An Unsupervised Cascade Fusion Network for Radiometrically-Accurate Vis-NIR-SWIR Hyperspectral Sharpening
Abstract
:1. Introduction
- (1)
- We proposed an image-specific unsupervised model for sharpening the Vis-NIR-SWIR hyperspectral image. Our method only needs one low-resolution hyperspectral image (LR-HSI) and high-resolution multispectral image (HR-MSI) pair in any sizes to perform the sharpening, which frees us from the requirements of a large dataset or a large image size in real-life tasks. In the training phase, the spectral loss is calculated as the difference between the spatially down-sampled reconstructed HR-HSI and the LR-HSI. For the spatial loss, due to the unavailability of the HR-MSI with SWIR bands covered, we spectrally integrate the Vis-NIR part of the reconstructed HR-HSI to compare it to the HR-MSI. This way, both high spatial and spectral precision are ensured.
- (2)
- A cascaded training strategy is used to progressively increase the spatial resolution of the LR-HSI, which considerably improves the robustness of the proposed method against large up-scale factors. Furthermore, the self-supervising loss is implemented under the cascade sharpening framework. The reconstructed HR-HSI obtained in the previous stage is used to calculate the loss between it and the degraded output obtained in the next stage. In this way, the stability of our method is further enhanced.
- (3)
- We implement the per-pixel classification on the reconstructed results yielded by the competing approaches to evaluate the radiometric accuracy from the task-based perspective. The details of this step are introduced in Section 4.2.
2. Related Works
3. Proposed Method
3.1. Problem Formulation
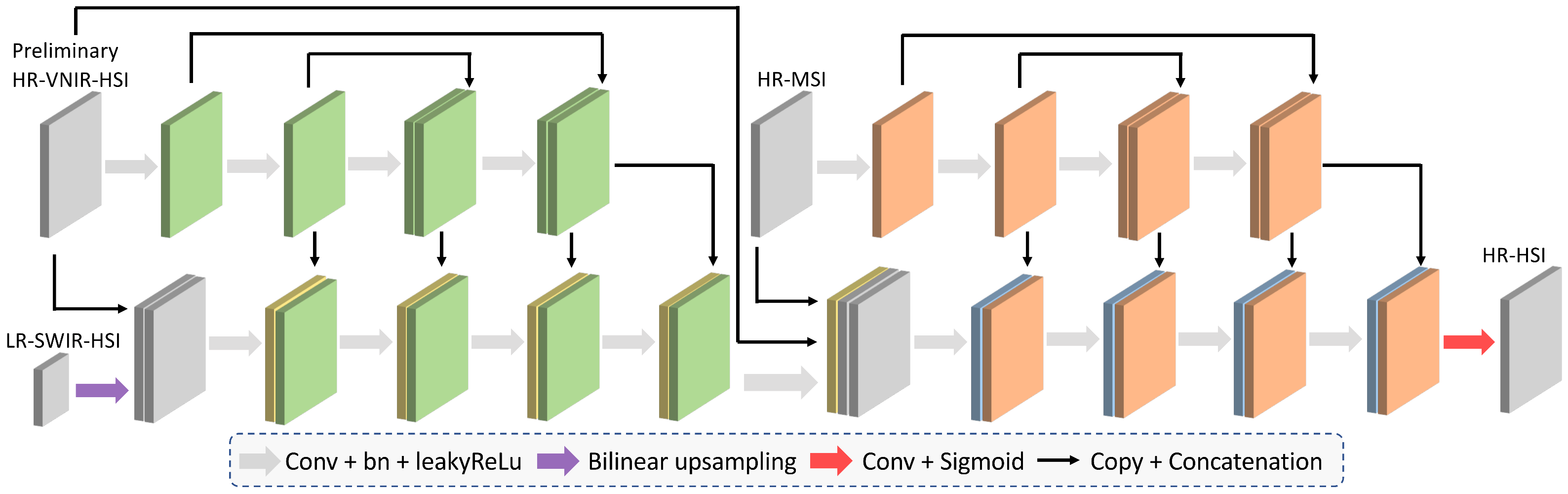
3.2. Network Structure
3.3. Loss Function
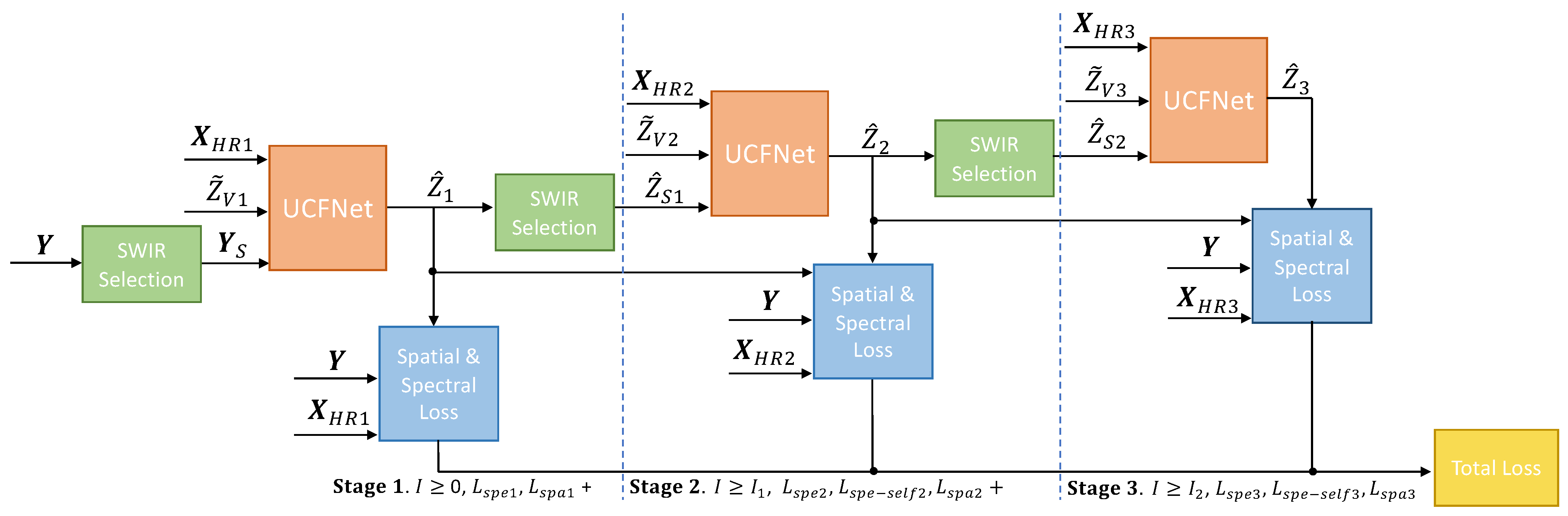
3.4. The Cascade Strategy
4. Experiments and Results
4.1. Synthetic Datasets
- (1)
- Dataset AVIRIS-NG-Cuprite [39] was acquired by the AVIRIS-NextGeneration sensor, which is an imaging spectrometer that records reflected radiance in the 380–2510 nm Visible to Shortwave Infrared (SWIR) spectral range. AVIRIS-NG-Cuprite is a diverse geologic dataset with more than 200 mineral classes. Several minerals have significant spectral characteristics in the SWIR bands that enable us to effectively test the performance of different approaches on the SWIR bands. A 360 × 360 region of interest (ROI) of the reference HR-HSI is selected for experiments.
- (2)
- Dataset SHARE2010 [40] was collected by the ProSpecTIR-VS sensor over the city of Rochester, NY, USA, in July 2010. The sensor was configured to collect the radiance ranging from 390 to 2450 nm with a spectral resolution of 5 [nm]. Sites for data collection include the Genesee River, sections of downtown Rochester, and the Rochester Institute of Technology (RIT) campus, and the ROI we selected in this paper is a 120 × 160 region of RIT.
4.2. Evaluation Criterion
4.3. Experiment Setup
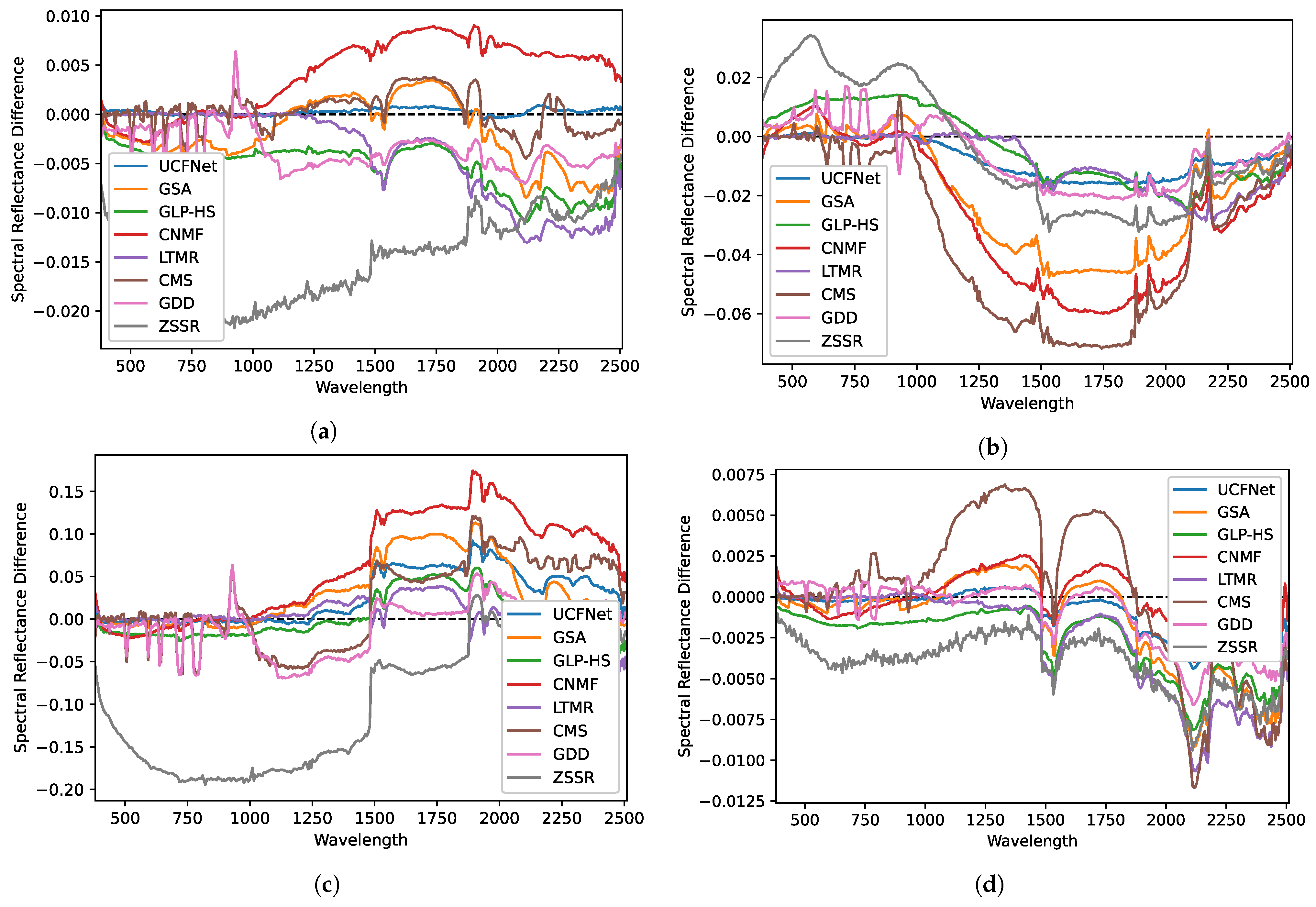
4.4. Results
4.5. Discussion
4.6. Ablation Study
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Carper, W.; Lillesand, T.; Kiefer, R. The use of intensity-hue-saturation transformations for merging SPOT panchromatic and multispectral image data. Photogramm. Eng. Remote Sens. 1990, 56, 459–467. [Google Scholar]
- Laben, C.A.; Brower, B.V. Process for Enhancing the Spatial Resolution of Multispectral Imagery Using Pan-Sharpening. U.S. Patent 6,011,875, 4 January 2000. [Google Scholar]
- Aiazzi, B.; Baronti, S.; Selva, M. Improving component substitution pansharpening through multivariate regression of MS + Pan data. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3230–3239. [Google Scholar] [CrossRef]
- Liu, J. Smoothing filter-based intensity modulation: A spectral preserve image fusion technique for improving spatial details. Int. J. Remote Sens. 2000, 21, 3461–3472. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Garzelli, A.; Selva, M. MTF-tailored multiscale fusion of high-resolution MS and Pan imagery. Photogramm. Eng. Remote Sens. 2006, 72, 591–596. [Google Scholar] [CrossRef]
- Yokoya, N.; Yairi, T.; Iwasaki, A. Coupled nonnegative matrix factorization unmixing for hyperspectral and multispectral data fusion. IEEE Trans. Geosci. Remote Sens. 2011, 50, 528–537. [Google Scholar] [CrossRef]
- Akhtar, N.; Shafait, F.; Mian, A. Sparse spatio-spectral representation for hyperspectral image super-resolution. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; Springer: Cham, Switzerland, 2014; pp. 63–78. [Google Scholar]
- Simoes, M.; Bioucas-Dias, J.; Almeida, L.B.; Chanussot, J. A convex formulation for hyperspectral image superresolution via subspace-based regularization. IEEE Trans. Geosci. Remote Sens. 2014, 53, 3373–3388. [Google Scholar] [CrossRef]
- Lanaras, C.; Baltsavias, E.; Schindler, K. Hyperspectral super-resolution by coupled spectral unmixing. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 3586–3594. [Google Scholar]
- Wei, Q.; Dobigeon, N.; Tourneret, J.Y. Bayesian fusion of multi-band images. IEEE J. Sel. Top. Signal Process. 2015, 9, 1117–1127. [Google Scholar] [CrossRef]
- Wei, Q.; Dobigeon, N.; Tourneret, J.Y. Fast fusion of multi-band images based on solving a Sylvester equation. IEEE Trans. Image Process. 2015, 24, 4109–4121. [Google Scholar] [CrossRef]
- Akhtar, N.; Shafait, F.; Mian, A. Bayesian sparse representation for hyperspectral image super resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3631–3640. [Google Scholar]
- Dian, R.; Fang, L.; Li, S. Hyperspectral image super-resolution via non-local sparse tensor factorization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 5344–5353. [Google Scholar]
- Zhang, L.; Wei, W.; Bai, C.; Gao, Y.; Zhang, Y. Exploiting clustering manifold structure for hyperspectral imagery super-resolution. IEEE Trans. Image Process. 2018, 27, 5969–5982. [Google Scholar] [CrossRef]
- Dian, R.; Li, S. Hyperspectral image super-resolution via subspace-based low tensor multi-rank regularization. IEEE Trans. Image Process. 2019, 28, 5135–5146. [Google Scholar] [CrossRef]
- Dian, R.; Li, S.; Kang, X. Regularizing hyperspectral and multispectral image fusion by CNN denoiser. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 1124–1135. [Google Scholar] [CrossRef] [PubMed]
- Selva, M.; Aiazzi, B.; Butera, F.; Chiarantini, L.; Baronti, S. Hyper-sharpening: A first approach on SIM-GA data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3008–3024. [Google Scholar] [CrossRef]
- Kwan, C.; Budavari, B.; Bovik, A.C.; Marchisio, G. Blind quality assessment of fused worldview-3 images by using the combinations of pansharpening and hypersharpening paradigms. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1835–1839. [Google Scholar] [CrossRef]
- Park, H.; Choi, J. A Comparison of Hyper-Sharpening Algorithms for Fusing VNIR and SWIR Bands of WorldView-3 Satellite Imagery. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 5124–5127. [Google Scholar]
- Selva, M.; Santurri, L.; Baronti, S. Improving hypersharpening for WorldView-3 data. IEEE Geosci. Remote Sens. Lett. 2018, 16, 987–991. [Google Scholar] [CrossRef]
- Ulyanov, D.; Vedaldi, A.; Lempitsky, V. Deep image prior. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 9446–9454. [Google Scholar]
- Shocher, A.; Cohen, N.; Irani, M. “zero-shot” super-resolution using deep internal learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 3118–3126. [Google Scholar]
- Haut, J.M.; Fernandez-Beltran, R.; Paoletti, M.E.; Plaza, J.; Plaza, A.; Pla, F. A new deep generative network for unsupervised remote sensing single-image super-resolution. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6792–6810. [Google Scholar] [CrossRef]
- Sidorov, O.; Yngve Hardeberg, J. Deep hyperspectral prior: Single-image denoising, inpainting, super-resolution. In Proceedings of the IEEE/CVF International Conference on Computer Vision Workshops, Seoul, Korea, 27–28 October 2019. [Google Scholar]
- Jiang, J.; Sun, H.; Liu, X.; Ma, J. Learning spatial-spectral prior for super-resolution of hyperspectral imagery. IEEE Trans. Comput. Imaging 2020, 6, 1082–1096. [Google Scholar] [CrossRef]
- Qu, Y.; Qi, H.; Kwan, C. Unsupervised sparse dirichlet-net for hyperspectral image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 2511–2520. [Google Scholar]
- Nguyen, H.V.; Ulfarsson, M.O.; Sveinsson, J.R.; Sigurdsson, J. Zero-shot sentinel-2 sharpening using a symmetric skipped connection convolutional neural network. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 613–616. [Google Scholar]
- Nguyen, H.V.; Ulfarsson, M.O.; Sveinsson, J.R.; Dalla Mura, M. Sentinel-2 Sharpening Using a Single Unsupervised Convolutional Neural Network With MTF-Based Degradation Model. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 6882–6896. [Google Scholar] [CrossRef]
- Salgueiro, L.; Marcello, J.; Vilaplana, V. Single-Image Super-Resolution of Sentinel-2 Low Resolution Bands with Residual Dense Convolutional Neural Networks. Remote Sens. 2021, 13, 5007. [Google Scholar] [CrossRef]
- Lanaras, C.; Bioucas-Dias, J.; Baltsavias, E.; Schindler, K. Super-resolution of multispectral multiresolution images from a single sensor. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 20–28. [Google Scholar]
- Lanaras, C.; Bioucas-Dias, J.; Galliani, S.; Baltsavias, E.; Schindler, K. Super-resolution of Sentinel-2 images: Learning a globally applicable deep neural network. ISPRS J. Photogramm. Remote Sens. 2018, 146, 305–319. [Google Scholar] [CrossRef]
- Huang, Q.; Li, W.; Hu, T.; Tao, R. Hyperspectral image super-resolution using generative adversarial network and residual learning. In Proceedings of the ICASSP 2019—2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 3012–3016. [Google Scholar]
- Shaham, T.R.; Dekel, T.; Michaeli, T. Singan: Learning a generative model from a single natural image. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Korea, 27–28 October 2019; pp. 4570–4580. [Google Scholar]
- Uezato, T.; Hong, D.; Yokoya, N.; He, W. Guided deep decoder: Unsupervised image pair fusion. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 87–102. [Google Scholar]
- Huang, S.; Messinger, D.W. An Unsupervised Laplacian Pyramid Network for Radiometrically Accurate Data Fusion of Hyperspectral and Multispectral Imagery. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5527517. [Google Scholar] [CrossRef]
- Gargiulo, M.; Mazza, A.; Gaetano, R.; Ruello, G.; Scarpa, G. A CNN-based fusion method for super-resolution of Sentinel-2 data. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 4713–4716. [Google Scholar]
- Pouliot, D.; Latifovic, R.; Pasher, J.; Duffe, J. Landsat super-resolution enhancement using convolution neural networks and Sentinel-2 for training. Remote Sens. 2018, 10, 394. [Google Scholar] [CrossRef] [Green Version]
- Kruse, F.A.; Lefkoff, A.; Boardman, J.; Heidebrecht, K.; Shapiro, A.; Barloon, P.; Goetz, A. The spectral image processing system (SIPS)-interactive visualization and analysis of imaging spectrometer data. In AIP Conference Proceedings; American Institute of Physics: College Park, MD, USA, 1993; Volume 283, pp. 192–201. [Google Scholar]
- The AVIRIS Next Generation Data.
- Herweg, J.A.; Kerekes, J.P.; Weatherbee, O.; Messinger, D.; van Aardt, J.; Ientilucci, E.; Ninkov, Z.; Faulring, J.; Raqueño, N.; Meola, J. Spectir hyperspectral airborne rochester experiment data collection campaign. In Proceedings of the Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XVIII, Baltimore, MD, USA, 23–27 April 2012; International Society for Optics and Photonics: Bellingham, WA, USA, 2012; Volume 8390, p. 839028. [Google Scholar]
- Wald, L.; Ranchin, T.; Mangolini, M. Fusion of satellite images of different spatial resolutions: Assessing the quality of resulting images. Photogramm. Eng. Remote Sens. 1997, 63, 691–699. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Canham, K.; Schlamm, A.; Ziemann, A.; Basener, B.; Messinger, D. Spatially adaptive hyperspectral unmixing. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4248–4262. [Google Scholar] [CrossRef]
- Messinger, D.W.; Ziemann, A.K.; Schlamm, A.; Basener, W. Metrics of spectral image complexity with application to large area search. Opt. Eng. 2012, 51, 036201. [Google Scholar] [CrossRef]
- Gunn, S.R. Support Vector Machines for Classification and Regression; ISIS Technical Report; University of Southampton: Southampton, UK, 1998; Volume 14, pp. 5–16. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]






| S | UCFNet | GSA | GLP-HS | CNMF | CMS | LTMR | GDD | ZSSR | |
|---|---|---|---|---|---|---|---|---|---|
| 2 | Mean SAM ↓ | 0.0084 | 0.0091 | 0.0120 | 0.0093 | 0.0204 | 0.0118 | 0.0101 | 0.0102 |
| Mean SSIM ↑ | 0.9962 | 0.9944 | 0.9920 | 0.9948 | 0.9458 | 0.9931 | 0.9949 | 0.9734 | |
| Mean PSNR ↑ | 49.0772 | 47.2153 | 45.3593 | 49.0620 | 36.6297 | 47.2524 | 47.7830 | 38.6947 | |
| 4 | Mean SAM ↓ | 0.0109 | 0.0134 | 0.0158 | 0.0130 | 0.0192 | 0.0163 | 0.0180 | 0.0153 |
| Mean SSIM ↑ | 0.9924 | 0.9874 | 0.9831 | 0.9871 | 0.9556 | 0.9843 | 0.9758 | 0.9281 | |
| Mean PSNR ↑ | 47.0997 | 43.9079 | 42.8805 | 43.2027 | 38.1846 | 45.0513 | 39.8599 | 34.1080 | |
| 8 | Mean SAM ↓ | 0.0141 | 0.0180 | 0.0208 | 0.0174 | 0.0248 | 0.0271 | 0.0303 | 0.0225 |
| Mean SSIM ↑ | 0.9872 | 0.9799 | 0.9737 | 0.9774 | 0.9387 | 0.9581 | 0.9481 | 0.8819 | |
| Mean PSNR ↑ | 44.6770 | 41.5907 | 40.6665 | 39.4293 | 37.1484 | 41.5918 | 34.4552 | 30.9458 |
| Methods | Reference | UCFNet | GSA | CNMF | GLP-HS | LTMR | CMS | GDD | ZSSR |
|---|---|---|---|---|---|---|---|---|---|
| Overall Accuracy (%) | 99.61 | 90.11 | 86.88 | 84.20 | 87.48 | 79.60 | 82.52 | 80.79 | 81.83 |
| Averaged Per-class Accuracy (%) | 98.39 | 80.23 | 70.54 | 62.51 | 76.77 | 70.08 | 63.42 | 70.95 | 66.61 |
| S | UCFNet | GSA | CNMF | GLP-HS | LTMR | CMS | GDD | ZSSR | |
|---|---|---|---|---|---|---|---|---|---|
| 2 | Mean SAM ↓ | 0.0197 | 0.0282 | 0.0295 | 0.0292 | 0.0300 | 0.0703 | 0.0226 | 0.0404 |
| Mean SSIM ↑ | 0.9979 | 0.9960 | 0.9964 | 0.9969 | 0.9968 | 0.9729 | 0.9967 | 0.9681 | |
| Mean PSNR ↑ | 49.7991 | 46.1933 | 46.9932 | 49.9470 | 49.2730 | 38.8847 | 49.7782 | 40.6667 | |
| 4 | Mean SAM ↓ | 0.0240 | 0.0468 | 0.0375 | 0.0420 | 0.0401 | 0.0773 | 0.0519 | 0.0628 |
| Mean SSIM ↑ | 0.9965 | 0.9889 | 0.9923 | 0.9905 | 0.9938 | 0.9637 | 0.9845 | 0.9138 | |
| Mean PSNR ↑ | 48.5506 | 41.9736 | 44.3017 | 42.3004 | 47.2764 | 38.2235 | 41.2772 | 30.3932 | |
| 8 | Mean SAM ↓ | 0.0348 | 0.0735 | 0.0478 | 0.0537 | 0.0596 | 0.0981 | 0.0672 | 0.0961 |
| Mean SSIM ↑ | 0.9923 | 0.9805 | 0.9876 | 0.9764 | 0.9767 | 0.9392 | 0.9815 | 0.8040 | |
| Mean PSNR ↑ | 43.1981 | 38.0056 | 42.0831 | 36.4299 | 44.4230 | 35.0870 | 39.6866 | 25.9654 |
| S | Mean SAM ↓ | Mean PSNR ↑ | Mean SSIM ↑ | |
|---|---|---|---|---|
| GLP-HS | 4 | 0.0240 | 48.5506 | 0.9965 |
| Bilinear | 4 | 0.0243 | 48.1867 | 0.9929 |
| GLP-HS | 8 | 0.0348 | 43.1981 | 0.9923 |
| Bilinear | 8 | 0.0355 | 42.6240 | 0.9913 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, S.; Messinger, D. An Unsupervised Cascade Fusion Network for Radiometrically-Accurate Vis-NIR-SWIR Hyperspectral Sharpening. Remote Sens. 2022, 14, 4390. https://doi.org/10.3390/rs14174390
Huang S, Messinger D. An Unsupervised Cascade Fusion Network for Radiometrically-Accurate Vis-NIR-SWIR Hyperspectral Sharpening. Remote Sensing. 2022; 14(17):4390. https://doi.org/10.3390/rs14174390
Chicago/Turabian StyleHuang, Sihan, and David Messinger. 2022. "An Unsupervised Cascade Fusion Network for Radiometrically-Accurate Vis-NIR-SWIR Hyperspectral Sharpening" Remote Sensing 14, no. 17: 4390. https://doi.org/10.3390/rs14174390
APA StyleHuang, S., & Messinger, D. (2022). An Unsupervised Cascade Fusion Network for Radiometrically-Accurate Vis-NIR-SWIR Hyperspectral Sharpening. Remote Sensing, 14(17), 4390. https://doi.org/10.3390/rs14174390







