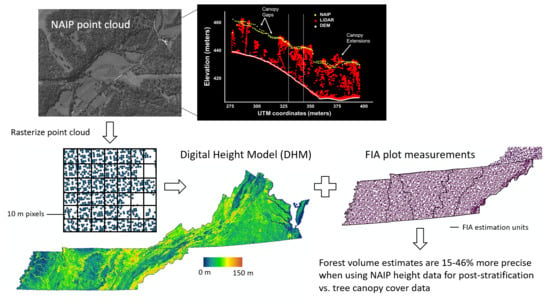
Evaluating Statewide NAIP Photogrammetric Point Clouds for Operational Improvement of National Forest Inventory Estimates in Mixed Hardwood Forests of the Southeastern U.S.
Abstract
:1. Introduction
1.1. National Forest Inventory
1.2. FIA and Nationwide Forest Attribute Estimation
1.3. Use of Point Clouds in Forest Inventory Applications
1.4. Using NAIP Digital Height Surfaces to Improve FIA Forest Inventory Estimates
1.5. Objectives
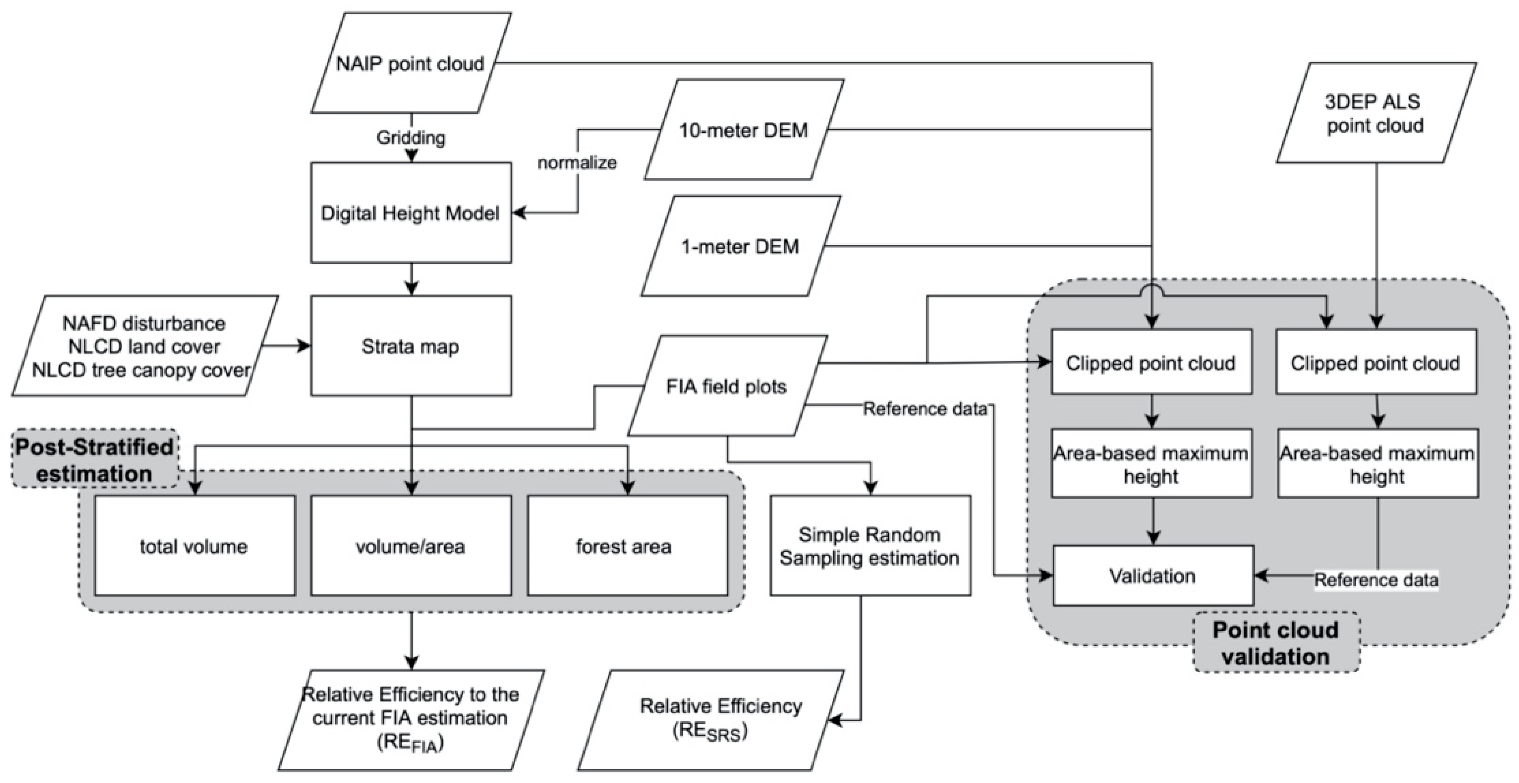
2. Materials and Methods
2.1. Study Area
2.2. Point Cloud Data
2.3. Digital Elevation Data
2.4. NAIP DHMs and Strata Map Processing
2.5. FIA Data
2.6. Point Cloud Tree Height Validation
2.7. Post-Stratified Estimation
3. Results
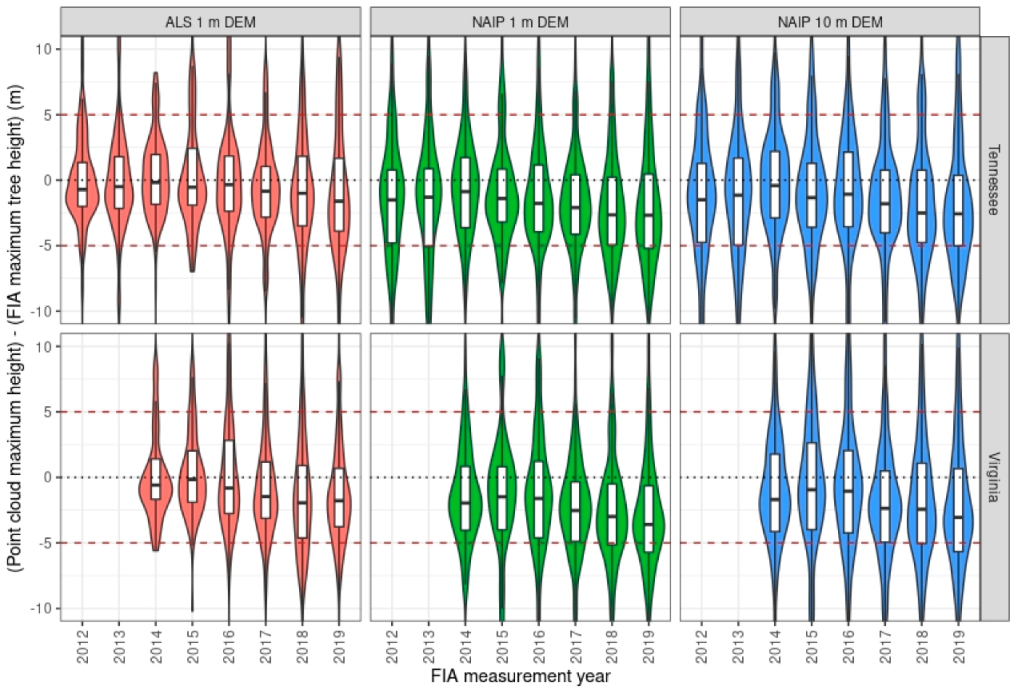
3.1. Point Cloud Validation
3.2. Post-Stratified Estimates
3.2.1. Forest Volume
3.2.2. Forest Area
3.2.3. Species Group Volume
4. Discussion
4.1. Validation of NAIP DAP and ALS Point Clouds
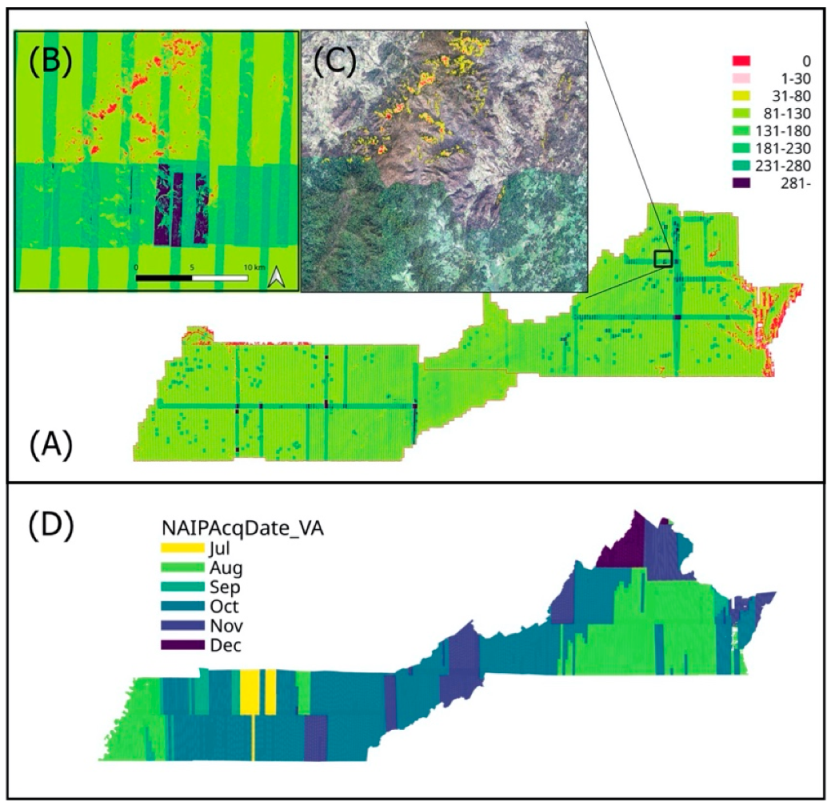
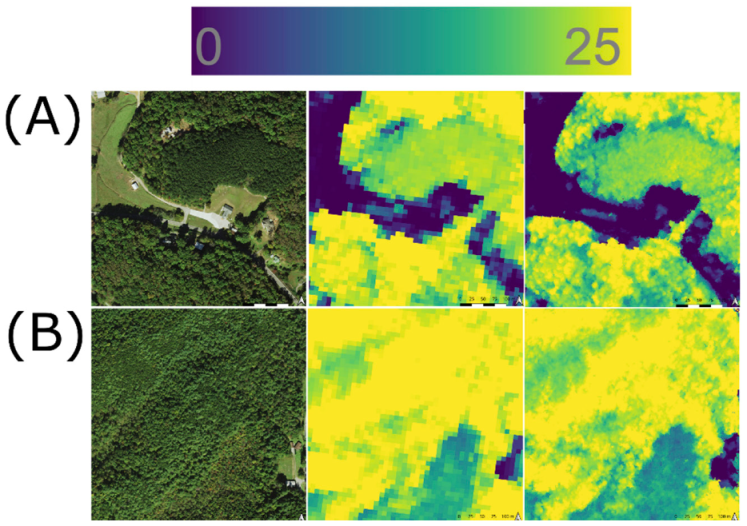
4.2. NAIP Point Cloud Anomalies
4.3. Other Factors Impacting NAIP Point Cloud Quality
4.3.1. Forest Disturbance
4.3.2. Temporal Offset
4.3.3. GPS Imprecision
4.3.4. FIA Tree Measurement Uncertainty
4.3.5. Post-Stratifying FIA Estimates with Digital Height Maps vs. Tree Canopy Cover Data
4.3.6. Potential for Operational Use of NAIP Point Clouds within FIA
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- FAO. Voluntary Guidelines on National Forest Monitoring; FAO: Rome, Italy, 2017; ISBN 978-92-5-109619-2. [Google Scholar]
- Nilsson, M.; Nordkvist, K.; Jonzén, J.; Lindgren, N.; Axensten, P.; Wallerman, J.; Egberth, M.; Larsson, S.; Nilsson, L.; Eriksson, J.; et al. A Nationwide Forest Attribute Map of Sweden Predicted Using Airborne Laser Scanning Data and Field Data from the National Forest Inventory. Remote Sens. Environ. 2017, 194, 447–454. [Google Scholar] [CrossRef]
- Tomppo, E.; Gschwantner, T.; Lawrence, M.; McRoberts, R.E.; Gabler, K.; Schadauer, K.; Vidal, C.; Lanz, A.; Ståhl, G.; Cienciala, E.; et al. National Forest Inventories; Tomppo, E., Gschwantner, T., Lawrence, M., McRoberts, R.E., Eds.; Springer: Dordrecht, The Netherlands, 2010; ISBN 978-90-481-3232-4. [Google Scholar]
- Breidenbach, J.; McRoberts, R.E.; Alberdi, I.; Antón-Fernández, C.; Tomppo, E. A Century of National Forest Inventories—Informing Past, Present and Future Decisions. For. Ecosyst. 2021, 8, 36. [Google Scholar] [CrossRef]
- Kangas, A.; Astrup, R.; Breidenbach, J.; Fridman, J.; Gobakken, T.; Korhonen, K.T.; Maltamo, M.; Nilsson, M.; Nord-Larsen, T.; Næsset, E.; et al. Remote Sensing and Forest Inventories in Nordic Countries—Roadmap for the Future. Scand. J. For. Res. 2018, 33, 397–412. [Google Scholar] [CrossRef]
- Mononen, L.; Auvinen, A.-P.; Ahokumpu, A.-L.; Rönkä, M.; Aarras, N.; Tolvanen, H.; Kamppinen, M.; Viirret, E.; Kumpula, T.; Vihervaara, P. National Ecosystem Service Indicators: Measures of Social–Ecological Sustainability. Ecol. Indic. 2016, 61, 27–37. [Google Scholar] [CrossRef]
- Blackard, J.A.; Patterson, P.L. National FIA Plot Intensification Procedure Report; RMRS-GTR-329; U.S. Department of Agriculture, Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA, 2014; p. 63.
- Goerndt, M.E.; Monleon, V.J.; Temesgen, H. Small-Area Estimation of County-Level Forest Attributes Using Ground Data and Remote Sensed Auxiliary Information. For. Sci. 2013, 59, 536–548. [Google Scholar] [CrossRef]
- Ståhl, G.; Saarela, S.; Schnell, S.; Holm, S.; Breidenbach, J.; Healey, S.P.; Patterson, P.L.; Magnussen, S.; Næsset, E.; McRoberts, R.E.; et al. Use of Models in Large-Area Forest Surveys: Comparing Model-Assisted, Model-Based and Hybrid Estimation. For. Ecosyst. 2016, 3, 5. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Nelson, M.D.; Wendt, D.G. Stratified Estimation of Forest Area Using Satellite Imagery, Inventory Data, and the k-Nearest Neighbors Technique. Remote Sens. Environ. 2002, 82, 457–468. [Google Scholar] [CrossRef]
- Bechtold, W.A.; Patterson, P.L. The Enhanced Forest Inventory and Analysis Program: National Sampling Design and Estimation Procedures; U.S. Department of Agriculture, Forest Service, Southern Research Station: Asheville, NC, USA, 2015.
- Tinkham, W.T.; Mahoney, P.R.; Hudak, A.T.; Domke, G.M.; Falkowski, M.J.; Woodall, C.W.; Smith, A.M.S. Applications of the United States Forest Inventory and Analysis Dataset: A Review and Future Directions. Can. J. For. Res. 2018, 48, 1251–1268. [Google Scholar] [CrossRef]
- Hu, H.; Wang, G.G. Changes in Forest Biomass Carbon Storage in the South Carolina Piedmont between 1936 and 2005. For. Ecol. Manag. 2008, 255, 1400–1408. [Google Scholar] [CrossRef]
- Brandeis, C.; Hodges, D.G.; Poudyal, N. Forest Resource Economics in Transition: Traditional and Emerging Markets; Gen. Tech. Rep. SRS-247; U.S. Department of Agriculture Forest Service, Southern Research Station: Asheville, NC, USA, 2018; 247, pp. 1–70. [CrossRef]
- Bechtold, W.A.; Ruark, G.A.; Lloyd, F.T. Changing Stand Structure and Regional Growth Reductions in Georgia’s Natural Pine Stands. For. Sci. 1991, 37, 703–717. [Google Scholar]
- Reams, G.A. Radial Growth Trends of Loblolly Pine in the Virginia Coastal Plain. Can. J. For. Res. 1996, 26, 9. [Google Scholar] [CrossRef]
- Brady, T.J.; Monleon, V.J.; Gray, A.N. Calibrating Vascular Plant Abundance for Detecting Future Climate Changes in Oregon and Washington, USA. Ecol. Indic. 2010, 10, 657–667. [Google Scholar] [CrossRef]
- Desprez, J.; Iannone, B.V.; Yang, P.; Oswalt, C.M.; Fei, S. Northward Migration under a Changing Climate: A Case Study of Blackgum (Nyssa Sylvatica). Clim. Chang. 2014, 126, 151–162. [Google Scholar] [CrossRef]
- Woodall, C.W.; Oswalt, C.M.; Westfall, J.A.; Perry, C.H.; Nelson, M.D.; Finley, A.O. An Indicator of Tree Migration in Forests of the Eastern United States. For. Ecol. Manag. 2009, 257, 1434–1444. [Google Scholar] [CrossRef]
- Patterson, P.L.; Coulston, J.W.; Roesch, F.A.; Westfall, J.A.; Hill, A.D. A Primer for Nonresponse in the US Forest Inventory and Analysis Program. Environ. Monit. Assess. 2012, 184, 1423–1433. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Wendt, D.G.; Nelson, M.D.; Hansen, M.H. Using a Land Cover Classification Based on Satellite Imagery to Improve the Precision of Forest Inventory Area Estimates. Remote Sens. Environ. 2002, 81, 36–44. [Google Scholar] [CrossRef]
- Tomppo, E.; Haakana, M.; Katila, M.; Peräsaari, J. Multi-Source National Forest Inventory: Methods and Applications; Springer: Dordrecht, The Netherlands, 2008; ISBN 978-1-4020-8712-7. [Google Scholar]
- Tomppo, E.; Olsson, H.; Ståhl, G.; Nilsson, M.; Hagner, O.; Katila, M. Combining National Forest Inventory Field Plots and Remote Sensing Data for Forest Databases. Remote Sens. Environ. 2008, 112, 1982–1999. [Google Scholar] [CrossRef]
- Hansen, M.H.; Wendt, D.G. Using Classified Landsat Thematic Mapper Data for Stratification in a Statewide Forest Inventory. In First Annual Forest Inventory and Analysis Symposium; US Department of Agriculture, Forest Service, North Central Research Station: St. Paul, MN, USA, 2000; pp. 20–27. [Google Scholar]
- McRoberts, R.E.; Liknes, G.C.; Domke, G.M. Using a Remote Sensing-Based, Percent Tree Cover Map to Enhance Forest Inventory Estimation. For. Ecol. Manag. 2014, 331, 12–18. [Google Scholar] [CrossRef]
- Schroeder, T.A.; Healey, S.P.; Moisen, G.G.; Frescino, T.S.; Cohen, W.B.; Huang, C.; Kennedy, R.E.; Yang, Z. Improving Estimates of Forest Disturbance by Combining Observations from Landsat Time Series with U.S. Forest Service Forest Inventory and Analysis Data. Remote Sens. Environ. 2014, 154, 61–73. [Google Scholar] [CrossRef]
- Strunk, J.; Packalen, P.; Gould, P.; Gatziolis, D.; Maki, C.; Andersen, H.-E.; McGaughey, R.J. Large Area Forest Yield Estimation with Pushbroom Digital Aerial Photogrammetry. Forests 2019, 10, 397. [Google Scholar] [CrossRef] [Green Version]
- Lister, A.J.; Andersen, H.; Frescino, T.; Gatziolis, D.; Healey, S.; Heath, L.S.; Liknes, G.C.; McRoberts, R.; Moisen, G.G.; Nelson, M.; et al. Use of Remote Sensing Data to Improve the Efficiency of National Forest Inventories: A Case Study from the United States National Forest Inventory. Forests 2020, 11, 1364. [Google Scholar] [CrossRef]
- Coulston, J.W.; Moisen, G.G.; Wilson, B.T.; Finco, M.V.; Cohen, W.B.; Brewer, C.K. Modeling Percent Tree Canopy Cover: A Pilot Study. Photogramm. Eng. Remote Sens. 2012, 78, 715–727. [Google Scholar] [CrossRef]
- Lu, D.; Chen, Q.; Wang, G.; Moran, E.; Batistella, M.; Zhang, M.; Vaglio Laurin, G.; Saah, D. Aboveground Forest Biomass Estimation with Landsat and LiDAR Data and Uncertainty Analysis of the Estimates. Int. J. For. Res. 2012, 2012, 436537. [Google Scholar] [CrossRef]
- Zhao, P.; Lu, D.; Wang, G.; Wu, C.; Huang, Y.; Yu, S. Examining Spectral Reflectance Saturation in Landsat Imagery and Corresponding Solutions to Improve Forest Aboveground Biomass Estimation. Remote Sens. 2016, 8, 469. [Google Scholar] [CrossRef]
- Zhu, X.; Liu, D. Improving Forest Aboveground Biomass Estimation Using Seasonal Landsat NDVI Time-Series. ISPRS J. Photogramm. Remote Sens. 2015, 102, 222–231. [Google Scholar] [CrossRef]
- Holmgren, J. Prediction of Tree Height, Basal Area and Stem Volume in Forest Stands Using Airborne Laser Scanning. Scand. J. For. Res. 2004, 19, 543–553. [Google Scholar] [CrossRef]
- Næsset, E. Determination of Mean Tree Height of Forest Stands Using Airborne Laser Scanner Data. ISPRS J. Photogramm. Remote Sens. 1997, 52, 49–56. [Google Scholar] [CrossRef]
- Noordermeer, L.; Bollandsås, O.M.; Ørka, H.O.; Næsset, E.; Gobakken, T. Comparing the Accuracies of Forest Attributes Predicted from Airborne Laser Scanning and Digital Aerial Photogrammetry in Operational Forest Inventories. Remote Sens. Environ. 2019, 226, 26–37. [Google Scholar] [CrossRef]
- Baltsavias, E.P. A Comparison between Photogrammetry and Laser Scanning. ISPRS J. Photogramm. Remote Sens. 1999, 54, 83–94. [Google Scholar] [CrossRef]
- Iglhaut, J.; Cabo, C.; Puliti, S.; Piermattei, L.; O’Connor, J.; Rosette, J. Structure from Motion Photogrammetry in Forestry: A Review. Curr. For. Rep. 2019, 5, 155–168. [Google Scholar] [CrossRef] [Green Version]
- Huang, W.; Dolan, K.; Swatantran, A.; Johnson, K.; Tang, H.; O’Neil-Dunne, J.; Dubayah, R.; Hurtt, G. High-Resolution Mapping of Aboveground Biomass for Forest Carbon Monitoring System in the Tri-State Region of Maryland, Pennsylvania and Delaware, USA. Environ. Res. Lett. 2019, 14, 095002. [Google Scholar] [CrossRef]
- Lisein, J.; Pierrot-Deseilligny, M.; Bonnet, S.; Lejeune, P. A Photogrammetric Workflow for the Creation of a Forest Canopy Height Model from Small Unmanned Aerial System Imagery. Forests 2013, 4, 922–944. [Google Scholar] [CrossRef]
- White, J.C.; Wulder, M.A.; Vastaranta, M.; Coops, N.C.; Pitt, D.; Woods, M. The Utility of Image-Based Point Clouds for Forest Inventory: A Comparison with Airborne Laser Scanning. Forests 2013, 4, 518–536. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Chen, Q.; Gormanson, D.D.; Walters, B.F. The Shelf-Life of Airborne Laser Scanning Data for Enhancing Forest Inventory Inferences. Remote Sens. Environ. 2018, 206, 254–259. [Google Scholar] [CrossRef]
- Goodbody, T.R.H.; Coops, N.C.; White, J.C. Digital Aerial Photogrammetry for Updating Area-Based Forest Inventories: A Review of Opportunities, Challenges, and Future Directions. Curr. For. Rep. 2019, 5, 55–75. [Google Scholar] [CrossRef]
- Vastaranta, M.; Wulder, M.A.; White, J.C.; Pekkarinen, A.; Tuominen, S.; Ginzler, C.; Kankare, V.; Holopainen, M.; Hyyppä, J.; Hyyppä, H. Airborne Laser Scanning and Digital Stereo Imagery Measures of Forest Structure: Comparative Results and Implications to Forest Mapping and Inventory Update. Can. J. Remote Sens. 2013, 39, 382–395. [Google Scholar] [CrossRef]
- White, J.C.; Stepper, C.; Tompalski, P.; Coops, N.C.; Wulder, M.A. Comparing ALS and Image-Based Point Cloud Metrics and Modelled Forest Inventory Attributes in a Complex Coastal Forest Environment. Forests 2015, 6, 3704–3732. [Google Scholar] [CrossRef]
- Gobakken, T.; Bollandsås, O.M.; Næsset, E. Comparing Biophysical Forest Characteristics Estimated from Photogrammetric Matching of Aerial Images and Airborne Laser Scanning Data. Scand. J. For. Res. 2015, 30, 73–86. [Google Scholar] [CrossRef]
- Ginzler, C.; Hobi, M. Countrywide Stereo-Image Matching for Updating Digital Surface Models in the Framework of the Swiss National Forest Inventory. Remote Sens. 2015, 7, 4343–4370. [Google Scholar] [CrossRef]
- Rahlf, J.; Breidenbach, J.; Solberg, S.; Næsset, E.; Astrup, R. Digital Aerial Photogrammetry Can Efficiently Support Large-Area Forest Inventories in Norway. For. Int. J. For. Res. 2017, 90, 710–718. [Google Scholar] [CrossRef]
- Bohlin, J.; Wallerman, J.; Fransson, J.E.S. Forest Variable Estimation Using Photogrammetric Matching of Digital Aerial Images in Combination with a High-Resolution DEM. Scand. J. For. Res. 2012, 27, 692–699. [Google Scholar] [CrossRef]
- Irulappa-Pillai-Vijayakumar, D.B.; Renaud, J.-P.; Morneau, F.; McRoberts, R.E.; Vega, C. Increasing Precision for French Forest Inventory Estimates Using the K-NN Technique with Optical and Photogrammetric Data and Model-Assisted Estimators. Remote Sens. 2019, 11, 991. [Google Scholar] [CrossRef]
- Jenkins, C.N.; Houtan, K.S.V.; Pimm, S.L.; Sexton, J.O. US Protected Lands Mismatch Biodiversity Priorities. Proc. Natl. Acad. Sci. USA 2015, 112, 5081–5086. [Google Scholar] [CrossRef] [PubMed]
- Cohen, W.B.; Yang, Z.; Stehman, S.V.; Schroeder, T.A.; Bell, D.M.; Masek, J.G.; Huang, C.; Meigs, G.W. Forest Disturbance across the Conterminous United States from 1985–2012: The Emerging Dominance of Forest Decline. For. Ecol. Manag. 2016, 360, 242–252. [Google Scholar] [CrossRef]
- Schleeweis, K.G.; Moisen, G.G.; Schroeder, T.A.; Toney, C.; Freeman, E.A.; Goward, S.N.; Huang, C.; Dungan, J.L. US National Maps Attributing Forest Change: 1986–2010. Forests 2020, 11, 653. [Google Scholar] [CrossRef]
- Oswalt, C.M.; Oswalt, S.N.; Johnson, T.G.; Brandeis, C.; Randolph, K.C. Tennessee’s Forests, 2009. In Resource Bulletin SRS-189; U.S. Department of Agriculture Forest Service, Southern Research Station: Asheville, NC, USA, 2012; pp. 1–165. [Google Scholar]
- Brandeis, T.J.; Hartsell, A.J.; Randolph, K.C.; Oswalt, C.M. Virginia’s Forests, 2016. In Resource Bulletin SRS–223; U.S. Department of Agriculture Forest Service, Southern Research Station: Asheville, NC, USA, 2018; pp. 1–116. [Google Scholar]
- Webb, J.; Schaaf, A.; Davenport, J.; Fisk, H.; Strunk, J.; McGaughey, R.J.; Anderson, H.; Gatziolis, D.; Bell, D.M. NAIP Point Clouds: Evaluating and Processing Statewide High-Resolution Elevation Data; U.S. Department of Agriculture, Forest Service, Geospatial Technology and Applications Center: Salt Lake City, UT, USA, 2020; p. 11.
- U.S. Geological Survey 3D Elevation Program. Available online: https://www.usgs.gov/core-science-systems/ngp/3dep (accessed on 10 October 2021).
- Sugarbaker, L.J.; Eldridge, D.F.; Saghy, D.L.; Stoker, J.M.; Thune, D.R. Status of the 3D Elevation Program, 2015; U.S. Geological Survey: Reston, VA, USA, 2017; p. 13.
- McGaughey, R.J. FUSION/LDV: Software for LIDAR Data Analysis and Visualization; United States Department of Agriculture Forest Service: Seattle, WA, USA, 2016; p. 217.
- Goward, S.N.; Huang, C.; Zhao, F.; Schleeweis, K.; Rishmawi, K.; Lindsey, M.; Dungan, J.L.; Michaelis, A.R. NACP NAFD Project: Forest Disturbance History from Landsat, 1986–2010; ORNL DAAC: Oak Ridge, TN, USA, 2016. [CrossRef]
- USDA Forest Service Rocky Mountain Research Station North American Forest Dynamics (NAFD). Available online: https://www.fs.usda.gov/rmrs/projects/north-american-forest-dynamics-nafd (accessed on 30 January 2022).
- Jin, S.; Homer, C.; Yang, L.; Danielson, P.; Dewitz, J.; Li, C.; Zhu, Z.; Xian, G.; Howard, D. Overall Methodology Design for the United States National Land Cover Database 2016 Products. Remote Sens. 2019, 11, 2971. [Google Scholar] [CrossRef]
- Multi-Resolution Land Characteristics Consortium NLCD 2016 Land Cover (CONUS). Available online: https://www.mrlc.gov/data/nlcd-2016-land-cover-conus (accessed on 30 January 2022).
- USDA Forest Service FIA DataMart. Available online: https://apps.fs.usda.gov/fia/datamart/CSV/datamart_csv.html (accessed on 30 January 2022).
- Burrill, E.A.; Wilson, A.M.; Turner, J.A.; Pugh, S.A.; Menlove, J.; Christensen, G.; Conkling, B.L.; David, W. The Forest Inventory and Analysis Database: Database Description and User Guide for Phase 2 (Version 7.2); U.S. Forest Service: Washington, DC, USA, 2018.
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
- Roussel, J.-R.; Auty, D.; Coops, N.C.; Tompalski, P.; Goodbody, T.R.H.; Meador, A.S.; Bourdon, J.-F.; de Boissieu, F.; Achim, A. LidR: An R Package for Analysis of Airborne Laser Scanning (ALS) Data. Remote Sens. Environ. 2020, 251, 112061. [Google Scholar] [CrossRef]
- Gobakken, T.; Næsset, E. Assessing Effects of Laser Point Density, Ground Sampling Intensity, and Field Sample Plot Size on Biophysical Stand Properties Derived from Airborne Laser Scanner Data. Can. J. For. Res. 2008, 38, 5. [Google Scholar] [CrossRef]
- Healey, S.P.; Cohen, W.B.; Yang, Z.; Kenneth Brewer, C.; Brooks, E.B.; Gorelick, N.; Hernandez, A.J.; Huang, C.; Joseph Hughes, M.; Kennedy, R.E.; et al. Mapping Forest Change Using Stacked Generalization: An Ensemble Approach. Remote Sens. Environ. 2018, 204, 717–728. [Google Scholar] [CrossRef]
- Næsset, E. Predicting Forest Stand Characteristics with Airborne Scanning Laser Using a Practical Two-Stage Procedure and Field Data. Remote Sens. Environ. 2002, 80, 88–99. [Google Scholar] [CrossRef]
- Næsset, E. Airborne Laser Scanning as a Method in Operational Forest Inventory: Status of Accuracy Assessments Accomplished in Scandinavia. Scand. J. For. Res. 2007, 22, 433–442. [Google Scholar] [CrossRef]
- Cohen, W.B.; Maiersperger, T.K.; Gower, S.T.; Turner, D.P. An Improved Strategy for Regression of Biophysical Variables and Landsat ETM+ Data. Remote Sens. Environ. 2003, 84, 561–571. [Google Scholar] [CrossRef]
- Frescino, T.S.; Patterson, P.L.; Freeman, E.A.; Moisen, G.G. An R-Based Tool for Analysts, to Look at Temporal Trends in Forest Estimates. In Moving from Status to Trends; Rocky Mountain Research Station, US Forest Service: Baltimore, MD, USA, 2012. [Google Scholar]
- Scott, C.T.; Bechtold, W.A.; Reams, G.A.; Smith, W.D.; Westfall, J.A.; Hansen, M.H.; Moisen, G.G. Sample-Based Estimators Used by the Forest Inventory and Analysis National Information Management System; Gen. Tech. Rep. SRS-80; U.S. Department of Agriculture, Forest Service, Southern Research Station: Asheville, NC, USA, 2005; pp. 53–77.
- Andersen, H.-E.; Reutebuch, S.E.; McGaughey, R.J. A Rigorous Assessment of Tree Height Measurements Obtained Using Airborne LIDAR and Conventional Field Methods. Can. J. Remote Sens. 2006, 32, 355–366. [Google Scholar] [CrossRef]
- Tesfamichael, S.G.; van Aardt, J.A.N.; Ahmed, F. Estimating Plot-Level Tree Height and Volume of Eucalyptus Grandis Plantations Using Small-Footprint, Discrete Return Lidar Data. Prog. Phys. Geogr. Earth Environ. 2010, 34, 515–540. [Google Scholar] [CrossRef]
- Prior, E.M.; Thomas, V.A.; Wynne, R.H. Estimation of mean dominant height using NAIP digital aerial photogrammetry and lidar over mixed deciduous forest in the southeastern USA. Int. J. Appl. Earth Obs. Geoinf. 2022, 110, 102813. [Google Scholar] [CrossRef]
- Ritz, A.L.; Thomas, V.A.; Wynne, R.H.; Green, P.C.; Schroeder, T.A.; Albaugh, T.J.; Burkhart, H.E.; Carter, D.R.; Cook, R.L.; Compoe, O.C.; et al. Assessing the utility of NAIP digital aerial photogrammetric point clouds for estimating canopy height of managed loblolly pine plantations in the southeastern United States. Int. J. Appl. Earth Obs. Geoinf. 2022; in review. [Google Scholar]
- Sibona, E.; Vitali, A.; Meloni, F.; Caffo, L.; Dotta, A.; Lingua, E.; Motta, R.; Garbarino, M. Direct Measurement of Tree Height Provides Different Results on the Assessment of LiDAR Accuracy. Forests 2016, 8, 7. [Google Scholar] [CrossRef]
- Wang, Y.; Lehtomäki, M.; Liang, X.; Pyörälä, J.; Kukko, A.; Jaakkola, A.; Liu, J.; Feng, Z.; Chen, R.; Hyyppä, J. Is Field-Measured Tree Height as Reliable as Believed—A Comparison Study of Tree Height Estimates from Field Measurement, Airborne Laser Scanning and Terrestrial Laser Scanning in a Boreal Forest. ISPRS J. Photogramm. Remote Sens. 2019, 147, 132–145. [Google Scholar] [CrossRef]
- Cao, Q.; Dettmann, G.T.; Radtke, P.J.; Coulston, J.W.; Derwin, J.; Thomas, V.A.; Burkhart, H.E.; Wynne, R.H. Increased precision in county-level volume estimates in the United States Forest Inventory with area-level small area estimation. Front. For. Glob. Chang. 2022, 5, 769917. [Google Scholar] [CrossRef]





| Survey Unit | Plots | Total Volume | Forest Area | VPA | Max Height | Mean Height | Forest Loss | Mean Elevation | Major Species Group |
|---|---|---|---|---|---|---|---|---|---|
| Million m3 | % | m3/ha | m | m | % | m | |||
| West (T1) | 457 | 0.91 | 36.91 | 166.86 | 24.12 | 16.22 | 35 | 128.56 | Loblolly and shortleaf pines |
| West Central (T2) | 412 | 0.91 | 66.03 | 139.4 | 23.98 | 16.3 | 41 | 198.52 | Select white oaks |
| Central (T3) | 541 | 1.10 | 43.15 | 157.51 | 23.86 | 16.23 | 11 | 246.34 | Hickory |
| Plateau (T4) | 546 | 1.20 | 66.39 | 165.49 | 24.98 | 16.54 | 34 | 480.59 | Other red oaks |
| East (T5) | 707 | 1.51 | 55.33 | 184.99 | 25.76 | 16.99 | 17 | 585.99 | Other white oaks |
| Coastal Plain (V1) | 694 | 1.52 | 59.36 | 190.63 | 23.14 | 15.7 | 51 | 35.49 | Loblolly and shortleaf pines |
| S. Piedmont (V2) | 694 | 1.56 | 68.36 | 165.4 | 22.91 | 15.78 | 48 | 205.78 | Loblolly and shortleaf pines |
| N. Piedmont (V3) | 474 | 1.01 | 56.19 | 203.34 | 25.94 | 17.52 | 28 | 253.92 | Yellow-poplar |
| N. Mountains (V4) | 503 | 1.12 | 64.51 | 172.34 | 22.78 | 15.66 | 14 | 626.32 | Other white oaks |
| S. Mountains(V5) | 584 | 1.24 | 64 | 191.05 | 24.97 | 17.04 | 19 | 757.8 | Yellow-poplar |
| (A) Percentage of NAIP imagery in each acquisition month (%). | ||||||||||
| July | August | September | October | November | December | |||||
| Tennessee | 4.13 | 12.20 | 6.43 | 64.25 | 12.99 | 0.00 | ||||
| Virginia | 0.00 | 35.71 | 0.88 | 38.08 | 19.14 | 6.18 | ||||
| (B) Percentage of 10 m pixels in each point density class (%) and the Min, Mean and Maximum point density in each state. | ||||||||||
| 0–30 | 31–80 | 81–130 | 131–180 | 181–230 | 231–280 | 280+ | Min | Mean | Max | |
| Tennessee | 0.95 | 67.92 | 12.42 | 15.51 | 2.63 | 0.57 | 0.24 | 0 | 86.41 | 566 |
| Virginia | 4.21 | 64.19 | 8.38 | 19.42 | 3.12 | 0.68 | 0.19 | 0 | 88.12 | 447 |
| Source | State | Resolution | Species | Plots | Avg. Point Cloud Height | Avg. FIA Height | r | RMSE | Bias |
|---|---|---|---|---|---|---|---|---|---|
| Meter | n | Meter | Meter | Meter | Meter | ||||
| NAIP | TN | 1 | Softwood | 224 | 19.27 | 20.54 | 0.82 | 3.46 | −1.28 |
| NAIP | TN | 1 | Hardwood | 1429 | 24.00 | 25.05 | 0.71 | 3.96 | −1.05 |
| NAIP | TN | 10 | Softwood | 224 | 19.95 | 20.81 | 0.81 | 3.43 | −0.85 |
| NAIP | TN | 10 | Hardwood | 1429 | 24.23 | 25.02 | 0.70 | 4.12 | −0.79 |
| ALS | TN | 1 | Softwood | 126 | 20.08 | 19.89 | 0.87 | 2.56 | 0.20 |
| ALS | TN | 1 | Hardwood | 794 | 24.91 | 24.71 | 0.79 | 3.20 | 0.20 |
| NAIP | VA | 1 | Softwood | 162 | 17.84 | 20.76 | 0.89 | 3.38 | −2.92 |
| NAIP | VA | 1 | Hardwood | 634 | 23.25 | 25.40 | 0.63 | 4.90 | −2.15 |
| NAIP | VA | 10 | Softwood | 462 | 18.32 | 20.40 | 0.77 | 3.70 | −2.08 |
| NAIP | VA | 10 | Hardwood | 1447 | 23.34 | 24.69 | 0.58 | 5.30 | −1.35 |
| ALS | VA | 1 | Softwood | 154 | 18.62 | 20.73 | 0.88 | 3.42 | −2.11 |
| ALS | VA | 1 | Hardwood | 628 | 25.42 | 25.15 | 0.74 | 3.58 | 0.28 |
| Tennessee | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Forest Volume/Area (m3/ha) | |||||||||
| Survey unit | REFIA | Volume/Area (m3/ha) * | Apparent Sample Size | ||||||
| Plots | PSDHM | PSCHM | PSCHM+FT | RESRS * | SE% * | Plot Gain/Loss | |||
| T1 | 457 | 1.19 | 1.28 | 1.09 | 1.49 | 166.82 | 2.88 | 126 | 583 |
| T2 | 412 | 1.30 | 1.34 | 1.20 | 1.58 | 140.06 | 2.48 | 138 | 550 |
| T3 | 541 | 1.27 | 1.31 | 1.33 | 1.33 | 155.47 | 2.42 | 179 | 720 |
| T4 | 546 | 1.34 | 1.44 | 1.46 | 1.39 | 168.73 | 2.06 | 251 | 797 |
| T5 | 707 | 1.26 | 1.30 | 1.27 | 1.32 | 184.46 | 1.88 | 211 | 918 |
| Total forest volume (million m3) | |||||||||
| Survey unit | REFIA | Total volume (million m3) * | Apparent Sample Size | ||||||
| Plots | PSDHM | PSCHM | PSCHM+FT | RESRS * | SE% * | Plot Gain/Loss | |||
| T1 | 457 | 1.33 | 1.34 | 1.16 | 2.74 | 156.17 | 3.02 | 155 | 612 |
| T2 | 412 | 1.45 | 1.46 | 1.27 | 2.51 | 127.30 | 2.60 | 190 | 602 |
| T3 | 541 | 1.32 | 1.32 | 1.33 | 2.87 | 165.75 | 2.63 | 180 | 721 |
| T4 | 546 | 1.37 | 1.37 | 1.33 | 2.39 | 203.29 | 2.14 | 203 | 749 |
| T5 | 707 | 1.29 | 1.30 | 1.28 | 2.81 | 275.77 | 2.02 | 211 | 918 |
| Forest area (thousand ha) | |||||||||
| Survey unit | REFIA | Forest area (thousand ha) * | Apparent Sample Size | ||||||
| Plots | PSDHM | PSCHM | PSCHM+FT | RESRS * | SE% * | Plot Gain/Loss | |||
| T1 ** | 457 | 0.66 | 0.78 | 0.79 | 3.93 | 927.51 | 1.88 | −96 | 361 |
| T2 | 412 | 0.89 | 1.24 | 0.69 | 4.05 | 908.86 | 1.38 | 100 | 512 |
| T3 | 541 | 0.78 | 0.89 | 1.01 | 3.80 | 1066.18 | 1.74 | 6 | 547 |
| T4 | 546 | 0.83 | 1.11 | 1.06 | 3.65 | 1209.48 | 1.24 | 61 | 607 |
| T5 | 707 | 0.80 | 1.02 | 0.97 | 3.80 | 1495.00 | 1.29 | 15 | 722 |
| Virginia | |||||||||
| Forest Volume/area (m3/ha) | |||||||||
| Survey unit | REFIA | ||||||||
| Plots | PSDHM | PSCHM | PSCHM+FT | RESRS * | Volume/area (m3/ha) * | SE% * | Plot Gain/Loss | Apparent Sample Size | |
| V1 | 694 | 1.19 | 1.18 | 1.18 | 1.42 | 191.04 | 2.14 | 130 | 824 |
| V2 | 694 | 1.28 | 1.22 | 1.24 | 1.54 | 161.97 | 2.21 | 196 | 890 |
| V3 | 474 | 1.07 | 1.15 | 1.01 | 1.24 | 201.46 | 2.26 | 71 | 545 |
| V4 | 503 | 1.14 | 1.33 | 1.20 | 1.37 | 171.40 | 2.07 | 167 | 670 |
| V5 | 584 | 1.20 | 1.26 | 1.20 | 1.29 | 192.15 | 2.18 | 150 | 734 |
| Total forest volume (million m3) | |||||||||
| Survey unit | REFIA | ||||||||
| Plots | PSDHM | PSCHM | PSCHM+FT | RESRS * | Total volume (million m3) * | SE% * | Plot Gain/Loss | Apparent Sample Size | |
| V1 | 694 | 1.34 | 1.36 | 1.23 | 2.39 | 284.15 | 2.24 | 248 | 942 |
| V2 | 694 | 1.36 | 1.38 | 1.23 | 2.33 | 247.98 | 2.31 | 265 | 959 |
| V3 | 474 | 1.29 | 1.29 | 1.20 | 2.37 | 204.04 | 2.51 | 139 | 613 |
| V4 | 503 | 1.31 | 1.32 | 1.27 | 2.46 | 197.35 | 2.18 | 163 | 666 |
| V5 | 584 | 1.23 | 1.20 | 1.15 | 2.28 | 245.77 | 2.25 | 136 | 720 |
| Forest area (thousand ha) | |||||||||
| Survey unit | REFIA | ||||||||
| Plots | PSDHM | PSCHM | PSCHM+FT | RESRS * | Forest area (thousand ha) * | SE% * | Plot Gain/Loss | Apparent Sample Size | |
| V1 ** | 694 | 0.71 | 0.83 | 0.78 | 3.07 | 1523.16 | 1.77 | −119 | 575 |
| V2 | 694 | 0.77 | 1.08 | 0.77 | 2.48 | 1539.16 | 1.27 | 55 | 749 |
| V3 ** | 474 | 0.64 | 0.88 | 0.85 | 3.19 | 1006.63 | 1.31 | −58 | 416 |
| V4 ** | 503 | 0.60 | 0.96 | 0.95 | 3.54 | 1118.82 | 1.32 | −22 | 481 |
| V5 ** | 584 | 0.71 | 0.87 | 0.79 | 3.70 | 1240.08 | 1.88 | −73 | 511 |
| Survey Units | Improved Survey Units | Best PS Map | Plot Gain/Loss (%) | |||||
|---|---|---|---|---|---|---|---|---|
| PSDHM | PSCHM | PSCHM+FT | Avg. | Min | Max | |||
| TN Forest Area (acres) | 5 | 4 | 0 | 3 | 1 | 4 | −21 | 24 |
| TN Total Forest Volume (m3) | 5 | 5 | 1 | 4 | 1 | 36 | 30 | 46 |
| TN Total Forest Vol/Area (m3/acre) | 5 | 5 | 0 | 3 | 2 | 34 | 28 | 46 |
| VA Forest Area (acres) | 5 | 1 | 0 | 1 | 0 | −8 | −17 | 8 |
| VA Total Forest Volume (m3) | 5 | 5 | 2 | 4 | 0 | 32 | 23 | 38 |
| VA Total Forest Vol/Area (m3/acre) | 5 | 5 | 2 | 3 | 0 | 24 | 15 | 33 |
| Total | 30 | 25 | 5 | 18 | 4 | - | - | - |
| Total Species | Improved Species | Best PS Map | Softwood Plot Gain/Loss (%) | Hardwood Plot Gain/Loss (%) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| PSDHM | PSCHM | PSCHM+FT | Avg. | Min | Max | Avg. | Min | Max | |||
| TN Total Forest Volume (m3) | 84 | 63 | 4 | 21 | 44 | 17 | −2 | 64 | 4 | −7 | 18 |
| TN Total Forest Volume/Area (m3/acre) | 84 | 71 | 23 | 8 | 44 | 20 | 2 | 72 | 6 | −4 | 20 |
| VA Total Forest Volume (m3) | 80 | 53 | 7 | 19 | 35 | 10 | −6 | 52 | 4 | −7 | 28 |
| VA Total Forest Vol/Area (m3/acre) | 80 | 69 | 32 | 21 | 29 | 14 | −5 | 60 | 7 | −4 | 29 |
| Total | 328 | 256 | 66 | 69 | 152 | - | - | - | - | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schroeder, T.A.; Obata, S.; Papeş, M.; Branoff, B. Evaluating Statewide NAIP Photogrammetric Point Clouds for Operational Improvement of National Forest Inventory Estimates in Mixed Hardwood Forests of the Southeastern U.S. Remote Sens. 2022, 14, 4386. https://doi.org/10.3390/rs14174386
Schroeder TA, Obata S, Papeş M, Branoff B. Evaluating Statewide NAIP Photogrammetric Point Clouds for Operational Improvement of National Forest Inventory Estimates in Mixed Hardwood Forests of the Southeastern U.S. Remote Sensing. 2022; 14(17):4386. https://doi.org/10.3390/rs14174386
Chicago/Turabian StyleSchroeder, Todd A., Shingo Obata, Monica Papeş, and Benjamin Branoff. 2022. "Evaluating Statewide NAIP Photogrammetric Point Clouds for Operational Improvement of National Forest Inventory Estimates in Mixed Hardwood Forests of the Southeastern U.S." Remote Sensing 14, no. 17: 4386. https://doi.org/10.3390/rs14174386
APA StyleSchroeder, T. A., Obata, S., Papeş, M., & Branoff, B. (2022). Evaluating Statewide NAIP Photogrammetric Point Clouds for Operational Improvement of National Forest Inventory Estimates in Mixed Hardwood Forests of the Southeastern U.S. Remote Sensing, 14(17), 4386. https://doi.org/10.3390/rs14174386