Identification of Old-Growth Mediterranean Forests Using Airborne Laser Scanning and Geostatistical Analysis
Abstract
1. Introduction
2. Materials and Methods
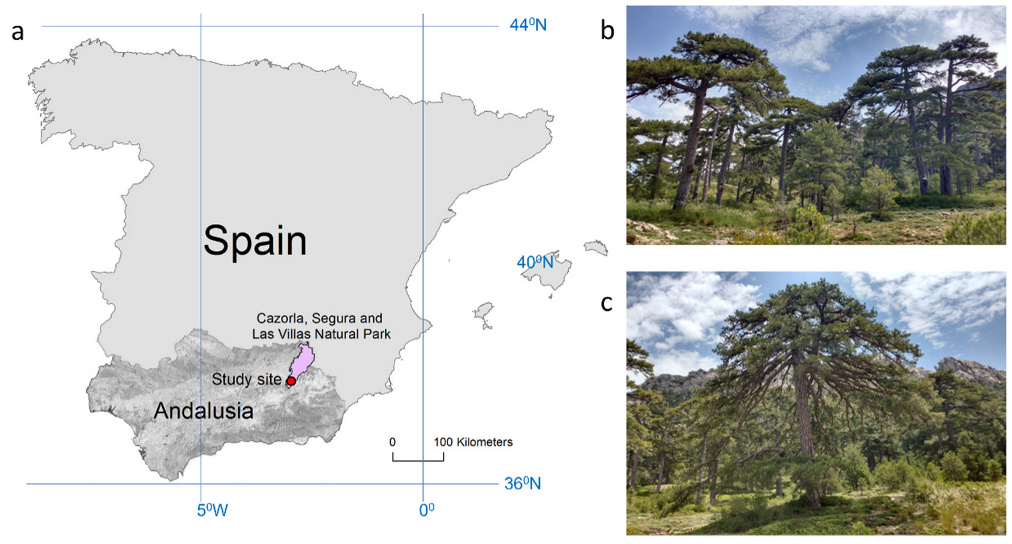
2.1. The Study Area
2.2. Forest Inventory Data
2.3. Calculation of Old-Growth Indices
2.4. Geostatistical Modeling
2.5. ALS Data Analysis
3. Results
3.1. Selection of Structural Parameters and OGI
3.2. Geostatistical Model
3.3. ALS Model
4. Discussion
4.1. Stand Structure Differences between Young and Old-Growth Forests
4.2. OGIs to Distinguish Old Growth from Young Forests
4.3. Geostatistics and ALS to Estimate OGIs
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bauhus, J.; Puettmann, K.; Messier, C. Silviculture for old-growth attributes. For. Ecol. Manag. 2009, 258, 525–537. [Google Scholar] [CrossRef]
- Spies, T.A.; Hemstrom, M.A.; Youngblood, A.; Hummel, S. Conserving old-growth forest diversity in disturbance-prone landscapes. Conserv. Biol. 2006, 20, 351–362. [Google Scholar] [CrossRef] [PubMed]
- Mackey, B.; DellaSala, D.A.; Kormos, C.; Lindenmayer, D.; Kumpel, N.; Zimmerman, B.; Watson, J.E.M. Policy options for the world’s primary forests in multilateral environmental agreements. Conserv. Lett. 2015, 8, 139–147. [Google Scholar] [CrossRef]
- Spies, T.A. Ecological concepts and diversity of old-growth forests. J. For. 2004, 102, 14–20. [Google Scholar] [CrossRef]
- Wirth, C.; Gleixner, G.; Heimann, M. Old-growth forests. Function, Fate and Value. Ecolo. Stud. 2009, 207, 3–7. [Google Scholar] [CrossRef]
- Leverett, R. Definitions and history. In Eastern Old-Growth Forests: Prospects for Rediscovery and Recovery; Davis, M.B., Ed.; Island Press: Washington, WA, USA, 1996; pp. 3–17. [Google Scholar]
- Peterken, G.F. Natural Woodland. Ecology and Conservation on Northern temperate Regions; Cambridge University Press: Cambridge, UK, 1996; 522p. [Google Scholar]
- Acker, S.; Sabin, T.E.; Ganio, M.; McKee, W.A. Development of old growth structure and timber volume growth trends in maturing Douglas-fir stands. For. Ecol. Manag. 1998, 104, 265–280. [Google Scholar] [CrossRef]
- Kuuluvainen, T.; Syrjänen, K.; Kalliola, R. Structure of a pristine Picea abies forest in northeastern Europe. J. Veg. Sci. 1998, 9, 563–574. [Google Scholar] [CrossRef]
- Mosseler, A.; Lynds, J.A.; Major, J.E. Old-growth forests of the Acadian Forest Region. Environ. Rev. 2003, 11, S47–S77. [Google Scholar] [CrossRef]
- Mosseler, A.; Thompson, I.; Pendrel, B.A. Overview of old-growth forests in Canada from a science perspective. Environ. Rev. 2003, 11, S1–S7. [Google Scholar] [CrossRef]
- Franklin, J.F.; Spies, T.A.; Van Pelt, R. Definition and Inventory of Old-Growth Forests on DNR-Managed State Lands; Washington State Department of Natural Resources: Washington, DC, USA, 2005; 74p.
- Rozas, V. Regeneration patterns, dendroecology, and forest-use history in an old-growth beech-oak lowland forest in Northern Spain. For. Ecol. Manag. 2003, 18, 175–194. [Google Scholar] [CrossRef]
- Lindner, M.; Sievanen, R.; Pretzsch, H. Improving the simulation of stand structure in a forest gap model. For. Ecol. Manag. 1997, 95, 183–195. [Google Scholar] [CrossRef]
- Nagel, T.A.; Svoboda, M.; Diaci, J. Regeneration patterns after intermediate wind disturbance in an old growth Fagus-Abies forest in Southeastern Slovenia. For. Ecol. Manag. 2006, 226, 268–278. [Google Scholar] [CrossRef]
- Siitonen, P.; Martikainen, P.; Punttila, P.; Rauh, J. Coarse woody debris and stand characteristics in mature and oldgrowth boreal mesic forests in southern Finland. For. Ecol. Manag. 2000, 128, 211–225. [Google Scholar] [CrossRef]
- Lombardi, F.; Chirici, G.; Marchetti, M.; Tognetti, R.; Lasserre, B.; Corona, P.; Barbati, A.; Ferrari, B.; Di Paolo, S.; Giuliarelli, D.; et al. Deadwood in forest stands close to old-growthness under Mediterranean conditions in the Italian Peninsula. Ital. J. For. Mt. Environ. 2010, 65, 481–501. [Google Scholar] [CrossRef][Green Version]
- Franklin, J.F.; Spies, T.A. Composition, function, and structure of old-growth Douglas-fir forests. In Wildlife and Vegetation of Unmanaged Douglas-Fir Forests; General Technical Report PNW-GTR-285; Ruggiero, L.F., Aubry, K.B., Carey, A.B., Huff, M.H., Eds.; USDA Forest Service: Washington, DC, USA, 1991; pp. 71–80. [Google Scholar]
- Gibson, L.; Lee, T.M.; Koh, L.P.; Brook, B.W.; Gardner, T.A.; Barlow, J.; Peres, C.A.; Bradshaw, C.J.A.; Laurance, W.F.; Lovejoy, T.E.; et al. Primary forests are irreplaceable for sustaining tropical biodiversity. Nature 2011, 478, 378–381. [Google Scholar] [CrossRef]
- Mansourian, S.; Rossi, M.; Vallauri, D. Ancient Forests in the Northern Mediterranean: Neglected High Conservation Value Areas; WWF: Marseille, France, 2013; 80p. [Google Scholar]
- FAO. Global Forest Resources Assessment 2015. Terms and definitions. In Forest Resources Assessment Working Paper 180; FAO: Rome, Italy, 2015; p. 36. [Google Scholar]
- Knorn, J.A.N.; Kuemmerle, T.; Radeloff, V.C.; Keeton, W.S. Continued loss of temperate old-growth forests in the Romanian Carpathians despite an increasing protected area network. Environ. Conserv. 2013, 40, 182–193. [Google Scholar] [CrossRef]
- Potapov, P.; Hansen, M.C.; Laestadius, L.; Turubanova, S.; Yaroshrenko, A.; Thies, C.; Esipova, E. The last frontiers of wilderness: Tracking loss of intact forest landscapes from 2000 to 2013. Sci. Adv. 2017, 3, e1600821. [Google Scholar] [CrossRef]
- Forest Europe 2015. State of Europe’s Forests 2015 Report. Available online: https://www.foresteurope.org/docs/fullsoef2015.pdf (accessed on 21 April 2021).
- Sabatini, F.M.; Burrascano, S.; Keeton, W.S.; Levers, C.; Lindner, M.; Pötzschner, F.; Verkerk, P.J.; Bauhus, J.; Buchwald, E.; Chaskovsky, O.; et al. Where are Europe’s last primary forests? Divers. Distrib. 2018, 24, 1426–1439. [Google Scholar] [CrossRef]
- Zhengquan, W.; Qingcheng, W.; Yandong, Z.; Li, H. Quantification of spatial heterogeneity in old growth forests of Korean pine. J. For. Res. 1997, 8, 65. [Google Scholar] [CrossRef]
- Tíscar, P.A.; Linares, J.C. Structure and regeneration patterns of Pinus nigra subsp. salzmannii natural forests: A basic knowledge for adaptive management in a changing climate. Forests 2011, 2, 1013–1030. [Google Scholar] [CrossRef]
- Noss, R.F. Beyond Kyoto: Forest management in a time of rapid climate change. Conserv. Biol. 2001, 15, 578–590. [Google Scholar] [CrossRef]
- Millar, C.I.; Stephenson, N.L.; Stephens, S.L. Climate change and forests of the future: Managing in the face of uncertainty. Ecol. Appl. 2007, 17, 2145–2151. [Google Scholar] [CrossRef] [PubMed]
- Paci, M.; Salbitano, F. The role of studies on vegetation dynamics in undisturbed natural reserves towards the need of knowledge for close-to-nature silvicultural treatments: The case study of Natural Reserve of Sasso Fratino (Foreste Casentinesi, northern-central Apennines). In Proceedings of the AISF-EFI International Conference on “Forest Management in Designated Conservation & Recreation Areas, Florence, Italy, 7–11 October 1998; Morandini, R., Merlo, M., Paivinnen, R., Eds.; University of Padua Press: Padua, Italy, 1998; pp. 45–156. [Google Scholar]
- Piovesan, G.; di Filippo, A.; Alessandrini, A.; Biondi, F.; Schirone, B. Structure, dynamics and dendroecology of an old-growth Fagus forest in the Apennines. J. Veg. Sci. 2005, 16, 13–28. [Google Scholar] [CrossRef]
- Lombardi, F.; Cherubini, P.; Lasserre, B.; Tognetti, R.; Marchetti, M. Tree rings used to assess time-since-death of deadwood of different decay classes in beech and silver fir forests in the Central Apennines (Molise, Italy). Can. J. For. Res. 2008, 38, 821–833. [Google Scholar] [CrossRef]
- Mittermeier, R.A.; Hoffmann, M.; Pilgrim, J.; Brooks, T.; Lamoreux, J.; Mittermeier, C.G.; Gil, P.R.; Da Fonseca, G.A.B. Hotspots Revisited: Earth’s Biologically Richest and Most Endangered Terrestrial Ecoregions; CEMEX: Mexico City, Mexico, 2004; 392p. [Google Scholar]
- FAO. Plan Bleu 2018. In State of Mediterranean Forests 2018; Food and Agriculture Organization of the United Nations, Rome and Plan Bleu: Marseille, France, 2018; 331p. [Google Scholar]
- Firm, D.; Nagel, T.A.; Diaci, J. Disturbance history and dynamics of an old-growth mixed species mountain forest in the Slovenian Alps. For. Ecol. Manag. 2009, 257, 1893–1901. [Google Scholar] [CrossRef]
- Keren, S.; Motta, R.; Govedar, Z.; Lucic, R.; Medarevic, M.; Diaci, J. Comparative structural dynamics of the Janj Mixed old-growth mountain forest in Bosnia and Herzegovina: Are conifers in a long-term decline? Forests 2014, 5, 1243–1266. [Google Scholar] [CrossRef]
- Nilsson, S.G.; Niklasson, M.; Hedin, J.; Aronsson, G.; Gutowski, J.; Linder, P.; Ljunberg, H.; Mikusinski, G.; Ranius, T. Densities of large living and dead trees in old-growth temperate and boreal forests. For. Ecol. Manag. 2002, 161, 189–204, Erratum in For. Ecol. Manag. 2003, 178, 355–370. [Google Scholar] [CrossRef]
- Carrión, J.S.; Munera, M.; Dupre, M.; Andrade, A. Abrupt Vegetation Changes in the Segura Mountains of Southern Spain Throughout the Holocene. J. Ecol. 2001, 89, 783–797. Available online: https://www.jstor.org/stable/3072152 (accessed on 16 May 2021). [CrossRef]
- Tíscar, P.A.; Lucas-Borja, M.E. Structure of old-growth and managed stands and growth of old trees in a Mediterranean Pinus nigra forest in southern Spain. For. Int. J. For. Res. 2016, 89, 201–207. [Google Scholar] [CrossRef]
- Abellanas, B.; Pérez Moreno, P.J. Assessing spatial dynamics of a Pinus nigra subsp. salzmannii natural stand combining point and polygon patterns analysis. For. Ecol. Manag. 2018, 424, 136–153. [Google Scholar] [CrossRef]
- Barros, L.A. Mapping Old-Growth Forests with Airbone LiDAR Delivered Forest Metrics Report. University of Northern British Columbia. Available online: https://scholars.esri.ca/wp-content/uploads/profiles/318/Barros_Report.pdf (accessed on 1 October 2020).
- González-Ferreiro, E.; Arellano-Pérez, S.; Castedo-Dorado, F.; Hevia, A.; Vega, J.A.; Vega-Nieva, D.; Álvarez-González, J.G.; Ruiz-González, A.D. Modelling the vertical distribution of canopy fuel load using national forest inventory and low-density airbone laser scanning data. PLoS ONE 2017, 12, e0176114. [Google Scholar] [CrossRef] [PubMed]
- Bater, C.W.; Coops, N.C.; Gergel, S.E.; LeMay, V.; Collins, D. Estimation of standing dead tree class distributions in northwest coastal forests using lidar remote sensing. Can. J. For. Res. 2009, 39, 1080–1091. [Google Scholar] [CrossRef]
- Racine, E.B.; Coops, N.C.; St-Onge, B.; Bégin, J. Estimating Forest Stand Age from LiDAR-Derived Predictors and Nearest Neighbor Imputation. For. Sci. 2014, 60, 128–136. [Google Scholar] [CrossRef]
- White, J.C.; Tompalski, P.; Coops, N.C.; Wulder, M.A. Comparison of airborne laser scanning and digital stereo imagery for characterizing forest canopy gaps in coastal temperate rainforests. Remote Sens. Environ. 2018, 208, 1–14. [Google Scholar] [CrossRef]
- Kane, V.R.; McGaughey, R.J.; Bakker, J.D.; Gersonde, R.F.; Lutz, J.A.; Franklin, J.F. Comparisons between field- and LiDAR-based measures of stand structural complexity. Can. J. For. Res. 2010, 40, 761–773. [Google Scholar] [CrossRef]
- Zimble, D.A.; Evans, D.L.; Carlson, G.C.; Parker, R.C.; Grado, S.C.; Gerard, P.D. Characterizing vertical forest structure using small-footprint airborne LiDAR. Remote Sens. Environ. 2003, 87, 171–182. [Google Scholar] [CrossRef]
- Falkowski, M.J.; Evans, J.S.; Martinuzzi, S.; Gessler, P.E.; Hudak, A.T. Characterizing forest succession with lidar data: An evaluation for the Inland Northwest, USA. Remote Sens. Environ. 2009, 113, 946–956. [Google Scholar] [CrossRef]
- Barros, L.A.; Elkin, C. An index for tracking old-growth value in disturbance-prone forest landscapes. Ecol. Indic. 2021, 121, 107175. [Google Scholar] [CrossRef]
- Spracklen, B.; Spracklen, D.V. Determination of structural characteristics of old-growth forest in Ukraine using spaceborne LiDAR. Remote Sens. 2021, 13, 1233. [Google Scholar] [CrossRef]
- Kent, R.; Lindsell, J.A.; Laurin, G.V.; Valentini, R.; Coomes, D.A. Airborne LiDAR Detects Selectively Logged Tropical Forest Even in an Advanced Stage of Recovery. Remote Sens. 2015, 7, 8348–8367. [Google Scholar] [CrossRef]
- Martin, M.; Cerrejón, C.; Valeria, O. Complementary airborne LiDAR and satellite indices are reliable predictors of disturbance-induced structural diversity in mixed old-growth forest landscapes. Remote Sens. Environ. 2021, 267, 112746. [Google Scholar] [CrossRef]
- Tíscar, P.A. Estructura, Regeneración y Crecimiento de Pinus nigra en el área de Reserva Navahondona-Guadahornillos (Sierra de Cazorla, Jaén). Ph.D. Thesis, Universidad Politécnica de Madrid, Madrid, Spain, 2004. [Google Scholar]
- Alejano, R. Regeneración Natural de Pinus nigra Arn. ssp. salzmannii en las Sierras Béticas. Ph.D. Thesis, Universidad Politécnica de Madrid, Madrid, Spain, 1997. [Google Scholar]
- Spies, T.A.; Franklin, J.F. The structure of natural young, mature and old-growth Douglas- fir forests in Oregon and Washington. Wildlife and Vegetation of Unmanaged Douglas-Fir. Forests 1991, 285, 91–109. [Google Scholar]
- Whitford, T.C. Defining Old-Growth Douglas-Fir Forests of Central Montana and Use of the Northern Goshawk (Accipiter gentilis) as a Management Indicator Species. Ph.D. Thesis, University of Montana, Missoula, MT, USA, 1991. [Google Scholar]
- Zhang, Z.; Papaik, M.J.; Wang, X.; Hao, Z.; Ye, J.; Lin, F.; Yuan, Z. The effect of tree size, neighborhood competition and environment on tree growth in an old-growth temperate forest. J. Plant Ecol. 2017, 10, 970–980. [Google Scholar] [CrossRef]
- Lexerød, N.L.; Eid, T. An evaluation of different diameter diversity indices based on criteria related to forest management planning. For. Ecol. Manag. 2006, 222, 17–28. [Google Scholar] [CrossRef]
- Burrascano, S.; Keeton, W.S.; Sabatini, F.M.; Blasi, C. Commonality and variability in the structural attributes of moist temperate old-growth forests: A global review. For. Ecol. Manag. 2013, 291, 458–479. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- McGaughey, R.J. Fusion/LDV: Software for LiDAR Data Analysis and Visualization; USDA Forest Service, Pacific Northwest Research Station: Portland, OR, USA, 2015; 119p.
- Arias-Rodil, M.; Diéguez-Aranda, U.; Álvarez-González, J.G.; Pérez-Cuadrado, C.; Castedo-Dorado, F.; González-Ferreiro, E. Modeling diameter distributions in radiata pine plantations in Spain with existing countrywide LiDAR data. Ann. For. Sci. 2018, 75, 36. [Google Scholar] [CrossRef]
- Hevia, A.; Álvarez-González, J.G.; Ruiz-Fernández, E.; Prendes, C.; Ruiz-González, A.D.; Majada, J.; González-Ferreiro, E. Modelling canopy fuel and forest stand variables and characterizing the influence of the thinning treatments in the stand structure using airborne LiDAR. Rev. Teledetec. 2016, 45, 41–55. [Google Scholar] [CrossRef]
- Novo-Fernández, A.; Barrio-Anta, M.; Recondo, C.; Cámara-Obregón, A.; López-Sánchez, C.A. Integration of national forest inventory and nationwide airborne laser scanning data to improve forest yield predictions in North-Western Spain. Remote Sens. 2019, 11, 1693. [Google Scholar] [CrossRef]
- Whittingham, M.J.; Stephens, P.A.; Bradbury, R.B.; Freckleton, R.P. Why do we still use stepwise modeling in ecology and behaviour? J. Anim. Ecol. 2006, 75, 1182–1189. [Google Scholar] [CrossRef]
- Andersen, H.E.; McGaughey, R.J.; Reutebuch, S.E. Estimating forest canopy fuel parameters using LIDAR data. Remote Sens. Environ. 2005, 94, 441–449. [Google Scholar] [CrossRef]
- Næsset, E. Estimating above-ground biomass in young forests with airborne laser scanning. Int. J. Remote Sens. 2011, 32, 473–501. [Google Scholar] [CrossRef]
- Guerra-Hernández, J.; Görgens, E.B.; García-Gutiérrez, J.; Rodriguez, L.C.E.; Tomé, M.; González-Ferreiro, E. Comparison of ALS based models for estimating aboveground biomass in three types of Mediterranean forest. Eur. J. Remote Sens. 2016, 49, 85–204. [Google Scholar] [CrossRef]
- Montealegre, A.L.; Lamelas, M.T.; de la Riva, J.; García-Martín, A.; Escribano, F. Use of low point density ALS data to estimate stand-level structural variables in Mediterranean Aleppo pine forest. Forestry. Int. J. For. Res. 2016, 89, 373–382. [Google Scholar] [CrossRef]
- Rcmdr: R Commander.R Package Version 2.7-1. Available online: https://socialsciences.mcmaster.ca/jfox/Misc/Rcmdr/ (accessed on 28 January 2021).
- R Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing: Vienna, Austria. Available online: https://www.R-project.org/ (accessed on 28 January 2021).
- Alin, A. Multicollinearity. WIREs Comp. Stat. 2010, 2, 370–374. [Google Scholar] [CrossRef]
- Torresan, C.; Corona, P.; Scrinzi, G.; Valls Marsal, J. Using classification trees to predict forest structure types from LiDAR data. Ann. For. Res. 2016, 59, 281–298. [Google Scholar] [CrossRef]
- Lindenmayer, D.B.; Laurance, W.F.; Franklin, J.F. Global decline in large old trees. Science 2012, 338, 1305–1306. [Google Scholar] [CrossRef]
- Franklin, J.F.; Spies, T.A.; van Pelt, R.; Carey, A.B.; Thornburgh, D.A.; Berg, D.R.; Lindenmayer, D.B.; Harmon, M.E.; Keeton, W.S.; Shaw, D.C.; et al. Disturbances and structural development of natural forest ecosystems with silvicultural implications, using Douglas-fir forests as an example. For. Ecol. Manag. 2002, 155, 399–423. [Google Scholar] [CrossRef]
- Hansen, A.J.; Spies, T.A.; Swanson, F.J.; Ohmann, J.L. Conserving biodiversity in managed forests. BioScience 1991, 41, 382–392. [Google Scholar] [CrossRef]
- Holt, R.F.; Braumandl, T.F.; Mackillop, D.J. An Index of Old-Growthness for Two BEC Variants in the Nelson Forest Region. Final Report; Inter-agency Management Committee, Land Use Coordination Office, Ministry of Environment Lands and Parks: Victoria, BC, Canada, 1999; 47p.
- Freund, J.A.; Franklin, J.F.; Lutz, J.A. Structure of early old-growth Douglas-fir forests in the Pacific Northwest. For. Ecol. Manag. 2015, 335, 11–25. [Google Scholar] [CrossRef]
- Sabatini, F.M.; Burrascano, S.; Lombardi, F.; Chirici, G.; Blasi, C. An index of structural complexity for Apennine beech forests. iForest 2015, 8, 314–323. [Google Scholar] [CrossRef]
- Molino, F. Los Coleópteros Saproxílicos de Andalucía. Ph.D. Thesis, University of Granada, Granada, Spain, 1996. [Google Scholar]
- Ponce, D.B.; Donoso, P.J.; Salas-Eljatib, C. Differentiating structural and compositional attributes across successional stages in chilean temperate rainforests. Forests 2017, 8, 329. [Google Scholar] [CrossRef]
- Fulé, P.Z.; Ribas, M.; Gutiérrez, E.; Vallejo, R.; Kaye, M.W. Forest structure and fire history in an old Pinus nigra forest, eastern Spain. For. Ecol. Manag. 2008, 255, 1234–1242. [Google Scholar] [CrossRef]
- Seidl, R.; Thom, D.; Kautz, M.; Martin-Benito, D.; Peltoniemi, M.; Vacchiano, G.; Wild, J.; Ascoli, D.; Petr, M.; Honkaniemi, J. Forest disturbances under climate change. Nat. Clim. Chang. 2017, 7, 395–402. [Google Scholar] [CrossRef] [PubMed]
- Luyssaert, S.; Schulze, E.D.; Börner, A.; Knohl, A.; Hessenmöller, D.; Law, B.E.; Ciais, P.; Grace, J. Old-growth forests as global carbon sinks. Nature 2008, 455, 213. [Google Scholar] [CrossRef]
- Giorgi, F.; Lionello, P. Climate change projections for the Mediterranean region. Glob. Planet Chang. 2008, 63, 90–104. [Google Scholar] [CrossRef]
- Seidling, W.; Mues, V. Statistical and geostatistical modelling of preliminarily adjusted defoliation on a European scale. Environ. Monit. Assess. 2005, 101, 223–247. [Google Scholar] [CrossRef]
- White, J.C.; Tompalski, P.; Vastaranta, M.; Wulder, M.A.; Saarinen, N.; Stepper, C.; Coops, N.C. A Model Development and Application Guide for Generating an Enhanced Forest Inventory Using Airborne Laser Scanning Data and an Area-Based Approach; Information Report FI-X-018; Canadian Wood Fibre Centre: Ottawa, ON, Canada, 2017; 38p. [Google Scholar]
- Ozdemir, I.; Donoghue, D.M.N. Modelling tree size diversity from airborne laser scanning using canopy height models with image texture measures. For. Ecol. Manag. 2013, 295, 28–37. [Google Scholar] [CrossRef]
- Valbuena, R.; Maltamo, M.; Mehtätalo, L.; Packalen, P. Key structural features of Boreal forests may be detected directly using L-moments from airborne LiDAR data. Remote Sens. Environ. 2017, 194, 437–446. [Google Scholar] [CrossRef]
- Moran, C.J.; Rowell, E.M.; Seielstad, C.A. A data-driven framework to identify and compare forest structure classes using LiDAR. Remote Sens. Environ. 2018, 211, 154–166. [Google Scholar] [CrossRef]
- Hosking, J.R.M. L-moments analysis and estimation of distributions using linear combinations of order statistics. J. Royal Stat. Soc. 1990, 52, 105–124. [Google Scholar] [CrossRef]
- White, J.C.; Wulder, M.A.; Varhola, A.; Vastaranta, M.; Coops, N.C.; Cook, B.D.; Pitt, D.; Woods, M. A best practices guide for generating forest inventory attributes from airborne laser scanning data using an area-based approach. For. Chron. 2013, 89, 722–723. [Google Scholar] [CrossRef]
- Frazer, G.W.; Magnussen, S.; Wulder, M.A.; Niemann, K.O. Simulated impact of sample plot size and co-registration error on the accuracy and uncertainty of LiDAR-derived estimates of forest stand biomass. Remote Sens. Environ. 2011, 115, 636–649. [Google Scholar] [CrossRef]





| Structural Parameters | ||
|---|---|---|
| OGI Type | DBH Variability | Density of Large Trees |
| 1 | STDDBH | Density of trees > 50 cm DBH |
| 2 | STDDBH | Density of trees > 70 cm DBH |
| 3 | STDDBH | Density of trees > 100 cm DBH |
| 4 | GC | Density of trees > 50 cm DBH |
| 5 | GC | Density of trees > 70 cm DBH |
| 6 | GC | Density of trees > 100 cm DBH |
| 7 | - | Density of trees > 50 cm DBH |
| 8 | - | Density of trees > 70 cm DBH |
| 9 | - | Density of trees > 100 cm DBH |
| 10 | STDDBH | Basal area of trees > 50 cm DBH |
| 11 | STDDBH | Basal area of trees > 70 cm DBH |
| 12 | STDDBH | Basal area of trees > 100 cm DBH |
| 13 | - | Basal area of trees > 50 cm DBH |
| 14 | - | Basal area of trees > 70 cm DBH |
| 15 | - | Basal area of trees > 100 cm DBH |
| ALS Metrics | Description |
|---|---|
| hmean, hmode | mean, mode |
| hmin, hmax | minimum, maximum |
| hSD, hCV | standard deviation, coefficient of variation |
| hSkw | skewness |
| hkurt | kurtosis |
| hID, | interquartile range, |
| hAAD | average absolute deviation |
| hMADmedian | median of the absolute deviations from the overall median |
| hMADmode | median of the absolute deviations from the overall mode |
| hL1, hL2, hL3, hL4 | L-moments |
| hLskw | L-moments of skewness |
| hLkur | L-moments of kurtosis |
| h01, h05, h10, h20, h25, …, h90, h95, h99 | Percentiles |
| CRR | canopy relief ratio: mean height-min height/max height-min height |
| CC | canopy cover: percentage of first returns above 4.5 m/total returns |
| PARA3 | percentage of all returns above 3 m/total all returns |
| ARA3.TFR | ratio between all returns above 3 m and total of first returns |
| PFRAM | percentage of first returns above mean/total all returns |
| PARAM | percentage of all returns above mean/total all returns |
| PARAMO | percentage of all returns above mode/total all returns |
| PFRAMO | percentage of first returns above mode/total all returns |
| ARAM.TFR | ratio between all returns above mean and total of first returns |
| ARAMO.TFR | ratio between all returns above mode and total of first returns |
| Structural Variables | Old Forests (n = 21) | Young Forests (n = 18) | F (p > F) |
|---|---|---|---|
| Mean tree diameter (mDBH, cm) | 70.48 (15.0) a | 17.58 (2.01) b | 219.55 (<0.0001) |
| Diameter standard deviation (STDDBH) | 30.89 (17.2) a | 4.28 (2.23) b | 42.45 (<0.0001) |
| Basal area (G, m2 ha−1) | 36.08 (15.2) a | 5.74 (5.75) b | 47.88 (<0.0001) |
| Basal area of trees > 50 cm DBH (BA50, m2 ha−1) | 34.69 (15.2) a | 1.67 (0.71) b | 91.92 (<0.0001) |
| Basal area of trees > 70 cm DBH (BA70, m2 ha−1) | 31.35 (12.0) a | 0 (0) b | 86.98 (<0.0001) |
| Basal area of trees > 100 cm DBH (BA100, m2 ha−1) | 27.26 (10.5) a | 0 (0) b | 12.35 (0.0012) |
| Density (N, trees ha−1) | 83.15 (41.9) b | 285.30 (277.7) a | 10.88 (0.0022) |
| Density of trees > 50 cm DBH (N50, trees ha−1) | 58.94 (29.9) a | 0.78 (3.33) b | 67.00 (<0.0001) |
| Density of trees > 70 cm DBH (N70, trees ha−1) | 42.10 (19.6) a | 0 (0) b | 82.30 (<0.0001) |
| Density of trees > 100 cm DBH (N100, trees ha−1) | 11.57 (13.3) a | 0 (0) b | 13.59 (0.0007) |
| Gini coefficient (GC) | 0.45 (0.21) a | 0.26 (0.11) b | 11.67 (0.006) |
| Model | Description | −2LL | AIC |
|---|---|---|---|
| 1 | With nugget, covariates, and different spatial covariance in areas North and South | 6545.5 | 6575.5 |
| 2 | = Model 1 but same spatial covariance in areas North and South | 6549.4 | 6575.4 |
| 3 | = Model 2 but without nugget | 6751.6 | 6775.6 |
| 4 | With covariates but no spatial covariance | 6563.5 | 6585.5 |
| 5 | = Model 2 but without covariates | 6560.4 | 6568.4 |
| Parameter | Estimate | Standard Error | t-Value | p >|t| |
|---|---|---|---|---|
| Intercept | −30.14945 | 5.25588 | −5.736 | <0.0001 |
| ARAM.TFR | −0.25675 | 0.08158 | −3.147 | 0.0018 |
| h95 | 1.90980 | 0.38434 | 4.969 | <0.0001 |
| hL2 | 8.86526 | 2.12298 | 4.176 | <0.0001 |
| CRR | 32.37033 | 10.86575 | 2.979 | 0.0031 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hevia, A.; Calzado, A.; Alejano, R.; Vázquez-Piqué, J. Identification of Old-Growth Mediterranean Forests Using Airborne Laser Scanning and Geostatistical Analysis. Remote Sens. 2022, 14, 4040. https://doi.org/10.3390/rs14164040
Hevia A, Calzado A, Alejano R, Vázquez-Piqué J. Identification of Old-Growth Mediterranean Forests Using Airborne Laser Scanning and Geostatistical Analysis. Remote Sensing. 2022; 14(16):4040. https://doi.org/10.3390/rs14164040
Chicago/Turabian StyleHevia, Andrea, Anabel Calzado, Reyes Alejano, and Javier Vázquez-Piqué. 2022. "Identification of Old-Growth Mediterranean Forests Using Airborne Laser Scanning and Geostatistical Analysis" Remote Sensing 14, no. 16: 4040. https://doi.org/10.3390/rs14164040
APA StyleHevia, A., Calzado, A., Alejano, R., & Vázquez-Piqué, J. (2022). Identification of Old-Growth Mediterranean Forests Using Airborne Laser Scanning and Geostatistical Analysis. Remote Sensing, 14(16), 4040. https://doi.org/10.3390/rs14164040






