Joint Satellite-Transmitter and Ground-Receiver Digital Pre-Distortion for Active Phased Arrays in LEO Satellite Communications

Abstract

A novel joint satellite-transmitter and ground-receiver (JSG) digital pre-distortion (DPD) (JSG-DPD) technique is proposed to improve the linearity and power efficiency of the space-borne active phased arrays (APAs) in low Earth orbit (LEO) satellite communications. Different from the conventional DPD technique that requires a complex RF feedback loop, the DPD coefficients based on a generalized memory polynomial (GMP) model are extracted at the ground-receiver and then transmitted to the digital baseband front-end of the LEO satellite-transmitter via a satellite–ground bi-directional transmission link. The issue of the additive white Gaussian noise (AWGN) of the satellite–ground channel affecting the extraction of DPD coefficients is tackled using a superimposing training sequences (STS) method. The proposed technique has been experimentally verified using a 28 GHz phased array. The performance improvements in terms of error vector amplitude (EVM) and adjacent channel power ratio (ACPR) are 7.5% and 3.6 dB, respectively. Requiring limited space-borne resources, this technique offers a promising solution to achieve APA DPD for LEO satellite communications.

1. Introduction

With the rapid rise of fifth-generation (5G) millimeter-wave (mmWave) communications and broadband low Earth orbit (LEO) satellites [1,2], active phased array (APA) antennas have seen unprecedented development in recent years [3,4,5]. Compared with conventional antennas, APA antennas do not require bulky servo tracking systems. They can change the radiation pattern by adjusting the excitation phases of the antenna elements in the array, thus bringing advantages such as flexible beam control and high reliability [6,7]. Higher power efficiency is required to support high data rates operation while driving power amplifiers (PAs) close to their saturation state will introduce severe nonlinear distortion. Nonlinear distortion leads to non-negligible problems such as: interference to other satellite and terrestrial communication systems due to the increased adjacent channel power ratio (ACPR), and deterioration of the error vector magnitude (EVM) leading to higher bit error rates.

To address this problem, power backoff techniques and digital pre-distortion (DPD) [8,9,10,11,12,13,14] techniques are often adopted, of which DPD techniques have drawn widespread attention because they can better improve power efficiency to fully utilize the space-borne power resources. As shown in Figure 1a,b, the DPD techniques with 4-by-4 array antennas as an example can be further divided into two categories: one is individual DPD [8,9,11], and the other is overall DPD [12,13,14]. The impact of PA nonlinear distortion of a massive multiple-input multiple-output (MIMO) generalized frequency division multiplexing (GFDM) (MIMO-GFDM) system on the spectral shape, the peak to average power ratio (PAPR), and the bit error rate (BER) in the additive white Gaussian noise (AWGN) channel was researched and analyzed in [8]. It proposes a linearization technique for applying each PA pre-distorter separately at the transmitter side of the MIMO-GFDM system. Ref. [9] offers a method to simultaneously compensate for PA nonlinearity, antenna crosstalk, and mismatch in a broadband multi-antenna transmitter. Each transmit path is provided with a dual input DPD, which matches a linear model of the crosstalk and mismatch features of the antenna array shared by all transmitting paths. The DPD technique proposed by [11] includes overall multibeam compensation and separate dual-band compensation. The multibeam compensation deals with multibeam interference, while the dual-band compensation is designed to eliminate the nonlinear distortion of the PA. Nevertheless, these one-to-one DPD techniques are unsuitable for large-scale APAs because of the high complexity and the mutual disturbance between channels.

For large-scale APA linearization, approaches with overall DPD of PAs for all array cells at the transmitter give more generic and effective solutions. The fundamental coefficients of the single-input single-output (SISO) array model include beamforming weights, antenna cross-coupling, channel coefficients, etc. As a result, many sets of trained DPD coefficients are sufficient to reduce the nonlinear distortion of mm-wave radio frequency beamforming array [12]. Ref. [13] assumed that the PAs are similar in all branches, the main beam is generated by collecting the output signal of one PA, and the memory polynomial (MP) model is used to calculate the overall DPD from the main beam and the input of the sub-array. Ref. [14] implements full-angle DPD for 5G mmWave large-scale MIMO transmitters by first compensating for differences of PAs in different transmitter chains and then linearizing the entire subarray using a common digital block. Unfortunately, since the DPD is done within the digital domain before the front-end, these approaches necessitate an RF feedback loop, and the resulting hardware resource consumption is almost equivalent to an space-borne receiver, which is unacceptably high for LEO satellite communications. Therefore, a joint satellite-transmitter and ground-receiver digital pre-distortion (JSG-DPD) technique, by reusing the ground-receiver as the "feedback loop", is proposed in this paper to achieve linearization of the space-borne APA. It is experimentally demonstrated that this technique can dramatically save space-borne resources and can achieve a promising 7.5% EVM improvement. To the best of our knowledge, this paper is the first attempt to join the receiver and transmitter for DPD in order to obtain desirable results with less cost. With the future deployment of a large number of LEO satellite systems, the search for effective high-power-efficient satellite communication techniques becomes increasingly urgent.

The rest of the paper is organized as follows: Section 2 presents the main principles of the proposed technique. Section 3 explains the algorithm for calculating the DPD coefficients of the GMP model. Section 4 shows the experimental results and analysis. Conclusions are given in Section 5.

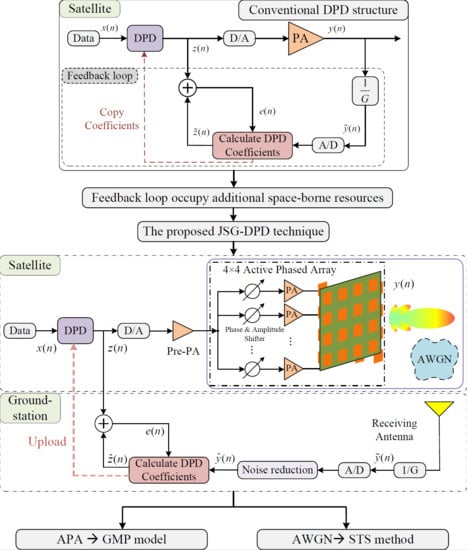
2. Principle Analysis of the Proposed JSG-DPD Technique

In this section, we demonstrate the structure of the proposed JSG-DPD technique and present the adopted signal standard, the channel model, and the solution for a low SNR.

2.1. The Proposed JSD-DPD Technique

The proposed system architecture depicted in Figure 2 is mainly based on the overall DPD structure of Figure 1b. However, the space-borne feedback loop is eliminated and replaced by a noise reduction and DPD coefficient extraction system at the ground station to save satellite resources. Certainly, the ground station faces the challenge of a low signal-noise ratio (SNR) resulting from high AWGN. To address this concern, the superimposed training sequences (STS) method is proposed. The nonlinearly compressed STS signals pass through the AWGN channel between the satellite and the ground and are captured by the receiving antenna of the ground station. Noise reduction is performed by exploiting the irrelevancy of the noise, as explained in the following Section 2.4. Then the DPD coefficients of the selected model are calculated with a suitable adaptive algorithm and uploaded to the baseband front-end of the LEO satellite using the satellite–ground bi-directional link. Hence, this joint satellite–ground DPD (JSG-DPD) structure does not occupy additional space-borne resources. It can greatly improve the linearity and the power efficiency of APA, enabling the application of DPD techniques to LEO satellite communications.

2.2. OFDM Technique

Conventional digital modulation is performed on a single carrier, such as QPSK, 16QAM, etc. These single-carrier modulation methods are susceptible to inter-symbol interference (ISI), deteriorating the BER. It is subject to Rayleigh fading in a multipath propagation environment, which can cause burst BER. While orthogonal frequency division multiplexing (OFDM) divides the channel into several orthogonal subchannels in the frequency domain and adopts a subcarrier transmitted in parallel for modulation on each subchannel. In addition, a cyclic prefix is usually inserted between each OFDM symbol as a guard interval. Therefore, the OFDM system offers excellent anti-fading and anti-ISI capabilities, high spectrum efficiency, and is applicable to high-speed digital communication. The mathematical expression for the continuous OFDM baseband signal is

$$x\left(t\right)=\frac{1}{\sqrt{M}}\underset{u=-\infty }{\sum ^{+\infty }}\underset{m=0}{\sum ^{M-1}}{\mathbf{X}}_{\mathbf{u},\mathbf{m}}g\left(t-u{T}_s\right)e^{j2\pi m\frac{\left(t-u{T}_s\right)}{T_s}},$$

(1)

where M represents the number of subcarriers, ${\mathbf{X}}_{\mathbf{u},\mathbf{m}}$ denotes the information carried on the m-th subcarrier in the u-th OFDM symbol, $T_s$ is the duration of an OFDM symbol, and $g\left(t\right)$ is the window function. The discrete OFDM baseband signal is derived by sampling the continuous OFDM baseband signal at the Nyquist sampling rate $t=(w+uM)T_s/M$, denoted as

$$x_{u,w}=\frac{1}{\sqrt{M}}\underset{u=-\infty }{\sum ^{+\infty }}\underset{m=0}{\sum ^{M-1}}{\mathbf{X}}_{\mathbf{u},\mathbf{m}}g\left[\frac{w{T}_s}{M}\right]e^{j2\pi \frac{mw}{M}},$$

(2)

where $w=0,1,\dots ,M-1$. In order to enhance the LEO satellite-to-ground data transmission rate, this paper adopts such an OFDM signal with a high PAPR of 11.69 dB

$$\mathrm{PAPR}=\frac{max\left\{{\left|x_{u,w}\right|}^2\right\}}{E\left\{{\left|x_{u,w}\right|}^2\right\}}.$$

(3)

Given that OFDM symbols are composed of several independently modulated subcarrier signals, when each subcarrier is in the same or comparable phase, the superimposed signal will be modulated by the same beginning phase signal, resulting in a huge instantaneous power peak, thus bringing a high PAPR. Since the limited linear operating range of a typical PA, OFDM signals with large PAPR are likely to get into the nonlinear region of the PA, causing serious degradation of the overall system performance.

2.3. LEO Satellite-Ground Channel

As for LEO satellite communications, it is commonly necessary to consider the Doppler effect [15] and multipath effect [16]. The multipath effect is the propagation phenomenon of radio frequency (RF) signals arriving at the receiving antenna through various paths from the transmitting antenna. The electromagnetic waves of each path arrive at the receiver at different times, and thus at different phases. The superposition of multiple signals with different phases at the receiver results in a change in the amplitude of the received signal, which produces the so-called multipath fading.

When considering that the received signal consists of only multipath signal components, the probability density function (PDF) of the signal obeys the Rayleigh distribution

$$f_r\left(r\right)=\frac{r}{{\sigma }^2}·exp\left[-\frac{r^2}{2{\sigma }^2}\right],$$

(4)

where r and ${\sigma }^2$ denote the received signal amplitude, and the average multipath power, respectively. While considering the received signal is composed of a line of sight (LOS) signal and multipath signal, the PDF of the signal obeys the Rice distribution

$$f_r\left(r\right)=\frac{r}{{\sigma }^2}·exp\left[-\frac{r^2+z^2}{2{\sigma }^2}\right]I_0\left(\frac{rz}{{\sigma }^2}\right),$$

(5)

where r indicates the received signal amplitude, z represents the LOS signal amplitude, and ${\sigma }^2$ is the average multipath power [17]. Generally, we assume ground stations are built in non-urban open areas, thus ignoring the effect of reflections caused by buildings. Due to different atmospheric densities, scattering is typically generated in the troposphere at an altitude of about 10–20 km above the ground. For LEO satellites above several hundred km, such a link length is only 2–3% of the total link length, so the resulting multipath effect is insignificant. In addition, the inter-symbol interference (ISI) from multipath can be maximally eliminated by inserting a guard interval between OFDM symbols, where the guard interval is larger than the maximum multipath delay extension of the satellite communication channel. If the cyclic prefix (CP) is filled in the guard interval, the inter-channel interference (ICI) from multipath can also be avoided. This is the commonly used means of OFDM signal transmission. Therefore, the impact of the multipath effect is ignored in this paper.

When there is relative motion between the satellite and the ground station, the transmitted carrier frequency received by the ground station is frequency shifted, which is the Doppler shift phenomenon. It is harmful to digital communication using correlation demodulation, and thus cannot be ignored. As depicted in Figure 3, the actual velocity of the satellite is v, and the relative speed of the satellite to the ground station is

$$v^{\prime }=v·sin\theta ,$$

(6)

which varies dynamically. The Doppler shift is defined as

$$\Delta f_c=\frac{v^{\prime }}{c}·f_c,$$

(7)

where $f_c$ denotes the carrier frequency, $\Delta f_c$ represents the carrier frequency offset, i.e., Doppler frequency offset, and $c=3·{10}^8$ m/s is the speed of light. According to the standard 401.0-B of the Consultative Committee for Space Data Systems (CCSDS) [18], the maximum relative motion speed between a LEO satellite and a ground station is 10 km/s, and the maximum speed change rate is 380 m/s ${}^2$. The maximum Doppler frequency offset of the LEO satellite–ground data transmission system based on Ka-band (28 GHz) is $\pm 930$ kHz, and the maximum Doppler frequency offset change rate is 35 kHz/s. Therefore, the time-varying Doppler effect makes it difficult for the receiver to accurately track the carrier of the signal, which undoubtedly increases the design difficulty of the receiver. In addition, the Doppler effect causes a spreading/compression of

$$\Delta B=\frac{v^{\prime }}{c}·B$$

(8)

for a transmitted signal with bandwidth B.

For the Ka-band 100 MHz signal applied in this paper, the maximum spreading of the bandwidth is 3.3 kHz. Given that the time-varying Doppler effect has been solved by mature techniques [19,20,21,22], so it is not the focus of our study. Consequently, the LEO satellite–ground transmission channel is modeled as an AWGN channel in this paper. The magnitude of white Gaussian noise follows a Gaussian distribution, while the power spectral density (PSD) obeys a uniform distribution.

2.4. Noise Reduction Method

The transmission frame structure of the proposed superimposing training sequences method is illustrated in Figure 4, which mainly consists of three parts: frame header, data block, and pilot signal. The pilot signal is composed of H identical training sequences. Assume that the discrete OFDM signal subject to AWGN interference is

$$x\left(n\right)=s\left(n\right)+u\left(n\right),n=0,1,\cdots ,N,$$

(9)

where $s\left(n\right)$ and $u\left(n\right)$ denote the discrete OFDM signal and the noise signal, respectively. After superimposing the above equation for H times, we obtain

$$x_h\left(n\right)=\underset{h=1}{\sum ^H}{s}_h\left(n\right)+\underset{h=1}{\sum ^H}{u}_h\left(n\right),n=0,1,\cdots ,N.$$

(10)

Since AWGN is not only irrelevant between random variables at any two distinct moments, it is also statistically independent. Hence, the noise part ${\displaystyle \sum _{h=1}^H}{u}_h\left(n\right)$ is almost zero, while the signal part is amplified H times, and the above equation is then averaged and divided by H on both sides to yield

$$x^{\prime }\left(n\right)=s\left(n\right)+{\mathit{U}}^{\prime },n=0,1,\cdots ,N.$$

(11)

When the number H of superpositions is large enough, theoretically ${\mathit{U}}^{\prime }\approx 0$, $x^{\prime }\left(n\right)\approx x\left(n\right)$. With this method, the valuable signal is coherent and can be accumulated, while the noise signal is irrelevant and cannot be gathered. Therefore, the SNR of the received signal is improved by increasing the signal power, which can be equivalent to noise reduction. Moreover, the frame length and the propagation time occupied by the pilot signal consisting of the superimposed training sequence, etc., can be acceptable during several minutes of LEO satellite data transmission.

Furthermore, for non-Gaussian noise such as heavy-tailed noise [23,24], other methods [25,26,27] are needed for noise reduction.

3. DPD Coefficients Recognition Algorithm

In this section, we present an indirect learning structure based on the proposed JSG-DPD technique, focusing on the principle of computing the DPD coefficients of the GMP model using the least squares (LS) algorithm.

3.1. The JSG-DPD Indirect Learning Structure

In [28], the indirect learning architecture applied to PA linearization is proposed for the first time. As shown in Figure 5, in the field of satellite communications, the feedback loop for coefficient calculation is almost equivalent to a receiver that would be included in the satellite-transmitter. Therefore, the required cost is unacceptable for satellites; it is also for this reason that dynamic DPD techniques are not widely used in satellite communications. Ref. [29] provides a fifth order static DPD, which means that only the static nonlinearity of the PA can be handled, while the memory effect is ignored. Such a static DPD method would not improve the performance a lot, especially for broadband signals.

The indirect learning structure of the proposed JSG-DPD technique is illustrated in Figure 6, in which the pre-distorter is not working until the DPD coefficients are identified. At this time, the input signal of the APA $x\left(n\right)=z\left(n\right)$, $z\left(n\right)$ is taken as the expected output signal of the DPD coefficients estimation module, and the signal $\widehat{y}\left(n\right)$ after noise reduction of the received signal $\tilde{y}\left(n\right)$ is taken as the input of the pre-distortion coefficients estimation module, where G is the gain of the pre-PA and linear APA. The signal $\widehat{y}\left(n\right)$ is passed through the DPD coefficients estimation module (i.e., post-distortion) to obtain the output signal $\widehat{z}\left(n\right)$, which is subtracted from the desired output signal $z\left(n\right)$ to obtain the error signal $e\left(n\right)$. The adaptive discrimination algorithm obtains the coefficients w of the optimal DPD coefficients estimation module by iterating the error signal. Finally, the coefficient w is directly copied as the coefficient of the pre-distorter to make the pre-distorter operate. It is worth pointing out that for the general Volterra system, the P-order post-inverse is the same as the P-order pre-inverse [30]. Thus, for our application, the post-distortion response is the same as the pre-distortion response, and that is why the coefficients can be copied directly to the pre-distorter before the APA. In addition, the Volterra series are generalized nonlinear models with memory, and DPD of Volterra models is usually implemented using P-order inverse techniques [31].

Notably, another communication link is not required because the pilot signal $z\left(n\right)$ is only a fixed segment of the signal known to the ground station for the purpose of calculating the DPD coefficients. Therefore, the proposed JSG-DPD indirect learning structure does not occupy additional space-borne resources.

The calculation of the DPD coefficients is very fast after the ground station receives the pilot signal, and this calculation time is even negligible because the computing resources of the ground station are very powerful. Instead, the time to be concerned is the time to upload the DPD coefficients, which depends on the communication rate of the uplink. For this paper, the number of coefficients of the generalized memory polynomial model obtained is several tens, which can be uploaded in a short time (ms level).

Therefore, both the DPD coefficient calculation time and the DPD coefficient upload time are very short and do not illegally emit large amounts of spurious emissions to other satellites, which can affect the communication quality.

It is only possible that while waiting for the coefficients to be uploaded, the received signal quality of the ground station will degrade because the space-borne DPD coefficients have not been updated yet. After the coefficients are uploaded and the DPD coefficients are updated, the received signal quality at the ground station will be greatly improved. There is a mode that can be set to avoid the problem of temporary degradation of communication quality: when the received signal quality degrades, only the pilot signal used for updating DPD coefficients is transmitted. Normal scientific data will be transmitted after the DPD coefficients have been updated. Hence, although it takes time to upload DPD coefficients, it is not required for each transition, and the number of uploaded coefficients is extremely small.

3.2. Generalized Memory Polynomial (GMP) Model

For narrow-band signals, where the memory effect is not obvious, it can usually be implemented using polynomial models, Saleh models [32], etc. For wideband signals, the influence of the memory effect cannot be ignored, and the output signal of the APA is not only related to the current input signal, but also related to the past input signal, so it is necessary to use a nonlinear model with memory for wideband APA modeling. Memory models mainly include Volterra series models [33] and their simplified forms, such as memory polynomial (MP) [28], generalized memory polynomial (GMP) [34], Wiener model [35], Hammerstein model [36], etc. Recently, neural network models [37] have also been investigated for modeling nonlinear systems.

Usually, the MP model and Volterra series are used to model narrowband memory APAs and wideband memory APAs, respectively. While the coefficients of Volterra series model are too complex and the coefficients of MP model are too simplified. As a compromise, the GMP model can achieve better modeling results than the MP model by considering the generalized memory effect and the number of coefficients can be acceptable for LEO satellite communication.

The significance of the APA behavior model is that it can inverse model the APA and be used to compensate for the signal distortion caused by the APA nonlinearity. In this broadband OFDM signal and array antennas for the LEO satellite communication application scenario, it is necessary to trade off the computational complexity and algorithm performance. The MP model is a simplified form of Volterra for narrowband signals as well as unit antenna systems with few model coefficients. The MP model with nonlinear order K and memory depth Q can be written as

$$y_{MP}\left(n\right)=\sum _{k=0}^{K-1}\sum _{q=0}^{Q-1}{c}_{kq}x(n-q){\left|x(n-q)\right|}^k,$$

(12)

where $x\left(n\right)$ and $y_{MP}\left(n\right)$ are the input and output signals of the model, and $c_{kq}$ represents the coefficients of the model. The total number of coefficients is $O_{MP}=K·Q$.

Its performance is limited because it contains only the diagonal terms of Volterra. While in some application scenarios, non-diagonal terms can significantly impact the model accuracy. Although the neural network model is very flexible and adaptable, the large number of coefficients requires a large number of space-borne computing resources, so it cannot be deployed on satellites by far. The GMP model performs better for strongly nonlinear dynamical systems because it supplements the consideration of generalized memory effects than the MP model. Therefore, the GMP model is adopted as the model of pre-distorter in this paper

$$\begin{array}{cc}\hfill y_{GMP}\left(n\right)& =\sum _{k=0}^{K_a-1}\sum _{l=0}^{L_a-1}{a}_{kl}x(n-l){\left|x(n-l)\right|}^k\hfill \\ \hfill & +\sum _{k=1}^{K_b}\sum _{l=0}^{L_b-1}\sum _{m=1}^{M_b}{b}_{klm}x(n-l){\left|x(n-l-m)\right|}^k\hfill \\ \hfill & +\sum _{k=1}^{K_c}\sum _{l=0}^{L_c-1}\sum _{m=1}^{M_c}{c}_{klm}x(n-l){\left|x(n-l+m)\right|}^k,\hfill \end{array}$$

(13)

where $x\left(n\right)$ and $y_{GMP}\left(n\right)$ are the input and output signals of the model, $a_{kl}$, $b_{klm}$, and $c_{klm}$ represent the model coefficients of the MP sub-model, the lagging term, and the leading term, respectively. $K_a$, $K_b$, and $K_c$ stand for the nonlinear order of each branch term, $L_a$, $L_b$, and $L_c$ denote the memory depth of each branch term, and $M_b$, $M_c$ are the additional degrees of freedom, which determine the maximum selectable range of memory depths for the lagging and leading terms, respectively. The total number of coefficients is $O_{GMP}=K_a{L}_a+K_b{L}_b{M}_b+K_c{L}_c{M}_c$.

3.3. Coefficient Estimation Algorithm

Classical adaptive estimation algorithms include the LS algorithm, the least mean square (LMS) algorithm, and the recursive least squares (RLS) algorithm. These methods are also widely applied in adaptive equalization [38,39]. The LMS algorithm has the advantages of no matrix inversion, simple structure, and easy implementation. Still, it is unsuitable for DPD application scenarios since it is prone to poorly conditioned covariance matrices, resulting in extremely slow convergence. The RLS algorithm is more computationally intensive and may also have poorly conditioned covariance matrices leading to unstable convergence. Therefore, in this paper, we employ the batch processing LS algorithm to estimate model coefficients.

The core idea of the LS algorithm is to search for the best function of the data for matching by minimizing the sum of squares of the errors. By replacing $x(n-l)$ and $y_{GMP}\left(n\right)$ of Equation (13) with ${\widehat{y}}_{GMP}(n-l)$ and $z\left(n\right)$, respectively, we can write the equation as

$$\mathit{z}=\mathit{U}\mathit{c},$$

(14)

where

$$\mathit{z}={\left[z\right(N),z(N-1),...,z(1\left)\right]}^{\mathrm{T}},$$

(15)

$$\mathit{U}=\left[\mathit{u}\right(N),\mathit{u}(N-1),...,\mathit{u}(1\left)\right],$$

(16)

$$\mathit{u}\left(n\right)={[u\left(n\right),...,u(n-L_c+1){\left|u(n-L_c+1+M_c)\right|}^{K_c}]}^{\mathrm{T}},$$

(17)

$$\mathit{c}={[a_{00},...,a_{(K_a-1)(L_a-1)},...,c_{K_c(L_c-1)M_c}]}^{\mathrm{T}},$$

(18)

where $K_a,L_a,K_b,L_b,M_b,K_c,L_c,M_c$ are the parameters of the GMP model, and the LS solution of Equation (14) is

$$\widehat{\mathit{c}}={\left({\mathit{U}}^H\mathit{U}\right)}^{-1}{\mathit{U}}^H\mathit{z},$$

(19)

where ${(·)}^H$ denotes the complex conjugate transpose of the matrix, and $\widehat{\mathit{c}}$ is the estimated GMP coefficients (including $\left\{a_{kl},b_{klm},c_{klm}\right\}$). With such an approach, the APA and DPD coefficients of the GMP model can be obtained based on the corresponding input and output data.

In addition, it is worth noting that the GMP model has as many as eight parameters, while the MP model has only two. Parameter selection is usually performed scan-by-scan to obtain a set of parameters to achieve a trade-off between the modeling error and model size. This approach is appropriate for the MP model, but for the GMP model with eight parameters, it takes a lot of combinations and time to obtain the proper set of parameters. There have been studies, such as the simulated annealing (SA) method, the particle swarm optimization with the Akaike information criterion (PSO-AIC) method [40], to develop fast and efficient strategies to determine the optimal parameters, allowing a suitable balance of performance and computing complexity.

4. Experimental Validation and Results Analysis

In this section, the experimental system is presented, followed by the determination of the training sequence length and the analysis of the JSG-DPD results for two power levels.

4.1. Experimental Setup

The structural block diagrams of the over-the-air (OTA) measurement equipment and the actual laboratory equipment photo are presented in Figure 7 and Figure 8, respectively. The 5G new radio (NR) intermediate frequency (IF) signal with a bandwidth of 100 MHz centered at 3 GHz is generated from a vector signal generator (VSG)(R&S SMBV100B). The Agilent E3247C outputs an unmodulated signal of 12.5 GHz, which is multiplied to 25 GHz by a MITEQ-MAX2M200400 frequency multiplier, and then sent to a power divider as a local oscillator (LO) signal for the up-converter (KTX321840) and down-converter (KRX321840). The 28 GHz bandpass filtered signal is linearly amplified by a pre-amplifier (Ducommum APH-26063325) away from its saturation region to drive the APA into its compression state. The APA device is based on the Amotech AAiPK428GC-A0404, which consists of four Anokiwave AWMF-0158 transceivers and incorporates 16 branches attenuators, phase shifters, and PAs in a 4-by-4 APA, as well as 16 patch antennas. The main beam signal is captured by an observation horn antenna. After down-conversion to IF, it is collected and converted to a baseband signal by an R&S FSW spectrum analyzer. Lastly, the baseband signal is processed by MATLAB.

4.2. Experimental Results and Analysis

Generally, to obtain higher drain efficiency, the PA is required to operate in 2–3 dB gain compression; thus, we choose two input power levels of −24 dBm and −25 dBm from VSG for testing. The nonlinear characteristics of such points are meaningful and significantly impact the quality of the transmitted signal without DPD techniques.

For the JSG-DPD technique proposed in this paper, it is necessary to trade-off the model performance and the frame length occupation to select a suitable length of training sequences to model and linearize the APA. Therefore, we first conduct experiments in the noiseless scenario to determine the length of training sequences by observing the improvement of ACPR and EVM. The expression of ACPR and EVM are as follows

$$\mathrm{ACPR}\left(\mathrm{dB}\right)=10lg\left[\frac{P_{adj\_n\_L}\left(w\right)+P_{adj\_n\_R}\left(w\right)}{P_{ch\_main}\left(w\right)}\right],$$

(20)

where $P_{adj\_n\_L}\left(w\right)$, $P_{adj\_n\_R}\left(w\right)$ are the signal power of the left channel and the right channel adjacent to the main channel, respectively, and $P_{ch\_main}\left(w\right)$ is the power of the signal of the main channel (transmit channel).

$$\mathrm{EVM}=\sqrt{\frac{\frac{1}{N}{\displaystyle \sum _{n=1}^N}{e}_n}{\frac{1}{N}{\displaystyle \sum _{n=1}^N}({I_n}^2+{Q_n}^2)}}\times 100\%,$$

(21)

where the vector error signal $e_n=({\tilde{I}}_n-{I_n)}^2+({\tilde{Q}}_n-{Q_n)}^2$, $I_n$, $Q_n$ are the expected signal’s quadrature components, and ${\tilde{I}}_n$, ${\tilde{Q}}_n$ are the two quadrature signals of the real measurement, respectively.

Since this part of the test is performed at the ground station (before the satellite launch), the prior knowledge about APA and an almost noise-free experimental scenario can be obtained. The experimental results are shown in Figure 9. For these two input power levels, the improvement of both ACPR and EVM is optimal for a training sequence length of 40,000. Although the EVM improvement may be better after the training length exceeds 100,000, an extra-long frame length is needed to obtain a slight improvement. Especially after hundreds or thousands of superpositions, the slight performance improvement is negligible in comparison to the cost of the frame length. Hence, the training sequence length is chosen to be 40,000 after a trade-off.

In order to verify the effect of AWGN on the transmitted signal without loss of generality, an SNR of 10 dB is assumed for each satellite transit to establish communication with the ground station.

In actual communication scenarios, as shown in Figure 10, when the angle between the satellite and the ground station is 5 degrees from the horizontal, the communication is established, and the communication distance is the longest and the SNR is the smallest. It is at this moment that our proposed method starts to operate. The relative position between transceivers will change, which will lead to fluctuations in SNR. The SNR variation throughout the communication window may exceed 10 dB [41], but our proposed method is only used when communication is just established. The SNR fluctuation range is approximately 10 dB to 10.5 dB, which is not a large enough fluctuation to affect the experimental results. Therefore, for the convenience of the calculation, we assume a constant SNR of 10 dB.

The unprocessed received signal at this point is shown in Figure 11a, and the critical sidelobe information of the APA nonlinear system is completely drowned in the noise. After 10, 100, and 1000 superimposed training sequences, the sidelobe information is gradually revealed. As the time domain signal results shown in Figure 11b, the noise reduction processed signal and the original signal almost overlap. Hence, the nonlinear characteristics of the APA system can be extracted.

According to the DPD structure introduced in the previous sections, the GMP model is applied to model the APA system and generate the predistorted signal. Figure 12 shows the AM-AM and AM-PM curves of this APA system. The predistorted signal forms an inverse relationship with the original APA output signal, which makes the combined pre-distorter and the APA approximately linear. The time-domain signal comparison in Figure 13 reveals that the most effective strategy of the DPD technique is to pre-amplify the signal at high amplitude so that after the nonlinear APA gain compression, the same linear gain can be achieved as at other low amplitude.

Empirically and based on several attempts to obtain the minimum normalized mean square error (NMSE)

$$\mathrm{NMSE}\left(\mathrm{dB}\right)=10lg\left[\frac{{\displaystyle \sum _{n=0}^{N-1}}\left|y\left(n\right)-\overline{y}\left(n\right)\right|}{{\displaystyle \sum _{n=0}^{N-1}}{\left|y\left(n\right)\right|}^2}\right],$$

(22)

where $y\left(n\right)$ is the actual output of the APA, and $\overline{y}\left(n\right)$ is the output of the APA obtained by model fitting. Thus, the optimal parameters selected for the GMP model are 3, 5, 2, 3, 2, 3, 2, 2, which represent the nonlinear order and memory depth of the MP sub-model, lagging envelope term, and leading envelope term, as well as the additional degrees of freedom of the lagging and leading term. In this paper, experiments were also conducted on the MP model for comparison. For fairness, the nonlinear order and memory depth were chosen as three and five, respectively, which are consistent with the MP sub-model of the GMP model. As can be seen from the results in Figure 14 and

Table 1. Measured ACPR and EVM results with different methods for different input power levels from VSG.

Power Level	${\mathit{P}}_{\mathbf{in}}$: −25 dBm		${\mathit{P}}_{\mathbf{in}}$: −24 dBm
Scheme	ACPR (dBc) Lower & Upper	EVM	ACPR (dBc) Lower & Upper	EVM
Original signal (APA input)	−45.48/−45.93	–	−45.48/−45.93	–
Original signal (APA output)	−34.77/−32.81	11.26%	−33.36/−31.58	12.18%
w/Ideal DPD (GMP)	−36.50/−36.56	4.11%	−36.42/−36.36	4.46%
w/JSG-DPD (GMP STS1000)	−36.43/−36.20	4.33%	−36.55/−36.23	4.67%
w/JSG-DPD (GMP STS100)	−36.12/−35.44	4.73%	−35.71/−35.63	4.84%
w/JSG-DPD (GMP STS10)	−35.10/−34.34	4.95%	−34.46/−35.06	5.84%
w/JSG-DPD (GMP w/o STS)	−30.68/−32.14	10.68%	−30.14/−32.99	10.51%
w/Ideal DPD (MP)	−35.00/−34.95	4.83%	−36.96/−35.19	4.65%
w/JSG-DPD (MP STS1000)	−34.80/−34.38	4.56%	−36.85/−35.23	4.88%
w/JSG-DPD (MP STS100)	−34.63/−33.35	5.44%	−36.22/−35.64	5.13%
w/JSG-DPD (MP STS10)	−35.27/−33.08	5.80%	−35.63/−35.83	6.22%
w/JSG-DPD (MP w/o STS)	−35.85/−35.24	10.31%	−34.52/−35.27	11.44%

, for the case of stronger nonlinearity (input power level: −24 dBm), the application of the proposed JSG-DPD method improves the upper and lower ACPR average performance by nearly 4 dB for a training sequence superposition of 1000 or 100 times with the GMP model, especially the EVM performance by more than 7.5%, which undoubtedly enhances the quality of the transmitted signal significantly. The ground station is more concerned about the improvement status of EVM than ACPR. When the number of training sequence superposition is 10, there is also an improvement of nearly 6.5% in EVM, which is still promising. In contrast, the results without the STS method improved the EVM slightly. In addition, for the results of the MP model, the improvement in EVM is not as good as that of the GMP model, with a difference of about 0.2% to 0.4%. Nevertheless, it is noteworthy that using the MP model without the STS method still improves the ACPR by 2.5 dB, while the ACPR results with the GMP model without the STS method have deteriorated to the extent that it seriously affects the signal transmission in the adjacent channels.

For the case of slightly weaker nonlinearity (input power level: −25 dBm), applying the proposed JSG-DPD method, the EVM performance is improved by 6.3% to 6.9% for the training sequence superpositions of 1000, 100, and 10 times with the GMP model. For the results of the MP model, the improvement of EVM is not as good as that of the GMP model, and the difference is about 0.2–0.8%. Moreover, the MP model is still more robust than the GMP model for ACPR improvement, which might depend on its low number of parameters and insensitivity to low SNR responses.

In summary, the problem of low SNR due to AWGN channels can be effectively solved after 1000 or 100 times of superimposed training sequences. For the 10 to 15 min of LEO satellite transit, the pilot sequence length of 40,000 times 1000 or 100 is acceptable, accounting for less than 1 min. More critically, it is not necessary to re-adjust the DPD coefficients for each transit. However, only when the communication quality degrades significantly and the BER of the ground station crosses the preset threshold. It is at this point that the DPD coefficients are re-adjusted based on the operational status of the space-borne APA using the proposed JSG-DPD technique to restore the normal transmission state, allowing the linearity and power efficiency of the space-borne APA to be enhanced without taking any additional space-borne resources. Although the STS method used in this paper to improve SNR appears simple, it validates the feasibility of the proposed JSG-DPD technique. There is still a lot of room for further exploration and performance improvement, such as adopting deep learning approaches.

5. Conclusions

In this paper, a joint satellite-transmitter and ground-receiver (JSG) digital pre-distortion (DPD) (JSG-DPD) technique is proposed to linearize a low Earth orbit (LEO) space-borne active phased array (APA). The method takes the approach of DPD coefficients extraction at the ground station, which saves a complete set of feedback loop at the satellite-transmitter side compared to the conventional DPD techniques. The issue of sidelobe information drowning in the additive white Gaussian noise (AWGN) is addressed by employing the superimposed training sequences (STS) method. The proposed method is experimentally verified to improve the adjacent channel power ratio (ACPR) by 4 dB, especially the error vector amplitude (EVM) greatly by 7.5%. In addition, the performance difference between the GMP model and the MP model is analytically compared. The proposed technique provides a feasible means for the linearization of space-borne power amplifiers (PAs) or APAs. In the future, we will address the problem of accurate synchronization of training sequences and seek opportunities for in-orbit validation in actual LEO satellite communication projects.