Deep-Learning-Based Method for Estimating Permittivity of Ground-Penetrating Radar Targets
Abstract
:1. Introduction
- (1)
- A method combining the physical mechanism of GPR and using CNN to detect the high-level features of B-SCAN images is proposed to effectively obtain the main parameter information for inversion of the GPR scattering field.
- (2)
- We propose a regression-model-based approach to estimate the permittivity of subsurface targets. Specifically, by analyzing the physical characteristics of the GPR echo data in the reflection measurement mode [36], the target scattering intensity, buried depth, and the permittivity of the background medium are used as input parameters of the regression network, and the estimation result of the target permittivity is output by non-linear mapping transformation.
- (3)
- According to the MAXWELL equations, we discuss the validity of using regression models to estimate target permittivity after generalizing the subsurface half-space from a single-layer medium to a layered structure, which is verified by numerical simulations and field experiments.
2. Materials and Methods
2.1. GPR Physical Mechanism
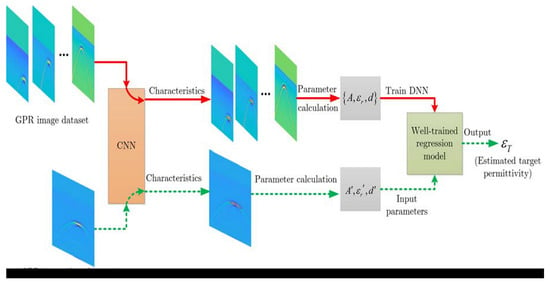
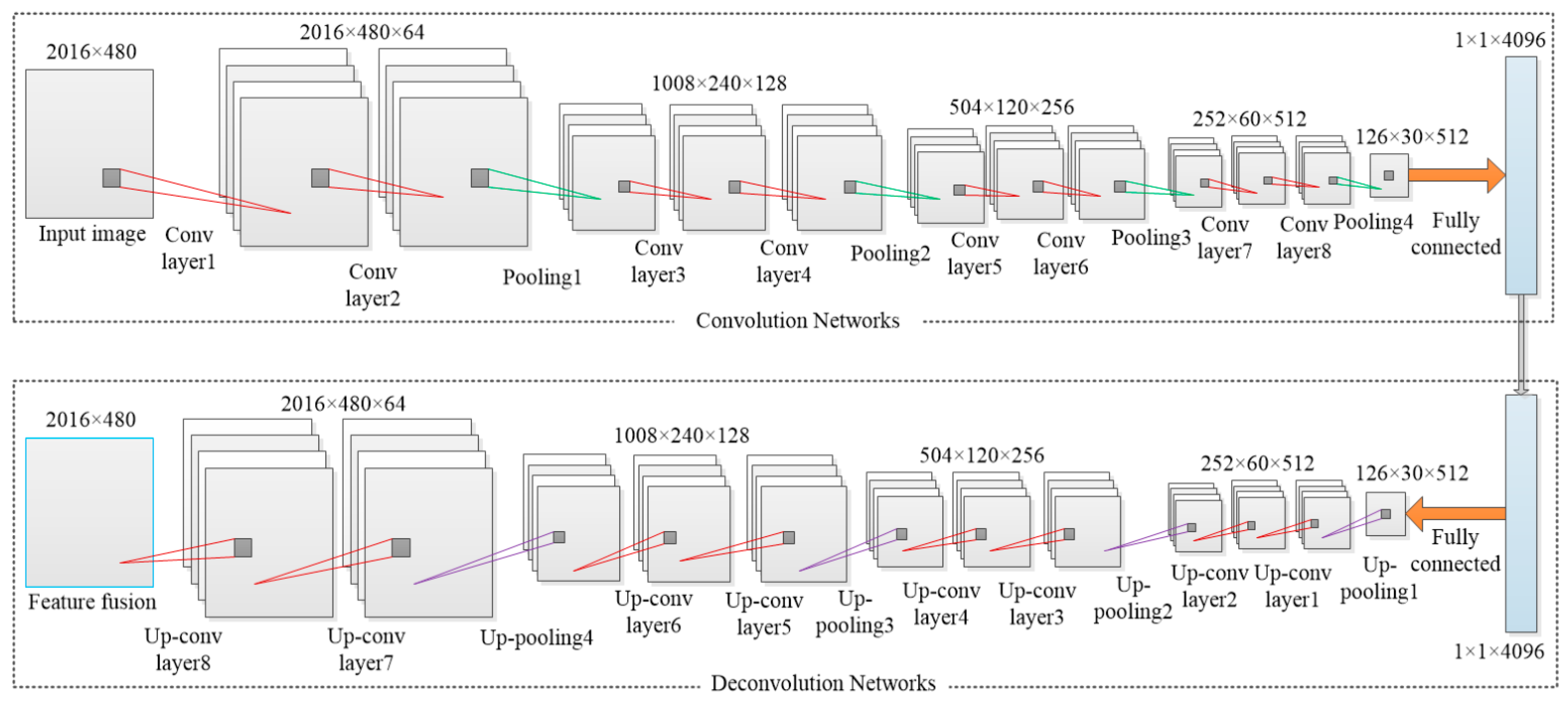
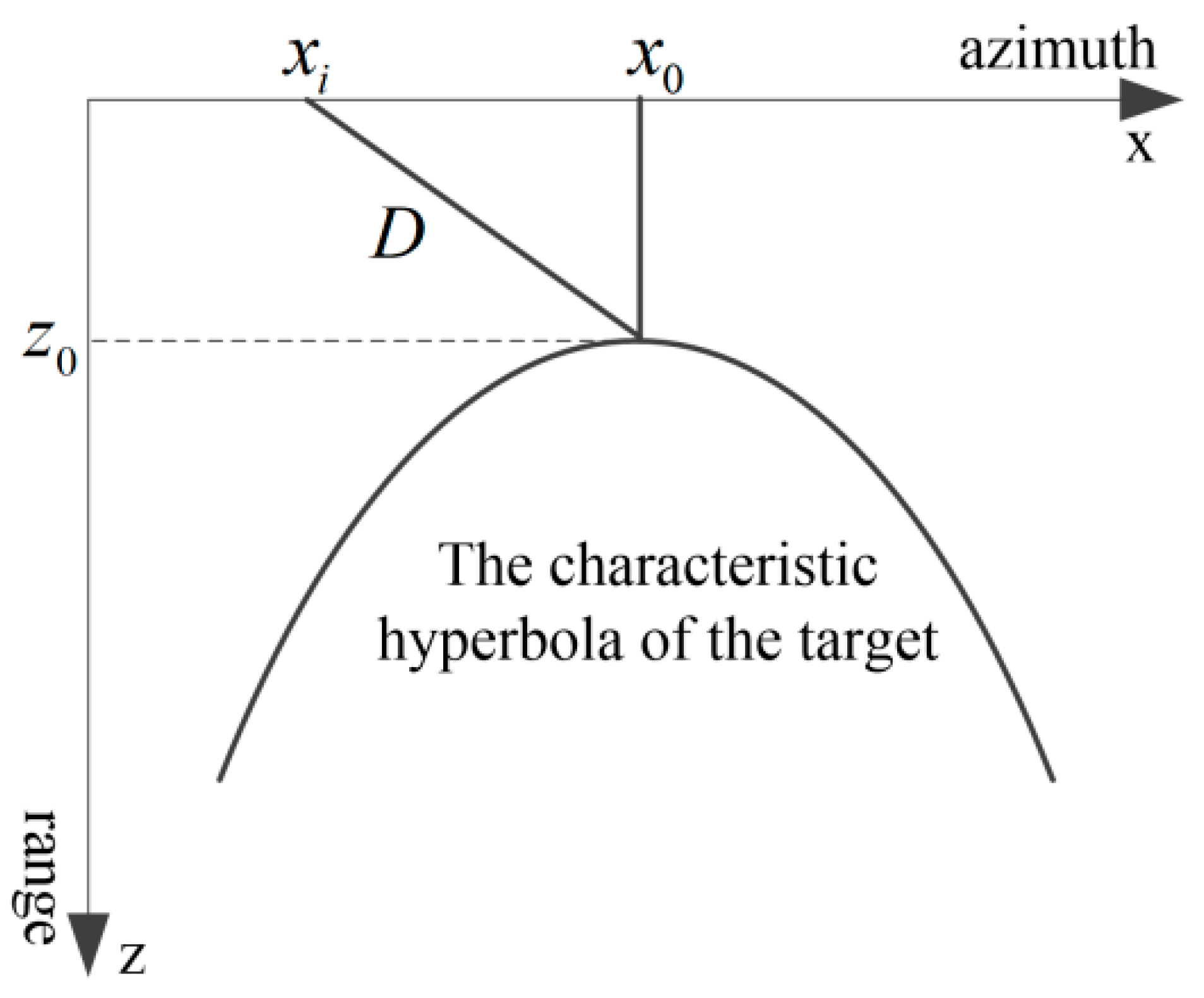
2.2. CNN-Based Feature Hyperbola Detection Method
2.3. Background Dielectric Permittivity Calculation Method
2.4. Regression Network-Based Permittivity Estimation Method
- (1)
- Make a data set for training the DNN:
- (2)
- The non-linear mapping is expanded into an layer DNN, and the network model is trained on the example set. In general, empirical risk can be used to evaluate the results of model training, that is, to measure the degree of fit between the model and the training set in an average sense, where the empirical risk can be defined as
- (3)
- For the observation value of the input DNN, through non-linear mapping transformation, the output value is the parameter inversion result.
3. Results and Analysis
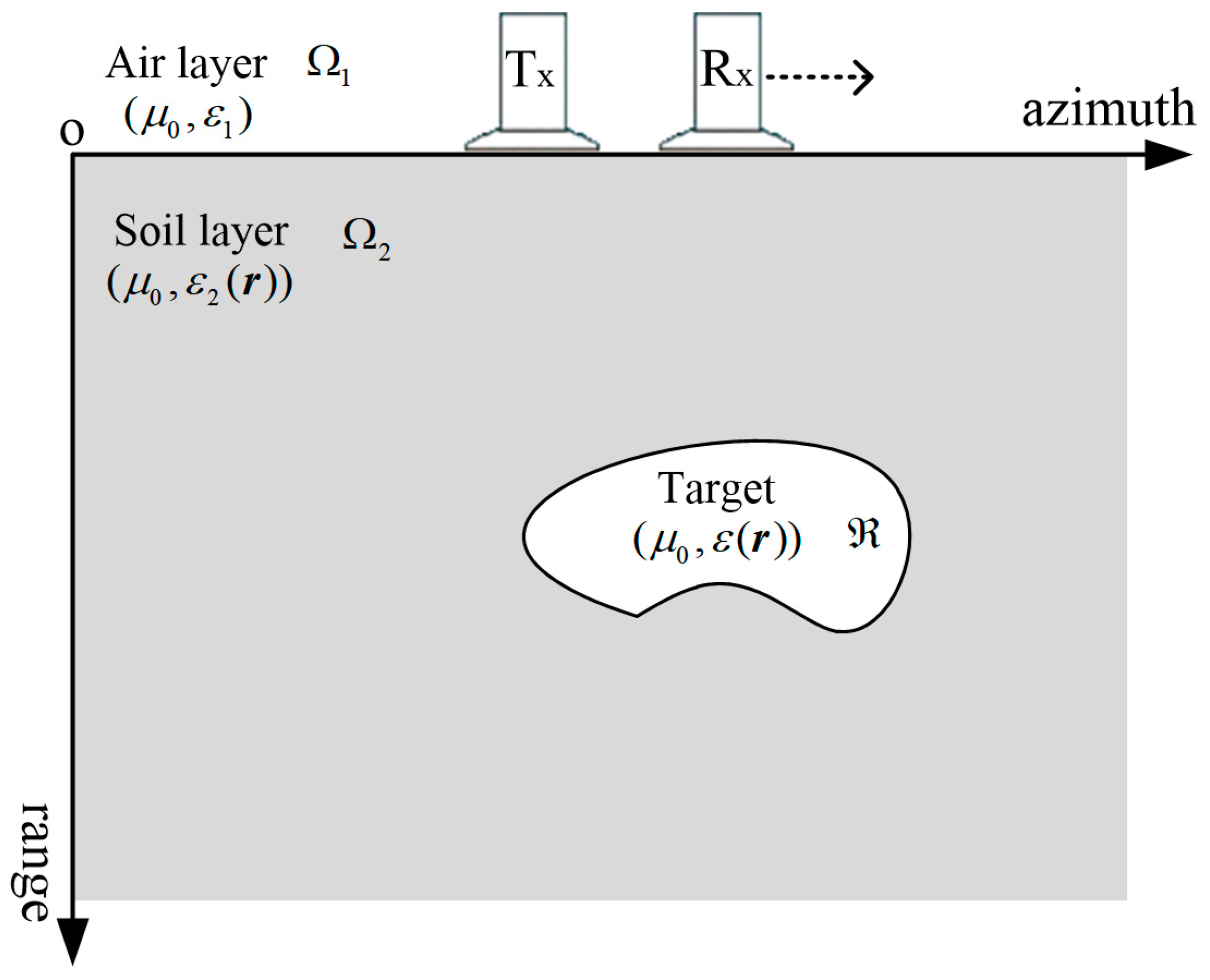
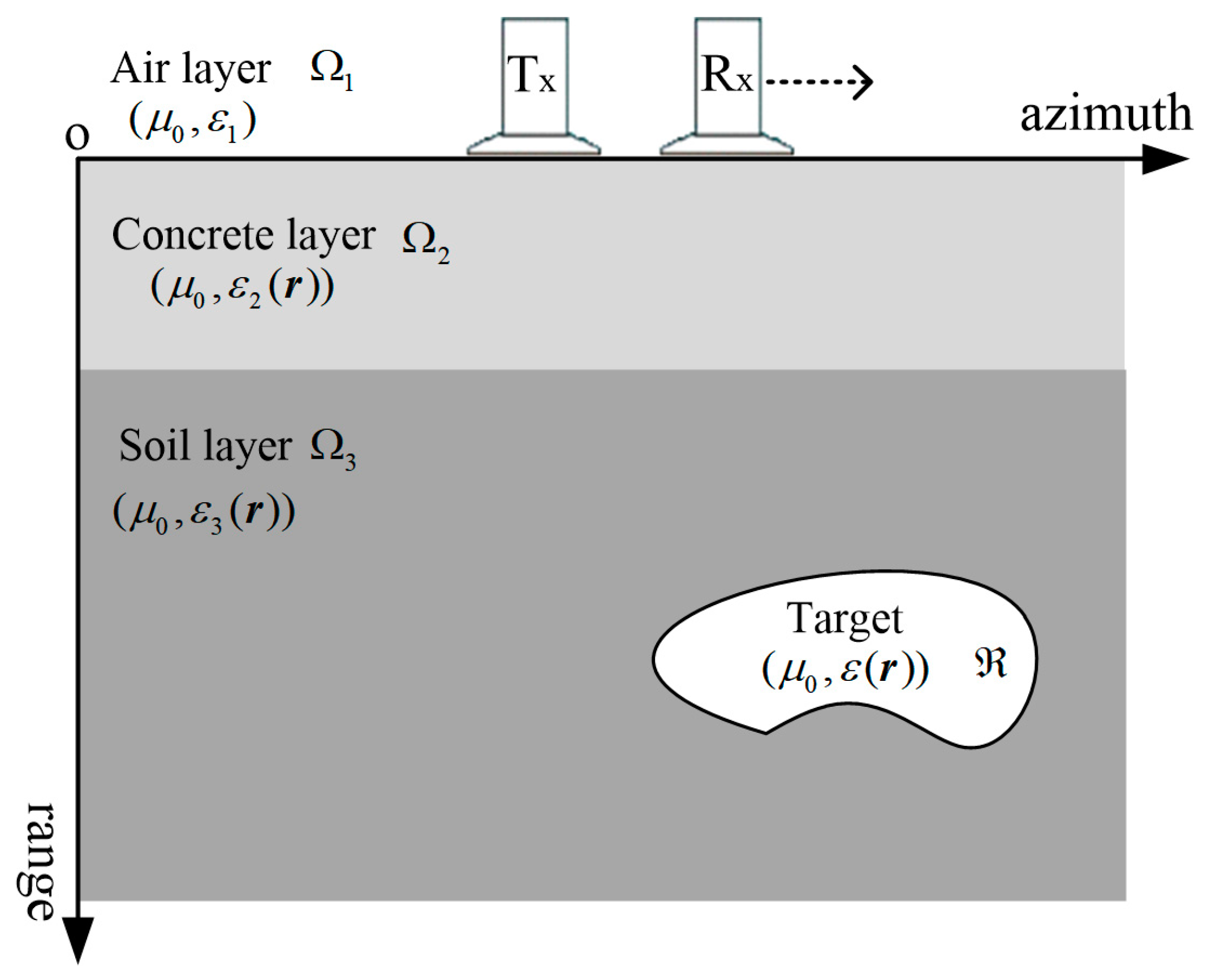
3.1. Numerical Simulation Description
- (1)
- The width along the azimuth direction is 5 m, the depth along the range direction is 2 m, and the average thickness of the concrete layer is 0.25 m.
- (2)
- There are 4–6 concave and convex blocks with a maximum width and height of 0.3 m and 0.05 m, respectively, which are randomly generated at the lower boundary of the concrete layer to simulate the rough interface between concrete and soil.
- (3)
- The permittivity of soil along the range direction is generated in a random way; considering the influence of water content in soil at different depths, the range is set to 9–25.
- (4)
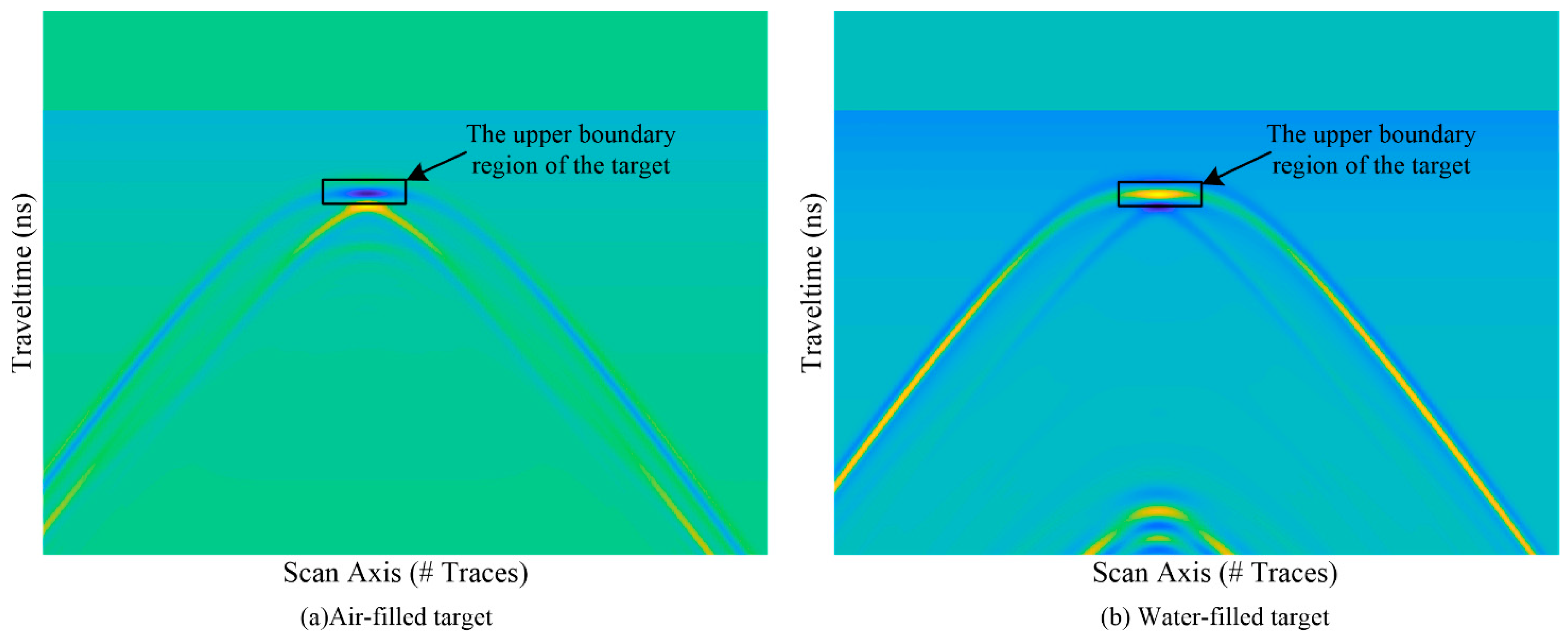
- The number of targets is set to 1 or 2, and the shape is set to a rectangle (the size of the air-filled target is randomly generated between 0.3–0.5 m in width and 0.3–0.4 m in height; the width and height of the water-filled target are randomly generated between 0.25–0.65 m and 0.25–0.45 m, respectively). A single target is randomly distributed in the soil layer, and two targets are randomly distributed in the left and right half of the soil layer, respectively.
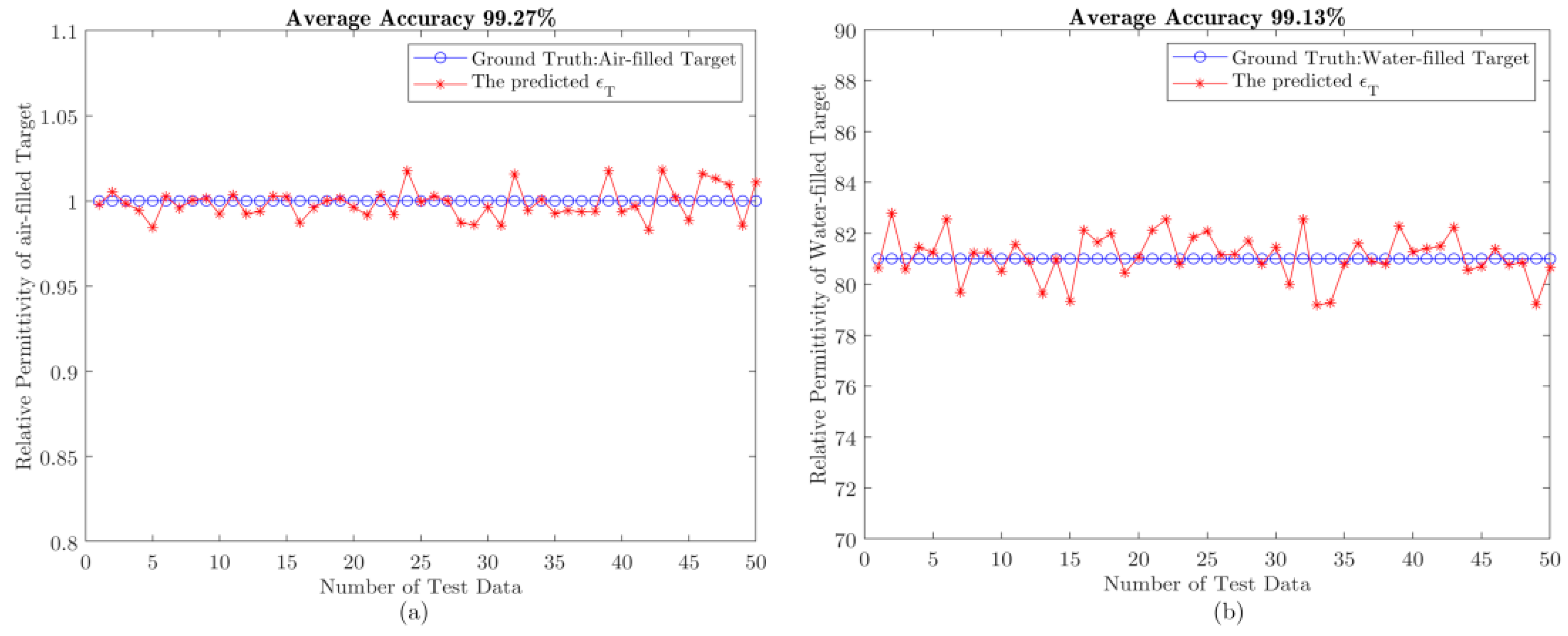
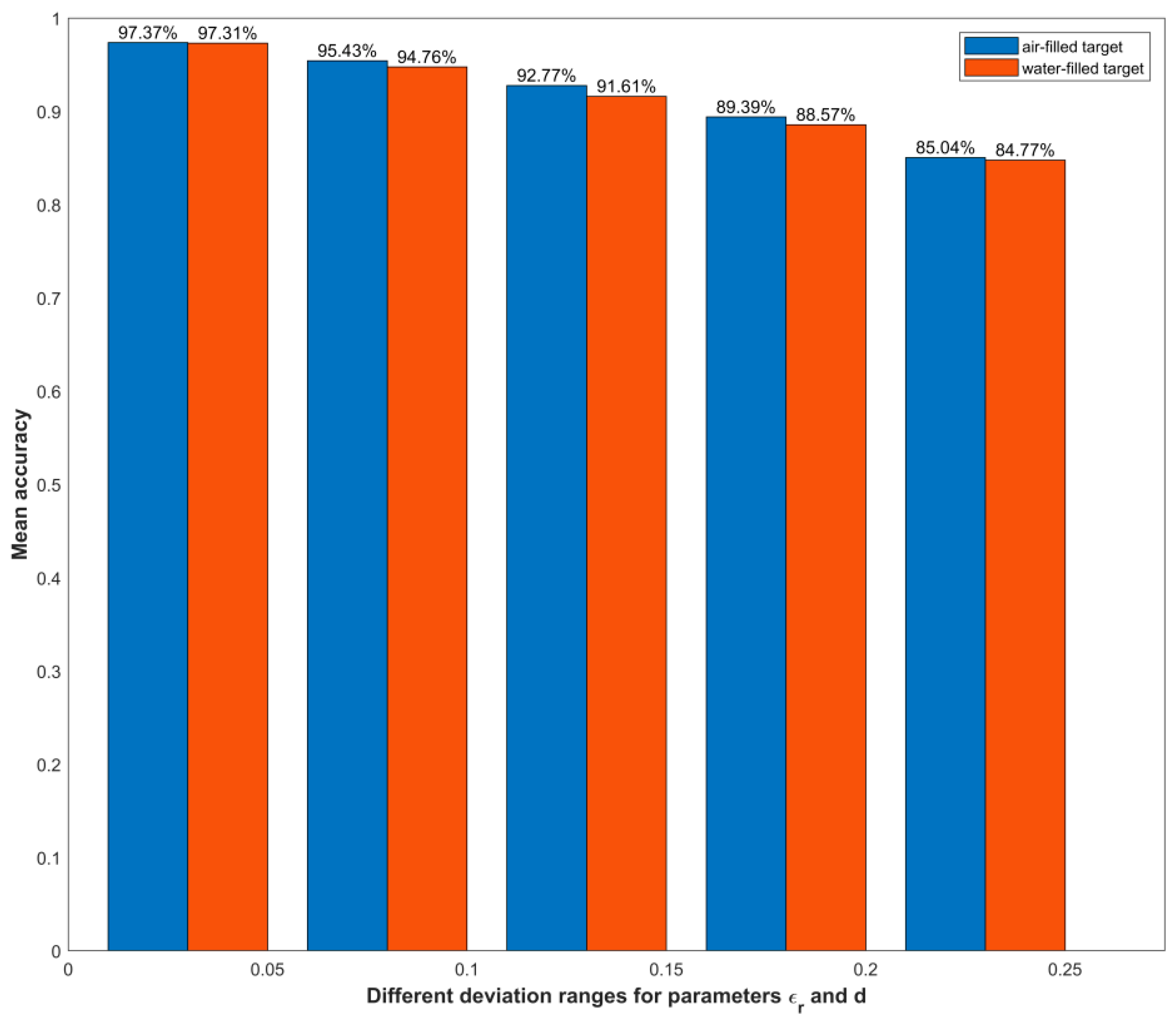
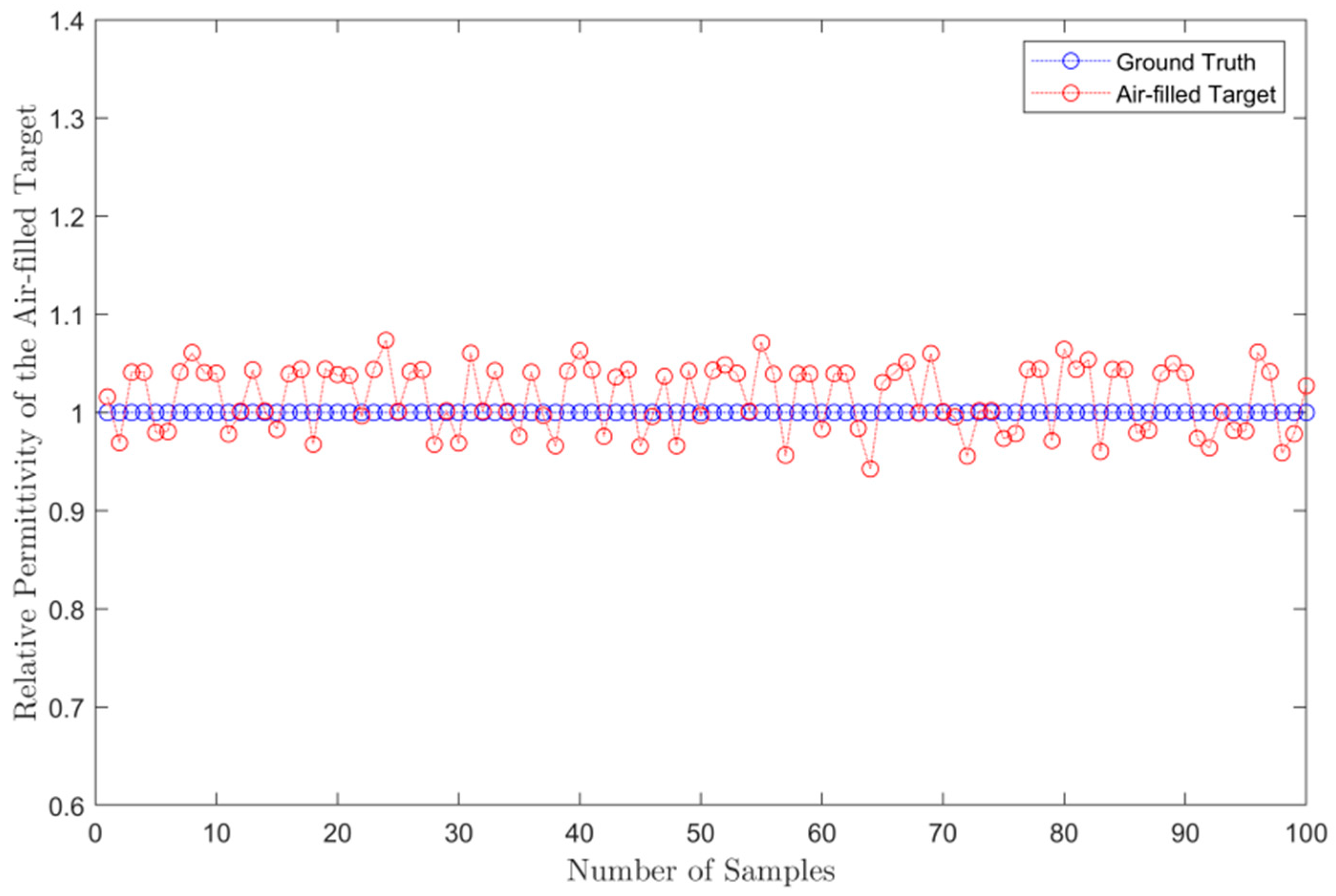
3.2. Simulation Results and Analysis
3.2.1. Single-Layer Background Medium Scene
3.2.2. Layered Background Medium Scene
3.3. Field Results and Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shen, R.; Zhao, Y.; Hu, S.; Li, B.; Bi, W. Reverse-time migration imaging of ground-penetrating radar in NDT of reinforced concrete structures. Remote Sens. 2021, 13, 2020. [Google Scholar] [CrossRef]
- Liu, S.; Lu, Q.; Li, H.; Wang, Y. Estimation of moisture content in railway subgrade by ground penetrating radar. Remote Sens. 2020, 12, 2912. [Google Scholar] [CrossRef]
- Mangel, A.R.; Moysey, S.; Bradford, J. Reflection tomography of time-lapse GPR data for studying dynamic unsaturated flow phenomena. Hydrol. Earth Syst. Sci. 2020, 24, 159–167. [Google Scholar] [CrossRef]
- Liu, T.; Klotzsche, A.; Pondkule, M.; Vereecken, H.; Su, Y.; van der Kruk, J. Radius estimation of subsurface cylindrical objects from ground-penetrating-radar data using full-waveform inversion. Geophysics 2018, 83, H43–H54. [Google Scholar] [CrossRef]
- Zhong, S.; Wang, Y.; Zheng, Y.; Chang, X. Reverse time migration of ground-penetrating radar with full wavefield decomposition based on the Hilbert transform. Geophys. Prospect. 2020, 68, 1097–1112. [Google Scholar] [CrossRef]
- Xiao, J.; Tang, X.; Liang, B.; Han, F.; Liu, H.; Liu, Q.H. Subsurface reconstruction from GPR data by 1-D DBIM and RTM in frequency domain. IEEE Geosci. Remote Sens. Lett. 2020, 17, 582–586. [Google Scholar] [CrossRef]
- Wang, H.H.; Liu, H.; Cui, J.; Hu, X.Y.; Sato, M. Velocity analysis of CMP gathers acquired by an array GPR system ‘Yakumo’: Results from field application to tsunami deposits. Explor. Geophys. 2018, 49, 669–674. [Google Scholar] [CrossRef]
- Vânia, M.; Fontul, S.; Solla, M.; Antunes, M.D.L. Evaluation of the feasibility of common mid-point approach for air–coupled GPR applied to road pavement assessment. Measurement 2018, 128, 295–305. [Google Scholar] [CrossRef]
- Monte, L.; Erricolo, D.; Soldovieri, F.; Wicks, M.C. Radio frequency tomography for tunnel detection. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1128–1137. [Google Scholar] [CrossRef]
- Qu, L.; Yin, Y.; Sun, Y.; Zhang, L. Diffraction tomographic ground-penetrating radar multibistatic imaging algorithm with compressive frequency measurements. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2011–2015. [Google Scholar] [CrossRef]
- Zhou, Z.; Klotzsche, A.; Schmack, J.; Vereecken, H.; Van Der Kruk, J. Improvement of ground-penetrating radar full-waveform inversion images using cone penetration test data. Geophysics 2021, 86, H13–H25. [Google Scholar] [CrossRef]
- Feng, D.; Wang, X.; Zhang, B. A frequency-domain quasi-newton-based biparameter synchronous imaging scheme for ground-penetrating radar with applications in full waveform inversion. IEEE Trans. Geosci. Remote Sens. 2021, 59, 1949–1966. [Google Scholar] [CrossRef]
- Van den Berg, P.M.; Abubakar, A. Contrast source inversion method: State of art. Prog. Electromagn. 2001, 34, 189–218. [Google Scholar] [CrossRef]
- Babcock, E.; Bradford, J.H. Reflection waveform inversion of ground-penetrating radar data for characterizing thin and ultrathin layers of nonaqueous phase liquid contaminants in stratified media. Geophysics 2015, 80, H1–H11. [Google Scholar] [CrossRef]
- Feng, D.S.; Wang, X.; Zhang, B. Improving reconstruction of tunnel lining defects from ground-penetrating radar profiles by multi-scale inversion and bi-parametric full-waveform inversion. Adv. Eng. Inform. 2019, 41, 100931. [Google Scholar] [CrossRef]
- Feng, D.S.; Ding, S.Y.; Wang, X. Wavefield reconstruction inversion of GPR data for permittivity and conductivity models in the frequency domain based on modified total variation regularization. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Persico, R.; Bernini, R.; Soldovieri, F. The role of the measurement configuration in inverse scattering from buried objects under the born approximation. IEEE Trans. Antennas Propag. 2005, 53, 1875–1887. [Google Scholar] [CrossRef]
- Oliveri, G.; Poli, L.; Rocca, P.; Massa, A. Bayesian compressive optical imaging within the Rytov approximation. Opt. Lett. 2012, 37, 1760–1762. [Google Scholar] [CrossRef]
- Yang, Y.; Lai, B.; Soatto, S. DyStaB: Unsupervised object segmentation via dynamic-static bootstrapping. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021. [Google Scholar] [CrossRef]
- Fan, Q.; Zhuo, W.; Tang, C.K.; Tai, Y.W. Few-shot object detection with attention-RPN and multi-relation detector. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020. [Google Scholar] [CrossRef]
- Li, H.; Wu, G.; Zheng, W.S. Combined depth space based architecture search for person re-identification. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021. [Google Scholar] [CrossRef]
- Zhou, R.S.; Yao, X.M.; Wang, Y.J.; Hu, G.M.; Yu, F.C. Seismic fault detection with progressive transfer learning. Acta Geophys. 2021, 69, 2187–2203. [Google Scholar] [CrossRef]
- Gao, K.; Huang, L.; Zheng, Y. Fault detection on seismic structural images using a nested residual U-net. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Wrona, T.; Pan, I.; Gawthorpe, R.L.; Fossen, H. Seismic facies analysis using machine learning. Geophysics 2018, 83, O83–O95. [Google Scholar] [CrossRef]
- Wang, Z.; Li, F.; Taha, T.R.; Arabnia, H.R. Improved automating seismic facies analysis using deep dilated attention autoencoders. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Long Beach, CA, USA, 15–20 June 2019. [Google Scholar] [CrossRef]
- Pham, M.T.; Lefèvre, S. Buried object detection from B-scan ground penetrating radar data using Faster-RCNN. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018. [Google Scholar] [CrossRef]
- Lei, W.T.; Hou, F.F.; Xi, J.C.; Tan, Q.Y. Automatic hyperbola detection and fitting in GPR B-SCAN image. Autom. Constr. 2019, 106, 102839. [Google Scholar] [CrossRef]
- Yang, J.; Duan, Y.L. Wavelet scattering network-based machine learning for ground penetrating radar imaging: Application in pipeline identification. Remote Sens. 2020, 12, 3655. [Google Scholar] [CrossRef]
- Tong, Z.; Gao, J.; Zhang, H. Recognition location measurement and 3D reconstruction of concealed cracks using convolutional neural networks. Constr. Build. Mater. 2017, 146, 775–787. [Google Scholar] [CrossRef]
- Zhang, W.; Gao, J.; Gao, Z.; Chen, H. Adjoint-driven deep-learning seismic full-waveform inversion. IEEE Trans. Geosci. Remote Sens. 2021, 59, 8913–8932. [Google Scholar] [CrossRef]
- Ren, Y.X.; Liu, B. Seismic data inversion with acquisition adaptive convolutional neural network for geologic forward prospecting in tunnels. Geophysics 2021, 86, 659–670. [Google Scholar] [CrossRef]
- Zhang, H.; Yang, P.; Liu, Y.; Luo, Y.; Xu, J. Deep learning-based low-frequency extrapolation and impedance inversion of seismic data. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Liu, B.; Ren, Y.X.; Liu, H.C.L. GPRInvNet: Deep learning-based ground penetrating radar data inversion for tunnel lining. IEEE Trans. Geosci. Remote Sens. 2021, 59, 8305–8325. [Google Scholar] [CrossRef]
- Leong, Z.X.; Zhu, T. Direct velocity inversion of ground penetrating radar data using GPRNet. J. Geophys. Res. Solid Earth 2021, 126, 21047. [Google Scholar] [CrossRef]
- Ji, Y.T.; Zhang, F.K.; Wang, J.; Wang, Z.F.; Jiang, P.; Liu, H.C.; Sui, Q.M. Deep neural network-based permittivity inversions for ground penetrating radar data. IEEE Sens. J. 2021, 21, 8172–8818. [Google Scholar] [CrossRef]
- Wang, H.; Ouyang, S.; Liao, K.F.; Jing, N.L. GPR B-SCAN image hyperbola detection method based on deep learning. Actc Electron. Sin. 2021, 49, 953–963. [Google Scholar] [CrossRef]
- Wang, H.; Ouyang, S.; Liu, Q.H.; Liao, K.F.; Zhou, L.J. Buried target detection method for ground penetrating radar based on deep learning. J. Appl. Remote Sens. 2022, 16, 018503. [Google Scholar] [CrossRef]
- Wang, H.; Ouyang, S.; Liu, Q.H.; Liao, K.F.; Zhou, L.J. Structure feature detection method for ground penetrating radar two-dimensional profile image based on deep learning. J. Electron. Inf. Technol. 2022, 44, 1284–1294. [Google Scholar] [CrossRef]
- Mendonca, J.T.; Shukla, P.K. Time Refraction and Time Reflection: Two Basic Concepts. Phys. Scr. 2002, 44, 160–163. [Google Scholar] [CrossRef]
- Balanis, C.A. Advanced Engineering Electromagnetics; Wiley: New York, NY, USA, 1989; pp. 73–84. [Google Scholar]
- Hornik, K.; Stinchcombe, M.; White, H. Universal approximation of an unknown mapping and its derivatives using multilayer feedforward networks. Neural Netw. 1990, 3, 551–560. [Google Scholar] [CrossRef]
- Warren, C.; Giannopoulos, A.; Giannakis, I. GPRMAX: Open source software to simulate electromagnetic wave propagation for ground penetrating radar. Comput. Phys. Commun. 2016, 209, 163–170. [Google Scholar] [CrossRef] [Green Version]
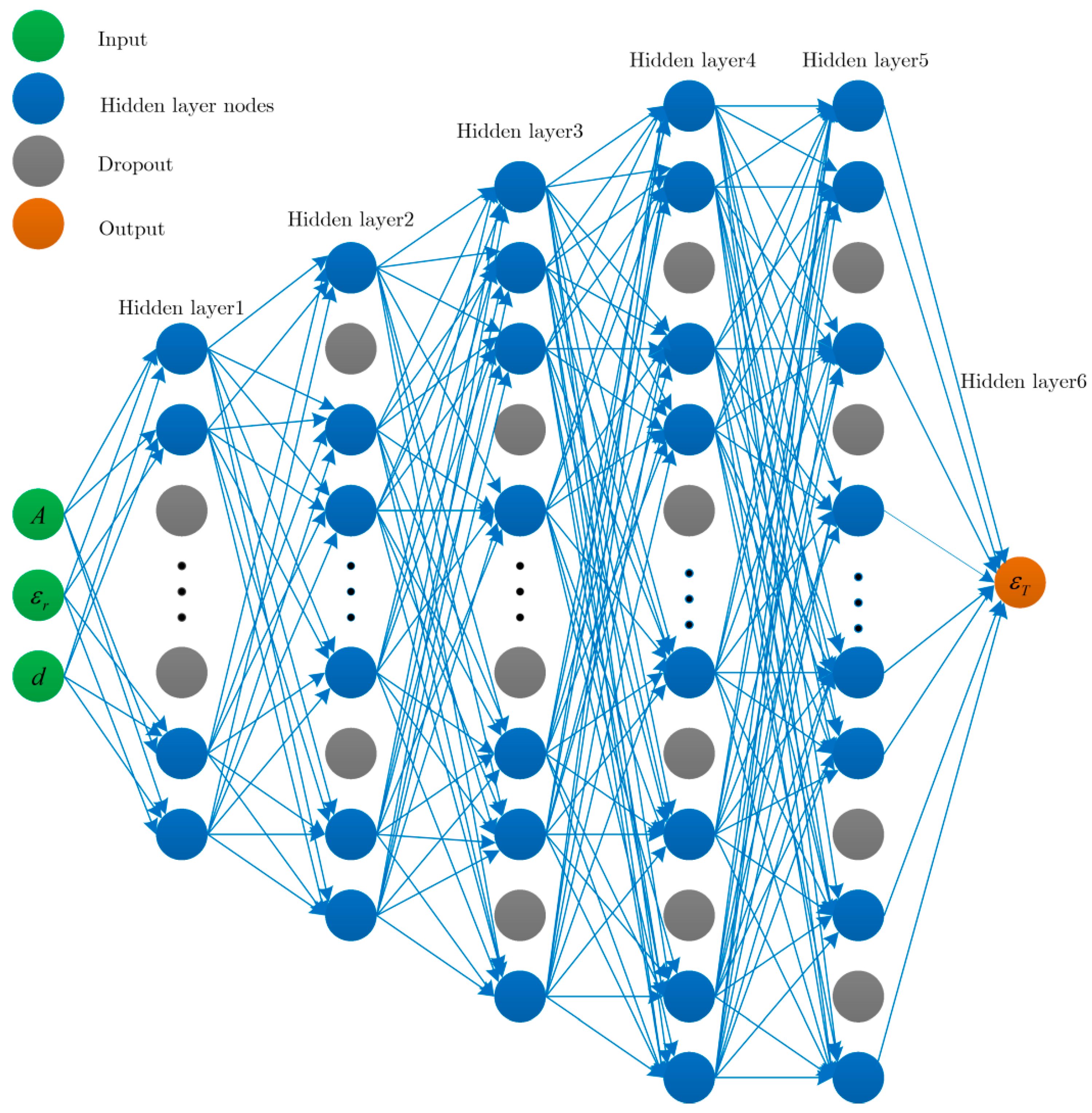



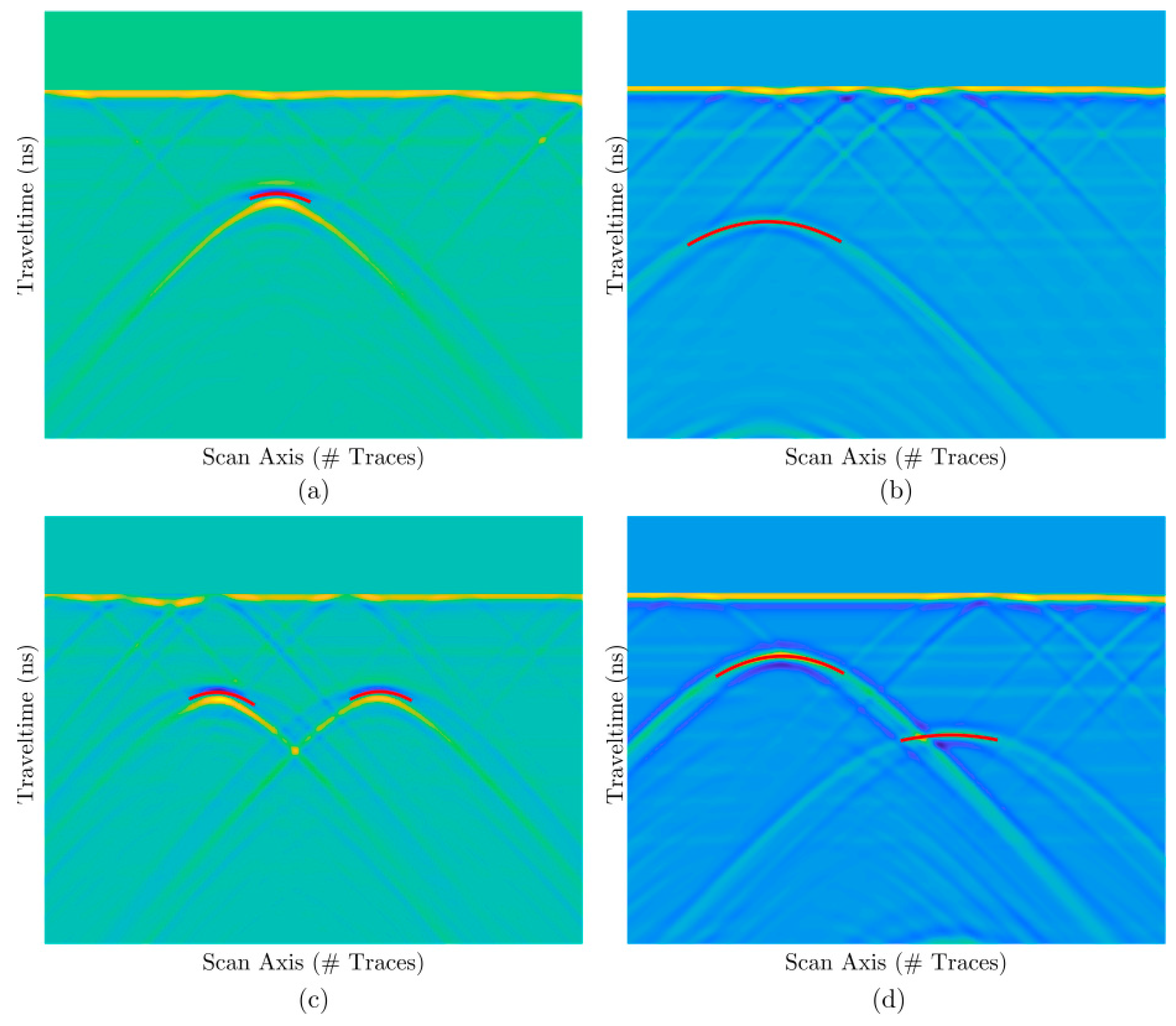
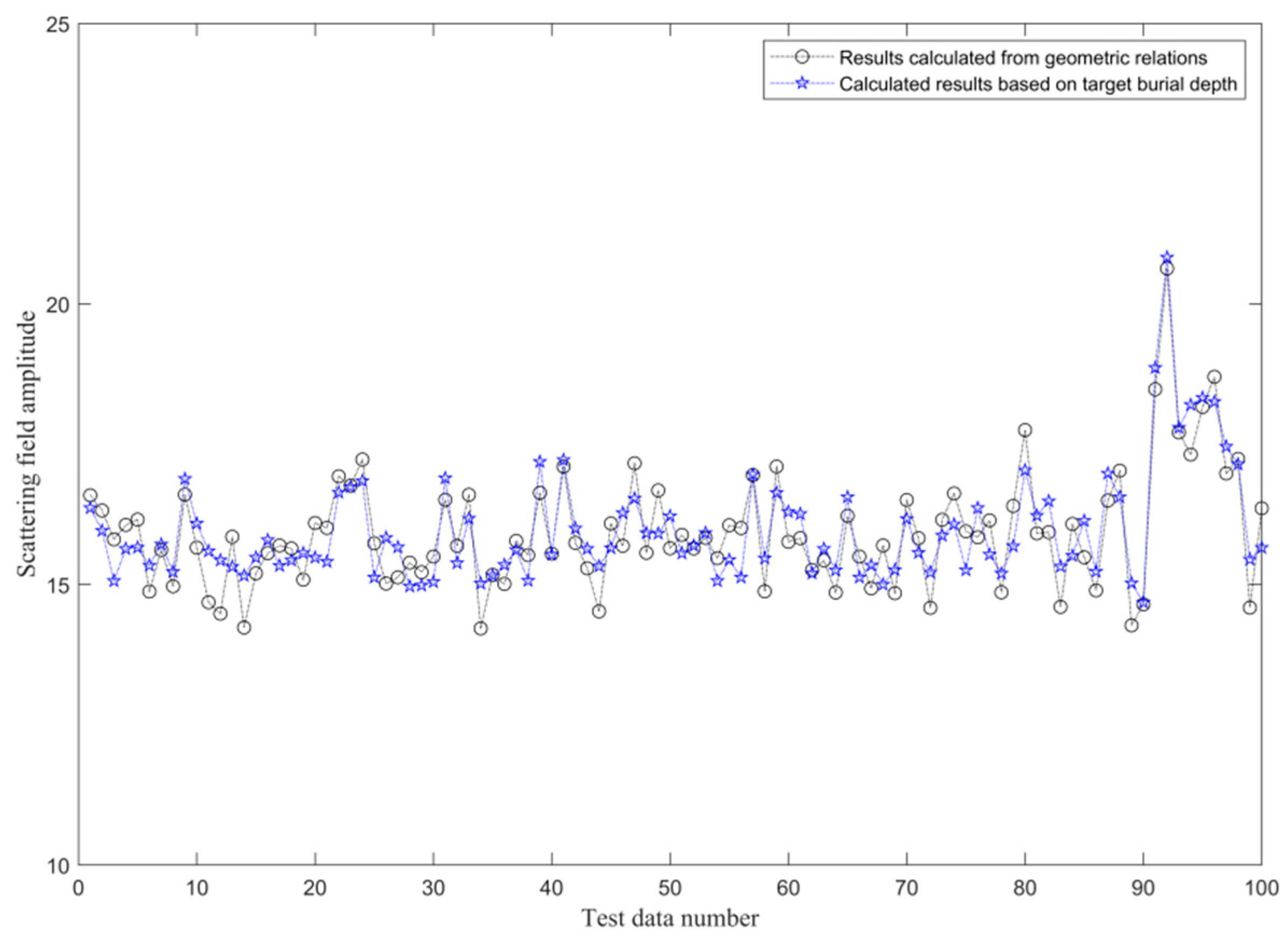
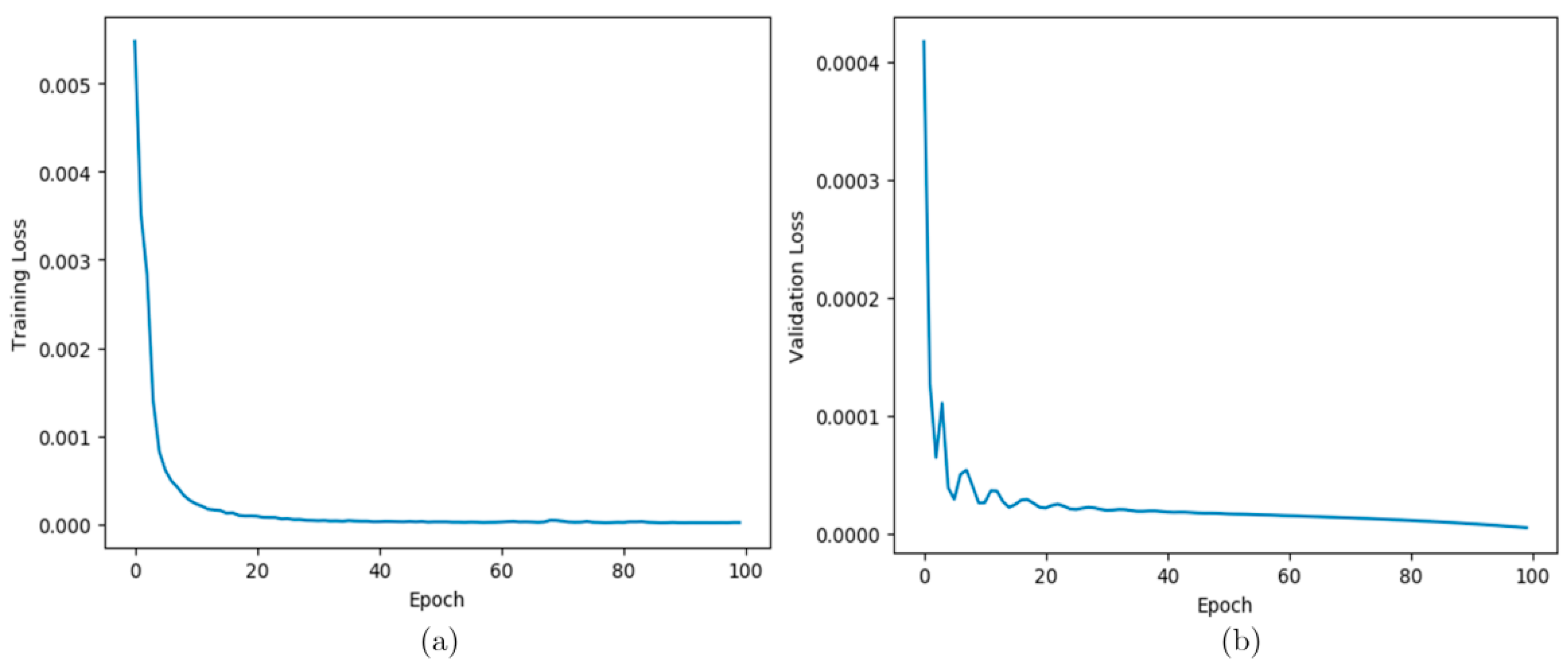
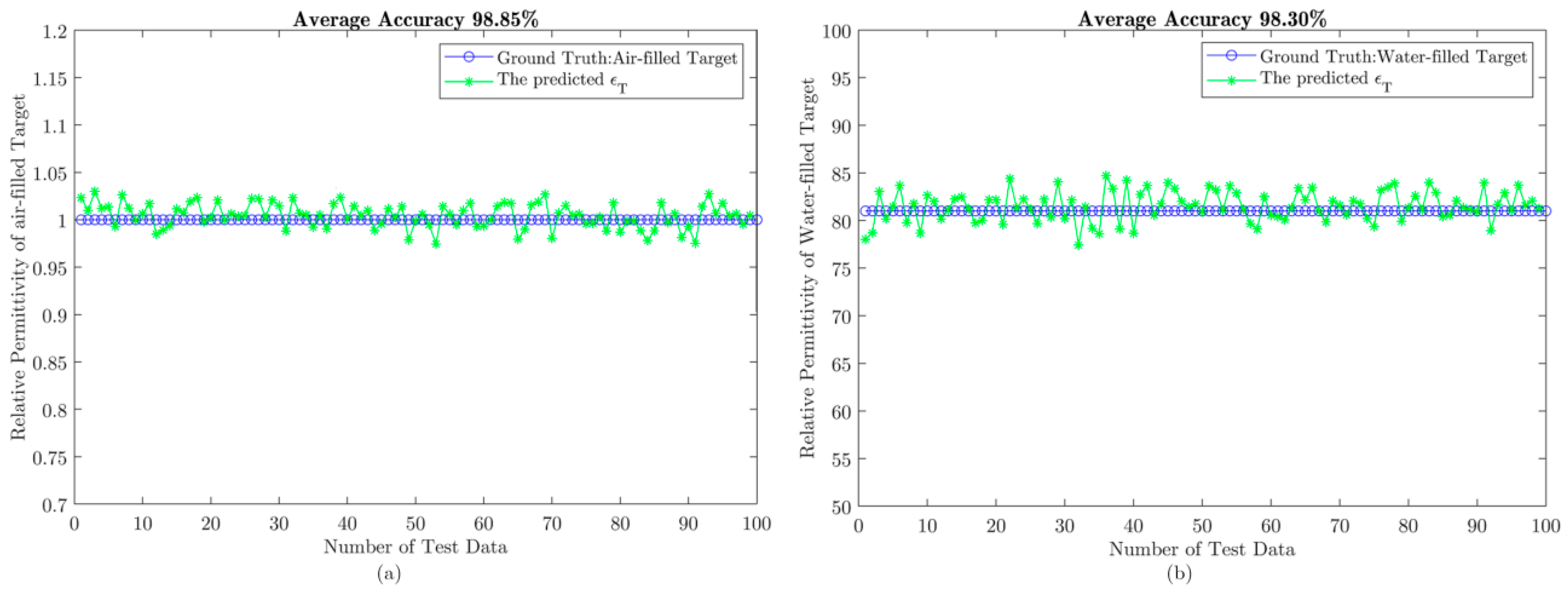

| Layer | Ouput_Dim | Layer Details |
|---|---|---|
| Hidden layer 1 | 64 | Input_dim: 3 Activation: Relu Dropout: 0.2 |
| Hidden layer 2 | 128 | Input_dim: 3 Activation: Relu Dropout: 0.2 |
| Hidden layer 3 | 256 | Input_dim: 3 Activation: Relu Dropout: 0.2 |
| Hidden layer 4 | 512 | Input_dim: 3 Activation: Relu Dropout: 0.3 |
| Hidden layer 5 | 512 | Input_dim: 3 Activation: Relu Dropout: 0.3 |
| Hidden layer 6 | 1 | — |
| Index | Average Accuracy | Estimated Range | Time Consuming | |
|---|---|---|---|---|
| Algorithm | ||||
| FWI-based | 89.13% | 0.86–1.18 | 2820 s | |
| DNN-based | 95.52% | 0.93–1.05 | 0.023 s | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Ouyang, S.; Liu, Q.; Liao, K.; Zhou, L. Deep-Learning-Based Method for Estimating Permittivity of Ground-Penetrating Radar Targets. Remote Sens. 2022, 14, 4293. https://doi.org/10.3390/rs14174293
Wang H, Ouyang S, Liu Q, Liao K, Zhou L. Deep-Learning-Based Method for Estimating Permittivity of Ground-Penetrating Radar Targets. Remote Sensing. 2022; 14(17):4293. https://doi.org/10.3390/rs14174293
Chicago/Turabian StyleWang, Hui, Shan Ouyang, Qinghua Liu, Kefei Liao, and Lijun Zhou. 2022. "Deep-Learning-Based Method for Estimating Permittivity of Ground-Penetrating Radar Targets" Remote Sensing 14, no. 17: 4293. https://doi.org/10.3390/rs14174293
APA StyleWang, H., Ouyang, S., Liu, Q., Liao, K., & Zhou, L. (2022). Deep-Learning-Based Method for Estimating Permittivity of Ground-Penetrating Radar Targets. Remote Sensing, 14(17), 4293. https://doi.org/10.3390/rs14174293