Detection of Vertical Changes in the Ionospheric Electron Density Structures by the Radio Occultation Technique Onboard the FORMOSAT-7/COSMIC2 Mission over the Eruption of the Tonga Underwater Volcano on 15 January 2022
Abstract
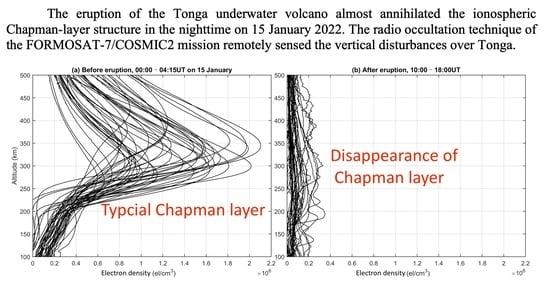
:1. Introduction
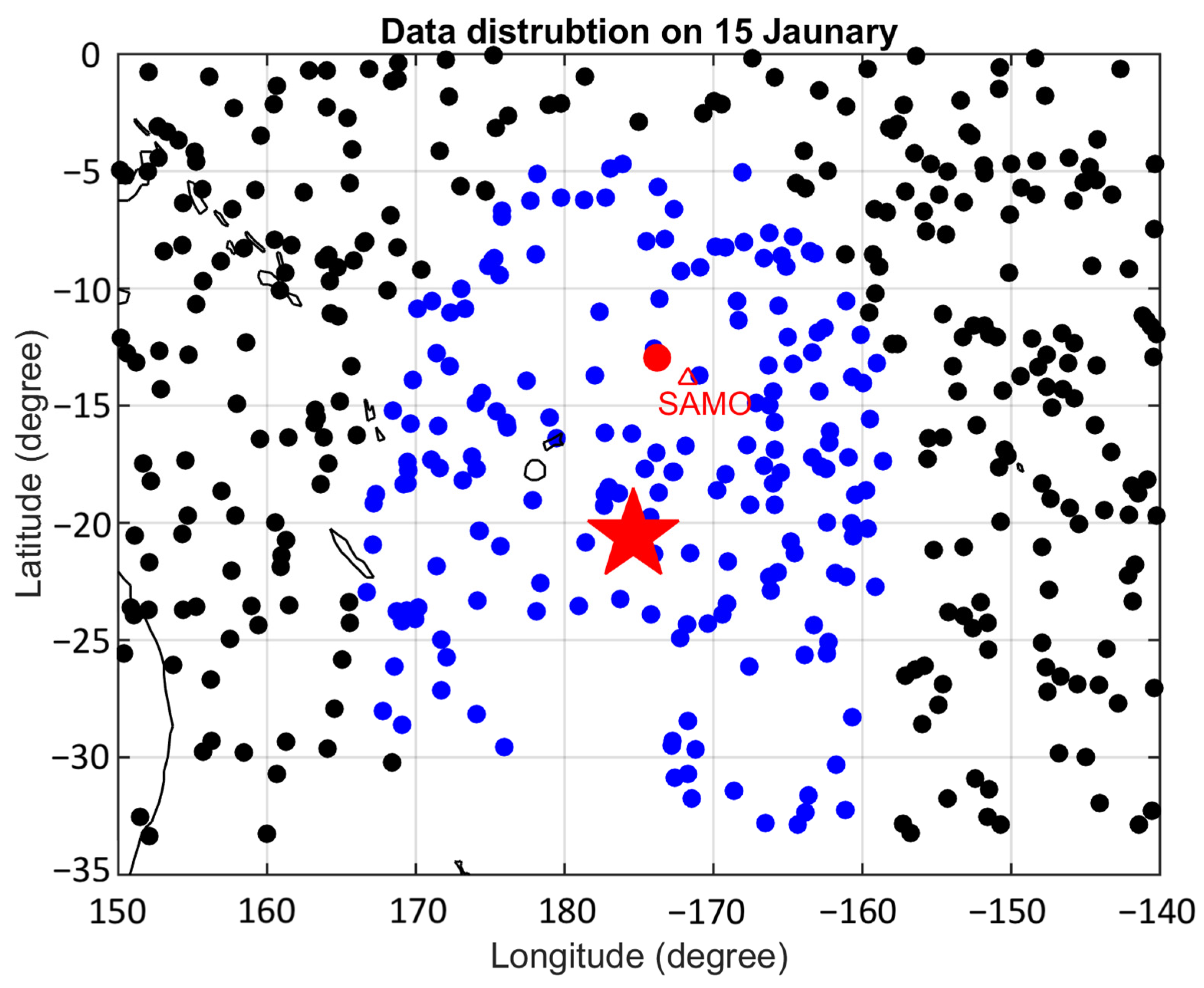
2. Data and Methodology
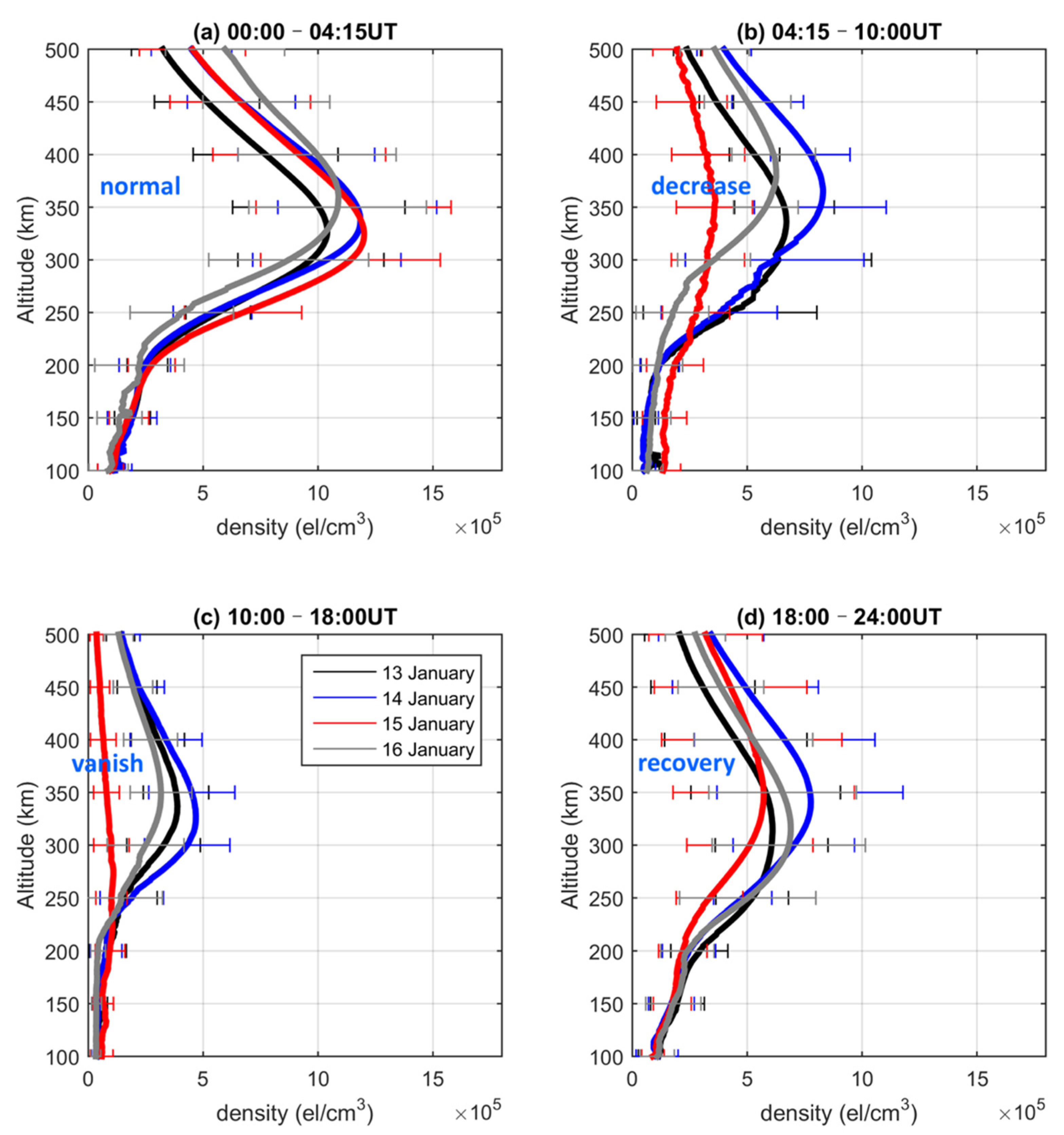
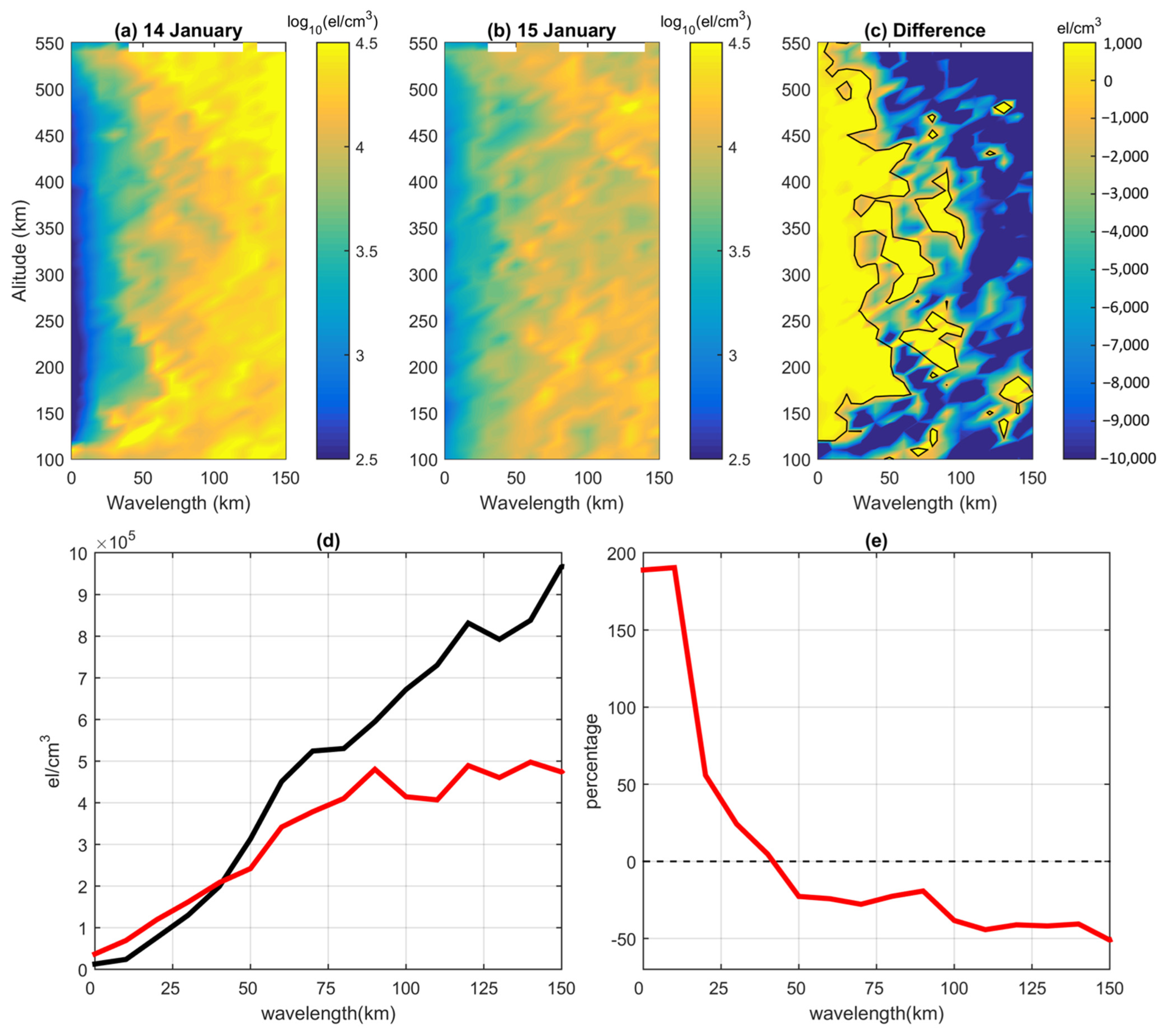
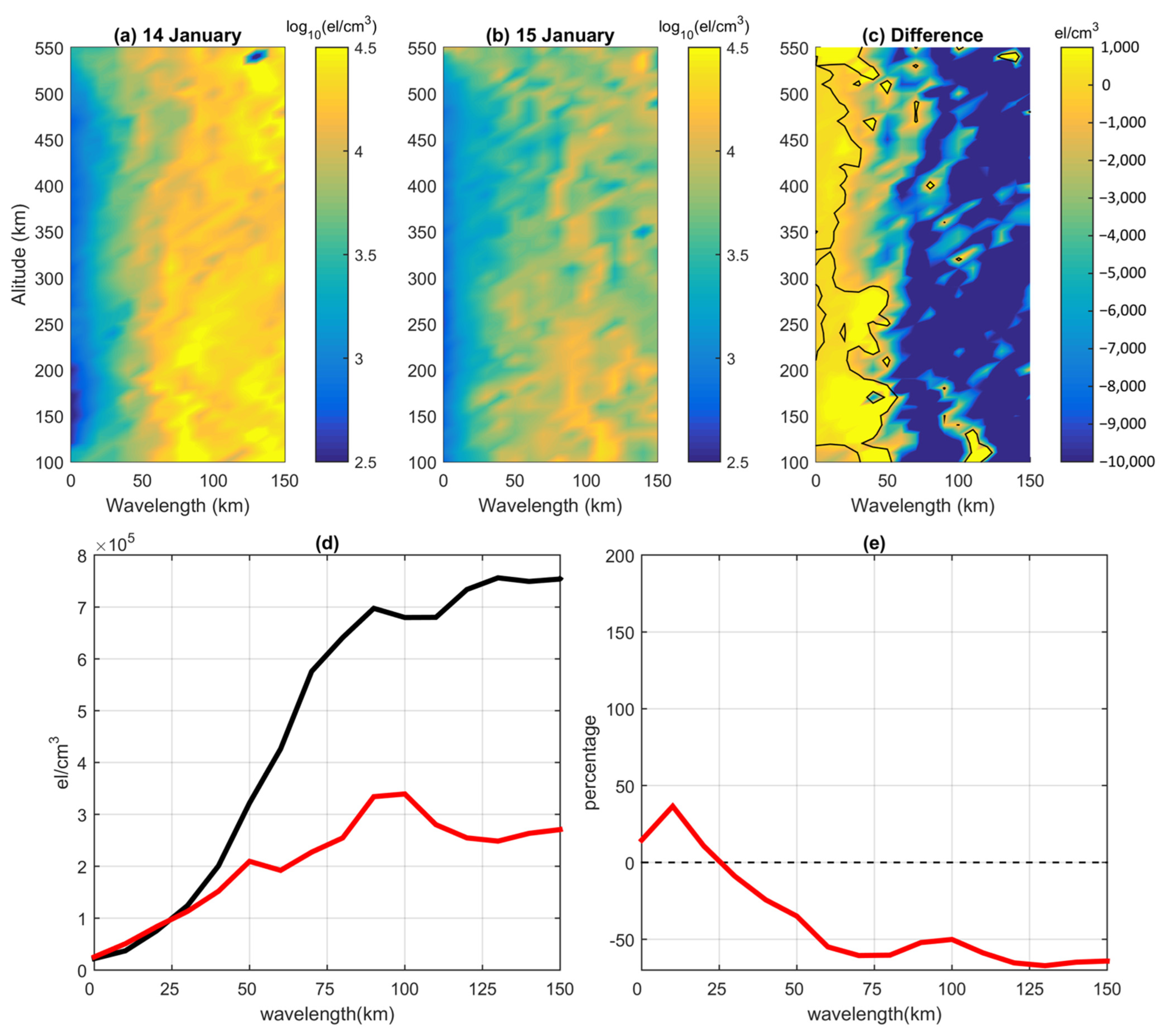
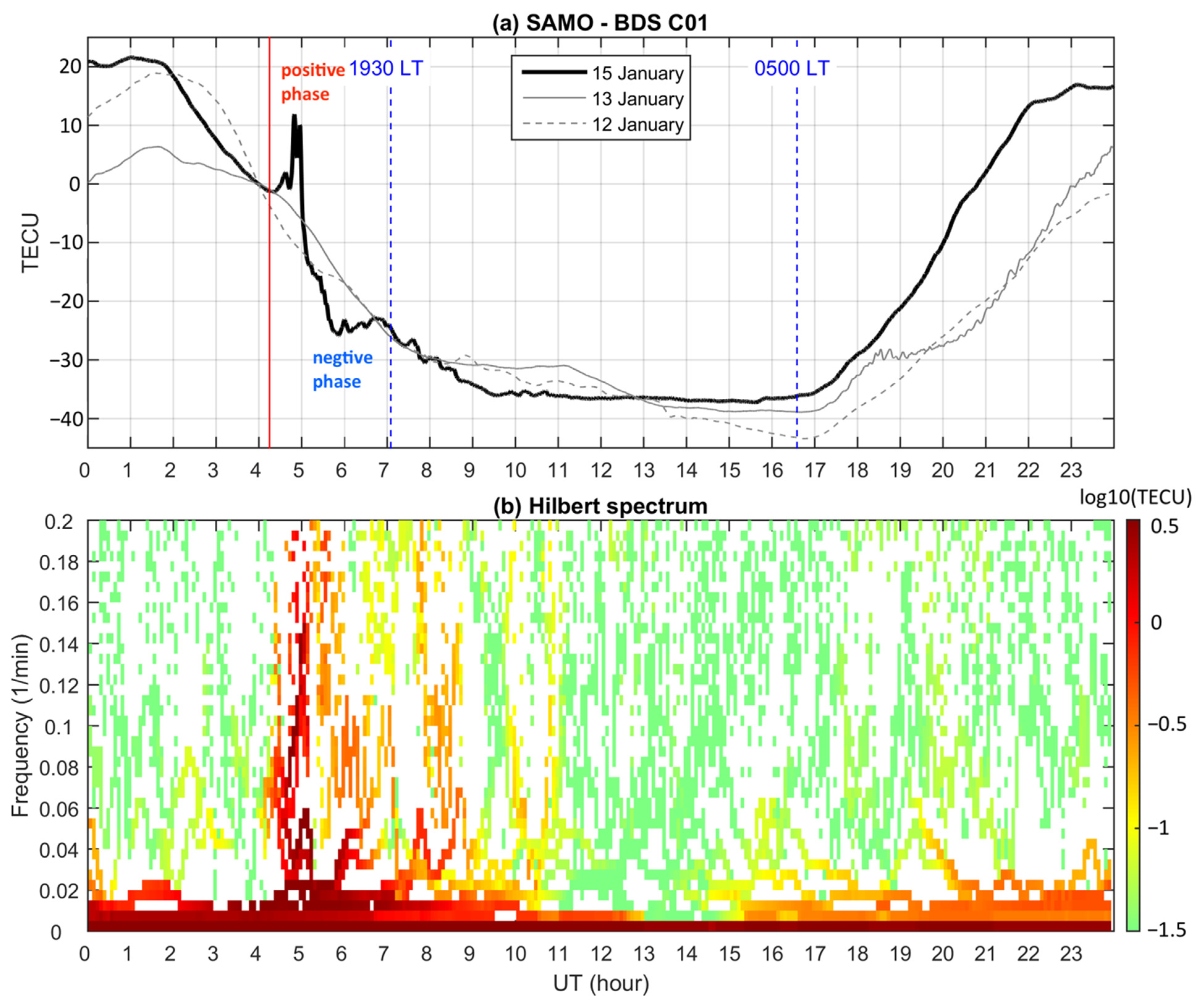
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, J.Y.; Tsai, Y.B.; Chen, S.W.; Lee, C.P.; Chen, Y.C.; Yen, H.Y.; Chang, W.Y.; Liu, C. Giant ionospheric disturbances excited by the M9.3 Sumatra earthquake of 26 December 2004. Geophys. Res. Lett. 2006, 33, L02103. [Google Scholar] [CrossRef]
- Liu, J.-Y.; Chen, C.-H.; Lin, C.-H.; Tsai, H.-F.; Chen, C.-H.; Kamogawa, M. Ionospheric disturbances triggered by the 11 March 2011 M9.0 Tohoku earthquake. J. Geophys. Res. Earth Surf. 2011, 116, A06319. [Google Scholar] [CrossRef]
- Otsuka, Y.; Kotake, N.; Tsugawa, T.; Shiokawa, K.; Ogawa, T.; Effendy; Saito, S.; Kawamura, M.; Maruyama, T.; Hemmakorn, N.; et al. GPS detection of total electron content variations over Indonesia and Thailand following the 26 December 2004 earthquake. Earth Planets Space 2006, 58, 159–165. [Google Scholar] [CrossRef]
- Tsugawa, T.; Saito, A.; Otsuka, Y.; Nishioka, M.; Maruyama, T.; Kato, H.; Nagatsuma, T.; Murata, K.T. Ionospheric disturbances detected by GPS total electron content observation after the 2011 off the Pacific coast of Tohoku Earthquake. Earth Planets Space 2011, 63, 875–879. [Google Scholar] [CrossRef]
- Chen, C.H.; Saito, A.; Lin, C.C.H.; Liu, J.Y.; Tsai, H.F.; Tsugawa, T.; Otsuka, Y.; Nishioka, M.; Matsumura, M. Long-distance propagation of ionospheric disturbance generated by the 2011 off the Pacific coast of Tohoku earthquake. Earth Planets Space 2011, 63, 881–884. [Google Scholar] [CrossRef]
- Nishioka, M.; Tsugawa, T.; Kubota, M.; Ishii, M. Concentric waves and short-period oscillations observed in the ionosphere after the 2013 Moore EF5 tornado. Geophys. Res. Lett. 2013, 40, 5581–5586. [Google Scholar] [CrossRef]
- Chou, M.Y.; Lin, C.C.H.; Yue, J.; Tsai, H.F.; Sun, Y.Y.; Liu, J.Y.; Chen, C.H. Concentric traveling ionosphere disturbances triggered by Super Typhoon Meranti (2016). Geophys. Res. Lett. 2017, 44, 1219–1226. [Google Scholar] [CrossRef]
- Chou, M.-Y.; Cherniak, I.; Lin, C.C.; Pedatella, N. The Persistent Ionospheric Responses Over Japan After the Impact of the 2011 Tohoku Earthquake. Space Weather 2020, 18, e2019SW002302. [Google Scholar] [CrossRef]
- Heki, K. Explosion energy of the 2004 eruption of the Asama Volcano, central Japan, inferred from ionospheric disturbances. Geophys. Res. Lett. 2006, 33, L14303. [Google Scholar] [CrossRef]
- Dautermann, T.; Calais, E.; Mattioli, G. Global Positioning System detection and energy estimation of the ionospheric wave caused by the 13 July 2003 explosion of the Soufrière Hills Volcano, Montserrat. J. Geophys. Res. Earth Surf. 2009, 114, B02202. [Google Scholar] [CrossRef]
- Shults, K.; Astafyeva, E.; Adourian, S. Ionospheric detection and localization of volcano eruptions on the example of the April 2015 Calbuco events. J. Geophys. Res. Space Phys. 2016, 121, 10303–10315. [Google Scholar] [CrossRef]
- Astafyeva, E. Ionospheric detection of natural hazards. Rev. Geophys. 2019, 57, 1265–1288. [Google Scholar] [CrossRef]
- Liu, J.-Y.; Sun, Y.-Y. Seismo-traveling ionospheric disturbances of ionograms observed during the 11 March 2011 M9.0 Tohoku earthquake. Earth Planets Space 2011, 63, 897–902. [Google Scholar] [CrossRef]
- Liu, J.Y.; Chen, C.H.; Sun, Y.Y.; Tsai, H.F.; Yen, H.Y.; Chum, J.; Lastovicka, J.; Yang, Q.S.; Chen, W.S.; Wen, S. The vertical propagation of disturbances triggered by seismic waves of the 11 March 2011 M9.0 Tohoku earthquake over Taiwan. Geophys. Res. Lett. 2016, 43, 1759–1765. [Google Scholar] [CrossRef]
- Maruyama, T.; Tsugawa, T.; Kato, H.; Saito, A.; Otsuka, Y.; Nishioka, M. Ionospheric multiple stratifications and irregularities induced by the 2011 off the Pacific coast of Tohoku Earthquake. Earth Planets Space 2011, 63, 869–873. [Google Scholar] [CrossRef]
- Maruyama, T.; Yusupov, K.; Akchurin, A. Ionosonde tracking of infrasound wavefronts in the thermosphere launched by seismic waves after the 2010 M8.8 Chile earthquake. J. Geophys. Res. Space Phys. 2016, 121, 2683–2692. [Google Scholar] [CrossRef]
- Wang, J.; Zuo, X.; Sun, Y.-Y.; Yu, T.; Wang, Y.; Qiu, L.; Mao, T.; Yan, X.; Yang, N.; Qi, Y.; et al. Multilayered sporadic-E response to the annular solar eclipse on June 21, 2020. Space Weather 2021, 19, e2020SW002643. [Google Scholar] [CrossRef]
- Borchevkina, O.P.; Kurdyaeva, Y.A.; Dyakov, Y.A.; Karpov, I.V.; Golubkov, G.V.; Wang, P.K.; Golubkov, M.G. Disturbances of the Thermosphere and the Ionosphere during a Meteorological Storm. Atmosphere 2021, 12, 1384. [Google Scholar] [CrossRef]
- Chen, C.-H.; Sun, Y.-Y.; Lin, K.; Zhou, C.; Xu, R.; Qing, H.; Gao, Y.; Chen, T.; Wang, F.; Yu, H.; et al. A new instrumental array in Sichuan, China, to monitor vibrations and perturbations of the lithosphere, atmosphere and ionosphere. Surv. Geophys. 2021, 42, 1425–1442. [Google Scholar] [CrossRef]
- Coïsson, P.; Lognonné, P.; Walwer, D.; Rolland, L.M. First tsunami gravity wave detection in ionospheric radio occultation data. Earth Space Sci. 2015, 2, 125–133. [Google Scholar] [CrossRef]
- Sun, Y.-Y.; Liu, J.-Y.; Lin, C.-Y.; Tsai, H.-F.; Chang, L.C.; Chen, C.-Y.; Chen, C.-H. Ionospheric F2 region perturbed by the 25 April 2015 Nepal earthquake. J. Geophys. Res. Space Phys. 2016, 121, 5778–5784. [Google Scholar] [CrossRef]
- Liu, J.-Y.; Chen, C.-Y.; Sun, Y.-Y.; Lee, I.-T.; Chum, J. Fluctuations on vertical profiles of the ionospheric electron density perturbed by the 11 March, 2011 M9.0 Tohoku earthquake and tsunami. GPS Solut. 2019, 23, 76. [Google Scholar] [CrossRef]
- Sun, Y.-Y. GNSS brings us back on the ground from ionosphere. Geosci. Lett. 2019, 6, 14. [Google Scholar] [CrossRef]
- Yan, X.; Sun, Y.-Y.; Yu, T.; Liu, J.-Y.; Qi, Y.; Xia, C.; Zuo, X.; Yang, N. Stratosphere perturbed by the 2011 Mw9.0 Tohoku earthquake. Geophys. Res. Lett. 2018, 45, 10050–10056. [Google Scholar] [CrossRef]
- Themens, D.R.; Watson, C.; Žagar, N.; Vasylkevych, S.; Elvidge, S.; McCaffrey, A.; Prikryl, P.; Reid, B.; Wood, A.; Jayachandran, P.T. Global Propagation of Ionospheric Disturbances Associated With the 2022 Tonga Volcanic Eruption. Geophys. Res. Lett. 2022, 49, e2022GL098158. [Google Scholar] [CrossRef]
- Lin, J.; Rajesh, P.K.; Lin, C.C.H.; Chou, M.; Liu, J.; Yue, J.; Hsiao, T.; Tsai, H.; Chao, H.; Kung, M. Rapid Conjugate Appearance of the Giant Ionospheric Lamb Wave Signatures in the Northern Hemisphere After Hunga-Tonga Volcano Eruptions. Geophys. Res. Lett. 2022, 49, e2022GL098222. [Google Scholar] [CrossRef]
- Astafyeva, E.; Maletckii, B.; Mikesell, T.D.; Munaibari, E.; Ravanelli, M.; Coisson, P.; Manta, F.; Rolland, L. The 15 January 2022 Hunga Tonga Eruption History as Inferred From Ionospheric Observations. Geophys. Res. Lett. 2022, 49, e2022GL098827. [Google Scholar] [CrossRef]
- Chen, C.-H.; Zhang, X.; Sun, Y.-Y.; Wang, F.; Liu, T.-C.; Lin, C.-Y.; Gao, Y.; Lyu, J.; Jin, X.; Zhao, X.; et al. Individual Wave Propagations in Ionosphere and Troposphere Triggered by the Hunga Tonga-Hunga Ha’apai Underwater Volcano Eruption on 15 January 2022. Remote Sens. 2022, 14, 2179. [Google Scholar] [CrossRef]
- Zhang, S.-R.; Vierinen, J.; Aa, E.; Goncharenko, L.P.; Erickson, P.J.; Rideout, W.; Coster, A.J.; Spicher, A. 2022 Tonga volcanic eruption induced global propagation of ionospheric disturbances via Lamb waves. Front. Astron. Space Sci. 2022, 9, 871275. [Google Scholar] [CrossRef]
- Saito, S. Ionospheric disturbances observed over Japan following the eruption of Hunga Tonga-Hunga Ha’apai on 15 January 2022. Earth Planets Space 2022, 74, 57. [Google Scholar] [CrossRef]
- Sun, Y.-Y.; Chen, C.-H.; Zhang, P.-Y.; Li, S.; Xu, H.-R.; Yu, T.; Lin, K.; Mao, Z.; Zhang, D.; Lin, C.-Y.; et al. Explosive eruption of the Tonga underwater volcano modulates the ionospheric E-region current on 15 January 2022. Geophys. Res. Lett. 2022, 49, e2022GL099621. [Google Scholar] [CrossRef]
- Lin, C.-Y.; Lin, C.C.-H.; Liu, J.-Y.; Rajesh, P.K.; Matsuo, T.; Chou, M.-Y.; Tsai, H.-F.; Yeh, W.-H. The early results and validation of FORMOSAT-7/COSMIC-2 space weather products: Global ionospheric specification and Ne-aided Abel electron density profile. J. Geophys. Res. Space Phys. 2020, 125, e2020JA028028. [Google Scholar] [CrossRef]
- Liu, T.J.-Y.; Lin, C.C.; Lin, C.-Y.; Lee, I.-T.; Sun, Y.-Y.; Chen, S.-P.; Chang, F.-Y.; Rajesh, P.K.; Hsu, C.-T.; Matsuo, T.; et al. Retrospect and prospect of ionospheric weather observed by FORMOSAT-3/COSMIC and FORMOSAT-7/COSMIC-2. Terr. Atmos. Ocean. Sci. 2022, 33, 20. [Google Scholar] [CrossRef]
- Chen, C.-H.; Sun, Y.-Y.; Xu, R.; Lin, K.; Wang, F.; Zhang, D.; Zhou, Y.; Gao, Y.; Zhang, X.; Yu, H.; et al. Resident waves in the ionosphere before the M6.1 Dali and M7.3 Qinghai earthquakes of 21–22 May 2021. Earth Space Sci. 2022, 9, e2021EA002159. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A-Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Sun, Y.-Y.; Shen, M.M.; Tsai, Y.-L.; Lin, C.-Y.; Chou, M.-Y.; Yu, T.; Lin, K.; Huang, Q.; Wang, J.; Qiu, L.; et al. Wave steepening in ionospheric total electron density due to the 21 August 2017 total solar eclipse. J. Geophys. Res. Space Phys. 2021, 126, e2020JA028931. [Google Scholar] [CrossRef]
- Sun, Y.-Y.; Oyama, K.-I.; Liu, J.-Y.; Jhuang, H.-K.; Cheng, C.-Z. The neutral temperature in the ionospheric dynamo region and the ionospheric F region density during Wenchuan and Pingtung Doublet earthquakes. Nat. Hazards Earth Syst. Sci. 2011, 11, 1759–1768. [Google Scholar] [CrossRef]
- Davies, K. Ionospheric Radio; Peregrinus: London, UK, 1990. [Google Scholar]
- Wang, J.; Sun, Y.-Y.; Yu, T.; Wang, Y.; Mao, T.; Yang, H.; Xia, C.; Yan, X.; Yang, N.; Huang, G.; et al. Convergence effects on the ionosphere during and after the annular solar eclipse on 21 June 2020. J. Geophys. Res.-Space Phys. 2022, 127, e2022JA030471. [Google Scholar] [CrossRef]
- Chou, M.-Y.; Shen, M.-H.; Lin, C.C.H.; Yue, J.; Chen, C.-H.; Liu, J.-Y.; Lin, J.-T. Gigantic circular shock acoustic waves in the ionosphere triggered by the launch of FORMOSAT-5 satellite. Space Weather 2018, 16, 172–184. [Google Scholar] [CrossRef]
- Kakinami, Y.; Kamogawa, M.; Tanioka, Y.; Watanabe, S.; Gusman, A.R.; Liu, J.-Y.; Watanabe, Y.; Mogi, T. Tsunamigenic ionospheric hole. Geophys. Res. Lett. 2012, 39, L00G27. [Google Scholar] [CrossRef]
- Kamogawa, M.; Orihara, Y.; Tsurudome, C.; Tomida, Y.; Kanaya, T.; Ikeda, D.; Gusman, A.R.; Kakinami, Y.; Liu, J.-Y.; Toyoda, A. A possible space-based tsunami early warning system using observations of the tsunami ionospheric hole. Sci. Rep. 2016, 6, 37989. [Google Scholar] [CrossRef] [PubMed]
- Shirbhate, P.A.; Goel, M.D. A Critical Review of Blast Wave Parameters and Approaches for Blast Load Mitigation. Arch. Comput. Methods Eng. 2020, 28, 1713–1730. [Google Scholar] [CrossRef]
- Borchevkina, O.P.; Adamson, S.O.; Dyakov, Y.A.; Karpov, I.V.; Golubkov, G.V.; Wang, P.-K.; Golubkov, M.G. The Influence of Tropospheric Processes on Disturbances in the D and E Ionospheric Layers. Atmosphere 2021, 12, 1116. [Google Scholar] [CrossRef]
- Song, Q.; Ding, F.; Wan, W.; Ning, B.; Liu, L.; Zhao, B.; Li, Q.; Zhang, R. Statistical study of large-scale traveling ionospheric disturbances generated by the solar terminator over China. J. Geophys. Res. Space Phys. 2013, 118, 4583–4593. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.-Y.; Chen, C.-H.; Lin, C.-Y. Detection of Vertical Changes in the Ionospheric Electron Density Structures by the Radio Occultation Technique Onboard the FORMOSAT-7/COSMIC2 Mission over the Eruption of the Tonga Underwater Volcano on 15 January 2022. Remote Sens. 2022, 14, 4266. https://doi.org/10.3390/rs14174266
Sun Y-Y, Chen C-H, Lin C-Y. Detection of Vertical Changes in the Ionospheric Electron Density Structures by the Radio Occultation Technique Onboard the FORMOSAT-7/COSMIC2 Mission over the Eruption of the Tonga Underwater Volcano on 15 January 2022. Remote Sensing. 2022; 14(17):4266. https://doi.org/10.3390/rs14174266
Chicago/Turabian StyleSun, Yang-Yi, Chieh-Hung Chen, and Chi-Yen Lin. 2022. "Detection of Vertical Changes in the Ionospheric Electron Density Structures by the Radio Occultation Technique Onboard the FORMOSAT-7/COSMIC2 Mission over the Eruption of the Tonga Underwater Volcano on 15 January 2022" Remote Sensing 14, no. 17: 4266. https://doi.org/10.3390/rs14174266
APA StyleSun, Y.-Y., Chen, C.-H., & Lin, C.-Y. (2022). Detection of Vertical Changes in the Ionospheric Electron Density Structures by the Radio Occultation Technique Onboard the FORMOSAT-7/COSMIC2 Mission over the Eruption of the Tonga Underwater Volcano on 15 January 2022. Remote Sensing, 14(17), 4266. https://doi.org/10.3390/rs14174266