Evaluation of HY-2 Series Satellites Mapping Capability on Mesoscale Eddies
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.1.1. Along-Track Altimeter Data
2.1.2. Ocean Model Data
2.1.3. DUACS DT2018 Data
2.2. Methods
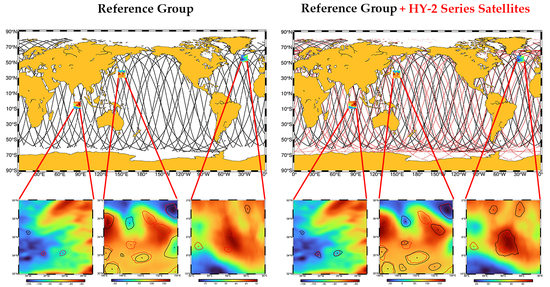
2.2.1. Experimental Design
2.2.2. Optimal Interpolation
2.2.3. Eddy Identification Algorithm
3. Results
3.1. Comparing Along-Track Coverage
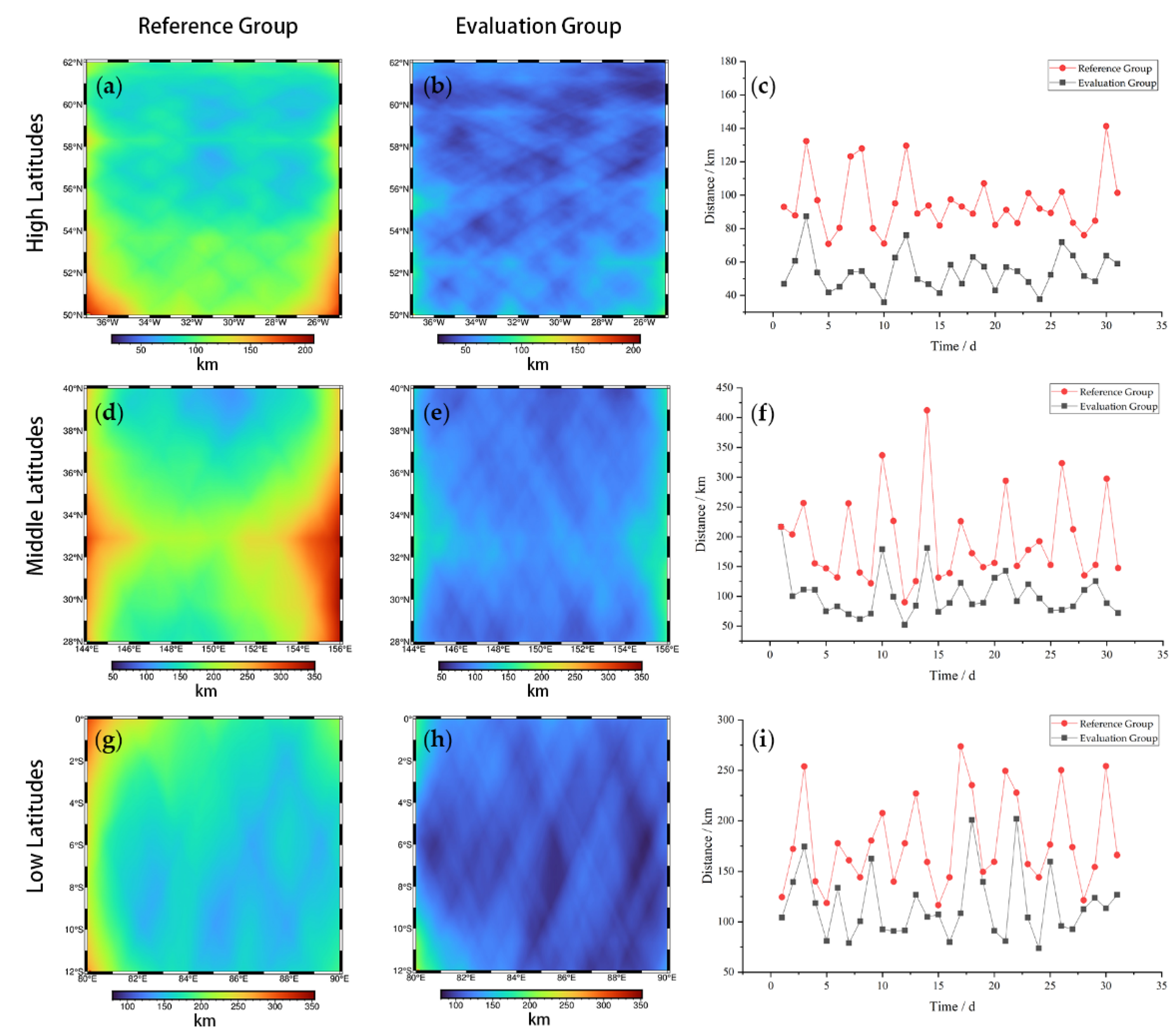
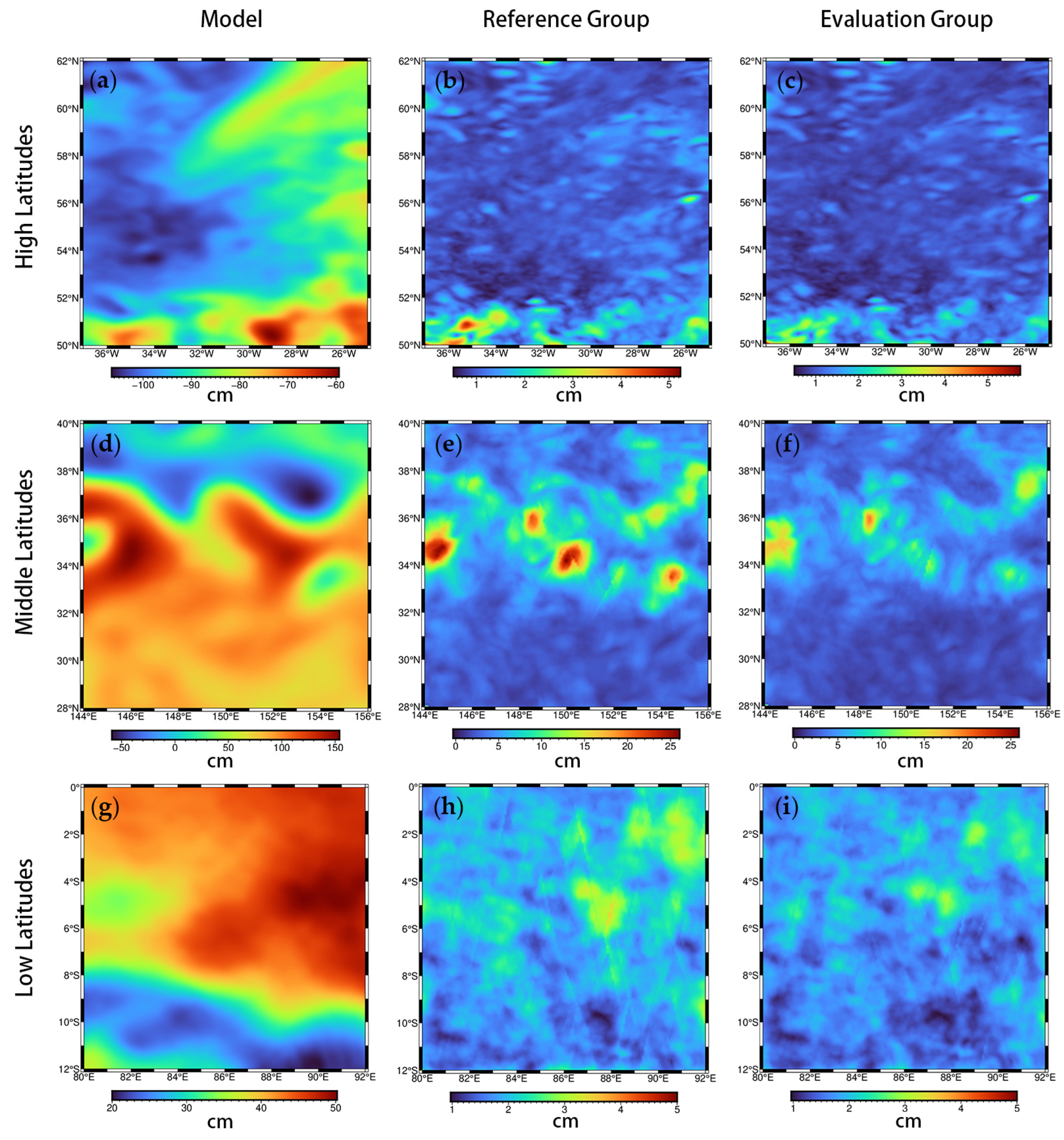
3.2. Comparing OI Gridded Product
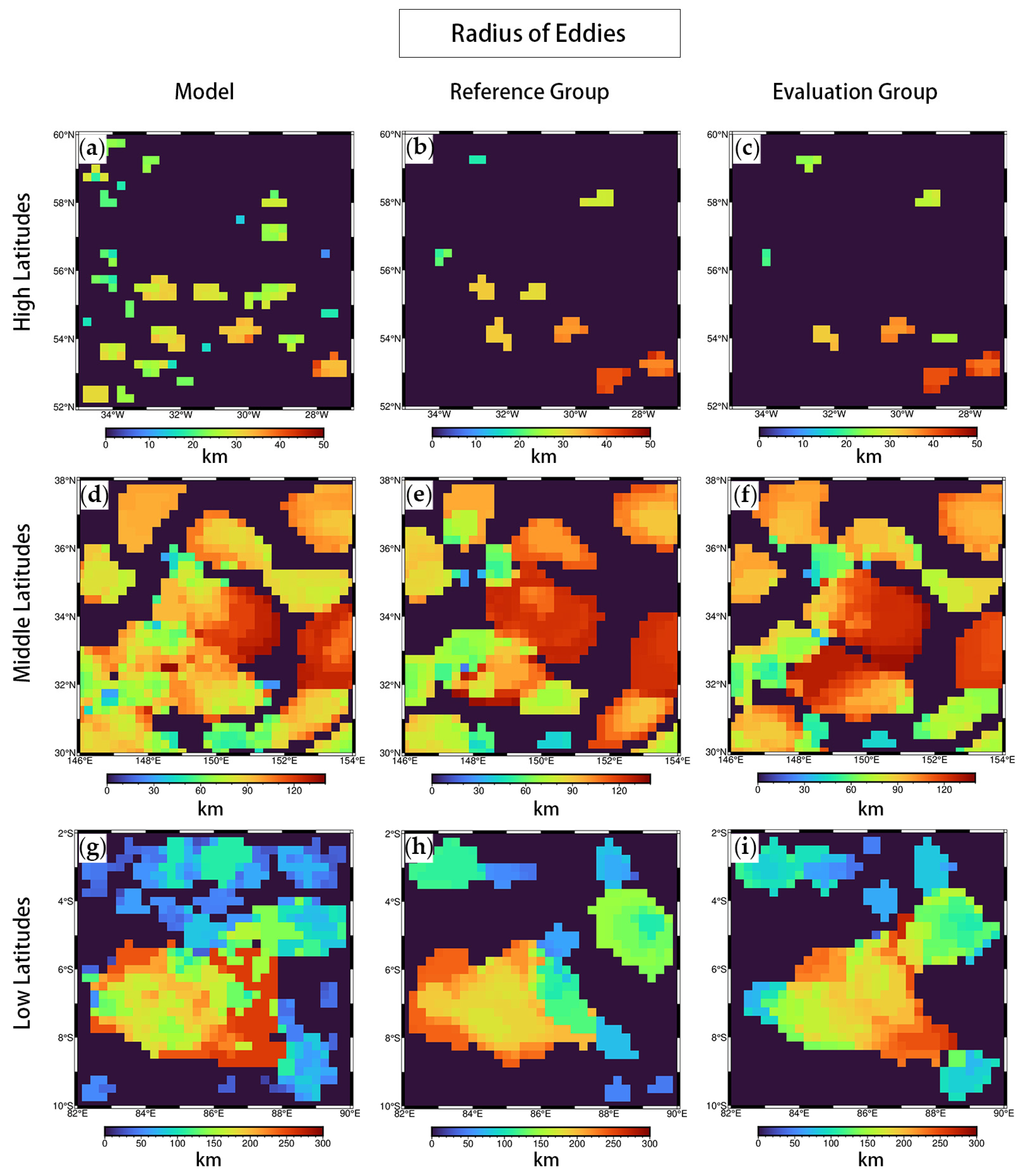
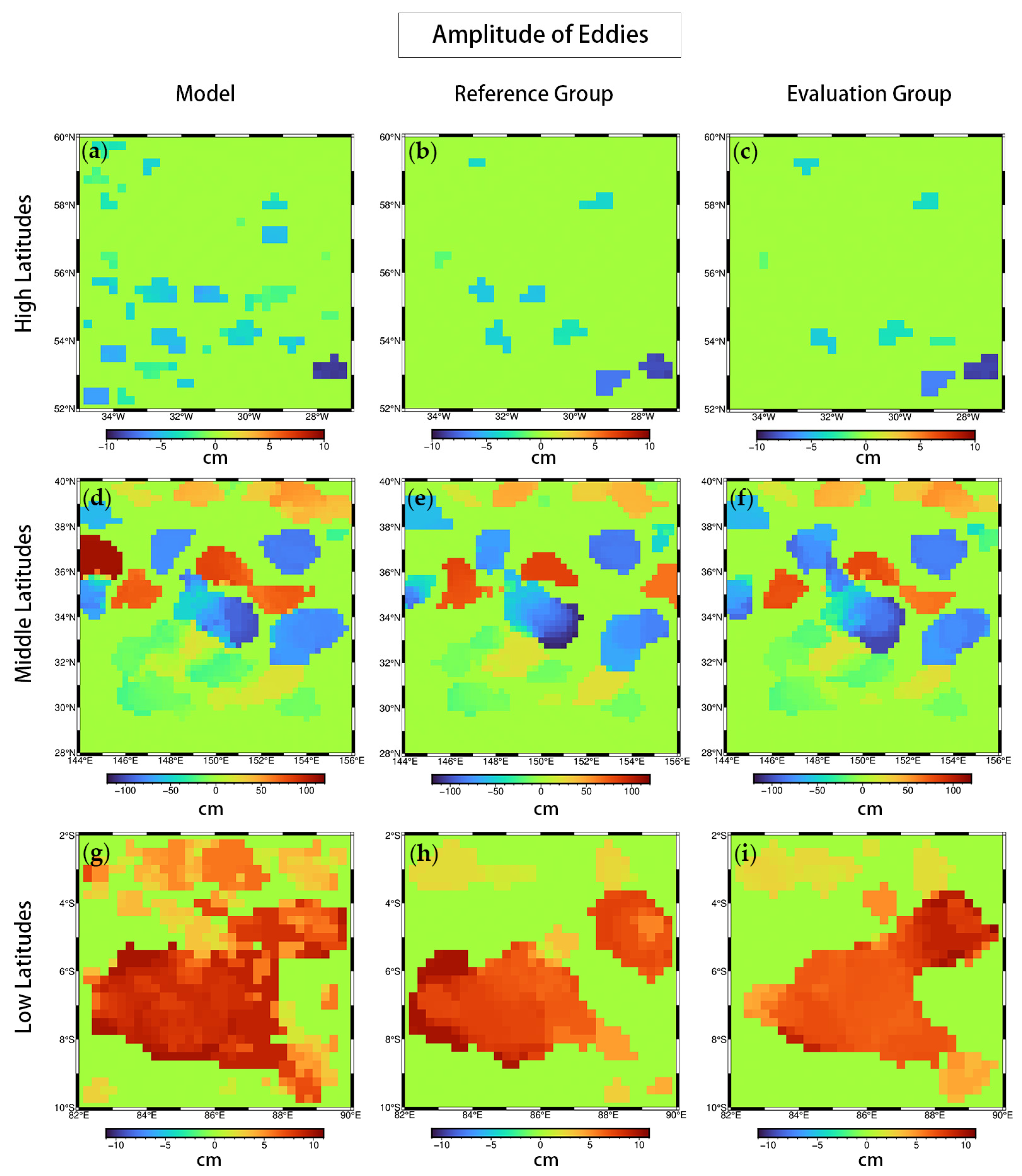
3.3. Comparing Identified Mesoscale Eddies
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| HY-2 | Haiyang-2 |
| HY-2B | Haiyang-2B |
| HY-2C | Haiyang-2C |
| HY-2D | Haiyang-2D |
| NSOAS | National Satellite Ocean Application Service |
| NOAA | National Oceanic and Atmospheric Administration |
| NASA | National Aeronautics and Space Administration |
| CNES | Center National ďEtudes Spatiales |
| EUMETSAT | European Organization for Exploitation of Meteorological Satellites |
| ESA | European Space Agency |
| HYCOM | Hybrid Coordinate Ocean Model |
| DUACS | Data Unification and Altimeter Combination System |
| CLS | Collect Localization Satellites |
| CMEMS | Copernicus Marine and Environment Monitoring Service |
| SLA | Sea Level Anomaly |
| OI | Optimal Interpolation |
| SSH | Sea Surface Height |
| CLS | Collect Localization Satellites |
References
- Zhen, Y.C.; Tandeo, P.; Leroux, S.; Metref, S.; Penduff, T.; Le Sommer, J. An Adaptive Optimal Interpolation Based on Analog Forecasting: Application to SSH in the Gulf of Mexico. J. Atmos. Ocean. Tech. 2020, 37, 1697–1711. [Google Scholar] [CrossRef]
- Taburet, G.; Sanchez-Roman, A.; Ballarotta, M.; Pujol, M.I.; Legeais, J.F.; Fournier, F.; Faugere, Y.; Dibarboure, G. DUACS DT2018: 25 years of reprocessed sea level altimetry products. Ocean Sci. 2019, 15, 1207–1224. [Google Scholar] [CrossRef]
- Chelton, D.B.; Schlax, M.G.; Samelson, R.M.; de Szoeke, R.A. Global observations of large oceanic eddies. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Samelson, R.M.; Schlax, M.G.; Chelton, D.B. Global observations of nonlinear mesoscale eddies. J. Phys. Oceanogr. 2014, 44, 2588–2589. [Google Scholar] [CrossRef]
- Fu, L.L.; Ubelmann, C. On the Transition from Profile Altimeter to Swath Altimeter for Observing Global Ocean Surface Topography. J. Atmos. Ocean. Tech. 2014, 31, 560–568. [Google Scholar] [CrossRef]
- Gandin, L.S. Objective Analysis of Meteorological Fields. Isr. Program Sci. Transl. 1963, 286. [Google Scholar]
- Ducet, N.; Le Traon, P.Y.; Reverdin, G. Global high-resolution mapping of ocean circulation from TOPEX/Poseidon and ERS-1 and-2. J. Geophys. Res. Ocean. 2000, 105, 19477–19498. [Google Scholar] [CrossRef]
- Le Traon, P.Y.; Dibarboure, G. Mesoscale mapping capabilities of multiple-satellite altimeter missions. J. Atmos. Ocean. Tech. 1999, 16, 1208–1223. [Google Scholar] [CrossRef]
- Koblinsky, C. Oceans and climate change: The future of spaceborne altimetry. Trans. Am. Geophys. Union 1992, 73, 403. [Google Scholar] [CrossRef]
- Morrow, R.; Le Traon, P.Y. Recent advances in observing mesoscale ocean dynamics with satellite altimetry. Adv. Space Res. 2012, 50, 1062–1076. [Google Scholar] [CrossRef]
- Le Traon, P.Y.; Dibarboure, G. Velocity mapping capabilities of present and future altimeter missions: The role of high-frequency signals. J. Atmos. Ocean. Tech. 2002, 19, 2077–2087. [Google Scholar]
- Fu, L.L.; Christensen, E.J.; Yamarone, C.A.; Lefebvre, M.; Menard, Y.; Dorrer, M.; Escudier, P. TOPEX/POSEIDON mission overview. J. Geophys. Res. Ocean. 1994, 99, 24369–24381. [Google Scholar]
- Wang, Z.X.; Zou, J.H.; Zhang, Y.G.; Stoffelen, A.; Lin, W.M.; He, Y.J.; Feng, Q.; Zhang, Y.; Mu, B.; Lin, M.S. Intercalibration of Backscatter Measurements among Ku-Band Scatterometers Onboard the Chinese HY-2 Satellite Constellation. Remote Sens. 2021, 13, 4783. [Google Scholar]
- Guo, Q. China Launches HY-2B Satellite Atop a LM-4B. Aerosp. China 2018, 19, 59. [Google Scholar]
- Yueming, R. LM-4B Successfully Launched HY-2C Satellite. Aerosp. China 2020, 21, 56. [Google Scholar]
- Zou, J.; Mu, B.; Bao, Q.; Wang, Z.; Lang, S.; Yang, S.; Lin, M. Calibration and Validation of Scatterometer Product of CFOSAT and HY-2 Series Satellites. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 8138–8141. [Google Scholar]
- Guo, J.Y.; Wang, G.Z.; Guo, H.Y.; Lin, M.S.; Peng, H.L.; Chang, X.T.; Jiang, Y.M. Validating Precise Orbit Determination from Satellite-Borne GPS Data of Haiyang-2D. Remote Sens. 2022, 14, 2477. [Google Scholar]
- Lin, M.S.; Jia, Y.J. Past, Present and Future Marine Microwave Satellite Missions in China. Remote Sens. 2022, 14, 1330. [Google Scholar]
- Zhou, X.; Yang, L.; Lin, M.; Lei, N.; Tang, Q.; Mu, B. Absolute calibration of HY-2, Jason-2 and Saral/AltiKa from China in-situ calibration site: Qian Li Yan. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 3659–3662. [Google Scholar]
- Liu, Q.X.; Babanin, A.V.; Guan, C.L.; Zieger, S.; Sun, J.; Jia, Y.J. Calibration and Validation of HY-2 Altimeter Wave Height. J. Atmos. Ocean. Tech. 2016, 33, 919–936. [Google Scholar]
- Jia, Y.; Lin, M.; Zhang, Y. Current status of the HY-2A satellite radar altimeter and its prospect. In Proceedings of the Geoscience & Remote Sensing Symposium, Quebec City, QC, Canada, 3–18 July 2014. [Google Scholar]
- Mingsen, L.; Xingwei, J. Ocean observation from Haiyang satellites. Chin. J. Space Sci. 2020, 40, 898–907. [Google Scholar]
- Xingwei, J.; Mingsen, L. Ocean Observation from Haiyang Satellites: 2012–2014. Chin. J. Space Sci. 2014, 34, 710–720. [Google Scholar]
- Pascual, A.; Faugère, Y.; Larnicol, G.; Le Traon, P.Y. Improved description of the ocean mesoscale variability by combining four satellite altimeters. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef] [Green Version]
- Le Traon, P.; Faugère, Y.; Hernandez, F.; Dorandeu, J.; Mertz, F.; Ablain, M. Can we merge GEOSAT follow-on with TOPEX/Poseidon and ERS-2 for an improved description of the ocean circulation? J. Atmos. Ocean. Tech. 2003, 20, 889–895. [Google Scholar]
- Pujol, M.I.; Faugere, Y.; Taburet, G.; Dupuy, S.; Pelloquin, C.; Ablain, M.; Picot, N. DUACS DT2014: The new multi-mission altimeter data set reprocessed over 20 years. Ocean Sci. 2016, 12, 1067–1090. [Google Scholar]
- Dibarboure, G.; Renaudie, C.; Pujol, M.I.; Labroue, S.; Picot, N. A demonstration of the potential of Cryosat-2 to contribute to mesoscale observation. Adv. Space Res. 2012, 50, 1046–1061. [Google Scholar]
- Dibarboure, G.; Lamy, A.; Pujol, M.I.; Jettou, G. The Drifting Phase of SARAL: Securing Stable Ocean Mesoscale Sampling with an Unmaintained Decaying Altitude. Remote Sens. 2018, 10, 1051. [Google Scholar]
- Donlon, C.J.; Cullen, R.; Giulicchi, L.; Vuilleumier, P.; Francis, C.R.; Kuschnerus, M.; Simpson, W.; Bouridah, A.; Caleno, M.; Bertoni, R.; et al. The Copernicus Sentinel-6 mission: Enhanced continuity of satellite sea level measurements from space. Remote Sens. Environ. 2021, 258, 112395. [Google Scholar]
- Vaze, P.; Neeck, S.; Bannoura, W.; Green, J.; Wade, A.; Mignogno, M.; Zaouche, G.; Couderc, V.; Thouvenot, E.; Parisot, F. The jason-3 mission: Completing the transition of ocean altimetry from research to operations. In Proceedings of the Conference on Sensors, Systems, and Next-Generation Satellites XIV, Toulouse, France, 20–23 September 2010. [Google Scholar]
- Mavrocordatos, C.; Berruti, B.; Aguirre, M.; Drinkwater, M. The Sentinel-3 mission and its Topography element. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Barcelona, Spain, 23–27 July 2007; pp. 3529–3532. [Google Scholar]
- Chassignet, E.P.; Huriburt, H.E.; Smedstad, O.M.; Halliwell, G.R.; Hogan, P.J.; Wallcraft, A.J.; Bleck, R. Ocean prediction with the hybrid coordinate ocean model (HYCOM). In Proceedings of the International Summer School of Oceanography, Agelonde in Lalonde-Les Maures, Agelonde, France, 20 September–1 October 2004; pp. 413–426. [Google Scholar]
- Meyers, G.; Phillips, H.; Smith, N.; Sprintall, J. Space and time scales for optimal interpolation of temperature—Tropical Pacific Ocean. Prog. Oceanogr. 1991, 28, 189–218. [Google Scholar]
- Le Traon, P.Y.; Ogor, F. ERS-1/2 orbit improvement using TOPEX/POSEIDON: The 2 cm challenge. J. Geophys. Res. Ocean. 1998, 103, 8045–8057. [Google Scholar]
- Dong, C.M.; Nencioli, F.; Liu, Y.; McWilliams, J.C. An Automated Approach to Detect Oceanic Eddies From Satellite Remotely Sensed Sea Surface Temperature Data. IEEE Geosci. Remote Sens. Lett. 2011, 8, 1055–1059. [Google Scholar] [CrossRef]
- Kurian, J.; Colas, F.; Capet, X.; McWilliams, J.C.; Chelton, D.B. Eddy properties in the California current system. J. Geophys. Res. Ocean. 2011, 116. [Google Scholar] [CrossRef]
- Li, Q.Y.; Sun, L.; Lin, S.F. GEM: A dynamic tracking model for mesoscale eddies in the ocean. Ocean Sci. 2016, 12, 1249–1267. [Google Scholar]
- Faghmous, J.H.; Le, M.; Uluyol, M.; Kumar, V.; Chatterjee, S. A parameter-free spatio-temporal pattern mining model to catalog global ocean dynamics. In Proceedings of the IEEE 13th International Conference on Data Mining (ICDM), Dallas, TX, USA, 7–10 December 2013; pp. 151–160. [Google Scholar]
- Nencioli, F.; Dong, C.M.; Dickey, T.; Washburn, L.; McWilliams, J.C. A Vector Geometry-Based Eddy Detection Algorithm and Its Application to a High-Resolution Numerical Model Product and High-Frequency Radar Surface Velocities in the Southern California Bight. J. Atmos. Ocean. Tech. 2010, 27, 564–579. [Google Scholar]
- Meng, Y.; Liu, H.L.; Lin, P.F.; Ding, M.R.; Dong, C.M. Oceanic mesoscale eddy in the Kuroshio extension: Comparison of four datasets. Atmos. Ocean. Sci. Lett. 2021, 14, 100011. [Google Scholar]
- Escudier, R.; Renault, L.; Pascual, A.; Brasseur, P.; Chelton, D.; Beuvier, J. Eddy properties in the Western Mediterranean Sea from satellite altimetry and a numerical simulation. J. Geophys. Res. Ocean. 2016, 121, 3990–4006. [Google Scholar]
- Martinez-Moreno, J.; Hogg, A.M.; Kiss, A.E.; Constantinou, N.C.; Morrison, A.K. Kinetic Energy of Eddy-Like Features From Sea Surface Altimetry. J. Adv. Modeling Earth Syst. 2019, 11, 3090–3105. [Google Scholar]
- Amores, A.; Jordà, G.; Arsouze, T.; Le Sommer, J. Up to what extent can we characterize ocean eddies using present-day gridded altimetric products? J. Geophys. Res. Ocean. 2018, 123, 7220–7236. [Google Scholar]





| Satellite | Agency | Launch | Inclination | Sun- Synchronous | Waveband | Repetitive |
|---|---|---|---|---|---|---|
| HY-2B | NSOAS | 2018.10 | 99.3° | Yes | Ku/C | 14day |
| HY-2C | NSOAS | 2020.09 | 66° | No | Ku | 10day |
| HY-2D | NSOAS | 2021.05 | 66° | No | Ku | 10day |
| Jason-3 | NOAA&NASA& CNES&EUMETSAT | 2016.01 | 66° | No | Ku/C | 10day |
| Sentinel-3A | NOAA&NASA | 2016.02 | 98.6° | Yes | Ku/C | 27 day |
| Sentinel-3B | NOAA&NASA | 2018.04 | 98.6° | Yes | Ku/C | 27 day |
| Reference Group | Evaluation Group | |||||
|---|---|---|---|---|---|---|
| High Latitudes | Middle Latitudes | Low Latitudes | High Latitudes | Middle Latitudes | Low Latitudes | |
| /km | 80 | 100 | 120 | 70 | 90 | 120 |
| /day | 7 | 7 | 3 | 3 | 3 | 3 |
| High Latitudes | Middle Latitudes | Low Latitudes | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | Reference Group | Evaluation Group | Model | Reference Group | Evaluation Group | Model | Reference Group | Evaluation Group | |
| Ed. Amount | 114 | 110 | 108 | 291 | 306 | 304 | 117 | 52 | 55 |
| Ed. Radius/km | 25.10 | 32.20 | 32.64 | 69.04 | 73.20 | 72.42 | 56.19 | 109.03 | 104.96 |
| Ed. Amplitude/cm | −4.15 | −4.67 | −4.70 | −10.53 | −17.64 | −21.62 | 4.26 | 5.11 | 4.84 |
| Eddy Recognition Rate/% | Eddy Recognition Accuracy/% | |||||
|---|---|---|---|---|---|---|
| High Latitudes | Middle Latitudes | Low Latitudes | High Latitudes | Middle Latitudes | Low Latitudes | |
| Reference Group | 30.97 | 55.35 | 18.80 | 31.82 | 55.87 | 42.31 |
| Evaluation Group | 35.40 | 52.56 | 21.37 | 37.04 | 55.66 | 45.45 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, F.; Qi, J.; Jia, Y.; Chen, G. Evaluation of HY-2 Series Satellites Mapping Capability on Mesoscale Eddies. Remote Sens. 2022, 14, 4262. https://doi.org/10.3390/rs14174262
Yu F, Qi J, Jia Y, Chen G. Evaluation of HY-2 Series Satellites Mapping Capability on Mesoscale Eddies. Remote Sensing. 2022; 14(17):4262. https://doi.org/10.3390/rs14174262
Chicago/Turabian StyleYu, Fangjie, Juanjuan Qi, Yongjun Jia, and Ge Chen. 2022. "Evaluation of HY-2 Series Satellites Mapping Capability on Mesoscale Eddies" Remote Sensing 14, no. 17: 4262. https://doi.org/10.3390/rs14174262
APA StyleYu, F., Qi, J., Jia, Y., & Chen, G. (2022). Evaluation of HY-2 Series Satellites Mapping Capability on Mesoscale Eddies. Remote Sensing, 14(17), 4262. https://doi.org/10.3390/rs14174262