Experimental Measurement of Forward Scattering from Very Rough Sand Ripples in a Water Tank
Abstract
:1. Introduction
2. Method to Extract Scattered Waves
3. Results
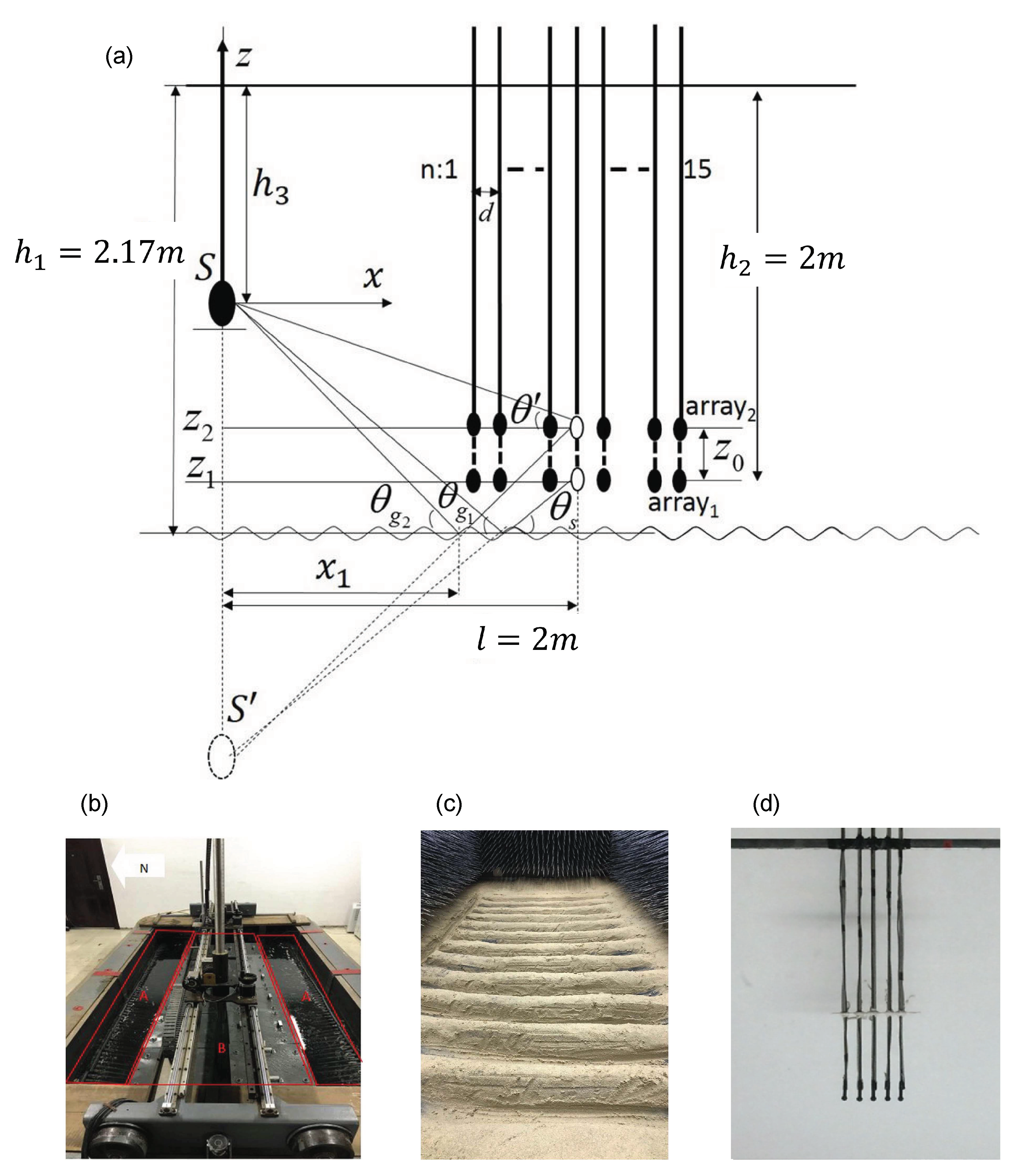
3.1. Experimental System
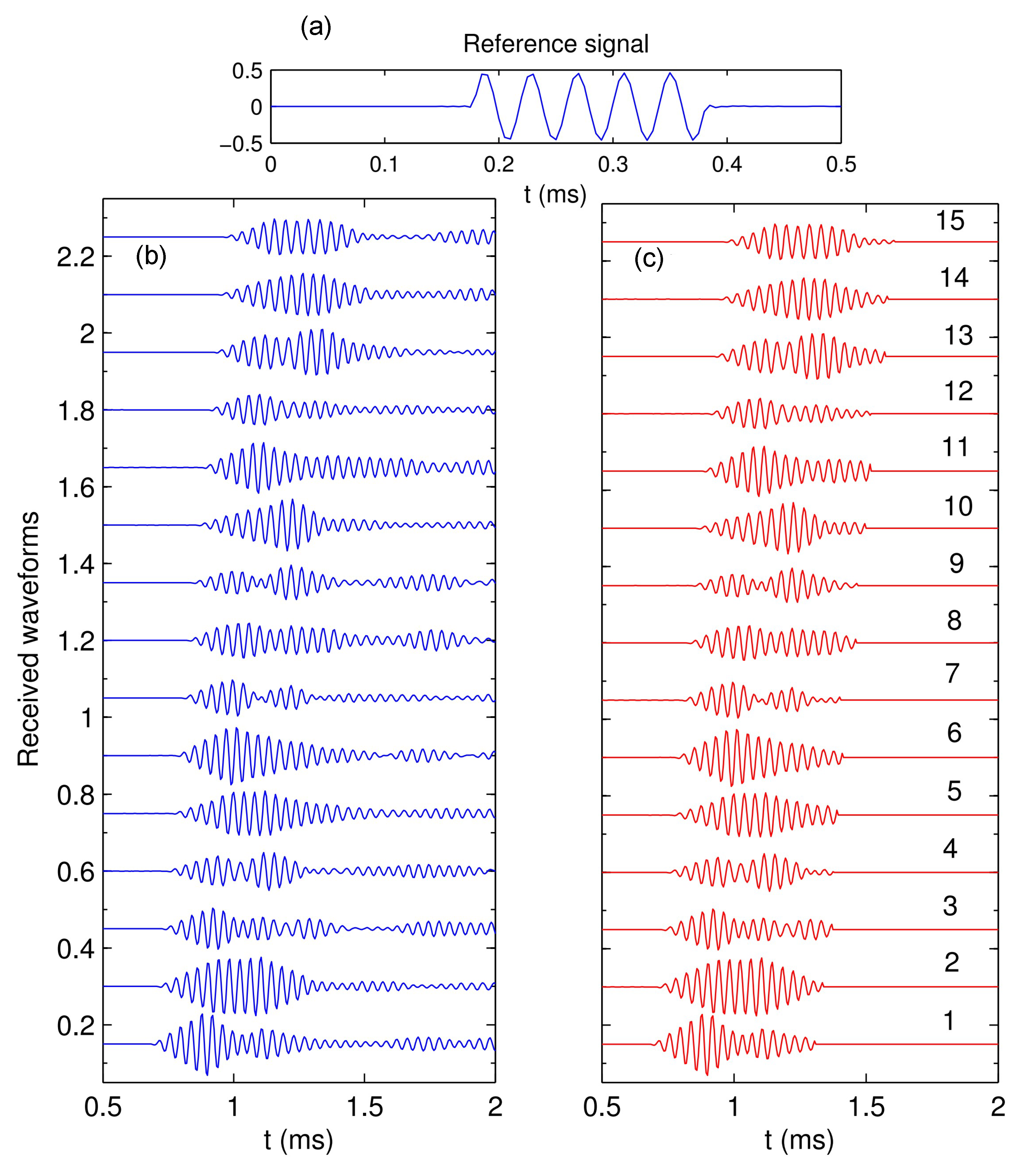
3.2. Processing Experimental Data
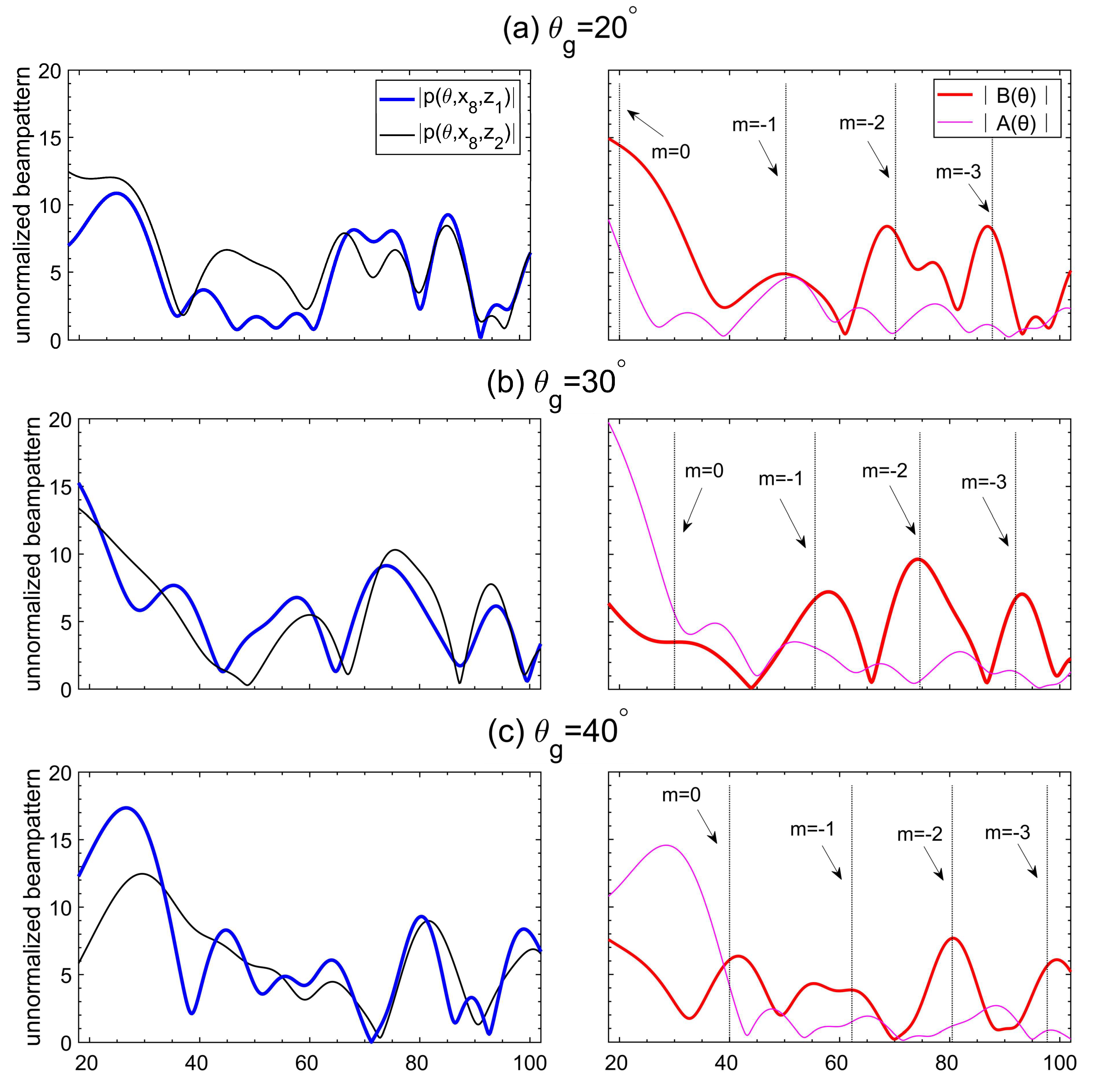
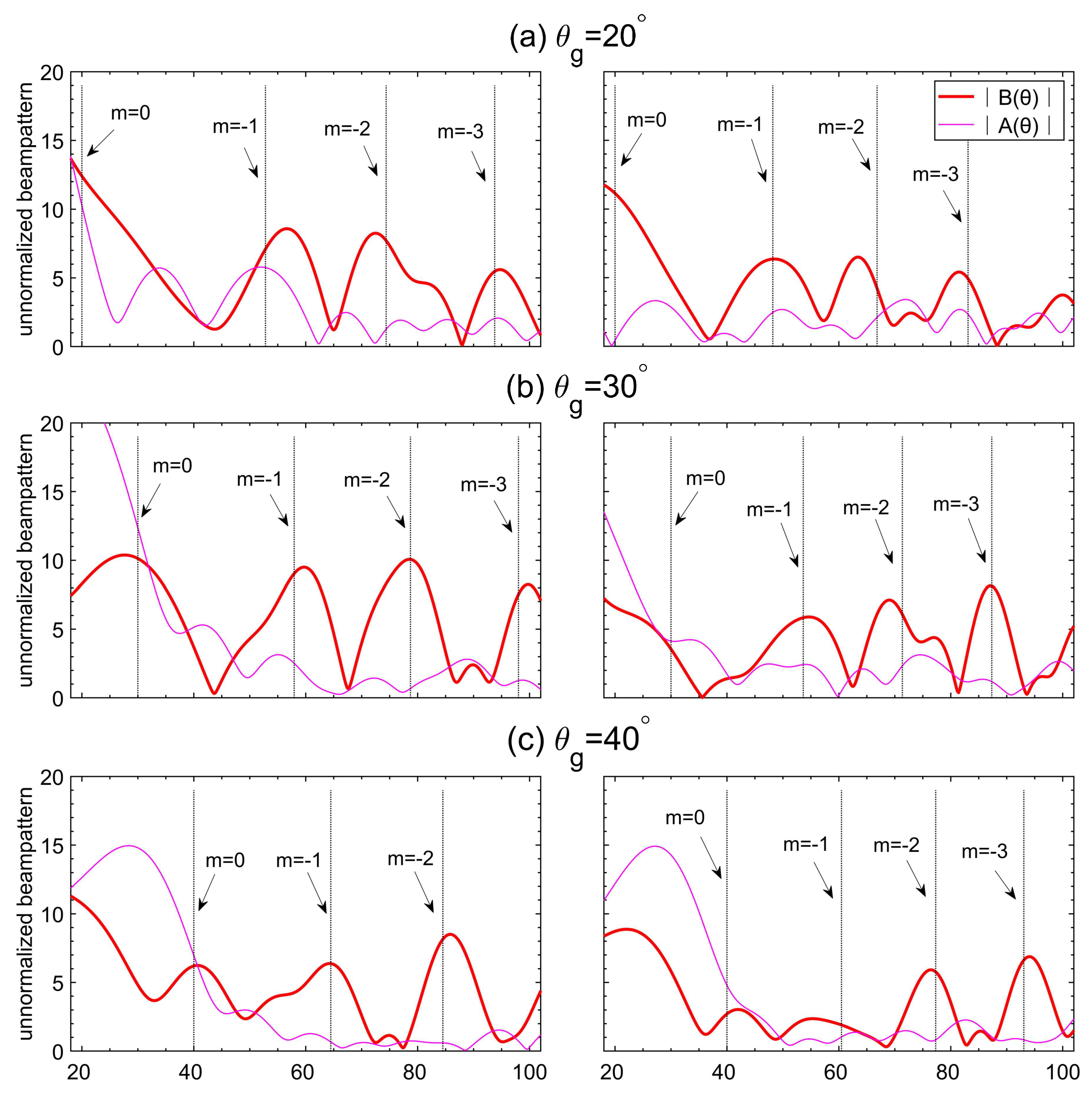
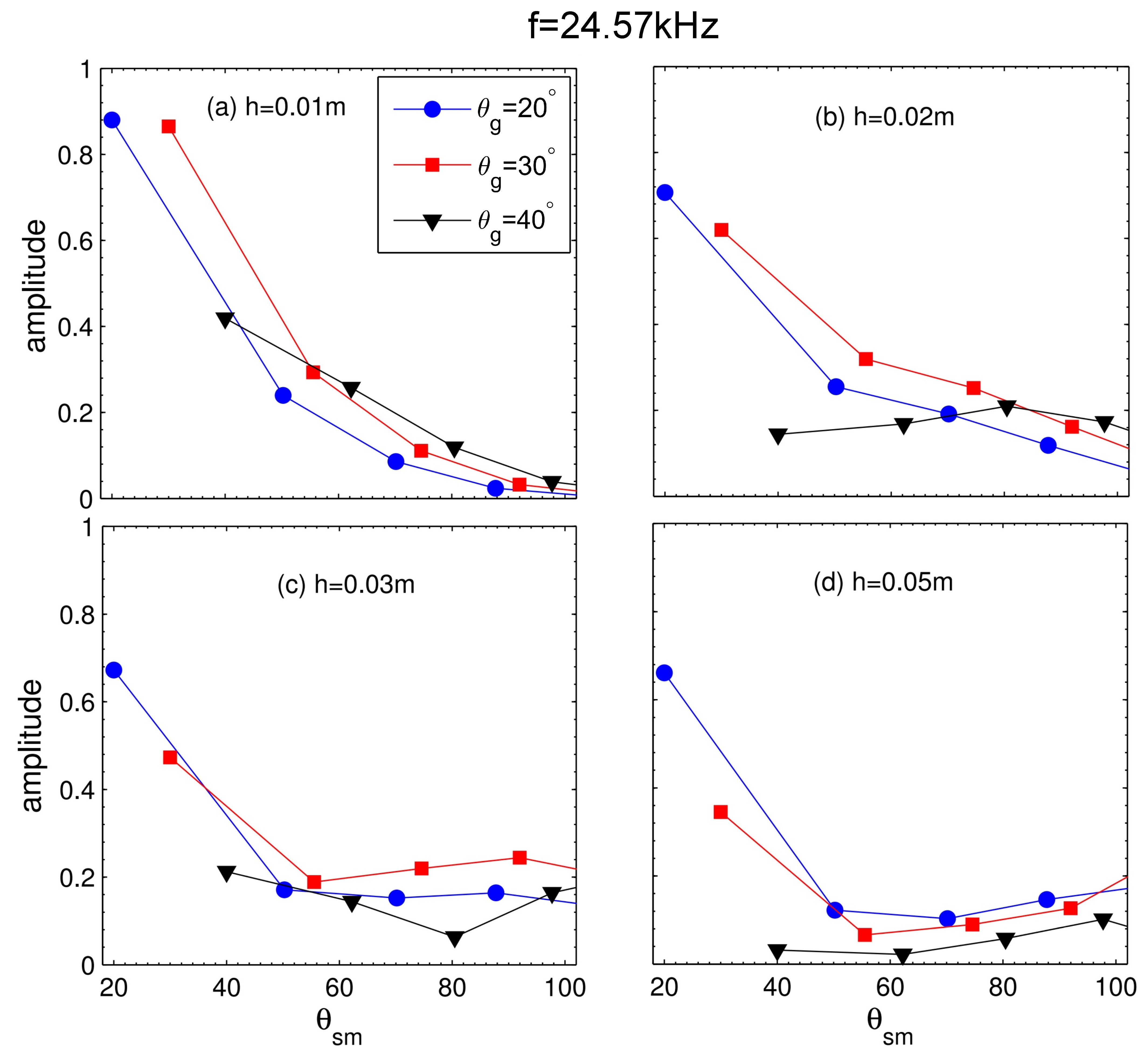
3.3. Analysis of Experimental Data
3.4. Theoretical Interpretation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Brown, D.C.; Brownstead, C.F.; Lyons, A.P.; Gabrielson, T.B. Measurements of two-dimensional spatial coherence of normal-incidence seafloor scattering. J. Acoust. Soc. Am. 2018, 144, 2095–2108. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Weber, T.C.; Ward, L.G. Observations of backscatter from sand and gravel seafloors between 170 and 250 kHz. J. Acoust. Soc. Am. 2015, 138, 2169–2180. [Google Scholar] [CrossRef] [PubMed]
- Hefner, B.; Hodgkiss, W. Reverberation due to a moving, narrowband source in an ocean waveguide. J. Acoust. Soc. Am. 2019, 146, 1661. [Google Scholar] [CrossRef] [PubMed]
- Lopes, J.; Williams, K.; Kargl, S.; Hefner, T.; Thorsos, E.; Marston, P.; Paustian, I.; Lim, R. Monostatic and bistatic measurements of targets resting on or buried under the seafloor. J. Acoust. Soc. Am. 2009, 125, 2701. [Google Scholar] [CrossRef]
- Sabra, K.G.; Roux, P.; Song, H.C.; Hodgkiss, W.S.; Kuperman, W.; Akal, T.; Stevenson, J.M. Experimental demonstration of iterative time-reversed reverberation focusing in a rough waveguide. Application to target detection. J. Acoust. Soc. Am. 2006, 120, 1305–1314. [Google Scholar] [CrossRef]
- Yildiz, S.; Roux, P.; Rakotonarivo, S.T.; Marandet, C.; Kuperman, W. Target localization through a data-based sensitivity kernel: A perturbation approach applied to a multistatic configuration. J. Acoust. Soc. Am. 2014, 135, 1800–1807. [Google Scholar] [CrossRef]
- Boehme, H.; Chotiros, N.; Rolleigh, L.; Pitt, S.; Garcia, A.; Goldsberry, T.; Lamb, R. Acoustic backscattering at low grazing angles from the ocean bottom. Part I. Bottom backscattering strength. J. Acoust. Soc. Am. 1985, 77, 962–974. [Google Scholar] [CrossRef]
- Chotiros, N.; Boehme, H.; Goldsberry, T.; Pitt, S.; Lamb, R.; Garcia, A.; Altenburg, R. Acoustic backscattering at low grazing angles from the ocean bottom. Part II. Statistical characteristics of bottom backscatter at a shallow water site. J. Acoust. Soc. Am. 1985, 77, 975–982. [Google Scholar] [CrossRef]
- Jackson, D.R.; Baird, A.M.; Crisp, J.J.; Thomson, P.A. High-frequency bottom backscatter measurements in shallow water. J. Acoust. Soc. Am. 1986, 80, 1188–1199. [Google Scholar] [CrossRef]
- Jackson, D.R.; Winebrenner, D.P.; Ishimaru, A. Application of the composite roughness model to high-frequency bottom backscattering. J. Acoust. Soc. Am. 1986, 79, 1410–1422. [Google Scholar] [CrossRef]
- Stanic, S.; Briggs, K.; Fleischer, P.; Ray, R.; Sawyer, W. Shallow-water high-frequency bottom scattering off panama city, florida. J. Acoust. Soc. Am. 1988, 83, 2134–2144. [Google Scholar] [CrossRef]
- Stanic, S.; Briggs, K.B.; Fleischer, P.; Sawyer, W.; Ray, R. High-frequency acoustic backscattering from a coarse shell ocean bottom. J. Acoust. Soc. Am. 1989, 85, 125–136. [Google Scholar] [CrossRef]
- de Moustier, C.; Alexandrou, D. Angular dependence of 12-kHz seafloor acoustic backscatter. J. Acoust. Soc. Am. 1991, 90, 522–531. [Google Scholar] [CrossRef]
- Jackson, D.R.; Briggs, K.B. High-frequency bottom backscattering: Roughness versus sediment volume scattering. J. Acoust. Soc. Am. 1992, 92, 962–977. [Google Scholar] [CrossRef]
- Jackson, D.R.; Briggs, K.B.; Williams, K.L.; Richardson, M.D. Tests of models for high-frequency seafloor backscatter. IEEE J. Ocean. Eng. 1996, 21, 458–470. [Google Scholar] [CrossRef]
- Stanic, S.; Goodman, R.R.; Briggs, K.B.; Chotiros, N.P.; Kennedy, E.T. Shallow-water bottom reverberation measurements. IEEE J. Ocean. Eng. 1998, 23, 203–210. [Google Scholar] [CrossRef]
- Holland, C.W.; Hollett, R.; Troiano, L. Measurement technique for bottom scattering in shallow water. J. Acoust. Soc. Am. 2000, 108, 997–1011. [Google Scholar] [CrossRef]
- Williams, K.L.; Jackson, D.R.; Thorsos, E.I.; Tang, D.; Briggs, K.B. Acoustic backscattering experiments in a well characterized sand sediment: Data/model comparisons using sediment fluid and Biot models. IEEE J. Ocean. Eng. 2002, 27, 376–387. [Google Scholar] [CrossRef]
- Soukup, R.J.; Gragg, R.F. Backscatter from a limestone seafloor at 2–3.5 kHz: Measurements and modeling. J. Acoust. Soc. Am. 2003, 113, 2501–2514. [Google Scholar] [CrossRef]
- Hines, P.C.; Osler, J.C.; MacDougald, D.J. Acoustic backscatter measurements from littoral seabeds at shallow grazing angles at 4 and 8 kHz. J. Acoust. Soc. Am. 2005, 117, 3504–3516. [Google Scholar] [CrossRef]
- Williams, K.L.; Jackson, D.R.; Tang, D.; Briggs, K.B.; Thorsos, E.I. Acoustic backscattering from a sand and a sand/mud environment: Experiments and data/model comparisons. IEEE J. Ocean. Eng. 2009, 34, 388–398. [Google Scholar] [CrossRef]
- La, H.; Choi, J.W. 8-kHz bottom backscattering measurements at low grazing angles in shallow water. J. Acoust. Soc. Am. 2010, 127, EL160–EL165. [Google Scholar] [CrossRef] [PubMed]
- Jackson, D.R.; Odom, R.I.; Boyd, M.L.; Ivakin, A.N. A geoacoustic bottom interaction model (GABIM). IEEE J. Ocean. Eng. 2010, 35, 603–617. [Google Scholar] [CrossRef]
- Yu, S.; Liu, B.; Yu, K.; Yang, Z.; Kan, G.; Feng, Z.; Zong, L. Measurements of midfrequency acoustic backscattering from a sandy bottom in the South Yellow Sea of China. IEEE J. Ocean. Eng. 2017, 43, 1179–1186. [Google Scholar] [CrossRef]
- Ellis, D.D.; Crowe, D.V. Bistatic reverberation calculations using a three-dimensional scattering function. J. Acoust. Soc. Am. 1991, 89, 2207–2214. [Google Scholar] [CrossRef]
- Williams, K.L.; Jackson, D.R. Bistatic bottom scattering: Model, experiments, and model/data comparison. J. Acoust. Soc. Am. 1998, 103, 169–181. [Google Scholar] [CrossRef]
- Urick, R. Side scattering of sound in shallow water. J. Acoust. Soc. Am. 1960, 32, 351–355. [Google Scholar] [CrossRef]
- Stanic, S.; Kennedy, E.; Ray, R. Variability of shallow-water bistatic bottom backscattering. J. Acoust. Soc. Am. 1991, 90, 547–553. [Google Scholar] [CrossRef]
- Stanic, S.; Kennedy, E.; Ray, R. High-frequency bistatic reverberation from a smooth ocean bottom. J. Acoust. Soc. Am. 1993, 93, 2633–2638. [Google Scholar] [CrossRef]
- Day, C.M.; Yamamoto, T. Low grazing angle bistatic sea floor scattering on the Florida Atlantic coastal shelf. J. Acoust. Soc. Am. 1999, 106, 1744–1754. [Google Scholar] [CrossRef]
- Choi, J.W.; Na, J.; Seong, W. 240-kHz bistatic bottom scattering measurements in shallow water. IEEE J. Ocean. Eng. 2001, 26, 54–62. [Google Scholar] [CrossRef]
- Choi, J.W.; Na, J.; Yoon, K.S. High-frequency bistatic sea-floor scattering from sandy ripple bottom. IEEE J. Ocean. Eng. 2003, 28, 711–719. [Google Scholar] [CrossRef]
- Jackson, D.R.; Williams, K.L.; Thorsos, E.I.; Kargl, S.G. High-frequency subcritical acoustic penetration into a sandy sediment. IEEE J. Ocean. Eng. 2002, 27, 346–361. [Google Scholar] [CrossRef]
- Pouliquen, E.; Lyons, A.; Pace, N. Penetration of acoustic waves into rippled sandy seafloors. J. Acoust. Soc. Am. 2000, 108, 2071–2081. [Google Scholar] [CrossRef]
- Hefner, B.T.; Jackson, D.R.; Williams, K.L.; Thorsos, E.I. Mid-to high-frequency acoustic penetration and propagation measurements in a sandy sediment. IEEE J. Ocean. Eng. 2009, 34, 372–387. [Google Scholar] [CrossRef]
- Peng, L.; Yu, G. Subcritical penetration into rough seafloors due to Bragg scattering. J. Acoust. Soc. Am. 2013, 134, 166–175. [Google Scholar] [CrossRef]
- Jaud, V.; Sessarego, J.P.; Gervaise, C.; Stephan, Y. Bistatic scattering from an anisotropic rough surface in water tank. In Proceedings of the 4th International Conference on Underwater Acoustics Measurements, Kos Island, Greece, 20–24 June 2011; pp. 809–816. [Google Scholar]
- Jaud, V.; Sessarego, J.P.; Gervaise, C.; Stephan, Y. High frequency roughness scattering from various rough surfaces: Theory and laboratory experiments. Open J. Acoust. 2012, 2, 50–59. [Google Scholar] [CrossRef] [Green Version]
- Calvo, D.C.; Nicholas, M.; Fialkowski, J.M.; Gauss, R.C.; Olson, D.R.; Lyons, A.P. Scale-model scattering experiments using 3D printed representations of ocean bottom features. In Proceedings of the OCEANS 2015-MTS/IEEE Washington, Washington, DC, USA, 19–22 October 2015; pp. 1–7. [Google Scholar]
- Tamura, M. Spatial Fourier transform method of measuring reflection coefficients at oblique incidence. I: Theory and numerical examples. J. Acoust. Soc. Am. 1990, 88, 2259–2264. [Google Scholar] [CrossRef]
- Tamura, M.; Allard, J.F.; Lafarge, D. Spatial Fourier-transform method for measuring reflection coefficients at oblique incidence. II. Experimental results. J. Acoust. Soc. Am. 1995, 97, 2255–2262. [Google Scholar] [CrossRef]
- Yu, G.; Peng, L. Range of validity of the Rayleigh hypothesis for sound wave scattering from a periodic seafloor. IEEE J. Ocean. Eng. 2014, 39, 779–787. [Google Scholar] [CrossRef]
- Welton, P.; Frey, H.; Moore, P. Experimental measurements of the scattering of acoustic waves by rough surfaces. J. Acoust. Soc. Am. 1972, 52, 1553–1563. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Yu, G.; Liang, M.; Ren, Y.; Peng, L. Experimental Measurement of Forward Scattering from Very Rough Sand Ripples in a Water Tank. Remote Sens. 2022, 14, 3865. https://doi.org/10.3390/rs14163865
Wang L, Yu G, Liang M, Ren Y, Peng L. Experimental Measurement of Forward Scattering from Very Rough Sand Ripples in a Water Tank. Remote Sensing. 2022; 14(16):3865. https://doi.org/10.3390/rs14163865
Chicago/Turabian StyleWang, Liang, Gaokun Yu, Minshuai Liang, Yun Ren, and Linhui Peng. 2022. "Experimental Measurement of Forward Scattering from Very Rough Sand Ripples in a Water Tank" Remote Sensing 14, no. 16: 3865. https://doi.org/10.3390/rs14163865
APA StyleWang, L., Yu, G., Liang, M., Ren, Y., & Peng, L. (2022). Experimental Measurement of Forward Scattering from Very Rough Sand Ripples in a Water Tank. Remote Sensing, 14(16), 3865. https://doi.org/10.3390/rs14163865





