1. Introduction
With the increasing complexity of the electromagnetic environment, radar systems are facing many great challenges, especially the demand of anti-jamming capability when monitoring or detecting targets [
1,
2,
3,
4]. At present, array antennas are extensively utilized in radar systems since they have the ability to provide high gain beam, multi-beam and beam scanning [
5,
6,
7,
8]. In practical scenarios, it is likely for a jammer to generate interference through sidelobe regions of an array antenna with high possibility, so it is important for the array antenna to maintain the sidelobes at a specified low level for radar applications [
9]. It is also noticed that the non-Gaussian noise has an important influence on the target detection performance of a radar system [
10,
11]. The peak sidelobe level (PSLL) is one of the critical systematic parameters of an array antenna in the task of reducing background noise and interference for radar systems [
12]. A low PSLL can prevent interference energy from entering the radar receiver through the sidelobe, thus effectively improving the anti-jamming performance of radar systems. Moreover, the generation of null(s) in the direction of interference sources can further enhance the anti-jamming capability of radar systems [
13]. However, the deviation of the antenna position or the rapid movement of the interference source would cause the null(s) of the antenna beampattern to become unaligned with the interference source. Under this circumstance, the wide-nulling technique has emerged as a way to increase the output signal-to-interference-plus-noise ratio (SINR) of radar systems by widening the null region of the beampattern around the interference direction [
14]. Therefore, either the low PSLL or wide-nulling beampattern synthesis of the array antenna can play an important role in improving the performance of radar systems.
Firstly, many typical and traditional amplitude tapering methods have been proposed, such as Chebyshev distribution [
15,
16], Taylor distribution [
17], Gaussian distribution [
18], Fourier transform [
19] and hybrid distributions [
20,
21,
22], to achieve a low sidelobe level (SLL). Secondly, with the development of metaheuristic optimization algorithms, more and more scholars have tried to utilize these algorithms to achieve a low SLL and wide null(s) by adjusting the amplitudes, phases and positions of the array elements. The genetic algorithm (GA) was introduced to obtain a low SLL beampattern synthesis and array thinning in [
23,
24,
25,
26]. Meanwhile, it was also applied to achieve multi-nulls by only adjusting the amplitudes and phases of a relatively small number of elements at the edge of the array [
27]. Compared with the GA, the particle swarm optimization (PSO) algorithm is much easier to understand and implement, and requires a minor mathematical preprocessing [
28]. The PSO algorithm was used to achieve a low SLL and null control by optimizing the positions of the array elements in [
29,
30,
31]. The hybridization of the PSO and ant lion optimization was employed to achieve sidelobe suppression by optimizing the amplitudes and phases of excitations, and element spacing in [
32]. Moreover, the differential evolution (DE) algorithm was utilized to realize a low SLL by properly optimizing the amplitudes, phases and positions of the array elements in [
33,
34,
35]. A quantized DE algorithm and bee algorithm were exploited for interference suppression, which can form single, multiple and wide nulls in prescribed directions by controlling the rotation phases and amplitudes of each element, in [
36,
37]. An analytical approach was proposed for the design of a uniformly spaced array to achieve an as low as possible SLL by only adjusting the mainlobe region in [
38]. A flexible covariance matrix tapering (CMT)-based null-widening method was proposed in [
39], which could produce wide nulls with a different desired width and asymmetry. A binary bat algorithm (BBA)-based amplitude control beamformer was proposed to create a pattern nulling for the uniform linear array to prevent interference in [
40], which has superiority in the convergence rate compared to binary PSO. Moreover, a BBA-based phase control approach for half-wave dipole uniform linear array (DULA) pattern nulling to suppress unknown interference was presented in [
41]. In practical applications, there are many inevitable array errors, such as the mutual coupling effects among elements, amplitude errors, phase errors and element position errors, which exist either inherently or are induced by the limited processing techniques and installing accuracy. These errors would drastically influence the beampattern shape, beam steering and SLL of the array antenna, and further degrade the radar performance of sensitivity and ambiguity suppression [
42]. Nevertheless, the array errors are not taken into consideration in most of the above reported investigations.
To improve the reliability of radar systems, it is of great importance to take these errors into consideration when implementing related researches. In [
43], an analytical approach was presented to investigate the influence of phase shifter errors on the beam collection efficiency of a planar array. Amplitude errors are taken into consideration in [
44] and [
45]. In [
46], an approach based on statistical analysis was proposed for the analysis of the influence of array antenna position errors on the beam collection efficiency. In [
47], the improved DE was adopted to achieve array synthesis for optimal microwave power transmission in the presence of excitation errors. A conical method for the representation of position errors is proposed in [
48], which considers both the relevance and the randomness of adjacent planar array elements. In [
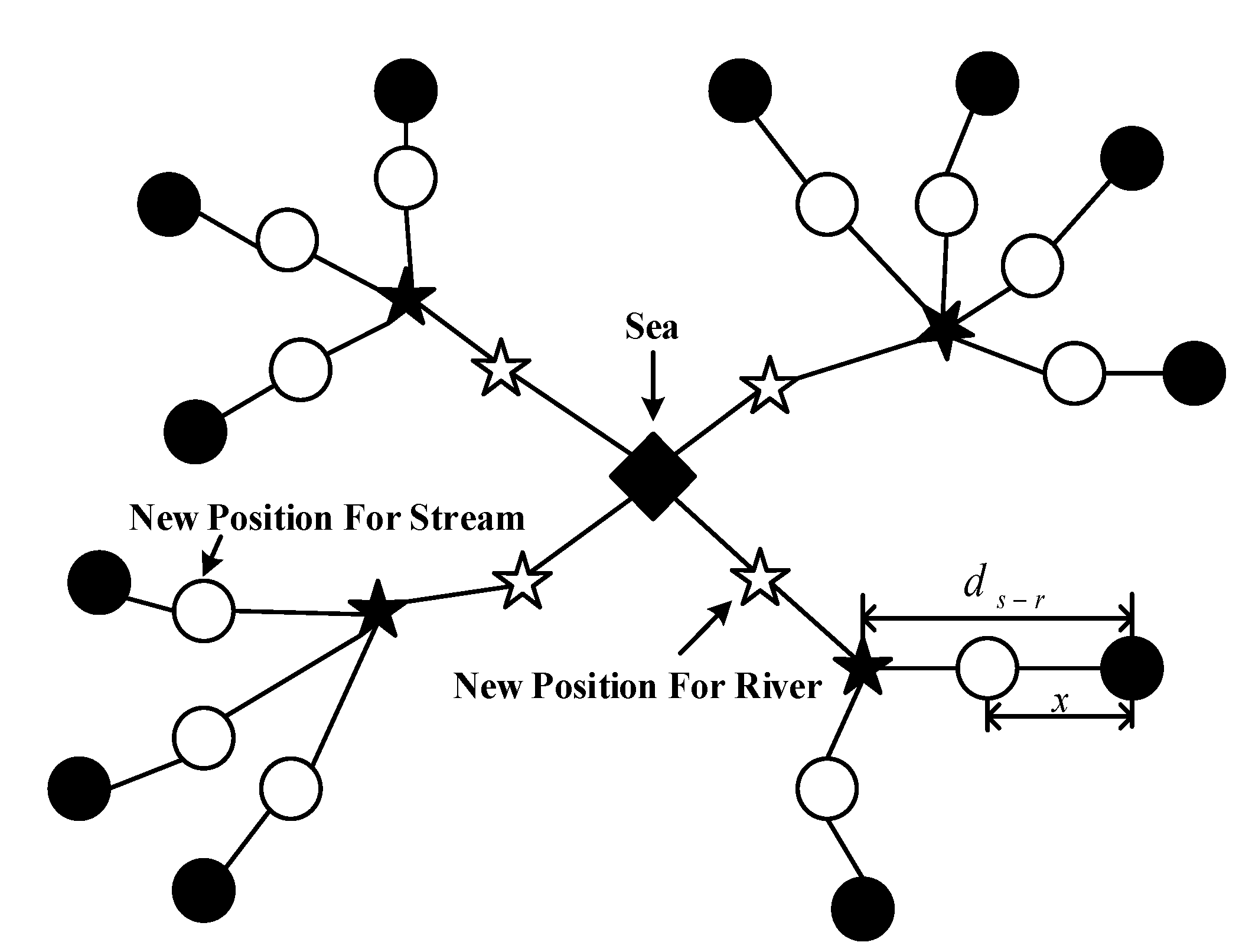
49], an approach was proposed to design sum and difference patterns with common nulls and low SLLs simultaneously in the presence of array errors for radar applications. After a thorough literature review, it was found that most of the current investigations only consider one or two kinds of factors when implementing relative researches, and quite limited investigations have been conducted on either the low PSLL or wide-nulling beampattern synthesis for radar applications in the presence of unavoidable array errors in the state-of-the-art methods. Inspired by the observation of the water cycle and how rivers and streams flow downhill in nature, Eskandar et al. [
50] proposed a new metaheuristic algorithm, i.e., WCA, in 2012. This algorithm has the advantages of a fast optimization rate and high iterative accuracy. This simple and robust algorithm has good potential for finding all global optimal solutions of multimodal functions and benchmark functions [
51,
52]. At present, it has only been introduced in array beampattern synthesis [
53] and antenna design [
54]. Aiming at improving the performance of radar systems in monitoring or detecting targets, an effective low PSLL and wide-nulling beampattern synthesis approach is proposed based on the advanced WCA in the presence of array errors. The main contributions of this work are summarized as follows.
- (1)
A more general array error model is established by summarizing all of the above mentioned factors on the array beamforming as the amplitude and phase response errors satisfying the Gaussian random distribution and zero mean uniformly random distribution, respectively.
- (2)
The WCA-based low PSLL and wide-nulling beampattern synthesis approach is proposed in the presence of array errors with proper constraints imposed on the mainbeam width and the PSLL. In particular, the covariance matrix of the sidelobe region (CMSR) is incorporated into the optimization problem based on the above error model.
- (3)
Theoretical analysis based on the signal processing technique and electromagnetic simulation based on the Ansoft HFSS workbench are combined to verify the effectiveness of the proposed low PSLL and wide-nulling beampattern synthesis in the presence of errors.
The rest of the paper is arranged as follows. In
Section 2, the basic signal models are established, and the consequent problems are introduced. The proposed WCA-based beampattern synthesis approach is presented in
Section 3 to separately achieve low PSLL and wide null(s) in the presence of array errors. Theoretical results using the MATLAB workbench and electromagnetic simulation results using the Ansoft HFSS workbench are provided and analyzed in
Section 4 to verify the effectiveness of the proposed approach. Finally,
Section 5 summarizes the work and draws the conclusion of this paper.
2. Signal Models and Problem Formulation
Take a uniformly spaced linear array composed of
M elements into consideration, the inter-element spacing of which is denoted by
d, as depicted in
Figure 1. Set the first element as the reference point, then the steering vector of the array can be expressed as [
55]
where
,
stands for the wave vector with
being the operational wavelength, the superscript
denotes the transpose operator and
is defined as the angle deviating from the positive
y-axis.
,
is the position vector of the
mth element.
In practical scenarios, it is known that many unavoidable errors exist due to many factors, such as the exciting errors, position errors, failure element(s) and the mutual coupling effects among elements. Therefore, the actual steering vector cannot be exactly expressed by Equation (1). In this case,
is utilized in lieu of
when formulating the actual power pattern of the array, i.e.,
where the superscript
denotes the conjugate transpose operator,
represents the weight vector of the array and
is the actual covariance matrix of the array in the presence of array errors. The aforementioned errors will drastically distort the array beampattern and consequently weaken the performance of radar systems. Usually, the above mentioned factors are merged together, and it is quite difficult to individually distinguish their influence on the array beamforming. In this case, it is reasonable to summarize the effects of all these factors on the array beamforming as the amplitude and phase response errors. Therefore, the actual steering vector can be constructed as
where
is the array error vector, and
stands for the Schur–Hadamard product. Specifically
where the parameters
and
represent the amplitude and phase response errors, respectively, and satisfy the Gaussian random distribution and zero mean uniformly random distribution, respectively. Herein, it should be highlighted that the maximum amplitude and phase response errors can be preliminarily estimated by measurement.
As is shown in Equation (2),
is important in forming the array pattern. To analyze the properties of
, we first examine the characteristic of
. Since Equation (4) can be equivalently written as
, the expectation value of
can be expressed as
where
denotes the expectation operator. Therefore, the expectation of the actual covariance matrix can be represented as
where
is the error matrix. From Equation (6), it is seen that the expectation of
in the presence of array errors converges to
. Namely, the existence of errors introduces a disturbance on the covariance matrix
.
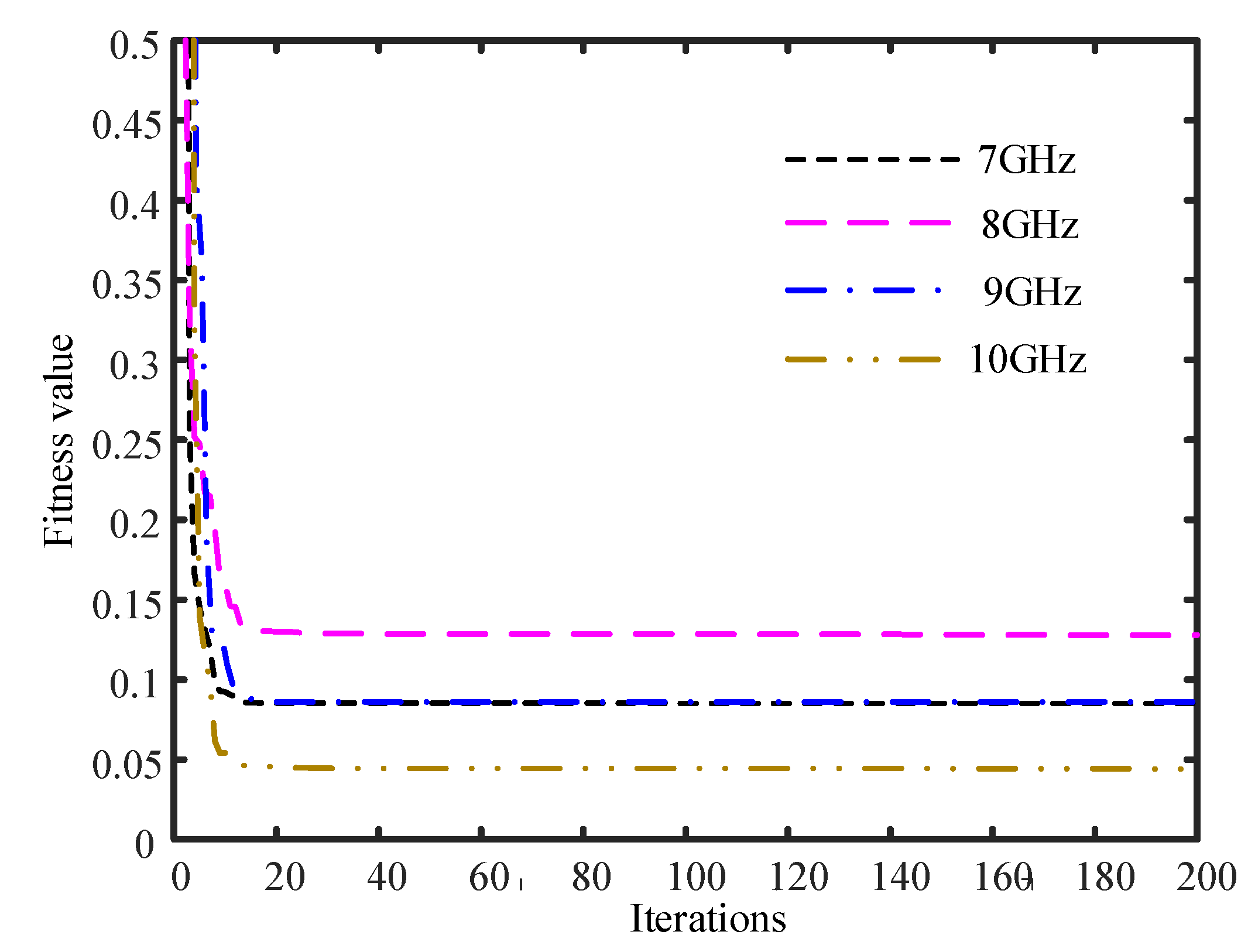
Generally, the CMSR is commonly utilized when implementing the beampattern synthesis. To accurately calculate the CMSR in the presence of array errors, the statistical mean method is exploited. Specifically,
Monte Carlo trials are executed, and then the mean of the CMSR in the existence of array errors can be written as
where
is the CMSR obtained in the
lth Monte Carlo trial with array errors taken into consideration,
and
denote the two boundaries of array sidelobe region, and
. Then the estimated
will be incorporated into the WCA-based low PSLL and wide-nulling beampattern synthesis presented in
Section 3.
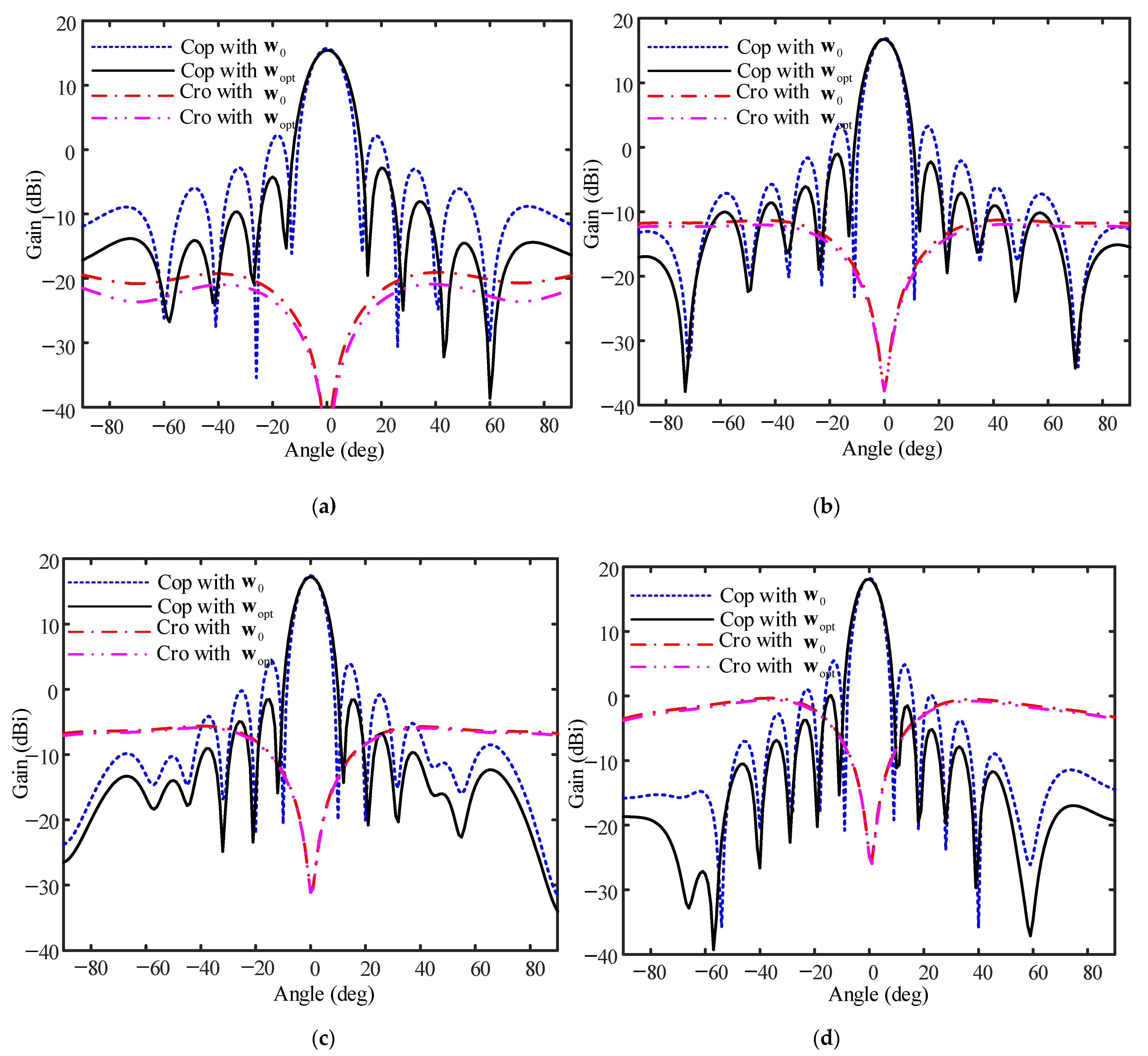
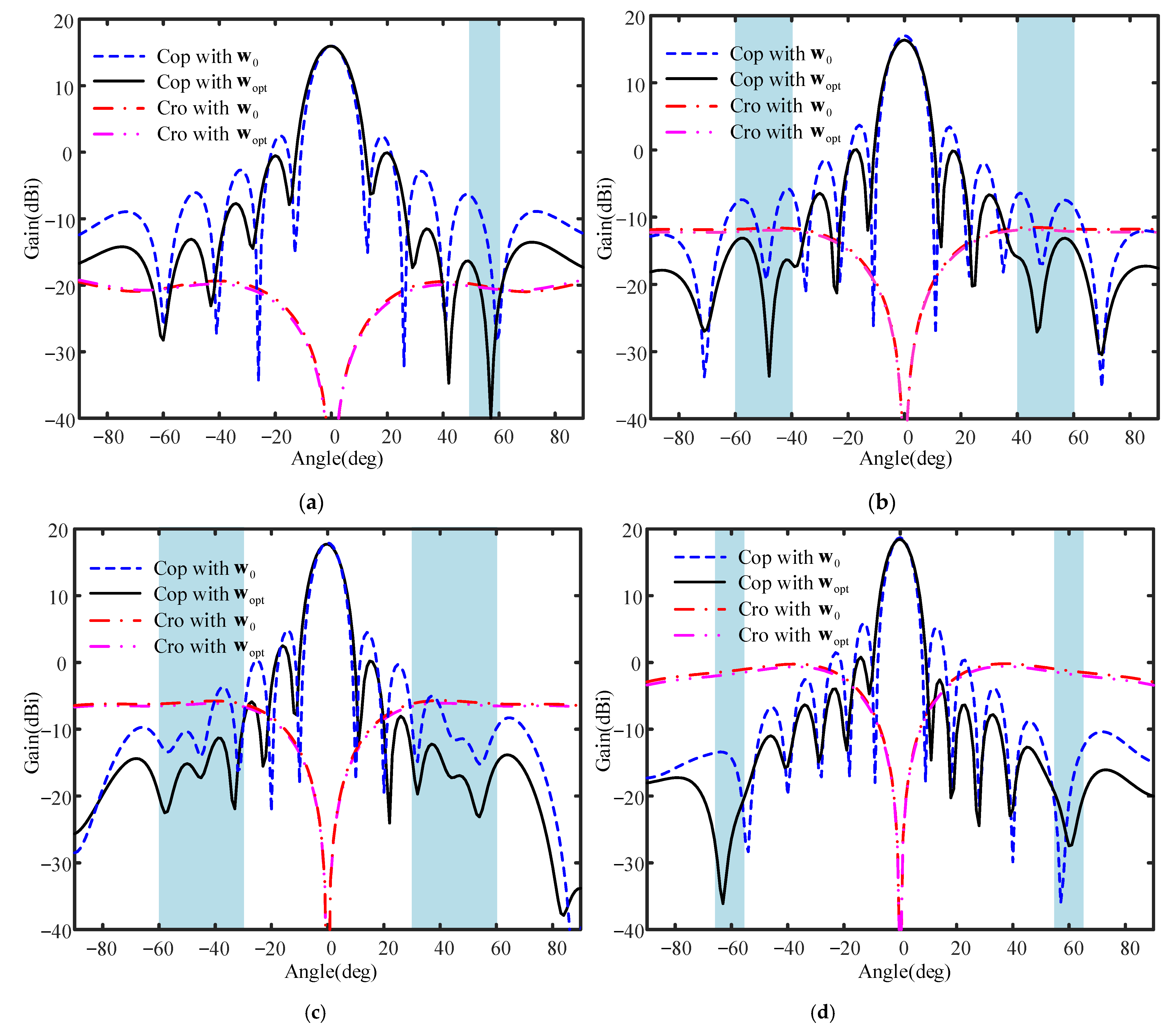
At the end of this section, an illustration is provided to show the possible negative influence that the array errors would have on the array beampattern. As depicted in
Figure 2, four normalized patterns are presented in four different situations. Specifically, pattern 1 and pattern 2 are generated with
, respectively, in an ideal situation and in the presence of 10% array errors, while pattern 3 and pattern 4 are formed with
, respectively, in an ideal situation and in the presence of 10% array errors, where
is an all one vector and
denotes the wide-nulling weight vector where the wide null is located at the angle region from 30° to 40° with a null level (NL) of −35 dB. Comparing pattern 2 with pattern 1, it is observed that the PSLL is increased from −12.8 dB to −8.8 dB due to the existence of array errors. Comparing pattern 4 with pattern 3, it is seen that not only is the wide null distorted, but also the PSLL is increased (from −20 dB to −16.3 dB) when the array errors exist.