Detecting Spatial Communities in Vehicle Movements by Combining Multi-Level Merging and Consensus Clustering
Abstract
:1. Introduction
2. Related Work
3. Study Area and Dataset
4. Method
4.1. Construction of a Weighted Spatially Embedded Network
4.2. Iterative Local Moving and Global Perturbation Approach
- (1)
- Spatially constrained local moving. We first initialize each vertex as a spatial community (Figure 4a). Then, each vertex vi was moved from the current community to a spatial adjacent community of vi that yields the largest increase in modularity. When modularity cannot be improved by moving each vertex, a local optimum solution is obtained (Figure 4b). Community Cj is a spatial adjacent community of vertex vi if at least one vertex in Cj is the spatial neighbor of vi. The gain of modularity for moving a vertex vi from community Cj to community Ck (j ≠ k) can be calculated as:where and are the sum of the weights of the edges inside Ck and Cj, respectively. and are the sums of the weights of the edges between vi and the vertices in Ck and Cj, respectively. is the sum of edge weights linked to vi. and are the sums of the weights of the edges linked to the vertices in Ck and Cj, respectively. The sum of the edge weights of the network is defined by m;
- (2)
- Spatially constrained global perturbation. After the local moving operation, we further used a global perturbation operation [38] to reconstruct the local optimum solution. An ideal global perturbation operation should not only jump out of the local optimum trap, but also guide the algorithm to find a possible better solution [27]. To achieve this purpose, for each vertex vi on the boundaries of communities, we first identified the spatial adjacent community of vi, which makes ∆Qi reaches its maximum value. Then, we sorted these vertices in a non-increasing order according to ∆Q. Finally, we selected the first Np vertices to forcibly move them from their original communities to their spatial adjacent communities, even if the ∆Q values are negative (Figure 4c). The spatial continuity of each community cannot be destroyed in the global perturbation process. After the global perturbation, a new round of spatially constrained local moving (Step 1) should be applied to optimize modularity. We performed the global perturbation operation Id times and recorded the community detection result with the highest modularity;
- (3)
- Refinement and network aggregation. After spatially constrained global perturbation, there may be some weakly-connected (even disconnected) spatial communities. The refinement operation of Leiden [35] was modified to handle this problem. Each spatial community was considered as a sub-network. The spatially constrained local moving method in Step 1 was performed within each sub-network (Figure 4d). A spatial community may be split into several small communities (but not always). After the refinement operation, a network aggregation operation [25] was used to construct a new weighted spatially embedded network, where each vertex is a spatial community and the weights between vertices are the sum of the weights between two communities (Figure 4e).
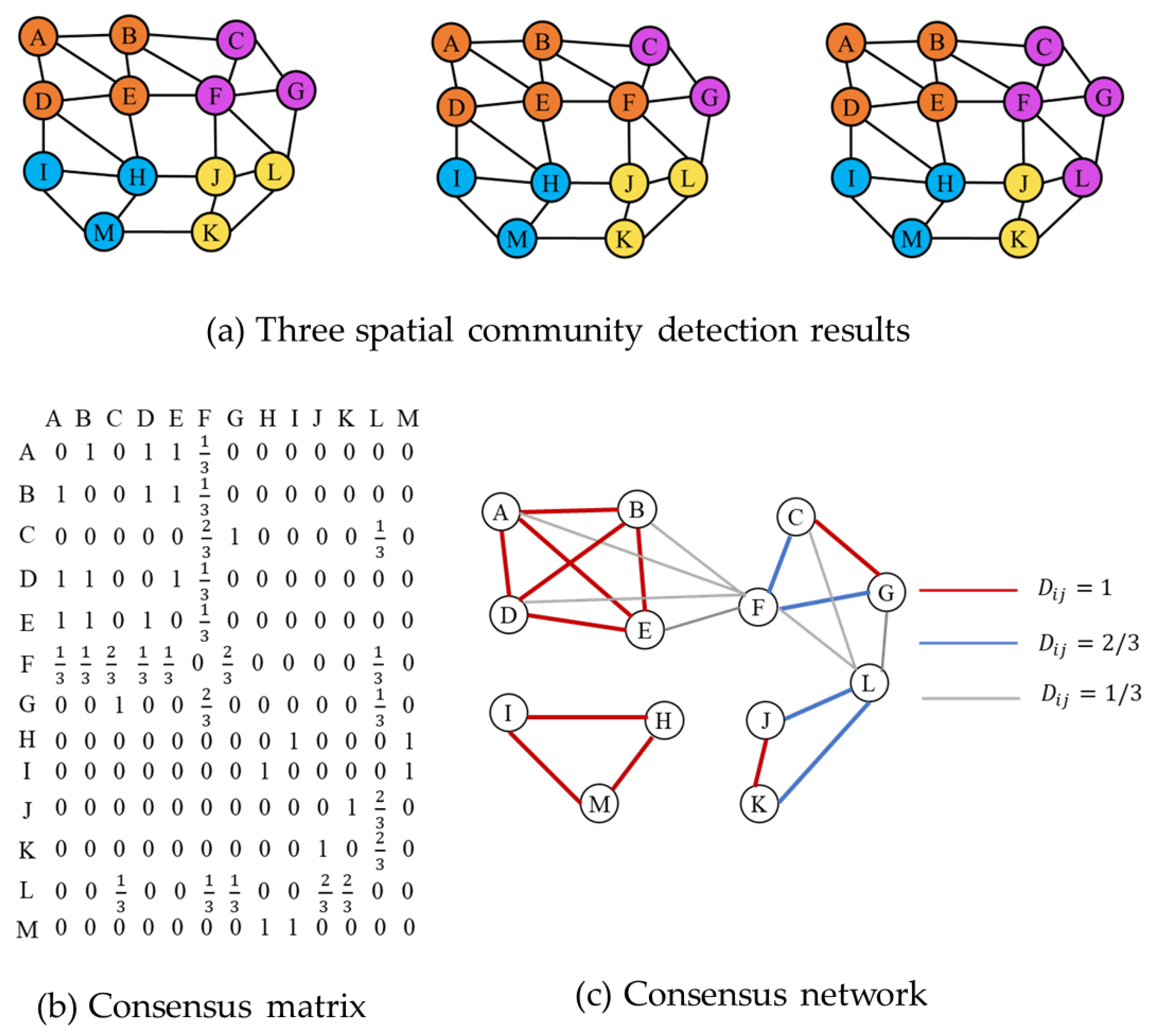
4.3. Identification of Stable Spatial Communities Based on Consensus Clustering
4.4. The Implementation of the Proposed Method
| Algorithm 1SCMiner (Input: R, Trj, Id, Np, Nc, t) |
| SpatialAdjacencyMatrix = SpatialAdjacencyMatrixConstructiI(R)//Construct the spatial adjacency matrix of the road network For r = 1: Nc Network = NetworkConstruction (Trj)//Construct the weighted spatially embedded network CommunityStructure = InitializeCommunityStructure (Network)//Initialize the spatial community structure CommunityStructure = SpatiallyConstrainedLocalMoving (CommunityStructure, Network, SpatialAdjacencyMatrix)//Optimize the communities under the contiguity constraint Flag = True while Flag = True: For i = 1: Id CommunityStructure = SpatiallyConstrainedGlobalPerturbation (CommunityStructure, Network, SpatialAdjacencyMatrix, Np)//Spatially constrained global perturbation CommunityStructure = SpatiallyConstrainedLocalMoving (CommunityStructure, Network, SpatialAdjacencyMatrix)//Optimize communities under the contiguity constraint End for i CommunityStructure = Refinement (CommunityStructure, Network, SpatialAdjacencyMatrix)//Refine the network CommunityStructure, Network = NetworkAggregation(CommunityStructure, Network)//Aggregate communities into vertices InitialQ = Modularity (CommunityStructure)//Calculate modularity of the spatial community structure CommunityStructure = SpatiallyConstrainedLocalMoving (CommunityStructure, Network, SpatialAdjacencyMatrix)//Optimize the communities under the contiguity constraint NewQ = Modularity (CommunityStructure)//Calculate modularity of the spatial community structure If NewQ = InitialQ: Flag = False End while Insert CommunityStructure into CandidateCommunityStructures End for r TrueCommunityStructure = ConsensusClustering (CandidateCommunityStructures, t)//Apply consensus clustering on Nc results return TrueCommunity |
5. Experimental Results
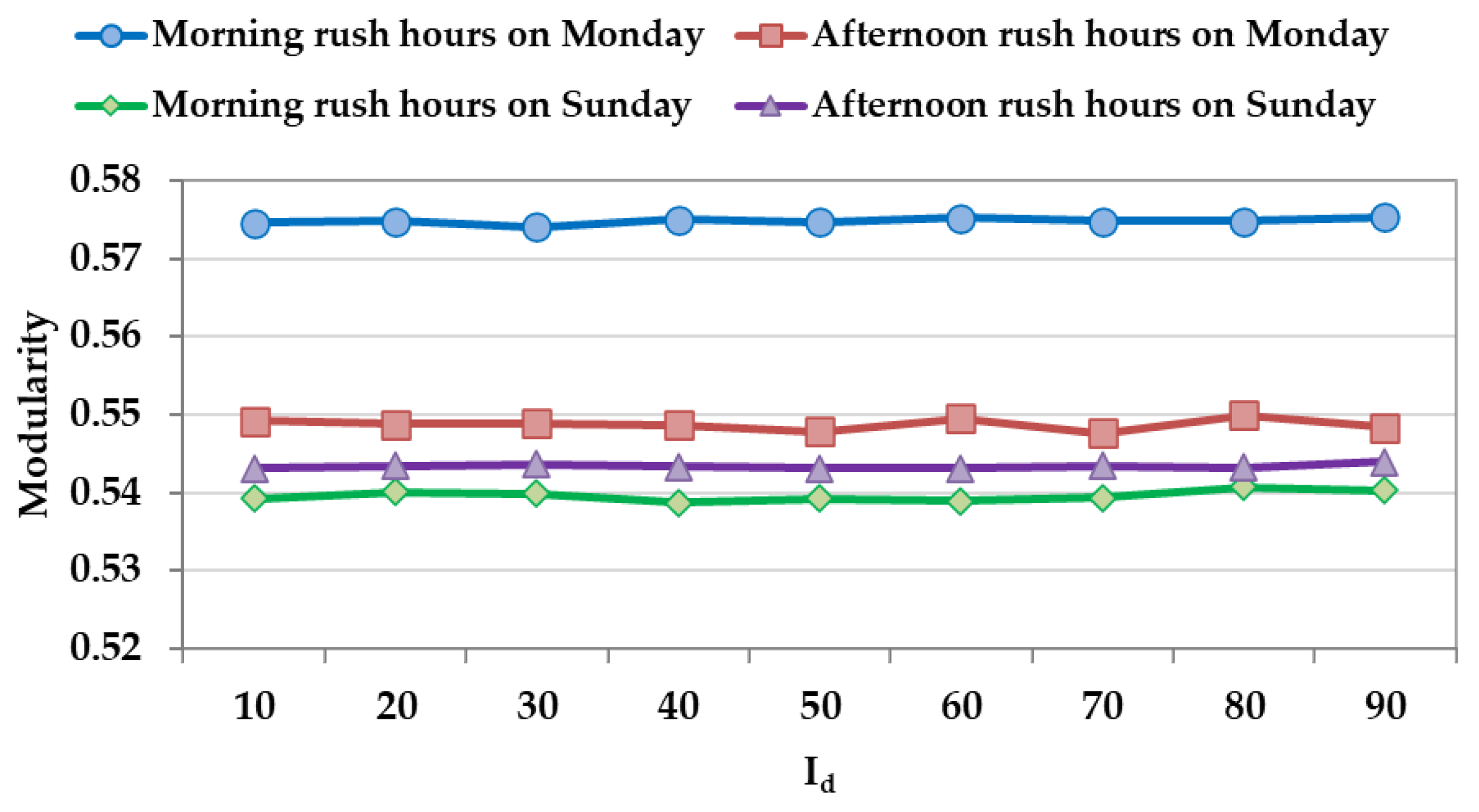
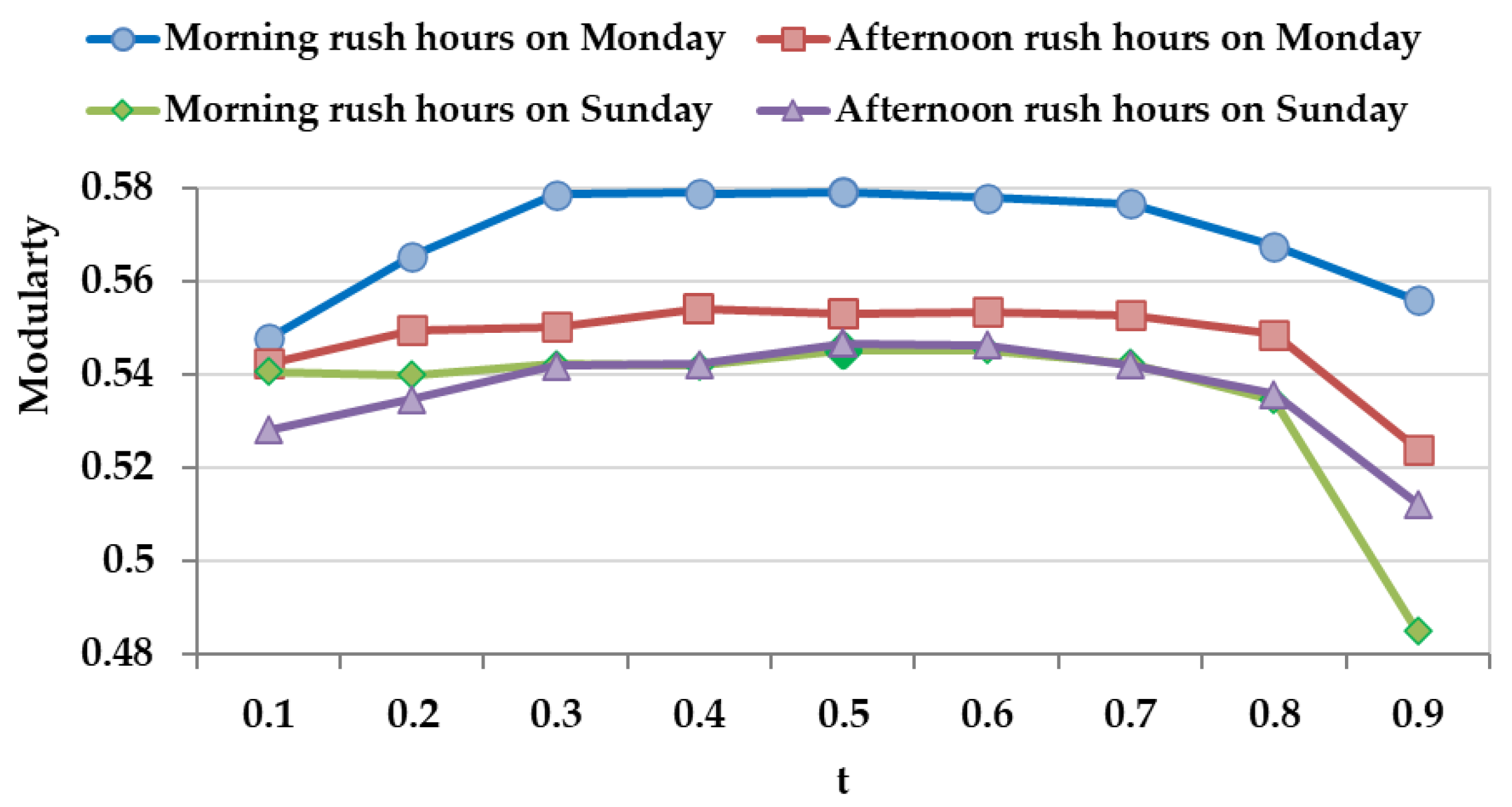
5.1. Parameters Setting
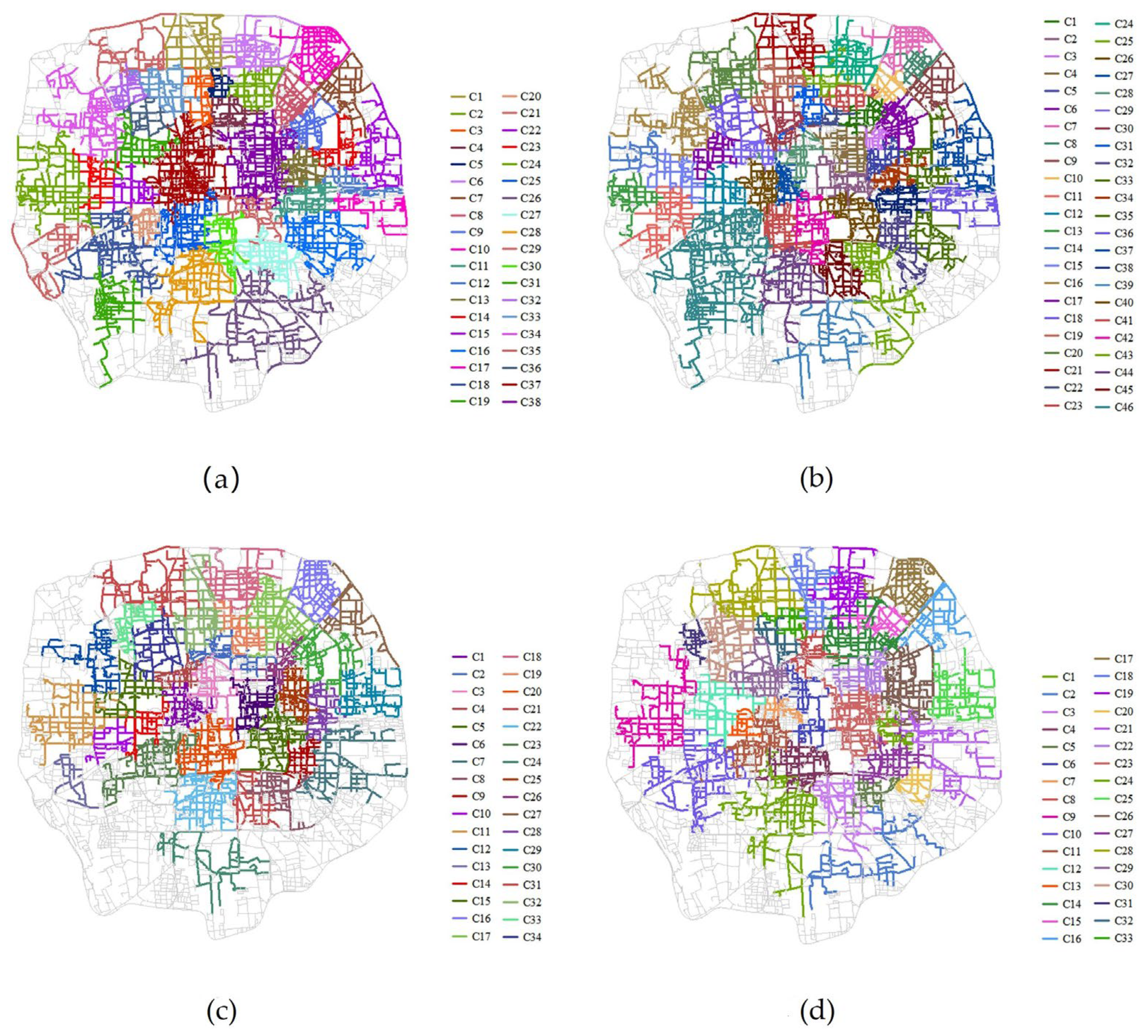
5.2. Spatial Communities during Morning Rush Hours
5.3. Spatial Communities during Afternoon Rush Hours
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Siła-Nowicka, K.; Vandrol, J.; Oshan, T.; Long, J.A.; Demšar, U.; Fotheringham, A.S. Analysis of human mobility patterns from GPS trajectories and contextual information. Int. J. Geogr. Inf. Sci. 2015, 30, 881–906. [Google Scholar] [CrossRef] [Green Version]
- Liu, K.; Gao, S.; Lu, F. Identifying spatial interaction patterns of vehicle movements on urban road networks by topic modelling. Comput. Environ. Urban Syst. 2019, 74, 50–61. [Google Scholar] [CrossRef]
- Zhu, D.; Wang, N.; Wu, L.; Liu, Y. Street as a big geo-data assembly and analysis unit in urban studies: A case study using Beijing taxi data. Appl. Geogr. 2017, 86, 152–164. [Google Scholar] [CrossRef]
- Liu, X.; Gong, L.; Gong, Y.; Liu, Y. Revealing travel patterns and city structure with taxi trip data. J. Transp. Geogr. 2015, 43, 78–90. [Google Scholar] [CrossRef] [Green Version]
- Zheng, Y.; Capra, L.; Wolfson, O.; Yang, H. Urban computing: Concepts, methodologies, and applications. ACM Trans. Intell. Syst. Technol. TIST 2014, 5, 1–55. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, X.; Gao, S.; Gong, L.; Kang, C.; Zhi, Y.; Chi, G.; Shi, L. Social sensing: A new approach to understanding our socioeconomic environments. Ann. Assoc. Am. Geogr. 2015, 105, 512–530. [Google Scholar] [CrossRef]
- Guo, D.; Jin, H.; Gao, P.; Zhu, X. Detecting spatial community structure in movements. Int. J. Geogr. Inf. Sci. 2018, 32, 1326–1347. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, J.; Xu, M. Finding community structure in spatially constrained complex networks. Int. J. Geogr. Inf. Sci. 2015, 29, 889–911. [Google Scholar] [CrossRef]
- Wang, C.; Wang, F.; Onega, T. Network Optimization Approach to Delineating Health Care Service Areas: Spatially Constrained Louvain and Leiden Algorithms. Trans. GIS 2021, 25, 1065–1081. [Google Scholar] [CrossRef]
- Zhong, C.; Arisona, S.M.; Huang, X.; Batty, M.; Schmitt, G. Detecting the dynamics of urban structure through spatial network analysis. Int. J. Geogr. Inf. Sci. 2014, 28, 2178–2199. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Y.; Tu, W.; Ratti, C. Do different datasets tell the same story about urban mobility—A comparative study of public transit and taxi usage. J. Transp. Geogr. 2018, 70, 78–90. [Google Scholar] [CrossRef]
- Lu, F.; Liu, K.; Duan, Y.; Cheng, S.; Du, F. Modeling the heterogeneous traffic correlations in urban road systems using traffic-enhanced community detection approach. Phys. A Stat. Mech. Appl. 2018, 501, 227–237. [Google Scholar] [CrossRef]
- Fortunato, S. Community detection in graphs. Phys. Rep. 2010, 486, 75–174. [Google Scholar] [CrossRef] [Green Version]
- Attea, B.A.A.; Abbood, A.D.; Hasan, A.A.; Pizzuti, C.; Al-Ani, M.; Özdemir, S.; Al-Dabbagh, R.D. A review of heuristics and metaheuristics for community detection in complex networks: Current usage, emerging development and future directions. Swarm Evol. Comput. 2021, 63, 100885. [Google Scholar] [CrossRef]
- Rossetti, G.; Cazabet, R. Community discovery in dynamic networks: A survey. ACM Comput. Surv. 2018, 51, 1–37. [Google Scholar] [CrossRef] [Green Version]
- Strehl, A.; Ghosh, J. Cluster ensembles-a knowledge reuse framework for combining multiple partitions. J. Mach. Learn. Res. 2002, 3, 583–617. [Google Scholar]
- Newman, M.E.; Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. E 2004, 69, 026113. [Google Scholar] [CrossRef] [Green Version]
- Clauset, A.; Newman, M.E.; Moore, C. Finding community structure in very large networks. Phys. Rev. E 2004, 70, 066111. [Google Scholar] [CrossRef] [Green Version]
- Chakraborty, T.; Dalmia, A.; Mukherjee, A.; Ganguly, N. Metrics for community analysis: A survey. ACM Comput. Surv. (CSUR) 2017, 50, 1–37. [Google Scholar] [CrossRef]
- Cafieri, S.; Hansen, P.; Liberti, L. Edge ratio and community structure in networks. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2010, 81, 026105. [Google Scholar] [CrossRef] [Green Version]
- Radicchi, F.; Castellano, C.; Cecconi, F.; Loreto, V.; Parisi, D. Defining and identifying communities in networks. Proc. Natl. Acad. Sci. USA 2004, 101, 2658–2663. [Google Scholar] [CrossRef] [Green Version]
- Shi, J.; Malik, J. Normalized cuts and image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 888–905. [Google Scholar]
- Rosvall, M.; Bergstrom, C.T. Maps of random walks on complex networks reveal community structure. Proc. Natl. Acad. Sci. USA 2008, 105, 1118–1123. [Google Scholar] [CrossRef] [Green Version]
- Rosvall, M.; Bergstrom, C.T. Multilevel compression of random walks on networks reveals hierarchical organization in large integrated systems. PLoS ONE 2011, 6, e18209. [Google Scholar] [CrossRef] [Green Version]
- Blondel, V.D.; Guillaume, J.-L.; Lambiotte, R.; Lefebvre, E. Fast unfolding of communities in large networks. J. Stat. Mech. Theory Exp. 2008, 2008, P10008. [Google Scholar] [CrossRef] [Green Version]
- Gach, O.; Hao, J.-K. Combined neighborhood tabu search for community detection in complex networks. RAIRO-Oper. Res. 2016, 50, 269–283. [Google Scholar] [CrossRef] [Green Version]
- Lu, Z.; Huang, W. Iterated tabu search for identifying community structure in complex networks. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2009, 80, 026130. [Google Scholar] [CrossRef]
- Pons, P.; Latapy, M. Computing communities in large networks using random walks. In Proceedings of the 20th International Symposium on Computer and Information Sciences, Istanbul, Turkey, 26–28 October 2005; pp. 284–293. [Google Scholar]
- Karimi, F.; Lotfi, S.; Izadkhah, H. Multiplex community detection in complex networks using an evolutionary approach. Expert Syst. Appl. 2020, 146, 113184. [Google Scholar] [CrossRef]
- Zhou, X.; Liu, Y.; Zhang, J.; Liu, T.; Zhang, D. An ant colony based algorithm for overlapping community detection in complex networks. Phys. A Stat. Mech. Appl. 2015, 427, 289–301. [Google Scholar] [CrossRef]
- Liu, Q.; Zhu, S.; Deng, M.; Liu, W.; Wu, Z. A Spatial Scan Statistic to Detect Spatial Communities of Vehicle Movements on Urban Road Networks. Geogr. Anal. 2021, 54, 124–148. [Google Scholar] [CrossRef]
- Expert, P.; Evans, T.S.; Blondel, V.D.; Lambiotte, R. Uncovering space-independent communities in spatial networks. Proc. Natl. Acad. Sci. USA 2011, 108, 7663–7668. [Google Scholar] [CrossRef] [Green Version]
- Gao, S.; Liu, Y.; Wang, Y.; Ma, X. Discovering Spatial Interaction Communities from Mobile Phone Data. Trans. GIS 2013, 17, 463–481. [Google Scholar] [CrossRef] [Green Version]
- Wan, Y.; Liu, Y. DASSCAN: A Density and Adjacency Expansion-Based Spatial Structural Community Detection Algorithm for Networks. ISPRS Int. J. Geo-Inf. 2018, 7, 159. [Google Scholar] [CrossRef] [Green Version]
- Traag, V.A.; Waltman, L.; van Eck, N.J. From Louvain to Leiden: Guaranteeing well-connected communities. Sci. Rep. 2019, 9, 5233. [Google Scholar] [CrossRef]
- Lancichinetti, A.; Fortunato, S. Consensus clustering in complex networks. Sci. Rep. 2012, 2, 336. [Google Scholar] [CrossRef]
- White, C.E.; Bernstein, D.; Kornhauser, A.L. Some map matching algorithms for personal navigation assistants. Transp. Res. Part C Emerg. Technol. 2000, 8, 91–108. [Google Scholar] [CrossRef]
- Lourenço, H.R.; Martin, O.C.; Stützle, T. Iterated local search. In Handbook of Metaheuristics; Springer: Berlin, Germany, 2003; pp. 320–353. [Google Scholar]
- Reichardt, J.; Bornholdt, S. Statistical mechanics of community detection. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2006, 74, 016110. [Google Scholar] [CrossRef] [Green Version]
- Ruan, J.; Zhang, W. Identifying network communities with a high resolution. Phys. Rev. E 2008, 77, 016104. [Google Scholar] [CrossRef] [Green Version]
- Newman, M.E. The structure and function of complex networks. SIAM Rev. 2003, 45, 167–256. [Google Scholar] [CrossRef] [Green Version]
- Danon, L.; Díaz-Guilera, A.; Duch, J.; Arenas, A. Comparing community structure identification. J. Stat. Mech. Theory Exp. 2005, 2005, P09008. [Google Scholar] [CrossRef]
- Cai, J.; Huang, B.; Song, Y. Using multi-source geospatial big data to identify the structure of polycentric cities. Remote Sens. Environ. 2017, 202, 210–221. [Google Scholar] [CrossRef]
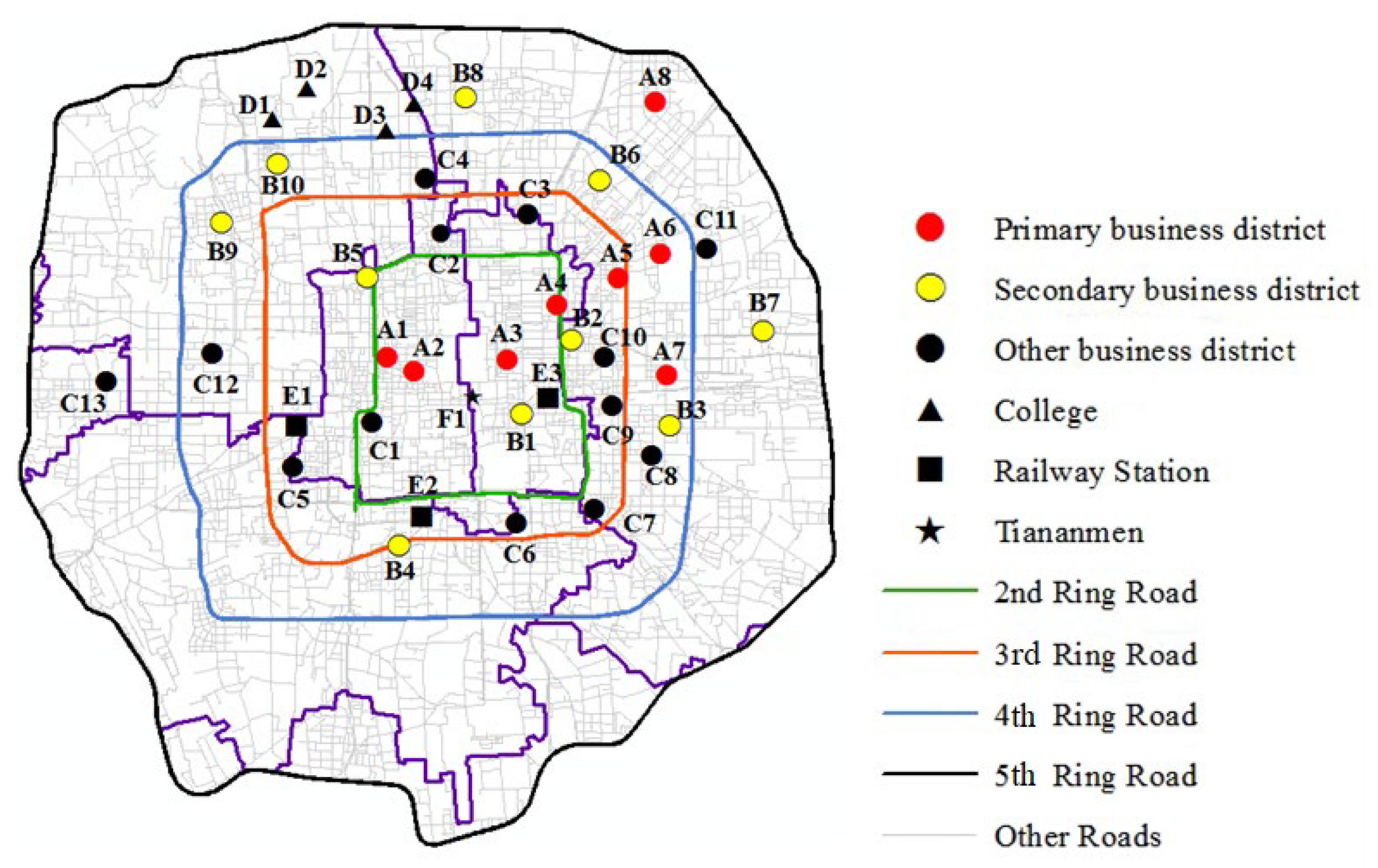








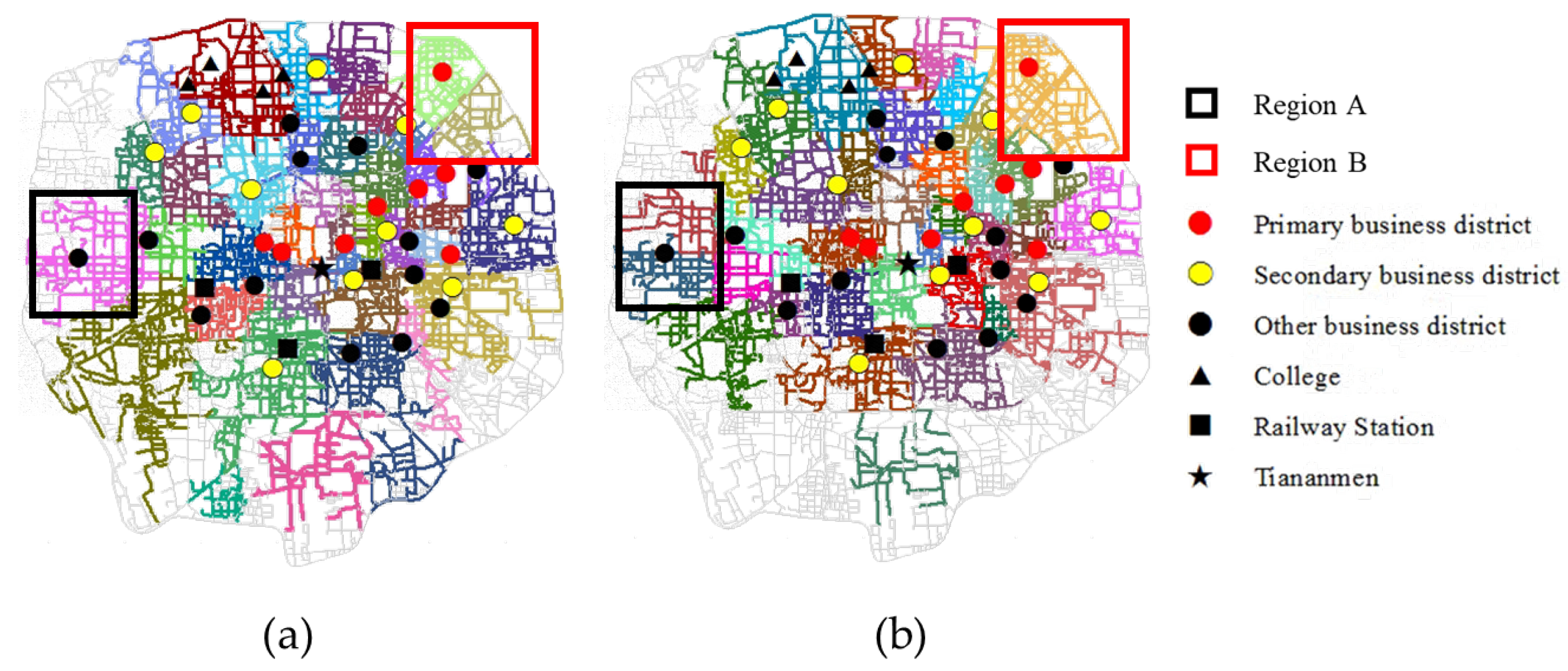
| Description of Locations | Name of Locations |
|---|---|
| Primary business district | A1: Financial Street, A2: Xidan, A3: Wangfujing, A4: Dongzhimen, A5: Sanlitun, A6: Yansha, A7: CBD, A8: Wangjing |
| Secondary business district | B1: Chongwenmen, B2: Zhaowai, B3: Shuangjing, B4: Gongzhufen, B5: Xizhimen, B6: Taiyanggong, B7: Chaoqing, B8: Yaao, B9: Wanliu, B10: Zhongguancun |
| Other business district | C1: Guanganmen, C2: Jishuitan, C3: Andingmen, C4: Beitaipingzhuang, C5: Lize, C6: Muxiyuan, C7: Fangzhuang, C8: Panjiayuan, C9: Guangqvmen, C10: Jianguomen, C11: Chaoyang Park, C12: Wukesong, C13: Lugu |
| College | D1: Peking University, D2: Tsinghua University, D3: Beijing University of Aeronautics and Astronautics, D4: University of Science and Technology Beijing |
| Railway Station | E1: Beijing West Railway Station, E2: Beijing South Railway Station, E3: Beijing Station |
| Tourist spot | F1: Tiananmen |
| The Proposed Method | Scleiden+ | |||||
|---|---|---|---|---|---|---|
| Maximum Value | Minimum Value | Average Value | Maximum Value | Minimum Value | Average Value | |
| low resolution results on Monday | 9.7 | 5.4 | 7.0 | 9.0 | 5.1 | 6.5 |
| high resolution results on Monday | 9.0 | 1.1 | 4.9 | 8.0 | 0.9 | 4.5 |
| low resolution results on Sunday | 7.4 | 3.7 | 4.8 | 6.7 | 2.6 | 4.3 |
| high resolution results on Sunday | 6.1 | 1.6 | 2.9 | 5.1 | 1.3 | 2.7 |
| The Proposed Method | Scleiden | Scleiden+ | |
|---|---|---|---|
| low resolution results on Monday | 0.579 | 0.568 | 0.568 |
| high resolution results on Monday | 0.478 | 0.419 | 0.429 |
| low resolution results on Sunday | 0.545 | 0.527 | 0.529 |
| high resolution results on Sunday | 0.422 | 0.375 | 0.370 |
| The Proposed Method | Scleiden+ | |||||
|---|---|---|---|---|---|---|
| Maximum Value | Minimum Value | Average Value | Maximum Value | Minimum Value | Average Value | |
| low resolution results on Monday | 12.6 | 6.2 | 9.0 | 11.2 | 5.9 | 8.9 |
| high resolution results on Monday | 12.7 | 2.9 | 6.1 | 11.9 | 2.3 | 5.7 |
| low resolution results on Sunday | 9.8 | 4.8 | 7.0 | 9.7 | 4.2 | 6.4 |
| high resolution results on Sunday | 10.3 | 2.1 | 4.5 | 8.8 | 1.6 | 4.1 |
| The Proposed Method | Scleiden | Scleiden+ | |
|---|---|---|---|
| low resolution results on Monday | 0.554 | 0.543 | 0.540 |
| high resolution results on Monday | 0.421 | 0.401 | 0.407 |
| low resolution results on Sunday | 0.546 | 0.538 | 0.539 |
| high resolution results on Sunday | 0.412 | 0.406 | 0.405 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Q.; Hou, Z.; Yang, J. Detecting Spatial Communities in Vehicle Movements by Combining Multi-Level Merging and Consensus Clustering. Remote Sens. 2022, 14, 4144. https://doi.org/10.3390/rs14174144
Liu Q, Hou Z, Yang J. Detecting Spatial Communities in Vehicle Movements by Combining Multi-Level Merging and Consensus Clustering. Remote Sensing. 2022; 14(17):4144. https://doi.org/10.3390/rs14174144
Chicago/Turabian StyleLiu, Qiliang, Zhaoyi Hou, and Jie Yang. 2022. "Detecting Spatial Communities in Vehicle Movements by Combining Multi-Level Merging and Consensus Clustering" Remote Sensing 14, no. 17: 4144. https://doi.org/10.3390/rs14174144
APA StyleLiu, Q., Hou, Z., & Yang, J. (2022). Detecting Spatial Communities in Vehicle Movements by Combining Multi-Level Merging and Consensus Clustering. Remote Sensing, 14(17), 4144. https://doi.org/10.3390/rs14174144







