Assessment and Prediction of Impact of Flight Configuration Factors on UAS-Based Photogrammetric Survey Accuracy
Abstract
:1. Introduction
- (1)
- flight height,
- (2)
- flight overlap,
- (3)
- the quantity of GCPs,
- (4)
- the focal length of the camera lens, and
- (5)
- the average image quality of each image dataset.
- (1)
- Evaluation of five main influence factors of UAS-based photogrammetric surveying and their significance level using the MR method.
- (2)
- MR modeling for prediction of the UAS-based photogrammetric accuracy with different flight configurations.
2. Background
2.1. Flight Heights
2.2. Image Overlap
2.3. GCP Quantities and Distribution
2.4. Georeferencing Methods
2.5. Multiple Factors
3. Methodology
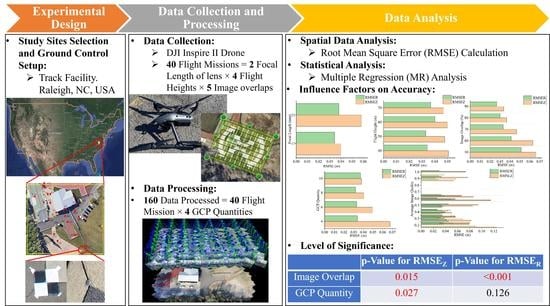
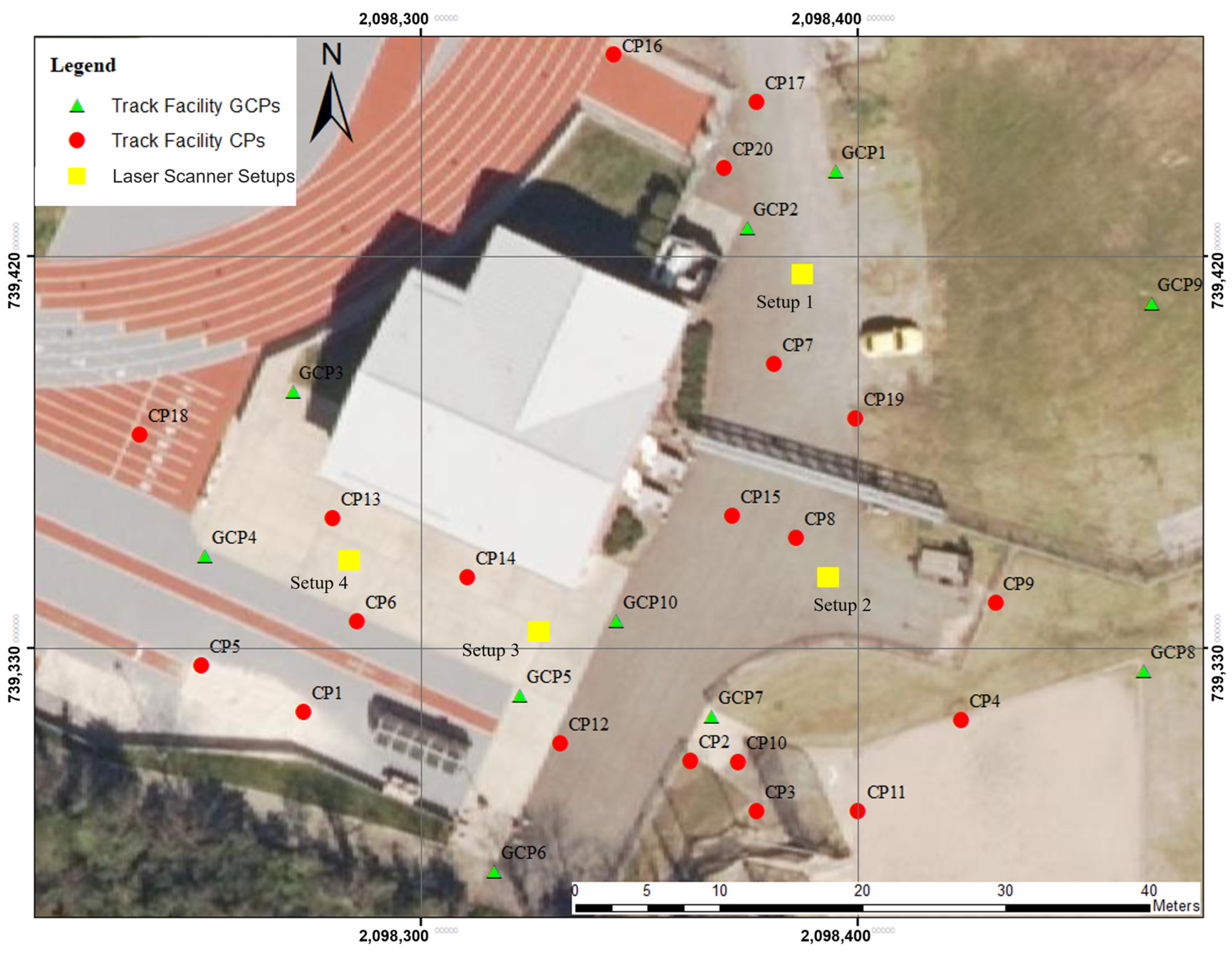
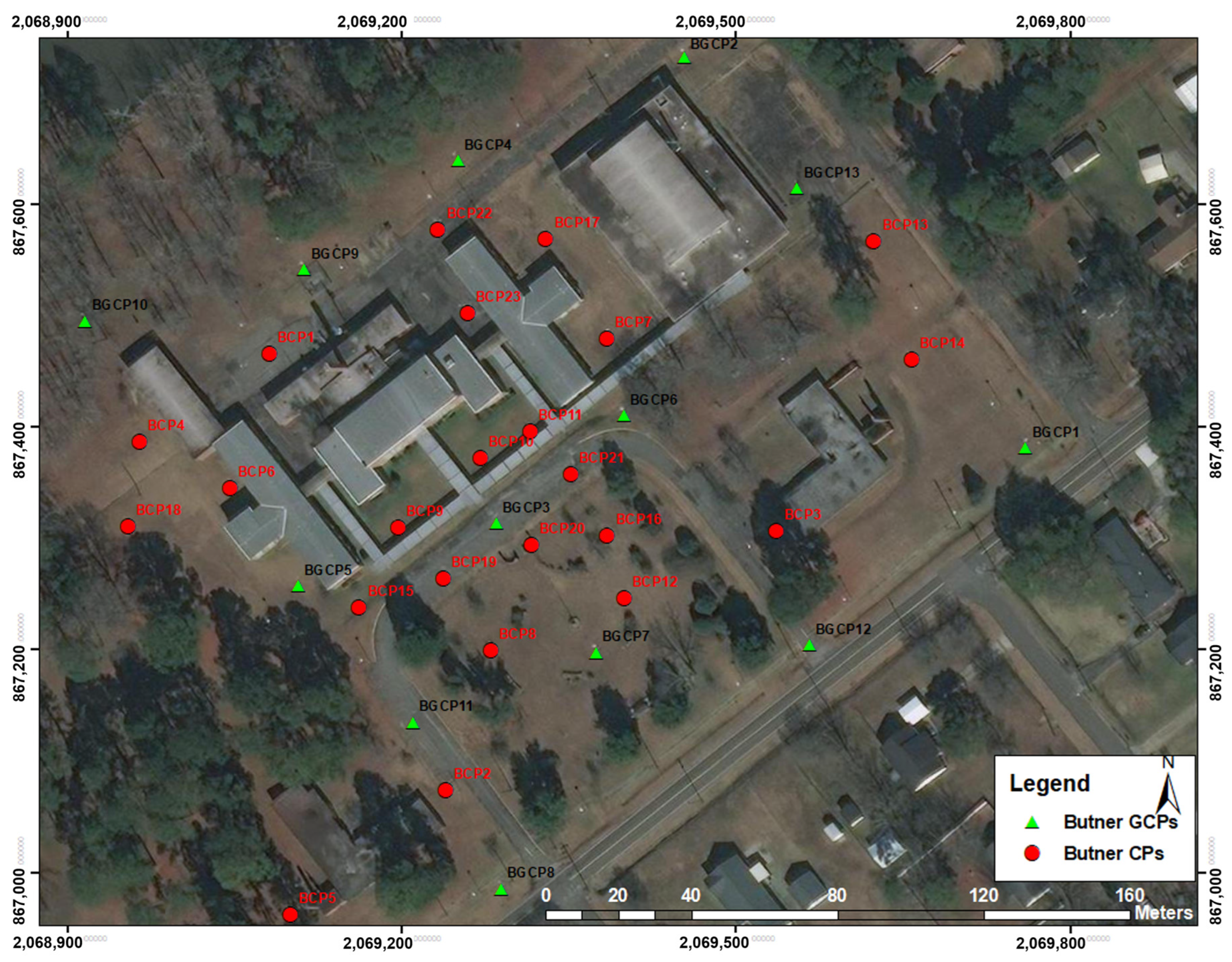
3.1. Experimental Design
3.2. Data Collection
- Flight Heights: 40 m (131 ft), 50 m (164 ft), 60 m (197 ft), and 70 m (229 ft)
- Image Overlap: 50%, 60%, 70%, 80%, and 90%
- Focal Length: 17 mm and 25 mm
3.3. Data Processing
3.4. Data Analysis
3.4.1. Spatial Data Analysis
3.4.2. Statistical Analysis
3.5. Validation
Data Collection
4. Results and Discussion
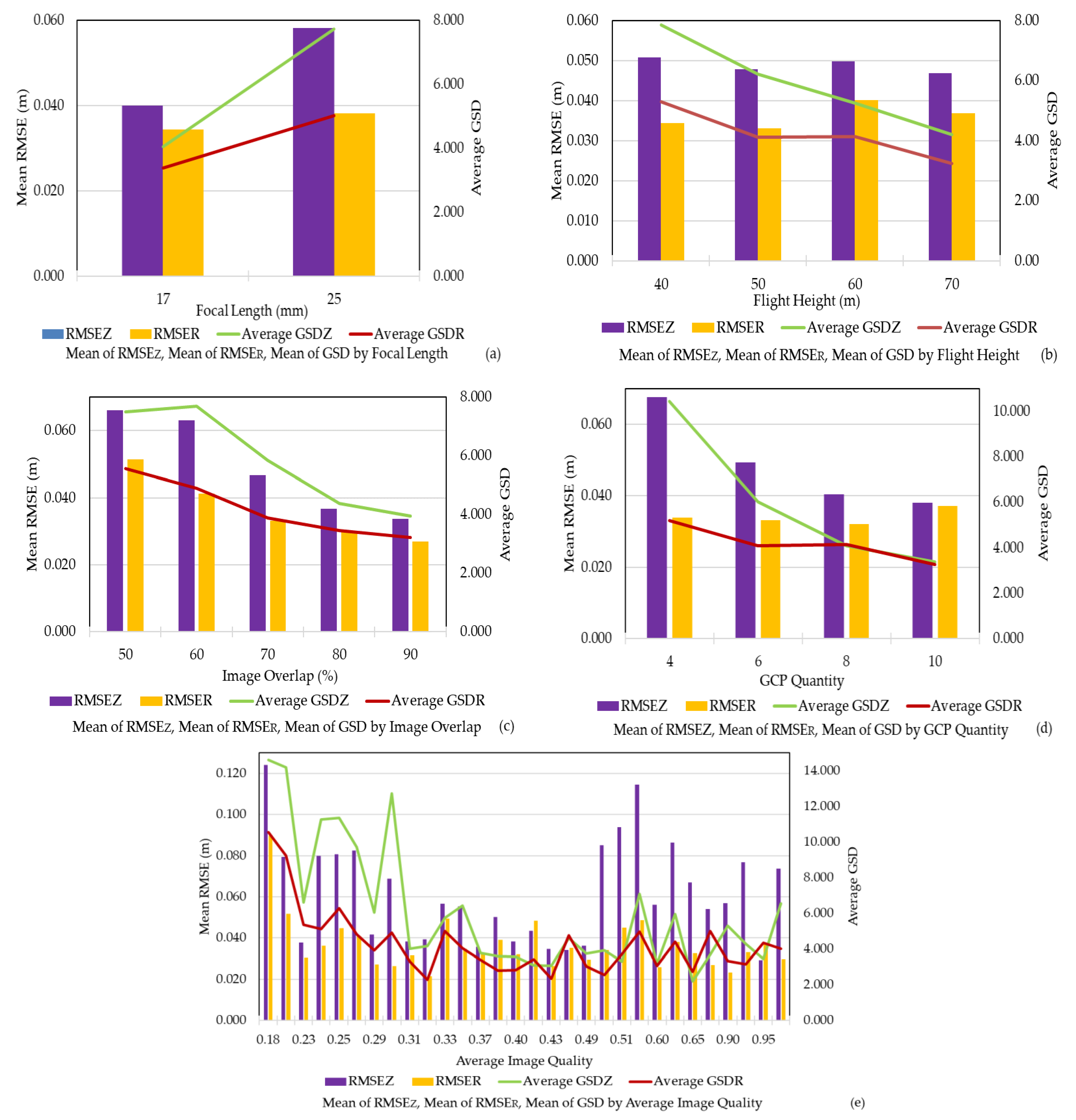
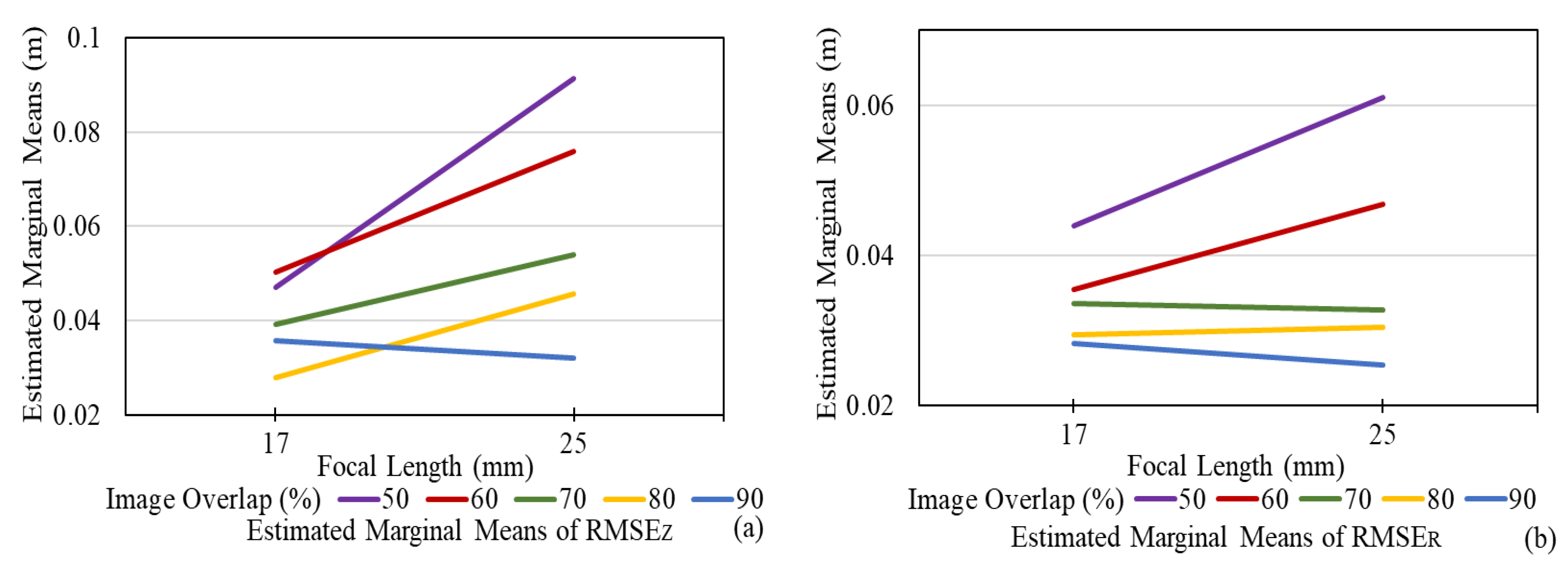
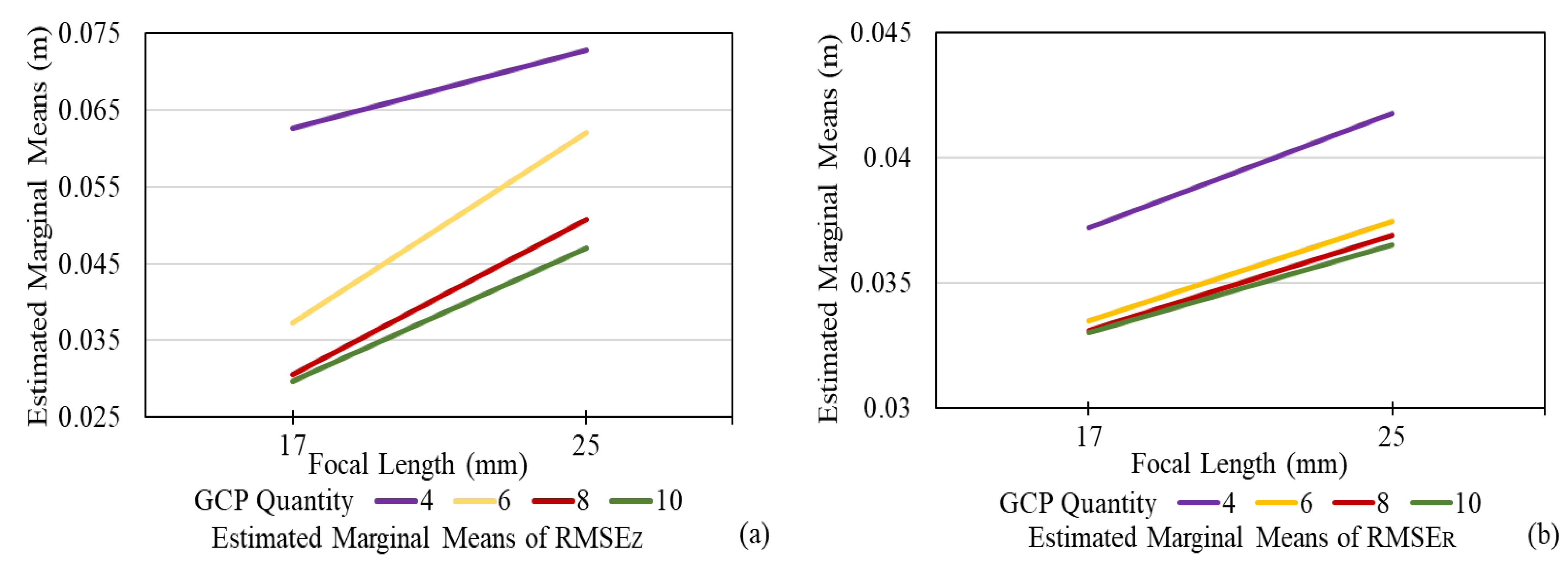
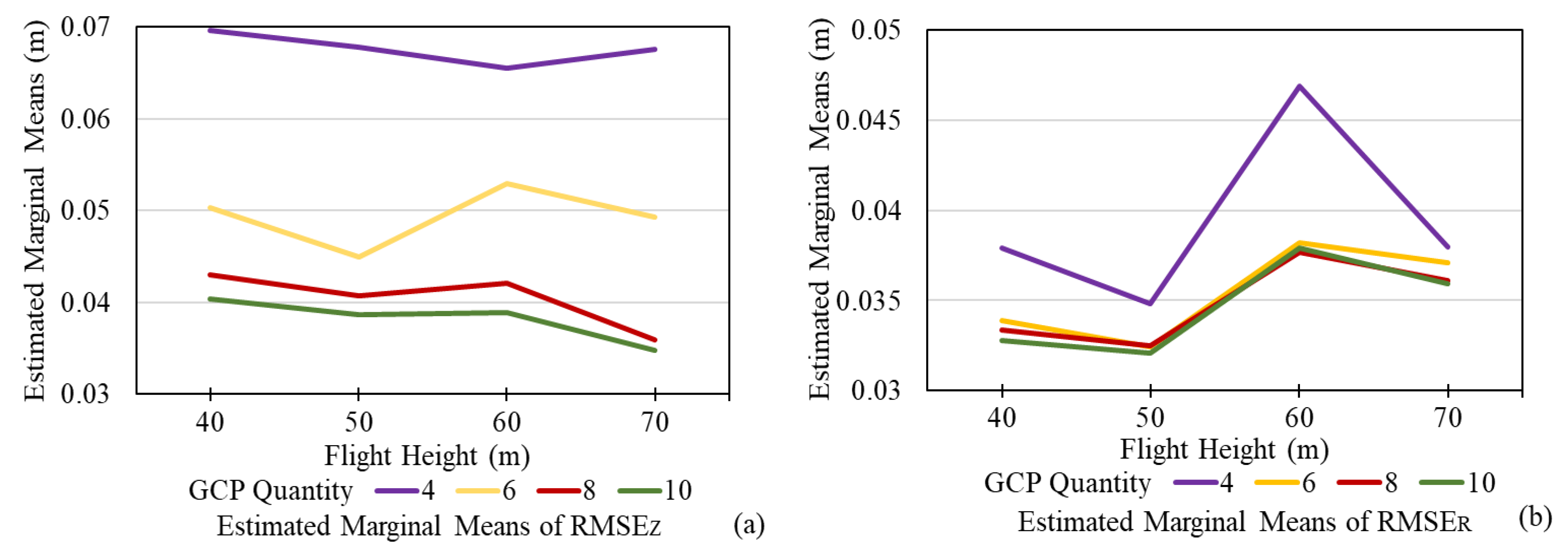
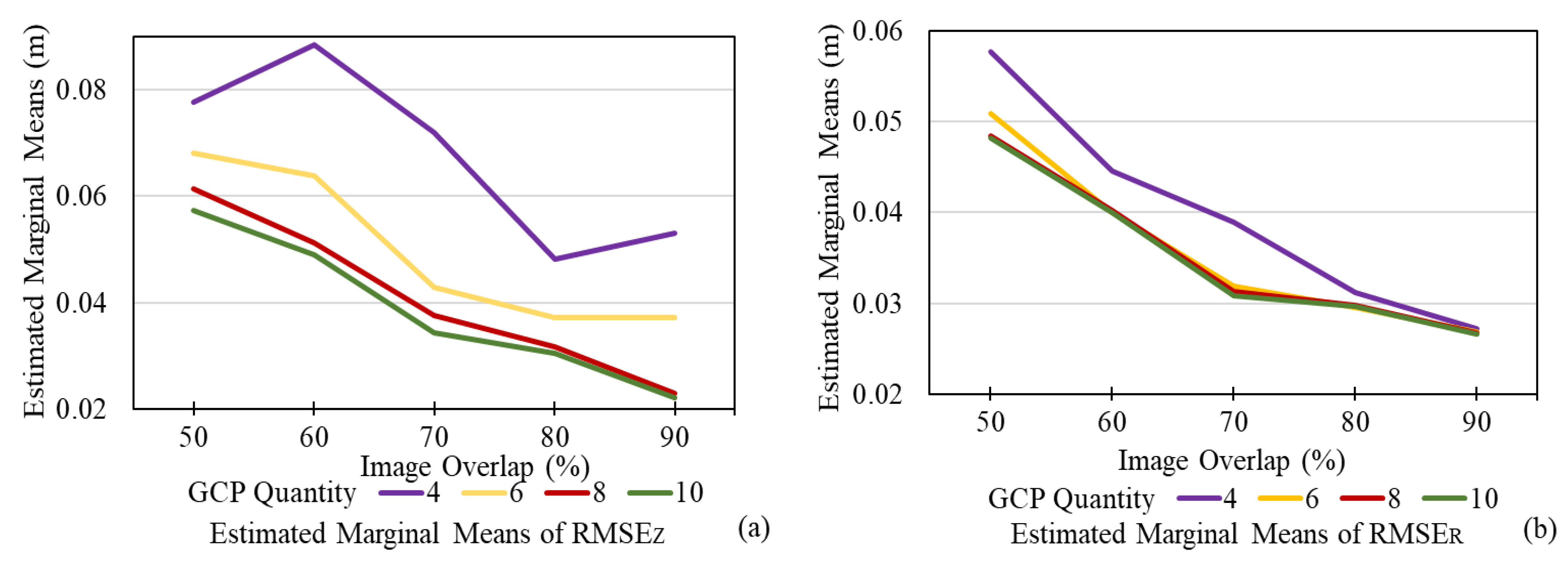
4.1. Influence and Significance of Five Influence Factors
4.2. MR Prediction Model Development and Validation
4.2.1. MR Model Development
4.2.2. MR Prediction Models Applied to Test Site
4.3. Practical Implications
4.4. Limitations and Future Work
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gabrlik, P.; la Cour-Harbo, A.; Kalvodova, P.; Zalud, L.; Janata, P. Calibration and Accuracy Assessment in a Direct Georeferencing System for UAS Photogrammetry. Int. J. Remote Sens. 2018, 39, 4931–4959. [Google Scholar] [CrossRef] [Green Version]
- Benjamin, A.R.; O’Brien, D.; Barnes, G.; Wilkinson, B.E.; Volkmann, W. Improving Data Acquisition Efficiency: Systematic Accuracy Evaluation of GNSS-Assisted Aerial Triangulation in UAS Operations. J. Surv. Eng. 2020, 146, 05019006. [Google Scholar] [CrossRef]
- Raeva, P.L.; Šedina, J.; Dlesk, A. Monitoring of Crop Fields Using Multispectral and Thermal Imagery from UAV. Eur. J. Remote Sens. 2019, 52, 192–201. [Google Scholar] [CrossRef] [Green Version]
- Hoffmann, H.; Nieto, H.; Jensen, R.; Guzinski, R.; Zarco-Tejada, P.; Friborg, T. Estimating Evaporation with Thermal UAV Data and Two-source Energy Balance Models. Hydrol. Earth Syst. Sci. 2016, 20, 697–713. [Google Scholar] [CrossRef] [Green Version]
- Guo, Y.; Senthilnath, J.; Wu, W.; Zhang, X.; Zeng, Z.; Huang, H. Radiometric Calibration for Multispectral Camera of Different Imaging Conditions Mounted on a UAV Platform. Sustainability 2019, 11, 978. [Google Scholar] [CrossRef] [Green Version]
- Navia, J.; Mondragon, I.; Patino, D.; Colorado, J. Multispectral Mapping in Agriculture: Terrain Mosaic Using an Autonomous Quadcopter UAV. In Proceedings of the 2016 International Conference on Unmanned Aircraft Systems, Arlington, VA, USA, 7–10 June 2016; pp. 1351–1358. [Google Scholar] [CrossRef]
- Lin, Y.C.; Cheng, Y.T.; Zhou, T.; Ravi, R.; Hasheminasab, S.; Flatt, J.; Troy, C.; Habib, A. Evaluation of UAV LiDAR for Mapping Coastal Environments. Remote Sens. 2019, 11, 2893. [Google Scholar] [CrossRef] [Green Version]
- Elaksher, A.F.; Bhandari, S.; Carreon-Limones, C.A.; Lauf, R. Potential of UAV lidar systems for geospatial mapping. In Proceedings of the Lidar Remote Sensing for Environmental Monitoring, San Diego, CA, USA, 8–9 August 2017; Volume 10406, pp. 121–133. [Google Scholar] [CrossRef]
- Nex, F.; Armenakis, C.; Cramer, M.; Cucci, D.A.; Gerke, M.; Honkavaara, E.; Kukko, A.; Persello, C.; Skaloudh, J. UAV in the Advent of the Twenties: Where We Stand and What is Next. ISPRS J. Photogramm. Remote Sens. 2022, 184, 215–242. [Google Scholar] [CrossRef]
- Ruzgiene, B.; Berteška, T.; Gečyte, S.; Jakubauskiene, E.; Aksamitauskas, V.Č. The Surface Modelling based on UAV Photogrammetry and Qualitative Estimation. Meas. J. Int. Meas. Confed. 2015, 73, 619–627. [Google Scholar] [CrossRef]
- Seifert, E.; Seifert, S.; Vogt, H.; Drew, D.; Van Aardt, J.; Kunneke, A.; Seifert, T. Influence of Drone Altitude, Image Overlap, and Optical Sensor Resolution on Multi-view Reconstruction of Forest Images. Remote Sens. 2019, 11, 1252. [Google Scholar] [CrossRef] [Green Version]
- Gerke, M.; Przybilla, H.J. Accuracy Analysis of Photogrammetric UAV Image Blocks: Influence of Onboard RTK-GNSS and Cross Flight Patterns. Photogramm. Fernerkund. Geoinf. 2016, 2016, 17–30. [Google Scholar] [CrossRef] [Green Version]
- Ajayi, O.G.; Palmer, M.; Salubi, A.A. Modelling Farmland Topography for Suitable Site Selection of Dam Construction Using Unmanned Aerial Vehicle (UAV) Photogrammetry. Remote Sens. Appl. Soc. Environ. 2018, 11, 220–230. [Google Scholar] [CrossRef]
- Catania, P.; Comparetti, A.; Febo, P.; Morello, G.; Orlando, S.; Roma, E.; Vallone, M. Positioning Accuracy Comparison of GNSS Receivers Used for Mapping and Guidance of Agricultural Machines. Agronomy 2020, 10, 924. [Google Scholar] [CrossRef]
- Padró, J.C.; Muñoz, F.J.; Planas, J.; Pons, X. Comparison of Four UAV Georeferencing Methods for Environmental Monitoring Purposes Focusing on the Combined Use with Airborne and Satellite Remote Sensing Platforms. Int. J. Appl. Earth Obs. Geoinf. 2019, 75, 130–140. [Google Scholar] [CrossRef]
- Shenbagaraj, N.; kumar, K.S.; Rasheed, A.M.; Leostalin, J.; Kumar, M.N. Mapping and Electronic Publishing of Shoreline Changes using UAV Remote Sensing and GIS. J. Indian Soc. Remote Sens. 2021, 49, 1769–1777. [Google Scholar] [CrossRef]
- Hemmelder, S.; Marra, W.; Markies, H.; de Jong, S.M. Monitoring River Morphology & Bank Erosion Using UAV Imagery—A Case study of the River Buëch, Hautes-Alpes, France. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 428–437. [Google Scholar] [CrossRef]
- Koucká, L.; Kopačková, V.; Fárová, K.; Gojda, M. UAV Mapping of an Archaeological Site Using RGB and NIR High-Resolution Data. Proceedings 2018, 2, 351. [Google Scholar] [CrossRef] [Green Version]
- arba, S.; Barbarella, M.; di Benedetto, A.; Fiani, M.; Gujski, L.; Limongiello, M. Accuracy Assessment of 3D Photogrammetric Models from an Unmanned Aerial Vehicle. Drones 2019, 3, 79. [Google Scholar] [CrossRef] [Green Version]
- Karachaliou, E.; Georgiou, E.; Psaltis, D.; Stylianidis, E. UAV for Mapping Historic Buildings: From 3D Modling to BIM. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, 42, 397–402. [Google Scholar] [CrossRef] [Green Version]
- Zulkipli, M.A.; Tahar, K.N. Multirotor UAV-Based Photogrammetric Mapping for Road Design. Int. J. Opt. 2018, 2018, 1871058. [Google Scholar] [CrossRef]
- Hubbard, B.; Hubbard, S. Unmanned Aircraft Systems (UAS) for Bridge Inspection Safety. Drones 2020, 4, 40. [Google Scholar] [CrossRef]
- Chen, S.; Laefer, D.F.; Mangina, E.; Zolanvari, S.M.I.; Byrne, J. UAV Bridge Inspection through Evaluated 3D Reconstructions. J. Bridge Eng. 2019, 24, 05019001. [Google Scholar] [CrossRef] [Green Version]
- Stampa, M.; Sutorma, A.; Jahn, U.; Willich, F.; Pratzler-Wanczura, S.; Thiem, J.; Röhrig, C.; Wolff, C. A Scenario for a Multi-UAV Mapping and Surveillance System in Emergency Response Applications. In Proceedings of the IDAACS-SWS 2020—5th IEEE International Symposium on Smart and Wireless Systems within the International Conferences on Intelligent Data Acquisition and Advanced Computing Systems, Dortmund, Germany, 17–18 September 2020. [Google Scholar] [CrossRef]
- Snavely, N.; Seitz, M.; Szeliski, R. Modeling the World from Internet Photo Collections. Int. J. Comput. Vis. 2007, 80, 189–210. [Google Scholar] [CrossRef] [Green Version]
- Förstner, W.; Wrobel, B.P. Photogrammetric Computer Vision Statistics, Geometry, Orientation and Reconstruction; Springer International Publishing: Cham, Switzerland, 2016; Volume 11. [Google Scholar] [CrossRef] [Green Version]
- Anders, N.; Smith, M.; Suomalainen, J.; Cammeraat, E.; Valente, J.; Keesstra, S. Impact of Flight Altitude and Cover Orientation on Digital Surface Model (DSM) Accuracy for Flood Damage Assessment in Murcia (Spain) Using a Fixed-Wing UAV. Earth Sci. Inform. 2020, 13, 391–404. [Google Scholar] [CrossRef] [Green Version]
- Agüera-Vega, F.; Carvajal-Ramírez, F.; Martínez-Carricondo, P. Accuracy of Digital Surface Models and Orthophotos Derived from Unmanned Aerial Vehicle Photogrammetry. J. Surv. Eng. 2017, 143, 04016025. [Google Scholar] [CrossRef]
- Zhang, D.; Watson, R.; Dobie, G.; MacLeod, C.; Khan, A.; Pierce, G. Quantifying Impacts on Remote Photogrammetric Inspection Using Unmanned Aerial Vehicles. Eng. Struct. 2020, 209, 109940. [Google Scholar] [CrossRef]
- Fraser, B.T.; Congalton, R.G. Issues in Unmanned Aerial Systems (UAS) Data Collection of Complex Forest Environments. Remote Sens. 2018, 10, 908. [Google Scholar] [CrossRef] [Green Version]
- Domingo, D.; Ørka, H.O.; Næsset, E.; Kachamba, D.; Gobakken, T. Effects of UAV Image Resolution, Camera Type, and Image Overlap on Accuracy of Biomass Predictions in a Tropical Woodland. Remote Sens. 2019, 11, 948. [Google Scholar] [CrossRef] [Green Version]
- Burdziakowski, P.; Bobkowska, K. UAV Photogrammetry under Poor Lighting Conditions—Accuracy Considerations. Sensors 2021, 21, 3531. [Google Scholar] [CrossRef]
- Taddia, Y.; Stecchi, F.; Pellegrinelli, A. Coastal Mapping Using DJI Phantom 4 RTK in Post-Processing Kinematic Mode. Drones 2020, 4, 9. [Google Scholar] [CrossRef] [Green Version]
- Toth, C.; Jozkow, G.; Grejner-Brzezinska, D. Mapping with Small UAS: A Point Cloud Accuracy Assessment. J. Appl. Geod. 2015, 9, 213–226. [Google Scholar] [CrossRef]
- Tomaštík, J.; Mokroš, M.; Saloš, S.; Chudỳ, F.; Tunák, D. Accuracy of Photogrammetric UAV-based Point Clouds under Conditions of Partially-Open Forest Canopy. Forests 2017, 8, 151. [Google Scholar] [CrossRef] [Green Version]
- Han, K.; Rasdorf, W.; Liu, Y. Applying Small UAS to Produce Survey Grade Geospatial Products for DOT Preconstruction & Construction. 2021. Available online: https://connect.ncdot.gov/projects/research/Pages/ProjDetails.aspx?ProjectID=2020-18 (accessed on 1 March 2022).
- American Society for Photogrammetry and Remote Sensing (ASPRS). ASPRS Positional Accuracy Standards for Digital Geospatial Data. Photogramm. Eng. Remote Sens. 2015, 81, A1–A26. [Google Scholar] [CrossRef]
- Ferrer-González, E.; Agüera-Vega, F.; Carvajal-Ramírez, F.; Martínez-Carricondo, P. UAV Photogrammetry Accuracy Assessment for Corridor Mping based on the Number and Distribution of Ground Control Points. Remote Sens. 2020, 12, 2447. [Google Scholar] [CrossRef]
- Gindraux, S.; Boesch, R.; Farinotti, D. Accuracy Assessment of Digital Surface Models from Unmanned Aerial Vehicles’ Imagery on Glaciers. Remote Sens. 2017, 9, 186. [Google Scholar] [CrossRef] [Green Version]
- Martínez-Carricondo, P.; Agüera-Vega, F.; Carvajal-Ramírez, F.; Mesas-Carrascosa, F.J.; García-Ferrer, A.; Pérez-Porras, F.J. Assessment of UAV-Photogrammetric Mapping Accuracy based on Variation of Ground Gontrol Points. Int. J. Appl. Earth Obs. Geoinf. 2018, 72, 1–10. [Google Scholar] [CrossRef]
- Oniga, E.’; Breaban, A.; Statescu, F. Determining the Optimum Number of Ground Control Points for Obtaining High Precision Results based on UAS Images. Multidiscip. Digit. Publ. Inst. Proc. 2018, 2, 5165. [Google Scholar] [CrossRef] [Green Version]
- Ridolfi, E.; Buffi, G.; Venturi, S.; Manciola, P. Accuracy Analysis of a Dam Model from Drone Surveys. Sensors 2017, 17, 1777. [Google Scholar] [CrossRef] [Green Version]
- Sanz-Ablanedo, E.; Chandler, J.H.; Rodríguez-Pérez, J.R.; Ordóñez, C. Accuracy of Unmanned Aerial Vehicle (UAV) and SfM Photogrammetry Survey as a Function of the Number and Location of Ground Control Points Used. Remote Sens. 2018, 10, 1606. [Google Scholar] [CrossRef] [Green Version]
- Stott, E.; Williams, R.D.; Hoey, T.B. Ground Control Point Distribution for Accurate Kilometre-scale Topographic Mapping using an RTK-GNSS Unmanned Aerial Vehicle and SfM Photogrammetry. Drones 2020, 4, 55. [Google Scholar] [CrossRef]
- Yu, J.J.; Kim, W.E.; Lee, J.; Son, S.W. Determining the Optimal Number of Ground Control Points for Varying Study Sites through Accuracy Evaluation of Unmanned Aerial System-based 3D Point Clouds and Digital Surface Model. Drones 2020, 4, 49. [Google Scholar] [CrossRef]
- James, M.R.; Robson, S.; d’Oleire-Oltmanns, S.; Niethammer, U. Optimising UAV Topographic Surveys Processed with Structure-from-Motion: Ground Control Quality, Quantity and Bundle Adjustment. Geomorphology 2017, 280, 51–66. [Google Scholar] [CrossRef] [Green Version]
- Wierzbicki, D. Multi-camera Imaging System for UAV Photogrammetry. Sensors 2018, 18, 2433. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, Y.; Rupnik, E.; Faure, P.H.; Pierrot-Deseilligny, M. GNSS-assisted Integrated Sensor Orientation with Sensor Pre-calibration for Accurate Corridor Mapping. Sensors 2018, 18, 2783. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alfio, V.S.; Costantino, D.; Pepe, M. Influence of Image TIFF Format and JPEG Compression Level in the Accuracy of the 3D Model and Auality of the Orthophoto in UAV Photogrammetry. J. Imaging 2020, 6, 30. [Google Scholar] [CrossRef]
- Yang, Y.; Lin, Z.; and Liu, F. Stable Imaging and Accuracy Issues of Low-Altitude Unmanned Aerial Vehicle Photogrammetry Systems. Remote Sens. 2016, 8, 316. [Google Scholar] [CrossRef] [Green Version]
- Benassi, F.; Dall’Asta, E.; Diotri, F.; Forlani, G.; Cella, U.; Roncella, R.; Santise, M. Testing Accuracy and Repeatability of UAV Blocks Oriented with GNSS-Supported Aerial Triangulation. Remote Sens. 2017, 9, 172. [Google Scholar] [CrossRef] [Green Version]
- Jurjević, L.; Gašparović, M.; Milas, A.S.; Balenović, I. Impact of UAS Image Orientation on Accuracy of Forest Inventory Attributes. Remote Sens. 2020, 12, 404. [Google Scholar] [CrossRef] [Green Version]
- Kalacska, M.; Lucanus, O.; Arroyo-Mora, J.P.; Laliberté, E.; Elmer, K.; Leblanc, G.; Groves, A. Accuracy of 3D Landscape Reconstruction without Ground Control Points Using Different UAS Platforms. Drones 2020, 4, 13. [Google Scholar] [CrossRef] [Green Version]
- Losè, L.T.; Chiabrando, F.; Tonolo, F.G. Boosting the Timeliness of UAV Large Scale Mapping. Direct Georeferencing Approaches: Operational Strategies and Best Practices. ISPRS Int. J. Geo-Inf. 2020, 9, 578. [Google Scholar] [CrossRef]
- Martinez, J.G.; Albeaino, G.; Gheisari, M.; Volkmann, W.; Alarcón, L.F. UAS Point Cloud Accuracy Assessment Using Structure from Motion–Based Photogrammetry and PPK Georeferencing Technique for Building Surveying Applications. J. Comput. Civ. Eng. 2020, 35, 05020004. [Google Scholar] [CrossRef]
- Tomaštík, J.; Mokroš, M.; Surový, P.; Grznárová, A.; Merganič, J. UAV RTK/PPK Method-An Optimal Solution for Mapping Inaccessible Forested Areas? Remote Sens. 2019, 11, 721. [Google Scholar] [CrossRef] [Green Version]
- Agüera-Vega, F.; Carvajal-Ramírez, F.; Martínez-Carricondo, P. Assessment of Photogrammetric Mapping Accuracy based on Variation Ground Control Points Number Using Unmanned Aerial Vehicle. Meas. J. Int. Meas. Confed. 2017, 98, 221–227. [Google Scholar] [CrossRef]
- Lee, S.; Park, J.; Choi, E.; Kim, D. Factors Influencing the Accuracy of Shallow Snow Depth Measured Using UAV-based Photogrammetry. Remote Sens. 2021, 13, 828. [Google Scholar] [CrossRef]
- Zimmerman, T.; Jansen, K.; Miller, J. Analysis of UAS Flight Altitude and Ground Control Point Parameters on DEM Accuracy along a Complex, Developed Coastline. Remote Sens. 2020, 12, 2305. [Google Scholar] [CrossRef]
- Harwin, S.; Lucieer, A.; Osborn, J. The Impact of the Calibration Method on the Accuracy of Point Clouds Derived Using Unmanned Aerial Vehicle multi-view stereopsis. Remote Sens. 2015, 7, 11933–11953. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Chen, J.C.; Dadi, G.B. Factors Influencing Measurement Accuracy of Unmanned Aerial Systems (UAS) and Photogrammetry in Construction Earthwork. In Computing in Civil Engineering 2019: Data, Sensing, and Analytics; American Society of Civil Engineers: Reston, VA, USA, 2019; pp. 408–414. [Google Scholar] [CrossRef]
- Griffiths, D.; Burningham, H. Comparison of Pre- and Self-Calibrated Camera Calibration Models for UAS-Derived Nadir Imagery for a SfM Application. Prog. Phys. Geog. 2019, 43, 215–235. [Google Scholar] [CrossRef] [Green Version]
- Cledat, E.; Jospin, L.V.; Cucci, D.A.; Skaloud, J. Mapping Quality Prediction for RTK/PPK-equipped Micro-drones Operating in Complex Natural Environment. ISPRS J. Photogramm. Remote Sens. 2020, 167, 24–38. [Google Scholar] [CrossRef]
- Unmanned Systems Technology. 2022. Available online: https://www.unmannedsystemstechnology.com/expo/uav-autopilot-systems/#:~:text=What%20is%20an%20UAV%20Autopilot%20Unit%3F (accessed on 14 August 2022).
- Scan Accuracy Checks for the Focus—FARO® Knowledge Base. Available online: https://knowledge.faro.com/Hardware/3D_Scanners/Focus/Scan_Accuracy_Checks_for_the_Focus (accessed on 19 August 2021).
- FARO® SCENE 3D Point Cloud Software | FARO. Available online: https://www.faro.com/en/Products/Software/SCENE-Software (accessed on 14 August 2022).








| Number of Influence Factors | Factors | Authors | Research Description | Highest MAE/RMSE Horizontal | Highest MAE/RMSE Vertical |
|---|---|---|---|---|---|
| Single Influence Factors | Flight Height | [27] | Evaluate the influence of flight height and area coverage orientations on the DSM and orthophoto accuracies for flood damage assessment. | N/A (consistently lower than 0.05 m, i.e., not more than 1–2 pixels) | N/A |
| [30] | Provide a solution of data collection and processing of UAS application in complex forest environment | N/A | N/A | ||
| GCP Quantity and Distribution | [10] | Assess the influence of numbers of GCPs on DSM accuracy. | N/A | 0.057 m | |
| [19] | Propose an algorithm to calculate the sparse point cloud roughness using associated angular interval. | N/A | N/A | ||
| [28] | Evaluate the impact of GCP quantities on UAS-based photogrammetry DSM and orthoimage accuracies. | 0.053 m | 0.049 m | ||
| [35] | Assess the influence of different grades of tree covers and GCP quantities and distributions on UAS-based point cloud in forest areas. | 0.031 m | 0.058 m | ||
| [2] | Evaluate the influence of additional GCPs on spatial accuracy when AAT is applied for georeferencing. | N/A | N/A | ||
| [38] | Identify the GCP quantities and distributions to generate a high accuracy for a corridor-shaped site. | 0.027 m | 0.055 m | ||
| [39] | Evaluate the effect of the location and quantity of GCPs on UAS-based DSMs in Glaciers. | N/A | N/A | ||
| [40] | Evaluate the impact of GCP quantities and distributions on UAS-based photogrammetry DSM and orthoimage accuracies. | 0.035 m | 0.048 m | ||
| [41] | Provide a solution about the optimal GCP quantity to generate high precision 3D models. | N/A | N/A | ||
| [42] | Provide information of the optimal GCP deployment for dam structures and high-rise structures. | 0.057 m | 0.012 m | ||
| [43] | Analyze the influence of the quantities and numbers of GCPs on 3D model accuracy. | N/A | N/A | ||
| [44] | Analyze the influence of GCP quantities on UAS photogrammetric mapping accuracy using RTK-GNSS system. | N/A | 0.003 m | ||
| [45] | Analyze 3D model and DSM accuracies to determine the optimal GCP quantities in various terrain types. | 0.044 m | 0.036 m | ||
| Camera Setting | [32] | Analyze the influence of photogrammetric process elements on the quality of UAS-based photogrammetric accuracy to identify artificial lighting at night | N/A | N/A | |
| [34] | Evaluate the influence of camera sensor types and configurations and SfM processing tools on UAS mapping accuracy. | N/A | N/A | ||
| [46] | Analyze the influence of the ground control quality and quantity on DEM accuracy using a Monte Carlo Method. | N/A | N/A | ||
| [47] | Generate a larger virtual image from five head cameras | 2.13 pixels | N/A | ||
| [48] | Investigate three issues of corridor aerial image block, including: focal length error, a gradually varied focal length, and rolling shutter effects. | 0.007 m | 0.008 m | ||
| Image Acquisition | [29] | Evaluate the impact of image parameters on the close-range UAS-based photogrammetric inspection accuracy. | N/A | N/A | |
| [49] | Evaluate the impact of image formats and levels of JPEG compression in UAS-based photogrammetric accuracy. | N/A | N/A | ||
| [50] | Evaluate the influence of low-height UAS photogrammetry systems on stable images, data processing and accuracy. | N/A | 0.059 m | ||
| Georeferencing Methods | [1] | Introduces a custom-built multi-sensor system for direct georeferencing. | 0.012 m | 0.020 m | |
| [14] | Evaluate the impact of GNSS receivers of techniques features and working modes on positioning accuracy. | N/A | N/A | ||
| [15] | Evaluate the geometric accuracy of using four different georeferencing techniques | 0.023 m | 0.03 m | ||
| [33] | Evaluate the quality of photogrammetric models and DTMs using PPK and RTK modes in coastline areas. | N/A | 0.016 m | ||
| [51] | Analyze the impact of UAS blocks and georeferencing methods on accuracy and repeatability. | 0.016 m | 0.014 m | ||
| [52] | Evaluate the influence of image block orientation methods on the accuracy of estimated forest attributes, especially the plot mean tree height. | N/A | N/A | ||
| [53] | Analyze the influence of different UAS platforms on positional and within-model accuracies without GCPs. | N/A | N/A | ||
| [54] | Provide operational guidelines and best practices of direct georeferencing methods on positional accuracy. | N/A | 0.019 m | ||
| [55] | Assess the influence of GNSS with PPK on the UAS-based accuracy in building surveying applications. | N/A | 0.01 m | ||
| [56] | Assess the influence of RTK/PPK on geospatial accuracies of photogrammetric products in forest areas. | 0.003 m | 0.006 m | ||
| Flight Height and Image Acquisition | [11] | Provide scientific evidence of the impact of flight height, image overlap, and image resolution on forest area reconstruction. | N/A | N/A | |
| Multiple Influence Factors | GCP Quantity and Distribution and Georeferencing Methods | [12] | Evaluate the impact of cross flight patterns, GCP distributions, and RTK-GNSS on camera self-calibration and bundle block adjustment quality. | N/A | N/A |
| Camera Setting and Image Acquisition | [31] | Evaluate the impact of image resolution, camera type, and side overlap on predicted biomass model accuracy. | N/A | N/A | |
| Flight Height and GCP Quantity and Distribution and Image Acquisition | [57] | Evaluate the impact of flight heights, terrain types, and GCP quantities on DSM and orthoimage accuracy in UAS-based photogrammetry | 0.000169 m | 0.047 m | |
| [58] | Evaluate the impact of flight height, image overlap, GCPs quantities and distribution, and time of survey on snow depth measurement. | N/A | N/A | ||
| [59] | Analyze the impact of flight heights and quantities and distribution of GCPs on survey error. | N/A | N/A | ||
| GCP Quantity and Distribution and Camera Setting | [60] | Evaluate the influence of camera calibration methods as well as quantities and distributions of GCPs on UAS photogrammetry accuracy. | 1.3 mm | 5.1 mm | |
| Flight Height and GCP Quantity and Distribution and Camera Setting | [61] | Assess the impact of flight height, image overlap, GCP quantities, and construction site conditions on measurement accuracy. | N/A | 0.085 m |
| Flight No. | Focal Length (mm) | Flight Height (m) | Overlap (%) | Average Image Quality | No. of Image |
|---|---|---|---|---|---|
| 1 | 25 | 40 | 90 | 0.88 | 539 |
| 2 | 25 | 40 | 80 | 0.23 | 161 |
| 3 | 25 | 40 | 70 | 0.30 | 94 |
| 4 | 25 | 40 | 60 | 0.22 | 57 |
| 5 | 25 | 40 | 50 | 0.96 | 48 |
| 6 | 25 | 50 | 90 | 0.29 | 473 |
| 7 | 25 | 50 | 80 | 0.90 | 156 |
| 8 | 25 | 50 | 70 | 0.24 | 64 |
| 9 | 25 | 50 | 60 | 0.63 | 48 |
| 10 | 25 | 50 | 50 | 0.25 | 39 |
| 11 | 25 | 60 | 90 | 0.60 | 391 |
| 12 | 25 | 60 | 80 | 0.34 | 86 |
| 13 | 25 | 60 | 70 | 0.95 | 47 |
| 14 | 25 | 60 | 60 | 0.28 | 30 |
| 15 | 25 | 60 | 50 | 0.18 | 22 |
| 16 | 25 | 70 | 90 | 0.32 | 171 |
| 17 | 25 | 70 | 80 | 0.40 | 98 |
| 18 | 25 | 70 | 70 | 0.31 | 39 |
| 19 | 25 | 70 | 60 | 0.33 | 30 |
| 20 | 25 | 70 | 50 | 0.58 | 20 |
| 21 | 17 | 40 | 90 | 0.49 | 345 |
| 22 | 17 | 40 | 80 | 1.01 | 148 |
| 23 | 17 | 40 | 70 | 0.48 | 55 |
| 24 | 17 | 40 | 60 | 1.01 | 46 |
| 25 | 17 | 40 | 50 | 0.63 | 35 |
| 26 | 17 | 50 | 90 | 0.92 | 321 |
| 27 | 17 | 50 | 80 | 0.37 | 77 |
| 28 | 17 | 50 | 70 | 0.37 | 48 |
| 29 | 17 | 50 | 60 | 0.63 | 31 |
| 30 | 17 | 50 | 50 | 0.63 | 21 |
| 31 | 17 | 60 | 90 | 0.43 | 226 |
| 32 | 17 | 60 | 80 | 0.63 | 85 |
| 33 | 17 | 60 | 70 | 0.65 | 48 |
| 34 | 17 | 60 | 60 | 0.92 | 28 |
| 35 | 17 | 60 | 50 | 0.51 | 23 |
| 36 | 17 | 70 | 90 | 0.49 | 120 |
| 37 | 17 | 70 | 80 | 0.40 | 75 |
| 38 | 17 | 70 | 70 | 0.50 | 30 |
| 39 | 17 | 70 | 60 | 0.39 | 30 |
| 40 | 17 | 70 | 50 | 0.42 | 20 |
| Processing Step | Parameters | Value |
|---|---|---|
| Alignment | Key points Image Scale | Full |
| Image Scale for Alignment | Original Size | |
| Matching Image Pairs | Aerial Grid or Corridor | |
| Calibration | Targeted Number of Key points | Automatic |
| Calibration Method | Standard | |
| Camera Optimization | Internal Parameters Optimization | All |
| External Parameters Optimization | All | |
| Dense Point Cloud Generation | Image Scale for Point Cloud Densification | Original Size with Multiscale |
| Point Density | High | |
| Minimum Number of Match | 3 |
| Processing Step | Parameters | Value |
|---|---|---|
| Processing Setting | Colorization | Colorize Scans |
| Find Targets | Find Checkerboards | |
| Registration | Automatic Registration | Target Based |
| Optimization and Verify | Cloud to Cloud |
| Flight Mission | Flight Height (m) | Overlap (%) | Focal Length (mm) | GCP Quantities | Average Image Quality | No. of Images | GSD (cm) |
|---|---|---|---|---|---|---|---|
| 1 | 116 | 90 | 25 | 13 | 0.85 | 684 | 1.6 |
| 2 | 86 | 80 | 17 | 12 | 0.48 | 280 | 1.65 |
| 3 | 116 | 90 | 25 | 10 | 0.85 | 684 | 1.6 |
| 4 | 86 | 70 | 17 | 12 | 0.48 | 280 | 1.65 |
| 5 | 86 | 70 | 17 | 10 | 0.48 | 140 | 1.65 |
| p-Value for RMSEZ | p-Value for RMSER | |
|---|---|---|
| Constant | 0.009 | <0.001 |
| Focal Length | 0.773 | 0.057 |
| Flight Height | 0.438 | 0.367 |
| Image Overlap | 0.015 | <0.001 |
| GCP Quantity | 0.027 | 0.126 |
| Average Image Quality | 0.427 | 0.103 |
| Flight Mission | RMSEZ from Pix4D (cm) | Z Direction Pixel Error from Pix4D | RMSER from Pix4D (cm) | R Direction Pixel Error from Pix4D | Predicted RMSEZ from MR Model (cm) | Predicted Z Direction Pixel Error from MR Model | Predicted RMSER from MR Model (cm) | Predicted R Direction Pixel Error from MR Model |
|---|---|---|---|---|---|---|---|---|
| 1 | 2.1 | 1.27 GSD | 2.4 | 1.50 GSD | 1.8 | 1.13 GSD | 2.6 | 1.63 GSD |
| 2 | 2.1 | 1.27 GSD | 2.5 | 1.52 GSD | 2.9 | 1.76 GSD | 2.3 | 1.39 GSD |
| 3 | 2.7 | 1.69 GSD | 2.9 | 1.81 GSD | 2.6 | 1.63 GSD | 3.1 | 1.94 GSD |
| 4 | 3.2 | 1.94 GSD | 3.1 | 1.88 GSD | 3.4 | 2.06 GSD | 2.6 | 1.58 GSD |
| 5 | 3.5 | 2.12 GSD | 3.3 | 2.00 GSD | 3.0 | 1.82 GSD | 2.8 | 1.70 GSD |
| RMSEZ Error Rate | RMSER Error Rate | Prediction Accuracy | Prediction Accuracy |
|---|---|---|---|
| 16.67 | 7.69 | 83.33 | 92.31 |
| 27.59 | 8.70 | 72.41 | 91.30 |
| 3.70 | 6.90 | 96.3 | 93.1 |
| 6.25 | 16.13 | 93.75 | 83.87 |
| 14.29 | 15.15 | 85.71 | 84.85 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Han, K.; Rasdorf, W. Assessment and Prediction of Impact of Flight Configuration Factors on UAS-Based Photogrammetric Survey Accuracy. Remote Sens. 2022, 14, 4119. https://doi.org/10.3390/rs14164119
Liu Y, Han K, Rasdorf W. Assessment and Prediction of Impact of Flight Configuration Factors on UAS-Based Photogrammetric Survey Accuracy. Remote Sensing. 2022; 14(16):4119. https://doi.org/10.3390/rs14164119
Chicago/Turabian StyleLiu, Yajie, Kevin Han, and William Rasdorf. 2022. "Assessment and Prediction of Impact of Flight Configuration Factors on UAS-Based Photogrammetric Survey Accuracy" Remote Sensing 14, no. 16: 4119. https://doi.org/10.3390/rs14164119
APA StyleLiu, Y., Han, K., & Rasdorf, W. (2022). Assessment and Prediction of Impact of Flight Configuration Factors on UAS-Based Photogrammetric Survey Accuracy. Remote Sensing, 14(16), 4119. https://doi.org/10.3390/rs14164119