Abstract
In the context of urban warming associated with rapid urbanization, the relationship between urban landscape patterns and land surface temperature (LST) has been paid much attention. However, few studies have comprehensively explored the effects of two/three-dimensional (2D/3D) building patterns on LST, particularly by comparing their relative contribution to the spatial variety of LST. This study adopted the ordinary least squares regression, spatial autoregression and variance partitioning methods to investigate the relationship between 2D/3D building patterns and summertime LST across 2016–2017 in Shanghai. The 2D and 3D building patterns in this study were quantified by four 2D and six 3D metrics. The results showed that: (1) During the daytime, 2D/3D building metrics had significant correlation with LST. However, 3D building patterns played a significant role in predicting LST. They explained 51.0% and 10.2% of the variance in LST, respectively. (2) The building coverage ratio, building density, mean building projection area, the standard deviation of building height, and mean building height highly correlated with LST. Specifically, the building coverage ratio was the main predictor, which was obviously positively correlated with LST. The correlation of building density and average projected area with LST was positive and significant, while the correlation of building height standard deviation and average building height with LST was negative. The increase in average height and standard deviation of buildings and the decrease in building coverage ratio, average projected area, and density of buildings, can effectively improve the urban thermal environment at the census tract level. (3) Spatial autocorrelation analysis can elaborate the spatial relationship between building patterns and LST. The findings from our research will provide important insights for urban planners and decision makers to mitigate urban heat island problems through urban planning and building design.
1. Introduction
Nowadays, China has become the most urbanized country globally, with an urbanization rate rising from 17.8% in 1978 to 64.72% in 2021 (NBSC, 2022). Along with rapid urbanization, the natural ecosystem has transformed into a human and nature coupled ecosystem [1,2], resulting in the commonly known urban heat island (UHI) effect. UHI is a phenomenon in which the temperature of a city is higher than that of its adjacent suburbs [3,4,5]. Previous studies reported the adverse consequences of the UHI effect, including urban air pollution [6,7,8], increasing urban energy consumption and water use during hot days [9,10,11], altering species distribution and composition [12,13], decreasing the human thermal comfort and causing more significant health risks [14,15], and increasing human risks of violence and mortality in cities. Thus, the linkage between the UHI effect and urban environmental sustainability has attracted attention worldwide [16,17].
Two approaches usually characterize the quantitative measurement of the UHI effect. The first is to compare the urban–rural air temperature using data from meteorological stations [18,19]. This approach has been traditionally used to study UHI [20,21]. However, the dispersed nature and low-density of meteorological stations means that this approach cannot generate spatially sufficient accuracy and thus limit its applicability in big cities [22,23]. The second is to measure the difference in urban–rural land surface temperature (LST) by using satellite and unmanned aerial vehicle remote sensing data [24,25,26]. As the most direct manifestation of surface urban heat island (SUHI) [1], LST is a good proxy for indicating energy balance in surface physical processes [27,28]. Due to its advantages of sizable spatial coverage [18,29,30,31], LST products retrieved from satellite-borne thermal infrared (TIR) bands have been widely applied to study the correlation between urban landscape patterns and SUHI effects.
Many studies have concentrated on the factors influencing the UHI effect associated with urban 2D or 3D patterns [19,32]. A considerable amount of research has demonstrated the significant effects of urban 2D patterns on LST and air temperature [33,34,35]. In contrast, very few studies have explored the relationship between urban 3D patterns and LST or air temperature [19,36], although vertical expansion is an essential feature of urbanization. Buildings are a key part of the 3D urban structure and are an important factor influencing the UHI effect [36,37]. Buildings will doubtless modify the reflection and absorption of radiation and thermal diffusion in urban areas [38]. Although 3D building patterns are of obvious importance to UHI, only a few studies have explored the impact of 3D urban structures such as street canyons, building height, and building volume on LST [36,38,39]. However, these studies only provide a binary association between 3D pattern factors and LST [37], while a comprehensive explanation of these factors in relation to LST and the relative importance of 2D/3D building patterns to UHI is still lacking. Therefore, in the sense of urban climate adaptation, the association between urban 3D building structure and UHI effect has to be further explored.
For the improvement of the urban thermal environment, the key issue is to identify the main influencing factors. Shanghai, the largest city in China, has undergone dramatic urbanization and its UHI intensity is particularly high [33,40,41], as of 1 August this year, Shanghai had 28 high-temperature days above 35 °C in 2022. This study concentrated on the summer daytime, because both the intensity and footprint of UHI are strongest during the summer daytime. In addition, its adverse impacts on the surrounding environment and the health of residents are most evident during the summer daytime [42,43]. Taking the large city of Shanghai as the study area, this study aims to answer two questions: (1) how do building patterns, particularly 3D building patterns, influence the distribution pattern of LST? (2) what is the relative importance of 2D/3D building patterns in explaining the spatial variability of LST? The findings of this study can deepen our insights into the impacts of 2D/3D building patterns on UHI and provide urban planners and policymakers with some enlightenment on how to alleviate the UHI effect through rational urban planning and architectural design.
2. Materials and Methods
2.1. Study Area
Shanghai is situated on the eastern coast of China (30°40′–31°53′N, 120°52′–122°12′E). Excluding the offshore sea area, its administrative boundary approximately covers an area of 6340.5 km2. The city has a subtropical monsoon climate, with an annual average temperature between 15.2 to 15.7 °C, annual rainfall of 1097.3 mm and an average altitude of about 4 m. Since its reform and opening up, Shanghai has undergone dramatic urbanization in both extent and intensity [33].
This study mainly focused on the central urban area within the outer ring road of Shanghai (Figure 1), as it is the most developed area in Shanghai and the most densely populated area in the world [44], with numerous skyscrapers and intensive UHI [26,33]. Therefore, it is an optimal area for exploring the correlation between building patterns and LST. The study area consists of 113 census tracts. The census tract was either all inside the outer ring or its centroid of mass was inside the outer ring (Figure 1). In the study, we selected census tracts as the analysis units because they were the smallest administrative divisions and the basic units of design and implementation in local urban planning and management [22].
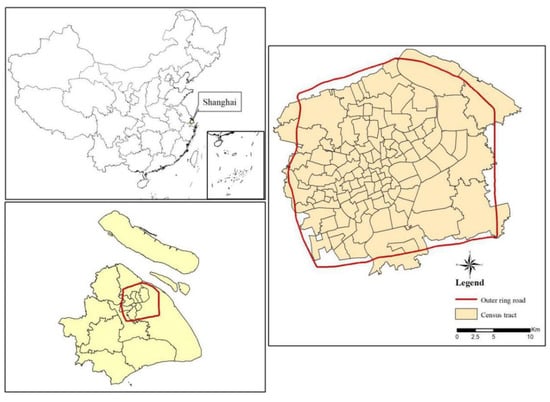
Figure 1.
Location of the study area and spatial distribution of the selected census tracts.
2.2. Methods
2.2.1. Retrieving LST
Data for two LSTs were retrieved from Landsat-8 images acquired during summer dates across 2016 and 2017 in order to coincide with the year of the building data. We first performed a comprehensive screening of all suitable images during the summer periods of 2016–2017 to remove images with cloud cover, and finally used two cloud-free Landsat-8 images from 20 July 2016 and 24 August 2017 for the LST retrieval. Thermal infrared sensor (TIRS) bands have been officially released in the form of 30-m resolution, using the cubic convolution algorithm [45]. In this research, band 10 was applied for the LST retrieval. The LST was evaluated by applying the radiative transfer equation (RTF) method by correcting atmospheric effects [46,47] and land surface emissivity [48]:
where Lλ is the top of atmosphere (TOA) radiance in W/(M2sr μm). ɛ is the land surface emissivity estimated from the NDVI-based method [33,48,49]. B(Ts) is the emitted radiance from the Earth’s surface, also as known as surface-leaving radiance, which can be derived by inversion of Planck’s law [48,50], and Ts refers to the LST. and are the downwelling and upwelling atmospheric radiance, respectively. is the atmospheric transmission. The atmospheric parameters such as , and were acquired from NASA’s atmospheric correction parameter calculator [51].
where LT is the surface-leaving radiance, which was transformed to at-satellite brightness temperature (TB) with the assumption that the earth’s surface is a black body.
for TIRS band 10, K1 is 774.89 W/(m2 sr μm) and K2 is 1321.08 K.
Finally, the land surface emissivity was calibrated and used to calculate the LST:
where λ is the wavelength of emitted radiance (10.9 μm for TIRS band 10), ρ = 1.438 × 10−2 mK. More details about LST retrieval are described in Weng (2009) [18] and Huang and Wang (2019) [37].
2.2.2. Measuring 2D/3D Building Patterns
The building data from 2017, including building footprint and total number of stories, were used to map 2D/3D building patterns. They can approximately represent the real building shape, since eccentric and unusual buildings are very few [52]. The building data were acquired from Baidu Map (map.baidu.com/ accessed on 8 July 2017) and the Shanghai Municipal Bureau of planning and natural resources. The building footprint was verified by a comparison of the building map and a historical high-resolution Google Earth image, which showed that the building boundary exactly matched the actual buildings (Figure 2). The building height was obtained from the number of floors multiplied by 3 m, then, using Baidu Quanjing Maps and the Lianjia real estate APP to compare and verify it, the results obtained were satisfactory.

Figure 2.
Examples of building footprints in: (a) Shanghai central city; (b) the enlarged image showing the details.
Many landscape metrics were applied to quantify building patterns [36,41,53]. Here, ten landscape metrics were selected to measure the building patterns (Table 1), including four 2D building metrics: (1) Building coverage ratio (BCR), (2) Mean building projection area (MBPA), (3) Mean patch shape index (MPSI), (4) Building density (BD), and six 3D building metrics: (1) Floor area ratio (FAR), (2) Mean building height (MBH), (3) Building height standard deviation (BHSD), (4) High-rise building density (HBD), (5) High-rise building ratio (HBR), (6) Building volume ratio (BVR). These building metrics reflect the primary characteristics of the 3D and 2D building patterns, including the size, density, roughness, complexity and fragmentation [53]. These metrics were selected using the following principles [25,54,55,56]: (1) they have important theory and practice, (2) they are easily interpreted and calculated, and (3) they have minimal redundancy. These metrics were calculated for each census tract using ArcGIS 10.6 (Environment System Research Institute, RedLands, CA, USA) and Fragstats 4.2 (University of Massachusetts, Amherst, MA, USA) [57].

Table 1.
Description of 2D and 3D building metrics.
2.2.3. Statistics Analysis
The mean LST of each unit was calculated as the response variable, and 2D/3D metrics were used as the predictive variables. There are many statistical analysis methods available to determine the correlation between LST and its influencing factors [22].
Firstly, the effects of building patterns on LST variation were analyzed using the ordinary least squares (OLS) multiple linear regression. A multiple stepwise selection procedure was used to decide which building metric was to be added or removed, and to calculate the comprehensive explanation efficiency of each stratification factor for LST variation, considering that there may be collinearity between the variables. The OLS regression is the most commonly applied statistical analysis methodology. It assumes that the error terms are independent. Nevertheless, spatial data usually has the characteristics of spatial autocorrelation, which may lead to the coefficient estimation bias of OLS regression variables [58,59]. The preliminary analyses showed that the residuals of the OLS model in this study have important significant spatial autocorrelation (p < 0.01). Therefore, the spatial autoregression (SAR) models integrating spatial autocorrelation are more suitable to explore the relationships between 2D/3D building metrics and LST [25].
Secondly, the SAR was performed, and the analysis results were compared with those of the OLS. SAR can measure the neighborhood relationship of response variables through an (n × n) spatial weight matrix, and integrate it into the standard multiple linear regression considering spatial autocorrelation [60]. SAR is usually modeled using the spatial lag model (SLM) and spatial error model (SEM) [25,59], which are the two main SAR models. The SLM assumes that spatial autocorrelation only exists in the response variable. The SLM is expressed in the form:
where Y is the response variable, ρ is a spatial autoregressive coefficient, Wy is a (n × 1) vector of the spatially lagged response variable, β is a (k × 1) vector of regression coefficients, X is a (n × k) matrix of explanatory variables, and ε is a (n × 1) matrix of independently distributed errors.
By contrast, the SEM assumes that the error term is spatially autocorrelated when the spatial effect is not completely interpreted by the explanatory variables involved. This model was written as:
where Wμ is a (n × 1) vector of spatially lagged errors, and λ is a spatial autoregressive coefficient.
Lagrange multiplier statistics were applied to make a comparison between the two models and determine which one was more appropriate for the data in this study [60]. The spatial regression was used with a maximum likelihood method, and the R2 calculated is comparable to that obtained from the OLS model [58].
The OLS model was performed using SPSS 16.0, and the SAR model was performed using Geoda 1.14.0 (Anselin, Chicago, IL, USA) [60].
Finally, we used the standardized coefficient (beta weights) to assess the relative importance of building metrics for predicting LST [61,62,63], and variance partitioning [25,64] was applied to analyze the relative contribution (the degree of LST change being explained) of 2D and 3D building metrics on the total LST variation. The LST variation was divided into four components: (1) unique effect of 2D building metrics, (2) unique effect of 3D building metrics, (3) joint effect of 2D and 3D building metrics, (4) unexplained change. The variance classification is detailed in Legendre (2008) [65], using Canoco software version 4.5 (ter Braak & Smilauer, Ithaca, NY, USA).
3. Results
3.1. The Spatial Pattern of Buildings and LST
The spatial distribution patterns of the buildings and LST are displayed in Figure 3. There exists a large spatial variability of LST, obviously. The average LST was 45.16 °C (ranging from 29.69 °C to 60.84 °C), and the standard deviation was 3.23 °C. The urban core area and the dock area at the northeast corner have relatively high LST, and the LST spatial pattern has a good spatial consistency with the distribution of buildings. The LST was higher where the building coverage is high. The average LST at the census tract level was 46.63 °C (ranging from 43.07 °C to 50.52 °C), and the standard deviation was 1.30 °C. LST showed significant positive spatial autocorrelation (Moran’s I = 0.48, p < 0.01) (Table 2).
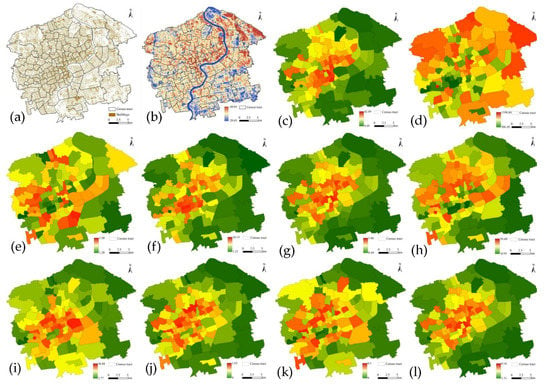
Figure 3.
The spatial distribution patterns of buildings characteristics and LST. (a) Buildings; (b) LST; (c) BCR; (d) MBPA; (e) MPSI; (f) BD; (g) FAR; (h) MBH; (i) BHSD; (j) HBD; (k) HBR; (l) BVR.

Table 2.
Descriptive statistics of 2D/3D building metrics and LST.
The 2D and 3D building metrics varied greatly in space for the research area. Buildings covered approximately 19.72% of the study area. BCR across census tracts ranged from 9.49% to 42.09%, with an average value of 24.52% and a standard deviation of 6.63%. FAR, MBH, BHSD, BVR, BD, and MBPA also had relatively large spatial heterogeneity among different units (Table 2). The average value of MBH was 17.75 m (ranging from 10.91 to 30.60 m), while the mean value of BHSD was 13.88 m (ranging from 2.77 to 36.88 m). MBPA varied from 306.45 m2 to 1398.84 m2, with a mean value of 24.52%. BD ranged from 1.23 to 10.19, and the maximum values of FAR and BVR were 3.06 and 9.18, respectively. In contrast, the ranges of HBD, HBR and MPSI were relatively small and the degree of variability was low. All 2D/3D building metrics presented a significant positive spatial autocorrelation (p < 0.01) (Table 2).
3.2. Relative Importance of 2D/3D Building Metrics in Determining the Variability of LST
The OLS multiple linear regressions results illustrated that BCR, BD, MBPA, BHSD, and MBH had significant effects on LST (Table 3). These metrics put together explained 65.8% of the full variance in LST. Judged by the standard coefficients, BCR was the foremost vital predictor of LST, and it played a greater role in predicting LST than the other 2D/3D building metrics. Among the five building metrics, three 2D metrics (BCR, BD, MBPA) had a relatively stronger prediction effect on LST and had a positive impact, while the two 3D metrics (BHSD, MBH) had a negative effect on LST.

Table 3.
Statistics of the OLS regression models.
The residuals of the OLS model had significant spatial autocorrelation (Moran’s I = 0.255, p < 0.01), suggesting a potential bias within the results of the OLS model (Table 4). The Lagrange Multiplier statistics indicated that LM Lag, Robust LM Lag, LM Error, and Robust LM Error were all significant. However, the SEM was more significant than the SLM, which suggested that the SEM was more appropriate for our data. The SEM results were significantly improved compared with the OLS model after considering the spatial autocorrelation, with the R2 value increasing from 65.8% to 78.5% and the AIC value decreasing from 262.08 to 216.34. At the same time, it should be noted that when spatial autocorrelation was considered, only three building metrics (BCR, MBPA, and BHSD) remained significant (Table 5). Whether OLS or SAR, the results of the standard coefficients recommended that BCR was the most important predictor of LST among the building metrics.

Table 4.
The diagnostics for spatial dependence of the OLS regression model.

Table 5.
The results of the spatial error models.
The variance partitioning results indicated that the two groups of variables together explained 65.8% of the whole variance of LST, while 34.2% were unexplained (Figure 4). 2D building metrics had taken on a more significant role than 3D building metrics. The 2D building metrics alone explained 51.0% of LST’s total variance while the unique effects of 3D building metrics and the joint effects 2D and 3D building metrics explained 10.2% and 4.6%, respectively.
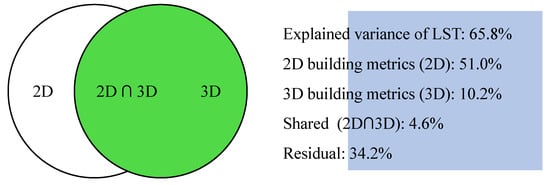
Figure 4.
Venn diagram showing the results of variance partitioning and percentages of explained variances of LST by 2D/3D building metrics.
4. Discussion
4.1. On the Associations between 2D/3D Building Spatial Patterns and LST
The building patterns will influence the distribution of energy balance. Thus, it will change the urban thermal environment [37], and a considerable amount of research has shown that 2D building patterns have an important impact on urban LST and air temperature [19,33,66,67]. However, few studies have examined the effects of 3D building patterns on LST [36,40,41] or compared the relative contribution rate of 2D and 3D building patterns to the variation of LST.
Among the 2D building metrics, BCR was the most critical predictor of LST and had a positive impact, which is similar to the findings of previous studies [26,33]. Our results showed that increasing the BCR can significantly increase LST. This reveals that extensive and contiguous building layout will significantly increase the LST at the census tract level. This phenomenon may be mainly due to the higher heat capacity, lower albedos, and evapotranspiration efficiency of building materials and impervious surfaces [68,69]. Besides, continuous building layouts impede ventilation and exacerbate the urban heat island effect [26,70] leading to broader use of air-conditioning systems and further deterioration of the urban thermal environment [37,71]. MBPA was another 2D metric exhibiting a significantly positive correlation with LST. Sun et al. and Li et al. also reached similar conclusions in their research [26,33]. An increase in MBPA may increase LST because greater and continuous buildings can generate stronger heat island effects [19,72,73]. Additionally, an increase in the average building base area will increase the total buildings’ boundaries, enhancing the energy flow and exchange between buildings and surrounding surfaces, thus leading to an increase in LST. We also discovered that there is a significant positive correlation between BD and LST, which indicated that with the increase of building density, LST would increase. The finding is consistent with previous studies that found that BD strongly affects urban LST [37,39]. In the same region, the average distance between adjacent buildings decreases as the building density increases. Previous studies have indicated that the shading effects of buildings increase when buildings are close to each other because of the shading facades supplied by adjacent buildings [19,36]. Moreover, dense buildings can obstruct wind and ventilation, which induces heat-trapping [39,41,74].
The relationship between 3D landscape patterns and the urban thermal environment has attracted more and more attention in urban ecology and landscape ecology. Our study indicated that the contribution rate of 3D building patterns is not as good as that of 2D building patterns in explaining LST variation. However, 3D building patterns also take on an important role in influencing LST during summer daytime. Among them, BHSD and MBH are the most significant 3D building metrics contributing to the LST. We found that there was a significant negative correlation between MBH and LST in summer daytime, and the LST decreases correspondingly with the increase of MBH, which is similar to the research results of previous studies [19,33,39,52,75], but diverges from others [36,70,76]. The different results may be due to the fact that some studies neglected other building metrics that have an impact on LST [39]. In fact, BD and BCR often changed with building height, and both have significant effects on LST. Considering the other building metrics, we discovered that there was a significant negative correlation between MBH and LST. First, high-rise buildings can effectively reduce the net solar radiation that reaches the land surfaces and cast more shadows, which reduces the LST of shaded areas [28,77,78]. Second, there is a significant difference in aerodynamics between low-rise and high-rise buildings in the lower boundary layer. In comparison with low-rise buildings, high-rise buildings have higher aerodynamic conductivity to take heat away from the surface [33]. BHSD was the most significant predictor of LST in the 3D building metrics and there is a significant negative correlation between BHSD and LST. This finding is consistent with the results of previous studies [19,26,70]. First, the uniform building height traps heat in a compact space and impedes the flow of wind [74,79]. Second, building height heterogeneity increases the surface roughness, which generates mechanical turbulence, thereby enhancing the convective heat dissipation [33]. However, the result differs from a similar study conducted in Wuhan, which discovered that BHSD explained LST variation inconspicuously in summer daytime [37]. This contradiction may be because the importance of BHSD on LST varies with the analysis scale [80,81] and across cities with different climatic conditions [19,25,82]. This deserves further study.
In addition, it should be pointed out that factors such as the sky view factor (SVF), street height–width ratio (H/W), and street orientation also affect local microclimate and air flow, and have an important impact on the urban thermal environment. The relationship between SVF and LST is mainly negative, but Scarano and Mancini found that the larger the SVF, the higher the LST [39], and their relationship may be affected by the spatiotemporal scale. H/W is negatively correlated with daytime air temperature in different climate regions. Whether it is a hot-dry climate or humid-hot climate, researchers have found that the smaller the H/W, the higher the temperature value [83,84]. Street orientation also has a certain impact on the urban thermal environment as east–west streets are exposed to solar radiation for a longer time, their daytime temperature is higher than those of north–south streets [85,86]. However, this study focuses on the impact of building patterns on LST at the census tract level, and the aforementioned factors are not particularly closely related to building characteristics. In addition, SVF and H/W are comprehensive indicators, and the basic building indicators such as building height and floor area ratio considered in this study can be directly applied to urban planning and architectural design, and it is more instructive to discuss their impact on the thermal environment. Therefore, these factors were not included in the establishment of the index system in this study.
4.2. The Methodical Implications
Our findings indicated that spatial autocorrelation analysis can elaborate the spatial relationship between building patterns and LST. In this research, the SAR model was more suitable for quantifying the effect of building patterns on LST than the OLS regression model. The OLS model residuals had significant spatial autocorrelation, which violated the assumption that the OLS error terms were independent. Such violation may cause the standard errors of OLS coefficient estimates to be underestimated and generate misleading results. Therefore, the selection of appropriate statistical methods is crucial. Other statistical approaches, such as the extreme gradient boosting regression model, boosted regression tree and hierarchical partitioning analysis have been increasingly applied to quantify the complex relationships between landscape patterns and the urban thermal environment [1,26,41], which potentially improve the quantitative study about the impacts of building structure on LST.
Furthermore, the statistical methods considering spatial autocorrelation could provide insights into understanding the relationship between building patterns and LST. The findings indicated that both LST and building metrics were spatially autocorrelated at the census tract scale, suggesting that LST in adjacent analysis units might interact with each other, and the building metrics values of adjacent units tend to be similar. This was probably the result of the regulation of unified planning and management of adjacent census tracts, and the building metrics (like building control height, floor area ratio and building density, etc.) in the controlled detailed plan of adjacent plots are similar.
4.3. Implications of Urban Planning and Management
The research showed that 2D and 3D building patterns significantly influence the summer daytime LST. The building patterns can influence the urban thermal environment by altering the absorption of solar radiation, the formation of airflow, and the generation of anthropogenic heat [37,85]. The relationships between building patterns and LST are of great significance for urban planning and management to improve the urban thermal environment. Previous studies [26,68,69] and ours suggest that building coverage contributes greatly to LST. But it is not realistic to decrease the urban building coverage ratio where the land source is scarce and valuable, such as in Shanghai. However, results from our study revealed that the 2D and 3D spatial configuration of buildings could also affect LST at the census tract level. Therefore, we can alleviate the UHI problem by optimizing 2D/3D building spatial configuration. However, it should be pointed out that in the study of the relationship between building patterns and the urban thermal environment, the selection of indicators mainly depends on the impact on the thermal environment, and less attention is paid to the guiding role of design. Many indicators have little relationship to planning and designing, so the research results cannot be directly applied to urban planning and architectural design. Therefore, when establishing the index system, its guiding significance for practice should be considered, and some basic architectural indicators commonly used in design, such as building height, density and floor area ratio, should be actively selected. The results of this study showed that more attention should be paid to the building density, mean building projection area, building height standard deviation, and mean building height during urban planning and management in highly urbanized areas. In addition to the building pattern, roof greening and vertical greening of buildings and the use of external wall materials with high albedo can also effectively alleviate the urban heat island effect [87,88,89].
5. Conclusions
This research quantified the association between building patterns and LST, particularly by measuring the relative importance of 2D/3D building metrics in determining the spatial variability of LST. We found that 2D and 3D building patterns have an important effect on LST. The 2D building patterns explained a more significant amount of variation in LST. However, the 3D building patterns also acted as a key player in predicting LST. Specifically, the building coverage ratio was the most critical predictor and had a significantly positive relationship with LST. The BD, MBPA, BHSD, and MBH also played dominant roles in predicting LST. In addition, spatial autocorrelation may influence the relationship between 2D/3D building metrics and LST. These results can extend our comprehension of the relationship between 2D/3D building patterns and LST at the census tract level and provide essential insights for urban planners and decision makers on alleviating the UHI problem through urban planning and architectural design.
It is widely recognized that decreasing building coverage can effectively alleviate UHI effects. However, with the massive influx of people into cities and dramatic urbanization, the increase in buildings has become an inevitable trend to meet urban living and working needs. Therefore, how to optimize the 2D and 3D building patterns to mitigate the UHI effect becomes particularly important. Our results indicate that an increase in the average height and standard deviation of buildings and a decrease in the average base area and density of buildings can also improve the urban thermal environment. However, it should be noted that the relationship between building patterns and LST may be scale-dependent and climate-dependent. This study was only carried out in the Shanghai metropolitan region at the census tract level, and whether these conclusions are applicable to other metropolitan areas with different scales or climate zone needs to be further explored. Therefore, comparative multi-scale and multi-city studies that take into account different climatic conditions are required for future research to deepen our insight into the relationship between building patterns and LST.
Author Contributions
Conceptualization, R.Z. and C.L.; methodology, R.Z. and J.Z.; software, R.Z., J.Z. and T.H.; validation, R.Z., H.Z. and C.L.; formal analysis, R.Z. and C.L.; investigation, R.Z. and J.Z.; resources, M.L. and J.G.; data curation, R.Z., M.L. and J.Z.; writing—original draft preparation, R.Z. and H.Z.; writing—review and editing, R.Z., H.X. and C.L.; visualization, R.Z., T.H. and C.L.; supervision, H.Z. and C.L.; project administration, R.Z. and C.L.; funding acquisition, R.Z., J.G. and C.L. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the National Natural Science Foundation of China (Nos. 41730642, 41871192), the General Science Foundation of Shanghai Normal University (No. SK202256), and the Soft Science Foundation of Shanghai, China (No. 19692108200).
Data Availability Statement
The data that support the findings of this study are available from the corresponding author on reasonable request.
Acknowledgments
The authors would like to thank the anonymous reviewers for their valuable comments to improve the quality of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Peng, J.; Xie, P.; Liu, Y.; Ma, J. Urban thermal environment dynamics and associated landscape pattern factors: A case study in the Beijing metropolitan region. Remote Sens. Environ. 2016, 173, 145–155. [Google Scholar] [CrossRef]
- Rhee, J.; Park, S.; Lu, Z. Relationship between land cover patterns and surface temperature in urban areas. GISci. Remote Sens. 2014, 51, 521–536. [Google Scholar] [CrossRef]
- Oke, T.R. The energetic basis of the urban heat island. Q. J. R. Meteorol. Soc. 1982, 108, 1–24. [Google Scholar] [CrossRef]
- Taha, H. Urban climates and heat islands: Albedo, evapotranspiration, and anthropogenic heat. Energy Build. 1997, 25, 99–103. [Google Scholar] [CrossRef] [Green Version]
- Voogt, J.A.; Oke, T.R. Thermal remote sensing of urban climates. Remote Sens. Environ. 2003, 86, 370–384. [Google Scholar] [CrossRef]
- Weng, Q.; Yang, S. Urban air pollution patterns, land use, and thermal landscape: An examination of the linkage using GIS. Environ. Monit. Assess. 2006, 117, 463–489. [Google Scholar] [CrossRef] [PubMed]
- Grimm, N.B.; Faeth, S.H.; Golubiewski, N.E.; Redman, C.L.; Wu, J.; Bai, X.; Briggs, J.M. Global change and the ecology of cities. Science 2008, 319, 756–760. [Google Scholar] [CrossRef] [Green Version]
- Gober, P.; Brazel, A.; Quay, R.; Myint, S.; Grossman-Clarke, S.; Miller, A.; Rossi, S. Using watered landscapes to manipulate urban heat island effects: How much water will it take to cool Phoenix? J. Am. Plan. Assoc. 2009, 76, 109–121. [Google Scholar] [CrossRef]
- Konopacki, S.; Akbari, H. Energy Savings for Heat Island Reduction Strategies in Chicago and Houston (Including Updates for Baton Rouge, Sacramento, and Salt Lake City); University of California: Berkeley, CA, USA, 2002. [Google Scholar]
- Wan, K.K.; Li, D.H.; Pan, W.; Lam, J.C. Impact of climate change on building energy use in different climate zones and mitigation and adaptation implications. Appl. Energy 2012, 97, 274–282. [Google Scholar] [CrossRef]
- Santamouris, M.; Cartalis, C.; Synnefa, A.; Kolokotsa, D. On the impact of urban heat island and global warming on the power demand and electricity consumption of buildings—A review. Energy Build. 2015, 98, 119–124. [Google Scholar] [CrossRef]
- White, M.A.; Nemani, R.R.; Thornton, P.E.; Running, S.W. Satellite evidence of phenological differences between urbanized and rural areas of the eastern United States deciduous broadleaf forest. Ecosystems 2002, 5, 260–273. [Google Scholar] [CrossRef]
- Niemelä, J. Ecology and urban planning. Biodivers. Conserv. 1999, 8, 119–131. [Google Scholar] [CrossRef]
- Poumadère, M.; Mays, C.; Le Mer, S.; Blong, R. The 2003 heat wave in France: Dangerous climate change here and now. Risk Anal. 2005, 25, 1483–1494. [Google Scholar] [CrossRef] [PubMed]
- Patz, J.A.; Campbell-Lendrum, D.; Holloway, T.; Foley, J.A. Impact of regional climate change on human health. Nature 2005, 438, 310–317. [Google Scholar] [CrossRef] [PubMed]
- Harlan, S.L.; Ruddell, D.M. Climate change and health in cities: Impacts of heat and air pollution and potential co-benefits from mitigation and adaptation. Curr. Opin. Environ. Sustain. 2011, 3, 126–134. [Google Scholar] [CrossRef]
- Jenerette, G.D.; Harlan, S.L.; Buyantuev, A.; Stefanov, W.L.; Declet-Barreto, J.; Ruddell, B.L.; Myint, S.W.; Kaplan, S.; Li, X. Micro-scale urban surface temperatures are related to land-cover features and residential heat related health impacts in Phoenix, AZ USA. Landsc. Ecol. 2016, 31, 745–760. [Google Scholar] [CrossRef]
- Weng, Q. Thermal infrared remote sensing for urban climate and environmental studies: Methods, applications, and trends. ISPRS J. Photogramm. Remote Sens. 2009, 64, 335–344. [Google Scholar] [CrossRef]
- Tian, Y.; Zhou, W.; Qian, Y.; Zheng, Z.; Yan, J. The effect of urban 2D and 3D morphology on air temperature in residential neighborhoods. Landsc. Ecol. 2019, 34, 1161–1178. [Google Scholar] [CrossRef]
- Eludoyin, O.M.; Adelekan, I.; Webster, R.; Eludoyin, A. Air temperature, relative humidity, climate regionalization and thermal comfort of Nigeria. Int. J. Clim. 2013, 34, 2000–2018. [Google Scholar] [CrossRef] [Green Version]
- Zeng, L.; Wardlow, B.D.; Tadesse, T.; Shan, J.; Hayes, M.J.; Li, D.; Xiang, D. Estimation of daily air temperature based on MODIS land surface temperature products over the corn belt in the US. Remote Sens. 2015, 7, 951–970. [Google Scholar] [CrossRef] [Green Version]
- Peng, J.; Jia, J.; Liu, Y.; Li, H.; Wu, J. Seasonal contrast of the dominant factors for spatial distribution of land surface temperature in urban areas. Remote Sens. Environ. 2018, 215, 255–267. [Google Scholar] [CrossRef]
- Zhang, H.; Li, T.-T.; Han, J.-J. Quantifying the relationship between land use features and intra-surface urban heat island effect: Study on downtown Shanghai. Appl. Geogr. 2020, 125, 102305. [Google Scholar] [CrossRef]
- Imhoff, M.L.; Zhang, P.; Wolfe, R.E.; Bounoua, L. Remote sensing of the urban heat island effect across biomes in the continental USA. Remote Sens. Environ. 2010, 114, 504–513. [Google Scholar] [CrossRef] [Green Version]
- Zhou, W.; Wang, J.; Cadenasso, M.L. Effects of the spatial configuration of trees on urban heat mitigation: A comparative study. Remote Sens. Environ. 2017, 195, 1–12. [Google Scholar] [CrossRef]
- Sun, F.; Liu, M.; Wang, Y.; Wang, H.; Che, Y. The effects of 3D architectural patterns on the urban surface temperature at a neighborhood scale: Relative contributions and marginal effects. J. Clean. Prod. 2020, 258, 120706. [Google Scholar] [CrossRef]
- Mildrexler, D.J.; Zhao, M.; Running, S.W. A global comparison between station air temperatures and MODIS land surface temperatures reveals the cooling role of forests. J. Geophys. Res. Earth Surf. 2011, 116, 15. [Google Scholar] [CrossRef]
- Kuang, W.; Dou, Y.; Zhang, C.; Chi, W.; Liu, A.; Liu, Y.; Zhang, R.; Liu, J. Quantifying the heat flux regulation of metropolitan land use/land cover components by coupling remote sensing modeling with in situ measurement. J. Geophys. Res. Atmos. 2015, 120, 113–130. [Google Scholar] [CrossRef]
- Clinton, N.; Gong, P. MODIS detected surface urban heat islands and sinks: Global locations and controls. Remote Sens. Environ. 2013, 134, 294–304. [Google Scholar] [CrossRef]
- Ayansina, A. Seasonality in the daytime and night-time intensity of land surface temperature in a tropical city area. Sci. Total Environ. 2016, 557, 415–424. [Google Scholar]
- Peng, J.; Dan, Y.; Qiao, R.; Liu, Y.; Dong, J.; Wu, J. How to quantify the cooling effect of urban parks? Linking maximum and accumulation perspectives. Remote Sens. Environ. 2021, 252, 112135. [Google Scholar] [CrossRef]
- Oke, T.R. Initial Guidance to Obtain Representative Meteorological Observations at Urban Sites; University of British Columbia: Vancouver, BC, Canada, 2004. [Google Scholar]
- Li, J.; Song, C.; Cao, L.; Zhu, F.; Meng, X.; Wu, J. Impacts of landscape structure on surface urban heat islands: A case study of Shanghai, China. Remote Sens. Environ. 2011, 115, 3249–3263. [Google Scholar] [CrossRef]
- Ma, Q.; Wu, J.; He, C. A hierarchical analysis of the relationship between urban impervious surfaces and land surface temperatures: Spatial scale dependence, temporal variations, and bioclimatic modulation. Landsc. Ecol. 2016, 31, 1139–1153. [Google Scholar] [CrossRef]
- Du, H.; Song, X.; Jiang, H.; Kan, Z.; Wang, Z.; Cai, Y. Research on the cooling island effects of water body: A case study of Shanghai, China. Ecol. Indic. 2016, 67, 31–38. [Google Scholar] [CrossRef]
- Berger, C.; Rosentreter, J.; Voltersen, M.; Baumgart, C.; Schmullius, C.; Hese, S. Spatio-temporal analysis of the relationship between 2D/3D urban site characteristics and land surface temperature. Remote Sens. Environ. 2017, 193, 225–243. [Google Scholar] [CrossRef]
- Huang, X.; Wang, Y. Investigating the effects of 3D urban morphology on the surface urban heat island effect in urban functional zones by using high-resolution remote sensing data: A case study of Wuhan, Central China. ISPRS J. Photogramm. Remote Sens. 2019, 152, 119–131. [Google Scholar] [CrossRef]
- Futcher, J.; Mills, G.; Emmanuel, R.; Korolija, I. Creating sustainable cities one building at a time: Towards an integrated urban design framework. Cities 2017, 66, 63–71. [Google Scholar] [CrossRef] [Green Version]
- Scarano, M.; Mancini, F. Assessing the relationship between sky view factor and land surface temperature to the spatial resolution. Int. J. Remote Sens. 2017, 38, 6910–6929. [Google Scholar] [CrossRef]
- Zheng, Z.; Zhou, W.; Yan, J.; Qian, Y.; Wang, J.; Li, W. The higher, the cooler? Effects of building height on land surface temperatures in residential areas of Beijing. Phys. Chem. Earth 2019, 110, 149–156. [Google Scholar] [CrossRef]
- Zhang, H.; Li, T.; Liu, Y.; Han, J.; Guo, Y. Understanding the contributions of land parcel features to intra-surface urban heat island intensity and magnitude: A study of downtown Shanghai, China. Land Degrad. Dev. 2020, 32, 1353–1367. [Google Scholar] [CrossRef]
- Yu, S.; Chen, Z.; Yu, B.; Wang, L.; Wu, B.; Wu, J.; Zhao, F. Exploring the relationship between 2D/3D landscape pattern and land surface temperature based on explainable eXtreme Gradient Boosting tree: A case study of Shanghai, China. Sci. Total Environ. 2020, 725, 138229. [Google Scholar] [CrossRef]
- Peng, S.; Piao, S.; Ciais, P.; Friedlingstein, P.; Ottle, C.; Bréon, F.-M.; Nan, H.; Zhou, L.; Myneni, R.B. Surface urban heat island across 419 global big cities. Environ. Sci. Technol. 2012, 46, 696–703. [Google Scholar] [CrossRef] [PubMed]
- Yang, Q.; Huang, X.; Tang, Q. The footprint of urban heat island effect in 302 Chinese cities: Temporal trends and associated factors. Sci. Total Environ. 2019, 655, 652–662. [Google Scholar] [CrossRef] [PubMed]
- United Nations. The World’s Cities in 2018; United Nations: New York, NY, USA, 2018. [Google Scholar]
- USGS. Landsat 8 (L8) Data Users Handbook; Department of the Interior, U.S. Geological Survey: Washington, DC, USA, 2016.
- Barsi, J.A.; Barker, J.L.; Schott, J.R. An atmospheric correction parameter calculator for a single thermal band earth-sensing instrument. In Proceedings of the IGARSS 2003. 2003 IEEE International Geoscience and Remote Sensing Symposium, Toulouse, France, 21–25 July 2003; Proceedings (IEEE Cat. No. 03CH37477). IEEE: Manhattan, NY, USA, 2003; pp. 3014–3016. [Google Scholar]
- Weng, Q.; Lu, D.; Schubring, J. Estimation of land surface temperature–vegetation abundance relationship for urban heat island studies. Remote Sens. Environ. 2004, 89, 467–483. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Jiménez-Muñoz, J.C.; Paolini, L. Land surface temperature retrieval from LANDSAT TM 5. Remote Sens. Environ. 2004, 90, 434–440. [Google Scholar] [CrossRef]
- Dash, P.; Göttsche, F.-M.; Olesen, F.-S.; Fischer, H. Land surface temperature and emissivity estimation from passive sensor data: Theory and practice-current trends. Int. J. Remote Sens. 2002, 23, 2563–2594. [Google Scholar] [CrossRef]
- Norman, J.M.; Becker, F. Terminology in thermal infrared remote sensing of natural surfaces. Remote Sens. Rev. 1995, 12, 159–173. [Google Scholar] [CrossRef]
- Barsi, J.A.; Butler, J.J.; Schott, J.R.; Palluconi, F.D.; Hook, S.J. Validation of a web-based atmospheric correction tool for single thermal band instruments. In Optics and Photonics 2005; SPIE: Bellingham, WA, USA, 2005; p. 7. [Google Scholar]
- Alavipanah, S.; Schreyer, J.; Haase, D.; Lakes, T.; Qureshi, S. The effect of multi-dimensional indicators on urban thermal conditions. J. Clean. Prod. 2017, 177, 115–123. [Google Scholar] [CrossRef]
- Liu, M.; Hu, Y.-M.; Li, C. Landscape metrics for three-dimensional urban building pattern recognition. Appl. Geogr. 2017, 87, 66–72. [Google Scholar] [CrossRef]
- Riitters, K.H.; O’Neill, R.V.; Hunsaker, C.T.; Wickham, J.D.; Yankee, D.H.; Timmins, S.P.; Jones, K.B.; Jackson, B.L. A factor analysis of landscape pattern and structure metrics. Landsc. Ecol. 1995, 10, 23–39. [Google Scholar] [CrossRef]
- Li, H.; Wu, J. Use and misuse of landscape indices. Landsc. Ecol. 2004, 19, 389–399. [Google Scholar] [CrossRef] [Green Version]
- Peng, J.; Wang, Y.; Zhang, Y.; Wu, J.; Li, W.; Li, Y. Evaluating the effectiveness of landscape metrics in quantifying spatial patterns. Ecol. Indic. 2010, 10, 217–223. [Google Scholar] [CrossRef]
- McGarigal, K.; Cushman, S.; Neel, M.; Ene, E. FRAGSTATS: Spatial Pattern Analysis Program for Categorical Maps; University of Massachusetts: Amherst, MA, USA, 2012. [Google Scholar]
- Lichstein, J.; Simons, T.; Shriner, S.; Franzreb, K. Spatial autocorrelation and autoregressive models in ecology. Ecol. Monogr. 2002, 72, 445–463. [Google Scholar] [CrossRef]
- Li, X.; Zhou, W.; Ouyang, Z.; Xu, W.; Zheng, H. Spatial pattern of greenspace affects land surface temperature: Evidence from the heavily urbanized Beijing metropolitan area, China. Landsc. Ecol. 2012, 27, 887–898. [Google Scholar] [CrossRef]
- Anselin, L. Exploring Spatial Data with GeoDa™: A Workbook; University of Illinois: Urbana, IL, USA, 2005. [Google Scholar]
- Weng, Q.; Lu, D.; Liang, B. Urban Surface Biophysical Descriptors and Land Surface Temperature Variations. Photogramm. Eng. Remote Sens. 2006, 72, 1275–1286. [Google Scholar] [CrossRef] [Green Version]
- Yan, H.; Fan, S.; Guo, C.; Wu, F.; Zhang, N.; Dong, L. Assessing the effects of landscape design parameters on intra-urban air temperature variability: The case of Beijing, China. Build. Environ. 2014, 76, 44–53. [Google Scholar] [CrossRef]
- Zhou, W.; Huang, G.; Cadenasso, M.L. Does spatial configuration matter? Understanding the effects of land cover pattern on land surface temperature in urban landscapes. Landsc. Urban Plan. 2011, 102, 54–63. [Google Scholar] [CrossRef]
- Anderson, M.J.; Gribble, N.A. Partitioning the variation among spatial, temporal and environmental components in a multivariate data set. Aust. J. Ecol. 1998, 23, 158–167. [Google Scholar] [CrossRef]
- Legendre, P. Studying beta diversity: Ecological variation partitioning by multiple regression and canonical analysis. J. Plant Ecol. 2007, 1, 3–8. [Google Scholar] [CrossRef] [Green Version]
- Srivanit, M.; Kazunori, H. The influence of urban morphology indicators on summer diurnal range of urban climate in Bangkok Metropolitan Area Thailand. Int. J. Civ. Environ. Eng. 2011, 11, 34–46. [Google Scholar]
- Chun, B.; Guldmann, J.-M. Spatial statistical analysis and simulation of the urban heat island in high-density central cities. Landsc. Urban Plan. 2014, 125, 76–88. [Google Scholar] [CrossRef]
- Wang, Y.; Akbari, H. Analysis of urban heat island phenomenon and mitigation solutions evaluation for Montreal. Sustain. Cities Soc. 2016, 26, 438–446. [Google Scholar] [CrossRef]
- Oke, T.R.; Mills, G.; Christen, A.; Voogt, J.A. Urban Climate; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Yang, L.; Li, Y. Thermal conditions and ventilation in an ideal city model of Hong Kong. Energy Build. 2010, 43, 1139–1148. [Google Scholar] [CrossRef]
- Wong, J.; Lau, L. From the ‘urban heat island’ to the ‘green island’? A preliminary investigation into the potential of retrofitting green roofs in Mongkok district of Hong Kong. Habitat Int. 2013, 39, 25–35. [Google Scholar] [CrossRef]
- Ryu, Y.-H.; Baik, J.-J. Quantitative Analysis of Factors Contributing to Urban Heat Island Intensity. J. Appl. Meteorol. Clim. 2012, 51, 842–854. [Google Scholar] [CrossRef]
- Konarska, J.; Holmer, B.; Lindberg, F.; Thorsson, S. Influence of vegetation and building geometry on the spatial variations of air temperature and cooling rates in a high-latitude city. Int. J. Climatol. 2016, 36, 2379–2395. [Google Scholar] [CrossRef] [Green Version]
- Jamei, E.; Rajagopalan, P. Urban development and pedestrian thermal comfort in Melbourne. Sol. Energy 2017, 144, 681–698. [Google Scholar] [CrossRef]
- Zhao, L.; Lee, X.; Smith, R.B.; Oleson, K. Strong contributions of local background climate to urban heat islands. Nature 2014, 511, 216–219. [Google Scholar] [CrossRef]
- Guo, G.; Zhou, X.; Wu, Z.; Xiao, R.; Chen, Y. Characterizing the impact of urban morphology heterogeneity on land surface temperature in Guangzhou, China. Environ. Model. Softw. 2016, 84, 427–439. [Google Scholar] [CrossRef]
- Nichol, J.E. Visualisation of urban surface temperatures derived from satellite images. Int. J. Remote Sens. 1998, 19, 1639–1649. [Google Scholar] [CrossRef]
- Perini, K.; Magliocco, A. Effects of vegetation, urban density, building height, and atmospheric conditions on local temperatures and thermal comfort. Urban For. Urban Green. 2014, 13, 495–506. [Google Scholar] [CrossRef]
- Allegrini, J. A wind tunnel study on three-dimensional buoyant flows in street canyons with different roof shapes and building lengths. Build. Environ. 2018, 143, 71–88. [Google Scholar] [CrossRef]
- Davis, A.Y.; Jung, J.; Pijanowski, B.C.; Minor, E.S. Combined vegetation volume and “greenness” affect urban air temperature. Appl. Geogr. 2016, 71, 106–114. [Google Scholar] [CrossRef] [Green Version]
- Howe, D.; Hathaway, J.; Ellis, K.; Mason, L. Spatial and temporal variability of air temperature across urban neighborhoods with varying amounts of tree canopy. Urban For. Urban Green. 2017, 27, 109–116. [Google Scholar] [CrossRef]
- Shashua-Bar, L.; Tzamir, Y.; Hoffman, M.E. Thermal effects of building geometry and spacing on the urban canopy layer microclimate in a hot-hunmid climate in summer. Int. J. Climatol. 2004, 24, 1729–1742. [Google Scholar] [CrossRef]
- Emmanuel, R.; Johansson, E. Influence of urban morphology and sea breeze on hot humid microclimate: The case of Colombo, Sri Lanka. Clim. Res. 2006, 30, 189–200. [Google Scholar] [CrossRef] [Green Version]
- Jamei, E.; Rajagopalan, P.; Seyedmahmoudian, M.; Jamei, Y. Review on the impact of urban geometry and pedestrian level greening on outdoor thermal comfort. Renew. Sustain. Energy Rev. 2016, 54, 1002–1017. [Google Scholar] [CrossRef]
- Shashua-Bar, L.; Hoffman, M.E. Quantitative evaluation of passive cooling of the UCL microclimate in hot regions in summer, case study: Urban streets and courtyards with trees. Build. Environ. 2004, 39, 1087–1099. [Google Scholar] [CrossRef]
- Yue, W.; Liu, X.; Zhou, Y.; Liu, Y. Impacts of urban configuration on urban heat island: An empirical study in China mega-cities. Sci. Total Environ. 2019, 671, 1036–1046. [Google Scholar] [CrossRef]
- Kikegawa, Y.; Genchi, Y.; Kondo, H.; Hanaki, K. Impacts of city-block-scale countermeasures against urban heat-island phenomena upon a building’s energy-consumption for air-conditioning. Appl. Energy 2006, 83, 649–668. [Google Scholar] [CrossRef]
- Aflaki, A.; Mirnezhad, M.; Ghaffarianhoseini, A.; Ghaffarianhoseini, A.; Omrany, H.; Wang, Z.-H.; Akbari, H. Urban heat island mitigation strategies: A state-of-the-art review on Kuala Lumpur, Singapore and Hong Kong. Cities 2017, 62, 131–145. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).