Inter-Comparison of Diverse Heatwave Definitions in the Analysis of Spatiotemporally Contiguous Heatwave Events over China
Abstract
:1. Introduction
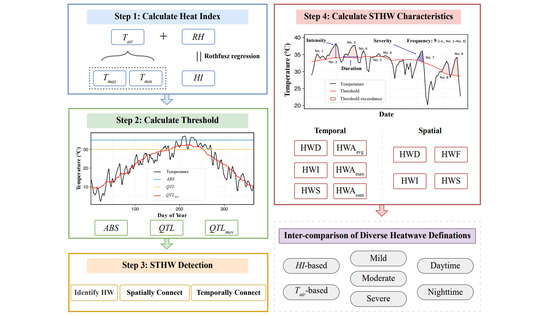
2. Data and Methods
2.1. Data
2.2. Heat Index
2.3. HW Thresholds
- (1)
- For the method, all grid cells share the same threshold and eastern China (longitude ≥ 105 °E) is used to compute the threshold. First, the regional area-weighted average of or is calculated at each time step. The thresholds are determined in accordance with certain percentiles (i.e., 90th, 95th and 99th corresponding to mild, moderate and severe HWs, respectively) during the 1961–1990 reference period from the time series.
- (2)
- For the method, each grid has a unique threshold. For each grid, the threshold is calculated as a certain percentile during the 1961–1990 reference period.
- (3)
- For the method, the threshold varies among each day of the year () from 1 to 366 in the Julian calendar. For each grid, a 15-day moving window (i.e., 7 days prior and posterior to the corresponding calendar day sampled from each year) for each is used to create a subset, and a specific quantile calculated during the 1961–1990 reference period is used as the threshold corresponding to the center date. For instance, all 1 January to 15 January data from 1961–1990 are selected, and the threshold for 8 January is the quantile of these 450 days. Due to the dramatic temperature changes that have occurred in China since the 1990s, it is appropriate to take 1961–1990 as the reference period for a historical comparison and climate change monitoring; this application is also recommended by the WMO [34].
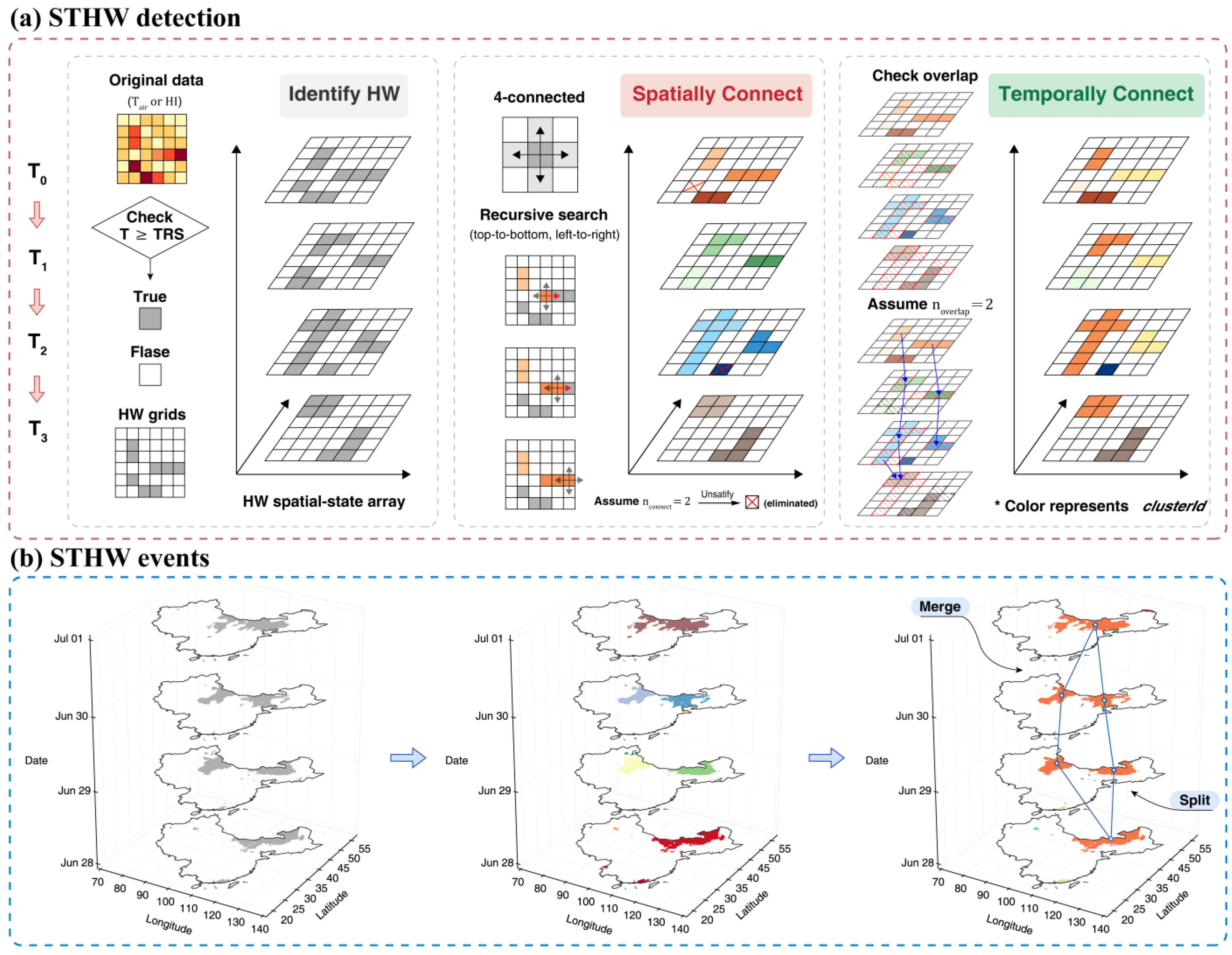
2.4. STHW Detection
- (1)
- The original data are converted to the HW spatial-state array. Initially, the original data have three dimensions (i.e., longitude × latitude × time). For each voxel, if the value is greater than the corresponding threshold, it is marked as “True” and considered as HW grid; otherwise, it is marked as “False”. The threshold is calculated as described in Section 2.3. Therefore, the data are converted to an HW spatial-state array that is stored in a “True/False” Boolean format.
- (2)
- Spatially adjacent HW grids are connected to spatial HW events. In this step, the HW state array is cyclically traversed moment-by-moment in a top-to-bottom, left-to-right order to search for spatially adjacent voxels in each time layer. If an HW grid is detected, it is given a unique . After that, according to the 4-connected neighborhood principle (i.e., two adjoining cells are part of the same object if they are both on and are connected along the horizontal or vertical direction), all recursively searched edge-adjacent HW grids are given the same . Here, a merged spatial HW event with a grid number less than is eliminated, because a small isolated HW event is usually unable to develop into a regional or impactful STHW event; is set to 16.
- (3)
- The spatial HW events are connected to spatiotemporally contiguous HW events. If there are at least grids at the same location in the preceding and following time steps from two spatial HW events, the events are merged into one STHW event and given a new (, where is the of the previous spatial HW event). Here, is set to correspond to . Because HW events usually have a small scale when appearing and dying, this threshold can be set to better distinguish different STHW events from the onset and demise. Finally, the values are stored in three dimensions as original data (i.e., longitude × latitude × time). Due to the thresholds, the identified STHW can ensure that the spatial coverage is not too small and lasts at least 2 days.
2.5. STHW Characteristics
3. Results
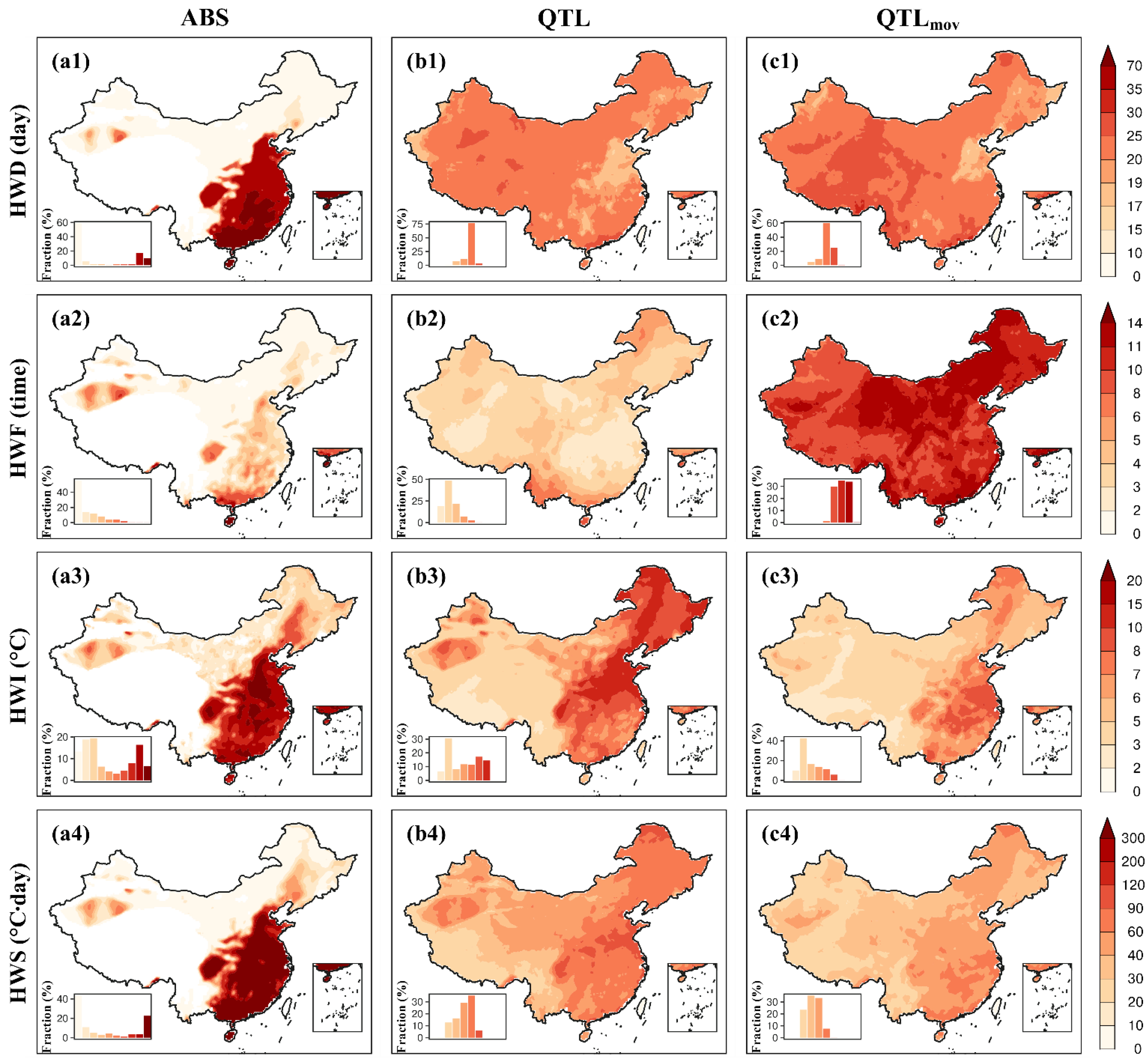
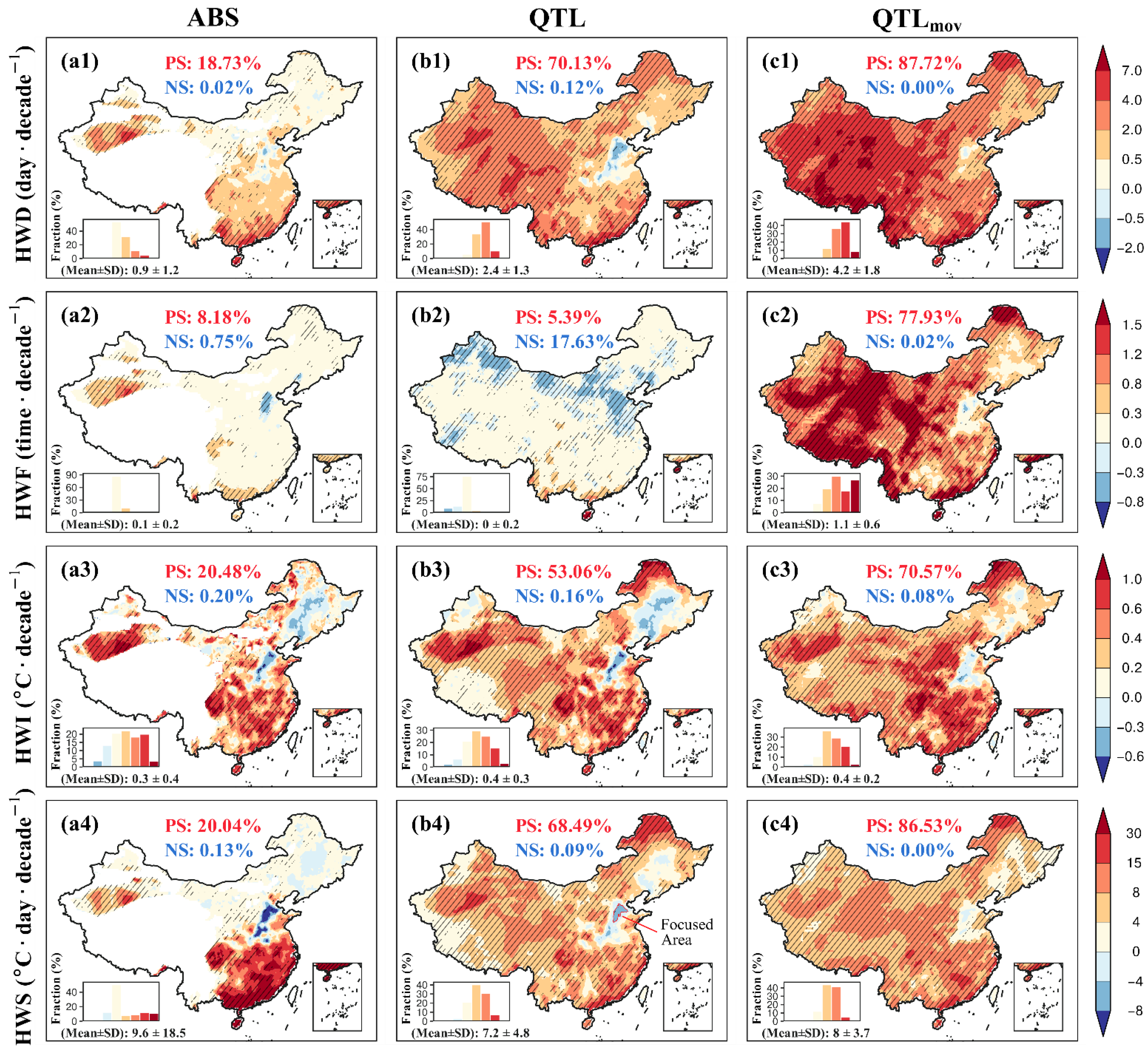
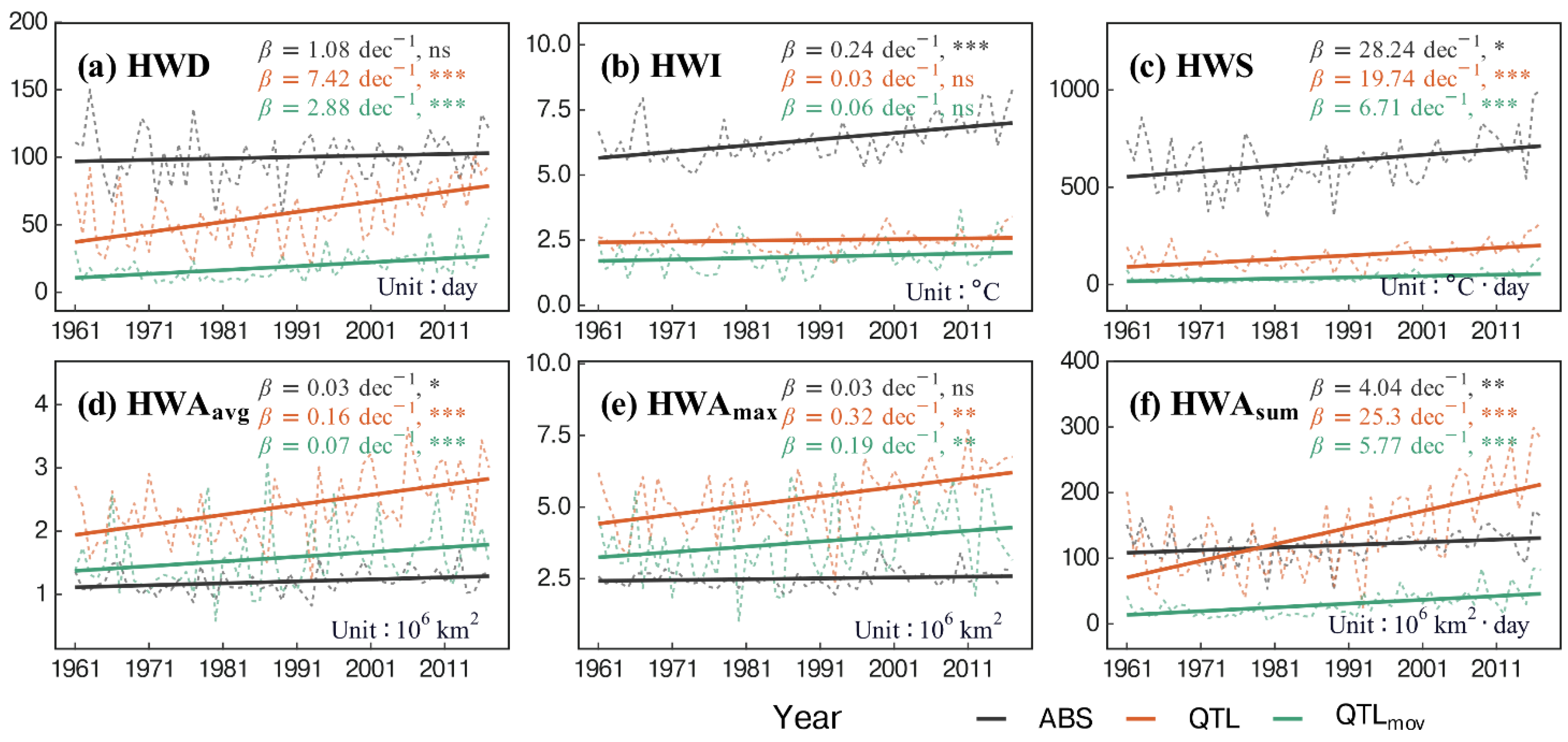
3.1. STHW Characteristics of Different Threshold Methods
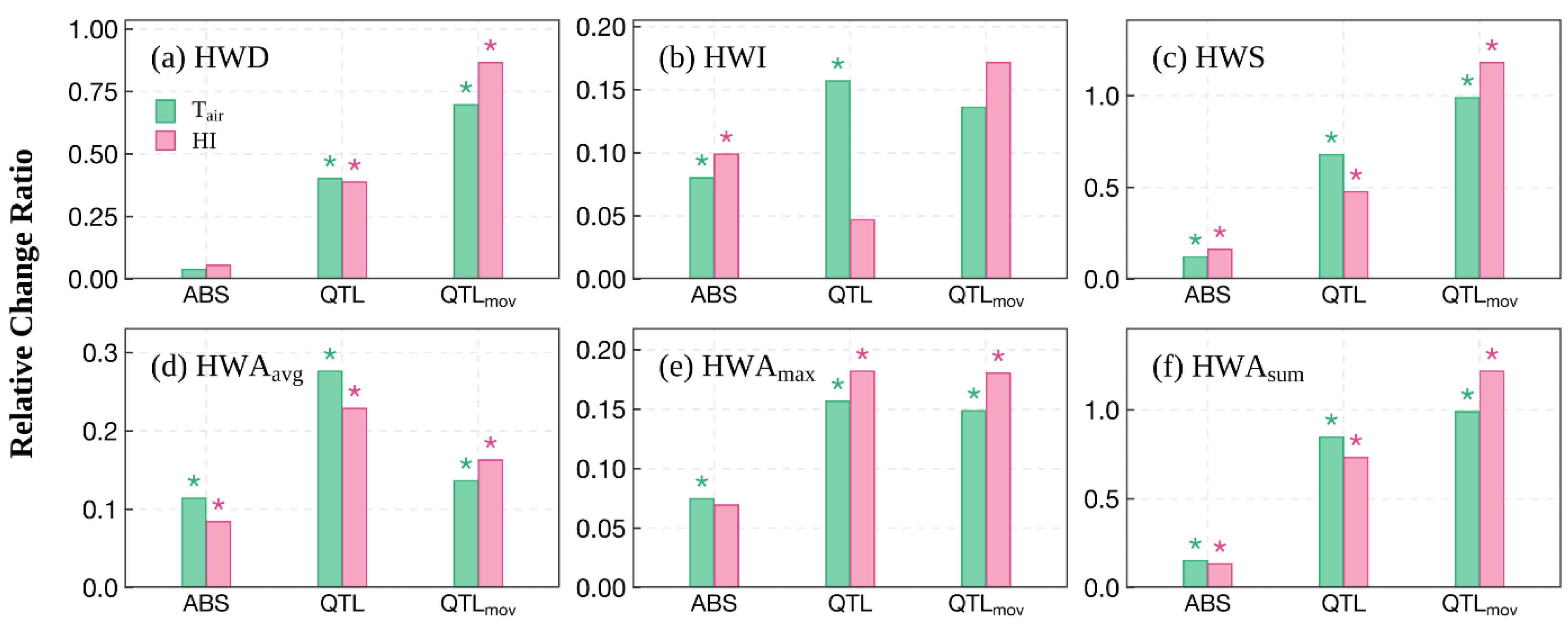
3.2. HI-Based and -Based STHWs
3.3. STHWs with Different Severity Levels

3.4. Daytime and Nighttime STHWs
4. Discussion
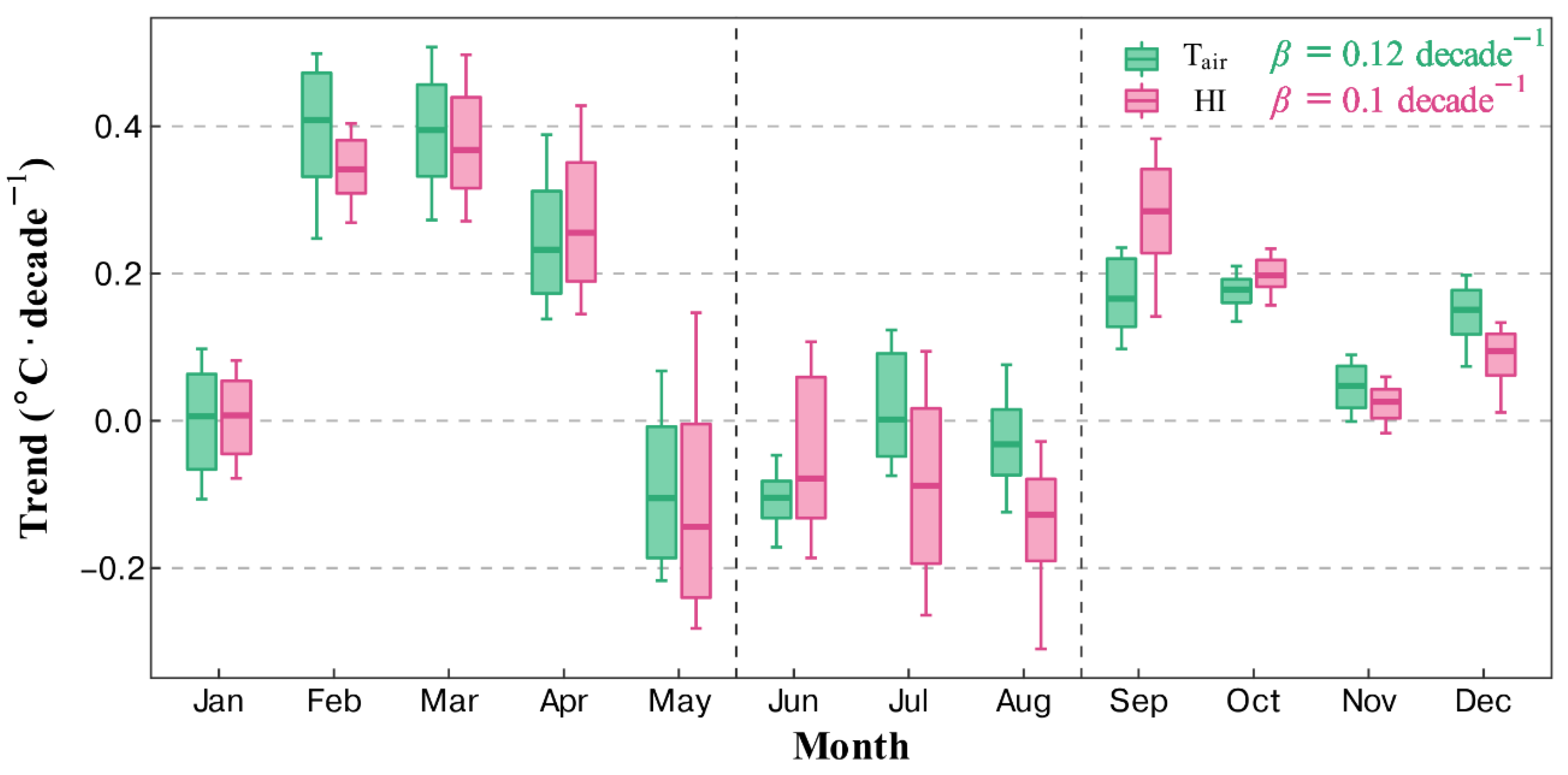
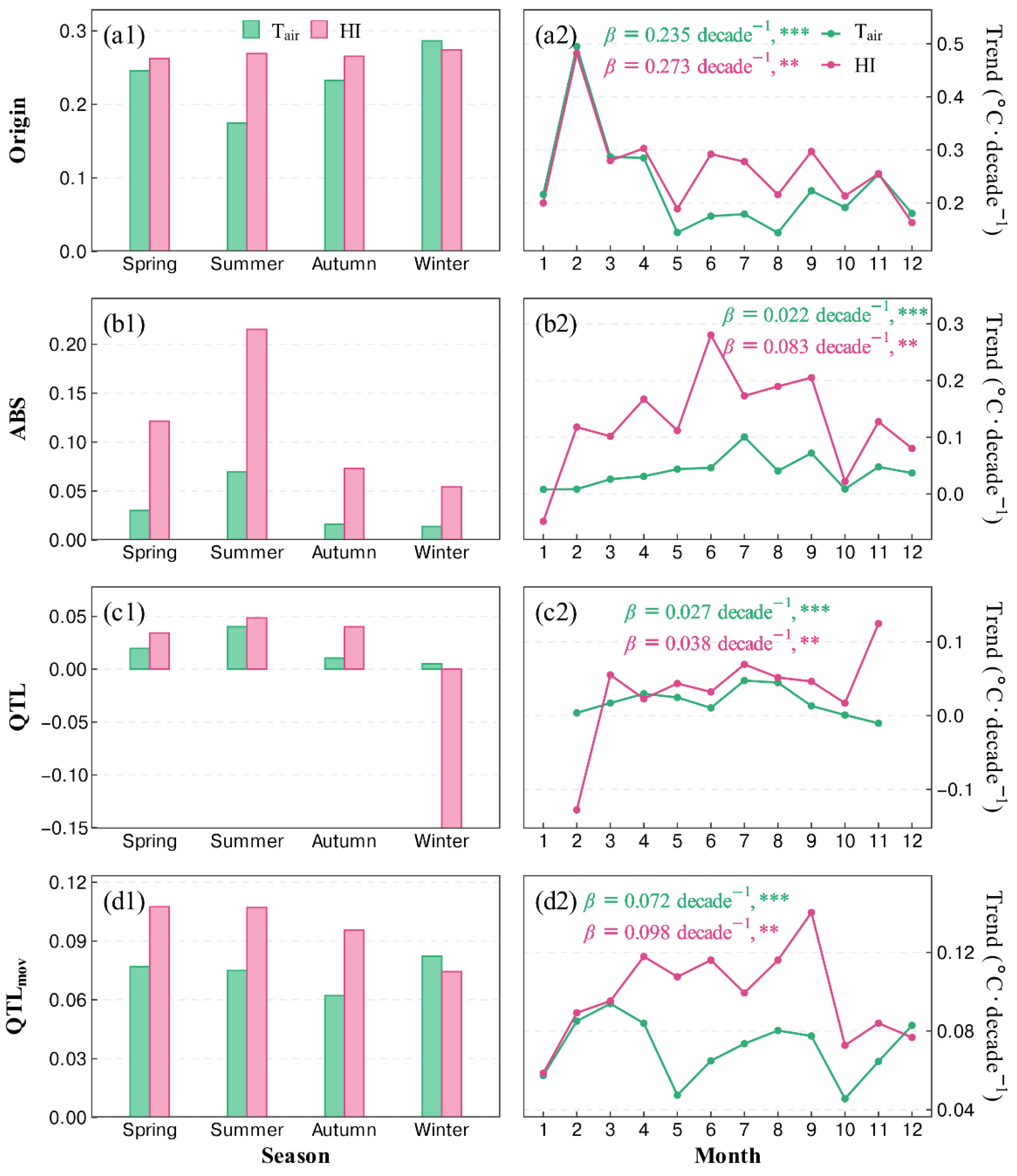
4.1. Explanation of Negative STHW Characteristic Trends in North China and Northeast China
4.2. Possible Reasons for the STHW Characteristic Differences among Different STHW Definitions
4.3. Significance and Limitations
- (1)
- An improved algorithm is used to detect STHWs. Instead of simply merging all temporally and spatially adjacent HW grids into a single STHW event, we set two thresholds: and . Compared to the ordinary 3D connection algorithm, this method considers the merging and splitting behaviors of STHW events during their development and diminution.
- (2)
- Past articles rarely used spatiotemporal clustering algorithms to compare the spatiotemporal patterns under different HW definitions. The majority of investigations of spatial or temporal variations focused only on the grid scale and ignored joint spatial and temporal evolution pattern. In addition, -based HWs are closely relevant to human perception, and while most past studies used either or , the difference among these variables remains largely unexplored. In our study, we compare these HW definitions as comprehensively as possible.
- (1)
- The data selection method may influence the results, especially for . According to our early study, using unhomogenized data can produce entirely different results. To ensure the objectivity of the results, we replaced the original with a homogenized . However, the differences introduced by different homogenization methods were not assessed. It is thus better to use multiple datasets to demonstrate the robustness of the results. In addition, the selection of temperature data may produce differences, as expressed in the trend magnitudes and the different distributions of spatial characteristics, but not to the same extent as the selection.
- (2)
- Different selections of the and thresholds were not investigated herein. Comparing the similarity of the results derived with different thresholds may enhance the robustness of our result.
5. Conclusions
- (1)
- Although the trends’ magnitudes were divergent, all threshold methods showed a consistent phenomenon in most regions of China: STHWs have become longer-lasting, more severe, and have impacted larger areas spatially. However, the increasing trends identified in most cases are insignificant. Moreover, the of the moderate STHWs has decreased mainly because the transfer of mild and moderate STHWs to extreme STHWs decreased the frequency of the former events. In small parts of central-eastern and northeast China, some negative STHW trends were observed due to asymmetric warming in these areas, i.e., these regions experience negative trends in summer but positive trends in other seasons. For threshold methods that do not consider any seasonal variation (i.e., and ), the spatial continuity of the exceedance is relatively weak, resulting in the increase rates of STHW characteristics being underestimated. In addition, the method uses eastern China to calculate the threshold, and it is difficult to identify HWs for the lower-elevation areas in western China (e.g., the Tibetan Plateau). In comparison, performs much better and is more suitable for use across China.
- (2)
- Regarding -based and -based STHWs, when using the threshold, the relative change ratios of all -based STHW characteristics are approximately 20% higher than the -based STHW characteristics, suggesting that the contribution of to HW variability is visible and causes human-perceived HWs to increase rapidly, as hot temperatures are even more unbearable as the presence of humidity in the environment reduces the ability of the human body to cool itself. Therefore, -based STHW should be priorly used. alone without considering may underestimate the increasing STHW magnitudes. However, this phenomenon is weak when considering the threshold and is even reversed when using the method due to the weak spatial continuity of these two methods.
- (3)
- Regarding different HW severity levels, the averaged relative change ratios of moderate and severe STHWs among different STHW characteristics are approximately 1.2 and 2.4 times higher than those of mild STHWs when using and threshold methods, respectively, implying that extreme STHWs will increase much faster than mild or moderate STHWs; this finding is inextricably related to climate warming. Therefore, this phenomenon requires preparation and mitigation programs to avoid or mitigate the effects of the rapid growth of extreme weather events.
- (4)
- Regarding daytime and nighttime STHWs, the increase in nighttime STHWs is approximately 60% faster than that of daytime STHWs when applying the threshold and approximately 120% faster when applying the method. Increasing nighttime exposures may increase the risk of heat-related illnesses.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| HW | Heatwave |
| STHW | Spatiotemporally continuous heatwave |
| Absolute threshold method | |
| Quantile-based threshold method | |
| Moving quantile-based threshold method | |
| Air temperature | |
| Daily maximum air temperature | |
| Daily minimum air temperature | |
| Relative humidity | |
| Heat index | |
| Day of year | |
| Heatwave duration | |
| Heatwave intensity | |
| Heatwave severity | |
| Heatwave mean occurrence area | |
| Heatwave maximum occurrence area | |
| Heatwave total occurrence area | |
| Heatwave frequency |
References
- Li, Y.; Ding, Y.; Li, W. Observed Trends in Various Aspects of Compound Heat Waves across China from 1961 to 2015. J. Meteorol. Res. 2017, 31, 455–467. [Google Scholar] [CrossRef]
- Meehl, G.A.; Tebaldi, C. More Intense, More Frequent, and Longer Lasting Heat Waves in the 21st Century. Science 2004, 305, 994–997. [Google Scholar] [CrossRef] [PubMed]
- Fischer, E.M.; Schär, C. Consistent Geographical Patterns of Changes in High-Impact European Heatwaves. Nat. Geosci. 2010, 3, 398–403. [Google Scholar] [CrossRef]
- Habeeb, D.; Vargo, J.; Stone, B. Rising Heat Wave Trends in Large US Cities. Nat. Hazards 2015, 76, 1651–1665. [Google Scholar] [CrossRef]
- Kenney, W.L.; Craighead, D.H.; Alexander, L.M. Heat Waves, Aging, and Human Cardiovascular Health. Med. Sci. Sports Exerc. 2014, 46, 1891–1899. [Google Scholar] [CrossRef]
- Mora, C.; Counsell, C.W.W.; Bielecki, C.R.; Louis, L.V. Twenty-Seven Ways a Heat Wave Can Kill You. Circ. Cardiovasc. Qual. Outcomes 2017, 10, e004233. [Google Scholar] [CrossRef]
- Yin, Q.; Wang, J. The Association between Consecutive Days’ Heat Wave and Cardiovascular Disease Mortality in Beijing, China. BMC Public Health 2017, 17, 223. [Google Scholar] [CrossRef]
- Carlson, C.J.; Albery, G.F.; Merow, C.; Trisos, C.H.; Zipfel, C.M.; Eskew, E.A.; Olival, K.J.; Ross, N.; Bansal, S. Climate Change Increases Cross-Species Viral Transmission Risk. Nature 2022, 607, 555–562. [Google Scholar] [CrossRef]
- Chung, U.; Gbegbelegbe, S.; Shiferaw, B.; Robertson, R.; Yun, J.I.; Tesfaye, K.; Hoogenboom, G.; Sonder, K. Modeling the Effect of a Heat Wave on Maize Production in the USA and Its Implications on Food Security in the Developing World. Weather Clim. Extrem. 2014, 5–6, 67–77. [Google Scholar] [CrossRef]
- Yuan, W.; Cai, W.; Chen, Y.; Liu, S.; Dong, W.; Zhang, H.; Yu, G.; Chen, Z.; He, H.; Guo, W.; et al. Severe Summer Heatwave and Drought Strongly Reduced Carbon Uptake in Southern China. Sci. Rep. 2016, 6, 18813. [Google Scholar] [CrossRef]
- Perkins, S.E. A Review on the Scientific Understanding of Heatwaves-Their Measurement, Driving Mechanisms, and Changes at the Global Scale. Atmos. Res. 2015, 164–165, 242–267. [Google Scholar] [CrossRef]
- Vogel, M.M.; Zscheischler, J.; Fischer, E.M.; Seneviratne, S.I. Development of Future Heatwaves for Different Hazard Thresholds. J. Geophys. Res. Atmos. 2020, 125, e2019JD032070. [Google Scholar] [CrossRef]
- You, Q.; Jiang, Z.; Kong, L.; Wu, Z.; Bao, Y.; Kang, S.; Pepin, N. A Comparison of Heat Wave Climatologies and Trends in China Based on Multiple Definitions. Clim. Dyn. 2016, 48, 3975–3989. [Google Scholar] [CrossRef]
- Brooke Anderson, G.; Bell, M.L. Heat Waves in the United States: Mortality Risk during Heat Waves and Effect Modification by Heat Wave Characteristics in 43 U.S. Communities. Environ. Health Perspect. 2011, 119, 210–218. [Google Scholar] [CrossRef] [PubMed]
- Su, Q.; Dong, B.W. Recent Decadal Changes in Heat Waves over China: Drivers and Mechanisms. J. Clim. 2019, 32, 4215–4234. [Google Scholar] [CrossRef]
- Wang, J.; Chen, Y.; Tett, S.F.B.; Yan, Z.; Zhai, P.; Feng, J.; Xia, J. Anthropogenically-Driven Increases in the Risks of Summertime Compound Hot Extremes. Nat. Commun. 2020, 11, 582. [Google Scholar] [CrossRef]
- Chen, Y.; Li, Y. An Inter-Comparison of Three Heat Wave Types in China during 1961–2010: Observed Basic Features and Linear Trends. Sci. Rep. 2017, 7, srep45619. [Google Scholar] [CrossRef]
- Li, J.; Chen, Y.D.; Gan, T.Y.; Lau, N.-C. Elevated Increases in Human-Perceived Temperature under Climate Warming. Nat. Clim. Chang. 2018, 8, 43–47. [Google Scholar] [CrossRef]
- Mora, C.; Dousset, B.; Caldwell, I.R.; Powell, F.E.; Geronimo, R.C.; Bielecki, C.R.; Counsell, C.W.W.; Dietrich, B.S.; Johnston, E.T.; Louis, L.V.; et al. Global Risk of Deadly Heat. Nat. Clim. Chang. 2017, 7, 501–506. [Google Scholar] [CrossRef]
- Russo, S.; Sillmann, J.; Sterl, A. Humid Heat Waves at Different Warming Levels. Sci. Rep. 2017, 7, 7477. [Google Scholar] [CrossRef]
- Luo, M.; Lau, N. Increasing Heat Stress in Urban Areas of Eastern China: Acceleration by Urbanization. Geophys. Res. Lett. 2018, 45, 13060–13069. [Google Scholar] [CrossRef]
- Kong, D.; Gu, X.; Li, J.; Ren, G.; Liu, J. Contributions of Global Warming and Urbanization to the Intensification of Human-Perceived Heatwaves Over China. J. Geophys. Res. Atmos. 2020, 125, e2019JD032175. [Google Scholar] [CrossRef]
- Diaz, V.; Corzo Perez, G.A.; Van Lanen, H.A.J.; Solomatine, D.; Varouchakis, E.A. An Approach to Characterise Spatio-Temporal Drought Dynamics. Adv. Water Resour. 2020, 137, 103512. [Google Scholar] [CrossRef]
- Samaniego, L.; Kumar, R.; Zink, M. Implications of Parameter Uncertainty on Soil Moisture Drought Analysis in Germany. J. Hydrometeorol. 2013, 14, 47–68. [Google Scholar] [CrossRef]
- Luo, M.; Lau, N.; Liu, Z.; Wu, S.; Wang, X. An Observational Investigation of Spatiotemporally Contiguous Heatwaves in China From a 3D Perspective. Geophys. Res. Lett. 2022, 49, e2022GL097714. [Google Scholar] [CrossRef]
- Lyon, B.; Barnston, A.G.; Coffel, E.; Horton, R.M. Projected Increase in the Spatial Extent of Contiguous US Summer Heat Waves and Associated Attributes. Environ. Res. Lett. 2019, 14, 114029. [Google Scholar] [CrossRef]
- Lo, S.H.; Chen, C.T.; Russo, S.; Huang, W.R.; Shih, M.F. Tracking Heatwave Extremes from an Event Perspective. Weather Clim. Extrem. 2021, 34, 100371. [Google Scholar] [CrossRef]
- Wu, J.; Gao, X.-J. A Gridded Daily Observation Dataset over China Region and Comparison with the Other Datasets. Chin. J. Geophys. 2013, 56, 1102–1111. [Google Scholar]
- Freychet, N.; Tett, S.F.B.; Yan, Z.; Li, Z. Underestimated Change of Wet-Bulb Temperatures over East and South China. Geophys. Res. Lett. 2020, 47, e2019GL086140. [Google Scholar] [CrossRef]
- Li, Z.; Yan, Z.; Zhu, Y.; Freychet, N.; Tett, S. Homogenized Daily Relative Humidity Series in China during 1960–2017. Adv. Atmos. Sci. 2020, 37, 318–327. [Google Scholar] [CrossRef]
- De Bono, A.; Peduzzi, P.; Kluser, S.; Giuliani, G. Impacts of Summer 2003 Heat Wave in Europe. Environ. Alert Bull. 2004, 2, 4. [Google Scholar]
- Steadman, R.G. A Universal Scale of Apparent Temperature. J. Clim. Appl. Meteorol. 1984, 23, 1674–1687. [Google Scholar] [CrossRef]
- Rothfusz, L.P.; NWS Southern Region Headquarters. The Heat Index Equation (or, More than You Ever Wanted to Know about Heat Index). Atmos. Clim. Sci. 1990, 4, 9023. [Google Scholar]
- Qi, L.; Wang, Y. Changes in the Observed Trends in Extreme Temperatures over China around 1990. J. Clim. 2012, 25, 5208–5222. [Google Scholar] [CrossRef]
- Lloyd-Hughes, B. A Spatio-Temporal Structure-Based Approach to Drought Characterisation. Int. J. Climatol. 2012, 32, 406–418. [Google Scholar] [CrossRef]
- Van der Walt, S.; Schönberger, J.L.; Nunez-Iglesias, J.; Boulogne, F.; Warner, J.D.; Yager, N.; Gouillart, E.; Yu, T. Scikit-Image: Image Processing in Python. PeerJ 2014, 2014, e453. [Google Scholar] [CrossRef]
- IPCC Summary for Policymakers. In Climate Change 2022: Mitigation of Climate Change. Contribution of Working Group III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Shukla, P.R.; Skea, J.; Slade, R.; al Khourdajie, A.; van Diemen, R.; McCollum, D.; Pathak, M.; Some, S.; Vyas, P.; Fradera, R.; et al. (Eds.) Cambridge University Press: Cambridge, UK; New York, NY, USA, 2022. [Google Scholar]
- Fu, D.; Ding, Y. The Study of Changing Characteristics of the Winter Temperature and Extreme Cold Events in China over the Past Six Decades. Int. J. Climatol. 2021, 41, 2480–2494. [Google Scholar] [CrossRef]
- Qian, W.; Lin, X. Regional Trends in Recent Temperature Indices in China. Clim. Res. 2004, 27, 119–134. [Google Scholar] [CrossRef]
- Zhang, Y.; Mao, G.; Chen, C.; Lu, Z.; Luo, Z.; Zhou, W. Population Exposure to Concurrent Daytime and Nighttime Heatwaves in Huai River Basin, China. Sustain. Cities Soc. 2020, 61, 102309. [Google Scholar] [CrossRef]
- An, N.; Zuo, Z. Changing Structures of Summertime Heatwaves over China during 1961–2017. Sci. China Earth Sci. 2021, 64, 1242–1253. [Google Scholar] [CrossRef]
- Du, Z.; Zhao, J.; Liu, X.; Wu, Z.; Zhang, H. Recent Asymmetric Warming Trends of Daytime versus Nighttime and Their Linkages with Vegetation Greenness in Temperate China. Environ. Sci. Pollut. Res. 2019, 26, 35717–35727. [Google Scholar] [CrossRef] [PubMed]
- Song, Z.; Yang, H.; Huang, X.; Yu, W.; Huang, J.; Ma, M. The Spatiotemporal Pattern and Influencing Factors of Land Surface Temperature Change in China from 2003 to 2019. Int. J. Appl. Earth Obs. Geoinf. 2021, 104, 102537. [Google Scholar] [CrossRef]
- Luo, M.; Lau, N.-C.; Liu, Z. Different Mechanisms for Daytime, Nighttime, and Compound Heatwaves in Southern China. Weather Clim. Extrem. 2022, 36, 100449. [Google Scholar] [CrossRef]


| Threshold | Mathematics | Spatially Variable | Temporally Variable | Description |
|---|---|---|---|---|
| Custom | No | No | Custom defined, the thresholds are static both with different grids and on different dates | |
| Quantile | Yes | No | Calculated by quantile, the thresholds vary spatially, but are temporally static | |
| Quantile | Yes | Yes | Calculated by rolling quantile, the thresholds vary both spatially and temporally |
| Metric | Equation | Unit | Description |
|---|---|---|---|
| Duration | day | For an STHW event, the number of days from onset to demise | |
| Intensity | °C | For an STHW event, the average daily area-weighted average anomaly over all grid cells | |
| Severity | °C·day | For an STHW event, the aggregate daily area-weighted average anomaly over all grid cells | |
| Mean Area | 106 km2 | For an STHW event, the average daily areas over all grid cells | |
| Maximum Area | 106 km2 | For an STHW event, the maximum daily areas over all grid cells | |
| Total Area | 106 km2 | For an STHW event, the aggregate daily areas over all grid cells |
| Metric | Equation | Unit | Description |
|---|---|---|---|
| Duration | day | For each grid , the number of days over which STHW event occurred; is the number of HW events that take place annually | |
| Frequency | time | For each grid , the number of STHW events that take place annually | |
| Intensity | °C | For each grid, , the average mean anomaly across all STHW events; is the number of STHW events that take place annually | |
| Severity | °C·day | For each grid , the average total anomaly across all STHW events; is the number of STHW events that take place annually |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, H.; Kong, D.; Xiong, L.; Gu, X.; Liu, J. Inter-Comparison of Diverse Heatwave Definitions in the Analysis of Spatiotemporally Contiguous Heatwave Events over China. Remote Sens. 2022, 14, 4082. https://doi.org/10.3390/rs14164082
Song H, Kong D, Xiong L, Gu X, Liu J. Inter-Comparison of Diverse Heatwave Definitions in the Analysis of Spatiotemporally Contiguous Heatwave Events over China. Remote Sensing. 2022; 14(16):4082. https://doi.org/10.3390/rs14164082
Chicago/Turabian StyleSong, Heyang, Dongdong Kong, Li Xiong, Xihui Gu, and Jianyu Liu. 2022. "Inter-Comparison of Diverse Heatwave Definitions in the Analysis of Spatiotemporally Contiguous Heatwave Events over China" Remote Sensing 14, no. 16: 4082. https://doi.org/10.3390/rs14164082
APA StyleSong, H., Kong, D., Xiong, L., Gu, X., & Liu, J. (2022). Inter-Comparison of Diverse Heatwave Definitions in the Analysis of Spatiotemporally Contiguous Heatwave Events over China. Remote Sensing, 14(16), 4082. https://doi.org/10.3390/rs14164082