A Multi-Feature Framework for Quantifying Information Content of Optical Remote Sensing Imagery
Abstract
:1. Introduction
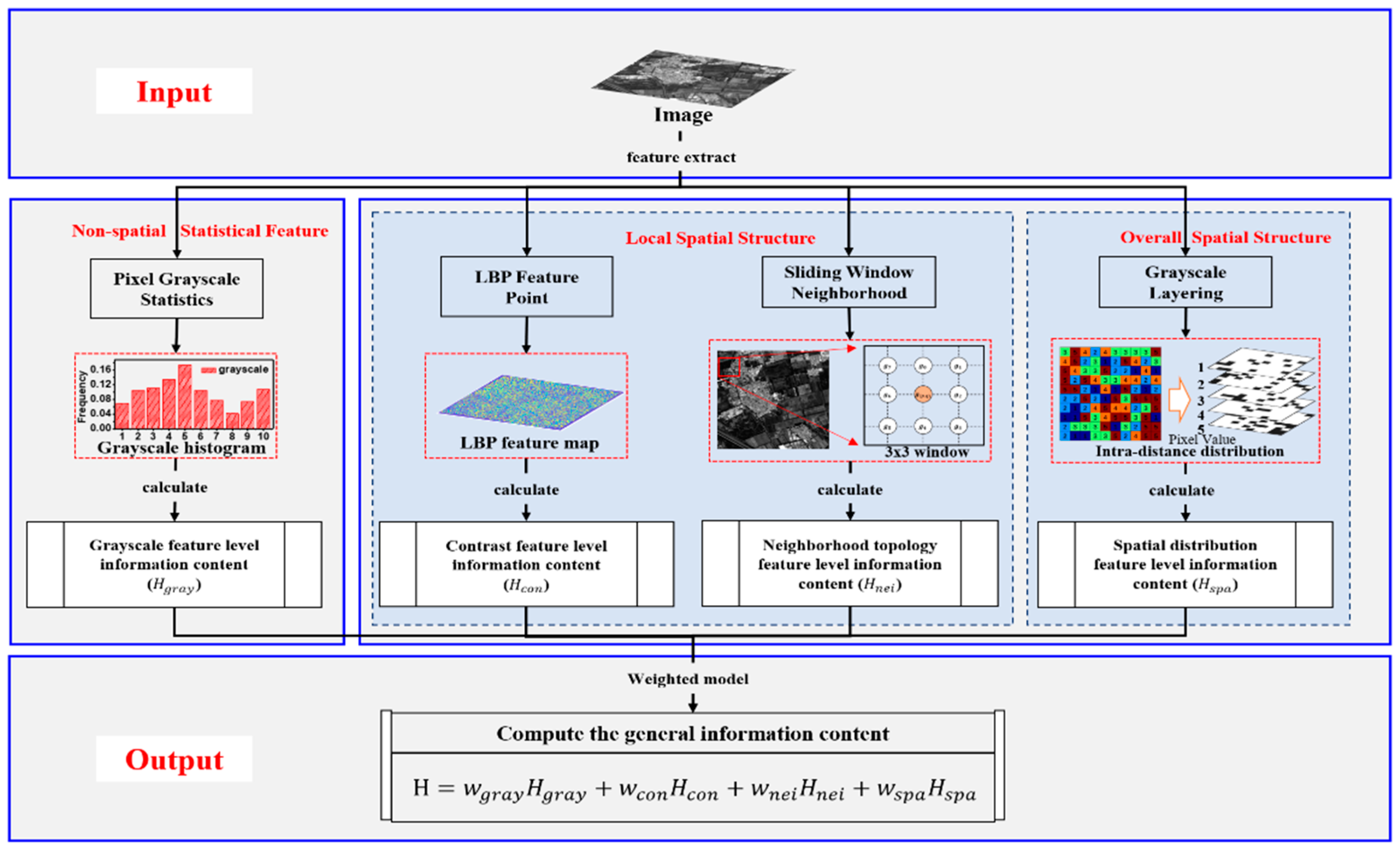
- A framework for measuring the information content of remote sensing images based on Shannon’s information theory is developed. In this framework, the information of an image is defined as the uncertainty of the pixels’ properties and spatial locations. Instead of simply measuring single feature information, multiple features including grayscale, contrast, neighborhood topology, and spatial distribution are modeled to calculate the information content of images. The spatial structure information content of the image at both the overall and local scales is measured as two parts of the comprehensive information.
- Entropy metrics at each feature are designed to quantify the uncertainty of the image in terms of pixel and spatial structure. Compared with state-of-the-art entropy models, our approach is the first study to systematically consider the multiple features of image information content based on Shannon entropy. It is comparable to existing models in terms of thermodynamic consistency.
2. Related Works
2.1. Shannon Entropy
2.2. Boltzmann Entropy
2.3. Imperfection of the Entropy-Based Information Model
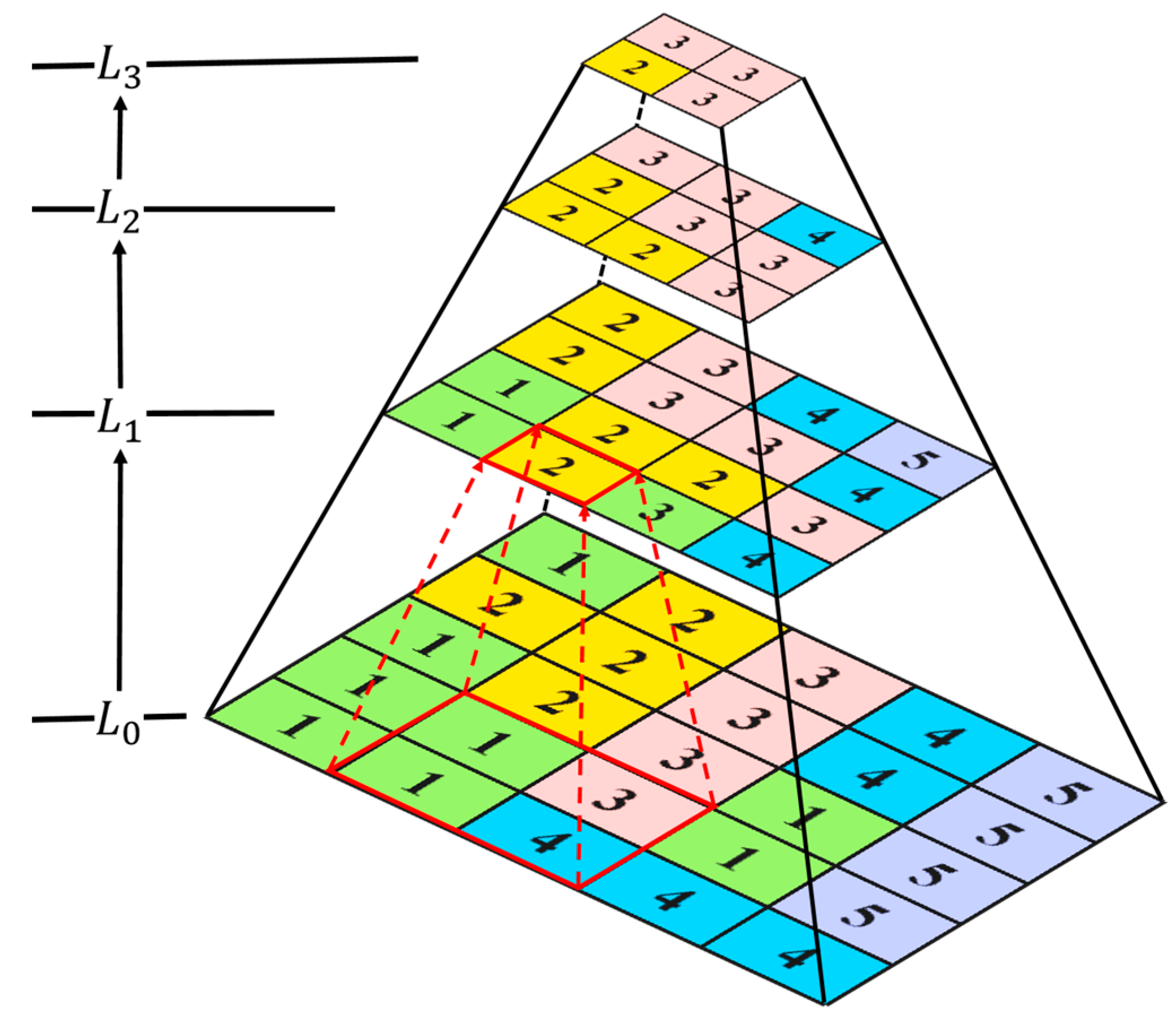
3. The Multi-Feature Framework for Image Information Measurement
3.1. The Multi-Feature Measurement Framework
3.2. Feature Selection of Images
- Grayscale is the most basic feature of remote sensing images. It reflects the spectral characteristics of different objects in the form of digital numbers (DN). Grayscale information content can be directly quantified by statistical histograms according to Shannon entropy;
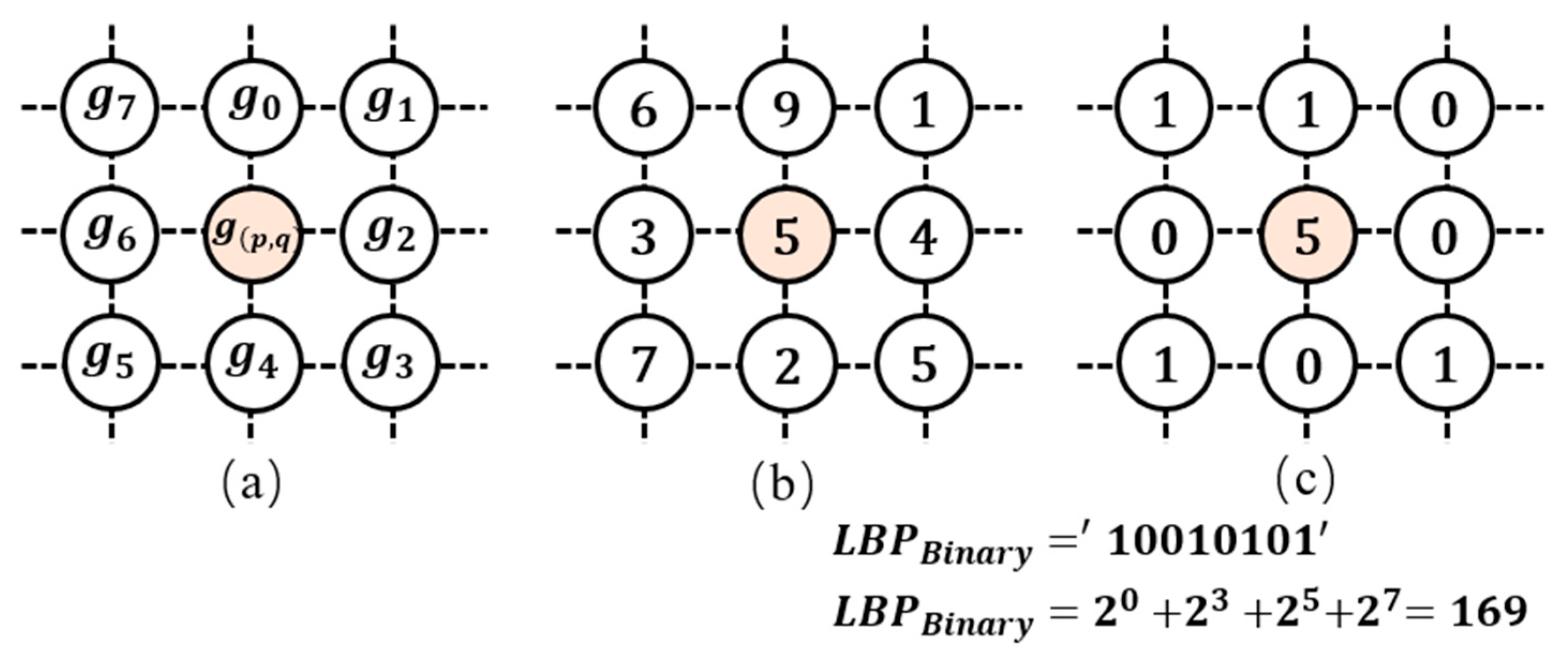
- Contrast is a common visual feature of images and is used to reflect ground objects’ texture and geometric characteristics. To keep the texture features of the image light invariant, LBP entropy is designed to quantify the contrast information;
- The complexity of the neighborhood topology relationship is measured by the neighborhood pixel differences. For a certain pixel, the more that adjacent pixels are similar, the less important the pixel is. Neighborhood topological information is measured using neighborhood topological entropy, which describes the relationship between a central pixel and its eight neighbor pixels;
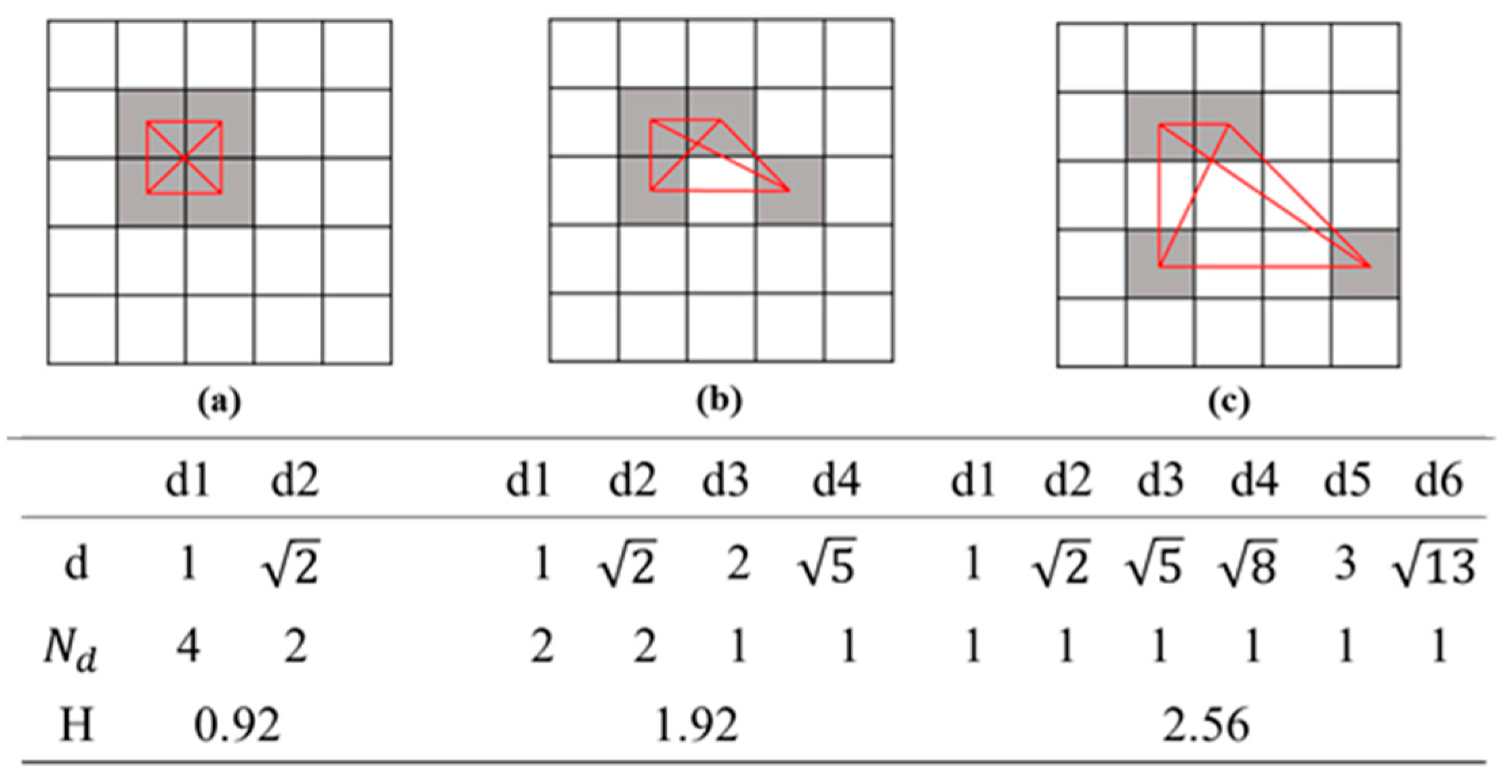
- The spatial distribution of pixels reflects the configuration of the spatial structure of the image as a whole. To measure the degree of disorder in the spatial distribution of pixels, the intra-class distance entropy is used to quantify the disorder of each grayscale pixel in the spatial distribution;
3.3. Information Quantification Model for Each Feature
3.3.1. Grayscale Information
3.3.2. Contrast Information
3.3.3. Neighborhood Topology Information
3.3.4. Spatial Distribution Information
3.4. Comprehensive Information Content of Images
4. Experiment and Discussion
- Experiment 1: A few images are randomly selected from the AID [67] image dataset to assess consistency trends between information content and scene complexity. The AID dataset includes 30 different aviation scenes and 10,000 samples of image size 600 × 600 × 3;
- Experiment 2: The large-scale Gaofen-2 (GF-2) satellite images from the GID dataset [68] were used to analyze the changing trends in image information content with spatial resolution;
- Experiment 3: Simulated images generated from an AID original image. Specifically, a series of disordered images are generated by exchanging the local spatial structure or by simulating the random motion of gas molecules in pixel units, which have the same grayscale histogram but different spatial structures. This experiment analyzes the ability of the proposed method to capture the spatial structure and the proposed method’s thermodynamic consistency in measuring disorder is evaluated;
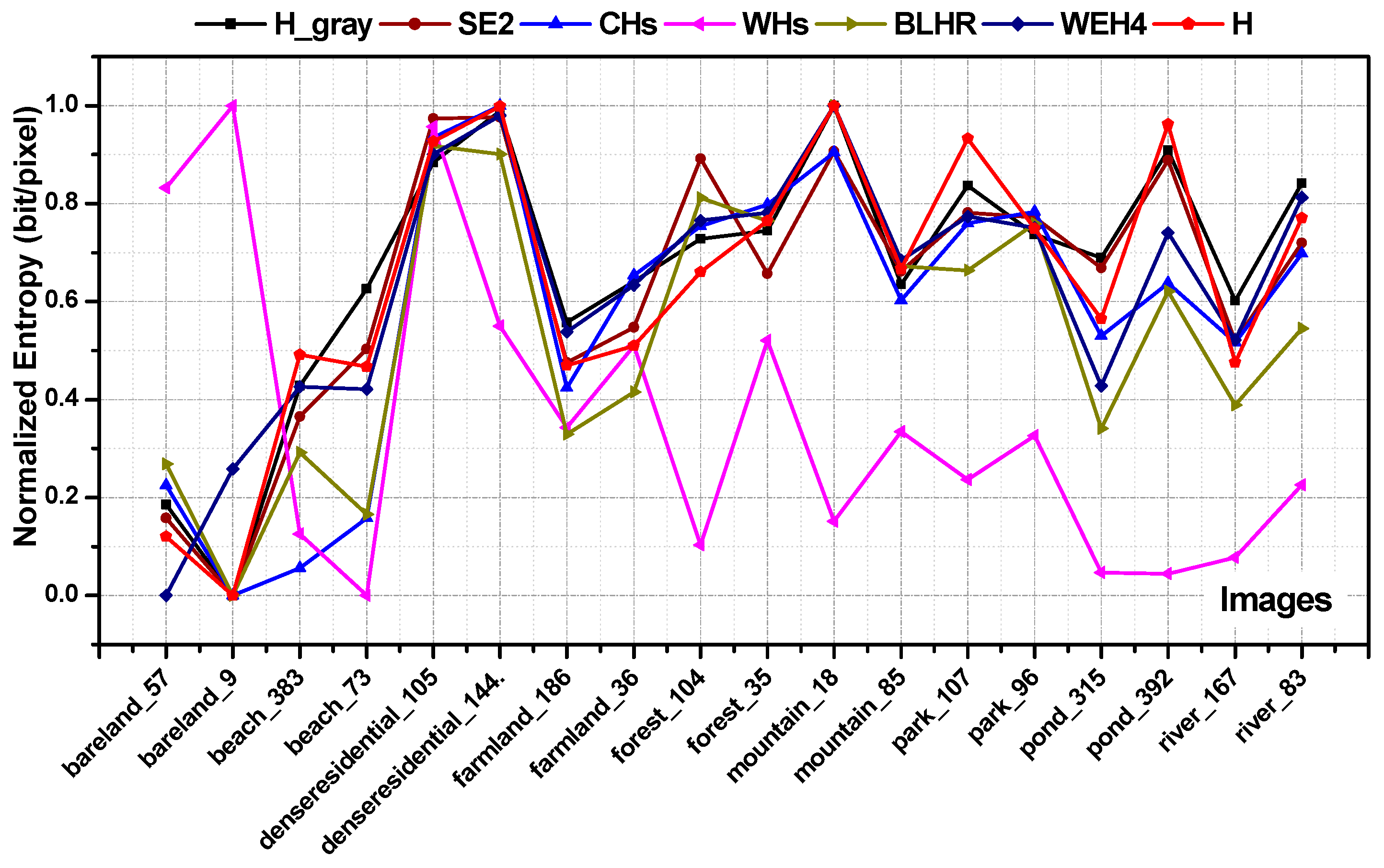
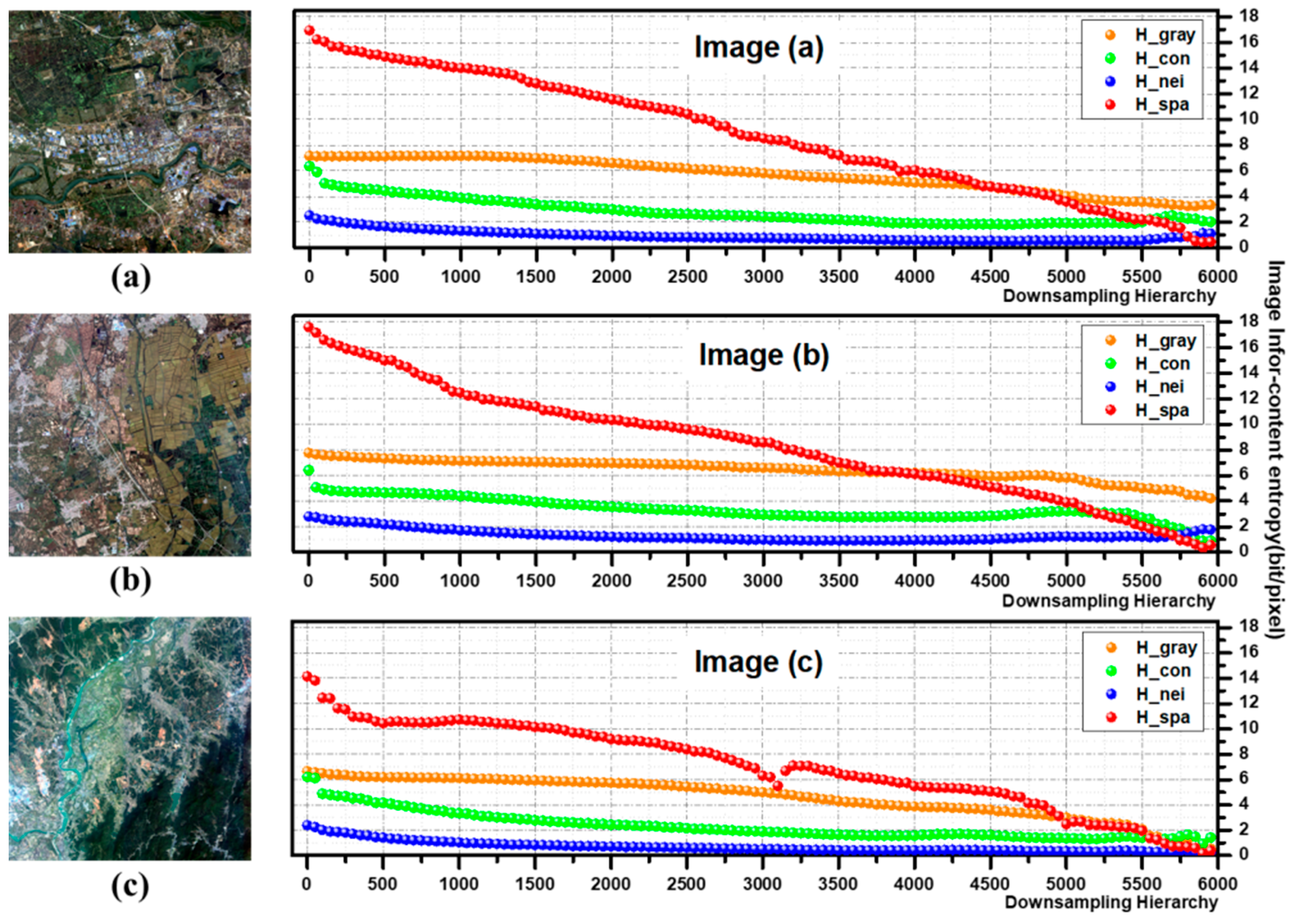
4.1. Analysis of Scene Image Information Content
4.2. Analysis of Information and Resolution
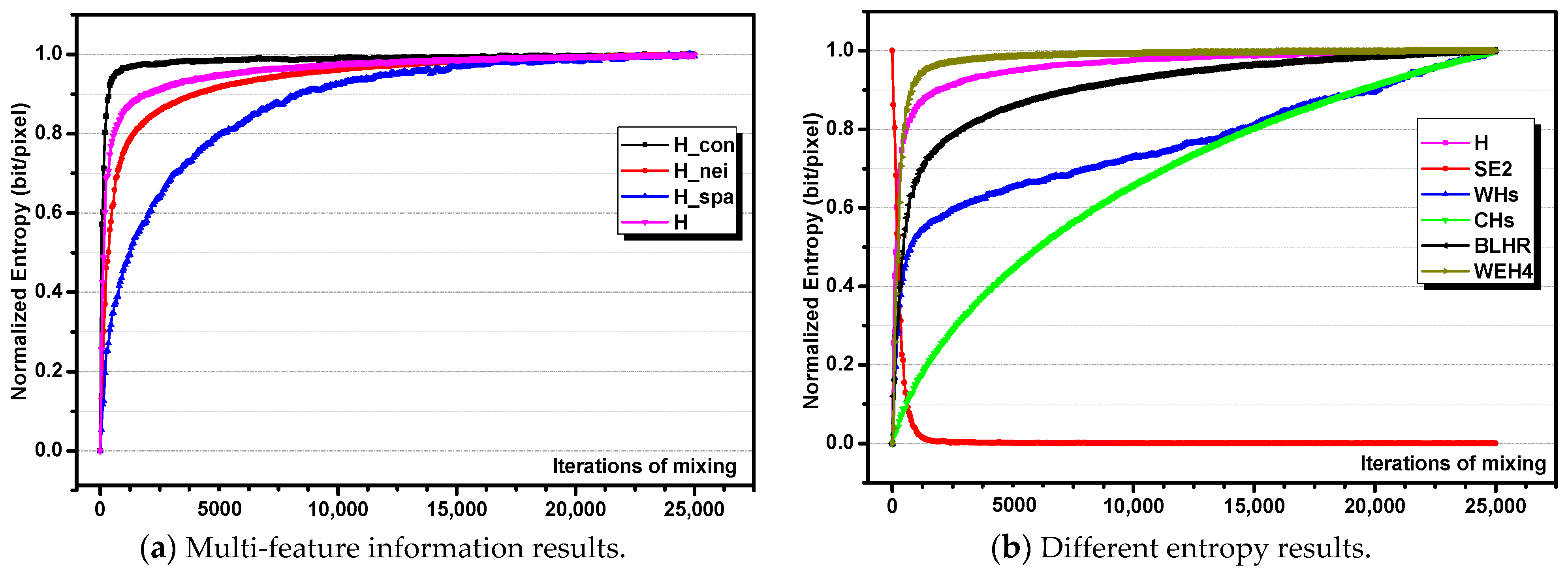
4.3. Analysis of Spatial Configuration and Disorder
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, B.; Deng, M.; Liu, H.; Shi, Y.; Zhao, B. A Multilevel Visual Feature-Based Approach for Measuring the Spatial Information in Remote Sensing Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 4110–4122. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, J.; Yang, W. Quantifying Information Content in Multispectral Remote-Sensing Images Based on Image Transforms and Geostatistical Modelling. Remote Sens. 2020, 12, 880. [Google Scholar] [CrossRef] [Green Version]
- Fang, S.; Zhou, X.; Zhang, J. A Multilevel Mapping Strategy to Calculate the Information Content of Remotely Sensed Imagery. ISPRS Int. J. Geo-Inf. 2019, 8, 464. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Zhang, J. Measure of Information Content of Remotely Sensed Images Accounting for Spatial Correlation. Acta Geod. Cartogr. Sin. 2015, 44, 1117–1124. [Google Scholar]
- Li, Z.L.; Gao, P.; Xu, Z. Information theory of cartography: An information-theoretic framework for cartographic communication. J. Geod. Geoinf. Sci. 2021, 4, 1–16. [Google Scholar]
- Li, Z.; Lan, T. GIScience from Viewpoint of Information Science. In New Thinking in GIScience; Li, B., Shi, X., Zhu, A.X., Wang, C., Lin, H., Eds.; Springer: Singapore, 2022; pp. 41–50. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1984, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]
- Batty, M. Spatial entropy. Geogr. Anal. 1974, 6, 1–31. [Google Scholar] [CrossRef]
- Batty, M. Entropy in spatial aggregation. Geogr. Anal. 1976, 8, 1–21. [Google Scholar] [CrossRef]
- Batty, M. Space, scale, and scaling in entropy maximizing. Geogr. Anal. 2010, 42, 395–421. [Google Scholar] [CrossRef]
- Batty, M.; Morphet, R.; Masucci, P.; Stanilov, K. Entropy, complexity, and spatial information. J. Geogr. Syst. 2014, 16, 363–385. [Google Scholar] [CrossRef] [Green Version]
- Quweider, M.K. Spatial entropy-based cost function for gray and color Image segmentation with dynamic optimal partitioning. Int. J. Comput. Sci. Netw. Secur. 2012, 12, 64–75. [Google Scholar]
- Claramunt. A Spatial form of Diversity. In Spatial Information Theory; Cohn, A.G., Mark, D.M., Eds.; Springer: Berlin, Germany, 2005; Volume 3693, pp. 218–231. [Google Scholar]
- Wang, C.; Zhao, H. Spatial heterogeneity analysis: Introducing a new form of spatial entropy. Entropy 2018, 20, 398. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Parvinnezhad, D.; Delavar, M.R.; Claramunt, C.; Pijanowski, B.C. A modified spatial entropy for urban sprawl assessment. Geocarto Int. 2021, 36, 1804–1819. [Google Scholar] [CrossRef]
- Gao, P.; Zhang, H.; Jia, D.; Song, C.; Cheng, C.; Shen, S. Efficient approach for computing the discrimination ratio-based variant of information entropy for image processing. IEEE Access 2020, 8, 92552–92564. [Google Scholar] [CrossRef]
- O’Neill, R.V.; Krummel, J.R.; Gardner, R.H.; Graham, R.L. Indices of landscape pattern. Landsc Ecol 1988, 1, 153–162. [Google Scholar] [CrossRef]
- Leibovici, D.G. Defining Spatial Entropy from Multivariate Distributions of Co-Occurrences. In Spatial Information Theory. COSIT 2009; Lecture Notes in Computer Science; Hornsby, K.S., Claramunt, C., Denis, M., Ligozat, G., Eds.; Springer: Berlin, Heidelberg, Germany, 2009; Volume 5756, pp. 392–404. [Google Scholar]
- Leibovici, D.G.; Claramunt, C.; Le Guyader, D.; Brosset, D. Local and global spatio-temporal entropy indices based on distance ratios and co-occurrences distributions. Int. J. Geogr. Inf. Sci. 2014, 28, 1061–1084. [Google Scholar] [CrossRef] [Green Version]
- Altieri, L.; Cocchi, D.; Roli, G. A new approach to spatial entropy measures. Environ. Ecol. Stat. 2018, 25, 95–110. [Google Scholar] [CrossRef]
- Altieri, L.; Cocchi, D.; Roli, G. Measuring heterogeneity in urban expansion via spatial entropy. Environmetrics 2019, 30, e2548.1–e2548.16. [Google Scholar] [CrossRef] [Green Version]
- Yu, J.; Peng, S.; Zhang, W.; Kang, S. Index for the Consistent Measurement of Spatial Heterogeneity for Large-Scale Land Cover Datasets. ISPRS Int. J. Geo-Inf. 2020, 9, 483. [Google Scholar] [CrossRef]
- Cushman, S.A. Calculating the configurational entropy of a landscape mosaic. Landsc. Ecol. 2016, 31, 481–489. [Google Scholar] [CrossRef]
- Cushman, S.A. Calculation of configurational entropy in complex landscapes. Entropy 2018, 20, 298. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, Y.; Zhang, X. Calculating spatial configurational entropy of a landscape mosaic based on the Wasserstein metric. Landsc. Ecol. 2019, 34, 1849–1858. [Google Scholar] [CrossRef]
- Zhang, H.; Wu, Z.; Lan, T.; Chen, Y.; Gao, P. Calculating the Wasserstein metric-based Boltzmann entropy of a landscape mosaic. Entropy 2020, 22, 381. [Google Scholar] [CrossRef] [Green Version]
- Gao, P.; Zhang, H.; Wu, Z. Wasserstein metric-based Boltzmann entropy of a landscape mosaic: A clarification, correction, and evaluation of thermodynamic consistency. Landsc. Ecol. 2021, 36, 815–827. [Google Scholar] [CrossRef]
- Gao, P.; Zhang, H.; Li, Z. A hierarchy-based solution to calculate the configurational entropy of landscape gradients. Landsc. Ecol. 2017, 32, 1133–1146. [Google Scholar] [CrossRef]
- Gao, P.; Zhang, H.; Li, Z. An efficient analytical method for computing the Boltzmann entropy of a landscape gradient. Trans. GIS 2018, 22, 1046–1063. [Google Scholar] [CrossRef]
- Zhang, H.; Wu, Z. A Head/Tail Breaks-Based Method for Efficiently Estimating the Absolute Boltzmann Entropy of Numerical Raster Data. ISPRS Int. J. Geo-Inf. 2020, 9, 103. [Google Scholar] [CrossRef] [Green Version]
- Gao, P.; Li, Z. Aggregation-based method for computing absolute Boltzmann entropy of landscape gradient with full thermodynamic consistency. Landsc. Ecol. 2019, 34, 1837–1847. [Google Scholar] [CrossRef]
- Sharma, M.; Kumar, S. Analysing the spatial patterns and trends of urban growth in Rohtak city, India. Sustain. Environ. 2022, 8, 1–10. [Google Scholar] [CrossRef]
- Talkhabi, H.; Ghalehteimouri, K.J.; Mehranjani, M.S.; Karami, T. Spatial and temporal population change in the Tehran Metropolitan Region and its consequences on urban decline and sprawl. Ecol. Inform. 2022, 70, 101731. [Google Scholar] [CrossRef]
- Deng, X.; Sun, G.; He, N.; Yu, Y. Landslide susceptibility mapping with the integration of information theory, fractal theory, and statistical analyses at a regional scale: A case study of Altay Prefecture, China. Environ. Earth Sci. 2022, 81, 1–17. [Google Scholar] [CrossRef]
- Sawant, S.S.; Manoharan, P. Unsupervised band selection based on weighted information entropy and 3D discrete cosine transform for hyperspectral image classification. Int. J. Remote Sens. 2020, 41, 3948–3969. [Google Scholar] [CrossRef]
- German, A.; Jenkin, M.R.; Lespérance, Y. Entropy-Based Image Merging. In Proceedings of the 2nd Canadian Conference on Computer and Robot Vision (CRV’05), NW Washington, DC, USA, 9–11 May 2005; pp. 81–86. [Google Scholar]
- Liu, Y.; Yang, X.; Zhang, R.; Albertini, M.K.; Celik, T.; Jeon, G. Entropy-Based Image Fusion with Joint Sparse Representation and Rolling Guidance Filter. Entropy 2020, 22, 118. [Google Scholar] [CrossRef] [Green Version]
- Long, D.; Singh, V.P. An entropy-based multispectral image classification algorithm. IEEE Trans. Geosci. Remote Sens. 2013, 51, 5225–5238. [Google Scholar] [CrossRef]
- Zhang, X.; Gao, Z.; Jiao, L.; Zhou, H. Multifeature hyperspectral image classification with local and nonlocal spatial information via Markov random field in semantic space. IEEE Trans. Geosci. Remote Sens. 2017, 56, 1409–1424. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Li, Z.; Gong, J. Multivariate statistical analysis of measures for assessing the quality of image fusion. Int. J. Image Data Fusion 2010, 1, 47–66. [Google Scholar] [CrossRef]
- Narayanan, R.M.; Desetty, M.K.; Reichenbach, S.E. Effect of spatial resolution on information content characterization in remote sensing imagery based on classification accuracy. Int. J. Remote Sens. 2010, 23, 537–553. [Google Scholar] [CrossRef]
- Wu, H.; Zhu, H.; Liu, Y. A Raster-Based Map Information Measurement for QoS. In Proceedings of the ISPRS, Istanbul, Turkey, 12–23 July 2004; pp. 365–370. [Google Scholar]
- Chen, Y.; Sun, K.; Lin, Z. Measures of Information in Remote Sensing Imagery and Area-Class Maps. J. Comput. Inf. Syst. 2010, 7, 1648–1654. [Google Scholar]
- Aiazzi, B.; Baronti, S.; Santurri, L.; Selva, M.; Alparone, L. Information-theoretic assessment of multi-dimensional signals. Signal Process. 2005, 85, 903–916. [Google Scholar] [CrossRef]
- Lin, Z.; Deng, B. Quantifying degrees of information in remote sensing imagery. In Proceedings of the 8th International Symposium on Spatial Accuracy Assessment in Natural Resources and Environmental Sciences, Shanghai, China, 25–27 June 2008; Volume 2527, pp. 201–205. [Google Scholar]
- Kowkabi, F.; Ghassemian, H.; Keshavarz, A. Hybrid preprocessing algorithm for endmember extraction using clustering, over-segmentation, and local entropy criterion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2940–2949. [Google Scholar] [CrossRef]
- Wu, Y.; Zhou, Y.; Saveriades, G.; Agaian, S.; Noonan, J.P.; Natarajan, P. Local Shannon entropy measure with statistical tests for image randomness. Inf. Sci. 2013, 222, 323–342. [Google Scholar] [CrossRef] [Green Version]
- Rao, M.; Chen, Y.; Vemuri, B.C.; Wang, F. Cumulative residual entropy: A new measure of information. IEEE Trans. Inf. Theory 2004, 50, 1220–1228. [Google Scholar] [CrossRef]
- Razlighi, Q.R.; Kehtarnavaz, N.; Nosratinia, A. Computation of image spatial entropy using quadrilateral Markov random field. IEEE Trans. Image Process. 2009, 18, 2629–2639. [Google Scholar] [CrossRef] [Green Version]
- Pralon, L.; Vasile, G.; Dalla Mura, M.; Chanussot, J. Evaluation of the New Information in the H/α Feature Space Provided by ICA in PolSAR Data Analysis. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6893–6909. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, M.; Xie, X.; Shi, G.; Sun, Z. Joint Entropy Degradation Based Blind Image Quality Assessment. In Proceedings of the 2018 IEEE Fourth International Conference on Multimedia Big Data (BigMM), 13–16 September 2018; pp. 1–6. [Google Scholar]
- Gao, P.; Li, Z.; Zhang, H. Thermodynamics-based evaluation of various improved Shannon entropies for configurational information of gray-level images. Entropy 2018, 20, 19. [Google Scholar] [CrossRef] [Green Version]
- Vranken, I.; Baudry, J.; Aubinet, M.; Visser, M.; Bogaert, J. A review on the use of entropy in landscape ecology: Heterogeneity, unpredictability, scale dependence and their links with thermodynamics. Landsc. Ecol. 2015, 30, 51–65. [Google Scholar] [CrossRef] [Green Version]
- Gao, P.; Wang, J.; Zhang, H.; Li, Z. Boltzmann entropy-based unsupervised band selection for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2018, 16, 462–466. [Google Scholar] [CrossRef]
- Zhang, H.; Wu, Z.; Wang, J.; Gao, P. Unsupervised band selection for hyperspectral image classification using the Wasserstein metric-based configuration entropy. Acta Geod. Cartogr. Sin. 2021, 50, 405–415. [Google Scholar]
- Jiao, Y.; Ding, Y.; Zha, Z.; Okuro, T. Crises of biodiversity and ecosystem services in Satoyama landscape of Japan: A review on the role of management. Sustainability 2019, 11, 454. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Liang, X.; Chen, H. Landscape sustainability evaluation of ecologically fragile areas based on Boltzmann entropy. ISPRS Int. J. Geo-Inf. 2020, 9, 77. [Google Scholar] [CrossRef] [Green Version]
- Gao, P.; Zhang, H.; Li, Z. Boltzmann Entropy for the Spatial Information of Raster Data. In Proceedings of the Abstracts of the ICA, Tokyo, Japan, 15 July 2019; pp. 15–20. [Google Scholar]
- Zhang, J.X.; Du, D.S. Field-based Models for Positional and Attribute Uncertainty. Acta Geod. Et Cartogr. Sin. 1999, 3, 244–249. [Google Scholar]
- Rocchini, D.; Foody, G.M.; Nagendra, H.; Ricotta, C.; Anand, M.; He, K.S.; Neteler, M. Uncertainty in ecosystem mapping by remote sensing. Comput. Geosci. 2013, 50, 128–135. [Google Scholar] [CrossRef]
- Haertel, V.F.; Shimabukuro, Y.E. Spectral linear mixing model in low spatial resolution image data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2555–2562. [Google Scholar] [CrossRef]
- Tamura, H.; Mori, S.; Yamawaki, T. Textural features corresponding to visual perception. IEEE Trans. Syst. Man Cybern. 1978, 8, 460–473. [Google Scholar] [CrossRef]
- Ojala, T.; Pietikainen, M.; Maenpaa, T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 971–987. [Google Scholar] [CrossRef]
- Ojala, T.; Pietik¨ainen, M.; Harwood, D. A comparative study of texture measures with classification based on featured distributions. Pattern Recognit. 1996, 29, 51–59. [Google Scholar] [CrossRef]
- Cressie, N. Statistics for Spatial Data; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Li, Z.; Huang, P. Quantitative measures for spatial information of maps. Int. J. Geogr. Inf. Sci. 2002, 16, 699–709. [Google Scholar] [CrossRef]
- Xia, G.S.; Hu, J.; Hu, F.; Shi, B.; Bai, X.; Zhong, Y.; Lu, X. AID: A benchmark data set for performance evaluation of aerial scene classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3965–3981. [Google Scholar] [CrossRef] [Green Version]
- Tong, X.Y.; Xia, G.S.; Lu, Q.; Shen, H.; Li, S.; You, S.; Zhang, L. Land-cover classification with high-resolution remote sensing images using transferable deep models. Remote Sens. Environ. 2020, 237, 111322. [Google Scholar] [CrossRef] [Green Version]
- Von Neumann, J. Theory of Self-Reproducing Automata; University of Illinois Press: Champaign, IL, USA, 1966. [Google Scholar]
- Wiener, N. Cybernetics or Control and Communication in the Animal and the Machine; MIT Press: Cambridge, MA, USA, 2019. [Google Scholar]
- Mingers, J.; Standing, C. What is information? toward a theory of information as objective and veridical. Soc. Sci. Electron. Publ. 2018, 33, 1–20. [Google Scholar] [CrossRef]
- Spinnangr, S.F. Energy, Entropy and Sustainable Development with Focus on Nuclear Fusion. Master’s Thesis, The University of Bergen, Bergen, Norway, 2017. [Google Scholar]






| Features | ||||
|---|---|---|---|---|
| 1.00 | 0.89 | 0.83 | 0.97 | |
| 0.89 | 1.00 | 0.91 | 0.81 | |
| 0.83 | 0.91 | 1.00 | 0.65 | |
| 0.97 | 0.81 | 0.65 | 1.00 |
| Image | |||||
|---|---|---|---|---|---|
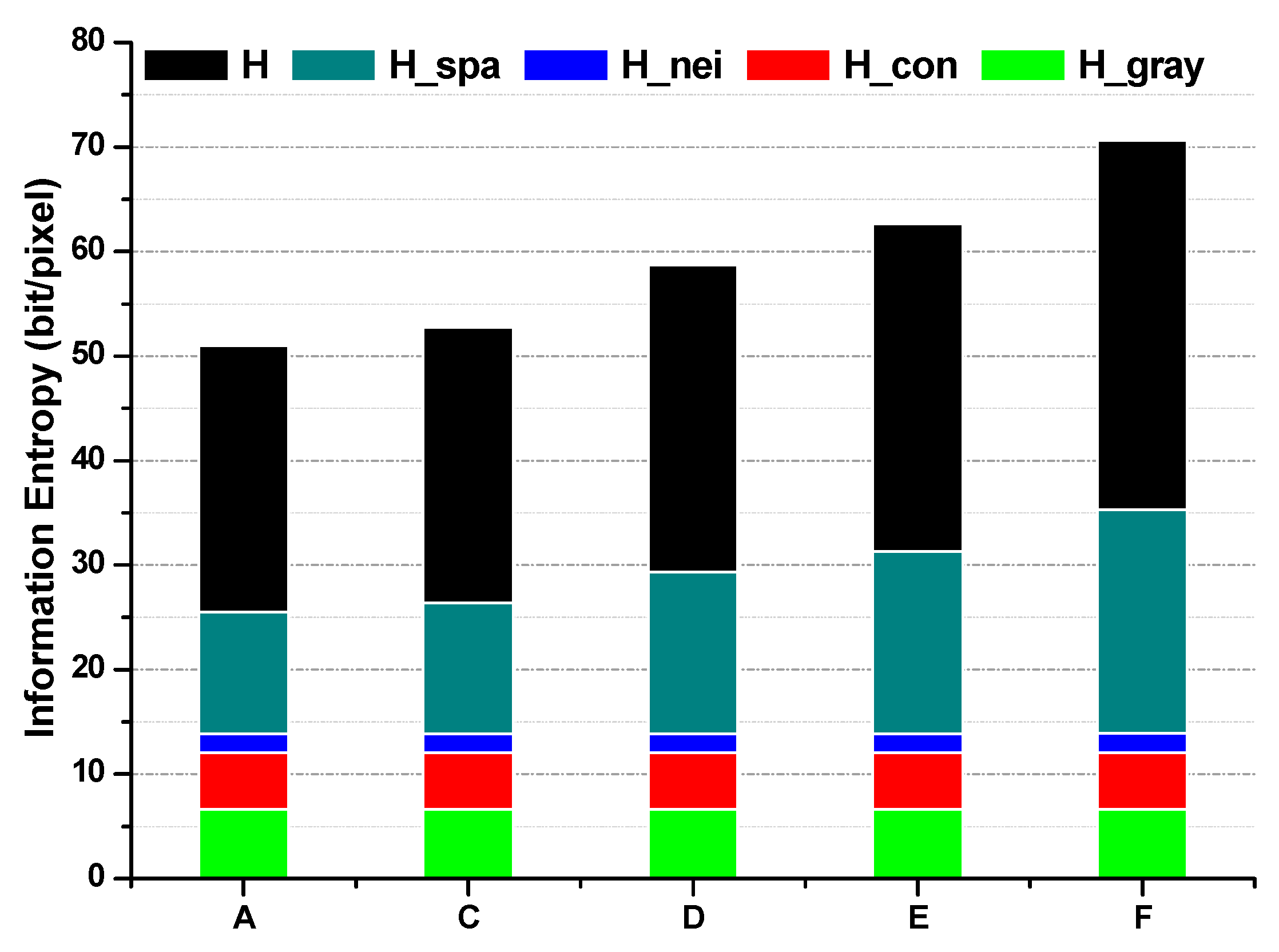
| A | 6.64 | 5.39 | 1.86 | 11.61 | 25.50 |
| C | 6.64 | 5.39 | 1.87 | 12.47 | 26.37 |
| D | 6.64 | 5.39 | 1.87 | 15.45 | 29.35 |
| E | 6.64 | 5.39 | 1.87 | 17.42 | 31.32 |
| F | 6.64 | 5.40 | 1.87 | 21.40 | 35.31 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silong, L.; Xiaoguang, Z.; Dongyang, H.; Ali, N.; Qiankun, K.; Sijia, W. A Multi-Feature Framework for Quantifying Information Content of Optical Remote Sensing Imagery. Remote Sens. 2022, 14, 4068. https://doi.org/10.3390/rs14164068
Silong L, Xiaoguang Z, Dongyang H, Ali N, Qiankun K, Sijia W. A Multi-Feature Framework for Quantifying Information Content of Optical Remote Sensing Imagery. Remote Sensing. 2022; 14(16):4068. https://doi.org/10.3390/rs14164068
Chicago/Turabian StyleSilong, Luo, Zhou Xiaoguang, Hou Dongyang, Nawaz Ali, Kang Qiankun, and Wang Sijia. 2022. "A Multi-Feature Framework for Quantifying Information Content of Optical Remote Sensing Imagery" Remote Sensing 14, no. 16: 4068. https://doi.org/10.3390/rs14164068
APA StyleSilong, L., Xiaoguang, Z., Dongyang, H., Ali, N., Qiankun, K., & Sijia, W. (2022). A Multi-Feature Framework for Quantifying Information Content of Optical Remote Sensing Imagery. Remote Sensing, 14(16), 4068. https://doi.org/10.3390/rs14164068









