Direct Assimilation of Radar Reflectivity Data Using Ensemble Kalman Filter Based on a Two-Moment Microphysics Scheme for the Analysis and Forecast of Typhoon Lekima (2019)
Abstract
:1. Introduction
2. Description of the Data Assimilation Experiments
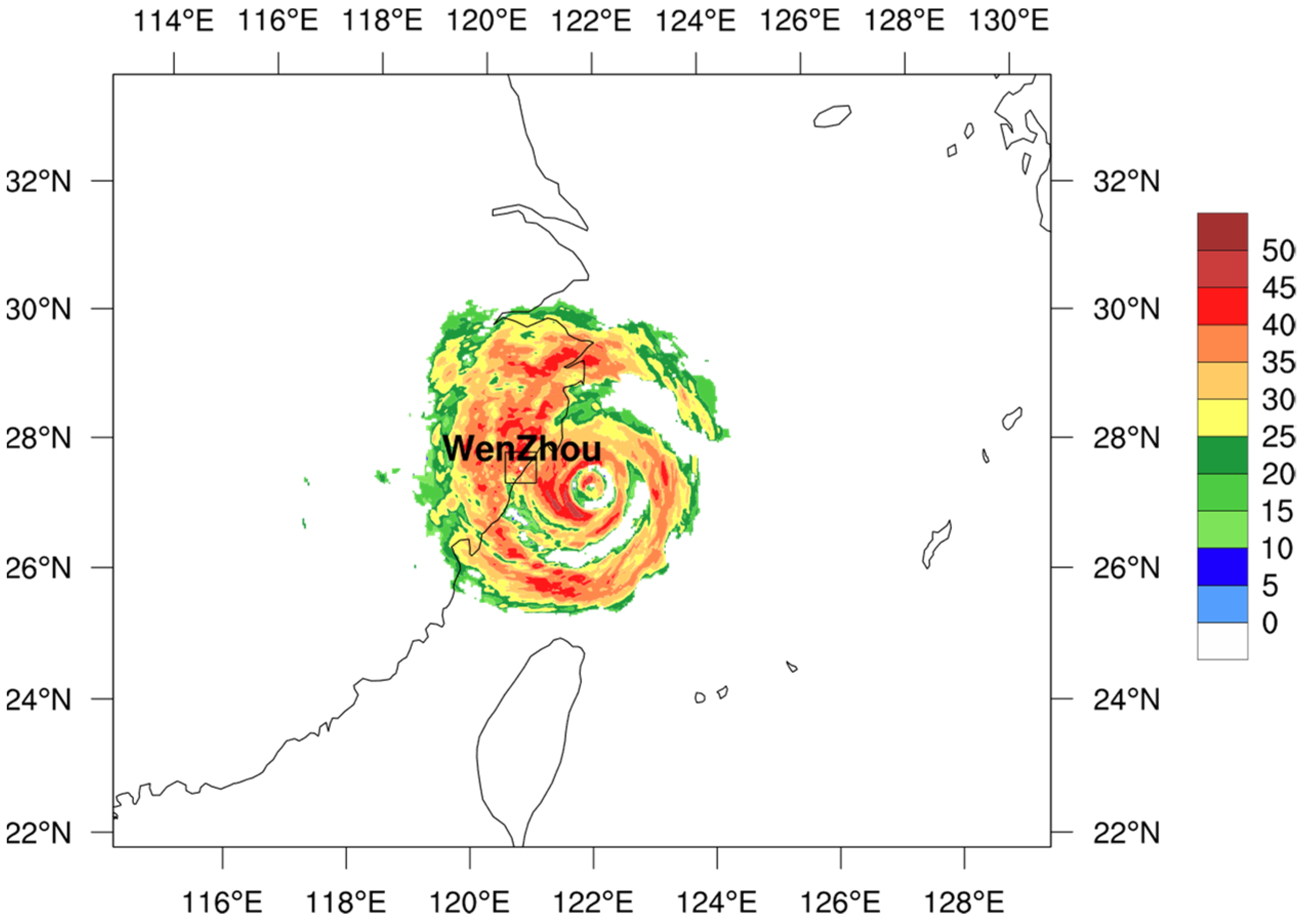
2.1. Case Overview
2.2. Numerical Model
2.3. Assimilation Data and Algorithms
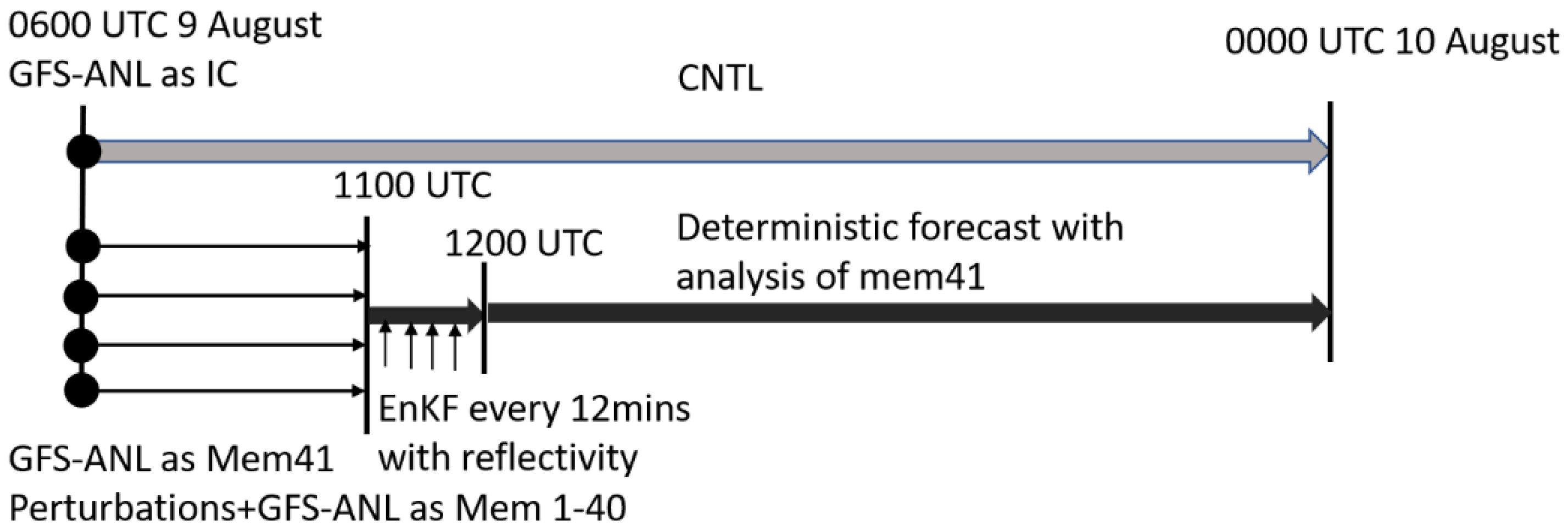
2.4. Experimental Design
3. Impact of Radar Reflectivity Assimilation
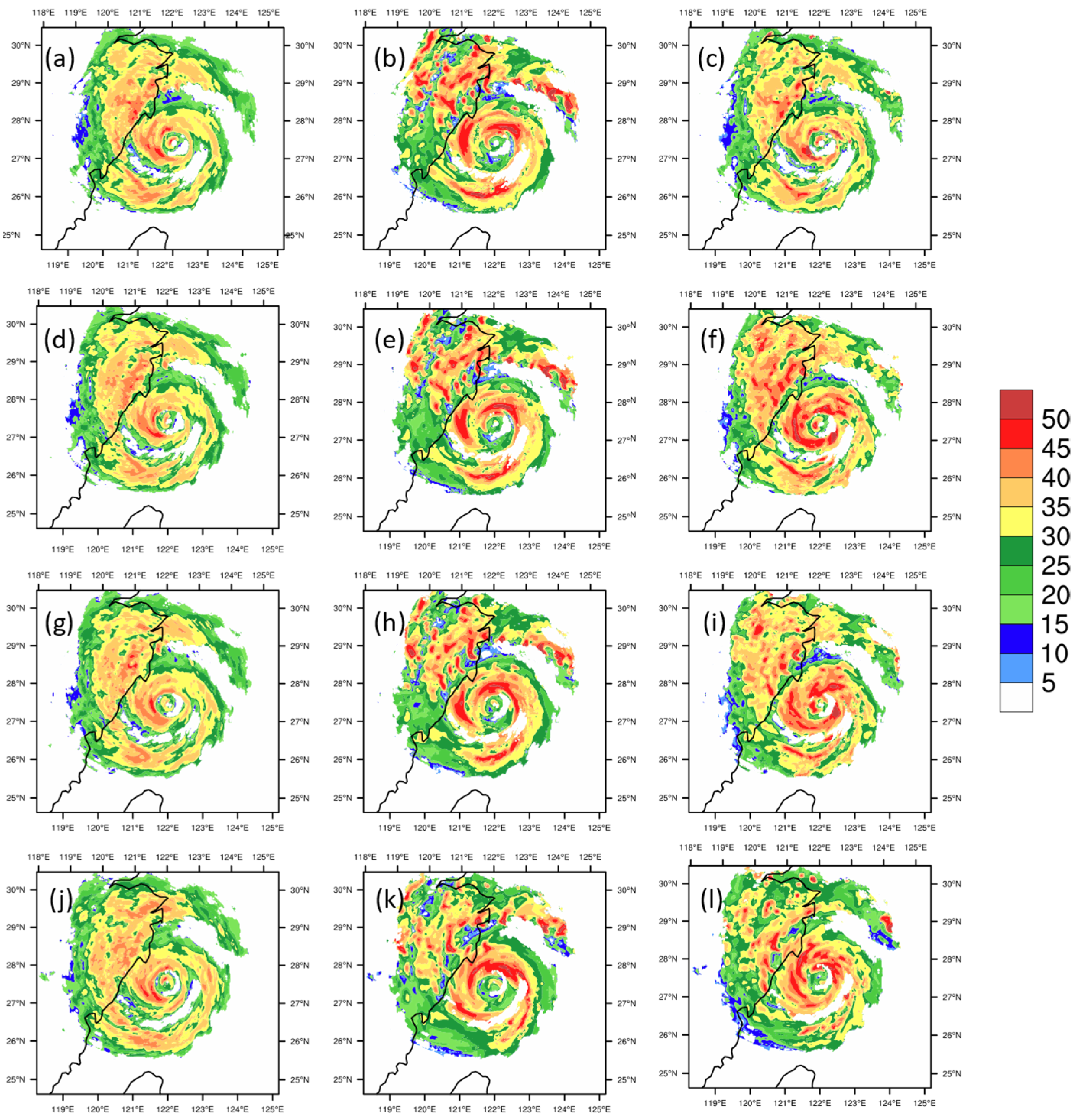
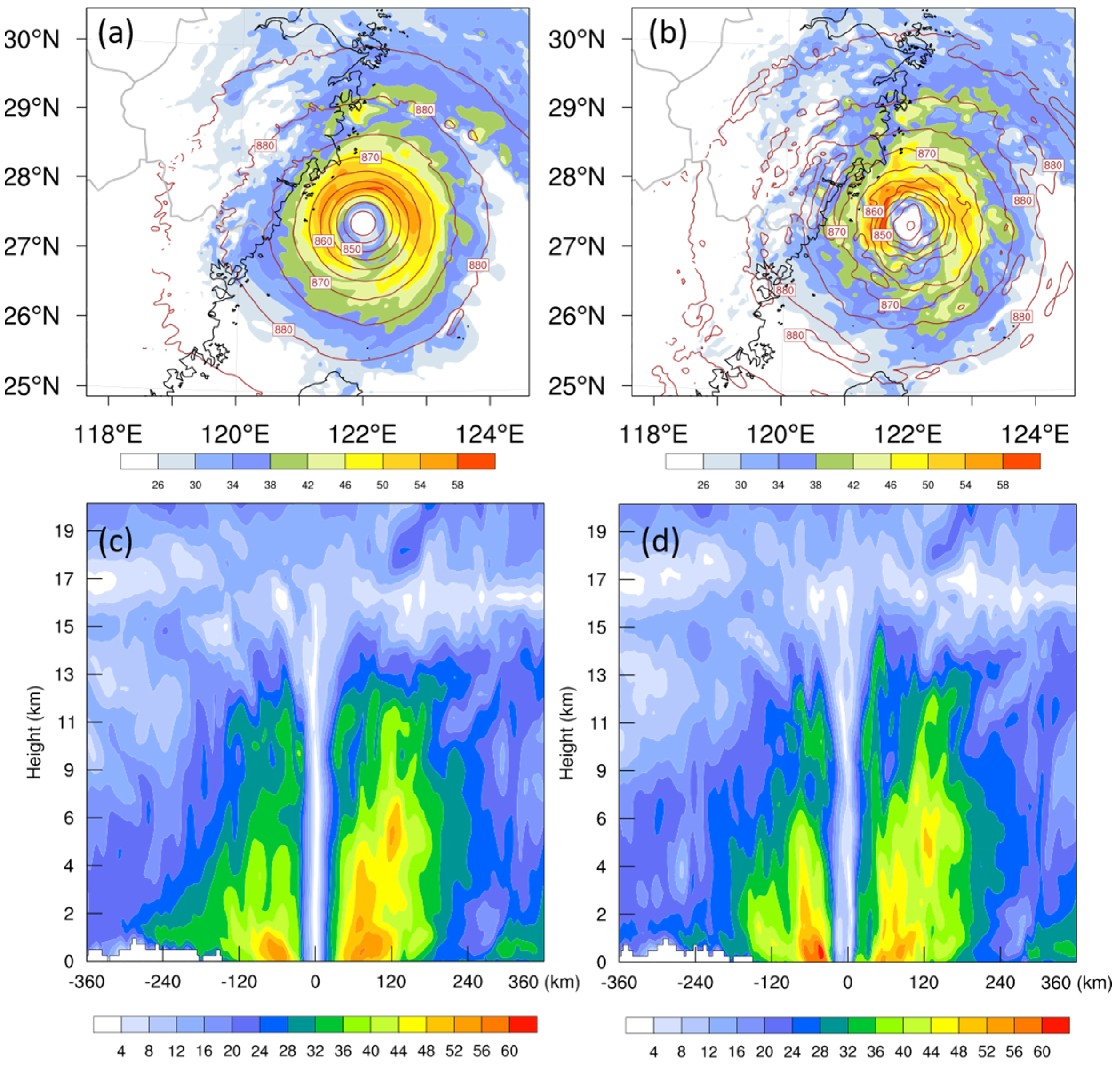
3.1. Impact on TC Analysis and Forecast
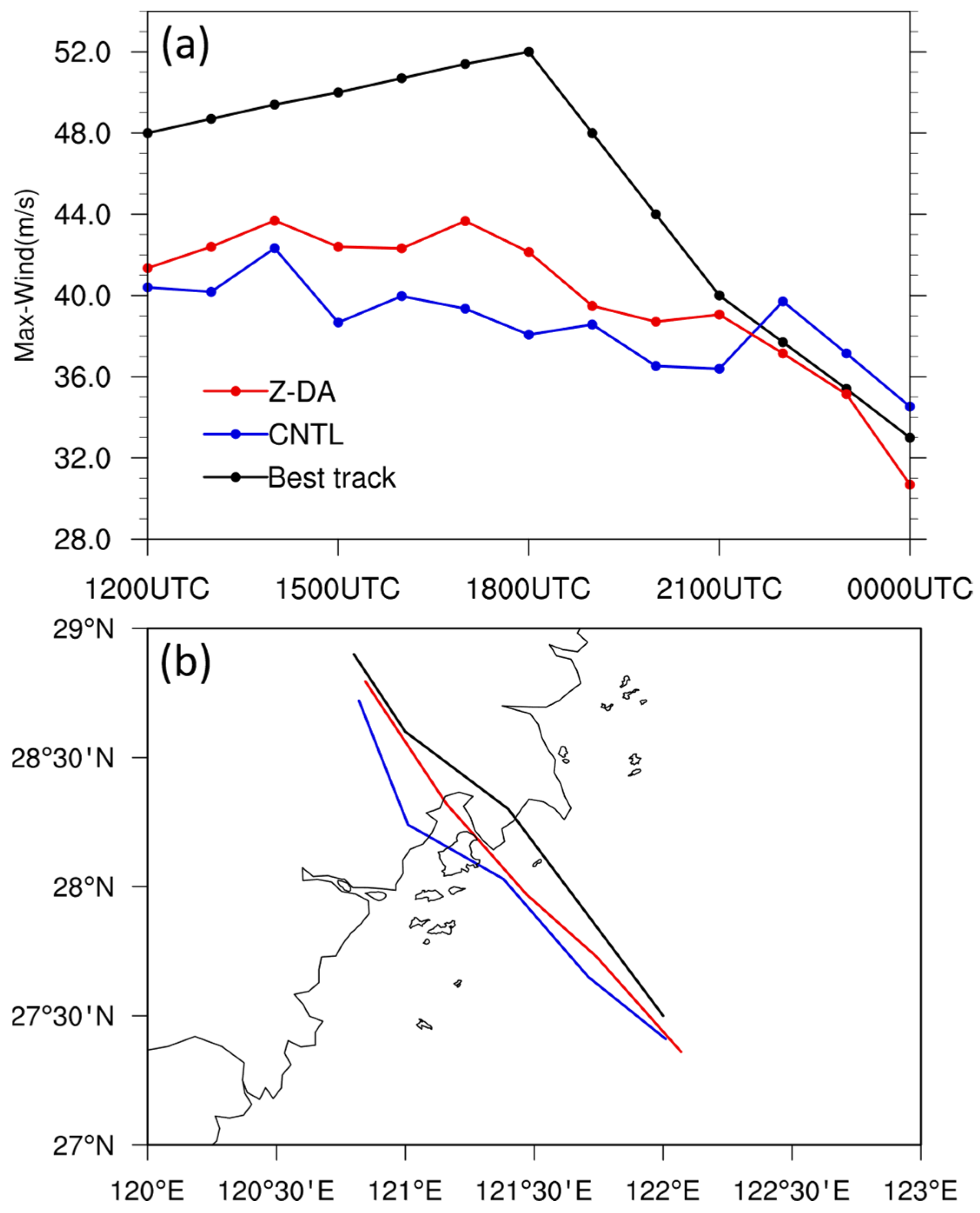
3.2. Intensity and Track Forecast
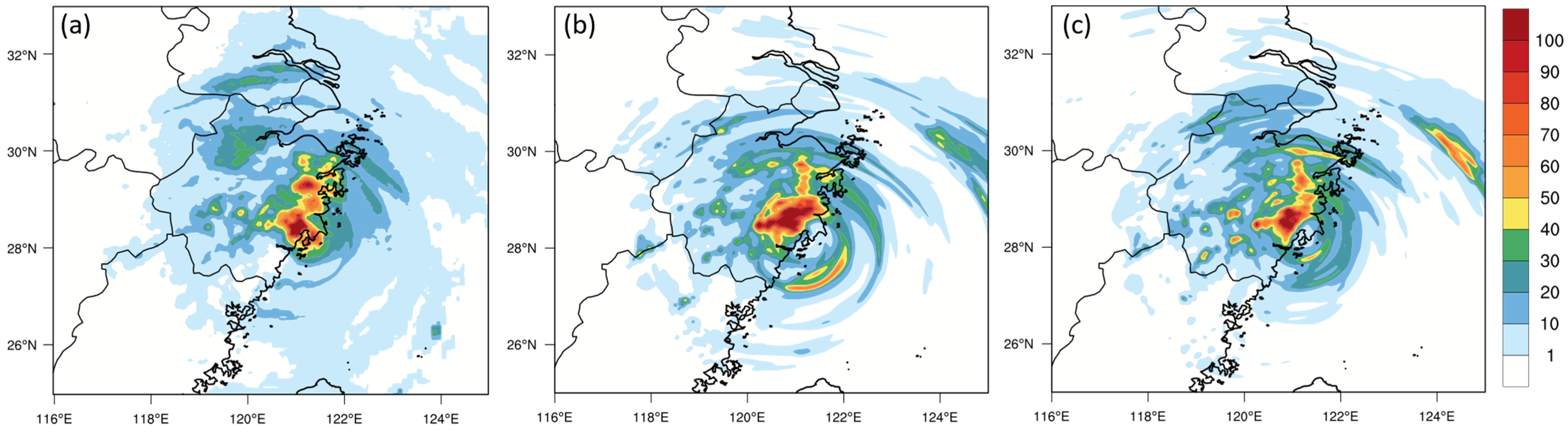
3.3. Precipitation Forecast
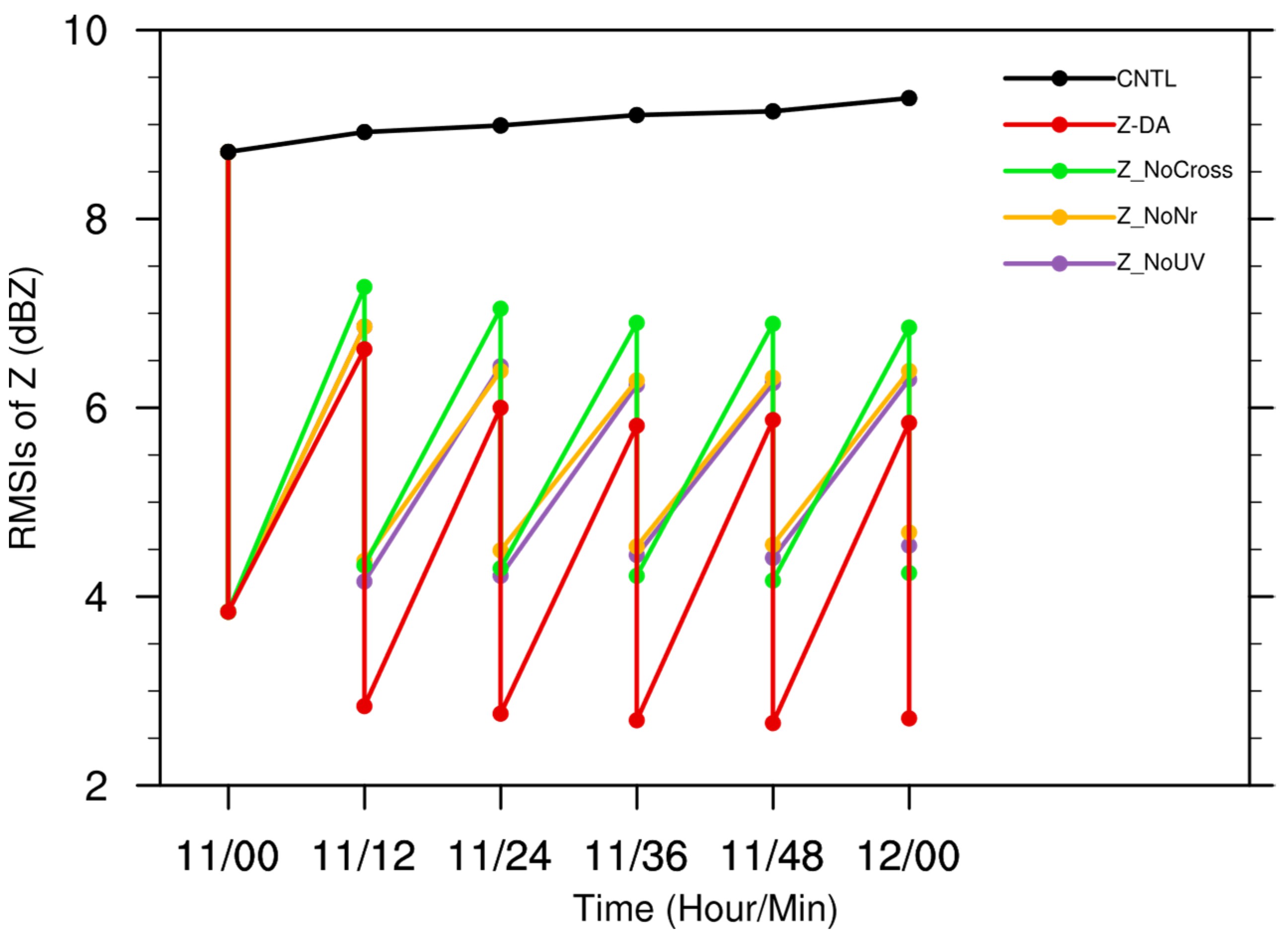
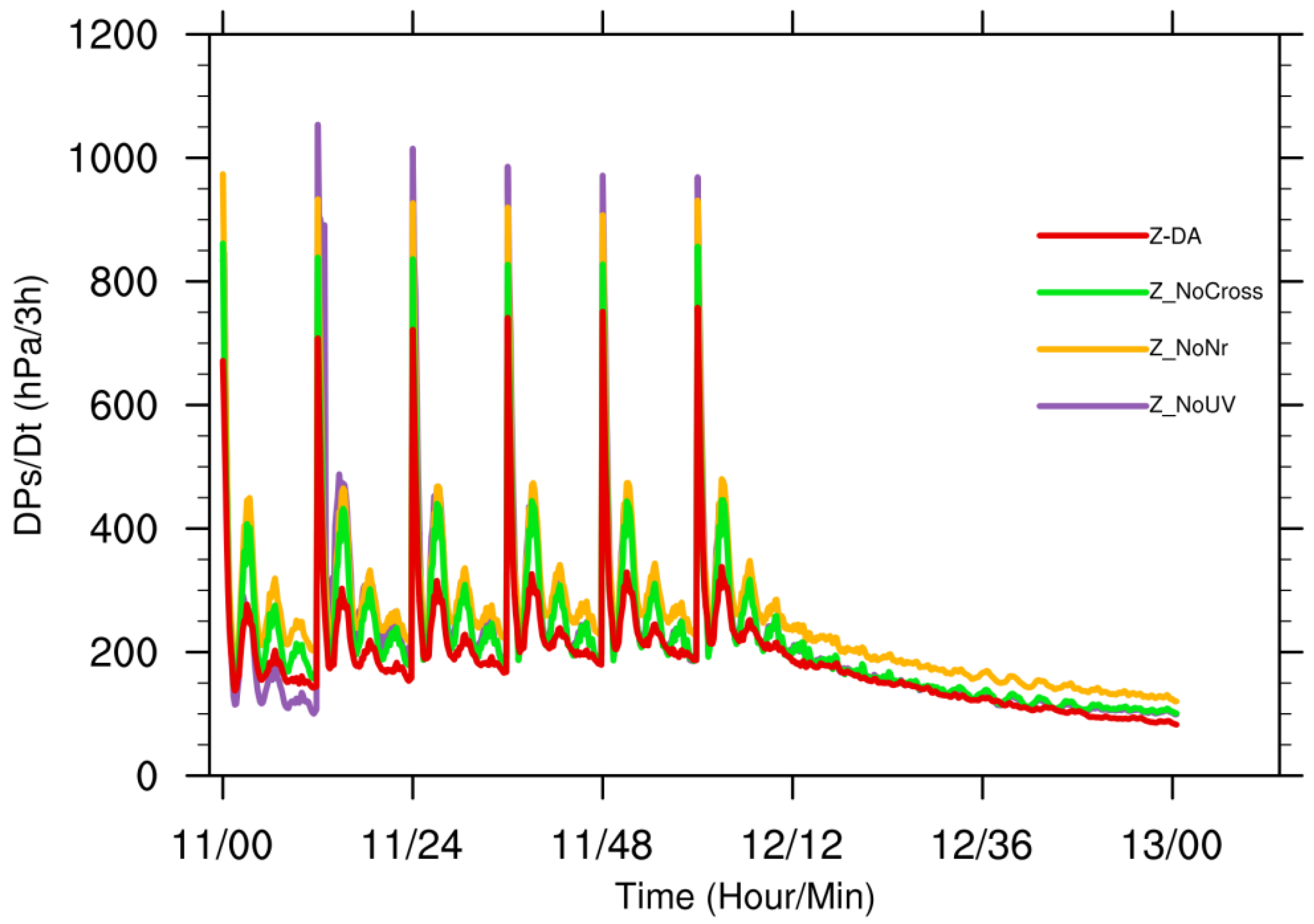
4. Sensitivity Experiments
5. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Marks, F.D., Jr. State of the science: Radar view of tropical cyclones. In Radar and Atmospheric Science; Meteorological Monograph No. 30; American Meteorological Society: Boston, MA, USA, 2003; pp. 33–73. [Google Scholar]
- Weng, Y.; Zhang, M.; Zhang, F. Advanced data assimilation for cloud-resolving hurricane initialization and prediction. Comput. Sci. Eng. 2011, 13, 40–49. [Google Scholar] [CrossRef]
- Zhang, F.; Weng, Y.; Gamache, J.F.; Marks, F.D. Performance of convection-permitting hurricane initialization and prediction during 2008–2010 with ensemble data assimilation of inner-core airborne Doppler radar observations. Geophys. Res. Lett. 2011, 38, L15810. [Google Scholar] [CrossRef]
- Zhao, Q.; Jin, Y. High-Resolution Radar Data Assimilation For Hurricane Isabel (2003) At Landfall. Bull. Am. Meteorol. Soc. 2008, 89, 1355–1372. [Google Scholar] [CrossRef]
- Pu, Z.; Li, X.; Sun, J. Impact of airborne Doppler radar data assimilation on the numerical simulation of intensity changes of hurricane Dennis near a landfall. J. Atmos. Sci. 2009, 66, 3351–3365. [Google Scholar] [CrossRef]
- Xiao, Q.; Zhang, X.; Davis, C.; Tuttle, J.; Holland, G.; Fitzpatrick, P.J. Experiments of hurricane initialization with airborne Doppler radar data for the advanced research hurricane WRF (AHW) model. Mon. Weather Rev. 2009, 137, 2758–2777. [Google Scholar] [CrossRef]
- Zhao, K.; Xue, M. Assimilation of coastal Doppler radar data with the ARPS 3DVAR and cloud analysis for the prediction of Hurricane Ike (2008). Geophys. Res. Lett. 2009, 36, L12803. [Google Scholar] [CrossRef]
- Zhao, K.; Xue, M.; Lee, W.-C. Assimilation of GBVTD-retrieved winds from single-Doppler radar for short-term forecasting of Super Typhoon Saomai (0608) at landfall. Q. J. R. Meteorol. Soc. 2012, 138, 1055–1071. [Google Scholar] [CrossRef]
- Wang, M.; Xue, M.; Zhao, K.; Dong, J. Assimilation of T-TREC-Retrieved Winds from Single-Doppler Radar with an Ensemble Kalman Filter for the Forecast of Typhoon Jangmi (2008). Mon. Weather Rev. 2014, 142, 1892–1907. [Google Scholar] [CrossRef]
- Zhu, L.; Wan, Q.; Shen, X.; Meng, Z.; Zhang, F.; Weng, Y.; Sippel, J.; Gao, Y.; Zhang, Y.; Yue, J. Prediction and Predictability of High-Impact Western Pacific Landfalling Tropical Cyclone Vicente (2012) through Convection-Permitting Ensemble Assimilation of Doppler Radar Velocity. Mon. Weather Rev. 2016, 144, 21–43. [Google Scholar] [CrossRef]
- Yue, J.; Meng, Z.; Yu, C.-K.; Cheng, L.-W. Impact of coastal radar observability on the forecast of the track and rainfall of Typhoon Morakot (2009) using WRF-based ensemble Kalman filter data assimilation. Adv. Atmos. Sci. 2017, 34, 66–78. [Google Scholar] [CrossRef]
- Dowell, D.C.; Wicker, L.J.; Snyder, C. Ensemble Kalman filter assimilation of radar observations of the 8 May 2003 Oklahoma City supercell: Influence of reflectivity observations on storm-scale analysis. Mon. Weather Rev. 2011, 139, 272–294. [Google Scholar] [CrossRef]
- Gao, J.; Stensrud, D.J. Assimilation of reflectivity data in a convective-scale, cycled 3DVAR framework with hydrometeor classification. J. Atmos. Sci. 2012, 69, 1054–1065. [Google Scholar] [CrossRef]
- Hu, M.; Xue, M.; Brewster, K. 3DVAR and cloud analysis with WSR-88D level-II data for the prediction of the Fort Worth, Texas, tornadic thunderstorms. Part I: Cloud analysis and its impact. Mon. Weather Rev. 2006, 134, 675–698. [Google Scholar] [CrossRef]
- Dawson, D.T.; Xue, M. Numerical Forecasts of the 15–16 June 2002 Southern Plains Mesoscale Convective System: Impact of Mesoscale Data and Cloud Analysis. Mon. Weather Rev. 2006, 134, 1607–1629. [Google Scholar] [CrossRef]
- Weygandt, S.; Benjamin, S. Radar reflectivity–based initialization of precipitation systems using a diabatic digital filter within the Rapid Update Cycle. In Proceedings of the 22nd Conference on Weather Analysis and Forecasting/18th Conference on Numerical Weather Prediction, Park City, UT, USA, 25 June 2007; Meteor. Soc., 1B.7.. Available online: https://ams.confex.com/ams/22WAF18NWP/techprogram/paper_124540.htm (accessed on 25 June 2007).
- Gao, J.; Ge, G.; Stensrud, D.J.; Xue, X. The relative importance of assimilating radial velocity and reflectivity data. In Proceedings of the 23nd Conference on Weather Analysis and Forecasting/19th Conference on Numerical Weather Prediction, Omaha, NB, USA, 1–5 June 2009; Meteor. Soc., 8A.1. 2009. Available online: http://ams.confex.com/ams/23WAF19NWP/techprogram/paper_154286.htm (accessed on 3 June 2009).
- Sun, J.; Crook, N.A. Dynamical and microphysical retrieval from Doppler radar observations using a cloud model and its adjoint. Part I: Model development and simulated data experiments. J. Atmos. Sci. 1997, 54, 1642–1661. [Google Scholar] [CrossRef]
- Wang, H.; Sun, J.; Fan, S.; Huang, X.-Y. Indirect assimilation of radar reflectivity with WRF 3D-Var and its impact on prediction of four summertime convective events. J. Appl. Meteor. Climatol. 2013, 52, 889–902. [Google Scholar] [CrossRef]
- Carley, J.R. Hybrid Ensemble-3DVar Radar Data Assimilation for the Short-Term Prediction of Convective Storms. Ph.D. Dissertation, Department of Earth, Atmospheric, and Planetary Sciences, Purdue University, West Lafayette, IN, USA, 2012; p. 205. [Google Scholar]
- Wang, Y.; Wang, X. Direct Assimilation of Radar Reflectivity without Tangent Linear and Adjoint of the Nonlinear Observation Operator in the GSI-Based EnVar System: Methodology and Experiment with the 8 May 2003 Oklahoma City Tornadic Supercell. Mon. Weather Rev. 2017, 145, 1447–1471. [Google Scholar] [CrossRef]
- Liu, C.; Xue, M.; Kong, R. Direct Assimilation of Radar Reflectivity Data Using 3DVAR: Treatment of Hydrometeor Background Errors and OSSE Tests. Mon. Weather Rev. 2019, 147, 17–29. [Google Scholar] [CrossRef]
- Chen, L.; Liu, C.; Xue, M.; Zhao, G.; Kong, R.; Jung, Y. Use of Power Transform Mixing Ratios as Hydrometeor Control Variables for Direct Assimilation of Radar Reflectivity in GSI En3DVar and Tests with Five Convective Storm Cases. Mon. Weather Rev. 2021, 149, 645–659. [Google Scholar] [CrossRef]
- Kong, R.; Xue, M.; Liu, C. Development of a Hybrid En3DVar Data Assimilation System and Comparisons with 3DVar and EnKF for Radar Data Assimilation with Observing System Simulation Experiments. Mon. Weather Rev. 2018, 146, 175–198. [Google Scholar] [CrossRef]
- Dowell, D.C.; Zhang, F.; Wicker, L.J.; Snyder, C.; Crook, N.A. Wind and temperature retrievals in the 17 May 1981 Arcadia, Oklahoma supercell: Ensemble Kalman filter experiments. Mon. Weather Rev. 2004, 132, 1982–2005. [Google Scholar] [CrossRef]
- Tong, M.; Xue, M. Ensemble Kalman filter assimilation of Doppler radar data with a compressible nonhydrostatic model: OSS experiments. Mon. Weather Rev. 2005, 133, 1789–1807. [Google Scholar] [CrossRef]
- Jung, Y.; Zhang, G.; Xue, M. Assimilation of simulated polarimetric radar data for a convective storm using ensemble Kalman fifilter. Part I: Observation operators for reflflectivity and polarimetric variables. Mon. Weather Rev. 2008, 136, 2228–2245. [Google Scholar] [CrossRef]
- Dong, J.; Xue, M. Assimilation of radial velocity and reflectivity data from coastal WSR-88D radars using an ensemble Kalman filter for the analysis and forecast of landfalling hurricane Ike (2008). Q. J. R. Meteorol. Soc. 2013, 139, 467–487. [Google Scholar] [CrossRef]
- Li, H.; Kalnay, E.; Miyoshi, T.; Danforth, C.M. Accounting for model errors in ensemble data assimilation. Mon. Weather Rev. 2009, 137, 3407–3419. [Google Scholar] [CrossRef]
- Seifert, A.; Beheng, K.D. A double-moment parameterization for simulating autoconversion, accretion and selfcollection. Atmos. Res. 2001, 59–60, 265–281. [Google Scholar] [CrossRef]
- Milbrandt, J.A.; Yau, M.K. A Multimoment Bulk Microphysics Parameterization. Part II: A Proposed Three-Moment Closure and Scheme Description. J. Atmos. Sci. 2005, 62, 3065–3081. [Google Scholar] [CrossRef]
- Morrison, H.; Grabowski, W.W. A Novel Approach for Representing Ice Microphysics in Models: Description and Tests Using a Kinematic Framework. J. Atmos. Sci. 2008, 65, 1528–1548. [Google Scholar] [CrossRef]
- Xue, M.; Jung, Y.; Zhang, G. State estimation of convective storms with a two-moment microphysics scheme and an ensemble Kalman filter: Experiments with simulated radar data. Q. J. R. Meteorol. Soc. 2010, 136, 685–700. [Google Scholar] [CrossRef]
- Jung, Y.; Xue, M.; Tong, M. Ensemble Kalman Filter Analyses of the 29–30 May 2004 Oklahoma Tornadic Thunderstorm Using One- and Two-Moment Bulk Microphysics Schemes, with Verification against Polarimetric Radar Data. Mon. Weather Rev. 2012, 140, 1457–1475. [Google Scholar] [CrossRef]
- Putnam, B.J.; Xue, M.; Jung, Y.; Snook, N.A.; Zhang, G. Ensemble Probabilistic Prediction of a Mesoscale Convective System and Associated Polarimetric Radar Variables Using Single-Moment and Double-Moment Microphysics Schemes and EnKF Radar Data Assimilation. Mon. Weather Rev. 2017, 145, 2257–2279. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Wang, W.; Powers, J.D. A Description of the Advanced Research WRF Version 2; (No. NCAR/TN-468+STR); University Corporation for Atmospheric Research: Boulder, CO, USA, 2005. [Google Scholar] [CrossRef]
- Thompson, G.; Field, P.R.; Rasmussen, R.M.; Hall, W.D. Explicit Forecasts of Winter Precipitation Using an Improved Bulk Microphysics Scheme. Part II: Implementation of a New Snow Parameterization. Mon. Weather Rev. 2008, 136, 5095–5115. [Google Scholar] [CrossRef]
- Hong, S.Y.; Noh, Y.; Dudhia, J. A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef]
- Chen, F.; Dudhia, J. Coupling an Advanced Land Surface–Hydrology Model with the Penn State–NCAR MM5 Modeling System. Part II: Preliminary Model Validation. Mon. Weather Rev. 2001, 129, 587–604. [Google Scholar] [CrossRef]
- Iacono, M.J.; Delamere, J.S.; Mlawer, E.J.; Shephard, M.W.; Clough, S.A.; Collins, W.D. Radiative forcing by long-lived greenhouse gases: Calculations with the AER radiative transfer models. J. Geophys. Res. 2008, 113, D13103. [Google Scholar] [CrossRef]
- Whitaker, J.S.; Hamill, T.M. Ensemble data assimilation without perturbed observations. Mon. Weather Rev. 2002, 130, 1913–1924. [Google Scholar] [CrossRef]
- Whitaker, J.S.; Hamill, T.M. Evaluating Methods to Account for System Errors in Ensemble Data Assimilation. Mon. Weather Rev. 2012, 140, 3078–3089. [Google Scholar] [CrossRef]
- Carlin, J.T.; Ryzhkov, A.V.; Snyder, J.C.; Khain, A. Hydrometeor mixing ratio retrievals for storm-scale radar data assimilation: Utility of current relations and potential benefits of polarimetry. Mon. Weather Rev. 2016, 144, 2981–3001. [Google Scholar] [CrossRef]
- Vivekanandan, J.; Raghavan, R.; Bringi, V.N. Polarimetric radar modeling of mixtures of precipitation particles. IEEE Trans. Geosci. Remote Sens. 1993, 31, 1017–1030. [Google Scholar] [CrossRef]
- Barker, D.M.; Huang, W.; Guo, Y.-R.; Bourgeois, A.; Xiao, Q. A three-dimensional variational data assimilation system for MM5: Implementation and initial results. Mon. Weather Rev. 2004, 132, 897–914. [Google Scholar] [CrossRef]
- Ying, M.; Zhang, W.; Yu, H.; Lu, X.; Feng, J.; Fan, Y.; Zhu, Y.; Chen, D. An overview of the China Meteorological Administration tropical cyclone database. J. Atmos. Ocean.Technol. 2014, 31, 287–301. [Google Scholar] [CrossRef]
- Lu, X.; Yu, H.; Ying, M.; Zhao, B.; Zhang, S.; Lin, L.; Bai, L.; Wan, R. Western North Pacific tropical cyclone database created by the China Meteorological Administration. Adv. Atmos. Sci. 2021, 38, 690–699. [Google Scholar] [CrossRef]
- Shen, Y.; Zhao, P.; Pan, Y.; Yu, J. A high spatiotemporal gauge-satellite merged precipitation analysis over China. J. Geophys. Res. 2014, 119, 3063–3075. [Google Scholar] [CrossRef]
- Lynch, P.; Huang, X.-Y. Initialization of the HIRLAM model using a digital filter. Mon. Weather Rev. 1992, 120, 1019–1034. [Google Scholar] [CrossRef]
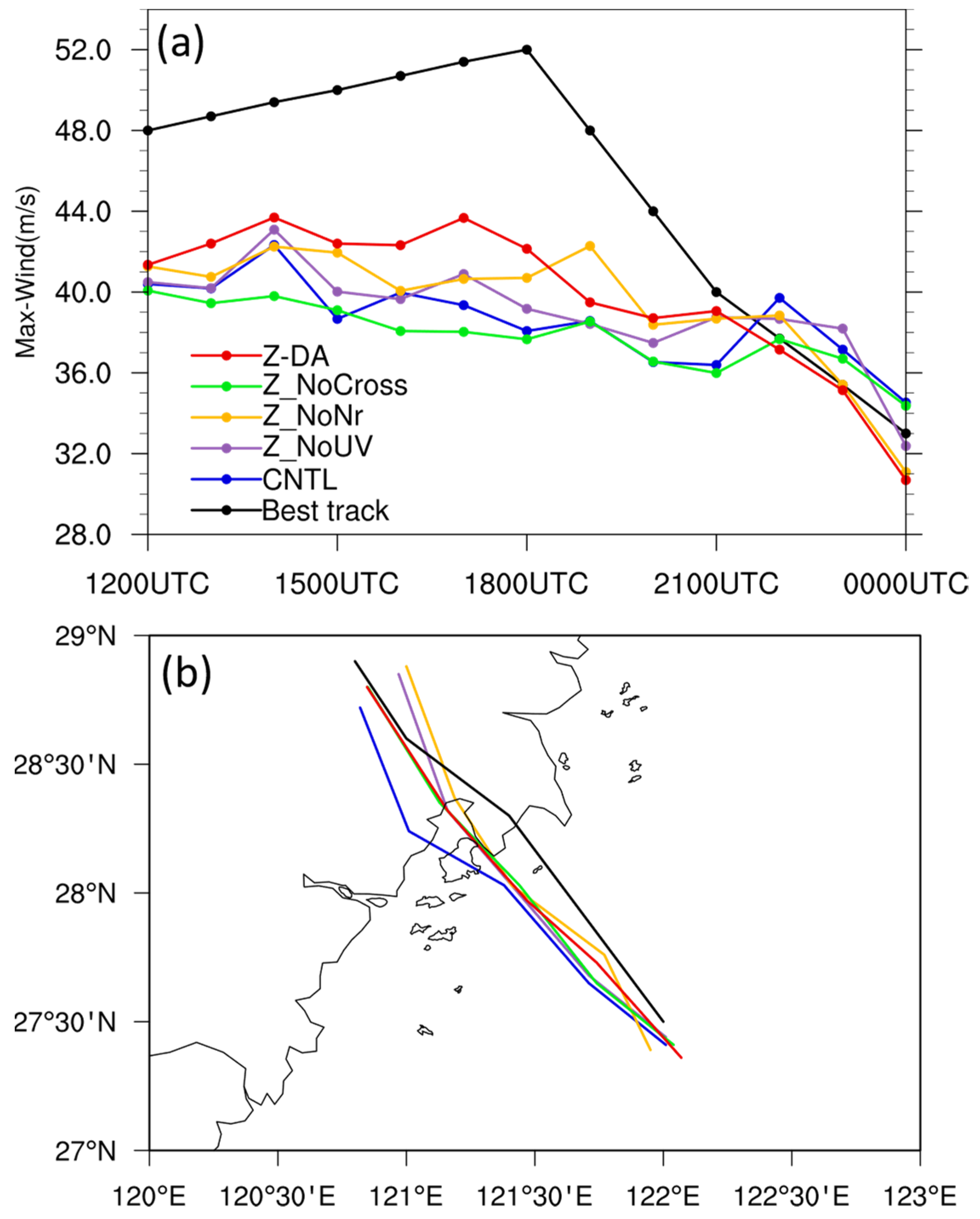
| Experiment Name | Assimilated Data | Analysis Variables Updated by EnKF |
|---|---|---|
| Z-DA | Radar reflectivity | u, v, w, MU, θ, qv, qc, qi, qr, qs, qg and Nr |
| Z_NoNr | Radar reflectivity | As in Z-DA, but Nr was not updated |
| Z_NoUV | Radar reflectivity | As in Z-DA, but u and v were not updated |
| Z_NoCross | Radar reflectivity | As in Z-DA, but u, v, w, MU, θ and qv were not updated |
| CNTL | None | None |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, J.; Li, H.; Xue, M.; Zhu, Y. Direct Assimilation of Radar Reflectivity Data Using Ensemble Kalman Filter Based on a Two-Moment Microphysics Scheme for the Analysis and Forecast of Typhoon Lekima (2019). Remote Sens. 2022, 14, 3987. https://doi.org/10.3390/rs14163987
Luo J, Li H, Xue M, Zhu Y. Direct Assimilation of Radar Reflectivity Data Using Ensemble Kalman Filter Based on a Two-Moment Microphysics Scheme for the Analysis and Forecast of Typhoon Lekima (2019). Remote Sensing. 2022; 14(16):3987. https://doi.org/10.3390/rs14163987
Chicago/Turabian StyleLuo, Jingyao, Hong Li, Ming Xue, and Yijie Zhu. 2022. "Direct Assimilation of Radar Reflectivity Data Using Ensemble Kalman Filter Based on a Two-Moment Microphysics Scheme for the Analysis and Forecast of Typhoon Lekima (2019)" Remote Sensing 14, no. 16: 3987. https://doi.org/10.3390/rs14163987
APA StyleLuo, J., Li, H., Xue, M., & Zhu, Y. (2022). Direct Assimilation of Radar Reflectivity Data Using Ensemble Kalman Filter Based on a Two-Moment Microphysics Scheme for the Analysis and Forecast of Typhoon Lekima (2019). Remote Sensing, 14(16), 3987. https://doi.org/10.3390/rs14163987






