Abstract
Soil moisture (SM) is critical in monitoring the time-lagged impacts of agrometeorological drought. In Australia and several south-west Pacific Small Island Developing States (SIDS), there are a limited number of in situ SM stations that can adequately assess soil-water availability in a near-real-time context. Satellite SM datasets provide a viable alternative for SM monitoring and agrometeorological drought provision in these regions. In this study, we investigated the performance of Soil Moisture Active Passive (SMAP), Soil Moisture and Ocean Salinity (SMOS), Soil Moisture Operational Products System (SMOPS), SM from the Advanced Microwave Scanning Radiometer 2 (AMSR-2) and SM from the Advanced Scatterometer (ASCAT) over Australia and south-west Pacific SIDS. Products were first evaluated in Australia, given the presence of several in-situ SM monitoring stations and a state-of-the-art hydrological model—the Australian Water Resources Assessment Landscape modelling system (AWRA-L). We further investigated the accuracy of SM satellite datasets in Australia and the south-west Pacific through Triple Collocation analysis with two other SM reference datasets—ERA5 reanalysis SM data and model data from the Global Land Data Assimilation System (GLDAS) dataset. All datasets have differing observation periods ranging from 1911-now, with a common period of observations between 2015–2021. Results demonstrated that ASCAT and SMOS were consistently superior in their performance. Analysis in the six south-west Pacific SIDS indicated reduced performance for all products, with ASCAT and SMOS still performing better than others for most SIDS with median R values ranging between 0.3–0.9. We conducted a case study of the 2015 El Niño and Positive Indian Ocean Dipole-induced drought in Papua New Guinea. It was shown that ASCAT is a valuable dataset indicative of agrometeorological drought for the nation, highlighting the value of using satellite SM products to provide early warning of drought in data-sparse regions in the south-west Pacific.
1. Introduction
Soil moisture (SM) is a key state variable that parametrises several hydrological processes such as infiltration, evaporation, and runoff. SM provides insight into the water availability of terrestrial ecosystems and modulates the primary productivity of several agricultural processes [1].
Information on the spatiotemporal variability of SM is of critical importance for monitoring meteorological, climatic, and hydrologic extremes such as drought. Defining a multi-faceted and slow-onset hazard like drought is a complex and sometimes arbitrary endeavour. For this reason, drought definitions tend to be categorised by propagation and impact, where an initial rainfall deficiency (meteorological drought) may be accompanied by time-lagged abiotic stress (agricultural drought), water supply stress (hydrological drought), and reduced financial productivity for drought-vulnerable communities (socioeconomic drought). SM is a key antecedent drought variable since it provides insight into surface and root zone water availability that can be used to track, monitor, and understand agricultural drought impacts before, during and after a drought event.
SM is monitored through in-situ observations or remote sensing retrieval and modelled using water balance land models. Generally, in-situ measurements of SM are considered the most reliable account of soil water profile [2,3]. Common SM instruments include neutron probes, electromagnetic sensors, heat pulse probes, and gamma radiation sensors [2]. However, given that such sensors are relatively discrete and point-based, they have limited ability to represent catchment-scale SM dynamics [4]. SM instruments can also be susceptible to errors from elevated salinity; reduced soil-sensor contact from soil shrinkage and ecological activity; limited performance at shallow depths; temperature extremes impacting performance; and limited soil-specific calibration [2]. Additionally, implementation of a high-density SM sensor network is a complex and financially infeasible process that is often of low priority in regions that are impacted by other hazards [5].
In gauge-sparse regions, like the south-west Pacific, where in-situ SM monitoring infrastructure may be limited in its availability, remote sensing of SM offers a promising solution. Microwave remote sensing is the prevailing technique deployed on various satellite missions owing to the longer than optical wavelengths of microwave radiation (1 mm–1 m wavelengths). This substantially eliminates the effects of atmospheric scattering from clouds, haze, dust, and rainfall that typically impact the accuracy of optical remote sensing methods [2,3]. Microwave remote sensing of SM can be conducted using passive or active sensors (or some combination of both) [2]. Active sensors (radars) emit pulses of microwave radiation and measure the backscattered fraction returned to the sensor. On the other hand, passive sensors (radiometers) do not actively emit microwave radiation. Instead, they measure the natural microwave emission of an emitting body through its brightness temperature [2,4]. Both passive and active retrieval methods rely on the naturally occurring contrast between the dielectric constants of dry and wet soil to estimate soil water capacity where wetter soils emit cooler brightness temperatures (passive) and reflect higher backscatter values (active) [6]. Passive remote sensing is more sensitive to surface SM and is commonly used to map global SM in X, C, and L band frequencies [3,7]. Passive SM satellite sensors require large antennas to allow for adequate detection of weak thermal emissions, which can result in coarser resolutions [6]. Active sensors, on the other hand, may have finer spatial resolutions but can be impacted by surface backscattering from vegetation and surface roughness. Both retrieval methods have an extensive array of advantages and disadvantages, which is why some SM space-missions deploy hybrid combinations that utilise attributes of both. This makes SM retrieval and algorithm generation an evolving area of SM research [2,3].
In the south-west Pacific region, monitoring soil moisture (and even rainfall) through a dense and uniform station network is a challenging task [8,9], owing in most part to the region’s remoteness and limited financial and infrastructural capacity for meteorological monitoring [10]. Additionally, given geographic distributions of orography, atolls, and low-lying islands, several regions in the Pacific are often vast distances away from capital islands where primary rain and soil moisture gauges are commonly placed [11]. Limited monitoring and forecasting abilities exacerbate the region’s vulnerability and exposure to drought, making it difficult to monitor and warn communities most at risk in the period leading up to drought. This means that historically, the region has experienced widespread devastation and loss of livelihood from drought episodes, with the notable El Niño periods of 1997–1998 and 2015–2016 leading to extensive crop losses, famine, and socioeconomic damage [11,12]. The El Niño-Southern Oscillation (ENSO) has varied drought impacts throughout the region as complex oceanic and atmospheric dynamics combined with other climate drivers that modulate drought [13]. For example, in Papua New Guinea (PNG), drought risk can be high for certain regions during both El Niño and La Niña periods. Regardless of the active ENSO phase influencing drought on the seasonal scale, impacts are expected to intensify on the multidecadal scale as anthropogenic climate change accelerates. The Intergovernmental Panel on Climate Change’s sixth assessment report notes Pacific Islands polewards of ±20° latitude have experienced a drying trend that is predicted to continue in the coming decades [14].
To aid, prepare and warn communities of drought, the operational implementation of satellite monitoring rainfall products is becoming more commonplace in the Pacific region as remote-sensing research progresses [15,16,17,18]. Yet, satellite SM evaluation is a relatively under-explored research space, owing to the minimal-to-none in situ SM stations or water balance models that can be used to evaluate satellite SM products in the Pacific region.
The objective of this study is to examine the performance of satellite SM products in Australia and the south-west Pacific region. Australia is chosen as an initial SM study area due to its range of climate zones; topographies; soil types; well-maintained SM station networks, and the availability of a state-of-the-art gridded water balance model used for operational SM provision by the Australian Bureau of Meteorology (BoM). The in-situ and gridded analysis is then accompanied by a Triple Collocation (TC) analysis over the South-West Pacific. All datasets have a common study period of 2015–2021. The TC analysis is a useful extension of the in-situ and gridded analysis that has not been performed for SM evaluation in this region before.
2. Data and Methods
In this study, we investigated the performance of Soil Moisture Active Passive (SMAP), Soil Moisture and Ocean Salinity (SMOS), Soil Moisture Operational Products System (SMOPS), SM from the Advanced Microwave Scanning Radiometer 2 (AMSR-2) and SM from the Advanced Scatterometer (ASCAT) over Australia and the south-west Pacific using a suite of statistical methods. A summary of dataset resolution, temporal coverage, latency, measurement unit, and sampling depth is provided in Table 1 and are discussed in detail in the following sections.

Table 1.
Summary of the datasets used in this study. Bold text indicates the resolution and sampling depths used in this study.
First, we validated satellite SM products against in-situ, point-based soil moisture data. Then a gridded analysis was performed—using monthly SM grids from a water balance model. Both the gridded and point-based analyses were performed over Australia. To expand our SM analysis to the south-west Pacific region, a TC analysis was conducted using global water balance models. The best-performing dataset from the TC analysis is then applied to a case study analysing the impacts of an extreme drought period in Papua New Guinea. For our analysis, all satellite, model, and in-situ data were either obtained in monthly pre-processed formats or were processed into monthly grids and values. This was done not only because drought impacts tend to occur on a multi-month timescale but also due to satellite swathes and sensor readings having sporadic daily data availability depending on passes, calibration algorithms, and SM instruments used [30]. The common period between each station, AWRA-L and TC triplets was used, 2015–2021. Additionally, all gridded datasets were resampled to a resolution of 0.25° using bilinear interpolation as a trade-off between higher resolution land-surface model data (0.05°) and some of the coarser resolution satellite data (0.10–0.5°).
2.1. Satellite Datasets
2.1.1. ASCAT
The Advanced Scatterometer (ASCAT) is a C-band radar onboard the MetOp-A and MetOp-B satellites. The ASCAT algorithm derives surface SM through a linear change detection retrieval algorithm developed by Wagner et al. (1999) [19]. ASCAT has a revisit frequency of 1–3 days with 9:30/21:30 LST overpass times. The algorithm detects SM in the degree of saturation (%) which we convert into volumetric SM (m3/m3) by multiplying ASCAT degree of saturation SM with soil porosity data obtained from the Harmonized World Soil Database (included within the ASCAT datasets). High resolution and monthly processed ASCAT SM was obtained from the Integrated Climate Data Centre (ICDC) [31], where we used descending overpasses (in the morning, i.e., AM) similar to previous studies that cite plant and soil temperatures, vertical profiles, and soil dielectric properties to be more consistent for AM overpasses [32,33].
2.1.2. SMOPS
The Soil Moisture Operational Products System (SMOPS) is a merged satellite SM product developed by the National Oceanic and Atmospheric Administration (NOAA) [21]. SMOPS was designed to increase the spatial and temporal coverage of existing satellite SM datasets [34] and has been an operational product at NOAA’s National Environmental Satellite Data and Information Service since 2013. SMOPS ingests SM data from ASCAT, SMOS, AMSR-2, and SMAP datasets and generates daily and 6-hourly global surface SM grids via the algorithm detailed in Zhan et al. (2016) [34]. For our study, we use monthly SMOPS grids at a 0.25° resolution provided by the World Meteorological Organization’s Space-based Weather and Climate Extremes Monitoring (SWCEM) [8].
2.1.3. SMOS
The Soil Moisture Ocean Salinity (SMOS) satellite mission was launched in November 2009 by the European Space Agency (ESA) with the goal of surveying surface SM and sea surface salinity globally. SMOS carries an L-band radiometer with 69 uniformly spaced dual polarization antennas that detect brightness temperatures emitted from Earth’s surface with an average spatial resolution of 43 km and a revisit time of 2–3 days [20]. The brightness temperatures are related to surface SM via a retrieval algorithm detailed by Kerr et al. (2010) [20]. Monthly processed data was obtained from the Barcelona Expert Centre (BEC), where raw point-based ESA SMOS L2 data is gridded to 0.25°, filtered, and binned through the algorithm described by Pablos et al. (2020) [35]. For consistency, we continue to use descending overpasses (AM).
2.1.4. AMSR-2
The Advanced Microwave Scanning Radiometer 2 (AMSR-2) is onboard the Japan Aerospace Exploration Agency’s (JAXA) GCOM-W satellite. AMSR-2 is the successor of AMSR-E, which retired in October 2011 and was onboard the National Aeronautics and Space Administration’s (NASA) Earth Observing System Aqua satellite. AMSR-2 detects emissions at several frequencies; for SM content specifically, AMSR-2 measures brightness temperatures in the C and X bands with a revisit time of 1–2 days [22,36]. Several studies have found that C-band SM retrievals have the potential to suffer from radio frequency interference which is why AMSR-2 is also equipped with X-band sensors [2,36]. For this study, we use C- and X-band L3 AMSR2 (LPRM algorithm) descending daily passes sourced from NASA’s Earth Data Center, which is processed into monthly grids [22]. To process monthly grids from daily swath passes, we use an approach similar to Wang et al. (2018) [37], where the monthly averaging conversion is only applied to grid cells with valid data of more than 15 days in a given month.
2.1.5. SMAP
The Soil Moisture Active Passive (SMAP) satellite used combined measurements from an L-band radar and an L-band radiometer to retrieve surface SM in the top 5 cm of soil. SMAP was launched in January 2015. However, a hardware mishap in July of the same year rendered the satellite’s radar instrument unworkable. SMAP’s working L-band radiometer provides observations with a revisit time of 2–3 days and a latency of 12–24 h [38]. In this study, we used dual-channel level 3 descending daily composite data sourced from NASA’s Earth Data Center and processed the swathes into monthly grids similarly to AMSR-2, described earlier [23]. We also used the 36 km resolution as 9 km datasets were too computationally demanding to process. Given that all our analysis uses a common resolution of 0.25°, we do not deem this to be a limiting factor in our evaluation.
2.2. Validation Metrics
Satellite products are commonly evaluated in their performance to some ‘truth’ dataset using conventional metrics such as Mean Bias Error (MBE), Mean Absolute Error (MAE), Root Mean Squared Error (RMSE), unbiased RMSE (ubRMSE), and Pearson correlation coefficient (R) [2,4,6]. A summary of the equations used in this study are provided in Table 2.

Table 2.
Summary of the validation metrics used in the point-based and gridded SM evaluations.
Here Ei is the estimated SM value at grid cell i, and Ti is the ‘true’ SM value at grid cell i.These metrics are used to evaluate satellite SM products in our point-based (Oi is station data) and gridded analysis (Oi is gridded water balance model data). For our TC analysis, a range of TC-specific mathematical metrics is used. We note that MBE, MAE, and RMSE are similar in exploring error characteristics. We retain their inclusion similar to other holistic satellite SM studies [32,38] that use MBE, MAE, and RMSE for bias and error spread insight and ubRMSE and correlations for insight into the systematic difference between datum pairs.
2.3. Point-Based Analysis Datasets
For the point-based analysis, in-situ SM data from three separate SM networks was processed. These datasets, OzFlux, OzNet, and CosmOz, are comprised of a combination of probes, reflectometers, and sensors with differing time periods (all ranging somewhere between 2001–the present) and with different spatial coverage throughout Australia. The distribution of these SM networks across different Australian climate zones is depicted in Figure 1. A detailed summary of each station’s metadata, including latitude, longitude, elevation, and sensor type, is provided in Appendix A. In cases with more than one station within a grid cell, the same grid cell is verified twice against the relevant station/s within it. Looking at Figure 1, this would only be the case for some OzNet stations.
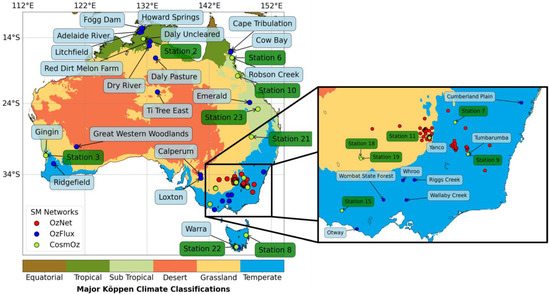
Figure 1.
In situ SM station networks and their distribution over different Australian Köppen climate zones (Climate Zone data sourced from BoM [39]).
SM is measured differently depending on the type of instrument and between networks [2]. This introduces certain systematic variations and biases between networks that Holgate et al. [40] note can be a point of interest when comparing to satellite datasets that also have systematic biases in their detection algorithms. Additionally, depth mismatches between different satellite datasets and instruments introduce other uncertainties into our analysis—pairing this in situ analysis with the varying SM depths of the gridded and TC analysis will help us scrutinize the extent to which depth mismatches can influence performance. We consulted network metadata to only include stations with active and calibrated, high-quality data. Raw station data ranged from hourly, tri-hourly, and daily values which were resampled into monthly averages to match satellite and water balance data temporal resolutions.
2.3.1. OzNet
The OzNet hydrological monitoring network is an SM sensor network located in the Murrumbidgee River Catchment in southern New South Wales [27]. OzNet data measures SM in several soil layers: 0–5, 0–8, 0–30, 30–60, and 60–90 cm using reflectometers and hydraprobes. We used 0–5/0–8 cm measurements to correspond with the soil surface measurements made by satellite products. Raw OzNet data is clustered in seasonal Excel workbooks that were cleaned and compiled into monthly data frames using the Pandas library in Python. In our study, we use SM data from sixty-two OzNet station sites (all clustered around the Murrumbidgee Catchment) with data ranging from 2001 to the present.
2.3.2. CosmOz
CosmOz is an Australian SM probe network that provides SM estimates using Cosmic Ray Probes (CRPs). These probes measure fast neutrons produced by cosmic rays (high-energy atomic nuclei produced from different astrophysical processes that travel close to the speed of light) moving through Earth’s atmosphere. Fast neutrons interact strongly with hydrogen atoms (mostly contained in water molecules) [2]. Thus, the intensity of scattered fast neutrons is inversely related to the abundance of hydrogen atoms in a certain region [28]. Unlike other SM reflectometers and sensors that measure volumetric SM in small quantities of soil, CRPs are recognized for their ability to deduce average SM on larger spatial scales up to 30 hectares [28]. In our study, we use Level 4 SM data from fourteen CosmOz station sites across Australia that have calibrated and real-time data available, all ranging from 2010–the present.
2.3.3. OzFlux
OzFlux is an SM flux tower network that is part of the international SM network, FluxNet [29]. Similar to OzNet data, SM is measured using a range of reflectometers and hydraprobes. For our study, we use Level 6 OzFlux grids for twenty-three sites available from the TERN/OzFlux THREDDS Data server. These pre-processed monthly NetCDF grids provide data for a range of terrestrial and climate variables, with data ranging between 2002–present.
2.4. Gridded Analysis—AWRA-L
The Australian Water Resource Assessment (AWRA-L) is the BoM’s operational gridded SM product. AWRA-L is a model that evolves the physical conditions of the atmosphere, soil, and ground water [24] to produce daily running water balances on a 0.05° × 0.05° Australian grid. AWRA-L outputs data for several hydrological state variables, with soil moisture outputs divided into the categories of upper (0–0.1 m), lower (0.1–1 m), root zone (0–1 m), and deep soil moisture (1–6 m) [24]. Since satellite SM products operate in the skin layer of soil (top ~5 cm), we used upper SM outputted by this model. For our analysis, we used version 6 of the product, which is open loop and has no data assimilation.
2.5. Triple Collocation Analysis
TC analysis defines error variances through the concept that the unknown truth can be derived through an additive or multiplicative combination of three independent, collocated datasets [41,42]. TC was first proposed by Stoffelen (1998) [42] to calibrate wind estimates and has now been broadly used to estimate error variance for satellite-based atmospheric and climatic state variables. TC has three underlying assumptions, (i) linearity and (ii) stationarity of datasets, as well as (iii) error independence of datasets. In this study, we use the additive TC model similar to other satellite SM TC studies [32,38], such that three SM datasets satisfy the linear relationship described in Equation (1).
where θ is the unknown truth, θi (i = 1,2,3) are values from the three independent datasets, and αi, βi, and εi are the intercepts, scale factor, and zero-mean random error, respectively, for each dataset. Then using TC assumptions, the unknown truth, θ, can be eliminated, and the linear relationship can be rearranged to provide the error variance (σε,i) term for each dataset (Equation (2)) in terms of the covariance, Qi,j, between datasets. This error variance term is analogous to conventional RMSE in that it measures the spread of errors in a particular dataset.
Draper et al. (2014) [43] proposed dividing this absolute error variance term by the standard deviation of each dataset to derive a relative error variance term, denoted by fRMSE, which we also use in our analysis.
Similarly, McColl et al. (2013) [44] solved the linear relationships outlined in Equation (1) for the Pearson correlation coefficient (R) between each dataset and the unknown truth that lies between all three (Equation (3)) in an approach they termed ‘Extended Triple Collocation’.
In our study, we create triplets between each satellite SM product; SM derived from a global water balance model (GLDAS) and SM from a reanalysis product (ERA5-Land), similar to Ming et al. (2022) [45]. Additionally, TC is most robust for anomaly error characterization because the errors of the seasonal cycle of different products can be cross-correlated, which would violate the TC assumption [12]. For this reason, all datasets used in our TC analysis had their seasonality removed before TC functions were performed. The south-west Pacific study domain for our TC analysis is depicted in Figure 2. This map was created in QGIS using topography data from ETOPO2v2 [46].
The two datasets used to form triplets with the satellite SM products are described in the following sections. In using GLDAS and ERA5-Land (both modelled products) for our TC analysis, we acknowledge the risk of error dependence between the two triplet datasets underlying the application of TC. Analysis of GLDAS and ERA5 metadata indicates fundamental algorithmic differences between the products and their various input parameters. We reference the work of Ming et al. (2022) [45], who also used GLDAS and ERA5-Land in TC triplets with satellite SM data and found the TC analysis to be “reasonable for the comparison and evaluation of satellite and model-based SM products” [45].
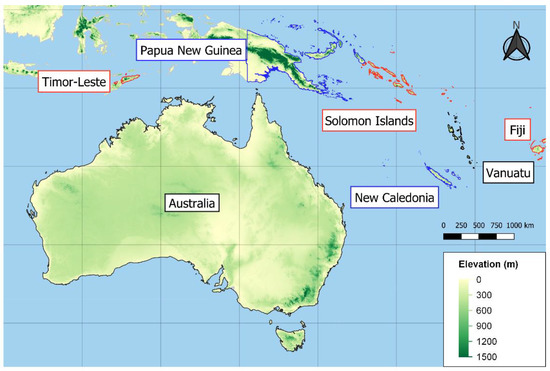
Figure 2.
TC Analysis domain with the six-country sub-domains of Australia, Timor-Leste, Papua New Guinea, Solomon Islands, New Caledonia, Fiji, and Vanuatu pictured.
2.5.1. GLDAS
The Global Land Data Assimilation System (GLDAS) ingests satellite data for several state variables (such as precipitation, brightness temperature, elevation, and leaf area index). It uses complex land surface modelling and assimilation methods to generate land surface states [25]. We obtain 0–10 cm monthly L4 SM GLDAS data from NASA’s Earth Data Center. We use GLDAS V2.1 data which are modelled using an “open-loop” approach (i.e. no data assimilation). GLDAS SM data has a resolution of 0.25° and is in units (kg/m2) which are converted to satellite SM units (m3/m3) using the method described in NASA’s Land Data Assimilation System Documentation, wherein kg/m2 SM values are divided by the mm depth of the SM layer (100 in this case), the assumption here being that the density of water in the soil is 1000 kg/m3 [47].
2.5.2. ERA5-Land
ERA5-Land is a reanalysis dataset produced by evolving the land component of the ERA5 global atmospheric reanalysis produced by the European Centre for Medium-Range Weather Forecasts (ECMWF). Unlike ERA5 global atmospheric reanalysis, ERA5-Land is evolved without coupling to the atmospheric module of the ECMWF forecasting system. ERA5-Land produces SM estimates for four soil layers, 0–7, 7–28, 28–100, and 100–289 cm, with data available from 1950–now [26]. For our analysis, we use the 0–7 cm layer and rescale it from its raw resolution of 0.10° to the study resolution of 0.25°.
2.6. Agrometeorological Drought Case Study
From the TC analysis, the best performing satellite SM dataset over PNG is used to analyze a critical drought period in the nation. We apply the Standardized Precipitation Index (SPI) and Vegetation Health Index (VHI) at 1,3- and 6-month accumulations to quantify the severity of the 2015 El Niño and Positive Indian Ocean Dipole (IOD) drought event in PNG. The SPI is commonly used to quantify precipitation deficit and involves fitting a region’s precipitation to a gamma distribution. SPI values then represent the number of standard deviations observed precipitation differs from the long-term median with −1 to −1.5; −1.5 to −2 and SPI < −2 indicative of moderate, severe, and extreme drought, respectively [48]. PNG’s rain gauge density is non-uniform and of limited capacity (less than ten rain gauges to capture over 460 000 km2 of land). Thus, we compute SPI using satellite-derived rainfall from JAXA’s Global Satellite Mapping of Precipitation (GSMaP) satellite which has been shown to have the promising performance in capturing precipitation over PNG [15]. For VHI, we use NASA’s MODIS-derived VHI dataset, which was also effective at capturing the vegetative stress associated with agricultural drought in PNG [15]. VHI indicates plant health; it is composed of the Vegetation Condition Index (calculated using the Normalized Difference Vegetation Index) and the Temperature Condition Index (calculated using land surface temperatures) [49]. VHI values of 20–30, 10–20, and 0–10 indicate moderately, severely, and extremely stressed vegetation, respectively.
3. Results
This section is presented in order of investigation—point-based analysis using in situ Australian SM data, followed by AWRA-L gridded analysis, and finally TC analysis conducted over a broader south-west Pacific domain.
3.1. Point-Based Analysis
The performance of the five SM satellite products is compared to station data in the box-whisker format in Figure 3. While SMOPS and AMSR-2 have marginally better performance across these metrics, there is no dominating satellite dataset that has significantly superior performance across SM stations.
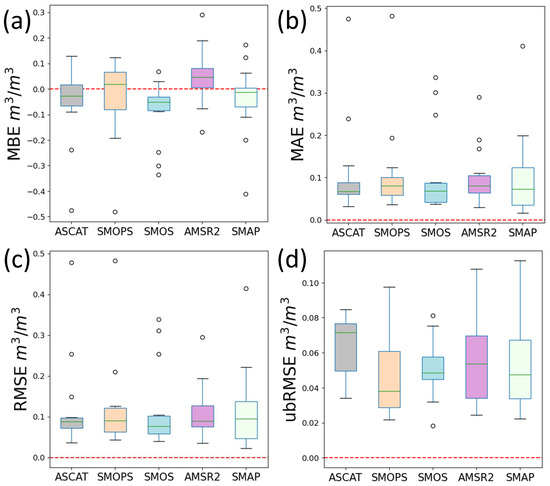
Figure 3.
Spatio-temporal box-whisker plots of (a) MBE, (b) MAE, (c) RMSE, and (d) ubRMSE with outliers that fall outside the interquartile range depicted as black circles, red dashed line indicates perfect value.
Figure 4 depicts both the spatial correlational performance of stations with significant correlations as well as the station averaged box plot. Unlike our earlier results, where SMOPS had only marginally better performance with MBE, MAE, RMSE, and ubRMSE metrics, in the correlational analysis, ASCAT has markedly superior performance with SM station time series. ASCAT not only had a higher positive correlation on average but also had a greater number of significant correlations than the other satellite SM products (this is why the ASCAT scatterplot of significant station correlations is most populated).
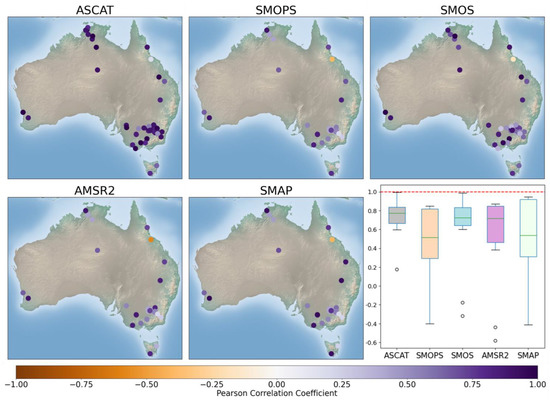
Figure 4.
Temporal correlation performance for ASCAT, SMOPS, SMOS, AMSR-2, and SMAP depicted spatially where only stations with a significant correlation are depicted. An accompanying box-whisker plot depicts the spatio-temporal results with outliers that fall outside the interquartile range depicted as black circles, red dashed line indicates perfect value.
An accompanying box-whisker plot demonstrates that ASCAT, SMOS, and AMSR-2 have the smallest positive spread of correlation coefficients across SM stations. The spatial analysis also highlights an outlier station along the northern QLD coast that has a negative correlation (orange dot) with SMOPS, SMOS, AMSR-2, and SMAP. This station is station 10 from the CosmOz network. It is not immediately clear why Station 10 had a negative correlation for all datasets aside from ASCAT. We investigated time series for this station and satellite datasets to verify the result. CosmOz data providers note that the ‘counting rates’ of all probes within the network are scaled to this station [28]. Intuitively this should yield a significant positive correlation similar to the other CosmOz stations in our analysis; however, the opposite was observed.
Figure 5 plots the satellite SM with the highest significant correlation for each station, we note that SMOS (teal) and ASCAT (purple) have superior time series performance for several stations, with ASCAT, SMOPS, SMOS, AMSR-2, and SMAP being the best performing for 12, 13, 29, 2 and 3 stations, respectively.
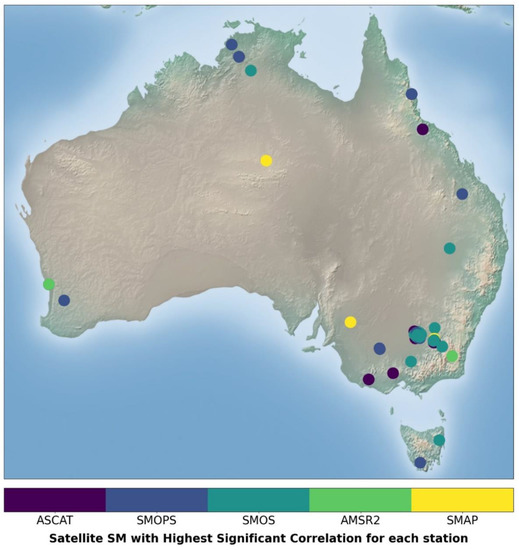
Figure 5.
Satellite SM product with the highest significant correlation for each station.
Referring back to ASCAT’s performance for MBE, MAE, RMSE, and ubRMSE, we note acceptable metrics of −0.019, 0.092, 0.108, and 0.067, respectively. Similarly, for our second-best correlative dataset, SMOS, we note MBE, MAE, RMSE, and ubRMSE performance as −0.029, 0.079, 0.092, and 0.054, respectively. Both SMOS and ASCAT have slight negative biases compared to station observed SM and similarly small RMSE values with a similar variation in their random error when systematic biases are removed (ubRMSE). Thus, from the point-based analysis, we conclude that ASCAT and SMOS have promising performance when using in situ SM station data.
3.2. Gridded Analysis
Figure 6 depicts the spatial MBE across the five satellite SM datasets spatially and as box-whisker plots. Unlike in situ results, we note a positive bias between AWRA-L upper SM grids and satellite SM products except for a small area in western Tasmania, which has slight negative biases for ASCAT and SMOS. Here, SMOPS, AMSR-2, and SMAP also have large positive biases along the southeast coast, and SMOPS has the highest mean bias on average.
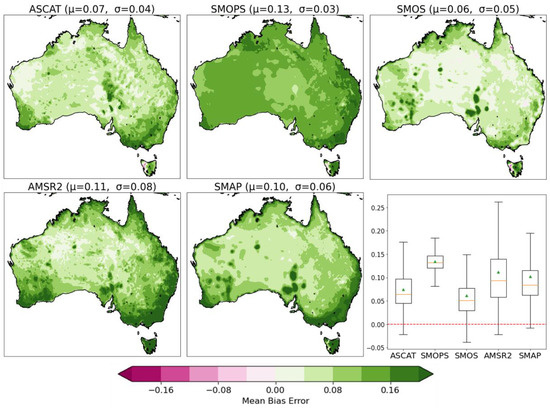
Figure 6.
Temporal MBE results depicted spatially for ASCAT, SMOPS, SMOS, AMSR-2, and SMAP. An accompanying box-whisker plot depicts the spatio-temporal results—whiskers extend out to show the interquartile range, the orange line indicates the distribution median, and the green triangle indicates the distribution mean, red dashed line indicates perfect value.
Similarly, for MAE (Figure 7) and RMSE (Figure 8), we find that AWRA-L average errors are similar in magnitude to average errors from the point-based analysis. Similar to MBE, SMOPS has the largest mean MAE and RMSE over Australia, and for AMSR-2, we note large MAE values over the south-eastern coast and southern Tasmania. For SMOS and ASCAT, there are also bullseye regions with high MAE values close to the Lake Eyre region of South Australia.
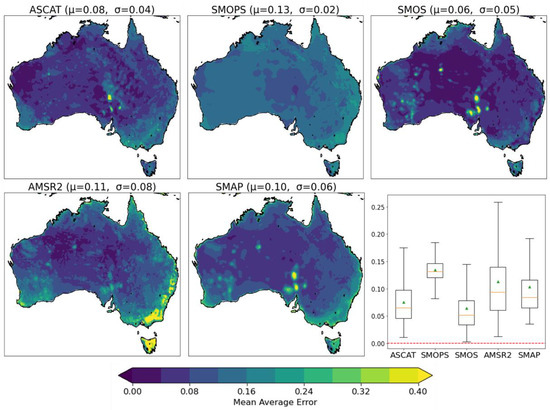
Figure 7.
Temporal MAE results depicted spatially for ASCAT, SMOPS, SMOS, AMSR-2, and SMAP. An accompanying box-whisker plot depicts the spatio-temporal results—whiskers extend out to show the interquartile range, the orange line indicates the distribution median, and the green triangle indicates the distribution mean, red dashed line indicates perfect value.
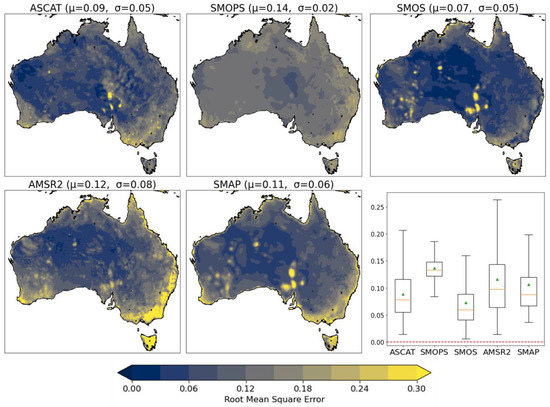
Figure 8.
Temporal RMSE results depicted spatially for ASCAT, SMOPS, SMOS, AMSR-2, and SMAP. An accompanying box-whisker plot depicts the spatio-temporal results—whiskers extend out to show the interquartile range, the orange line indicates the distribution median, and the green triangle indicates the distribution mean, red dashed line indicates perfect value.
Figure 9 depicts the spatial ubRMSE plots and the accompanying box-whisker plots. Despite ASCAT having comparatively lower RMSE values, we note its above-average ubRMSE values. This is also consistent with the point-based analysis where Figure 3d depicts ASCAT as having the highest average ubRMSE. This indicates a larger spread of ‘random’ errors that remain when systematic bias errors are removed for ASCAT.
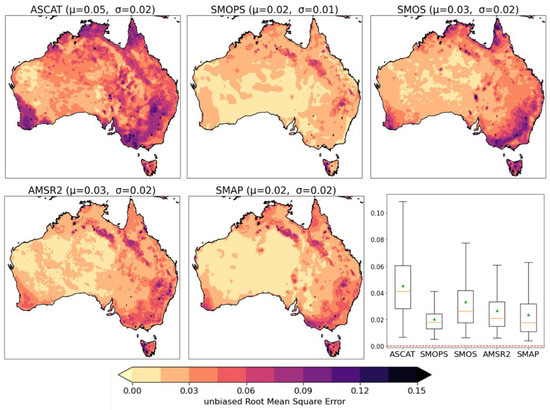
Figure 9.
Temporal ubRMSE results depicted spatially for ASCAT, SMOPS, SMOS, AMSR-2, and SMAP. An accompanying box-whisker plot depicts the spatio-temporal results—whiskers extend out to show the interquartile range, the orange line indicates the distribution median, and the green triangle indicates the distribution mean, red dashed line indicates perfect value.
Figure 10 depicts the results of the correlation between AWRA-L and the satellite SM datasets. Here only spatial plots of ASCAT, SMOPS, and SMOS are depicted as time series correlations between AMSR-2/SMAP and AWRA were insignificant. Furthermore, any grid cells that have insignificant correlations are masked. Despite SMOS having the higher correlation coefficient across Australia on average, we note that its performance along Australia’s southeast coast is considerably lower than ASCAT and even insignificant (masked) in several regions.
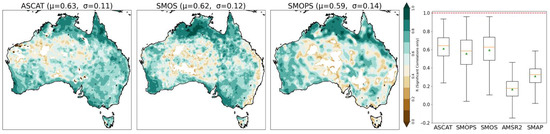
Figure 10.
Temporal correlation coefficient results depicted spatially for ASCAT, SMOPS, SMOS, AMSR-2, and SMAP. An accompanying box-whisker plot depicts the spatio-temporal results—whiskers extend out to show the interquartile range, the orange line indicates the distribution median, and the green triangle indicates the distribution mean, red dashed line indicates perfect value.
To visualize the best performing satellite SM datasets at each grid cell in our domain, we plot the dataset with the highest and second highest significant correlation for each grid cell in Figure 11; the percentage of each satellite dataset in both analyses is provided in Table 3.
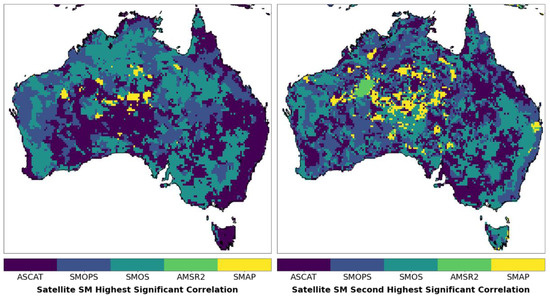
Figure 11.
ASCAT, SMOPS, SMOS, AMSR-2, and SMAP spatially ranked for best and second-best correlation performance (significant correlations only).
Table 3 depicts the percent totals of the ranked datasets from Figure 11. We see that ASCAT has the highest percentage of grid cells with the highest significant correlation, closely followed by SMOS. The third best-performing SM product is SMOPS. As expected in regions where ASCAT has insignificant correlations, SMOS is the best performing dataset, with the converse also being true. This is particularly observable along the south-eastern coast, where SMOS correlations are insignificant, leaving ASCAT as the better performing dataset in this region.

Table 3.
Percent totals of each satellite SM dataset in for highest significant correlations and second highest significant correlation. Best and second-best performing datasets are indicated in bold.
Table 3.
Percent totals of each satellite SM dataset in for highest significant correlations and second highest significant correlation. Best and second-best performing datasets are indicated in bold.
| ASCAT | SMOPS | SMOS | AMSR-2 | SMAP | |
|---|---|---|---|---|---|
| % Highest Significant Correlation | 38.36 | 24.79 | 35.18 | 0.02 | 1.65 |
| % Second Highest Significant Correlation | 32.07 | 29.44 | 32.17 | 1.08 | 5.24 |
To expand on this correlation analysis, correlation coefficients were averaged based on climate zone (Figure 12). Here we use the same climate zones depicted in Figure 1. These climate zones are classified using the same data used to create Figure 1 (BoM derived Köppen classification data derived from a 30-year climatology [39]).
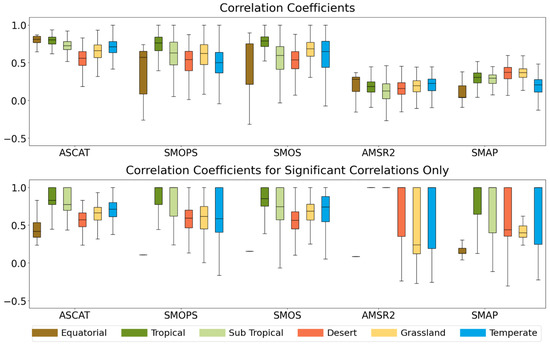
Figure 12.
Spatial correlation coefficients for ASCAT, SMOPS, SMOS, AMSR-2, and SMAP sectioned by climate zone—whiskers extend out to show the interquartile range; the black bar indicates the median value of the distribution.
Overall, performance in the Equatorial and Desert climate zones is considerably lower across all satellite datasets. When considering significant correlations only, most satellite SM datasets have average correlation coefficients close to 0 except for ASCAT. The lack of significant correlations for the Equatorial region is also likely due to only comprising 7.8% of the study area. In contrast, the Temperate and Grassland regions comprise 24.7% and 32.5% of the study region, respectively. Nonetheless, we again see that ASCAT and SMOS perform best across the six major climate zones, with SMOS performing best in the Grassland region and ASCAT performing best in the others.
In Figure 5, we noted that SMOS and SMAP have superior performance when compared with Western Australian stations and also several stations in the interior of the country that would largely be based in Desert and Grassland climate zones. Figure 12 indicates that in our gridded analysis ASCAT (μdesert = 0.55, μgrassland = 0.63) and SMOS (μdesert = 0.49, μgrassland = 0.58) have similar performance in Desert and Grassland regions, with Desert climate zones being the poorest area of performance for ASCAT and Equatorial climate zones being the poorest area of performance for SMOS.
3.3. Triple Collocation Analysis
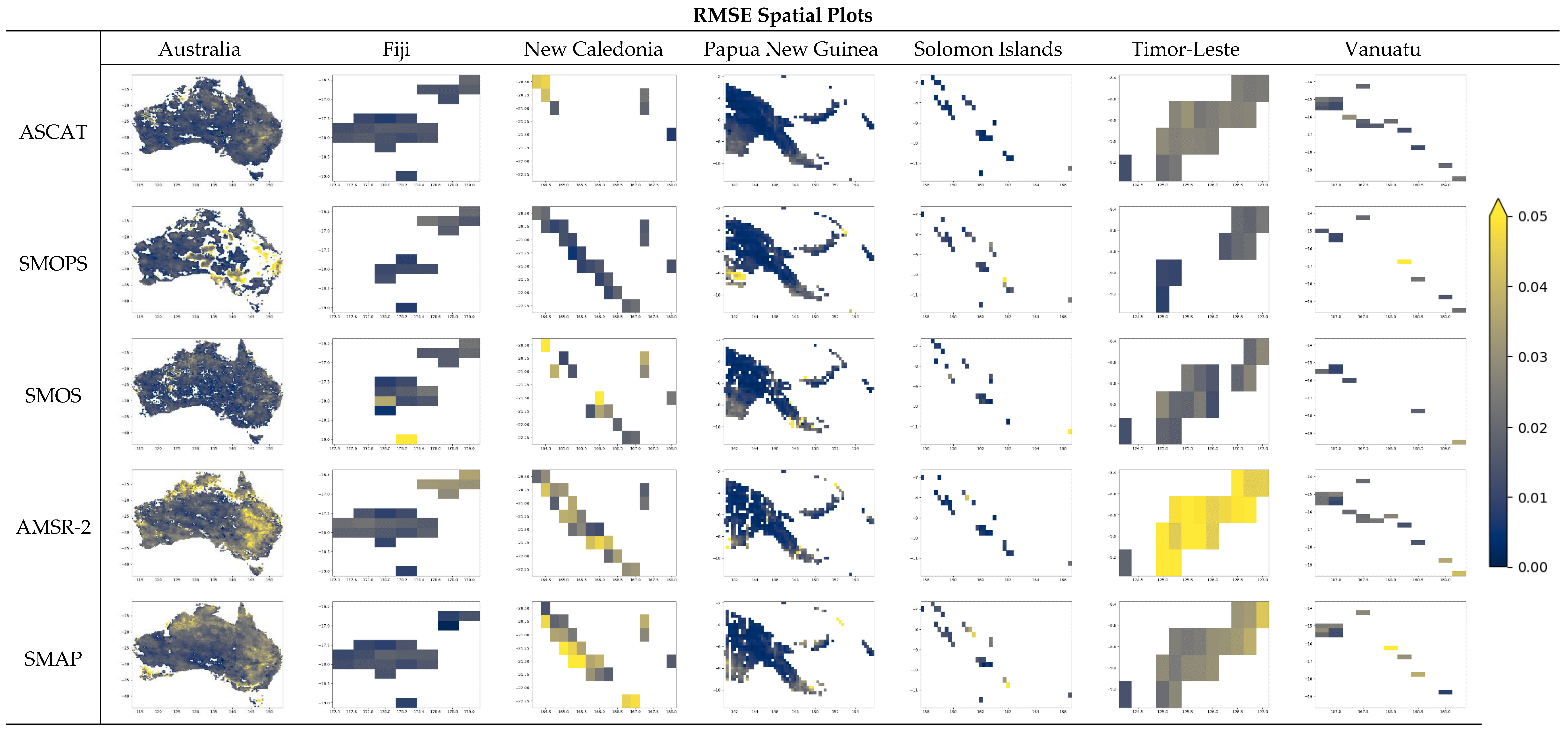
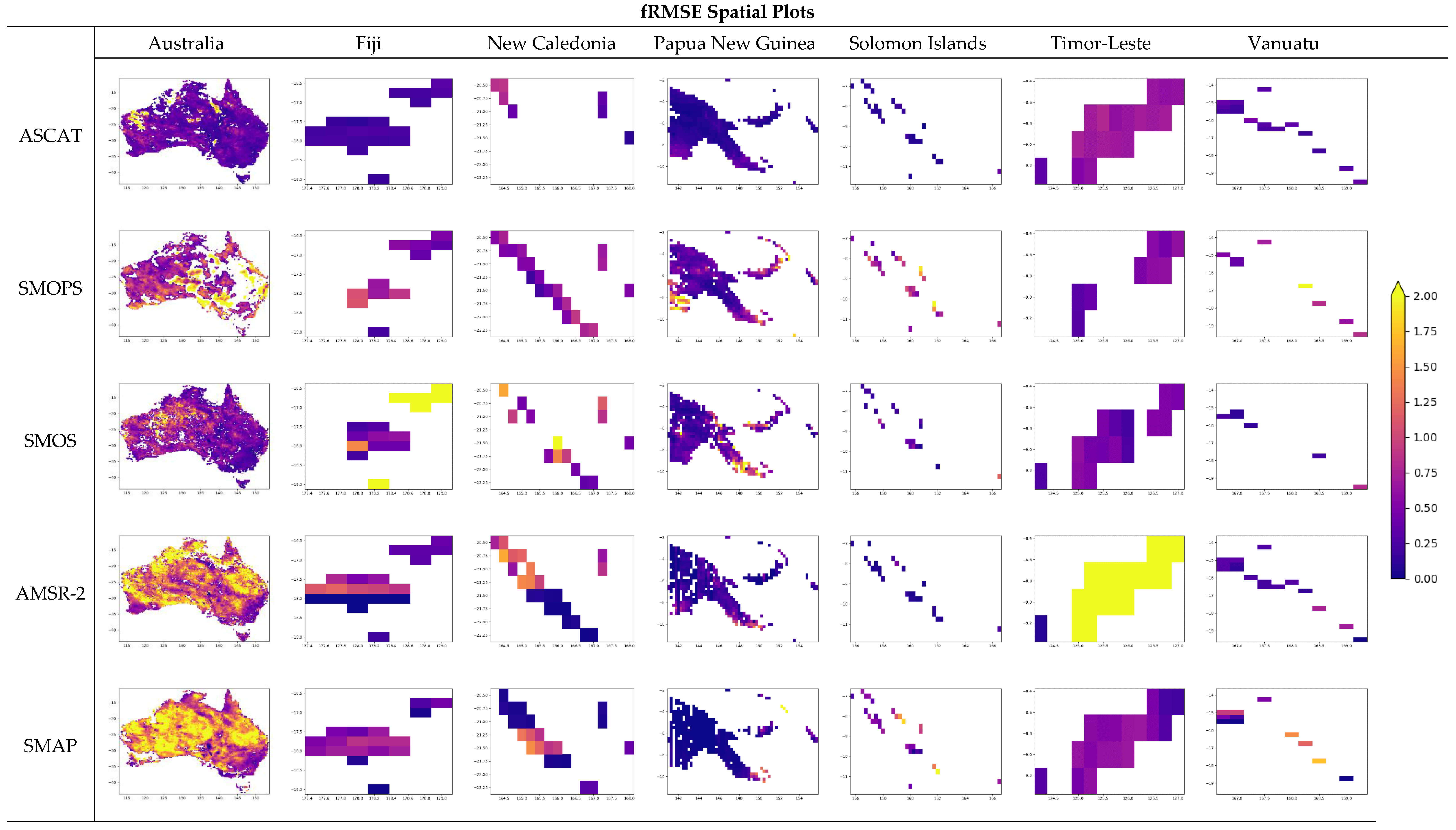
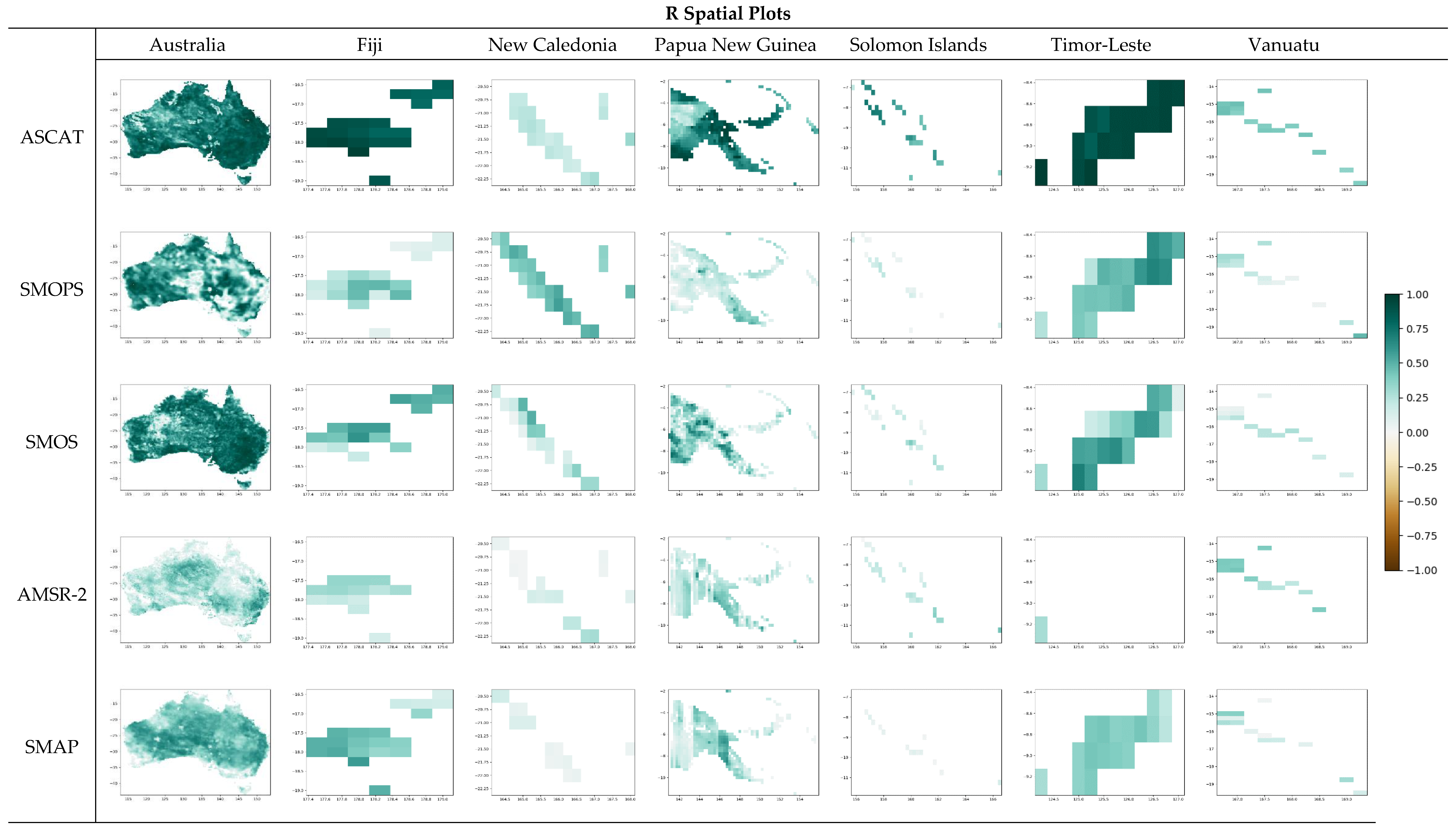
Figure 13 depicts the spatial results for each metric included in the TC analysis. For further details on TC results, consult the table in Appendix B. Spatial plots indicate generally superior performance of ASCAT and SMOS (which is consistent with AWRA-L results). However, it is difficult to consider the best-performing datasets in smaller SIDS. Thus Figure 14 depicts the results of the TC analysis as box-whisker plots categorized by country.
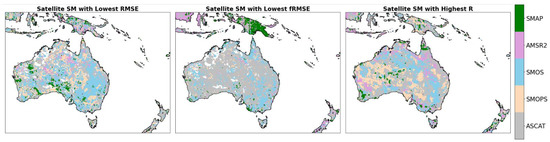
Figure 13.
ASCAT, SMOPS, SMOS, AMSR-2, and SMAP spatially ranked by best performance for RMSE, fRMSE, and R for each grid cell in the study domain.
Figure 14 indicates somewhat varying best-performing satellite SM candidates from country to country. Overall, we note that compared to Australia, satellite SM performance is generally lower for south-west Pacific countries. In Australia, PNG, Solomon Islands, Timor-Leste, and Fiji, ASCAT has stronger median correlational performance (and generally strong RMSE performance). However, unlike Australia, where ASCAT and SMOS generally have similar performance in PNG, Solomon Islands, and Fiji, ASCAT is the sole best-performing candidate. In New Caledonia, SMOPS has the superior median correlational performance. In Vanuatu, results vary, with ASCAT and AMSR-2 having the highest median correlational performance. Of all the SIDS considered here, Vanuatu has many islands with small land sizes. It is also comprised of several atolls and archipelagos, which would only be represented by a small plurality of pixels, if any. This may be contributing to the spread of correlational performance for Vanuatu. Ngridcells for each national sub-domain are included in brackets. We caution readers that our results have the most uncertainty over the smallest islands like Vanuatu. While these results are novel in their evaluation of satellite SM products over this region, we acknowledge the limiting effects of sea water on microwave SM retrieval over land. Even though such small islands may not have the capacity for SM sensor network implementation, even small-scale in situ research activities would contribute greatly to our understanding of microwave SM retrieval in these complex archipelagic regions.
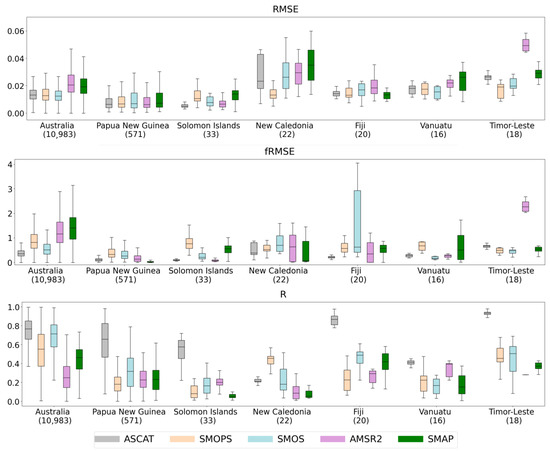
Figure 14.
TC RMSE, fRMSE, and R categorized by country in the study domain—whiskers extend out to show the interquartile range, and the black bar indicates the median value of the distribution. Ngridcells for each sub-domain are indicated in brackets—we caution the impact of sea water on coarse microwave SM land observations for these regions.
3.4. Case Study: Agrometeorological Drought in PNG
In 2015 a compound El Niño and Positive IOD led to severe and extreme drought conditions in PNG. This event had widespread impacts on the nation’s food supply, with drought-related frost prompting crop failure and famine conditions throughout PNG. It was estimated that up to 2.4 million people were affected, and many perished from famine conditions [12,50].
From Figure 14, we note ASCAT to have superior median correlational performance over PNG. Thus we analyze ASCAT SM time series and spatial plots for the onset, duration, and cessation of the 2015 drought period over PNG. Figure 15 plots the time series values of SPI-1-3-6, VHI-1-3-6, and ASCAT SM averaged over all of Papua New Guinea and plotted for the common period between all datasets (2014–2021).
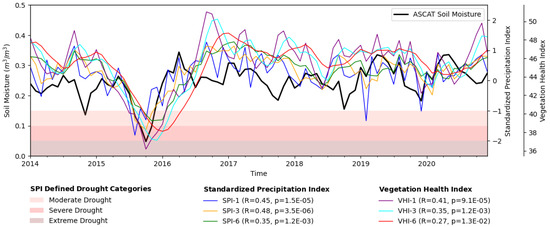
Figure 15.
Drought in Papua New Guinea—SPI 1-3-6, VHI-1-3-6, and ASCAT SM averaged over all PNG and plotted as a time series.
Correlation results between the time series and ASCAT SM are also provided in the legend within Figure 15. ASCAT has significant positive correlations for all SPI and VHI accumulations. For SPI, when averaged over time and over all of PNG, ASCAT SM correlates strongest with the 3-month accumulation, which is consistent with our understanding of the agrometeorological impacts associated with 3-month rainfall deficits. For VHI, ASCAT SM correlates strongest with the 1-month accumulation.
4. Discussion
4.1. Varying Dataset Performance
Our analysis found ASCAT and SMOS to perform consistently well across all analyses and AMSR-2 to be the consistently poorer candidate. SMOS is an L-band radiometer, and several studies note L-band radiometers to be more sensitive to SM retrieval than other bands (e.g., C and X) [2,51,52]. The increased L-band SM sensitivity varies from site to site but is believed to be strongest for vegetated sites as L-band radiometers are less sensitive to surface roughness, soil texture, topography, soil bunk density impacts, and may even have higher canopy penetration capability [2,52]. As a result, several studies acknowledge the high correlational performance of SMOS across the Australian landmass [40,51,53,54,55]. In evaluating SMAP, AMSR-2, and ASCAT over three global in-situ networks, Link et al. (2020) [51] similarly found SMOS to have overall better performance and AMSR-2 to have poor correlational performance over the Yanco stations in the OzNet network with R values 0.6–0.8 and 0.3–0.5 for SMOS and AMSR-2 respectively. They also found that despite ASCAT having high raw correlational performance, it had reduced anomaly correlation performance. However, it is important to note that their analysis was conducted for the Australian Yanco site, which is clustered predominantly in a Grasslands region and could yield varying anomaly results. Anomaly correlation results are not described in detail in our work as high-level anomaly analysis using AWRA-L as truth yielded very similar results. Thus, we maintained raw correlational results for our analysis (Aside from the TC analysis where maintaining raw correlations has potential to violate TC assumptions.), but further investigation could benefit from an in-depth seasonal anomaly investigation of all datasets considered to further validate the trends observed.
While the L-band radiometer, SMOS, performed highly in our analysis, ASCAT had comparable, if not superior, performance at times. Of all five satellite SM datasets analyzed, ASCAT is the only radar-based product. Unlike passive microwave sensors that measure brightness temperatures and derive SM using a radiative transfer model, ASCAT measures backscatter coefficients to derive relative SM content. ASCAT’s slightly superior performance over Australia may be attributed to its noted high sensitivity as an active sensor for detecting SM over sparsely vegetated areas [56]. Additionally, in our gridded analysis, we used AWRA version 6 and note that the BoM’s version 7 of AWRA-L will use ASCAT satellite data assimilation approaches for model output and calibration [57]. While the reason for switching from AMSR-derived calibration to ASCAT-derived calibration is not explicitly clear in AWRA documentation, our analysis, coupled with model evaluation reports, finds ASCAT to be an outperforming satellite SM dataset over Australia (except for desert regions where performance is markedly reduced).
Montzka et al. (2017) [53] evaluated AMSR-2, ASCAT, SMAP, SMOS, and GLDAS over a range of CRP sites in Germany, the USA, Kenya, India, and Australia. For Australia, they considered one station in NSW from the CosmOz network and found the following R values 0.5454 (AMSR-2), 0.7876 (ASCAT), 0.8818 (SMAP), 0.8674 (SMOS), and 0.7514 (GLDAS). They also found ASCAT, SMAP, and SMOS to have a negative bias (~0.05 m3/m3). Our point-based analysis detected the same for ASCAT and SMOS. For ASCAT, they note this underestimation bias may be related to uncertainties in the soil porosity information provided within the ASCAT dataset that is used to convert the degree of saturation SM (%) to volumetric SM (m3/m3) [53].
From our results, we also note that AMSR-2 and SMAP had a competitive performance with point-based data, which could indicate these two datasets may still have the potential to be effective SM detection datasets in Australia but that they have fundamentally different fingerprints than water balance models and reanalysis products which also have their own systematic biases [40]. Additionally, verifying different modelled, in situ, and satellite SM, all with differing depth coverage, also introduces uncertainties in our analysis. AMSR-2 detects SM in the top 10 mm of soil which is the thinnest depth coverage out of all the datasets included in our analysis—it is possible that SM in this skin layer correlates poorly with modelled SM in a larger surface layer.
Holgate et al. (2016) [40] investigated satellite SM and water balance datasets against a range of in situ Australian SM stations. They also found (i) SMAP and AMSR-2 to have moderate-high performance against station data and (ii) that at certain sites, station data correlate only moderately with AWRA-L and other water balance data (R values of 0.58–0.88 for AWRA-L). This is a further indicator of the complexities involved with using water balance and reanalysis SM data as ‘truth’.
4.2. Performance along the Southeast Coast
Our analysis also found decreased bias, RMSE, and R performance along Australia’s mountainous southeast coast. Satellite retrievals have notoriously inconsistent performance over topography [2,58]. In our results, SMOS has insignificant time series correlations, AMSR-2 has unfavorably high RMSE values, and all satellite SM datasets display some biases over this topographical southeast coastal region. Aside from this region’s topographically complex nature, parts of the Victorian and NSW eastern coast are also home to forested land cover types. Satellite SM retrieval algorithms have systematic variation between different climate zones and different land cover types [3]. In our gridded analysis against AWRA-L, satellite SM performance was poorest in Equatorial and Desert regions. Similarly, a comprehensive satellite SM study across different terrain, climate zone, and vegetation cover by Beck et al. (2021) found performance to be poorest in regions of dense vegetation and for cold and arid climates [58].
4.3. Drought Monitoring and Early Warning Implications
We found that across both Australia and the south-west Pacific, more broadly, SMOS and ASCAT had generally superior performance making both datasets a valuable candidate for drought detection in these regions. Raw daily satellite swath passes of ASCAT and SMOS have a latency of 12–24 h and are available from open-source platforms. This increases their appeal for inclusion in drought application in regions where in-situ or modelled SM provision is limited. In our work, building capacity for a drought Early Warning System (EWS) in PNG, we pair satellite monitoring datasets with seasonal forecasts to provide staged categorical warnings for drought at a provincial scale [59]. This drought EWS considers meteorological drought (through the SPI) and agricultural drought (through the VHI). We note that its agrometeorological nature could be made more robust with soil moisture information. Our results from the 2015 case study showed that ASCAT-derived SM could detect the severe drought period with a strong correlation with SPI-3 and VHI-1. This highlights the value of using satellite SM for drought monitoring in this study region. The ability to monitor SM conditions provides a valuable layer of complexity that can be used to accompany drought EWS warnings or even integrated into the EWS thresholds and decision rules. In other SIDS, similar to PNG, where in-situ SM monitoring is limited, drought management and response mechanisms could incorporate satellite SM data (amongst a suite of other inputs) to assist communities in managing drought proactively. Satellite SM data also has significant potential to be coupled with traditional knowledge indicators for local staple and cash crop management [10,60,61]. This is an evolving area of research with minimal exploration yet with significant potential for impact in Pacific communities most at risk from famine, socioeconomic instability, and ecosystem degradation resultant of drought.
5. Conclusions
In regions where in situ SM monitoring capacity is limited, satellite SM products provide a viable alternative to monitoring SM variation. Our study focused on SM use for drought monitoring and evaluated five monthly satellite SM datasets. ASCAT and SMOS performed consistently throughout the point-based, gridded, and TC analysis. On the other hand, AMSR-2 and SMAP were outliers in their gridded and TC performance. Their relatively promising performance compared to point-based data may indicate their systematically different fingerprint to modelled or reanalysis datasets with potential for further research for clarification. The gridded analysis found ASCAT to have superior performance over the Equatorial region of Australia with an average R-value of 0.77 (despite this region being spatially small in Australia). The TC analysis in the south-west Pacific found performance to be reduced across all datasets, albeit with smaller reductions in performance for ASCAT and SMOS, indicating their potential for use in this region. Our case study of a severe drought period in Papua New Guinea found ASCAT SM to be promising in its ability to capture the time-lagged impacts of precipitation deficit, with correlations strongest at the 3-month accumulation for SPI and 1-month accumulation for VHI. The results of this study pose interesting questions about the inclusion of satellite SM for proactive drought monitoring and early warning approaches in Australia and the south-west Pacific, both of which are expected to experience more frequent, intense, and severe droughts resultant of anthropogenic climate change in the future.
Author Contributions
Conceptualization, J.B. and Y.K.; methodology, J.B. and Y.K.; software, J.B. and Z.-W.C.; formal analysis, J.B.; investigation, J.B.; resources, J.B. and Y.K.; data curation, J.B. and Y.K.; writing—original draft preparation, J.B.; writing—review and editing, J.B., Z.-W.C., Y.K., A.B.W., S.C. and Q.S.; visualization, J.B.; supervision, Y.K., S.C. and Q.S.; project administration, Y.K.; funding acquisition, Y.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the World Meteorological Organization through the “Weather and Climate Early Warning System for Papua New Guinea (CREWS-PNG)” project 20170888.
Data Availability Statement
ASCAT data sourced from Integrated Climate Data Centre, (C) EUMETSAT. SMOPS data were sourced from the Space-based Weather and Climate Extremes Monitoring Project. SMOS data were sourced from the Barcelona Expert Centre. AMSR-2 data sourced from NASA Earth Data Centre. SMAP data were sourced from the NASA Earth Data Centre. OzNet data were sourced from https://www.oznet.org.au/, accessed on 6 June 2022. CosmOz data were sourced from https://cosmoz.csiro.au/, accessed on 6 June 2022. OzFlux data were sourced from the OzFlux THREDDS server. AWRA-L data were sourced from BoM. GLDAS data were sourced from NASA Earth Data Centre. ERA5-Land data were sourced from Copernicus Climate Data Store. This study contains modified Copernicus Climate Change ServiceInformation (2019). Neither the European Commission nor ECMWF is responsible for any use that may be made of the Copernicus Information or the data it contains.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Station Metadata
| Probe Type Key: (⊙) CS615/CS616, (❖), CS650, (★) Hydraprobe, (▪) Cosmic Ray Probe | |||||||
| CosmOz | |||||||
| Station | Latitude | Longitude | Elevation (m) | Station | Latitude | Longitude | Elevation (m) |
| Station 2 (Daly) ▪ | −14.16 | 131.39 | 75 | Station 11 (Yanco) ▪ | −35.01 | 146.3 | 124 |
| Station 3 (Gnangara) ▪ | −31.38 | 115.71 | 50 | Station 15 (Hamilton) ▪ | −37.8288 | 142.0895 | 199 |
| Station 6 (Robson) ▪ | −17.12 | 145.63 | 715 | Station 18 (Bishes) ▪ | −35.7694 | 142.9726 | 94 |
| Station 7 (Temora) ▪ | −34.4 | 147.53 | 294 | Station 19 (Bennets) ▪ | −35.8258 | 143.0039 | 98 |
| Station 8 (Tullochgorum) ▪ | −41.67 | 147.91 | 285 | Station 21 (Bullawarrie) ▪ | −28.8093 | 148.7651 | 166 |
| Station 9 (Tumbarumba) ▪ | −35.656 | 148.152 | 1200 | Station 22 (Scotts Peak) ▪ | −43.0418 | 146.337 | 305 |
| Station 10 (Weany) ▪ | −19.88 | 146.54 | 287 | Station 23 (Brigalow C3) ▪ | −24.812 | 149.8012 | 165 |
| OzNet | |||||||
| Station | Latitude | Longitude | Elevation (m) | Station | Latitude | Longitude | Elevation (m) |
| m1 ⊙ | −36.293 | 148.970567 | 937 | YA9 ★ | −34.7414 | 146.15364 | 133 |
| m2 ⊙ | −35.3088 | 149.2 | 639 | YB1 ★ | −34.9412 | 146.27654 | 123 |
| m3 ⊙ | −34.6299 | 148.0365 | 333 | YB3 ★ | −34.9427 | 146.34015 | 126 |
| m4 ⊙ | −33.9383 | 147.196183 | 258 | YB5a ★ | −34.9653 | 146.30262 | 123 |
| m5 ⊙ | −34.6584 | 143.54863 | 62 | YB5b ★ | −34.9634 | 146.31843 | 123 |
| m6 ⊙ | −34.5471 | 144.867 | 90 | YB5d ★ | −34.9848 | 146.29299 | 122 |
| m7 ⊙ | −34.249 | 146.07 | 137 | YB5e ★ | −34.9797 | 146.32052 | 121 |
| y1 ⊙★ | −34.6289 | 145.84895 | 120 | YB7a ★ | −34.9885 | 146.26941 | 126 |
| y2 ⊙★ | −34.6548 | 146.11028 | 130 | YB7c ★ | −34.9984 | 146.27852 | 125 |
| y3 ⊙ | −34.6208 | 146.4239 | 144 | YB7d ★ | −35.005 | 146.2685 | 126 |
| y4 ⊙★ | −34.7194 | 146.02003 | 130 | YB7e ★ | −35.0077 | 146.28805 | 121 |
| y5 ⊙★ | −34.7284 | 146.29317 | 136 | YB9 ★ | −35.0022 | 146.33978 | 121 |
| y6 ⊙★ | −34.8426 | 145.86692 | 121 | a1 ⊙ | −35.4975 | 148.106488 | 772 |
| y7 ⊙★ | −34.8518 | 146.1153 | 128 | a2 ⊙ | −35.4283 | 148.131626 | 595 |
| y8 ⊙★ | −34.847 | 146.41398 | 149 | a3 ⊙ | −35.3997 | 148.101076 | 472 |
| y9 ⊙★ | −34.9678 | 146.01632 | 122 | a4 ⊙ | −35.3731 | 148.066082 | 457 |
| y10 ⊙★ | −35.0054 | 146.30988 | 119 | a5 ⊙ | −35.3602 | 148.085427 | 379 |
| y11 ⊙★ | −35.1098 | 145.93553 | 113 | k1 ⊙ | −35.4932 | 147.55912 | 437 |
| y12 ⊙★ | −35.0696 | 146.16893 | 120 | k2 ⊙ | −35.4353 | 147.53052 | 351 |
| y13 ⊙★ | −35.0903 | 146.30648 | 121 | k3 ⊙ | −35.4341 | 147.56893 | 318 |
| YA1 ★ | −34.6843 | 146.089695 | 131 | k4 ⊙ | −35.4269 | 147.6 | 296 |
| YA3 ★ | −34.6772 | 146.1397 | 132 | k5 ⊙ | −35.4193 | 147.60408 | 306 |
| YA4a ★ | −34.706 | 146.07937 | 131 | k6 ⊙★ | −35.3898 | 147.4572 | 317 |
| YA4b ★ | −34.7031 | 146.10529 | 132 | k7 ⊙★ | −35.3939 | 147.56618 | 259 |
| YA4c ★ | −34.7142 | 146.09425 | 132 | k8 ⊙★ | −35.3163 | 147.34387 | 326 |
| YA4d ★ | −34.7142 | 146.07506 | 130 | k9 ⊙★ | −35.3198 | 147.43633 | 241 |
| YA4e ★ | −34.7214 | 146.10297 | 132 | k10 ⊙★ | −35.324 | 147.5348 | 232 |
| YA5 ★ | −34.7129 | 146.127712 | 132 | k11 ⊙★ | −35.272 | 147.42902 | 327 |
| YA7a ★ | −34.7352 | 146.08197 | 130 | k12 ⊙★ | −35.2275 | 147.485 | 220 |
| YA7b ★ | −34.7378 | 146.09867 | 131 | k13 ⊙★ | −35.2389 | 147.5333 | 261 |
| YA7d ★ | −34.7544 | 146.07777 | 129 | k14 ⊙★ | −35.1249 | 147.4974 | 184 |
| YA7e ★ | −34.7507 | 146.09493 | 131 | ||||
| OzFlux | |||||||
| Station | Latitude | Longitude | Elevation (m) | Station | Latitude | Longitude | Elevation (m) |
| Adelaide River ⊙ | −13.0769 | 131.1178 | 90 | Loxton | −34.4704 | 140.6551 | - |
| Calperum ❖ | −34.0027 | 140.5875 | 65 | Otway ⊙ | −38.525 | 142.81 | 54 |
| Cape Tribulation ⊙ | −16.1032 | 145.4469 | 66 | Red Dirt Melon Farm | −14.5636 | 132.4776 | - |
| Cow Bay ⊙ | −16.2382 | 145.4272 | 86 | Ridgefield ★ | −32.5061 | 116.9668 | 330 |
| Cumberland Plain | −33.6153 | 150.7236 | 23 | Riggs Creek ⊙ | −36.656 | 145.576 | 152 |
| Daly Pasture ⊙ | −17.1507 | 133.3502 | 70 | Robson Creek ⊙ | −17.1175 | 145.6301 | 710 |
| Daly Uncleared ⊙ | −14.1592 | 131.3881 | 110 | Ti Tree East ⊙ | −22.287 | 133.64 | 553 |
| Dry River ⊙ | −15.2588 | 132.3706 | 175 | Tumbarumba | −35.6566 | 148.1516 | 1200 |
| Emerald | −23.8587 | 148.4746 | - | Wallaby Creek ⊙ | −37.4259 | 145.1878 | 600 |
| Fogg Dam ⊙ | −12.5452 | 131.3072 | 4 | Warra ⊙ | −43.095 | 146.6545 | 100 |
| Gingin ⊙ | −31.3764 | 115.7138 | 51 | Whroo ⊙ | −36.6732 | 145.0294 | 165 |
| Great Western Woodlands ⊙ | −30.1914 | 120.6542 | 500 | Wombat State Forest ⊙ | −37.4222 | 144.0944 | 713 |
| Howard Springs ⊙ | −12.4952 | 131.1501 | 64 | Yanco | −34.9878 | 146.2908 | - |
| Litchfield ⊙ | −13.179 | 130.7945 | - | ||||
Appendix B. Detailed TC Results
References
- Heimann, M.; Reichstein, M. Terrestrial Ecosystem Carbon Dynamics and Climate Feedbacks. Nature 2008, 451, 289–292. [Google Scholar] [CrossRef] [PubMed]
- Babaeian, E.; Sadeghi, M.; Jones, S.B.; Montzka, C.; Vereecken, H.; Tuller, M. Ground, Proximal, and Satellite Remote Sensing of Soil Moisture. Rev. Geophys. 2019, 57, 530–616. [Google Scholar] [CrossRef]
- Mohanty, B.P.; Cosh, M.H.; Lakshmi, V.; Montzka, C. Soil Moisture Remote Sensing: State-of-the-Science. Vadose Zone J. 2017, 16, 1–9. [Google Scholar] [CrossRef]
- Wang, L.; Qu, J.J. Satellite Remote Sensing Applications for Surface Soil Moisture Monitoring: A Review. Front. Earth Sci. China 2009, 3, 237–247. [Google Scholar] [CrossRef]
- Gruber, A.; Dorigo, W.A.; Zwieback, S.; Xaver, A.; Wagner, W. Characterizing Coarse-Scale Representativeness of in Situ Soil Moisture Measurements from the International Soil Moisture Network. Vadose Zone J. 2013, 12, 1–16. [Google Scholar] [CrossRef]
- Kim, S.; Zhang, R.; Pham, H.; Sharma, A. A Review of Satellite-Derived Soil Moisture and Its Usage for Flood Estimation. Remote Sens. Earth Syst. Sci. 2019, 2, 225–246. [Google Scholar] [CrossRef]
- Jackson, T.J.; Le Vine, D.M.; Hsu, A.Y.; Oldak, A.; Starks, P.J.; Swift, C.T.; Isham, J.D.; Haken, M. Soil Moisture Mapping at Regional Scales Using Microwave Radiometry: The Southern Great Plains Hydrology Experiment. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2136–2151. [Google Scholar] [CrossRef]
- Kuleshov, Y.; Kurino, T.; Kubota, T.; Tashima, T.; Xie, P. WMO Space-Based Weather and Climate Extremes Monitoring Demonstration Project (SEMDP): First Outcomes of Regional Cooperation on Drought and Heavy Precipitation Monitoring for Australia and Southeast Asia. In Rainfall—Extremes, Distribution and Properties; IntechOpen: London, UK, 2019; ISBN 978-1-78984-734-5. [Google Scholar]
- McGree, S.; Schreider, S.; Kuleshov, Y. Trends and Variability in Droughts in the Pacific Islands and Northeast Australia. J. Clim. 2016, 29, 8377–8397. [Google Scholar] [CrossRef]
- Mcleod, E.; Bruton-Adams, M.; Förster, J.; Franco, C.; Gaines, G.; Gorong, B.; James, R.; Posing-Kulwaum, G.; Tara, M.; Terk, E. Lessons from the Pacific Islands—Adapting to Climate Change by Supporting Social and Ecological Resilience. Front. Mar. Sci. 2019, 6, 289. [Google Scholar] [CrossRef]
- Luchetti, N.T.; Sutton, J.R.P.; Wright, E.E.; Kruk, M.C.; Marra, J.J. When El Niño Rages: How Satellite Data Can Help Water-Stressed Islands. Bull. Am. Meteorol. Soc. 2016, 97, 2249–2255. [Google Scholar] [CrossRef]
- Jacka, J.K. In the Time of Frost: El Niño and the Political Ecology of Vulnerability in Papua New Guinea. Anthropol. Forum 2020, 30, 141–156. [Google Scholar] [CrossRef]
- Murphy, B.F.; Power, S.B.; McGree, S. The Varied Impacts of El Niño–Southern Oscillation on Pacific Island Climates. J. Clim. 2014, 27, 4015–4036. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC); Masson-Delmotte, V.; Zhai, P.; Pirani, A.; Connors, S.L.; Péan, C.; Berger, S.; Caud, N.; Chen, Y.; Goldfarb, L.; et al. Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2021. [Google Scholar]
- Chua, Z.-W.; Kuleshov, Y.; Watkins, A.B. Drought Detection over Papua New Guinea Using Satellite-Derived Products. Remote Sens. 2020, 12, 3859. [Google Scholar] [CrossRef]
- Wild, A.; Chua, Z.-W.; Kuleshov, Y. Evaluation of Satellite Precipitation Estimates over the South West Pacific Region. Remote Sens. 2021, 13, 3929. [Google Scholar] [CrossRef]
- Wimhurst, J.J.; Greene, J.S. Updated Analysis of Gauge-Based Rainfall Patterns over the Western Tropical Pacific Ocean. Weather Clim. Extrem. 2021, 32, 100319. [Google Scholar] [CrossRef]
- Pariyar, S.K.; Keenlyside, N.; Sorteberg, A.; Spengler, T.; Chandra Bhatt, B.; Ogawa, F. Factors Affecting Extreme Rainfall Events in the South Pacific. Weather Clim. Extrem. 2020, 29, 100262. [Google Scholar] [CrossRef]
- Wagner, W.; Lemoine, G.; Rott, H. A Method for Estimating Soil Moisture from ERS Scatterometer and Soil Data. Remote Sens. Environ. 1999, 70, 191–207. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.P.; Delwart, S.; Cabot, F.; Boutin, J.; Escorihuela, M.J.; Font, J.; Reul, N.; Gruhier, C.; et al. The SMOS L: New Tool for Monitoring Key Elements Ofthe Global Water Cycle. Proc. IEEE 2010, 98, 666–687. [Google Scholar] [CrossRef]
- Liu, J.; Zhan, X.; Hain, C.; Yin, J.; Fang, L.; Li, Z.; Zhao, L. NOAA Soil Moisture Operational Product System (SMOPS) and Its Validations. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 3477–3480. [Google Scholar]
- De Jeu, R.; Owe, M.; GES DISC; Teng, B. AMSR2/GCOM-W1 Surface Soil Moisture (LPRM) L3 1 Day 10 Km × 10 Km Descending V001; Goddard Earth Sciences Data and Information Services Center: Greenbelt, MD, USA, 2014.
- O’Neill, P.E.; Chan, S.; Njoku, E.G.; Jackson, T.; Bindlish, R.; Chaubell, J. SMAP L3 Radiometer Global Daily 36 km EASE-Grid Soil Moisture; Version 7; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2020; pp. 1–28.
- Frost, A.J.; Ramchurn, A.; Smith, A. The Australian Landscape Water Balance Model (AWRA-L v6); Technical Description of the Australian Water Resources Assessment Landscape Model Version 6; Bureau of Meteorology Technical Report; Bureau of Meteorology: Melbourne, Australia, 2018.
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The Global Land Data Assimilation System. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Muñoz Sabater, J. ERA5-Land Monthly Averaged Data from 1950 to 1980. Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-land-monthly-means?tab=overview (accessed on 6 June 2022).
- Smith, A.B.; Walker, J.P.; Western, A.W.; Young, R.I.; Ellett, K.M.; Pipunic, R.C.; Grayson, R.B.; Siriwardena, L.; Chiew, F.H.S.; Richter, H. The Murrumbidgee Soil Moisture Monitoring Network Data Set. Water Resour. Res. 2012, 48, W07701. [Google Scholar] [CrossRef]
- Hawdon, A.; McJannet, D.; Wallace, J. Calibration and Correction Procedures for Cosmic-Ray Neutron Soil Moisture Probes Located across Australia. Water Resour. Res. 2014, 50, 5029–5043. [Google Scholar] [CrossRef]
- Beringer, J.; Hutley, L.B.; McHugh, I.; Arndt, S.K.; Campbell, D.; Cleugh, H.A.; Cleverly, J.; De Dios, V.R.; Eamus, D.; Evans, B.; et al. An Introduction to the Australian and New Zealand Flux Tower Network—OzFlux. Biogeosciences 2016, 13, 5895–5916. [Google Scholar] [CrossRef]
- Yuan, X.; Ma, Z.; Pan, M.; Shi, C. Microwave Remote Sensing of Short-Term Droughts during Crop Growing Seasons. Geophys. Res. Lett. 2015, 42, 4394–4401. [Google Scholar] [CrossRef]
- Integrated Climate Data Center (ICDC). Globally Gridded Monthly Mean ASCAT Soil Moisture Maps. 2022. Available online: https://www.fdr.uni-hamburg.de/record/10196 (accessed on 6 June 2022).
- Wu, X.; Lu, G.; Wu, Z.; He, H.; Scanlon, T.; Dorigo, W. Triple Collocation-Based Assessment of Satellite Soil Moisture Products with in Situ Measurements in China: Understanding the Error Sources. Remote Sens. 2020, 12, 2275. [Google Scholar] [CrossRef]
- Molero, B.; Merlin, O.; Malbéteau, Y.; Al Bitar, A.; Cabot, F.; Stefan, V.; Kerr, Y.; Bacon, S.; Cosh, M.H.; Bindlish, R.; et al. SMOS Disaggregated Soil Moisture Product at 1 Km Resolution: Processor Overview and First Validation Results. Remote Sens. Environ. 2016, 180, 361–376. [Google Scholar] [CrossRef]
- Zhan, X.; Liu, J.; Zhao, L. Soil Moisture Operational Product System (SMOPS): Algorithm Theoretical Basis Document—Version 4.0; NOAA NESDIS STAR: Suitland, MD, USA, 2016.
- Pablos, M.; González-Haro, C.; Piles, M.; BEC Team. BEC SMOS Soil Moisture Products Description (V. 1.0). 2020. Available online: https://bec.icm.csic.es/data/available-products/#SoilMoisture (accessed on 6 June 2022).
- Owe, M.; de Jeu, R.; Holmes, T. Multisensor Historical Climatology of Satellite-Derived Global Land Surface Moisture. J. Geophys. Res. Earth Surf. 2008, 113. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, J.; Chen, Y.; De Maeyer, P.; Li, Z.; Duan, W. Detecting the Causal Effect of Soil Moisture on Precipitation Using Convergent Cross Mapping. Sci. Rep. 2018, 8, 12171. [Google Scholar] [CrossRef]
- Mousa, B.G.; Shu, H. Spatial Evaluation and Assimilation of SMAP, SMOS, and ASCAT Satellite Soil Moisture Products Over Africa Using Statistical Techniques. Earth Sp. Sci. 2020, 7, e2019EA000841. [Google Scholar] [CrossRef]
- Bureau of Meteorology Climate Classification Maps (Köppen—Major Classes). Available online: http://www.bom.gov.au/jsp/ncc/climate_averages/climate-classifications/index.jsp?maptype=kpngrp#maps (accessed on 6 June 2022).
- Holgate, C.M.; De Jeu, R.A.M.; van Dijk, A.I.J.M.; Liu, Y.Y.; Renzullo, L.J.; Vinodkumar; Dharssi, I.; Parinussa, R.M.; Van Der Schalie, R.; Gevaert, A.; et al. Comparison of Remotely Sensed and Modelled Soil Moisture Data Sets across Australia. Remote Sens. Environ. 2016, 186, 479–500. [Google Scholar] [CrossRef]
- Scipal, K.; Holmes, T.; De Jeu, R.; Naeimi, V.; Wagner, W. A Possible Solution for the Problem of Estimating the Error Structure of Global Soil Moisture Data Sets. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Stoffelen, A. Toward the True Near-Surface Wind Speed: Error Modeling and Calibration Using Triple Collocation. J. Geophys. Res. Ocean. 1998, 103, 7755–7766. [Google Scholar] [CrossRef]
- Draper, C.; Reichle, R.; de Jeu, R.; Naeimi, V.; Parinussa, R.; Wagner, W. Estimating Root Mean Square Errors in Remotely Sensed Soil Moisture over Continental Scale Domains. Remote Sens. Environ. 2013, 137, 288–298. [Google Scholar] [CrossRef]
- McColl, K.A.; Vogelzang, J.; Konings, A.G.; Entekhabi, D.; Piles, M.; Stoffelen, A. Extended Triple Collocation: Estimating Errors and Correlation Coefficients with Respect to an Unknown Target. Geophys. Res. Lett. 2014, 41, 6229–6236. [Google Scholar] [CrossRef]
- Ming, W.; Ji, X.; Zhang, M.; Li, Y.; Liu, C.; Wang, Y.; Li, J. A Hybrid Triple Collocation-Deep Learning Approach for Improving Soil Moisture Estimation from Satellite and Model-Based Data. Remote Sens. 2022, 14, 1744. [Google Scholar] [CrossRef]
- NOAA National Geophysical Data Center. ETOPO1 1 Arc-Minute Global Relief Model; NOAA National Centers for Environmental Information: Asheville, NC, USA, 2009. [CrossRef]
- National Aeronautics and Space Administration (NASA). How Can I Obtain Volumetric Soil Moisture [M3 m−3] from the LDAS Data? Available online: https://ldas.gsfc.nasa.gov/faq/LDAS#:~:text=To convert to units of,%5Bkg m-3%5D (accessed on 6 June 2022).
- McKee, T.B. Drought Monitoring with Multiple Time Scales. In Proceedings of the 9th Conference on Applied Climatology, Boston, MA, USA, 15–20 January 1995. [Google Scholar]
- Kogan, F.N. Droughts of the Late 1980s in the United States as Derived from NOAA Polar-Orbiting Satellite Data. Bull.-Am. Meteorol. Soc. 1995, 76, 655–668. [Google Scholar] [CrossRef]
- Schmidt, E.; Gilbert, R.; Holtemeyer, B.; Mahrt, K. Poverty Analysis in the Lowlands of Papua New Guinea Underscores Climate Vulnerability and Need for Income Flexibility. Aust. J. Agric. Resour. Econ. 2021, 65, 171–191. [Google Scholar] [CrossRef]
- Link, M.; Drusch, M.; Scipal, K. Soil Moisture Information Content in SMOS, SMAP, AMSR2, and ASCAT Level-1 Data over Selected in Situ Sites. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1213–1217. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Richaume, P.; Wigneron, J.P.; Ferrazzoli, P.; Mahmoodi, A.; Al Bitar, A.; Cabot, F.; Gruhier, C.; Juglea, S.E.; et al. The SMOS Soil Moisture Retrieval Algorithm. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1384–1403. [Google Scholar] [CrossRef]
- Montzka, C.; Bogena, H.R.; Zreda, M.; Monerris, A.; Morrison, R.; Muddu, S.; Vereecken, H. Validation of Spaceborne and Modelled Surface Soil Moisture Products with Cosmic-Ray Neutron Probes. Remote Sens. 2017, 9, 103. [Google Scholar] [CrossRef]
- Su, C.H.; Zhang, J.; Gruber, A.; Parinussa, R.; Ryu, D.; Crow, W.T.; Wagner, W. Error Decomposition of Nine Passive and Active Microwave Satellite Soil Moisture Data Sets over Australia. Remote Sens. Environ. 2016, 182, 128–140. [Google Scholar] [CrossRef]
- Albergel, C.; de Rosnay, P.; Gruhier, C.; Muñoz-Sabater, J.; Hasenauer, S.; Isaksen, L.; Kerr, Y.; Wagner, W. Evaluation of Remotely Sensed and Modelled Soil Moisture Products Using Global Ground-Based in Situ Observations. Remote Sens. Environ. 2012, 118, 215–226. [Google Scholar] [CrossRef]
- Wagner, W.; Hahn, S.; Kidd, R.; Melzer, T.; Bartalis, Z.; Hasenauer, S.; Figa-Saldaña, J.; De Rosnay, P.; Jann, A.; Schneider, S.; et al. The ASCAT Soil Moisture Product: A Review of Its Specifications, Validation Results, and Emerging Applications. Meteorol. Z. 2013, 22, 5–33. [Google Scholar] [CrossRef]
- Frost, A.J.; Shokri, A. The Australian Landscape Water Balance Model (AWRA-L v7); Technical Description of the Australian Water Resources Assessment Landscape Model Version 7; Bureau of Meteorology: Melbourne, Australia, 2021.
- Beck, H.E.; Pan, M.; Miralles, D.G.; Reichle, R.H.; Dorigo, W.A.; Hahn, S.; Sheffield, J.; Karthikeyan, L.; Balsamo, G.; Parinussa, R.M.; et al. Evaluation of 18 Satellite—And Model-Based Soil Moisture Products Using in Situ Measurements from 826 Sensors. Hydrol. Earth Syst. Sci. 2021, 25, 17–40. [Google Scholar] [CrossRef]
- Bhardwaj, J.; Kuleshov, Y.; Chua, Z.-W.; Watkins, A.B.; Choy, S.; Sun, Q. Building Capacity for a User-Centred Integrated Early Warning System for Drought in Papua New Guinea. Remote Sens. 2021, 13, 3307. [Google Scholar] [CrossRef]
- Ilan, K.; Jessica, M.; Gaillard, J.C. Indigenous Knowledge and Disaster Risk Reduction. Geography 2012, 97, 12–21. [Google Scholar] [CrossRef]
- Granderson, A.A. The Role of Traditional Knowledge in Building Adaptive Capacity for Climate Change: Perspectives from Vanuatu. Weather. Clim. Soc. 2017, 9, 545–561. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).