Abstract
The elastic response of solid earth to glacier and ice sheet melting, the most important consequences of climate change, is a contemporaneous uplift. Here, we use interferometric synthetic aperture radar (InSAR) measurements to detect crustal deformation and mass loss near the Helheim glacier, one of the largest glaciers in southeastern Greenland. The InSAR time series of Sentinel-1 data between April 2016 and July 2020 suggest that there is a maximum cumulative displacement of ~6 cm in the line of sight (LOS) direction from the satellite to the ground near Helheim. We use an exponentially decreasing model of the thinning rate, which assumes that the mass loss starts at the lower-elevation terminal region of the glacier and continues to the higher-elevation interior. A linear inversion of the derived crustal uplift in the vicinity of bedrock using this model for surface loading in an elastic half-space suggests a mass loss of 8.33 Gt/year, which agrees with the results from other studies.
1. Introduction
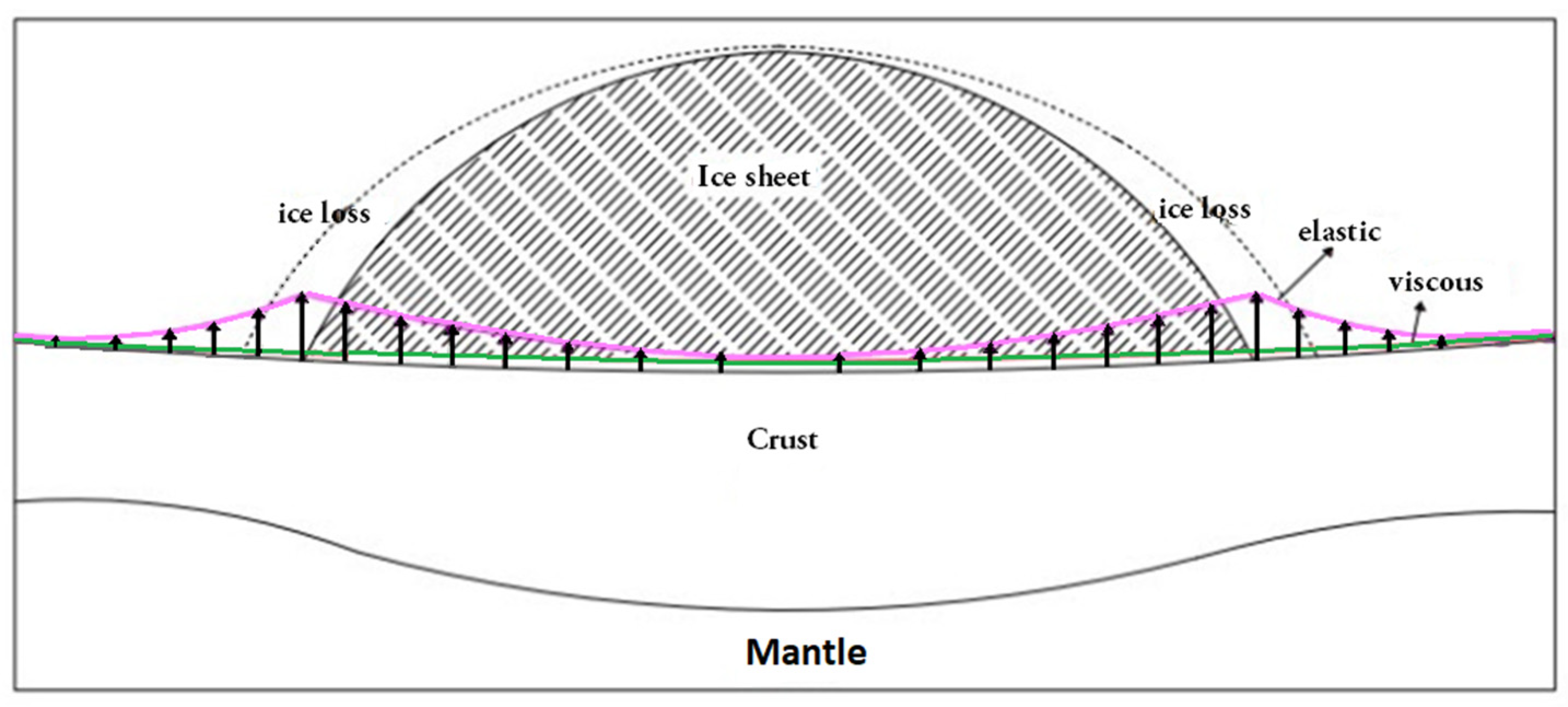
The balance of ice mass in glaciers, ice caps, and ice sheets is a very important issue associated with global climate change. Several studies have indicated rapid ice melting in Greenland over the last two decades [1,2,3,4]. The total volume of ice melting raises the global mean sea level at a rate of approximately 0.7–1.8 mm/year [5,6], which likely will increase in the future due to further global warming. The solid earth beneath glaciers is under the pressure of ice accumulation and ice melting. The response of the ground to current and past ice mass loss is an uplift signal, which consists of two components: (1) an instantaneous elastic component, and (2) a delayed viscous component (Figure 1) [7,8,9].
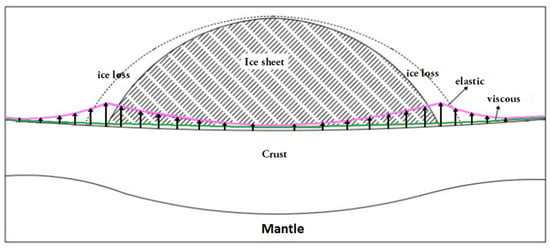
Figure 1.
Earth response to the discharge. The magenta line represents the contemporaneous elastic response due to the current ice loss and the green line represents the long-term viscous response due to the prior ice melting.
The elastic component indicates current uplift in response to the existing melting. The viscous component, on the other hand, is the response to deglaciation of the Pleistocene ice sheets that occupied a significant proportion of the Northern Hemisphere, and the advance and retreat cycles of the Antarctic and Greenland ice sheets since the Last Glacial Maximum (LGM) approximately 20,000 years ago [10]. The viscous component is related to flow in the mantle, more than 40 km below the surface, above which the lithosphere behaves like an elastically bending plate, resulting in displacements at wavelengths of several hundred kilometers [11]. To interpret ground deformation with respect to mass balance, it is essential to separate these spatial and temporal components (Figure 1).
Space geodetic techniques provide important observations for estimating ice mass balance. For example, laser and radar altimetry [2], space gravimetry [12], global navigation satellite system (GNSS) [13], and InSAR [14,15] have been used to resolve ice mass balance for glaciers, ice caps, and ice sheets in regions that cannot be easily accessed. The integration of such space geodetic techniques with ice thickness data and regional models can be used to estimate changes in mass balance [16,17].
Given the global availability of suitable SAR data derived from various national and international missions, spaceborne differential interferometric synthetic aperture radar (DInSAR) allows high-density measurements of surface deformation over large areas by combining the information from two SAR radar images acquired from approximately the same position in space over a length of time. DInSAR has been utilized for a variety of applications, such as volcanoes [18,19], earthquakes [20,21], landslides [22,23,24,25], surface subsidence due to groundwater pumping [26,27,28], glacier kinematics and surface unloading [29,30], and infrastructure monitoring [31,32,33,34].
The ability of DInSAR to measure large gradient displacements is limited due to problems arising from phase unwrapping [35], for which other techniques such as offset tracking can be used [36,37]. Furthermore, DInSAR fails if coherence, a measure of the radar reflection between two SAR observations, is lost due to, e.g., vegetation and snow cover [38]. Additionally, atmospheric artifacts can seriously affect the accuracy of DInSAR measurements, particularly if the rate of deformation is small (few cm/year—mm/year). To overcome such limitations, multiple interferograms using a stack of SAR acquisitions are generated and analyzed using InSAR time series techniques to obtain a time series of surface deformation. This approach is known as multi-temporal InSAR (MT-InSAR), which can be divided into three main categories: (1) persistent scatterer InSAR (PSI or PSInSAR), focusing on permanent/persistent scatterers (PS) defined as individual pixels with stable scattering properties over time, (2) small baseline subset, or SBAS, focusing on distributed scatterers (DS) defined as pixels whose neighboring pixels share similar statistical behavior [39], and (3) combined MT-InSAR methods that incorporate information from both PS and DS [40,41,42].
The InSAR-based measurements from older SAR missions such as ERS and Envisat presented a major challenge for assessing the elastic response to ice sheet melting due to their small temporal resolution, i.e., their sampling intervals of several weeks. This disadvantage has been improved with the launch of the Sentinel-1A satellite in 2014 and the Sentinel-1B in 2016, providing a repeat cycle of 6 days over Europe and 12 days for the rest of the world [43]. Sentinel-1 has four operational modes (SM, IW, EW, and WV). Interferometric wide swath (IW) is its main operational mode over land, featuring data products in single (HH or VV) or double (HH plus HV or VV plus VH) polarization at 5 20 m spatial resolution and a 250 km swath. Sentinel-1 SAR images are free and available for all users around the world [43].
Since the early 1990s, the Greenland ice sheet has experienced an increase in mass loss. Space geodetic techniques such as satellite altimetry [44,45,46], satellite gravity anomaly experiments [47,48,49], and flux-balance calculations [14,16] reveal an increase in the mass loss rate between 1992 and 2011. Recently, the observations from the CryoSat-2 altimeter have demonstrated that the volume loss rates for the period 2011–2014 were 2.5 times greater than those for the period 2003–2009 [50]. The rapid unloading of ice from southeastern Greenland has caused an elastic uplift of ~16 mm/year at a GPS site on the Helheim glacier between 2001 and 2006 [1].
This study is one of the few to use SAR data from the more recent Sentinel-1 satellite to assess ice-unloading-induced deformations at rocky outcrops near glaciers. Previous studies such as Liu et al. (2012), Auriac et al. (2013) [51], or Zhao et al. (2014) all predated the Sentinel-1 era: Liu et al. (2012) used RADARSAT-1 SAR data to measure elastic crustal uplift in west Greenland, Auriac et al. (2013) utilized ERS-1, ERS2 and Envisat SAR data to constrain uplift of the ground all the way up to the edge of the largest ice cap in Iceland, and Zhao et al. (2014) used C-band ERS imagery and the SBAS method for measuring the contemporaneous deformation in Iceland.
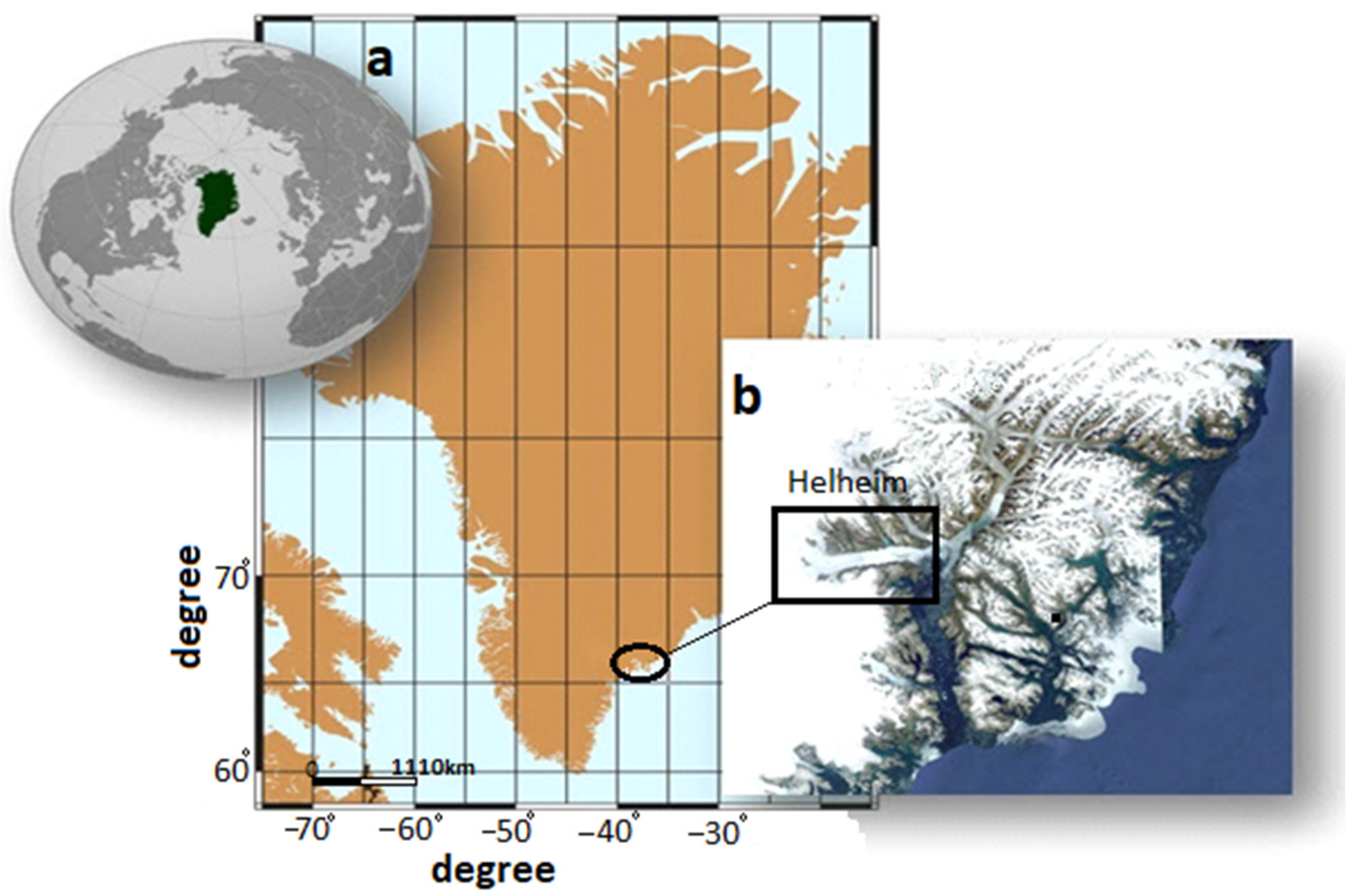
In this paper, we use the latest archive of Sentinel-1 to assess the contemporaneous displacement due to mass loss at the Helheim glacier, one of the largest glaciers in southeastern Greenland [66.5°N, 38°W] (Figure 2). Previous studies suggest that the rate of thinning of the Helheim glacier has not been constant in the last two decades. For example, Stearns et al. (2007) [52] analyzed sequential digital elevation models (DEMs) and showed that the thinning rate was 44 ± 21 mm/year between 2002–2003, 15 ± 21 mm/year between 2003–2004, 60 ± 13 mm/year between 2004–2005, and 7 ± 21 mm/year between 2005–2006. Using optical and SAR remote sensing data analysis, Bevan et al. (2012) [53] suggested a greater glacier discharge of the Helheim glacier since the mid-1990s. In this research, multi-temporal InSAR (MT-InSAR) analysis using the SBAS method is carried out to constrain the spatial and temporal pattern of the thinning rate for the period 2016–2020. The thinning rate is calculated by an exponential decreasing model which assumes the mass loss begins from the lower-elevation near the edge of glacier towards the higher-elevation interior and by a linear inversion-derived surface loading in an elastic half-space.
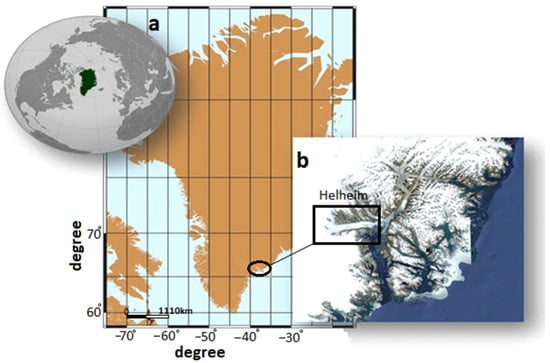
Figure 2.
(a) Helheim glacier located in the southeast of Greenland, which is one of the important glaciers in Greenland under dramatic ice melting in the last two decades. The black square in (b) shows the study area. (b) A close-up view of the study area (circle in (a)) from Google Earth.
2. Materials and Methods
2.1. Interferometric Analysis of Crustal Uplift
For the MT-InSAR analysis, we used GMTSAR software and the SBAS technique. The interferometric processing in GMTSAR comprises three major elements: (1) a pre-processor for each type of satellite data to convert the native format and orbital data into a generic form; (2) an InSAR processor to coregister a stack of images and convert topography into phase; and (3) a post-processor built on GMT [54,55], which is used for filtering interferograms and creating interferometric products such as coherence and line-of-sight displacement in both geographic and radar coordinates. The small baseline subset (SBAS) technique [39] was utilized as implemented in GMTSAR software [56] to observe the temporal and spatial changes in crustal deformation around the Helheim glacier. The SBAS technique uses all interferometric pairs with short baselines, either in temporal or spatial terms, to estimate the unknown deformation at each acquisition time. Including a large number of interferometric pairs in SBAS time series analysis, on one hand, reduces temporary uncorrelated effects caused by the atmosphere or decorrelation noises; on the other hand, this approach increases the density of measurement points on the resultant displacement maps [39,57,58].
Our study area was well covered by SAR images from Sentinel-1A that were collected in the 5 years from April 2016 to July 2020. In glacial regions, acquisitions in seasons with less snowfall are more suited for interferometric processing than those in other seasons due to snow cover that causes significant signal decorrelation in C-band interferograms. We used 73 SLC images in IW mode that were acquired in a descending track (path 112 and frame 370). We did not use ascending track images as all of them were acquired in winter (the last days of December to the beginning of February), hindering us from making a reliable network for SBAS analysis. Excluding the winter images leads to missing the elastic response of the earth due to the snow load collected in winter, and makes it impossible to identify the seasonal signal.
We used HH polarization data, which have a higher signal-to-noise ratio. Unwrapping of the differential interferograms was performed using the Snaphu technique [59]. We adapted a multilooking factor of 16 4 in range and azimuth to further suppress the noise and improve the efficiency of phase unwrapping. We used 2 by 2 m elevation cells for topography phase correction and geocoding. These cells were designed by the National Science Geospatial-intelligence Agency (NGA) and the National Science Foundation (NSF) public-private initiative, and they automatically produce a high-resolution, high-quality digital surface model (DSM) of the Arctic (ArcticDEM).
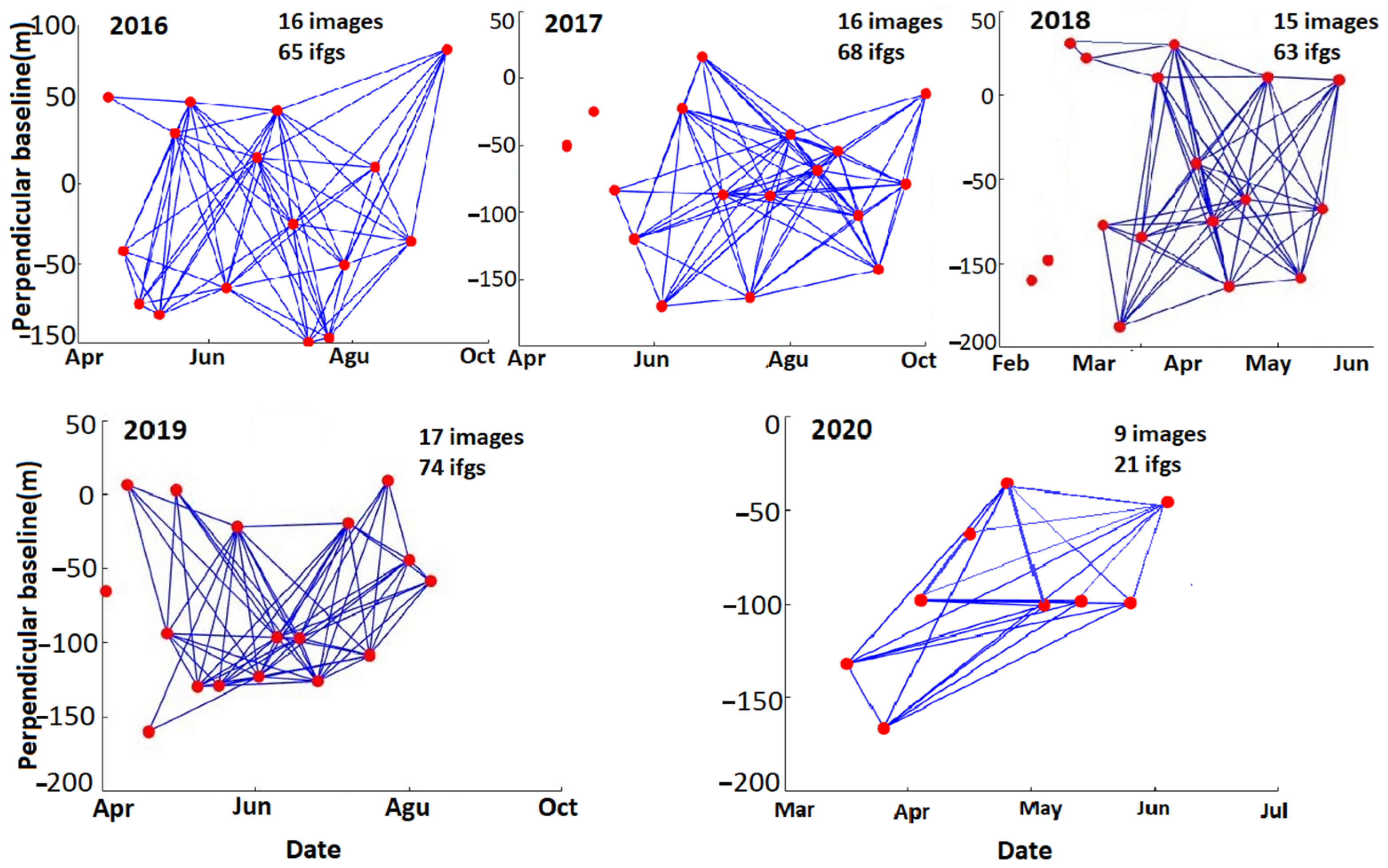
For the SBAS analysis, we focused on interferograms with small perpendicular and temporal baselines (<150 m and 150 days) to ensure that errors imposed by topography and temporal decorrelation remained small, and we minimized orbital gradients across the interferograms by utilizing coherent data from the entire SAR frame to flatten the phase. A coherence threshold of 0.3 was used to select reliable pixels as measurement points after phase unwrapping. To minimize the effect of temporal decorrelation caused by interferograms covering the winter seasons, the time period has been divided into five phases, each covering a different summer season. The networks of each year are shown in Figure 3; interferograms with low quality were excluded from the networks before the least-squares inversion.
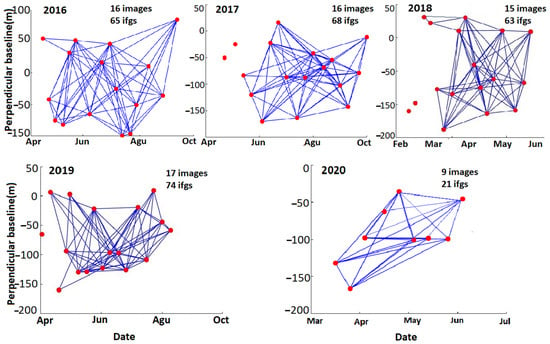
Figure 3.
The SBAS networks for the five summer periods analyzed in this study years. The red circles are the SAR acquisitions and the blue lines illustrate the interferograms.
Usually, orbital errors appear as a large extended signal, formed like a ramp that does not affect local deformations and cannot be mistakenly interpreted as a deformation signal. Fattahi and Amelung (2014) [60] showed that for Sentinel-1, the range uncertainty depends on the magnitude of the orbital errors, about 0.2 mm/year per 100 km, and the azimuth uncertainty is about 0.5 mm/year per 100 km. We used precise orbital determination (POD) data from ESA (https://scihub.copernicus.eu/gnss) (accessed on 29 August 2020) to filter out orbital errors from the interferograms.
The stratified atmospheric delay is a major error source in the SBAS time series analysis which is computed in GMTSAR by a method that uses a common point stacking technique to estimate the delays in the radar phase induced by propagation through the atmosphere [61]. It is worth noting that at high latitudes, it is possible for InSAR measurements to also be influenced by ionospheric disturbances. However, this effect is usually insignificant for C-band data [50,62] and appears as a ramp in high latitudes such as Greenland (https://iono.jpl.nasa.gov) (accessed on 24 May 2020). Accordingly, we estimated this effect by fitting a first order polynomial to the interferograms during the SBAS analysis. The set of small baseline interferograms were finally translated into a range-change time series that describes the time-dependent surface deformation by a least-squares inversion [63].
2.2. Ice Mass Loss Modeling
Ice melting in glaciers results in unloading that causes crustal uplift due to the viscoelastic deformation of the Earth’s crust and mantle. The viscous component is a long-wavelength phase contribution to glacial rebound and needs many years of observations to be determined due to its rather small uplift rate. Thus, for a short period of time such as the one considered in this paper, the viscous effect is very small and was ignored in our analysis.
To model the surface displacements observed by the MT-InSAR measurements, we use a model developed by Zhao et al. [30]. The model assumes a unit point mass in elastic half-space cylindrical coordinates with axial symmetry [30,64], as follows:
where is the vertical and is the radial displacement, ϑ is the Poisson’s ratio, is the gravitational acceleration, is the distance from the point source, and is the Young modulus. Under the assumption that the mass loss rate remains constant with time, it is possible to use velocities instead of displacements in Equations (2) and (3). As the trend of ice melting decreases from the edge of the glacier to the internal parts, an exponential decay function to describe the thinning rate in the margin of the glacier is considered [30]:
where is the thinning rate, is the decay factor, indicates the thinning rate of the inland portion (away from the ice edge), denotes distance from the ice edge, and is the thinning rate of the ice edge (). A negative means ice accumulation at an area away from the ice edge. In an attempt to extend this one-dimensional model (Equation (3)) into a two-dimensional model, the load change (Equations (1) and (2)) is split into a series of square blocks and the displacement rate is computed for each block. In the next step, solutions for all blocks are added as follows [65]:
where stands for displacement, and the vertical, north, and east directions are depicted by the superscripts , , and , respectively. indicates the distance of an ice block from the ice edge for i = 1…, ( is the number of blocks), is the ice density, denotes the block dimension, and represents the distance of point load from observation point with = 1, 2, …, ( indicates the number of observations). For a given , a linear system of equations can be constructed as follows:
where is the vector of observation velocities (LOS), is the vector of model parameters (the unknown parameters and ), and is the design matrix of the equation system, which acts as a mapping function. The -th line of reveals mapping of the mass loss rate onto the -th velocity field [30]. This system of equations has more equations than variables and is an overdetermined system of linear equations that can be solved using the least squares technique [66]:
where is the model standard error of the th ice block and is the standard error of the th velocity field. in Equation (6) is constructed from the two matrices of and as follows:
where B is a matrix generated from Equations (4) and (5) in which the first columns correspond to the vertical component of displacement, the second columns correspond to the east component, and the third columns correspond to the north component. , , and contain the mapping parameters from the three-dimensional velocities to LOS direction, is the looking angle of the satellite, is the incidence angle, and is a matrix for the thinning model parameters. The mass loss estimated by this approach is reasonable for glaciers with exponential thinning from the edge of glaciers towards the interior of glaciers. Therefore, a thickness reduction of the load points that are estimated by the model is multiplied the area and ice density to find the mass loss volume and ice mass loss, respectively. The modeling approach discussed above was implemented in an in-house Matlab code.
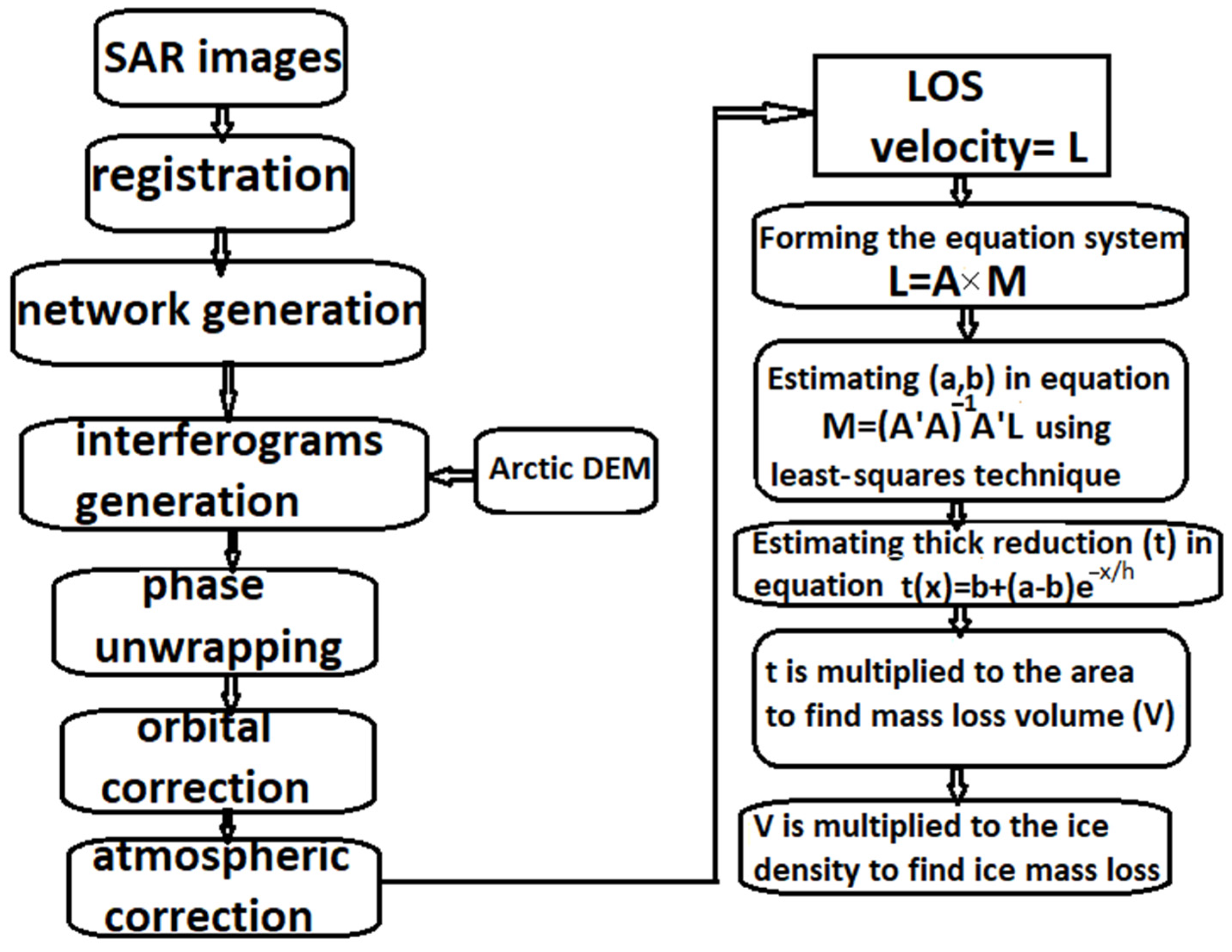
The overall flowchart of the InSAR processing and model development is illustrated in Figure 4.
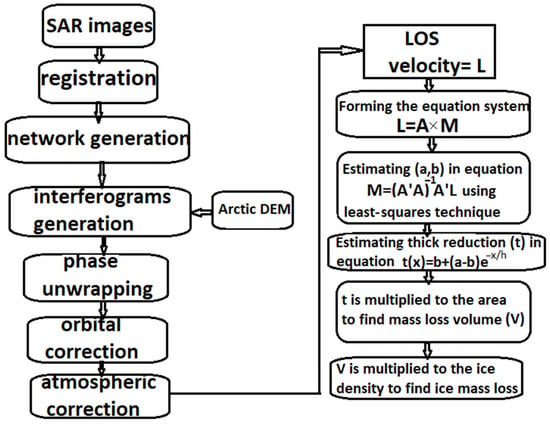
Figure 4.
Flowchart of the InSAR processing and model development.
2.3. Auxiliary Data
To investigate the relation between the local land surface temperature (LST) on the ice mass loss in the study area, we used LST data from Moderate Resolution Imaging Spectroradiometer (MODIS). MODIS is a sensor operating on the Terra and Aqua satellites, which were launched by NASA in December 1999 and May 2002, respectively. It helps scientists to determine the amount of water vapor in a column of the atmosphere and the vertical distribution of temperature and water vapor, measurements that are crucial to understanding Earth’s climate system. The MODIS Land Surface Temperature and Emissivity weekly data (MOD11C2) in the study area are collected for the time span of InSAR observations, and the LST measurements were extracted at a 1 km resolution to use them as local land surface temperature data.
3. Results
3.1. InSAR Velocity Field
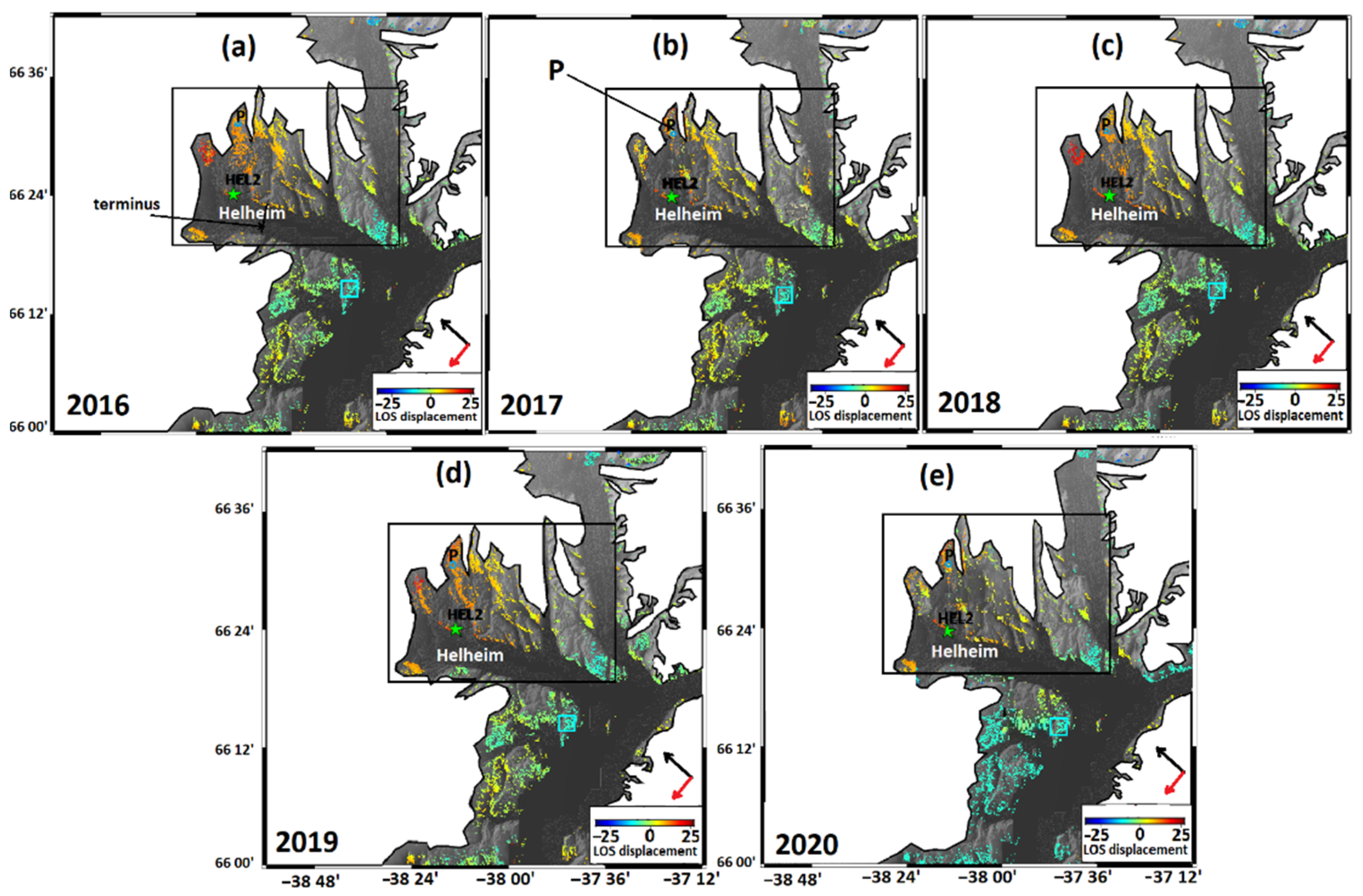
Figure 5 shows the LOS displacements resulting from the SBAS analysis for the five summer seasons between 2016 and 2020. Although the area is glacial and rugged and snow and ice cover reduce the coherence of the interferograms, InSAR has been able to show a clear signal of deformation. All five plots in Figure 5a–e show a 15–25 wide yellow-red area in the northern flank of the Helheim glacier, illustrating uplift in an LOS direction. The rate of uplift, however, is not constant. The maximum rates of approximately 18 mm/year occurred in the summer 2019 at the edge of the ice sheet in the northern flank of the Helheim glacier. The average standard error of the LOS velocity fields is 0.59 mm/year, following Zhao et al. [30], which was calculated in a non-deforming area by using the velocity of the points in that area, as shown by the cyan rectangle in Figure 5a–e, and then was averaging it as a standard error for all the LOS velocity fields.
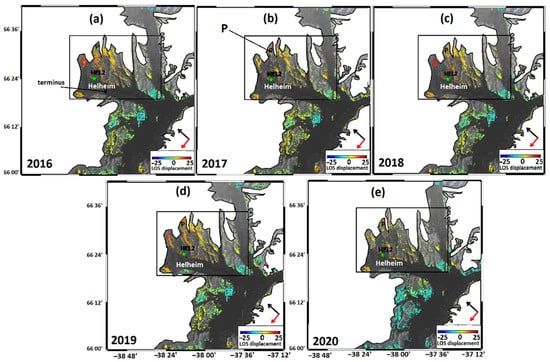
Figure 5.
(a–e) LOS displacements around Helheim for the five observation periods. The blue circle P is a point near the ice edge. The black rectangle is the region that shows uplift and is chosen as the study area. The white area is an ice sheet. The cyan rectangle shows a non-deforming region. The black and red arrows show the LOS and flight directions, respectively. The green star shows GPS permanent station Hel2.
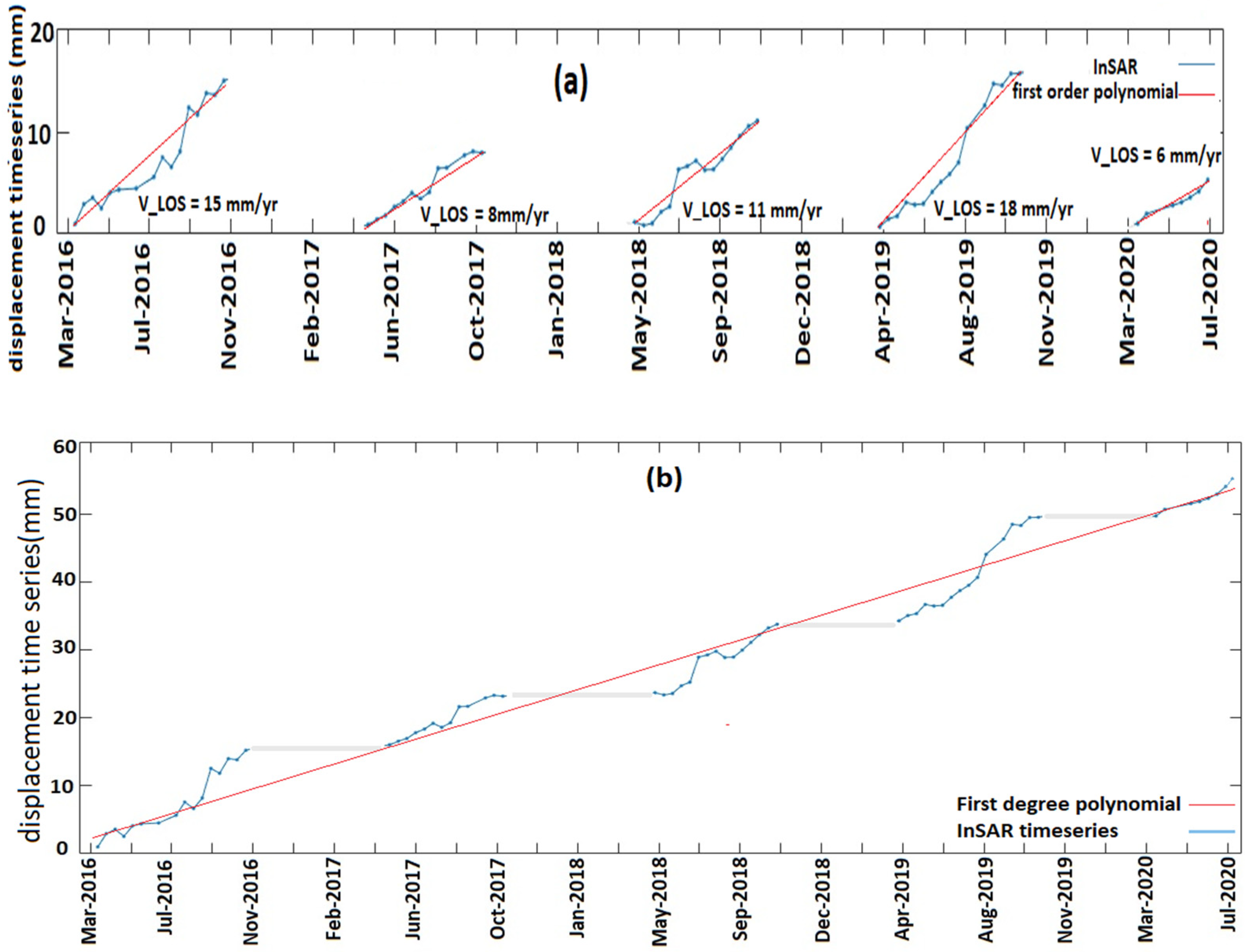
To better illustrate the temporal behavior of the displacement field, we selected a point (P) near the ice edge and plotted its LOS time series for all five periods. The velocity of the point was estimated using a linear regression (a constant velocity at each period). As illustrated in Figure 6a, point P shows uplift with a rate of 15 mm/year in summer 2016, decreasing by up to 46% and 26% in 2017 and 2018, respectively, and increasing again by 20% to 18 mm/year in summer 2019. The rate of uplift at point P in summer 2020 is reduced by more than 60% as compared to summer 2019.
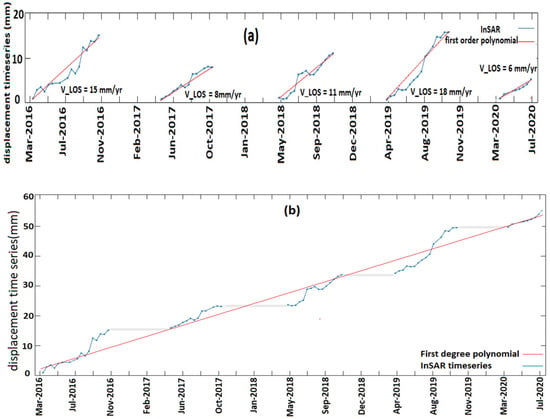
Figure 6.
(a) The blue line is the LOS displacement time series of point P for the five observation periods. The red lines are first-degree polynomials fitted to each time series. (b) The cumulative displacement time series for the summer times at point P. The gray lines are the time span between summer acquisitions. The blue circles show the InSAR images. The red line is a first-degree polynomial fit to the displacement time series.
In order to provide an assessment of the overall cumulative displacement in the summertime from 2016 to 2020, we assume that there is not any significant deformation in the period between November to March, and we merge the individual time series in Figure 6a by shifting the beginning of each time series to the end of the previous one in order to derive an estimation for the cumulative uplift during 2016–2020 (Figure 6b). The results show a cumulative displacement of up to 58 mm in the summer of the years 2016–2020, a long-term LOS uplift rate of 12.7 mm/year (assuming a constant velocity). The fluctuations with respect to the linear trend observed in Figure 6a,b are caused either by transient melting during the summer months, the remaining atmospheric artefacts from InSAR processing, or the temporary effect of precipitation in the elastic response of the crust in this area. To study the mass loss that caused the observed uplift in Figure 5, an area containing the uplift on the northern flank of Helheim is selected (black rectangle in Figure 5a–c) and the LOS velocities are used as observations in the model equations.
3.2. Mass Loss Estimation
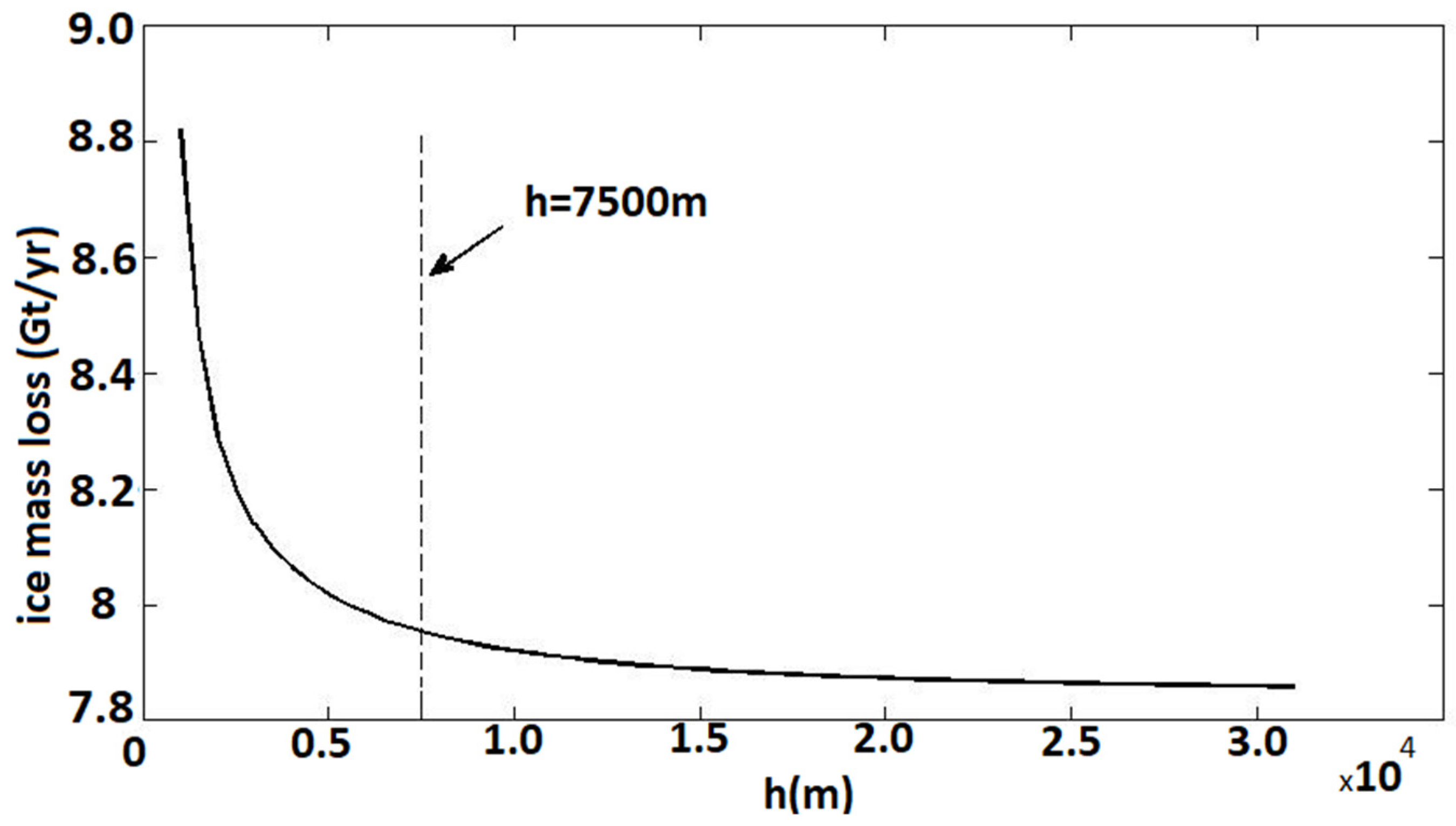
The method described in Section 2 is applied to model displacements and to estimate the mass loss rate for the five observation periods. An area around the northern flank of Helheim (the black rectangle in Figure 5; area ~1500 km2 (30 km × 50 km)) was selected for the modeling. To construct the model, we chose a snow block with a radius of 30 km around the velocity field as a load in the model. The load change was applied via a gridded point source based on square blocks with a size of 1 km. The decay factor h in Equation (4) was changed from 1 to 30 km with a step size of 1 km (Figure 7) to obtain the best decay factor in the model.
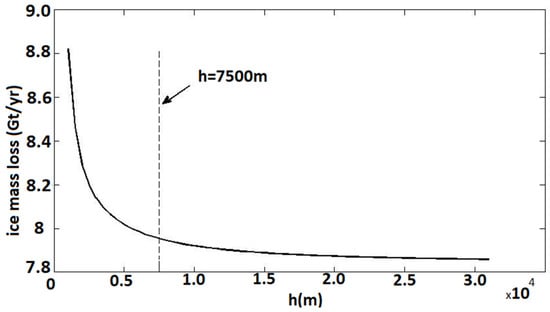
Figure 7.
Mass loss rate of ice as a function of the decay factor h. The dashed line indicates the model of choice at h = 7.5 km.
The best fit between observations and models occurred at h = 7500 m. The cumulative estimated ice volume loss of all periods of observation is 8.65–9.53 /year, equivalent to an ice mass loss of 7.93–8.75 Gt/year, assuming a snow density of 916.7 kg/m3. This range of 0.81 Gt/year between the minimum and maximum suggests that variations in h are largely compensated by variations in the parameters a and b. The fit of the model to the data is presented by the root mean square error: , where is the observation, is the model prediction, and L is the number of observations. We assume unit variance for all observation points and observe that as changes, the RMSE does not vary significantly (h = 1–30 km, RMSE = 1.58–1.67 mm/year). Therefore, the data are not sufficient to resolve h. According to the residuals of the data and model, the best fit of the model occurs at h = 7500 m, which we selected to find the parameters of the model to estimate the ice mass loss for each observation period. The average of the model parameters for all observation time spans is a = 5.07 m/year and b = −2.42 m/year. The model parameters and the estimated ice mass loss for each period of observation are listed in Table 1.

Table 1.
Model parameters and ice mass loss and its averages estimated for the five periods of observation.
By comparing the average of the ice mass loss in the years 2016–2020, we found that the maximum ice mass loss occurred in 2019. The increase in ice mass loss in 2019 in comparison to 2020, 2018, 2017, and 2016 is about 46%, 39%, 45%, and 31%, respectively.
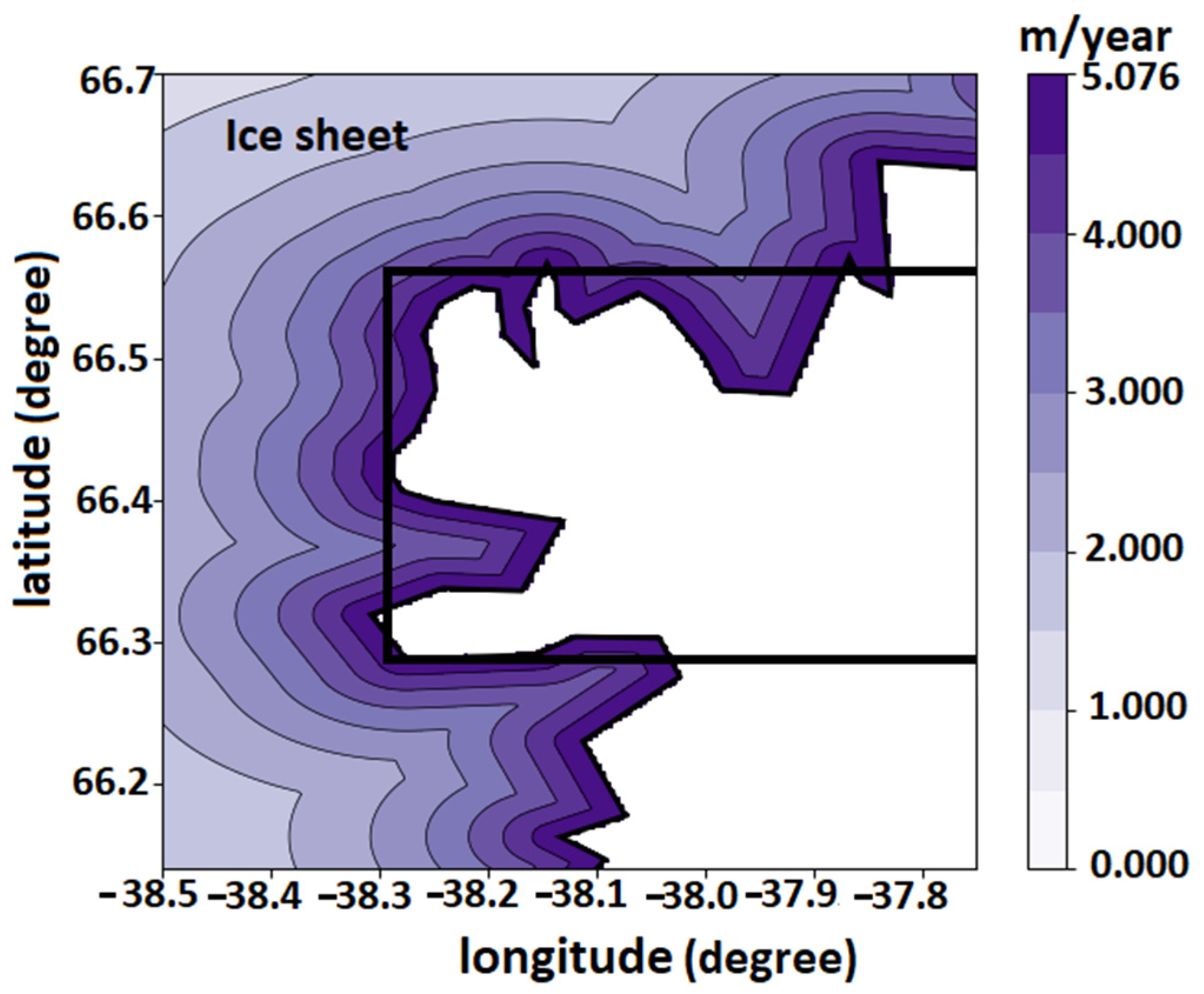
In order to assess how our model illustrates ice sheet/block melting, we plotted two-dimensional average thinning rates of the ice sheet near the edge of the Helheim glacier in Figure 8. The figure shows how the thinning rate decreases from the front of the ice sheet to the interior. On average, the maximum thinning rate of 5.07 m/year occurs at the edge of the ice sheet at the northern flank of the Helheim glacier. By moving away from the edge, the ice sheet height increases while the thinning rate decreases.
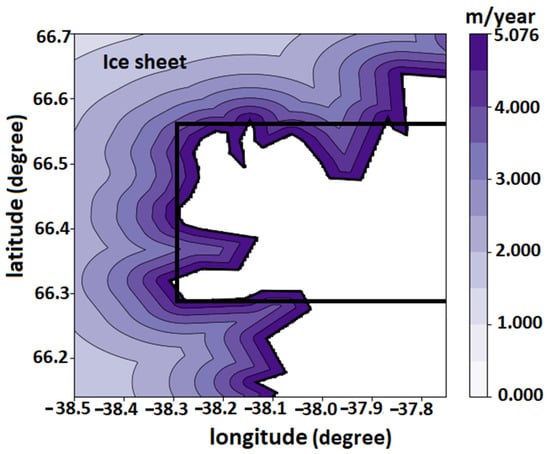
Figure 8.
Average two-dimensional thinning rates estimated for the edge of the ice sheet in the northern flank of the Helheim glacier (white area). The black rectangle shows our study area.
4. Discussion
4.1. InSAR and Modeling
In this study, we investigated how InSAR-based measurements of spatial and temporal variations in crustal uplift along the northern flank of the Helheim glacier in southeastern Greenland could be used to model and estimate the amount of ice melting in the region as an unloading problem. The model that we used to detect the thinning rate in the study area is based on the direct effect of ice melting near the edge of the ice sheet. As we assumed that ice melting decreases from the edge of a glacier to its interior, we selected a portion of the InSAR results for modeling, which was located close to the edge and clearly shows the rebound effect.
The InSAR displacement time series results showed a maximum cumulative LOS uplift of 58 mm for 2016–2020 and 40.86 ice volume loss in an area of approximately 1500 in the time span from 2016 April to 2020 July. Simpson et al. (2011) [67] showed that the viscous uplift rates for their best fitting earth model are about ± 0.2 mm/year all around Greenland, although Khan et al. (2016) [68] argued that the viscous deformation is larger in this region and estimated a viscous uplift rate of about 3–5 mm/year in southeast Greenland. Therefore, we also accounted for the viscous component in our results and removed the modeled viscous deformation (4 mm/year) from the InSAR measurements before inferring the present-day mass change. Our findings suggest that ignoring the viscous component leads to an estimation of 7.92 Gt/year for the ice mass loss, and so it will change our results by only 5%, indicating the result was not sensitive to the viscous deformation.
It is worth noting that for homogeneous elastic half-space modeling, it is important to justify our Young modulus, E, because the surface displacement due to loading is inversely proportional to the Young modulus (Equations (1) and (2)). Auriac et al. (2013) showed that one method to select the appropriate Young modulus is by minimizing the residuals between the observed and modeled values of the InSAR phase. Therefore, we applied this method and varied E between 1 GPa and 90 GPa. The minimum value for the residuals occurred at E = 48 GPa, which we used in our model.
The Poisson’s ratio of 0.23 in our model was adapted from the study by Dahl-Jensen et al. (2003) [69]. To consider the sensitivity of our model to this factor, we changed it from 0.2 to 0.4 by 0.01 steps and considered the results. The RMSE of the residuals did not change significantly, indicating that the model is not sensitive to this factor.
Figure 9 shows the comparison between observations (a, d, g, j, and m) and the models (b, e, h, k, and n) with h = 7.5 km. In this area, the model predictions closely resemble the observations (see the residuals in Figure 9). The standard deviation of the residuals is 2.52–3.77 mm/year and the RMSE between the observation and model varies from 1.493 to 1.789 mm/year for the observation periods (Table 2).
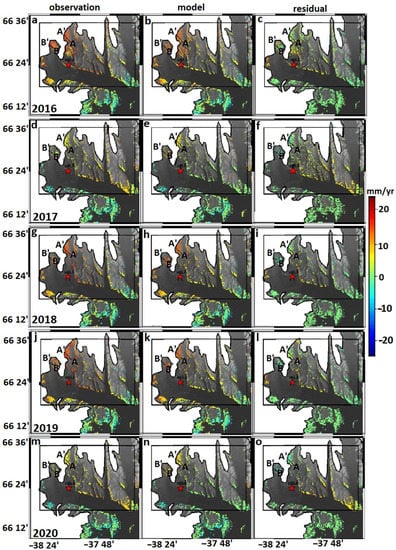
Figure 9.
The (a,d,g,j,m) observations, (b,e,h,k,n) models, and (c,f,i,l,o) residuals for the five periods. The modelled velocities are calculated for the decay distance h = 7.5 km. The red star shows the position of the permanent GPS station, Hel2.

Table 2.
Standard deviation of the residuals and the RMSE between the observations and models of the five periods.
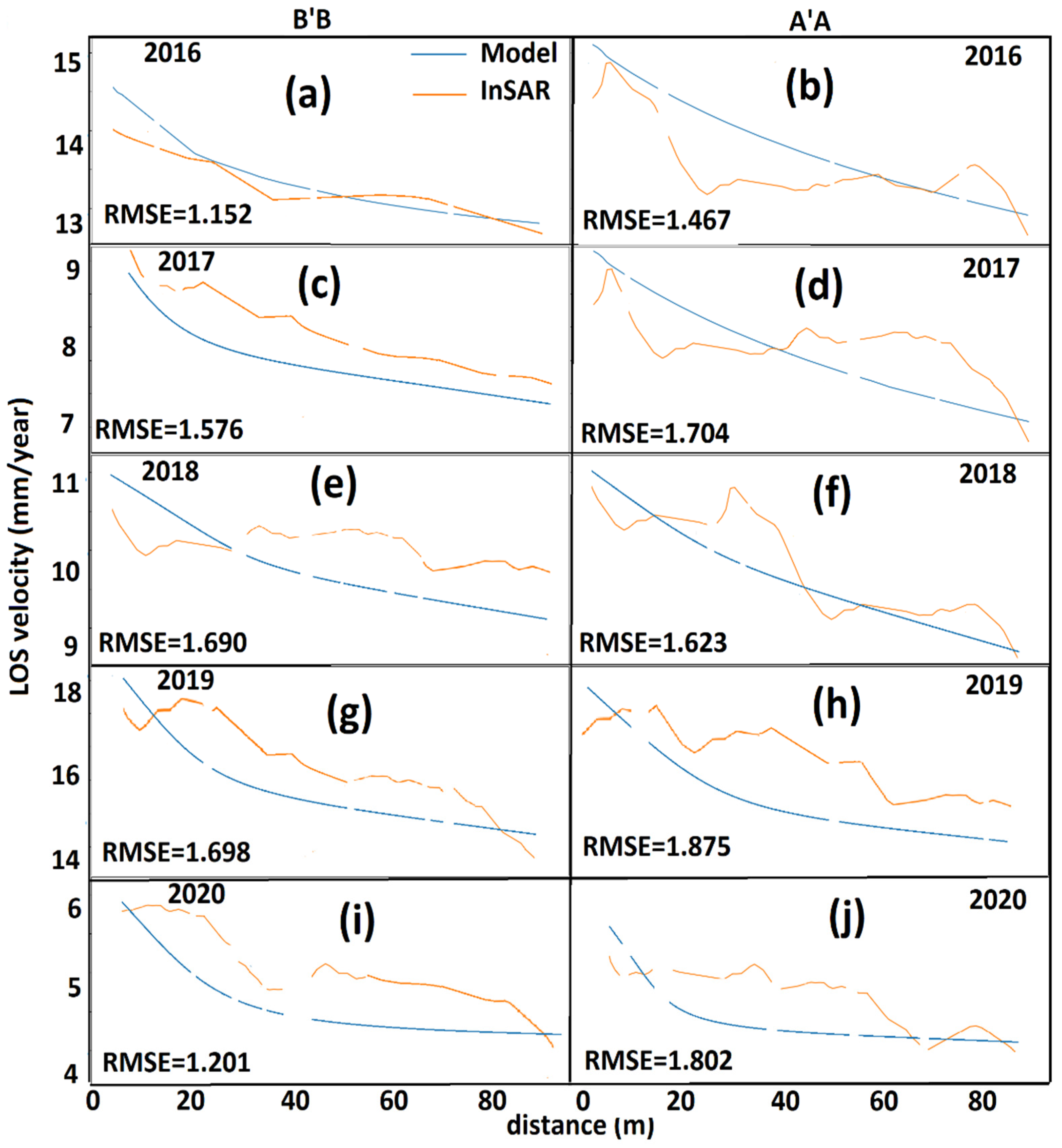
Despite the strongly scattered measurement points in this region, the model aligns well with the observations. To show the consistency of the observations and model, we considered two profiles, A′A and B′B, at the edge of the ice sheet for each observation period, and we compared the discrepancy between the observation and model along the profiles. The plots in Figure 10 illustrate how the model fits to the observation. The RMSE values are between 1.467 and 1.875 mm/year for A′A and between 1.152 and 1.698 mm/year for B′B.
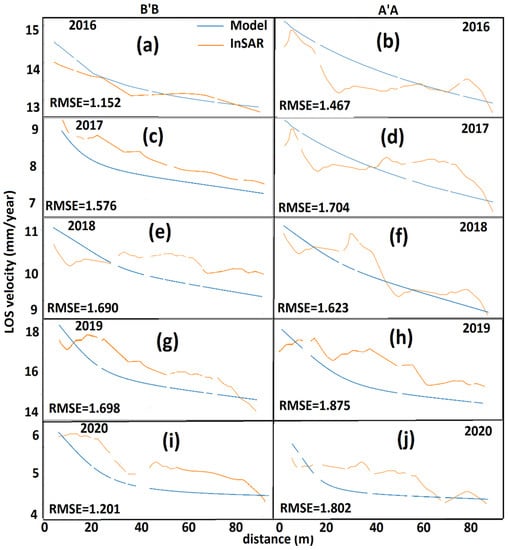
Figure 10.
Comparison between the model (blue lines) and the observations (orange lines) along the profiles A′A (b,d,f,h,j) and B′B (a,c,e,f,g,i) for five years in Figure 9.
In order to consider the absolute difference between the observation and model in Figure 10, we used the average of absolute percentage deviation (AAPD) [70] as follows:
where computes the absolute values. The minimum (maximum) values of the AAPD correspond to the best (worst) performance of the model to the observation.
Table 3 shows that in Figure 10, the best performance of the model is 1.8%, while the worst is 4.9%. Therefore, the model is fitted to the observations with a maximum five percent difference and the RMSE values are acceptable.

Table 3.
AAPD between the observations and models of the five periods in Figure 10.
4.2. Inferring Elastic Rebound from GPS
In order to infer the elastic rebound from the GPS, we used a GPS time series of displacement recorded at the permanent GPS station, Hel2, which is the only GPS station in the study area, from http://geodesy.unr.edu/gps_timeseries/txyz/IGS14/HEL2.txyz2 (accessed on 14 January 2021). The data were analyzed in the Nevada Geodetic Laboratory using GipsyX software that was developed at JPL. The precision of the GPS components is reported 0.9, 0.8, and 3 mm in the north, east, and up directions. As we had only one GPS station in the study area, we could not directly compare the SBAS and GPS measurements with each other; as DInSAR is a relative measuring system, we would need at least two GPS stations for comparison. Therefore, in the following, we do not focus on the direct comparison between the GPS and InSAR, but rather on the interpretation that we infer from the GPS. To do this, we first converted the GPS time-series displacement into the LOS direction by using the following equations:
where , , and are the three components of the displacement vector in the north, east, and up directions, respectively. is the incidence angle and is the azimuth of the satellite heading. is the projection of the horizontal components on the azimuth look direction [71].
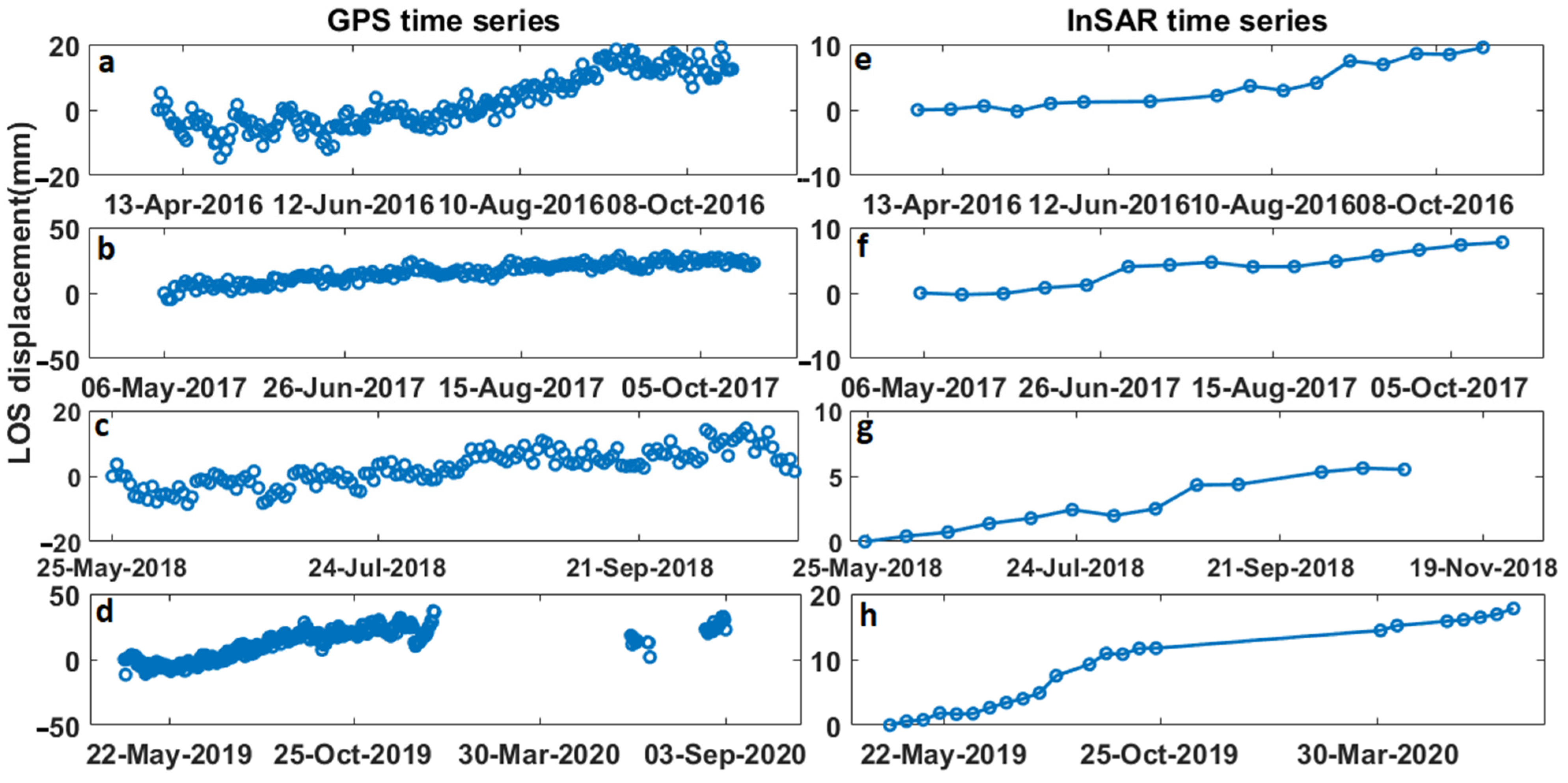
Figure 11 shows InSAR and GPS time series for four periods (due to the gap in the GPS data for 2020, the years 2019–2020 are assumed as one period), where the former was calculated based on the average of points within a radius of 100 m around the permanent GPS station Hel2. Both the GPS and InSAR time series show an increasing trend in the LOS displacement time series. In general, the GPS time series data are noisier than the InSAR, and they have much more fluctuations. The higher fluctuations in the GPS time series might be due to the continuous record of data that can affected by environmental effects such as rain and snowfall. In contrast, the InSAR data are discontinuous and are collected every 12 days, and so they may miss such effects. In addition, due to the employment of temporal filters in the SBAS analysis, the InSAR displacement time series are much smoother than the GPS, which may mask part of the ground displacement related to ice melting. As seen in Figure 11, the maximum LOS displacement in the GPS is more than the InSAR. It may be because the GPS time series is in an absolute reference frame, while the InSAR is relative to a reference area. The reference area experiences many of the same geophysical phenomena as the area close to the GPS, e.g., the seasonal elastic deformation due to snow cover would be similar for the area around the GPS station and for the reference area. The differencing will consequently remove a part of the displacement signal in the InSAR, while the signal remains in the un-differenced GPS. This causes the differences in the amount of uplift between the GPS and InSAR time series. The absolute precision of the GPS is ~3 mm and the relative precision of the InSAR is ~0.6 mm. Therefore, the integration of the InSAR measurements from the missions with shorter revisit times (1–3 days) with more continuous GPS stations in the region would improve the capability for a better interpretation of non-linearity related to ice melting in different seasons and glacier areas.
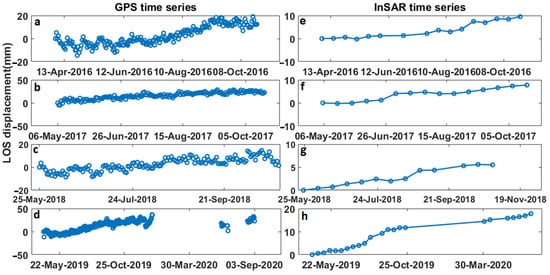
Figure 11.
GPS-derived LOS time series in the four periods of InSAR observation: (a) April–October 2016, (b) May–October 2017, (c) May–October 2018, and (d) May 2019–September 2020. (e–h) illustrate the average of the LOS displacement time series of the InSAR measurement points around the GPS station to a radius of 100 m in the same periods as (a–d), respectively.
4.3. Comparison with Previous Studies
As the observation period covered by our SAR data is relatively short and the detected average uplift of ~13 mm/year around the Helheim glacier in our study can be assigned to the elastic component of the crust, triggered by the very quick response of crust to atmospheric and oceanic fluctuations in short time scales. Khan et al. (2007) used the dem-extraction method to estimate the volume changes in Helheim and determined that there was 16.6 mm of uplift in this region and 180 volume loss for 2002–2005 in an area larger than 48,000 . Our study has revealed a maximum cumulative line-of-sight uplift of 58 mm during 2016–2020, corresponding to a cumulative volume loss of 40.56 in an area of about 1500 . If we divide the volume loss by the area in these two studies, the results show that the peak rates of ice melting near the Helheim glacier increased by almost four times between 2016 and 2020. This temporal acceleration of ice melting has also been mentioned in previous studies. For example, Bevis et al. (2012) used GPS data recorded at the Hel2 station and showed that the velocity of the vertical displacement was 11.8 mm/year between 2007 and April 2010, but it increased to 15.3 mm/year between April 2010 and March 2011, which the authors attributed to the summer of 2010 being the hottest and longest on record over most of southern Greenland (until 2011). Helm et al. (2014), using Cryosat-2 altimeter observations, showed that the volume loss rate at the Helheim glacier between 2011 and 2014 was 2–5 times greater than that between 2003 and 2009. Wake et al. (2016), using GPS data from Hel2 for 2008 to 2013, suggested that Hel2 was uplifting at a rate of 16 ± 0.36 mm/year, with significant acceleration (3.7 ± 0.24 mm/year from April 2006 to September 2012). Mouginot et al. (2019) [72], using an extensive survey of surface elevation, thickness, velocity, and surface mass balance, suggested that the mass loss acceleration shifted from positive in the 2000–2010 period to negative in the 2010–2018 period. They suggested a 20 Gt/year mass loss for all glaciers in southeastern Greenland over 46 years. Sasgen et al. (2020) [73] observed a mass loss in 2017 and 2018 by GRACE and GRACE-FO and reported that these were lower than in any other two-year period between 2003 and 2019. In June and July 2019, the ice sheet experienced high rates of melt water runoff close to the maximum rates observed over the full 2003–2018 period. Williams et al. (2021) [74] used a range of remotely sensed datasets and showed that during 2014–2020, the Helheim glacier had continued to lose mass and thin, and it had retreated inland, up to 100 m thinner than it was during 2005. Our results also show that in 2017 and 2018, the LOS displacements related to ice mass loss were lower than other year periods between 2016 and 2019, and in 2019, the most LOS displacement took placed. Our InSAR-based analysis indicates that the Helheim glacier plays a significant role in this process, and it shows a large area of the regional mass loss in southeastern Greenland.
4.4. Influence of Land Surface Temperature
Snow et al. (2021) [75] examined the influence of the sea surface temperature (SST) and ocean currents near the Helheim glacier and showed that fluctuations in subsurface Atlantic water temperatures coincided with some of the variability in discharge rates previously found at Helheim, although this relationship is not straightforward. For example, the SST was increasing in 2000 when Helheim experienced discharge rates. However, the SST was relatively warm in 2010, although Helheim did not experience any substantial increase in ice discharge. These findings suggest that there is no straight relationship between the SST and discharge rate of the glacier. In addition to the SST and ocean currents, other environmental factors such as land surface temperature, glacier configuration, and mélange rigidity may influence glacier discharge rates.
As analyzed above, the InSAR time series suggest faster melting in 2019, in comparison to periods before and after. Reports from the World Meteorological Organization (WMO) indicate that 2016–2020 were the five warmest years on record [76], with 2019 being warmer than the record-level temperatures seen in 2016 and 2018, making 2019 a fast melt year for the ice sheets.
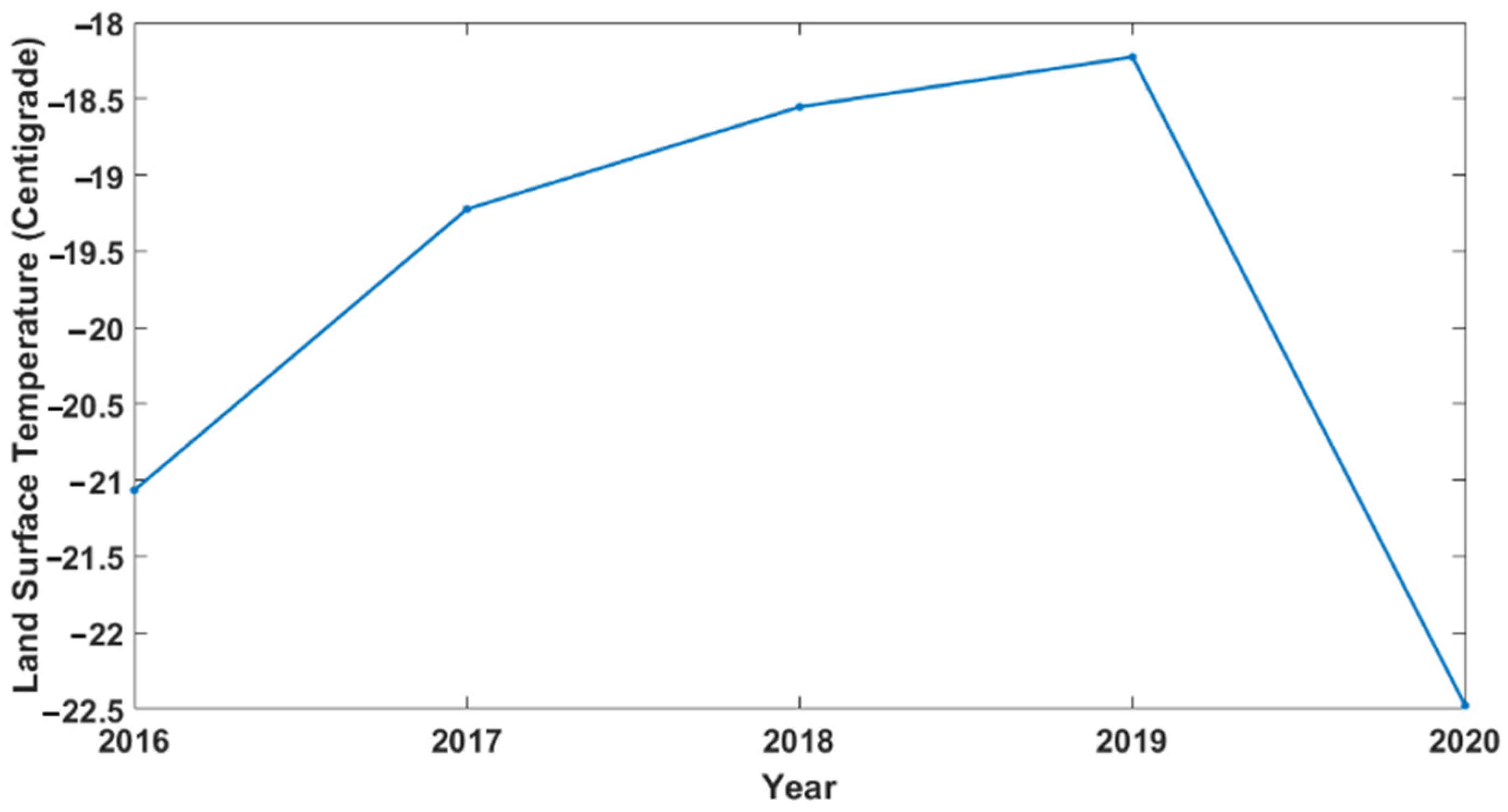
We compared the average of the local LST in our study area for each year by using MOD11C2 data from MODIS (Figure 12). For the 2020 local LST, the average of the first 9 months, for which we had InSAR data, is considered. As seen in Figure 12, the regional analysis from the LST shows that the LST rate increased from 2016 to 2019 but decreased in 2019–2020. However, as illustrated in Figure 6a, displacement rates decreased from 2016 to 2017 and 2018 and increased again in 2019, before decreasing in 2020. Thus, there is no direct link between elastic rebound of the crust and land surface temperature, and as stressed above, other parameters may also influence ice melting and the resulting unloading at the edges of the glaciers.
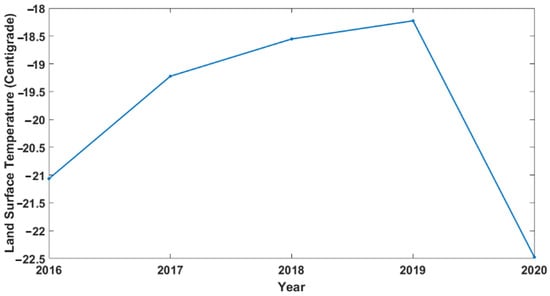
Figure 12.
Annual average of the local land surface temperature (LST) extracted from MOD11C2.
5. Conclusions
InSAR time series interferograms are useful for assessing the elastic surface deformation on the edges of large glaciers subject to ice melting, providing insight into the rheological characteristics of the region. Based on Sentinel-1 InSAR measurements covering summer seasons between 2016 and 2020 over the Helheim glacier, we could infer the uplift on the northern flank of the Helheim margin up to 58 mm in the LOS direction, attributed to the elastic response of solid earth to ice melting. InSAR time series analysis suggests faster melting in 2019 than in 2016, 2017, 2018, and 2020. Modeling the thinning rate of ice thickness and the mass loss rate due to unloading in this region results in an average thinning rate of 5.07 m/year at the edge of ice sheet and a mass loss of 8.33 Gt/year on the northern flank of the Helheim margin. Although the distribution of InSAR measurement points in this region is rather sparse, this study shows the ability of the Sentinel-1 SAR system to provide a reliable assessment of the surface deformation on the edges of a large glacier, which makes it promising for applying to other areas to evaluate the elastic response of solid earth to glacier and ice sheet melting.
Author Contributions
Conceptualization, Z.E.J. and M.M.; writing—review and editing, Z.E.J., M.M. and V.K. All authors have read and agreed to the published version of the manuscript.
Funding
The research of VK contributes to Advanced Earth System Modeling Capacity—ESM (Helmholtz-Association).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Khan, S.A.; Wahr, J.; Stearns, L.A.; Hamilton, G.S.; van Dam, T.; Larson, K.M.; Francis, O.; Khan, S.A.; Wahr, J.; Stearns, L.A.; et al. Elastic uplift in southeast Greenland due to rapid ice mass loss. Geophys. Res. Lett. 2007, 34, L21701. [Google Scholar] [CrossRef]
- Agency, E.S.; Howat, I.M.; Smith, B.E.; Joughin, I.; Scambos, T.A.; Wahr, J.; Stearns, L.A.; Hamilton, G.S. Rates of southeast Greenland ice volume loss from combined ICESat and ASTER observations. Geophys. Res. Lett. 2008, 35, 1–5. [Google Scholar] [CrossRef]
- Wouters, B.; Chambers, D.; Schrama, E.J.O. GRACE observes small-scale mass loss in Greenland. Geophys. Res. Lett. 2008, 35, L20501. [Google Scholar] [CrossRef]
- Khan, S.A.; Wahr, J.; Bevis, M.; Velicogna, I.; Kendrick, E. Spread of ice mass loss into northwest Greenland observed by GRACE and GPS. Geophys. Res. Lett. 2010, 37, 1–5. [Google Scholar] [CrossRef]
- Meier, M.F.; Dyurgerov, M.B.; Rick, U.K.; O’Neel, S.; Pfeffer, W.T.; Anderson, R.S.; Anderson, S.P.; Glazovsky, A.F. Glaciers Dominate Eustatic Sea-Level Rise in the 21st Century. Science 2007, 317, 1064–1067. [Google Scholar] [CrossRef] [PubMed]
- Gardner, A.S.; Moholdt, G.; Cogley, J.G.; Wouters, B.; Arendt, A.A.; Wahr, J.; Berthier, E.; Hock, R.; Pfeffer, W.T.; Kaser, G.; et al. A Reconciled Estimate of Glacier Contributions to Sea Level Rise: 2003 to 2009. Science 2013, 340, 852–857. [Google Scholar] [CrossRef] [PubMed]
- Peltier, W.R. The impulse response of a Maxwell Earth. Rev. Geophys. 1974, 12, 649. [Google Scholar] [CrossRef]
- Wu, P. Deformation of an incompressible viscoelastic flat earth with powerlaw creep: A finite element approach. Geophys. J. Int. 1992, 108, 35–51. [Google Scholar] [CrossRef]
- Mitrovica, J.X.; Milne, G.A.; Davis, J.L. Glacial isostatic adjustment on a rotating earth. Geophys. J. Int. 2001, 147, 562–578. [Google Scholar] [CrossRef]
- Wake, L.M.; Lecavalier, B.S.; Bevis, M. Glacial Isostatic Adjustment (GIA) in Greenland: A Review. Curr. Clim. Chang. Rep. 2016, 2, 101–111. [Google Scholar] [CrossRef]
- Watts, A. Isostasy and Flexure of the Lithosphere; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Slobbe, D.C.; Ditmar, P.; Lindenbergh, R.C. Estimating the rates of mass change, ice volume change and snow volume change in Greenland from ICESat and GRACE data. Geophys. J. Int. 2009, 176, 95–106. [Google Scholar] [CrossRef]
- Bevis, M.; Wahr, J.; Khan, S.A.; Madsen, F.B.; Brown, A.; Willis, M.; Kendrick, E.; Knudsen, P.; Box, J.E.; van Dam, T.; et al. Bedrock displacements in Greenland manifest ice mass variations, climate cycles and climate change. Proc. Natl. Acad. Sci. USA 2012, 109, 11944–11948. [Google Scholar] [CrossRef]
- Rignot, E.; Kanagaratnam, P. Changes in the velocity structure of the Greenland Ice Sheet. Science 2006, 311, 986–990. [Google Scholar] [CrossRef]
- Joughin, I.; Smith, B.E.; Abdalati, W. Glaciological advances made with interferometric synthetic aperture radar. J. Glaciol. 2011, 56, 1026–1042. [Google Scholar] [CrossRef]
- Rignot, E.; Bamber, J.L.; Van Den Broeke, M.R.; Davis, C.; Li, Y.; Van De Berg, W.J.; Van Meijgaard, E. Recent Antarctic ice mass loss from radar interferometry and regional climate modelling. Nat. Geosci. 2008, 1, 106–110. [Google Scholar] [CrossRef]
- Osmanoǧlu, B.; Braun, M.; Hock, R.; Navarro, F.J. Surface velocity and ice discharge of the ice cap on King George Island, Antarctica. Ann. Glaciol. 2013, 54, 111–119. [Google Scholar] [CrossRef]
- Hooper, A.; Zebker, H.; Segall, P.; Kampes, B. A new method for measuring deformation on volcanoes and other natural terrains using InSAR persistent scatterers. Geophys. Res. Lett. 2004, 31, 1–5. [Google Scholar] [CrossRef]
- Pritchard, M.E.; Biggs, J.; Wauthier, C.; Sansosti, E.; Arnold, D.W.; Delgado, F.; Zoffoli, S. Towards coordinated regional multi-satellite InSAR volcano observations: Results from the Latin America pilot project. J. Appl. Volcanol. 2018, 7, 5. [Google Scholar] [CrossRef]
- Chaussard, E.; Johnson, C.W.; Fattahi, H.; Bürgmann, R. Potential and limits of InSAR to characterize interseismic deformation independently of GPS data: Application to the southern San Andreas Fault system. Geochem. Geophys. Geosyst. 2016, 17, 1214–1229. [Google Scholar] [CrossRef]
- Motagh, M.; Bahroudi, A.; Haghighi, M.H.; Samsonov, S.; Fielding, E.; Wetzel, H.U. The 18 August 2014 Mw 6.2 Mormori, Iran, Earthquake: A thin-skinned faulting in the zagros mountain inferred from InSAR measurements. Seismol. Res. Lett. 2015, 86, 775–782. [Google Scholar] [CrossRef]
- Mirzaee, S.; Motagh, M.; Akbari, B.; Wetzel, H.U.; Roessner, S. Evaluating Three Insar Time-Series Methods To Assess Creep Motion, Case Study: Masouleh Landslide In North Iran. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 4, 223–228. [Google Scholar] [CrossRef]
- Motagh, M.; Wetzel, H.-U.; Roessner, S.; Kaufmann, H. A TerraSAR-X InSAR study of landslides in southern Kyrgyzstan, Central Asia. Remote Sens. Lett. 2013, 4, 657–666. [Google Scholar] [CrossRef]
- Xia, Z.; Motagh, M.; Li, T.; Roessner, S. The June 2020 Aniangzhai landslide in Sichuan Province, Southwest China: Slope instability analysis from radar and optical satellite remote sensing data. Landslides 2022, 19, 313–329. [Google Scholar] [CrossRef]
- Hu, X.; Bürgmann, R.; Fielding, E.J.; Lee, H. Internal kinematics of the Slumgullion landslide (USA) from high-resolution UAVSAR InSAR data. Remote Sens. Environ. 2020, 251, 112057. [Google Scholar] [CrossRef]
- Motagh, M.; Walter, T.R.; Sharifi, M.A.; Fielding, E.; Schenk, A.; Anderssohn, J.; Zschau, J. Land subsidence in Iran caused by widespread water reservoir overexploitation. Geophys. Res. Lett. 2008, 35, 1–5. [Google Scholar] [CrossRef]
- Motagh, M.; Shamshiri, R.; Haghshenas Haghighi, M.; Wetzel, H.U.; Akbari, B.; Nahavandchi, H.; Roessner, S.; Arabi, S. Quantifying groundwater exploitation induced subsidence in the Rafsanjan plain, southeastern Iran, using InSAR time-series and in situ measurements. Eng. Geol. 2017, 218, 134–151. [Google Scholar] [CrossRef]
- Cigna, F.; Esquivel Ramírez, R.; Tapete, D. Accuracy of Sentinel-1 PSI and SBAS InSAR Displacement Velocities against GNSS and Geodetic Leveling Monitoring Data. Remote Sens. 2021, 13, 4800. [Google Scholar] [CrossRef]
- Liu, L.; Wahr, J.; Howat, I.; Khan, S.A.; Joughin, I.; Furuya, M. Constraining ice mass loss from Jakobshavn Isbræ (Greenland) using InSAR-measured crustal uplift. Geophys. J. Int. 2012, 188, 994–1006. [Google Scholar] [CrossRef][Green Version]
- Zhao, W.; Amelung, F.; Dixon, T.H.; Wdowinski, S.; Malservisi, R. A method for estimating ice mass loss from relative InSAR observations: Application to the Vatnajökull ice cap, Iceland. Geochem. Geophys. Geosyst. 2014, 15, 108–120. [Google Scholar] [CrossRef]
- Shamshiri, R.; Motagh, M.; Baes, M.; Sharifi, M.A. Deformation analysis of the Lake Urmia causeway (LUC) embankments in northwest Iran: Insights from multi-sensor interferometry synthetic aperture radar (InSAR) data and finite element modeling (FEM). J. Geod. 2014, 88, 1171–1185. [Google Scholar] [CrossRef]
- Milillo, P.; Bürgmann, R.; Lundgren, P.; Salzer, J.; Perissin, D.; Fielding, E.; Biondi, F.; Milillo, G. Space geodetic monitoring of engineered structures: The ongoing destabilization of the Mosul dam, Iraq. Sci. Rep. 2016, 6, 37408. [Google Scholar] [CrossRef]
- Emadali, L.; Motagh, M.; Haghshenas Haghighi, M. Characterizing post-construction settlement of the Masjed-Soleyman embankment dam, Southwest Iran, using TerraSAR-X SpotLight radar imagery. Eng. Struct. 2017, 143, 261–273. [Google Scholar] [CrossRef]
- Montazeri, S. Geodetic synthetic aperture radar interferometry. DLR Dtsch. Zent. Fur Luft Und Raumfahrt E.V. Forsch. 2019, 2019, 1–197. [Google Scholar]
- Yun, S.; Zebker, H.; Segall, P.; Hooper, A.; Poland, M. Interferogram formation in the presence of complex and large deformation. Geophys. Res. Lett. 2007, 34, 1–6. [Google Scholar] [CrossRef]
- Singleton, A.; Li, Z.; Hoey, T.; Muller, J.-P. Evaluating sub-pixel offset techniques as an alternative to D-InSAR for monitoring episodic landslide movements in vegetated terrain. Remote Sens. Environ. 2014, 147, 133–144. [Google Scholar] [CrossRef]
- Sánchez-Gámez, P.; Navarro, F.J. Glacier surface velocity retrieval using D-InSAR and offset tracking techniques applied to ascending and descending passes of sentinel-1 data for southern ellesmere ice caps, Canadian Arctic. Remote Sens. 2017, 9, 442. [Google Scholar] [CrossRef]
- Zebker, H.A.; Villasenor, J. Decorrelation in interferometric radar echoes. IEEE Trans. Geosci. Remote Sens. 1992, 30, 950–959. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Hooper, A. A Combined Multi-Temporal Insar Method Incorporating Persistent Scatterer And Small Baseline Approaches. Geophys. Res. Lett. 2008, 35, 1–5. [Google Scholar] [CrossRef]
- Ferretti, A.; Fumagalli, A.; Novali, F.; Prati, C.; Rocca, F.; Rucci, A. A New Algorithm for Processing Interferometric Data-Stacks: SqueeSAR. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3460–3470. [Google Scholar] [CrossRef]
- Shamshiri, R.; Nahavandchi, H.; Motagh, M.; Hooper, A. Efficient Ground Surface Displacement Monitoring Using Sentinel-1 Data: Integrating Distributed Scatterers (DS) Identified Using Two-Sample t-Test with Persistent Scatterers (PS). Remote Sens. 2018, 10, 794. [Google Scholar] [CrossRef]
- Copernicus Space Component Mission Management Team. Sentinel High Level Operations Plan (HLOP); Uropian Space Agency: Paris, French, 2020. [Google Scholar]
- Pritchard, H.D.; Arthern, R.J.; Vaughan, D.G.; Edwards, L.A. Extensive dynamic thinning on the margins of the Greenland and Antarctic ice sheets. Nature 2009, 461, 971–975. [Google Scholar] [CrossRef] [PubMed]
- Johannessen, O.M.; Khvorostovsky, K.; Miles, M.W.; Bobylev, L.P. Recent Ice-Sheet Growth in the Interior of Greenland. Science 2003, 310, 2–5. [Google Scholar] [CrossRef]
- Zwally, H.J.; Li, J.; Brenner, A.C.; Beckley, M.; Cornejo, H.G.; Dimarzio, J.; Giovinetto, M.B.; Neumann, T.A.; Robbins, J.; Saba, J.L.; et al. Greenland ice sheet mass balance: Distribution of increased mass loss with climate warming; 2003–2007 versus 1992–2002. J. Glaciol. 2011, 57, 88–102. [Google Scholar] [CrossRef]
- Velicogna, I.; Wahr, J. Acceleration of Greenland ice mass loss in spring 2004. Nature 2006, 443, 329–331. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.L. Satellite Gravity Measurements Confirm Accelerated Melting of Greenland Ice Sheet. Science 2006, 313, 1958–1960. [Google Scholar] [CrossRef] [PubMed]
- Velicogna, I. Increasing rates of ice mass loss from the Greenland and Antarctic ice sheets revealed by GRACE. Geophys. Res. Lett. 2009, 36, 1–4. [Google Scholar] [CrossRef]
- Helm, V.; Humbert, A.; Miller, H. Elevation and elevation change of Greenland and Antarctica derived from CryoSat-2. Cryosph 2014, 8, 1539–1559. [Google Scholar] [CrossRef]
- Auriac, A.; Spaans, K.H.; Sigmundsson, F.; Hooper, A.; Schmidt, P.; Lund, B. Iceland rising: Solid Earth response to ice retreat inferred from satellite radar interferometry and visocelastic modeling. J. Geophys. Res. Solid Earth 2013, 118, 1331–1344. [Google Scholar] [CrossRef]
- Bevan, S.L.; Luckman, A.; Khan, S.A.; Murray, T. Seasonal dynamic thinning at Helheim Glacier. Earth Planet. Sci. Lett. 2015, 415, 47–53. [Google Scholar] [CrossRef]
- Stearns, L.A.; Hamilton, G.S. Rapid Volume Loss from Two East Greenland Outlet Glaciers Quantified Using Repeat Stereo Satellite Imagery. Geophys. Res. Lett. 2007, 34, 1–5. [Google Scholar] [CrossRef]
- Sandwell, D.; Mellors, R.; Tong, X.; Wei, M.; Wessel, P. Open radar interferometry software for mapping surface Deformation. Eos Trans. Am. Geophys. Union 2011, 92, 234. [Google Scholar] [CrossRef]
- Sandwell, D.; Mellors, R.; Tong, X.; Xu, X.; Wei, M.; Wessel, P. GMTSAR: An InSAR Processing System Based on Generic Mapping Tools. UC San Diego: Scripps Institution of Oceanography. Available online: http://topex.ucsd.edu/gmtsar/tar/GMTSAR_2ND_TEX.pdf (accessed on 1 June 2016).
- Xu, X.; Sandwell, D.T.; Tymofyeyeva, E.; Gonzalez-Ortega, A.; Tong, X. Tectonic and Anthropogenic Deformation at the Cerro Prieto Geothermal Step-Over Revealed by Sentinel-1A InSAR. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5284–5292. [Google Scholar] [CrossRef]
- Usai, S. A least squares database approach for SAR interferometric data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 753–760. [Google Scholar] [CrossRef]
- Hooper, A.; Zebker, H.A. Phase unwrapping in three dimensions with application to InSAR time series. J. Opt. Soc. Am. A 2007, 24, 2737. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.W.; Zebker, H.A. Network approaches to two-dimensional phase unwrapping: Intractability and two new algorithms. J. Opt. Soc. Am. A 2000, 17, 401. [Google Scholar] [CrossRef]
- Fattahi, H.; Amelung, F. InSAR uncertainty due to orbital errors. Geophys. J. Int. 2014, 199, 549–560. [Google Scholar] [CrossRef]
- Tymofyeyeva, E.; Fialko, Y. Mitigation of atmospheric phase delays in InSAR data, with application to the eastern California shear zone. J. Geophys. Res. Solid Earth 2015, 120, 5952–5963. [Google Scholar] [CrossRef]
- Meyer, F.J. Performance Requirements for Ionospheric Correction of Low-Frequency SAR Data. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3694–3702. [Google Scholar] [CrossRef]
- Tang, W.; Zhao, X.; Motagh, M.; Bi, G.; Li, J.; Chen, M.; Chen, H.; Liao, M. Land subsidence and rebound in the Taiyuan basin, northern China, in the context of inter-basin water transfer and groundwater management. Remote Sens. Environ. 2022, 269, 112792. [Google Scholar] [CrossRef]
- Khan, S.A.; Kjeldsen, K.K.; Kjær, K.H.; Bevan, S.; Luckman, A.; Bjørk, A.A.; Korsgaard, N.J.; Box, J.E.; Van Den Broeke, M.; Van Dam, T.M.; et al. Glacier dynamics at Helheim and Kangerdlugssuaq glaciers, southeast Greenland, since the Little Ice Age. Cryosphere 2014, 8, 1497–1507. [Google Scholar] [CrossRef]
- Nielsen, K.; Abbas, S.; Korsgaard, N.J.; Kjær, K.H.; Wahr, J.; Bevis, M.; Stearns, L.A.; Timm, L.H.; Khan, S.A.; Korsgaard, N.J.; et al. Crustal uplift due to ice mass variability on Upernavik Isstrøm, west Greenland. Earth Planet. Sci. Lett. 2012, 353–354, 182–189. [Google Scholar] [CrossRef]
- Gielsdorf, F.; Hillmann, T. Mathematics and Statistics. In Springer Handbook of Geographic Information; Springer: Berlin/Heidelberg, Germany, 2011; pp. 7–10. [Google Scholar]
- Simpson, M.J.R.; Wake, L.; Milne, G.A.; Huybrechts, P. The influence of decadal- to millennial-scale ice mass changes on present-day vertical land motion in Greenland: Implications for the interpretation of GPS observations. J. Geophys. Res. Solid Earth 2011, 116, 1–19. [Google Scholar] [CrossRef]
- Khan, S.A.; Sasgen, I.; Bevis, M.; Dam, T.V.; Bamber, J.L.; Wahr, J.; Willis, M. Geodetic measurements reveal similarities between post–Last Glacial Maximum and present-day mass loss from the Greenland ice sheet. Sci. Adv. 2016, 2, e1600931. [Google Scholar] [CrossRef]
- Dahl-Jensen, T.; Larsen, T.B.; Woelbern, I.; Bach, T.; Hanka, W.; Kind, R.; Gregersen, S. Depth to Moho in Greenland: Receiver-function analysis suggests two Proterozoic blocks in Greenland. Earth Planet. Sci. Lett. 2003, 205, 379–393. [Google Scholar] [CrossRef]
- Kosary, M.; Forootan, E.; Farzaneh, S.; Schumacher, M. A sequential calibration approach based on the ensemble Kalman filter (C-EnKF) for forecasting total selectron content (TEC). J. Geod. 2022, 29–96. [Google Scholar] [CrossRef]
- Hanssen, R.F. Radar Interferometry: Data Interpretation and Error Analysis; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2001; Volume 2. [Google Scholar]
- Mouginot, J.; Rignot, E.; Bjørk, A.A.; van den Broeke, M.; Millan, R.; Morlighem, M.; Noël, B.; Scheuchl, B.; Wood, M. Forty-six years of Greenland Ice Sheet mass balance from 1972 to 2018. Proc. Natl. Acad. Sci. USA 2019, 116, 9239–9244. [Google Scholar] [CrossRef]
- Sasgen, I.; Wouters, B.; Gardner, A.S.; King, M.D.; Tedesco, M.; Landerer, F.W. Return to rapid ice loss in Greenland and record loss in 2019 detected by the GRACE-FO satellites. Commun. Earth Env. 2021, 1, 8. [Google Scholar] [CrossRef]
- Williams, J.J.; Gourmelen, N.; Nienow, P.; Bunce, C.; Slater, D. Helheim Glacier Poised for Dramatic Retreat. Geophys Res Lett. 2021, 48, e2021GL094546. [Google Scholar] [CrossRef]
- Snow, T.; Straneo, F.; Holte, J.; Grigsby, S.; Abdalati, W.; Scambos, T. More than Skin Deep: Sea Surface Temperature as a Means of Inferring Atlantic Water Variability on the Southeast Greenland Continental Shelf Near Helheim Glacier. J. Geophys. Res. Ocean. 2021, 126, e2020JC016509. [Google Scholar] [CrossRef]
- Hansen, J.; Sato, M.; Ruedy, R.; Schmidt, G.A.; Lo, K.; Persin, A. Global Temperature in 2020; Columbia University: New York, NY, USA, 2021; Available online: http://www.columbia.edu/~jeh1/mailings/2021/20210114_Temperature2020.pdf (accessed on 14 January 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).