Inversion and Driving Force Analysis of Nutrient Concentrations in the Ecosystem of the Shenzhen-Hong Kong Bay Area
Abstract
:1. Introduction
2. Materials and Methods
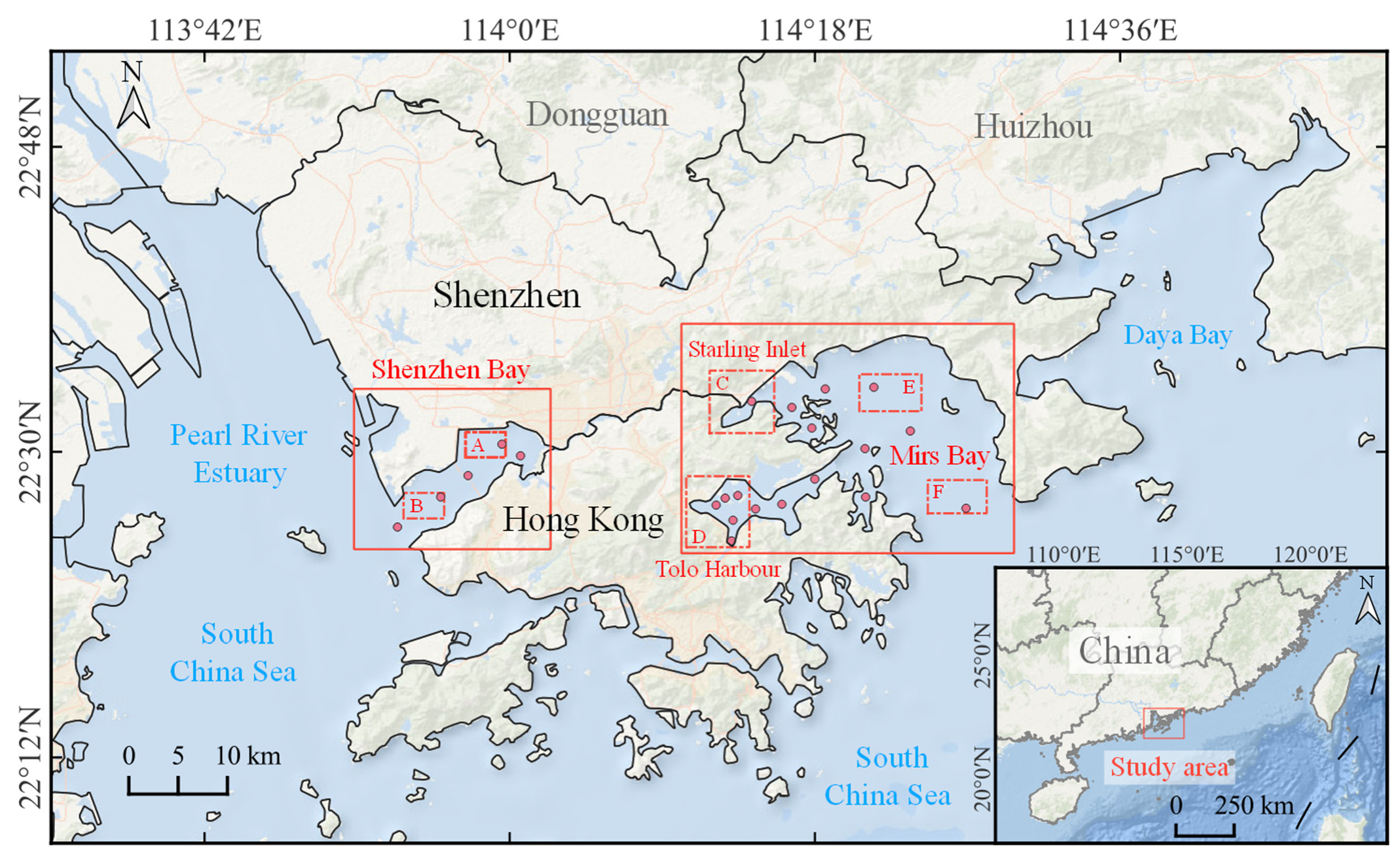
2.1. Study Area
2.2. Data Sources
2.3. Method of Model Building
2.3.1. Preprocessing
2.3.2. Tree Embedding (TE)
2.3.3. Support Vector Regression (SVR)
2.3.4. Gaussian Process Regression (GPR)
2.3.5. Back-Propagation Neural Network (BPNN)
2.3.6. Accuracy Assessment
2.3.7. Hyperparameter Optimization
3. Results
3.1. Comparison of the Methods Accuracy
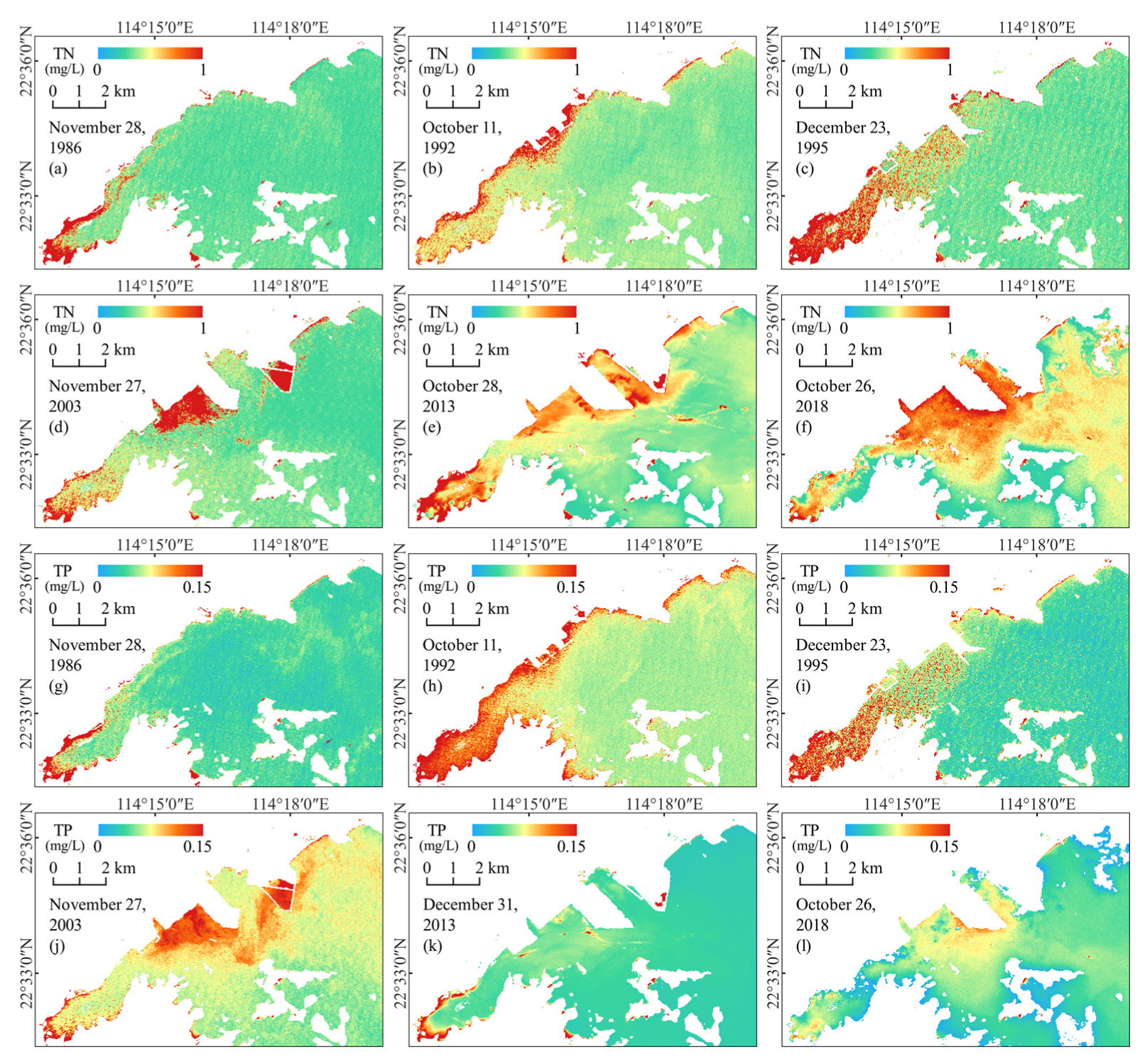
3.2. Spatial Distribution
3.3. Inter-Annual Changes
3.4. Intra-Annual Changes
4. Discussion
4.1. Impact of Urbanization
4.2. Impact of Rivers
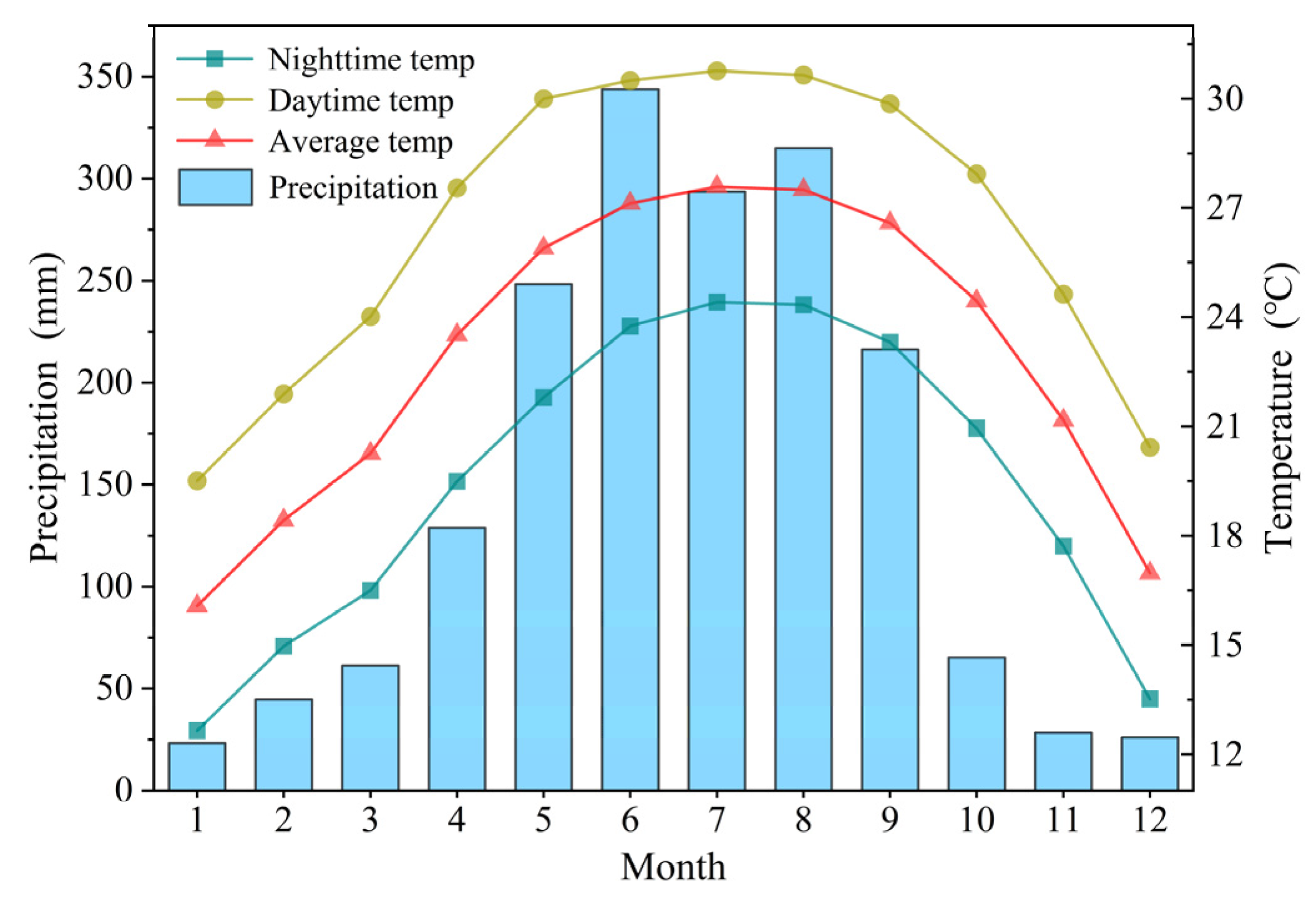
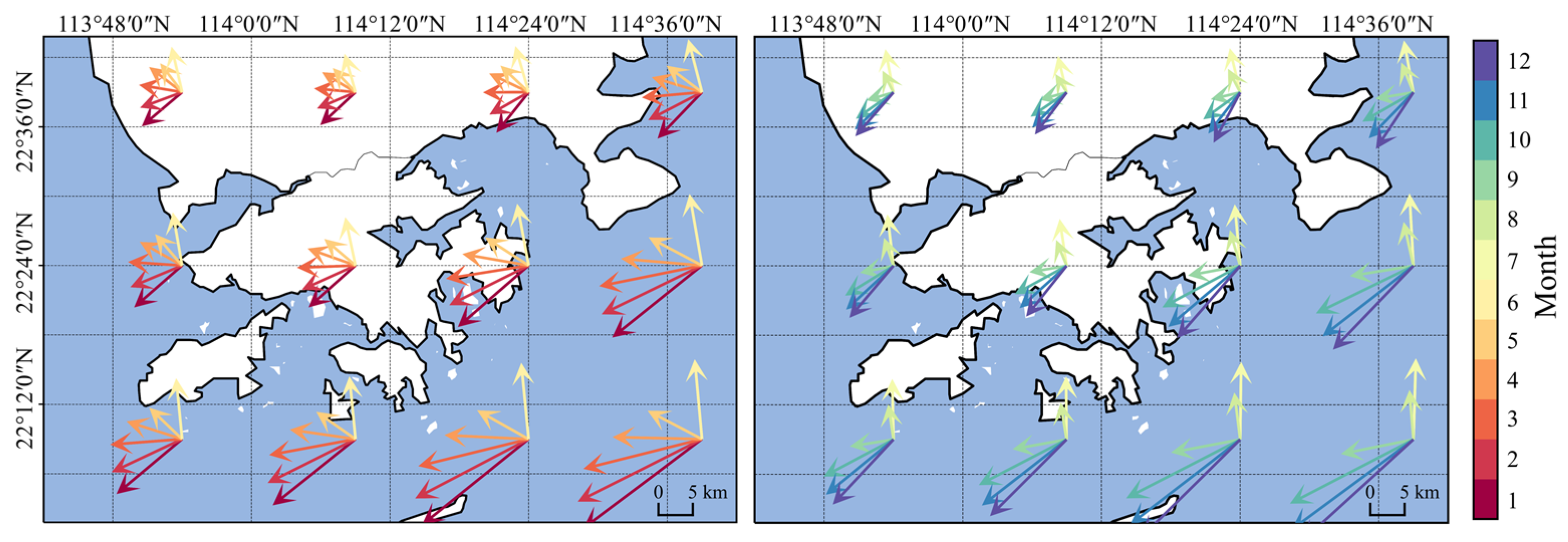
4.3. Impact of Climate
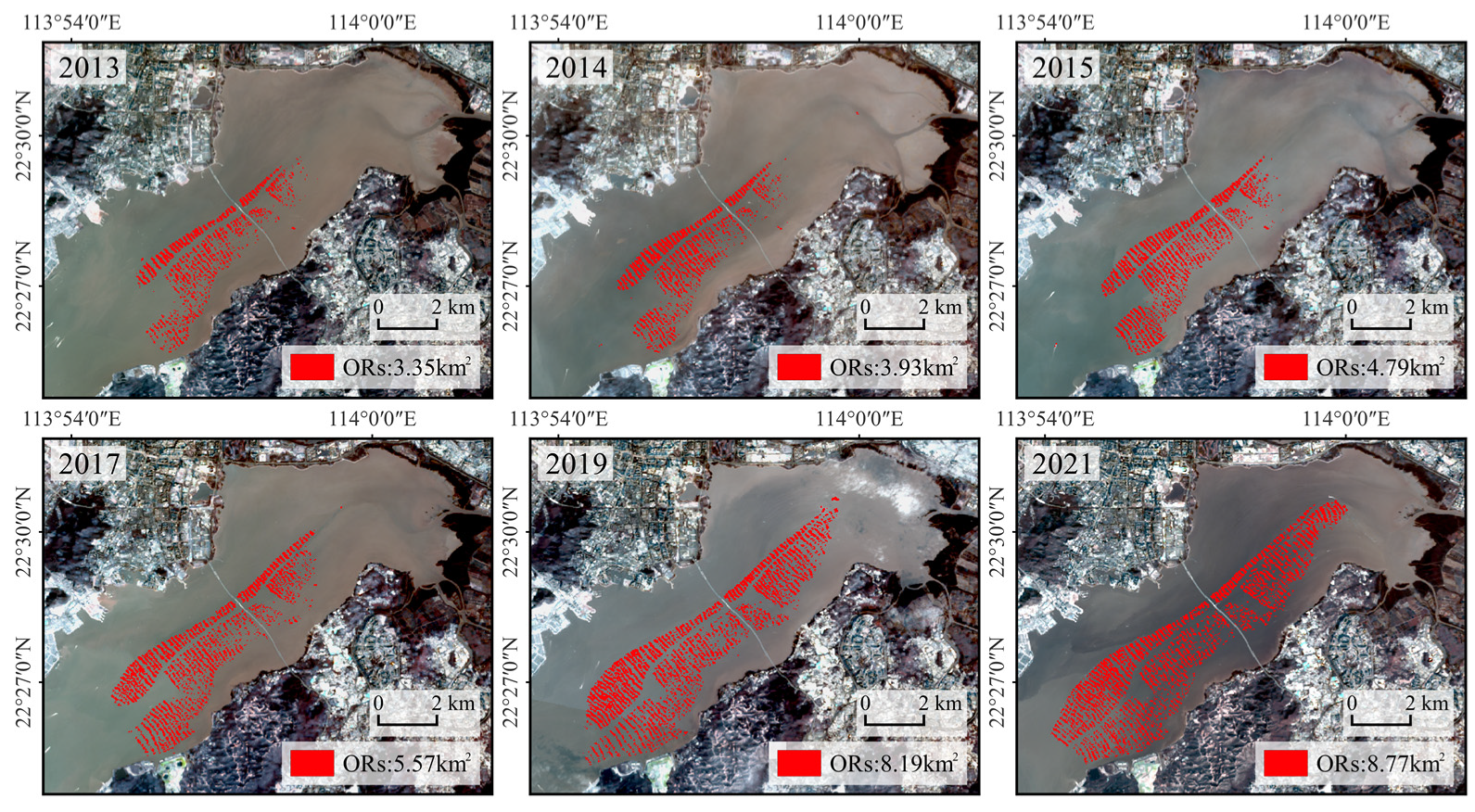
4.4. Impact of Oyster Farming
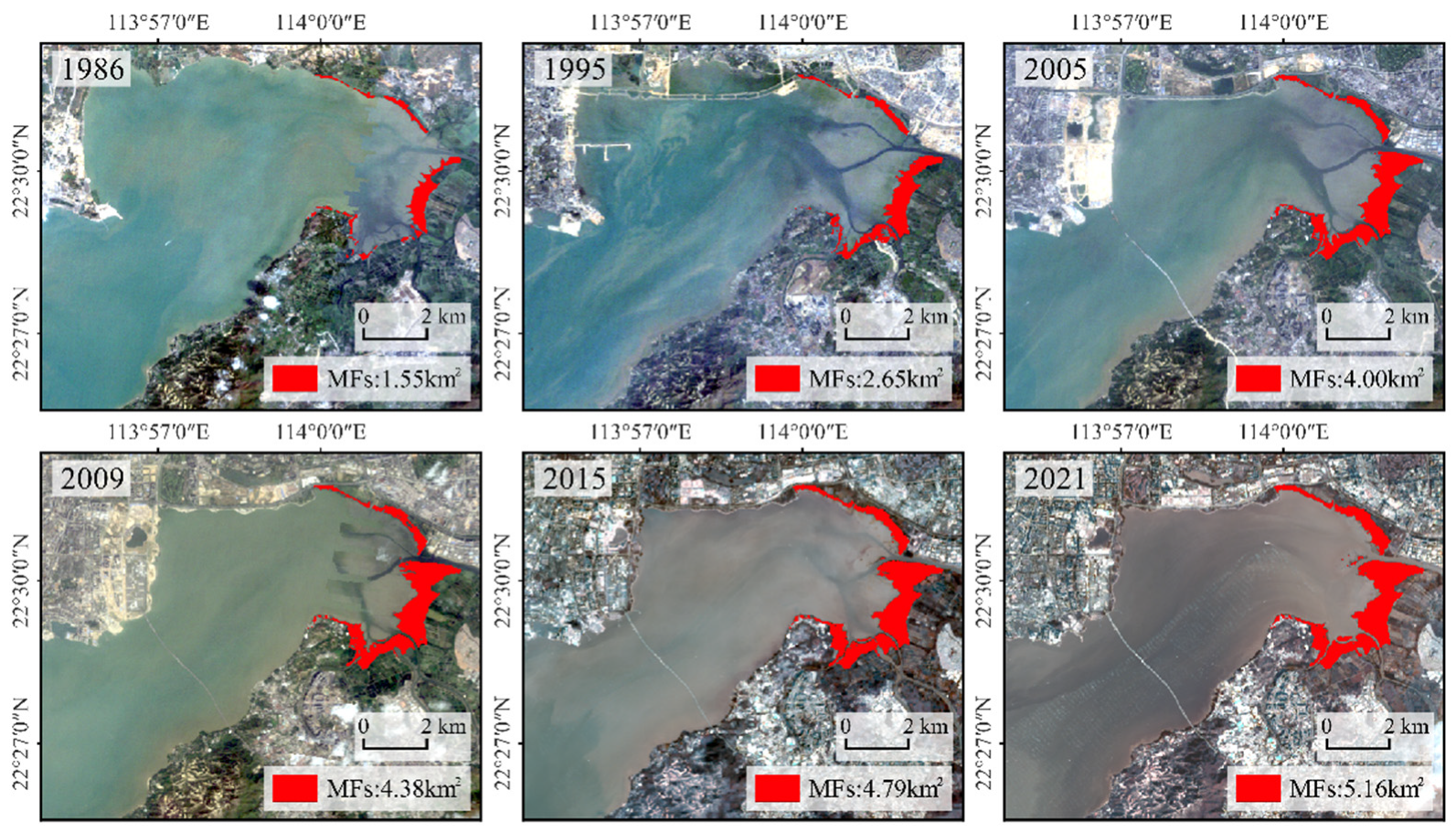
4.5. Impact of Mangrove Forests
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Neumann, B.; Vafeidis, A.T.; Zimmermann, J.; Nicholls, R.J. Future Coastal Population Growth and Exposure to Sea-Level Rise and Coastal Flooding—A Global Assessment. PLoS ONE 2015, 10, e0118571. [Google Scholar] [CrossRef] [Green Version]
- Kitamori, K.; Manders, T.; Dellink, R.; Tabeau, A. OECD Environmental Outlook to 2050: The Consequences of Inaction; 9264122168; OECD: Paris, France, 2012. [Google Scholar]
- World Health Organization; UNICEF. Meeting the MDG Drinking Water and Sanitation Target: The Urban and Rural Challenge of the Decade; World Health Organization: Geneva, Switzerland; UNICEF: New York, NY, USA, 2006. [Google Scholar]
- Ritchie, J.C.; Zimba, P.V.; Everitt, J.H. Remote sensing techniques to assess water quality. Photogramm. Eng. Remote Sens. 2003, 69, 695–704. [Google Scholar] [CrossRef] [Green Version]
- Mouw, C.B.; Greb, S.; Aurin, D.; DiGiacomo, P.M.; Lee, Z.; Twardowski, M.; Binding, C.; Hu, C.; Ma, R.; Moore, T.; et al. Aquatic color radiometry remote sensing of coastal and inland waters: Challenges and recommendations for future satellite missions. Remote Sens. Environ. 2015, 160, 15–30. [Google Scholar] [CrossRef]
- Doña, C.; Sánchez, J.M.; Caselles, V.; Domínguez, J.A.; Camacho, A. Empirical relationships for monitoring water quality of lakes and reservoirs through multispectral images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1632–1641. [Google Scholar] [CrossRef]
- Härmä, P.; Vepsäläinen, J.; Hannonen, T.; Pyhälahti, T.; Kämäri, J.; Kallio, K.; Eloheimo, K.; Koponen, S. Detection of water quality using simulated satellite data and semi-empirical algorithms in Finland. Sci. Total Environ. 2001, 268, 107–121. [Google Scholar] [CrossRef]
- Gordon, H.R.; Brown, O.B.; Jacobs, M.M. Computed Relationships Between the Inherent and Apparent Optical Properties of a Flat Homogeneous Ocean. Appl. Opt. 1975, 14, 417–427. [Google Scholar] [CrossRef]
- Dall’Olmo, G.; Gitelson, A.A.; Rundquist, D.C. Towards a unified approach for remote estimation of chlorophyll-a in both terrestrial vegetation and turbid productive waters. Geophys. Res. Lett. 2003, 30, 1938. [Google Scholar] [CrossRef] [Green Version]
- Chacon-Torres, A.; Ross, L.G.; Beveridge, M.C.M.; Watson, A.I. The application of SPOT multispectral imagery for the assessment of water quality in Lake Patzcuaro, Mexico. Int. J. Remote Sens. 1992, 13, 587–603. [Google Scholar] [CrossRef]
- Lim, J.; Choi, M. Assessment of water quality based on Landsat 8 operational land imager associated with human activities in Korea. Environ. Monit. Assess. 2015, 187, 384. [Google Scholar] [CrossRef]
- Gholizadeh, M.H.; Melesse, A.M.; Reddi, L. A Comprehensive Review on Water Quality Parameters Estimation Using Remote Sensing Techniques. Sensors 2016, 16, 1298. [Google Scholar] [CrossRef] [Green Version]
- Sagan, V.; Peterson, K.T.; Maimaitijiang, M.; Sidike, P.; Sloan, J.; Greeling, B.A.; Maalouf, S.; Adams, C. Monitoring inland water quality using remote sensing: Potential and limitations of spectral indices, bio-optical simulations, machine learning, and cloud computing. Earth-Sci. Rev. 2020, 205, 103187. [Google Scholar] [CrossRef]
- Niu, C.; Tan, K.; Jia, X.; Wang, X. Deep learning based regression for optically inactive inland water quality parameter estimation using airborne hyperspectral imagery. Environ. Pollut. 2021, 286, 117534. [Google Scholar] [CrossRef] [PubMed]
- Paerl, H.W.; Otten, T.G. Harmful Cyanobacterial Blooms: Causes, Consequences, and Controls. Microb. Ecol. 2013, 65, 995–1010. [Google Scholar] [CrossRef] [PubMed]
- Carlson, R.E. A trophic state index for lakes1. Limnol. Oceanogr. 1977, 22, 361–369. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Zhang, Y.; Shi, K.; Zhu, G.; Zhou, Y.; Zhang, Y.; Guo, Y. Monitoring spatiotemporal variations in nutrients in a large drinking water reservoir and their relationships with hydrological and meteorological conditions based on Landsat 8 imagery. Sci. Total Environ. 2017, 599–600, 1705–1717. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.; Zhang, Y.; Shi, K.; Zhang, Y.; Li, N.; Wang, W.; Huang, X.; Qin, B. Monitoring water quality using proximal remote sensing technology. Sci. Total Environ. 2022, 803, 149805. [Google Scholar] [CrossRef]
- Mathew, M.M.; Srinivasa Rao, N.; Mandla, V.R. Development of regression equation to study the Total Nitrogen, Total Phosphorus and Suspended Sediment using remote sensing data in Gujarat and Maharashtra coast of India. J. Coast. Conserv. 2017, 21, 917–927. [Google Scholar] [CrossRef]
- Gao, Y.; Gao, J.; Yin, H.; Liu, C.; Xia, T.; Wang, J.; Huang, Q. Remote sensing estimation of the total phosphorus concentration in a large lake using band combinations and regional multivariate statistical modeling techniques. J. Environ. Manag. 2015, 151, 33–43. [Google Scholar] [CrossRef]
- Dong, G.; Hu, Z.; Liu, X.; Fu, Y.; Zhang, W. Spatio-Temporal Variation of Total Nitrogen and Ammonia Nitrogen in the Water Source of the Middle Route of the South-To-North Water Diversion Project. Water 2020, 12, 2615. [Google Scholar] [CrossRef]
- Vakili, T.; Amanollahi, J. Determination of optically inactive water quality variables using Landsat 8 data: A case study in Geshlagh reservoir affected by agricultural land use. J. Clean. Prod. 2020, 247, 119134. [Google Scholar] [CrossRef]
- Xiong, J.; Lin, C.; Cao, Z.; Hu, M.; Xue, K.; Chen, X.; Ma, R. Development of remote sensing algorithm for total phosphorus concentration in eutrophic lakes: Conventional or machine learning? Water Res. 2022, 215, 118213. [Google Scholar] [CrossRef] [PubMed]
- Hafeez, S.; Wong, M.S.; Ho, H.C.; Nazeer, M.; Nichol, J.; Abbas, S.; Tang, D.; Lee, K.H.; Pun, L. Comparison of Machine Learning Algorithms for Retrieval of Water Quality Indicators in Case-II Waters: A Case Study of Hong Kong. Remote Sens. 2019, 11, 617. [Google Scholar] [CrossRef] [Green Version]
- Qiao, Z.; Sun, S.; Jiang, Q.O.; Xiao, L.; Wang, Y.; Yan, H. Retrieval of Total Phosphorus Concentration in the Surface Water of Miyun Reservoir Based on Remote Sensing Data and Machine Learning Algorithms. Remote Sens. 2021, 13, 4662. [Google Scholar] [CrossRef]
- Qun’ou, J.; Lidan, X.; Siyang, S.; Meilin, W.; Huijie, X. Retrieval model for total nitrogen concentration based on UAV hyper spectral remote sensing data and machine learning algorithms—A case study in the Miyun Reservoir, China. Ecol. Indic. 2021, 124, 107356. [Google Scholar] [CrossRef]
- Huang, J.; Wang, D.; Gong, F.; Bai, Y.; He, X. Changes in Nutrient Concentrations in Shenzhen Bay Detected Using Landsat Imagery between 1988 and 2020. Remote Sens. 2021, 13, 3469. [Google Scholar] [CrossRef]
- Wang, C.; Li, W.; Chen, S.; Li, D.; Wang, D.; Liu, J. The spatial and temporal variation of total suspended solid concentration in Pearl River Estuary during 1987–2015 based on remote sensing. Sci. Total Environ. 2018, 618, 1125–1138. [Google Scholar] [CrossRef]
- Nazeer, M.; Nichol, J.E. Combining Landsat TM/ETM+ and HJ-1 A/B CCD Sensors for Monitoring Coastal Water Quality in Hong Kong. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1898–1902. [Google Scholar] [CrossRef]
- Feng, T.; Xu, N. Satellite-Based Monitoring of Annual Coastal Reclamation in Shenzhen and Hong Kong since the 21st Century: A Comparative Study. J. Mar. Sci. Eng. 2021, 9, 48. [Google Scholar] [CrossRef]
- Huang, X.; Li, J.; Yang, J.; Zhang, Z.; Li, D.; Liu, X. 30 m global impervious surface area dynamics and urban expansion pattern observed by Landsat satellites: From 1972 to 2019. Sci. China Earth Sci. 2021, 64, 1922–1933. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [Green Version]
- Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Muñoz Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I.; et al. ERA5 monthly averaged data on single levels from 1959 to present. In Copernicus Climate Change Service (C3S) Climate Data Store (CDS); Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/10.24381/cds.f17050d7?tab=overview (accessed on 10 April 2022).
- Xu, H. Modification of normalised difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Routledge: London, UK, 1984. [Google Scholar]
- Sutton, C.D. 11—Classification and Regression Trees, Bagging, and Boosting. In Handbook of Statistics; Rao, C.R., Wegman, E.J., Solka, J.L., Eds.; Elsevier: Amsterdam, The Netherlands, 2005; Volume 24, pp. 303–329. [Google Scholar]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef] [Green Version]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- An, C.; Xie, C.; Meng, Y.; Shi, X.; Yang, C. Large Deformation Modeling of Wing-Like Structures Based on Support Vector Regression. Appl. Sci. 2020, 10, 5995. [Google Scholar] [CrossRef]
- Dibike, Y.B.; Velickov, S.; Solomatine, D.; Abbott Michael, B. Model Induction with Support Vector Machines: Introduction and Applications. J. Comput. Civ. Eng. 2001, 15, 208–216. [Google Scholar] [CrossRef]
- Verrelst, J.; Muñoz, J.; Alonso, L.; Delegido, J.; Rivera, J.P.; Camps-Valls, G.; Moreno, J. Machine learning regression algorithms for biophysical parameter retrieval: Opportunities for Sentinel-2 and -3. Remote Sens. Environ. 2012, 118, 127–139. [Google Scholar] [CrossRef]
- Yuan, J.; Wang, K.; Yu, T.; Fang, M. Reliable multi-objective optimization of high-speed WEDM process based on Gaussian process regression. Int. J. Mach. Tools Manuf. 2008, 48, 47–60. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Widrow, B.; Rumelhart, D.E.; Lehr, M.A. Neural networks: Applications in industry, business and science. Commun. ACM 1994, 37, 93–105. [Google Scholar] [CrossRef]
- Refaeilzadeh, P.; Tang, L.; Liu, H. Cross-validation. Encycl. Database Syst. 2009, 5, 532–538. [Google Scholar]
- Yang, L.; Shami, A. On hyperparameter optimization of machine learning algorithms: Theory and practice. Neurocomputing 2020, 415, 295–316. [Google Scholar] [CrossRef]
- Wu, J.; Chen, X.-Y.; Zhang, H.; Xiong, L.-D.; Lei, H.; Deng, S.-H. Hyperparameter Optimization for Machine Learning Models Based on Bayesian Optimizationb. J. Electron. Sci. Technol. 2019, 17, 26–40. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Y.; Li, Z.; Peng, J. Impervious surface impact on water quality in the process of rapid urbanization in Shenzhen, China. Environ. Earth Sci. 2013, 68, 2365–2373. [Google Scholar] [CrossRef]
- Luo, Y.; Zhao, Y.; Yang, K.; Chen, K.; Pan, M.; Zhou, X. Dianchi Lake watershed impervious surface area dynamics and their impact on lake water quality from 1988 to 2017. Environ. Sci. Pollut. Res. 2018, 25, 29643–29653. [Google Scholar] [CrossRef]
- He, L.; Wang, J.; Liu, Y.; Zhang, Y.; He, C.; Yu, Q.; Ma, W. Selection of onshore sites based on monitoring possibility evaluation of exhausts from individual ships for Yantian Port, China. Atmos. Environ. 2021, 247, 118187. [Google Scholar] [CrossRef]
- Shaikh, S.M.S.; Tagde, J.P.; Singh, P.R.; Dutta, S.; Sangolkar, L.N.; Kumar, M.S. Impact of Port and harbour activities on plankton distribution and dynamics: A multivariate approach. Mar. Pollut. Bull. 2021, 165, 112105. [Google Scholar] [CrossRef]
- Le Moal, M.; Gascuel-Odoux, C.; Ménesguen, A.; Souchon, Y.; Étrillard, C.; Levain, A.; Moatar, F.; Pannard, A.; Souchu, P.; Lefebvre, A.; et al. Eutrophication: A new wine in an old bottle? Sci. Total Environ. 2019, 651, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Wang, G.; Zhang, B.; Li, J.; Zhang, H.; Shen, Q.; Wu, D.; Song, Y. Study on Monitoring of Red Tide by Multi-Spectral Remote Sensing Based on HJ-CCD and MODIS. Procedia Environ. Sci. 2011, 11, 1561–1565. [Google Scholar] [CrossRef] [Green Version]
- Yudhistira, M.H.; Karimah, I.D.; Maghfira, N.R. The effect of port development on coastal water quality: Evidence of eutrophication states in Indonesia. Ecol. Econ. 2022, 196, 107415. [Google Scholar] [CrossRef]
- Sin, Y.S.; Chau, K.W. Eutrophication Studies on Tolo Harbour, Hong Kong. Water Sci. Technol. 1992, 26, 2551–2554. [Google Scholar] [CrossRef]
- HKEPD. Regional Collaboration with Shenzhen in Deep Bay (Shenzhen Bay). Available online: https://www.epd.gov.hk/epd/english/environmentinhk/water/hkwqrc/regional/deepbay.html (accessed on 5 May 2022).
- Bureau, S.M.E.A.E. Annual Environmental Status Bulletin. Available online: http://meeb.sz.gov.cn/xxgk/tjsj/ndhjzkgb (accessed on 5 May 2022).
- Deng, T.; Duan, H.-F.; Keramat, A. Spatiotemporal characterization and forecasting of coastal water quality in the semi-enclosed Tolo Harbour based on machine learning and EKC analysis. Eng. Appl. Comput. Fluid Mech. 2022, 16, 694–712. [Google Scholar] [CrossRef]
- Deng, T.; Chau, K.-W.; Duan, H.-F. Machine learning based marine water quality prediction for coastal hydro-environment management. J. Environ. Manag. 2021, 284, 112051. [Google Scholar] [CrossRef] [PubMed]
- HKEPD. Annual Marine Water Quality Reports. Available online: https://www.epd.gov.hk/epd/english/environmentinhk/water/hkwqrc/waterquality/marine-2.html (accessed on 5 May 2022).
- Delpla, I.; Jung, A.V.; Baures, E.; Clement, M.; Thomas, O. Impacts of climate change on surface water quality in relation to drinking water production. Environ. Int. 2009, 35, 1225–1233. [Google Scholar] [CrossRef]
- Sardans, J.; Peñuelas, J.; Estiarte, M. Changes in soil enzymes related to C and N cycle and in soil C and N content under prolonged warming and drought in a Mediterranean shrubland. Appl. Soil Ecol. 2008, 39, 223–235. [Google Scholar] [CrossRef]
- Dong, L.; Su, J.; Ah Wong, L.; Cao, Z.; Chen, J.-C. Seasonal variation and dynamics of the Pearl River plume. Cont. Shelf Res. 2004, 24, 1761–1777. [Google Scholar] [CrossRef]
- Harrison, P.J.; Yin, K.; Lee, J.H.W.; Gan, J.; Liu, H. Physical–biological coupling in the Pearl River Estuary. Cont. Shelf Res. 2008, 28, 1405–1415. [Google Scholar] [CrossRef]
- Zhao, Y.; Song, Y.; Cui, J.; Gan, S.; Yang, X.; Wu, R.; Guo, P. Assessment of Water Quality Evolution in the Pearl River Estuary (South Guangzhou) from 2008 to 2017. Water 2020, 12, 59. [Google Scholar]
- Ou, S.; Yang, Q.; Luo, X.; Zhu, F.; Luo, K.; Yang, H. The influence of runoff and wind on the dispersion patterns of suspended sediment in the Zhujiang (Pearl) River Estuary based on MODIS data. Acta Oceanol. Sin. 2019, 38, 26–35. [Google Scholar] [CrossRef]
- Kedong, Y. Monsoonal influence on seasonal variations in nutrients and phytoplankton biomass in coastal waters of Hong Kong in the vicinity of the Pearl River estuary. Mar. Ecol. Prog. Ser. 2002, 245, 111–122. [Google Scholar]
- Ray, N.E.; Li, J.; Kangas, P.C.; Terlizzi, D.E. Water quality upstream and downstream of a commercial oyster aquaculture facility in Chesapeake Bay, USA. Aquac. Eng. 2015, 68, 35–42. [Google Scholar] [CrossRef]
- Feng, Z.; Tan, G.; Xia, J.; Shu, C.; Chen, P.; Wu, M.; Wu, X. Dynamics of mangrove forests in Shenzhen Bay in response to natural and anthropogenic factors from 1988 to 2017. J. Hydrol. 2020, 591, 125271. [Google Scholar] [CrossRef]
- Lotfinasabasl, S.; Gunale, V.R.; Khosroshahi, M. Applying geographic information systems and remote sensing for water quality assessment of mangrove forest. Acta Ecol. Sin. 2018, 38, 135–143. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring vegetation systems in the great plains with ERTS. In Proceedings of the Third ERTS Symposium, NASA SP-351, I, Washington, DC, USA, 10–14 December 1973; pp. 309–317. [Google Scholar]
- Filella, I.; Penuelas, J. The red edge position and shape as indicators of plant chlorophyll content, biomass and hydric status. Int. J. Remote Sens. 1994, 15, 1459–1470. [Google Scholar] [CrossRef]
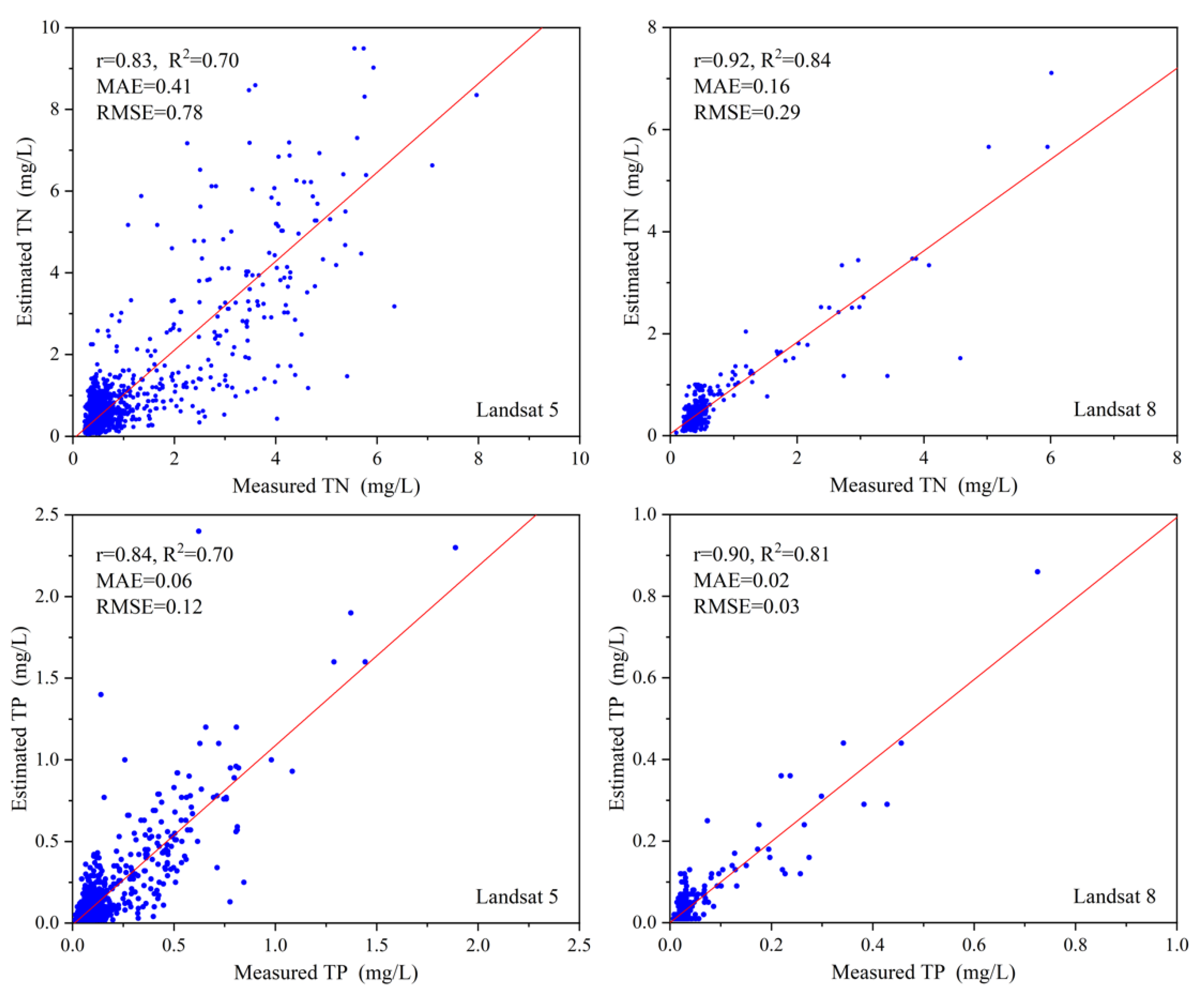
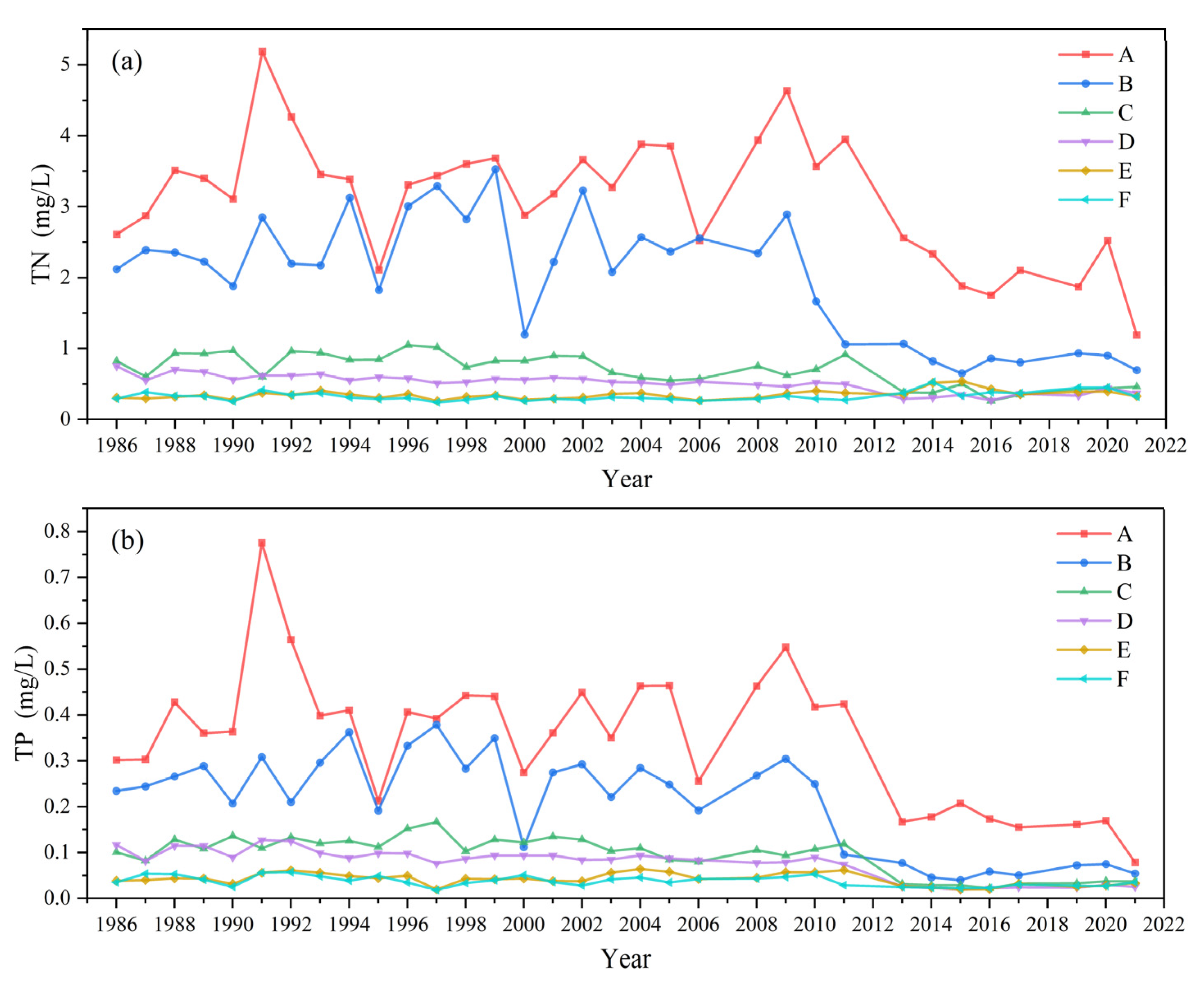
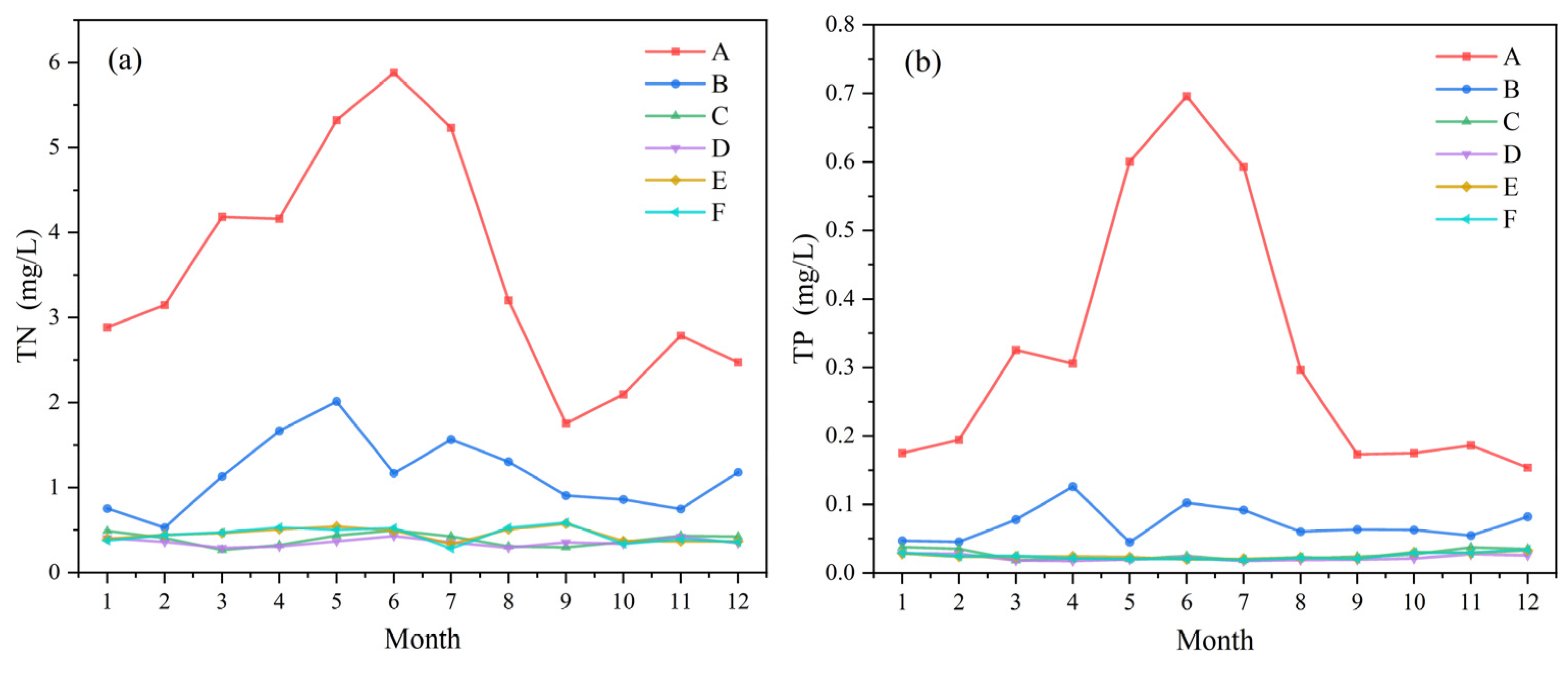
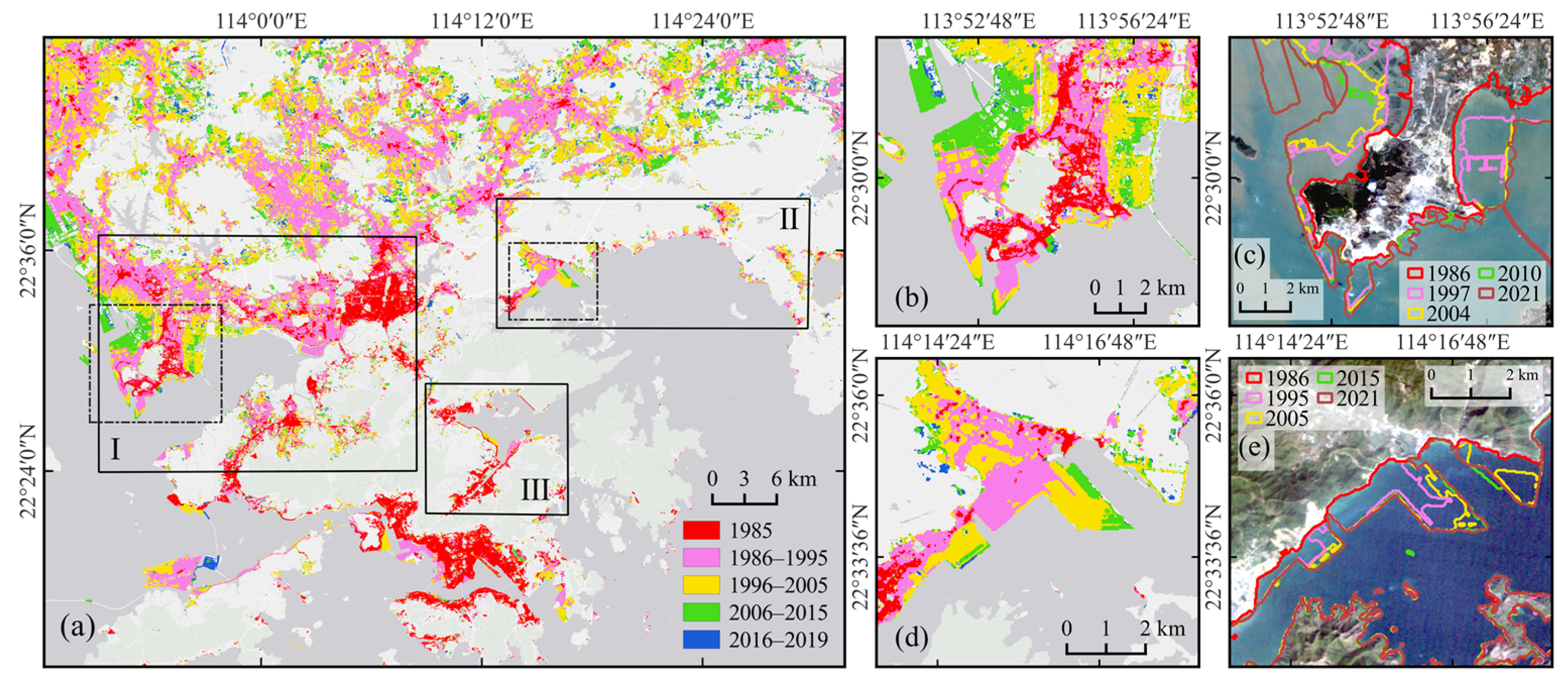
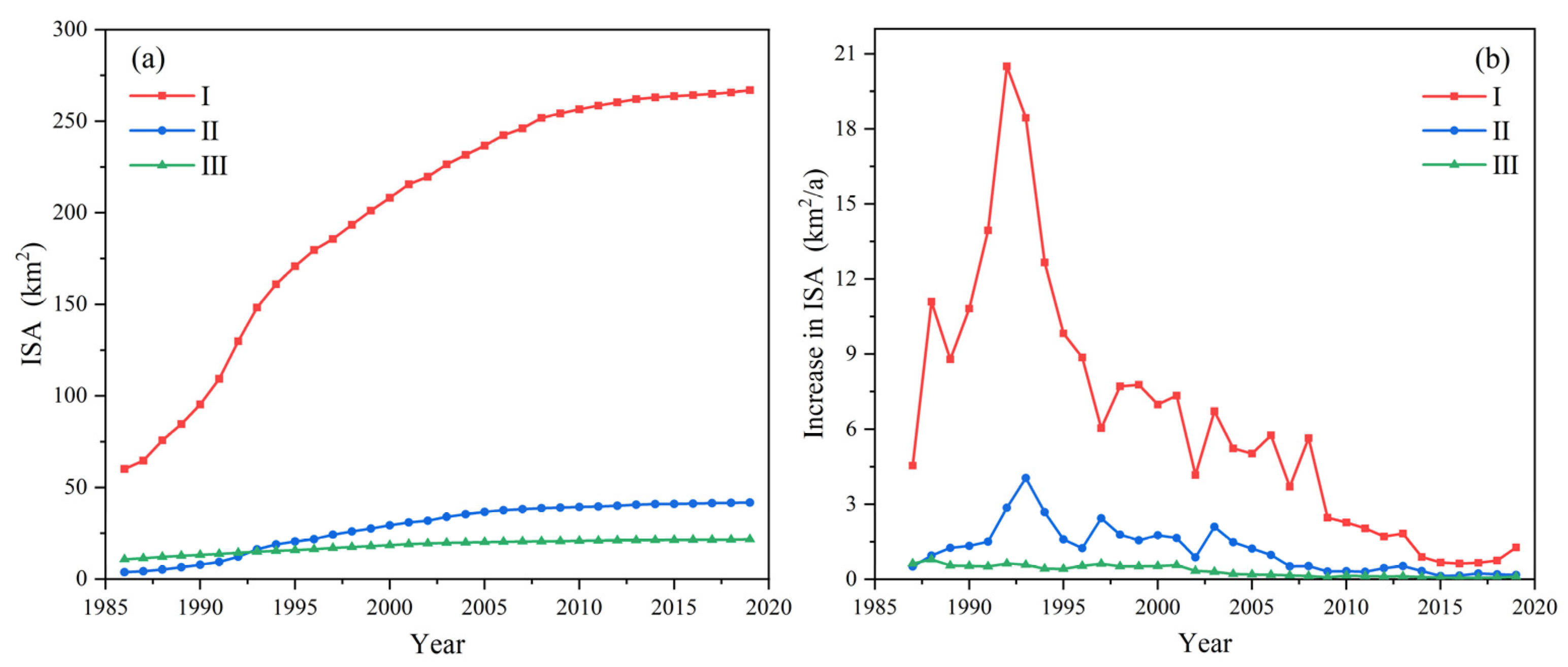
| Method | Hyperparameter | TN-L5 | TN-L8 | TP-L5 | TP-L8 |
|---|---|---|---|---|---|
| TE | Ensemble method | LS Boost | LS Boost | LS Boost | Bag |
| Isotropic Exponential | 448 | 18 | 399 | 28 | |
| Learning rate | 0.1343 | 0.4849 | 0.0254 | / | |
| Minimum leaf size | 2 | 1 | 2 | 2 | |
| SVM | Kernel function | Gaussian | Quadratic | Quadratic | Linear |
| Box constraint | 79.6126 | 0.0814 | 1.5765 | 0.6258 | |
| Kernel scale | 2.3638 | / | / | / | |
| Epsilon | 0.3972 | 2.49 × 10−4 | 0.1125 | 0.0048 | |
| GPR | Basis function | Constant | Linear | Zero | Linear |
| Kernel function | Non-isotropic Rational Quadratic | Non-isotropic Matem 3/2 | Isotropic Exponential | Isotropic Matem 5/2 | |
| Kernel scale | 1988.3 | / | 1114.7 | 3.46 | |
| Sigma | 1.89 × 10−4 | 0.0978 | 0.1081 | 0.0066 | |
| BPNN | Activation | ReLU | ReLU | ReLU | Sigmoid |
| Number of layers | 2 | 2 | 2 | 3 | |
| Regularization strength (Lambda) | 0.0143 | 0.0059 | 0.0007 | 2.95 × 10−5 | |
| Number of neurons in the first hidden layer | 82 | 256 | 47 | 139 | |
| Number of neurons in the second hidden layer | 115 | 101 | 3 | 4 | |
| Number of neurons in the third hidden layer | / | / | / | 4 |
| Model | Method | 5-fold | Training Set | Test Set | All Data | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | r | R2 | MAE | RMSE | r | R2 | MAE | RMSE | r | R2 | MAE | RMSE | ||
| TN-L5 | TE | 0.85 | 1.00 | 0.99 | 0.07 | 0.10 | 0.76 | 0.57 | 0.52 | 1.19 | 0.92 | 0.85 | 0.16 | 0.54 |
| SVR | 0.92 | 0.83 | 0.68 | 0.40 | 0.75 | 0.73 | 0.53 | 0.57 | 1.28 | 0.80 | 0.63 | 0.44 | 0.88 | |
| GPR | 0.85 | 1.00 | 1.00 | 0.00 | 0.00 | 0.80 | 0.63 | 0.46 | 1.11 | 0.94 | 0.88 | 0.09 | 0.50 | |
| BPNN | 0.83 | 0.86 | 0.73 | 0.38 | 0.67 | 0.79 | 0.62 | 0.51 | 1.13 | 0.83 | 0.70 | 0.41 | 0.78 | |
| TN-L8 | TE | 0.45 | 0.99 | 0.98 | 0.07 | 0.09 | 0.57 | 0.32 | 0.33 | 0.71 | 0.90 | 0.81 | 0.12 | 0.33 |
| SVR | 0.33 | 0.92 | 0.85 | 0.18 | 0.30 | 0.73 | 0.53 | 0.27 | 0.54 | 0.86 | 0.74 | 0.20 | 0.36 | |
| GPR | 0.34 | 0.98 | 0.96 | 0.11 | 0.14 | 0.70 | 0.49 | 0.28 | 0.59 | 0.92 | 0.84 | 0.14 | 0.29 | |
| BPNN | 0.35 | 0.96 | 0.93 | 0.14 | 0.20 | 0.82 | 0.67 | 0.24 | 0.51 | 0.92 | 0.84 | 0.16 | 0.29 | |
| TP-L5 | TE | 0.14 | 0.94 | 0.89 | 0.04 | 0.07 | 0.71 | 0.51 | 0.09 | 0.19 | 0.87 | 0.76 | 0.05 | 0.10 |
| SVR | 0.14 | 0.61 | 0.37 | 0.09 | 0.15 | 0.68 | 0.47 | 0.11 | 0.21 | 0.63 | 0.40 | 0.09 | 0.17 | |
| GPR | 0.14 | 1.00 | 1.00 | 0.00 | 0.00 | 0.76 | 0.58 | 0.08 | 0.18 | 0.93 | 0.86 | 0.02 | 0.08 | |
| BPNN | 0.14 | 0.87 | 0.75 | 0.06 | 0.10 | 0.77 | 0.60 | 0.08 | 0.17 | 0.84 | 0.70 | 0.06 | 0.12 | |
| TP-L8 | TE | 0.05 | 0.92 | 0.84 | 0.01 | 0.03 | 0.65 | 0.42 | 0.03 | 0.05 | 0.85 | 0.73 | 0.02 | 0.04 |
| SVR | 0.05 | 0.73 | 0.53 | 0.02 | 0.05 | 0.76 | 0.58 | 0.02 | 0.04 | 0.73 | 0.54 | 0.02 | 0.05 | |
| GPR | 0.05 | 0.95 | 0.89 | 0.02 | 0.02 | 0.68 | 0.46 | 0.03 | 0.06 | 0.87 | 0.76 | 0.02 | 0.04 | |
| BPNN | 0.05 | 0.92 | 0.85 | 0.02 | 0.03 | 0.79 | 0.63 | 0.02 | 0.04 | 0.90 | 0.81 | 0.02 | 0.03 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Zhang, G.; Zhu, Y.; Kaufmann, H.; Xu, G. Inversion and Driving Force Analysis of Nutrient Concentrations in the Ecosystem of the Shenzhen-Hong Kong Bay Area. Remote Sens. 2022, 14, 3694. https://doi.org/10.3390/rs14153694
Li H, Zhang G, Zhu Y, Kaufmann H, Xu G. Inversion and Driving Force Analysis of Nutrient Concentrations in the Ecosystem of the Shenzhen-Hong Kong Bay Area. Remote Sensing. 2022; 14(15):3694. https://doi.org/10.3390/rs14153694
Chicago/Turabian StyleLi, Hanyu, Guangzong Zhang, Yuyan Zhu, Hermann Kaufmann, and Guochang Xu. 2022. "Inversion and Driving Force Analysis of Nutrient Concentrations in the Ecosystem of the Shenzhen-Hong Kong Bay Area" Remote Sensing 14, no. 15: 3694. https://doi.org/10.3390/rs14153694
APA StyleLi, H., Zhang, G., Zhu, Y., Kaufmann, H., & Xu, G. (2022). Inversion and Driving Force Analysis of Nutrient Concentrations in the Ecosystem of the Shenzhen-Hong Kong Bay Area. Remote Sensing, 14(15), 3694. https://doi.org/10.3390/rs14153694







