A Novel Method to Simultaneously Measure Leaf Gas Exchange and Water Content

Abstract

Understanding the relationship between plant water status and productivity and between plant water status and plant mortality is required to effectively quantify and predict the effects of drought on plants. Plant water status is closely linked to leaf water content that may be estimated using remote sensing technologies. Here, we used an inexpensive miniature hyperspectral spectrometer in the 1550–1950 nm wavelength domain to measure changes in silver birch (Betula pendula Roth) leaf water content combined with leaf gas exchange measurements at a sub-minute time resolution, under increasing vapor pressure deficit, CO₂ concentrations, and light intensity within the measurement cuvette; we also developed a novel methodology for calibrating reflectance measurements to predict leaf water content for individual leaves. Based on reflectance at 1550 nm, linear regression modeling explained 98–99% of the variation in leaf water content, with a root mean square error of 0.31–0.43 g cm⁻². The prediction accuracy of the model represents a c. ten-fold improvement compared to previous studies that have used destructive sampling measurements of several leaves. This novel methodology allows the study of interlinkages between leaf water content, transpiration, and assimilation at a high time resolution that will increase understanding of the movement of water within plants and between plants and the atmosphere.

1. Introduction

Water is an essential element for all living organisms; for example, water content of plants tends to be >50%, facilitating key physiological processes such as the transport of nutrients and chemicals [1,2]. Understanding the mechanisms of tree–water relations requires careful measurements and quantification of leaf water content in different environmental conditions [3]. Water is drawn from the soil by tree roots under continual negative water potential, driven by atmospheric evaporative demand [4], where differences in water potential between the atmosphere and soil cause root water uptake and subsequent evaporation through stomata; adjustments in stomatal opening control the amount of evaporation and prevent hydraulic failure [5]. As leaf water potential decreases, water is drawn from neighboring tissues, causing water potentials of the branch, stem, roots, and soil to decrease sequentially and triggering water movement from the soil towards the upper canopy. Given the highly dynamic nature of water movement in trees, accurate and precise measurement of the process is required to allow the prediction, through modeling, of effects of altered water availability [6].

Plant and tree water status has traditionally been measured using destructive measurements, such as the use of a pressure chamber to record water potential [7], and non-destructive techniques, such as dendrometers that allow the measurement of diurnal stem diameter dynamics, which are closely linked to stem water potential [8,9], and psychrometers that can be used to measure stem and leaf water potential [10,11]. These traditional methods, however, are labor-intensive and spatially and temporally restricted, challenges that could be resolved using remote sensing. Given the electromagnetic spectrum is sensitive to water content, recent technological advancements have led to the development of leaf water content estimation applications using remote sensing [12,13], including optical imaging, laser, radar and microwave scanning, and Raman spectroscopy [14,15,16,17,18]. However, the accuracy of these applications at high time resolutions required for understanding leaf water dynamics is suboptimal [18].

The miniaturization of hyperspectral sensors presents novel opportunities for the use of remote sensing applications in improving estimations of leaf water content based on spectral signatures [19]. However, variation in leaf structure and density may be confounded with variation in leaf water content when leaf reflectance is sensed at similar wavelengths [12]. Thus, the elimination of effects of variation in leaf structure and density from measurements of reflectance allows for a more precise estimation of leaf water content [12,20].

Here, we test the use of a miniature hyperspectral sensor in the 1550–1950 nm wavelength domain to measure changes in leaf reflectance combined with leaf gas exchange measurements as a novel methodology for investigating leaf water dynamics in the studying of plant water relations. The tested sensor has shown high potential for measuring variations in leaf water content [20]. We hypothesize that we can use leaf transpiration measurements to calibrate leaf reflectance-based leaf water content measurements and improve the estimation accuracy of leaf water content. We demonstrate this novel approach using silver birch leaves measured under varying CO₂ concentration, light intensity, and vapor pressure deficit (VPD) within the measurement cuvette.

2. Materials and Methods

2.1. Experiment Design

We used a NIRONE S2.0 hyperspectral sensor (Spectral Engines Oy, Espoo, Finland), at 1550–1950 nm wavelength, fitted with a tungsten lamp as an illumination source; full width at half maximum of the sensor was 10 nm. Light entered the detector through a 1 mm diameter pin hole with a sensor opening angle of approximately 8°. The sensor parameters were a point average of 180 and a scan average of 10, where measurements were acquired every 10 s and at 5 nm intervals along the spectrum. Prior to recording the measurements, we allowed the sensor to warm up for at least 15 min, and a white reference target was used to calibrate the spectral measurements before the start of each measurement.

Given that shortwave infrared reflectance (SWIR) is affected at some wavelengths by the water vapor content of air, we investigated the spectral domain sensitivity of the sensor to changes in absolute water concentration of air using a leaf gas exchange analyzer (GFS-3000, Walz GmbH, Heinz, Germany) by recording content of an empty cuvette through a glass panel, as air water vapor concentration varied within the cuvette from 10,660 to 28,750 ppm at 30 °C; the flow was set to 650 µmol/s during this test. We set the NIRONE S2.0 sensor to measure at 2 nm intervals using a scan average of 7 and a point average of 195; a “magic arm” with a clamp (Articulating rosette arm, SmallRig, Kowloon, Hongkong) was used to attach the sensor to the measurement cuvette.

We randomly selected four healthy-looking leaves from the lower branches of a silver birch (Betula pendula Roth) tree (9 m high × 11 cm diameter at breast height) in an urban forest in Helsinki, Finland, for conducting the measurements. A single leaf (while attached to the tree) was placed in a cuvette on the leaf gas exchange analyzer, and the hyperspectral sensor was at the lower side of the cuvette, on top of the glass panel (Figure 1); each leaf was allowed to adjust to the cuvette conditions for 20 min. Then, three treatments were applied, comprising manipulation of vapor pressure deficit (VPD), carbon dioxide content, and light intensity within the cuvette while maintaining the other two variables constant. VPD was incrementally increased from 5 Pa kPa⁻¹ for 30 min to 45 Pa kPa⁻¹ by increasing temperature from 20 °C to 35 °C and decreasing relative humidity from 88% to 35% (

Table 1. Changing steps in vapor pressure deficit (VPD), CO₂ concentration, and light intensity, while the remaining two environmental parameters were kept constant.

VPD Manipulation
Increment	VPD (Pa kPa−1)	CO2 (ppm)	Light (µmol m−2 s−1)
1	5	400	1200
2	10	400	1200
3	15	400	1200
4	22	400	1200
5	32	400	1200
6	45	400	1200
CO2 Manipulation
Increment	VPD (Pa kPa−1)	CO2 (ppm)	Light (µmol m−2 s−1)
1	22	500	1200
2	22	350	1200
3	22	250	1200
4	22	150	1200
5	22	50	1200
Light Manipulation
Increment	VPD (Pa kPa−1)	CO2 (ppm)	Light (µmol m−2 s−1)
1	22	400	0
2	22	400	200
3	22	400	400
4	22	400	600
5	22	400	800
6	22	400	1000
7	22	400	1200
8	22	400	1400

), while CO₂ concentration was maintained at 400 ppm and the light was held constant at a level of high intensity (1200 µmol m⁻²); CO₂ concentrations ranged from 50 ppm to 500 ppm as light and VPD were held constant at 800 µmol/m² and 22 Pa kPa⁻¹; light intensity ranged from 0 to 1400 µmol m⁻² s⁻¹, while VPD and CO₂ concentration were maintained at 20 Pa kPa⁻¹ and 400 ppm, respectively. Temperature was set to 26 °C and relative humidity to 42% when CO₂ concentration and light were varied. Airflow in the cuvette was set to 650 µmol/s in all experiments.

To cut the water supply to the leaf blade and facilitate the calculation of the amount of water lost from the leaf from transpiration, we removed the petiole from the leaf blade following the final incremental increase in variables (VPD, CO₂, light), and continued the measurement of transpiration and assimilation. At the end of the measurement, leaf mass was recorded using a precision balance, and leaf area was measured using a flatbed scanner (Epson V370 Photo, Epson America, Inc., San Jose, CA, USA) at 800 dpi resolution. Leaf samples were then dried in an oven at 65 °C for 72 h before dry weight was measured for the calculation of equivalent water thickness (EWT, g m⁻²) as mass of water/leaf area.

2.2. Data Analysis

Changes in EWT during the drying period, following removal of the petiole, were calculated by a mass balance approach. As the leaf was completely cut from the water supply, the rate of decrease in leaf water content was calculated to be the same as the transpiration rate of the leaf by transformation of the mmol m⁻² s⁻¹ unit of transpiration rate to the cumulative amount of transpired water (g m⁻²). If peak transpiration occurred immediately after petiole removal, indicating the emptying of leaf veins to the mesophyll, 2 min of transpiration data were excluded from the analysis. Sometimes it was noticed that transpiration transiently increased immediately after cutting off the leaf vein. The reason for this could be, e.g., the sudden introduction of air to the cut xylem veins, which increases the pressure in the xylem veins and push water to the mesophyll, i.e., the transient capacitive effect of embolism [21].

We adopted the common assumptions of leaf water distribution in remote sensing studies that the water layer within the leaf is approximately uniform and that EWT describes the amount of water per leaf area. Thus, the relative change in EWT is equivalent to the change in relative water content (RWC) that describes the amount of leaf water in relation to full saturation; RWC is closely linked to leaf water potential that is both commonly used to describe plant water status [22,23]. EWT affects leaf reflectance in the SWIR domain (1300–1700 nm) due to the absorbance of energy by water, so changes in EWT using reflectance measurements is a proxy measurement for plant water status [12].

We calculated normalized ratio indices (NRIs) to understand the drivers of changes in EWT (Equation (1)) and to test their performance in estimating EWT. We used linear regression modeling to test the relationship between leaf reflectance at each wavelength, NRIs and EWT. Based on the regression models for each leaf, we used the coefficient of determination (R²) and root mean square error (RMSE) to estimate model accuracy. Then, the developed regression models were used to estimate changes in EWT during the incremental changes in environmental conditions. NRIs were calculated as follows:

$$\mathrm{NRI}=\frac{{\gamma }_1-{\gamma }_2}{{\gamma }_1+{\gamma }_2}$$

(1)

where γ₁ and γ₂ are the reflectance of each wavelength.

We also tested the sensitivity of the measured reflectance to air water vapor concentration using an empty cuvette and varying water vapor concentrations within the cuvette. Pearson’s correlation analysis was used to test the significance of the correlation between the reflectance of each wavelength and air water vapor concentration.

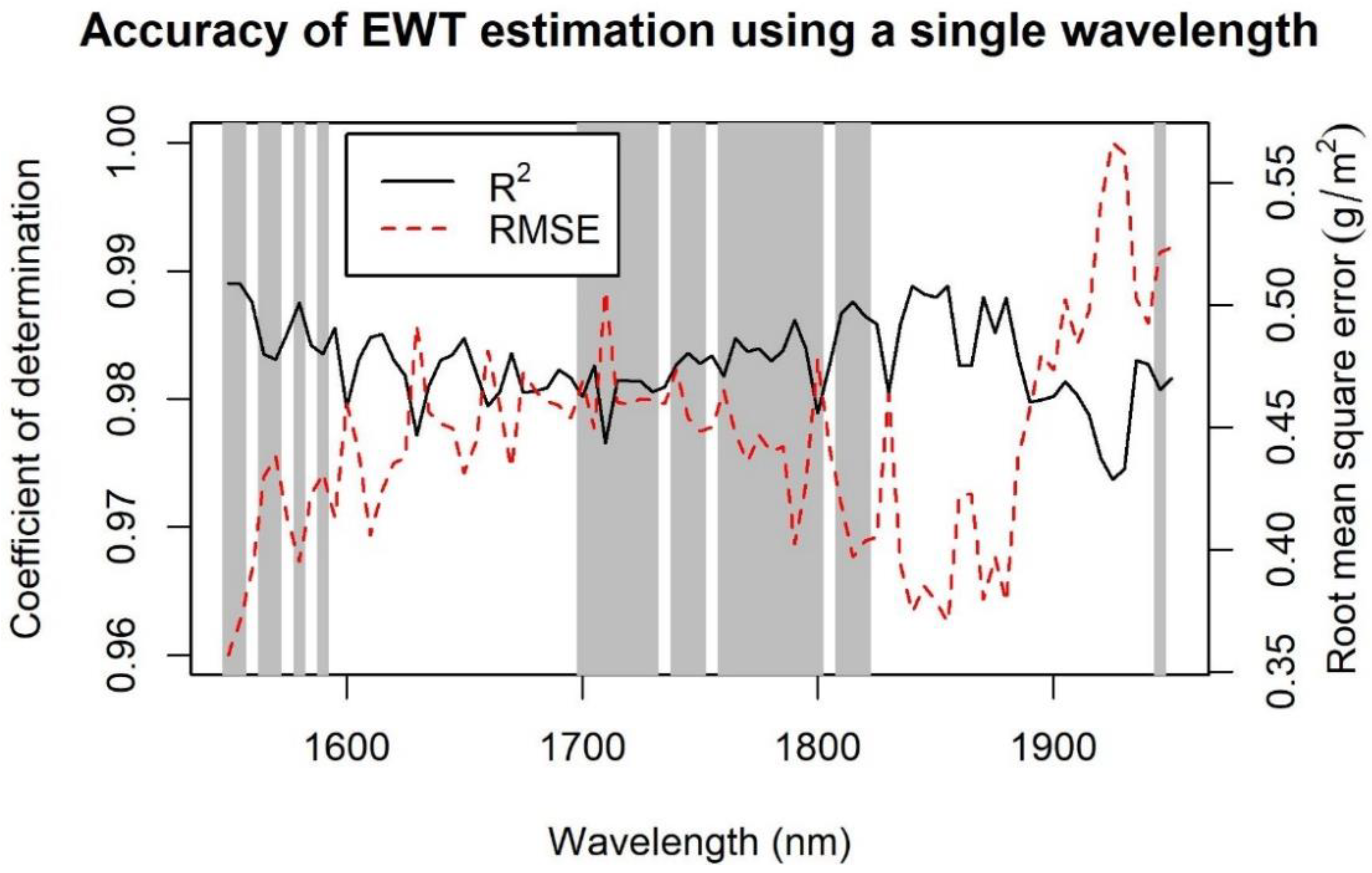
3. Results

We found strong linear relationships between reflectance in the 1550–1950 nm domain and EWT, where reflectance explained up to 99% of the variation in EWT (RMSE = 0.36 g m⁻²; Figure 2). There was a variation in wavelength that provided the lowest RMSE among the treatments, where the difference in EWT estimation accuracy tended to be small (0.2–0.5 g m⁻², see Appendix A). The lowest RMSE for the prediction of EWT was for single wavelengths (1550–1590 nm and 1820–1860 nm), but the 1820–1860 nm region also showed sensitivity to water vapor concentration (Figure 2). On average, reflectance at 1550 nm provided the lowest RMSE for predicting EWT. Performance of NRIs for the prediction of EWT was poor, as indicated by the 2–4-fold lower RMSEs than for single wavelength reflectance, and wavelengths used for the calculation of the best performing NRIs for EWT prediction were located at 1550–1720 nm and 1810–1860 nm wavelength regions (Figure 3). The performance of the top 10 regression models for EWT prediction for each treatment is shown in Appendix A 

Table A2. Coefficient of determination (R²) and root-mean-square-error (RMSE) for the top 10 most accurate linear regression models for estimating equivalent water thickness (g m⁻²) using normalized ratio indices calculated with wavelengths γ₁ and γ₁ under incremental increases in vapor pressure deficit (VPD) and constant CO₂ concentrations and light intensity (Leaf 1 and 2), light intensity and constant levels of VPD and CO₂ concentrations (Leaf 3), and D) CO₂ concentrations and constant levels of VPD and light intensity (Leaf 4).

VPD (Leaf 1)				VPD (Leaf 2)
γ1	γ2	R2	RMSE (g m−2)	γ1	γ2	R2	RMSE (g m−2)
1935	1690	0.938	0.783	1940	1715	0.867	0.949
1935	1750	0.935	0.802	1950	1715	0.857	0.982
1935	1730	0.929	0.838	1950	1735	0.855	0.989
1935	1720	0.927	0.850	1950	1740	0.839	1.044
1935	1660	0.921	0.885	1950	1695	0.838	1.048
1935	1680	0.920	0.889	1940	1640	0.837	1.051
1935	1740	0.918	0.898	1950	1710	0.834	1.060
1935	1710	0.909	0.947	1940	1655	0.831	1.070
1935	1695	0.908	0.952	1940	1710	0.831	1.070
1935	1640	0.907	0.957	1940	1675	0.830	1.071
CO2 (Leaf 3)				Light (Leaf 4)
γ1	γ2	R2	RMSE (g m−2)	γ1	γ2	R2	RMSE (g m−2)
1890	1665	0.985	1.483	1950	1665	0.943	0.803
1880	1670	0.985	1.487	1950	1710	0.943	0.805
1880	1675	0.985	1.511	1950	1695	0.943	0.805
1880	1700	0.984	1.529	1950	1610	0.942	0.808
1890	1735	0.984	1.538	1950	1685	0.942	0.812
1890	1730	0.984	1.539	1950	1765	0.941	0.817
1890	1675	0.984	1.542	1950	1700	0.940	0.823
1880	1695	0.984	1.558	1945	1715	0.940	0.825
1870	1655	0.984	1.570	1945	1770	0.940	0.827
1890	1680	0.983	1.577	1915	1695	0.940	0.828

.

We used reflectance at 1550 nm in the regression models for the prediction of EWT (Figure 4) due to high levels of insensitivity to water vapor content and sensitivity to EWT (Figure 2). We found that variation in EWT was greatest under increasing levels of VPD, where transpiration rate increased and EWT declined at VPD > 22 Pa kPa⁻¹ (Figure 5a,b). Increasing light intensity resulted in increased transpiration rate and decrease in EWT, albeit to a lower extent than under changes in VPD (Figure 5c), and decreasing CO₂ concentrations led to increases in transpiration rate, with no impact on EWT.

4. Discussion

We simultaneously measured leaf gas exchange and water content using a leaf gas analyzer and miniature hyperspectral sensor of the SWIR domain to demonstrate the feasibility of this novel approach for the study of plant-water status. We found that spectral reflectance measurements were related to leaf water content (R² > 0.98), driven by leaf transpiration, as demonstrated by the relationship between the cumulative amount of transpired water and spectral reflectance following removal of the petiole. This experimental approach allowed us to transform spectral reflectance to units of leaf water content (EWT), eliminating the need to weigh samples as has traditionally been required in the development of models that test and predict relations between leaf reflectance and water content. This approach allowed us to acquire tens of data points for each leaf with a high temporal resolution that could be used for model development.

Based on our results, the use of spectral reflectance data at single wavelengths in the 1550–1950 nm spectral domain accounts for greater amounts of variation in EWT than the use of NRIs (minimum RMSE = 0.78 g m⁻², see Appendix A Table A2). Previous estimates of EWT, using destructive sampling, have been based on NRIs that likely reduce between-leaf variation due to differences in leaf structure; however, this reduction in between-leaf variation leads to differences in spectral reflectance of single wavelengths [20]. In contrast, our novel approach allowed the development of regression models for single leaves that improved the estimation accuracy of EWT. For example, Junttila et al. [20] used similar sensors to the one used here with a destructive sampling of silver birch leaves and achieved an RMSE of 3.41 g m⁻² for the estimation of EWT based on NRIs, compared with a low accuracy and RMSE of 5.91 g m⁻² achieved based on the spectral reflectance of single wavelengths. Here, we achieved RMSEs of 0.27–0.41 g m⁻² with the best regression models for each leaf, representing almost a ten-fold improvement in the estimation accuracy of EWT by employing the novel methodology where transpiration measurements (instead of destructive sampling) are used to calibrate the prediction models of EWT.

The changes in EWT observed under variation in VPD, CO₂ concentrations, and light intensity support the current understanding of plant water relations. The greatest changes in EWT were observed under increasing VPD and led to higher transpiration rates; these changes in EWT and transpiration rapidly occurred following adjustment of VPD, indicating that stomatal control is slower than the change in VPD within the measurement cuvette. This is in accordance with previous findings from the literature that the rate of stomatal movement is typically of the order of minutes (e.g., [24]). When light intensity was sequentially increased, while other environmental parameters were kept constant, there was a slow increase in transpiration following a small decrease in EWT, whereas, under decreased CO₂ concentrations, transpiration rate increased, with small increases in EWT. This is likely caused by the movement of water between the cuvette and the rest of the leaf/plant as their environmental conditions change in a different way. Measurement of responses to increases in CO₂ concentrations and light intensity were conducted between 18:00 and 21:00 hrs when the ambient air temperature decreased from 21.3 to 17 °C; therefore, it is likely that transpiration of the entire tree decreased during this measurement period and the stem water potential increased enabling more efficient leaf hydration [25,26]. Increasing EWT during this measurement period may be due to the difference in environmental conditions within the cuvette (the leaf) and the whole tree.

The main limitation of this novel method for the estimation of leaf water content is the underlying assumption of a uniform water layer within the leaf. The hyperspectral sensor has a narrow field of view, resulting in the measurement of an area <1.5 mm in diameter, so variation in water content across an entire leaf and with veins may contribute to a measurement scaling error; we suggest that measurement of major leaf veins are avoided. Our second assumption, that EWT and spectral reflectance are linearly related, including at the higher levels of EWT that occur prior to petiole removal, may be problematic, although it was based on previous studies using the same species [20]. Leaves with a large area may be more difficult to measure using this proposed novel method because they may be too large for the measurement cuvette; however, we suggest this is not likely to be an issue when leaves are monitored under ambient environmental conditions but may be problematic if temperature and relative humidity are manipulated and contrast between ambient and cuvette conditions. The contrast could cause water movement also within one leaf between the parts of the leaf which are inside the cuvette and the parts which are outside the cuvette, depending on the difference in environmental conditions inside and outside the cuvette. The requirement of a leaf gas exchange measuring device limits the easy deployment of hyperspectral sensors in natural environments. In addition, accurate prediction of EWT for new leaves is challenging without the fitting of the regression models for each leaf. The direction of change in EWT can be interpreted directly from the spectral measurements without calibration based on the absorbance of water in the 1550–1950 nm domain, but the prediction of absolute EWT values requires fitting for each leaf.

Further development of this methodology may be achieved by fine-tuning the measured wavelengths and duration of measurements because wavelengths and averaging time of the NIRONE S2.0 miniature hyperspectral sensor may be set separately so that greater temporal accuracy may be achieved without the loss of spectral measurement details. We used a temporal resolution of 10 s, but this could be decreased to <1 s by reducing the number of measured wavelengths to facilitate greater temporal domains in the measurement of EWT. This methodology could also be used to investigate changes in RWC by measuring saturated leaf water content before dry weight measurements.

It is possible to adjust the environmental conditions in the measurement cuvette to achieve a slower dehydration process following the removal of the petiole. We found that desiccation of leaves that were subject to high VPD at the end of the measurement was rapid after petiole removal; quantification of this response requires high temporal matching of gas exchange and reflectance measurements. Reducing the rate of this desiccation process by increasing the humidity levels of the cuvette could result in more accurate regression models of changes in EWT.

The novel methodology described here is highly relevant for the study of plant-water relations and the role of leaf water content on leaf gas exchange and plant growth. Our innovation enables studying directly how changes in leaf water content affect leaf gas exchange and vice versa. This has not been possible so far, at least not at this accuracy and time resolution. In other words, leaf water content describes the internal state of the leaf, which might turn out to be a more direct driver of stomatal control, photosynthesis, and water use efficiency than environmental conditions, at least in some cases [27]. Coupling continuous leaf water content measurements with leaf or stem water potential measurements could also help in separating the dynamics of osmotic solutes from leaf water content measurements [28]. Simultaneous measurement of leaf carbon and water exchange, along with leaf water content, allows us to further understand the control of leaf physiological processes by leaf hydraulics and the associated impacts of environmental conditions on the relationship between leaf water content and leaf gas exchange. Climate change increases positive anomalies of VPD affecting leaf transpiration and associated carbon exchange resulting in reductions in global vegetation growth [29,30]. Understanding the influence of increased VPD on leaf water status and related carbon assimilation is required for modeling the growth of vegetation—a question that can be studied using our novel method. Future development work should include testing the developed methodology with different species and leaf structures encompassing a wide range of different forest biomes.