Self-Supervised Keypoint Detection and Cross-Fusion Matching Networks for Multimodal Remote Sensing Image Registration
Abstract
:1. Introduction
2. Related Works
2.1. Convolution Operation
2.1.1. Depthwise Separable Convolution
2.1.2. Deformable Convolutional Network
2.2. Fusion Module
3. Methodology
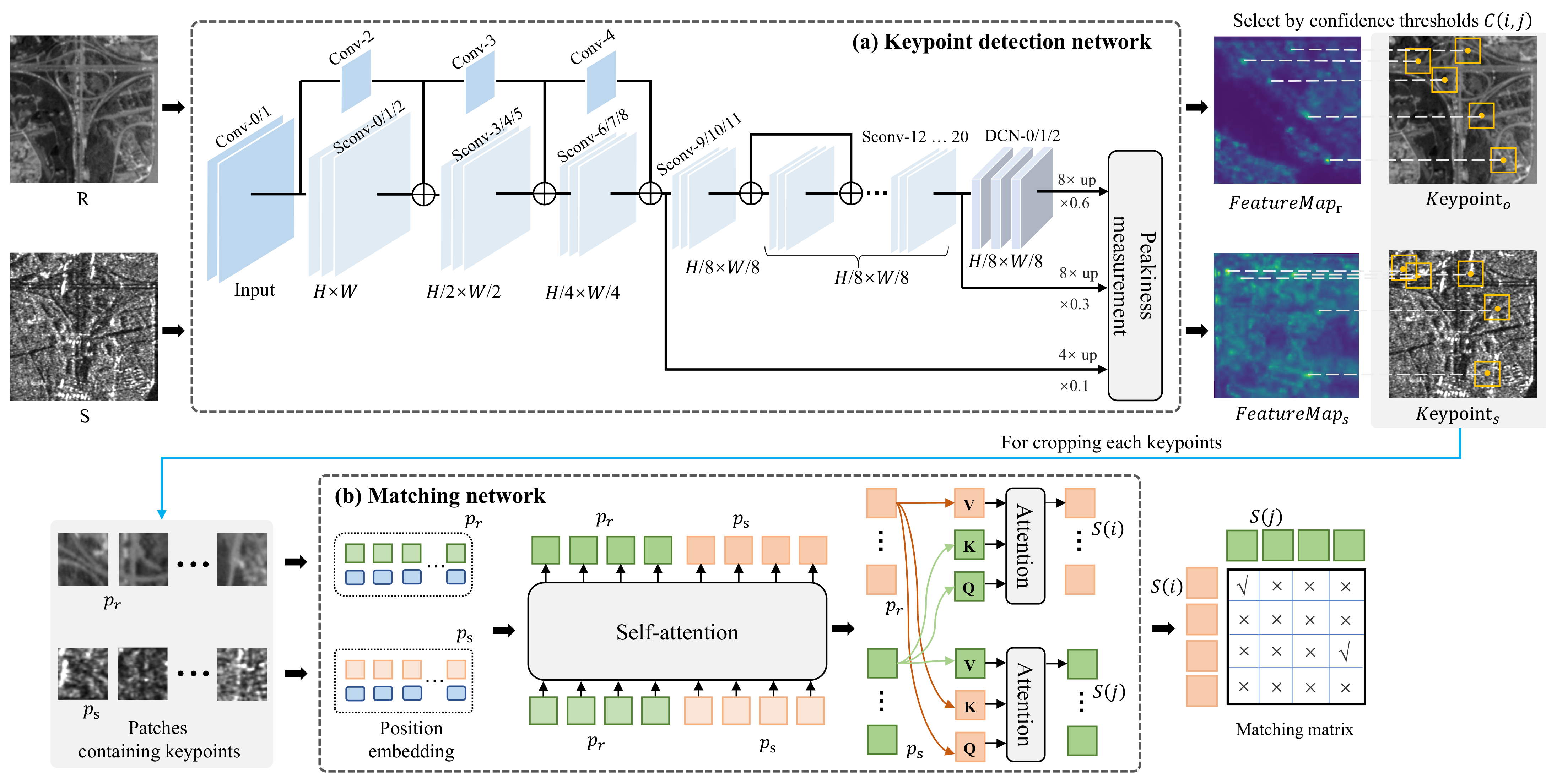
3.1. Overall Framework Description
3.2. Detection Network
3.3. Cross-Fusion Matching Network
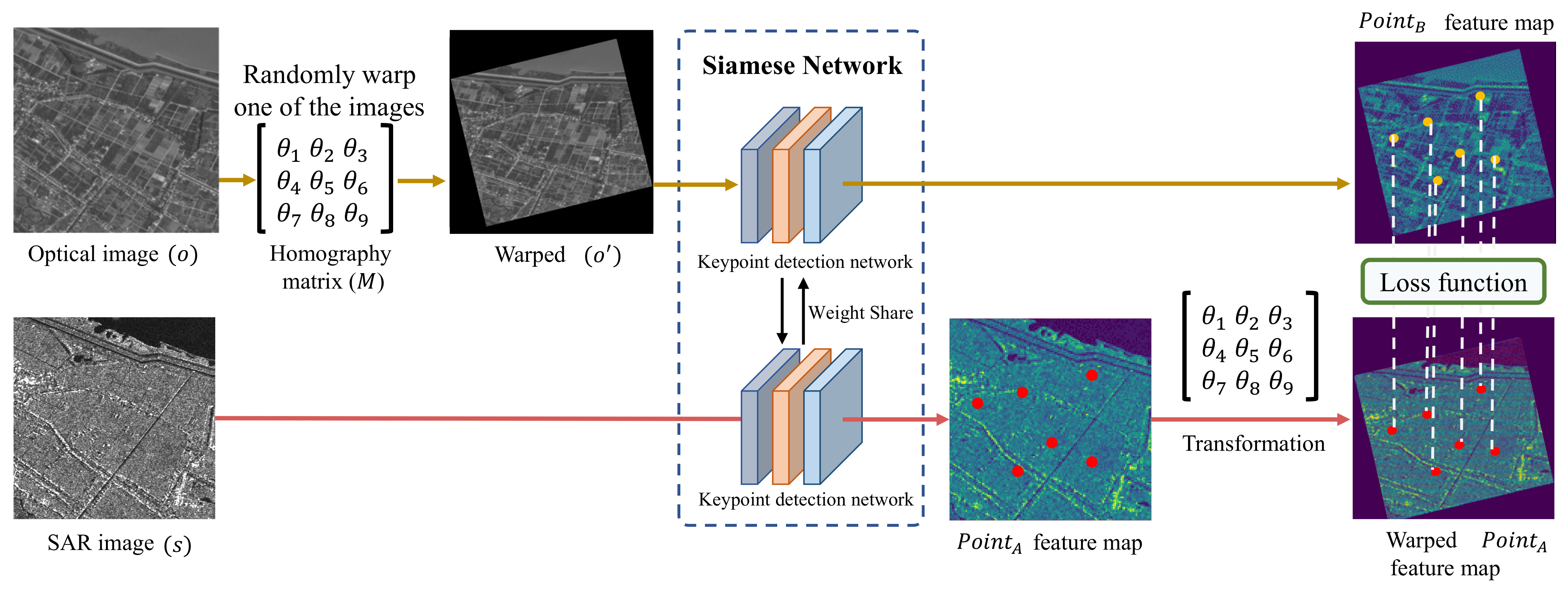
3.4. Positive and Negative Sample Generation
3.5. Matching and Parameter Setting
4. Experiments
4.1. Dataset
4.2. Evaluation Metrics
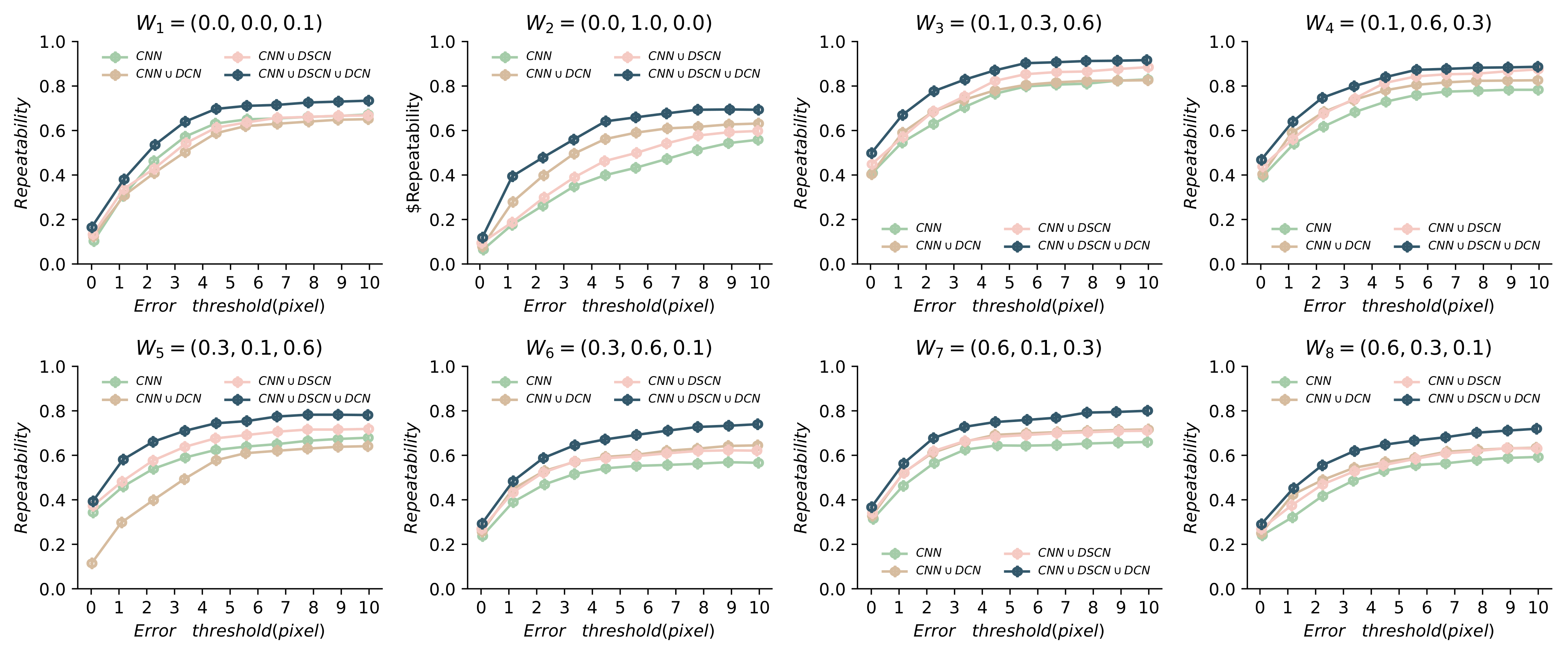
4.3. Ablation Study for the Detection Network
4.4. Ablation Study for the Matching Network
4.5. Repeatability of the Detection Network
4.6. Experimental Analysis of the Matching Network
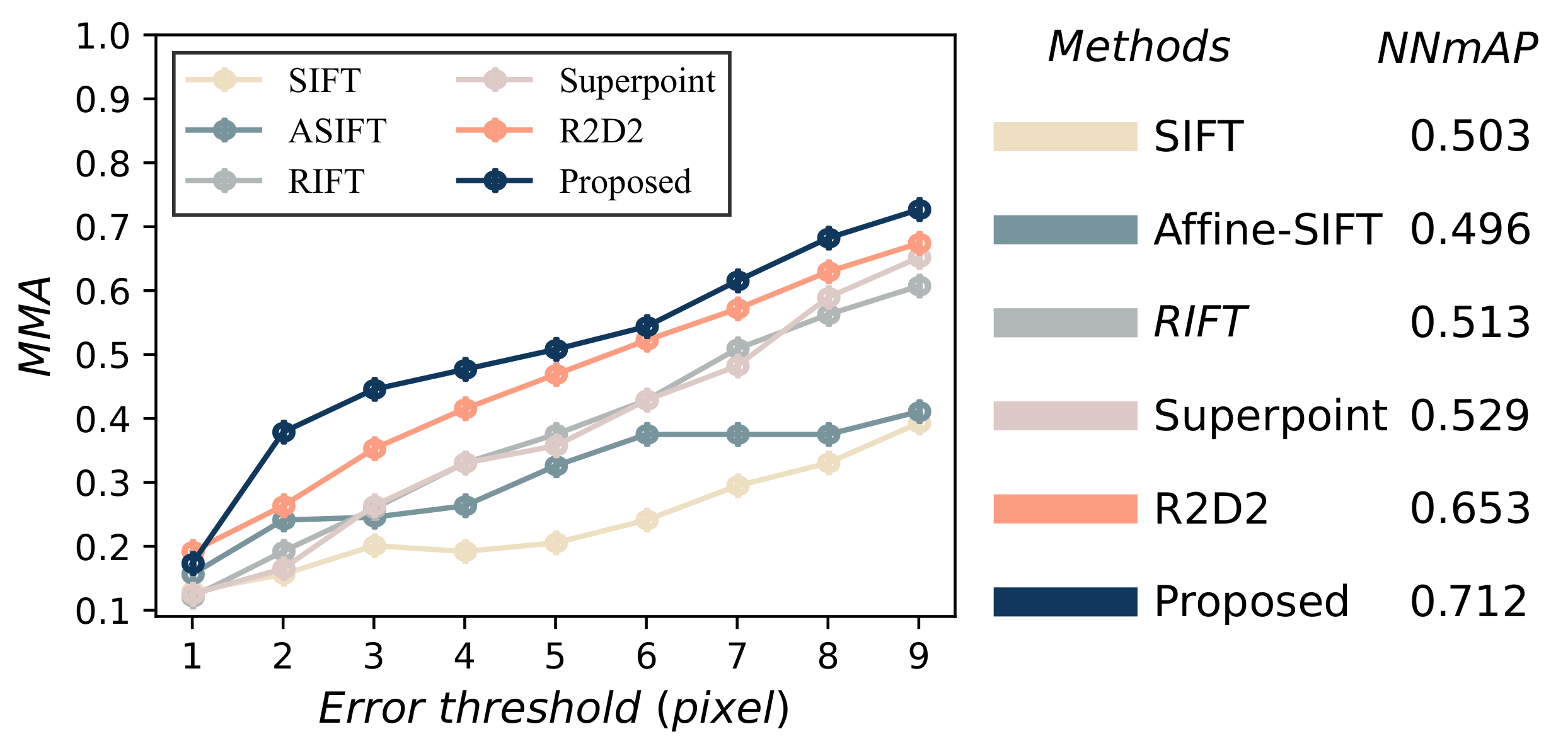
4.7. Overall Matching Performance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, X.; Leng, C.; Hong, Y.; Pei, Z.; Cheng, I.; Basu, A. Multimodal Remote Sensing Image Registration Methods and Advancements: A Survey. Remote Sens. 2021, 13, 5128. [Google Scholar] [CrossRef]
- Dawn, S.; Saxena, V.; Sharma, B. Remote sensing image registration techniques: A survey. In Proceedings of the International Conference on Image and Signal Processing; Springer: Berlin/Heidelberg, Germany, 2010; pp. 103–112. [Google Scholar]
- Tondewad, M.P.S.; Dale, M.M.P. Remote sensing image registration methodology: Review and discussion. Procedia Comput. Sci. 2020, 171, 2390–2399. [Google Scholar] [CrossRef]
- Feng, R.; Shen, H.; Jianjun, B.; Li, X. Advances and opportunities in remote sensing image geometric registration: A systematic review of state-of-the-art approaches and future research directions. IEEE Geosci. Remote Sens. Mag. 2021, 9, 120–142. [Google Scholar] [CrossRef]
- Jiang, X.; Ma, J.; Xiao, G.; Shao, Z.; Guo, X. A review of multimodal image matching: Methods and applications. Inf. Fusion 2021, 73, 22–71. [Google Scholar] [CrossRef]
- Johnson, H.J.; Christensen, G.E. Consistent landmark and intensity-based image registration. IEEE Trans. Med. Imaging 2002, 21, 450–461. [Google Scholar] [CrossRef]
- Ma, W.; Wen, Z.; Wu, Y.; Jiao, L.; Gong, M.; Zheng, Y.; Liu, L. Remote sensing image registration with modified SIFT and enhanced feature matching. IEEE Geosci. Remote Sens. Lett. 2016, 14, 3–7. [Google Scholar] [CrossRef]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing. 2002. Available online: https://www.codecool.ir/extra/2020816204611411Digital.Image.Processing.4th.Edition.www.EBooksWorld.ir.pdf (accessed on 25 June 2022).
- Reddy, B.S.; Chatterji, B.N. An FFT-based technique for translation, rotation, and scale-invariant image registration. IEEE Trans. Image Process. 1996, 5, 1266–1271. [Google Scholar] [CrossRef] [Green Version]
- Ye, Y.; Bruzzone, L.; Shan, J.; Bovolo, F.; Zhu, Q. Fast and robust matching for multimodal remote sensing image registration. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9059–9070. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Ma, W.; Wu, Y.; Jiao, L. Multimodal remote sensing image registration based on image transfer and local features. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1210–1214. [Google Scholar] [CrossRef]
- Ng, P.C.; Henikoff, S. SIFT: Predicting amino acid changes that affect protein function. Nucleic Acids Res. 2003, 31, 3812–3814. [Google Scholar] [CrossRef] [Green Version]
- Xiang, Y.; Wang, F.; You, H. OS-SIFT: A robust SIFT-like algorithm for high-resolution optical-to-SAR image registration in suburban areas. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3078–3090. [Google Scholar] [CrossRef]
- Fan, B.; Huo, C.; Pan, C.; Kong, Q. Registration of optical and SAR satellite images by exploring the spatial relationship of the improved SIFT. IEEE Geosci. Remote Sens. Lett. 2012, 10, 657–661. [Google Scholar] [CrossRef] [Green Version]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep learning in remote sensing: A comprehensive review and list of resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef] [Green Version]
- Tang, Y.; Zhu, M.; Chen, Z.; Wu, C.; Chen, B.; Li, C.; Li, L. Seismic performance evaluation of recycled aggregate concrete-filled steel tubular columns with field strain detected via a novel mark-free vision method. In Proceedings of the Structures; Elsevier: Amsterdam, The Netherlands, 2022; Volume 37, pp. 426–441. [Google Scholar]
- Kussul, N.; Lavreniuk, M.; Skakun, S.; Shelestov, A. Deep learning classification of land cover and crop types using remote sensing data. IEEE Geosci. Remote Sens. Lett. 2017, 14, 778–782. Available online: https://www.sciencedirect.com/science/article/abs/pii/S2352012421011747 (accessed on 25 June 2022). [CrossRef]
- Wang, H.; Lin, Y.; Xu, X.; Chen, Z.; Wu, Z.; Tang, Y. A Study on Long–Close Distance Coordination Control Strategy for Litchi Picking. Agronomy 2022, 12, 1520. [Google Scholar] [CrossRef]
- Yang, Z.; Dan, T.; Yang, Y. Multi-temporal remote sensing image registration using deep convolutional features. IEEE Access 2018, 6, 38544–38555. [Google Scholar] [CrossRef]
- Zhang, H.; Ni, W.; Yan, W.; Xiang, D.; Wu, J.; Yang, X.; Bian, H. Registration of multimodal remote sensing image based on deep fully convolutional neural network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3028–3042. [Google Scholar] [CrossRef]
- Li, L.; Han, L.; Ding, M.; Liu, Z.; Cao, H. Remote sensing image registration based on deep learning regression model. IEEE Geosci. Remote Sens. Lett. 2020, 19, 1–5. [Google Scholar] [CrossRef]
- Gong, M.; Yang, H.; Zhang, P. Feature learning and change feature classification based on deep learning for ternary change detection in SAR images. ISPRS J. Photogramm. Remote Sens. 2017, 129, 212–225. [Google Scholar] [CrossRef]
- Qi, G.; Zhang, Y.; Wang, K.; Mazur, N.; Liu, Y.; Malaviya, D. Small Object Detection Method Based on Adaptive Spatial Parallel Convolution and Fast Multi-Scale Fusion. Remote Sens. 2022, 14, 420. [Google Scholar] [CrossRef]
- Kuppala, K.; Banda, S.; Barige, T.R. An overview of deep learning methods for image registration with focus on feature-based approaches. Int. J. Image Data Fusion 2020, 11, 113–135. [Google Scholar] [CrossRef]
- Bürgmann, T.; Koppe, W.; Schmitt, M. Matching of TerraSAR-X derived ground control points to optical image patches using deep learning. ISPRS J. Photogramm. Remote Sens. 2019, 158, 241–248. [Google Scholar] [CrossRef]
- Wang, S.; Quan, D.; Liang, X.; Ning, M.; Guo, Y.; Jiao, L. A deep learning framework for remote sensing image registration. ISPRS J. Photogramm. Remote Sens. 2018, 145, 148–164. [Google Scholar] [CrossRef]
- Kalchbrenner, N.; Grefenstette, E.; Blunsom, P. A convolutional neural network for modelling sentences. arXiv 2014, arXiv:1404.2188. [Google Scholar]
- Zhou, L.; Ye, Y.; Tang, T.; Nan, K.; Qin, Y. Robust Matching for SAR and Optical Images Using Multiscale Convolutional Gradient Features. IEEE Geosci. Remote Sens. Lett. 2021, 19, 4017605. [Google Scholar] [CrossRef]
- Ye, Y.; Tang, T.; Zhu, B.; Yang, C.; Li, B.; Hao, S. A multiscale framework with unsupervised learning for remote sensing image registration. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Hughes, L.H.; Marcos, D.; Lobry, S.; Tuia, D.; Schmitt, M. A deep learning framework for matching of SAR and optical imagery. ISPRS J. Photogramm. Remote Sens. 2020, 169, 166–179. [Google Scholar] [CrossRef]
- Hughes, L.H.; Merkle, N.; Bürgmann, T.; Auer, S.; Schmitt, M. Deep learning for SAR-optical image matching. In Proceedings of the IGARSS 2019-2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 4877–4880. [Google Scholar]
- Li, L.; Han, L.; Ding, M.; Cao, H.; Hu, H. A deep learning semantic template matching framework for remote sensing image registration. ISPRS J. Photogramm. Remote Sens. 2021, 181, 205–217. [Google Scholar] [CrossRef]
- Dusmanu, M.; Rocco, I.; Pajdla, T.; Pollefeys, M.; Sivic, J.; Torii, A.; Sattler, T. D2-net: A trainable cnn for joint description and detection of local features. In Proceedings of the IEEE/cvf Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 8092–8101. [Google Scholar]
- DeTone, D.; Malisiewicz, T.; Rabinovich, A. Superpoint: Self-supervised interest point detection and description. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 224–236. [Google Scholar]
- Revaud, J.; Weinzaepfel, P.; De Souza, C.; Pion, N.; Csurka, G.; Cabon, Y.; Humenberger, M. R2D2: Repeatable and reliable detector and descriptor. arXiv 2019, arXiv:1906.06195. [Google Scholar]
- Hannun, A.; Lee, A.; Xu, Q.; Collobert, R. Sequence-to-sequence speech recognition with time-depth separable convolutions. arXiv 2019, arXiv:1904.02619. [Google Scholar]
- Dai, J.; Qi, H.; Xiong, Y.; Li, Y.; Zhang, G.; Hu, H.; Wei, Y. Deformable convolutional networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 764–773. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Spatial pyramid pooling in deep convolutional networks for visual recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 1904–1916. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.; Huang, D.; Wang, Y. Receptive field block net for accurate and fast object detection. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 385–400. [Google Scholar]
- Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 834–848. [Google Scholar] [CrossRef] [Green Version]
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid scene parsing network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2881–2890. [Google Scholar]
- Lin, T.Y.; Dollár, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature pyramid networks for object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2117–2125. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16 × 16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Agarap, A.F. Deep learning using rectified linear units (relu). arXiv 2018, arXiv:1803.08375. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the International Conference on Machine Learning, PMLR, Lille, France, 7–9 July 2015; pp. 448–456. [Google Scholar]
- Zheng, H.; Yang, Z.; Liu, W.; Liang, J.; Li, Y. Improving deep neural networks using softplus units. In Proceedings of the 2015 International Joint Conference on Neural Networks (IJCNN), Killarney, Ireland, 12–17 July 2015; pp. 1–4. [Google Scholar]
- Chum, O.; Matas, J.; Kittler, J. Locally optimized RANSAC. In Proceedings of the Joint Pattern Recognition Symposium; Springer: Berlin/Heidelberg, Germany, 2003; pp. 236–243. [Google Scholar]
- Yu, G.; Morel, J.M. ASIFT: An algorithm for fully affine invariant comparison. Image Process. Line 2011, 1, 11–38. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Hu, Q.; Ai, M. RIFT: Multi-modal image matching based on radiation-invariant feature transform. arXiv 2018, arXiv:1804.09493. [Google Scholar]





| Layer | Size | Operation |
|---|---|---|
| c-0/1 | 3 × 3 c | |
| c-2 | 3 × 3 c | |
| S-0/1/2 | 2 × 2 c; mp | |
| c-3 | 3 × 3 c | |
| S-3/4/5 | 1 × 1 c; 3 × 3 c; mp | |
| c-4 | 3 × 3 c | |
| S-6/7/8 | 1 × 1 c; 3 × 3 c; mp | |
| S-9/10/11 | 1 × 1 c; 3 × 3 c | |
| S-12…20 | … | 1 × 1 c; 3 × 3 c |
| D-0/1/2 | 3 × 3 c |
| ≤2 px(%) | ≤3 px(%) | ≤4 px(%) | ≤5 px(%) | ≤6 px(%) | |||
|---|---|---|---|---|---|---|---|
| 0.106 | 0.129 | 0.564 | 0.293 | 0.426 | 0.675 | ||
| 0.116 | 0.171 | 0.635 | 0.398 | 0.559 | 0.743 | ||
| 0.134 | 0.136 | 0.572 | 0.387 | 0.573 | 0.739 | ||
| 0.107 | 0.130 | 0.580 | 0.373 | 0.569 | 0.724 | ||
| Repeatability | ||||||
|---|---|---|---|---|---|---|
| SIFT | ASIFT | RIFT | Superpoint | R2D2 | Proposed | |
| 0.061 | 0.227 | 0.201 | 0.295 | 0.361 | 0.391 | |
| 0.087 | 0.133 | 0.327 | 0.290 | 0.459 | 0.503 | |
| 0.103 | 0.116 | 0.197 | 0.255 | 0.391 | 0.426 | |
| 0.093 | 0.235 | 0.249 | 0.407 | 0.489 | 0.473 | |
| 0.061 | 0.135 | 0.327 | 0.337 | 0.364 | 0.437 | |
| 0.085 | 0.096 | 0.207 | 0.340 | 0.420 | 0.466 | |
| 0.064 | 0.145 | 0.118 | 0.383 | 0.459 | 0.416 | |
| 0.053 | 0.230 | 0.301 | 0.374 | 0.252 | 0.398 | |
| 0.077 | 0.108 | 0.143 | 0.267 | 0.382 | 0.471 | |
| 0.078 | 0.098 | 0.315 | 0.354 | 0.463 | 0.452 | |
| 0.068 | 0.230 | 0.243 | 0.382 | 0.309 | 0.316 | |
| 0.115 | 0.138 | 0.225 | 0.451 | 0.471 | 0.473 | |
| M.S. | RMSE | M.S. | RMSE | M.S. | RMSE | M.S. | RMSE | M.S. | RMSE | M.S. | RMSE | M.S. | RMSE | M.S. | RMSE | M.S. | RMSE | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SIFT | 0.158 | 7.55 | 0.185 | 9.5 | 0.136 | 9.93 | 0.169 | 8.01 | 0.198 | 8.1 | 0.105 | 8.19 | 0.165 | 9.65 | 0.182 | 8.95 | 0.157 | 9.95 |
| POS-SIFT | 0.165 | 9.39 | 0.116 | 7.81 | 0.145 | 9.85 | 0.097 | 8.47 | 0.084 | 8.05 | 0.149 | 7.65 | 0.148 | 9.38 | 0.164 | 9.35 | 0.142 | 7.55 |
| SAR-SIFT | 0.163 | 5.74 | 0.247 | 5.86 | 0.188 | 5.74 | 0.226 | 5.06 | 0.245 | 6.03 | 0.155 | 5.79 | 0.227 | 6.53 | 0.158 | 5.43 | 0.205 | 6.14 |
| Superpoint | 0.245 | 3.95 | 0.241 | 4.72 | 0.255 | 3.65 | 0.278 | 3.35 | 0.295 | 4.22 | 0.291 | 4.95 | 0.211 | 4.36 | 0.306 | 4.59 | 0.306 | 3.81 |
| D2-Net | 0.313 | 3.87 | 0.198 | 4.67 | 0.191 | 4.62 | 0.228 | 3.87 | 0.191 | 4.46 | 0.178 | 4.95 | 0.213 | 4.29 | 0.325 | 4.15 | 0.240 | 4.93 |
| Proposed | 0.362 | 3.10 | 0.288 | 3.06 | 0.246 | 3.52 | 0.276 | 3.38 | 0.348 | 3.94 | 0.232 | 3.22 | 0.246 | 3.26 | 0.348 | 3.49 | 0.306 | 3.76 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Han, L.; Ye, Y. Self-Supervised Keypoint Detection and Cross-Fusion Matching Networks for Multimodal Remote Sensing Image Registration. Remote Sens. 2022, 14, 3599. https://doi.org/10.3390/rs14153599
Li L, Han L, Ye Y. Self-Supervised Keypoint Detection and Cross-Fusion Matching Networks for Multimodal Remote Sensing Image Registration. Remote Sensing. 2022; 14(15):3599. https://doi.org/10.3390/rs14153599
Chicago/Turabian StyleLi, Liangzhi, Ling Han, and Yuanxin Ye. 2022. "Self-Supervised Keypoint Detection and Cross-Fusion Matching Networks for Multimodal Remote Sensing Image Registration" Remote Sensing 14, no. 15: 3599. https://doi.org/10.3390/rs14153599
APA StyleLi, L., Han, L., & Ye, Y. (2022). Self-Supervised Keypoint Detection and Cross-Fusion Matching Networks for Multimodal Remote Sensing Image Registration. Remote Sensing, 14(15), 3599. https://doi.org/10.3390/rs14153599







