Next Article in Journal
Investigating Suppression of Cloud Return with a Novel Optical Configuration of a Doppler Lidar
Previous Article in Journal
Machine Learning to Identify Three Types of Oceanic Fronts Associated with the Changjiang Diluted Water in the East China Sea between 1997 and 2021
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 14
Issue 15
10.3390/rs14153575
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Mapping Soil Organic Carbon in Low-Relief Farmlands Based on Stratified Heterogeneous Relationship

by
Zihao Wu
1,2,
Yiyun Chen
3,*,
Zhen Yang
4,
Yuanli Zhu
1,2 and
Yiran Han
3
1
School of Public Policy & Management, China University of Mining and Technology, Xuzhou 221116, China
2
Research Center for Land Use and Ecological Security Governance in Mining Area, China University of Mining and Technology, Xuzhou 221116, China
3
School of Resource and Environmental Science, Wuhan University, Wuhan 430079, China
4
Qingdao Geotechnical Investigation and Surveying Institute, Qingdao 266000, China
*
Author to whom correspondence should be addressed.
Remote Sens. 2022, 14(15), 3575; https://doi.org/10.3390/rs14153575
Submission received: 16 June 2022 / Revised: 11 July 2022 / Accepted: 12 July 2022 / Published: 26 July 2022
(This article belongs to the Section Remote Sensing in Agriculture and Vegetation)
Browse Figures
Versions Notes

Abstract

:
Accurate mapping of farmland soil organic carbon (SOC) provides valuable information for evaluating soil quality and guiding agricultural management. The integration of natural factors, agricultural activities, and landscape patterns may well fit the high spatial variation of SOC in low-relief farmlands. However, commonly used prediction methods are global models, ignoring the stratified heterogeneous relationship between SOC and environmental variables and failing to reveal the determinants of SOC in different subregions. Using 242 topsoil samples collected from Jianghan Plain, China, this study explored the stratified heterogeneous relationship between SOC and natural factors, agricultural activities, and landscape metrics, determined the dominant factors of SOC in each stratum, and predicted the spatial distribution of SOC using the Cubist model. Ordinary kriging, stepwise linear regression (SLR), and random forest (RF) were used as references. SLR and RF results showed that land use types, multiple cropping index, straw return, and percentage of water bodies are global dominant factors of SOC. Cubist results exhibited that the dominant factors of SOC vary in different cropping systems. Compared with the SOC of paddy fields, the SOC of irrigated land was more affected by irrigation-related factors. The effect of straw return on SOC was diverse under different cropping intensities. The Cubist model outperformed the other models in explaining SOC variation and SOC mapping (fitting R2 = 0.370 and predicted R2 = 0.474). These results highlight the importance of exploring the stratified heterogeneous relationship between SOC and covariates, and this knowledge provides a scientific basis for farmland zoning management. The Cubist model, integrating natural factors, agricultural activities, and landscape metrics, is effective in explaining SOC variation and mapping SOC in low-relief farmlands.

Graphical Abstract

1. Introduction

The soil organic carbon (SOC) pool in farmland is the most active component of the soil carbon pool because it responds quickly to changes in agricultural practices [1,2]. It has great potential to become an important carbon sink if appropriate agricultural measures are taken, which will help alleviate the greenhouse effect and maintain ecological balance [3,4,5,6,7]. SOC content is an important index used to evaluate soil fertility and the quality of farmland, and its changes reflect the fixation or loss of soil carbon [8,9]. Therefore, accurate mapping of SOC content in farmland is of pivotal importance for soil quality evaluation, agricultural management, and climate change mitigation.
Identifying the dominant factors of SOC is the core of accurate SOC mapping [10,11,12]. However, in low-relief farmlands, long-term cultivation and flat terrain weaken the relationship between soil properties and natural factors. Some studies find that natural factors (e.g., soil type, climate factors, and terrain factors) can only slightly improve the accuracy of the SOC prediction model [13,14,15]. The dominant factors of SOC in low-relief farmlands remain unclear. Several studies have highlighted the importance of agricultural activities and landscape patterns in the spatial variation of farmland SOC [16,17]. Time-series vegetation indexes, crop type, crop rotation, crop phenological information, cropping systems, and landscape metrics have been successfully used to improve the mapping accuracy of SOC [1,14,18,19,20,21,22]. Hence, the integration of natural factors, agricultural activities, and landscape metrics may better explain SOC variation and improve SOC mapping accuracy in low-relief agricultural areas.
Commonly used data mining models, including stepwise linear regression (SLR), support vector machine, artificial neural network, gradient boosting regression tree, and random forest (RF), are global models that assume that the relationship between the dependent variable and covariates is homogeneous across the region [23,24,25,26,27,28]. However, many studies have found that the relationship between soil properties and environmental variables is often moderated by third-party variables [29,30,31,32,33]. Alidoust, Afyuni, Hajabbasi, and Mosaddeghi [32] found that the influencing factors of SOC in western central Iran vary considerably among different land uses, and the explanatory power of environmental variables on SOC variation of forests is higher than that of farmland and grassland. Zhou [34] determined that the relationship between SOC and environmental variables depends on soil types in the hilly agricultural areas of Chongqing, China. The two studies reveal a stratified heterogeneous relationship that the global prediction models cannot delineate. Therefore, effective methods should be employed to reveal the stratified heterogeneous relationship between SOC and environmental variables.
The Cubist model is a type of ensemble learning regression tree model based on the Quinlan M5 algorithm [35,36]. The Cubist model delineates the stratified heterogeneous relationship between the target variable and covariates by adopting a stratified linear regression strategy. Specifically, it creates stratification rules that divide the data into homogeneous strata and obtains the linear regression results of each stratum. This strategy avoids the interference of subjective stratification on fitting accuracy and can easily determine the main controlling factors of SOC in each stratum. The Cubist model is also notable because of its high accuracy. Several studies have found that the Cubist model outperforms the RF model in the spatial estimation of soil properties [26,37,38,39,40]. However, scholars mainly focus on the high prediction accuracy of the Cubist model, ignoring its vital role in revealing stratified heterogeneous relationships, and failing to explore the determinants of SOC in different subregions.
Using 242 topsoil samples collected from Jianghan Plain, China, this study aims to explore the stratified heterogeneous relationship between SOC and natural factors, agricultural activities, and landscape metrics, determine the dominant factors of SOC in each stratum, and predict the spatial distribution of SOC in low-relief farmlands using the Cubist model. Ordinary kriging (OK), SLR, and RF were used as references.

2. Materials and Methods

2.1. Study Area and Soil Samples

Chahe Town (29°55′–30°04′N and 113°21′–113°34′E) is situated in the Southeast Jianghan Plain, China, and it covers approximately 141.32 km2. The elevation ranges from 14–35 m, and the slope in most areas is less than 1.5°. The region is adjacent to Honghu Lake and has sufficient water for agricultural irrigation and aquaculture. The study area experiences a typical subtropical monsoon climate. It is warm and humid in summer and cold and dry in winter. The mean annual temperature (MAT) is approximately 16.6 °C and the mean annual precipitation (MAP) is roughly 1400 mm. The main soil types include fluvisols, anthrosols, and luvisols.
Chahe Town is an important agricultural area, and it mainly produces rice, wheat, cotton, sesame, and soybean. Paddy fields and irrigated land account for 90% and 10% of the farmland area, respectively (Figure 1). In summer, mid-season rice is planted in paddy fields, whereas cotton, sesame, and soybean are mainly planted in irrigated lands. In winter, parts of the farmland are planted with winter wheat, and the rest are fallow. As a result, the multiple cropping index (MCI) of farmlands is 1 or 2. All crops except cotton implement straw returns. After harvest, the straw is chopped and evenly covered on the ground, the soil is crushed by rotary tiller, and the straw and stubble are turned and buried in the soil. Water bodies (ponds and rivers) represent the second largest land use, which are mainly used for surface aquaculture. Dense irrigation canals ensure that all farmland is irrigated. The area of natural cover, including grassland and woodland, is very small and scattered.
A total of 242 topsoil samples (0–0.3 m) were collected in July 2013 to ensure full coverage of the study area (Figure 1), including 114 paddy fields and 128 irrigated land sampling points. The samples were air-dried for 14 days in a laboratory, then gently crushed in a porcelain mortar and made to pass through a 2 mm stainless steel sieve. The SOM content was measured via the potassium dichromate method [41], and SOC content (g/kg) was calculated using Bemmelen’s conversion coefficient [42]:
SOC   =   SOM × 0.58

2.2. Environmental Variables and Data Preprocessing

We selected the following 15 environmental variables as potential influencing factors of SOC (Table 1): (i) natural factors, namely, soil types, MAP, MAT, elevation, slope, and distance from the lake (Dis_Lake); (ii) agricultural activities, namely, land use (paddy field and irrigated land), MCI, normalized difference vegetation index (NDVI), and normalized difference index (NDI); (iii) landscape metrics: interspersion and juxtaposition index (IJI), patch cohesion index (COHESION), landscape shape index (LSI), and percentage of water bodies (WB) and irrigated canals (IC) (Figure 2).
The soil map was from the Harmonized World Soil Database (version 1.2), and its spatial resolution was 1 km [43]. The spatial distribution of MAP and MAT (500 m resolution) were obtained from the Chinese Resource and Environment Science and Data Center provided by the Institute of Geographic Sciences and Natural Resources Research (CAS) (http://www.resdc.cn/, accessed on 1 October 2020). The digital elevation model (DEM) data with 30 m resolution were from ASTER DEM images (http://www.gscloud.cn, accessed on 1 September 2019) [44], and the spatial distribution of slope was calculated using ArcGIS software (version 10.2.1).
MCI refers to the number of crops planted in a year, which can reflect the planting intensity of farmland [45,46]. With the planting and harvesting of crops, the NDVI will first rise and then decline. Therefore, the MCI can be determined by counting the number of peaks of the NDVI time-series images [47,48]. In this study, the NDVI time-series images were derived from HJ-1A/1B satellite time-series images (30 m resolution, every half a month, a year in total) using the following formula: NDVI = (band4 − band3)/(band4 + band3). The second-order difference method was used to extract the peak number of NDVI time-series images, and the spatial distribution of the MCI was thus obtained. The specific process of obtaining an MCI map is shown in the research of Wu, Liu, Han, Zhou, Liu, and Wu [14]. The NDVI image during the sampling period was also acquired.
NDI can distinguish crop residues from soil by capturing the unique absorption characteristics near 2100 nm of lignin and cellulose in crop residues [49,50,51]. Therefore, NDI is widely used to identify the relative amount of straw returned to the field. The NDI formula based on the Landsat 8 image is as follows:
NDI = NIR − SWIR 2 / NIR + SWIR 2
where NIR and SWIR2 are the reflectance of near infrared and second short wave infrared band of Landsat 8 image. Moreover, Zheng, et al. [52] suggested using a minimum value in NDI time-series data to avoid the influence of newborn crops, soil moisture, and cloud on NDI. Hence, we obtained three NDI images (23 April, 12 May, and 28 May 2013) after winter wheat harvest and before summer crop planting and then acquired the final NDI image (i.e., NDI minimum image).
The land use map (10 m resolution) was surveyed by the Hubei Provincial Department of Land and Resources [17]. The Dis_Lake was calculated using the “near” tool in ArcGIS, based on the land-use map. The landscape pattern of each sampling point was obtained using a 300 m circular buffer (optimal radius found by Wu, Wang, Huang, An, Jiang, Chen, and Liu [17]) based on land use map via ArcGIS software. The landscape metrics were calculated using FRAGSTATS software (version 4.2), which is a professional software of landscape ecology for the quantitative analysis of landscape patterns. Specifically, the IJI, COHESION, and LSI separately exhibit the fragmentation, connectivity, and shape complexity of the landscape, whereas the WB and IC reflect the landscape composition [53].

2.3. Prediction Models

2.3.1. Ordinary Kriging

OK is a local interpolation method based on variogram theory [54,55]. It computes the semi-variogram values of all point pairs and uses them to fit the theoretical semi-variogram to describe the spatial dependence of soil properties. The formula for the semi-variogram values is as follows:
γ * h = 1 2 m h ∑ i = 1 m h z x i − z x i + h 2
where γ * h is the semi-variogram value, h is the distance between point pair, m h is the number of point pairs with a distance of h, and z x i is the observed value at location x i. Then, OK identifies the optimal weighting factors via the theoretical semi-variogram on the principles of unbiased prediction and minimum variance, and the values to be predicted are equal to the linear weighted sum of the observed values in an effective space range. The formula for OK is expressed as follows:
z * x 0 = ∑ i = 1 n w i z x i
where z * x 0   is the predicted value at the non-sampled location x 0, z x i   is the observed value at location x i, and wi is the weighting factor for z x i .

2.3.2. Random Forest

RF is a form of a decision tree model, and it uses an ensemble learning strategy [56]. It can explore the non-linear relationship between target variables and independent variables without the assumption of normal distribution of dependent variable or collinearity test of independent variables. In the RF model, the randomized bootstrap sample method is used to form a series of new training sets, and the remaining samples are used as validation sets called out-of-bag (OOB) samples. Each new training set is used to separately construct a CART decision tree model, and the final regression prediction result is equal to the average of the prediction results of all trees. The %IncMSE value of a dependent variable denotes the increase in the mean square error when predicting OOB samples after removing the dependent variable. The higher the %IncMSE value of a dependent variable, the higher the relative importance of the dependent variable [57,58].
The RF model involves two key parameters, namely, “ntree” and “mtry.” The “ntree” is the number of trees, and we set it to its maximum of 1000. The “mtry” is the number of nodes, and it ranges from 1 to the number of dependent variables. The best mtry value will be determined and then used to develop the final prediction model. In this study, the fitting and prediction of the RF model were implemented on the R studio platform (version 1.4.1717) with the “randomForest” package.

2.3.3. Cubist Model

The Cubist model is a rule-based model that is an extension of the Quinlan M5 model tree [59]. It first establishes a set of rules by splitting each dependent variable and subsequently divides the data into multiple subsets, such as a tree structure. The linear regression of each subset is then obtained. The rules and regressions are constructed on the premise of minimum average absolute error for new case prediction. To sum up, the Cubist model employs the stratified linear regression strategy, and, thus, can explore the stratified heterogeneous relationship between the target variable and covariates. Moreover, its regression results are well interpretable [40,60]. Similar to the RF model, the Cubist model employs an ensemble learning strategy, and the final prediction result is equal to the average of the prediction results of all committees. The Cubist model reports the percentage of times a variable is used for conditions or in linear regression models, and the two indicators are positively related to the relative importance of variables.
“Committee” and “neighbor” are the two key parameters of the Cubist model. The “committee” is the number of committees, and we set it to its maximum of 100. The “neighbor” is only used for prediction, and the number of neighbors ranges from 0 to 9. The k neighbors denote that the final prediction value is equal to the sum of the predicted value of regressions and the average value of the regression residual of the most similar k points. The similarity of the point pairs is based on the covariate-value vector and the IBL method [35,61]. The optimal number of neighbors will be determined and then used to develop the final prediction model. In this study, the fitting and prediction of the Cubist model were implemented on an R studio platform using the “Cubist” package.

2.4. Model Evaluation

The 242 samples were randomly divided into a calibration set (80%, n = 194) and a validation set (20%, n = 48). Four indices were used for model evaluation: mean absolute error (MAE), root mean square error (RMSE), coefficient of determination (R2), and Lin’s concordance correlation coefficient (LCCC).
MAE = 1 n ∑ n 1 O i − P i
RMSE = 1 n × ∑ 1 n ( O i − P i ) 2 2
R 2 = 1 − ∑ 1 n O i − P i 2 / ∑ 1 n O i − O ¯ 2
LCCC = 2 r S O S P / S O 2 + S P 2 + O ¯ − P ¯ 2
where n is the number of samples, O i is the observed SOC content for sample i, O ¯ is the mean SOC content of the measured samples, and Pi is the predicted value for sample i. LCCC can describe both precision and accuracy. LCCC ranges from 0 to ±1. Its absolute value increases as the scatters approach the 45-degree line and reaching 1 denotes perfect concordance [62,63,64]. Generally, a well-performing prediction model has low MAE and RMSE and high R2 and LCCC.

3. Results

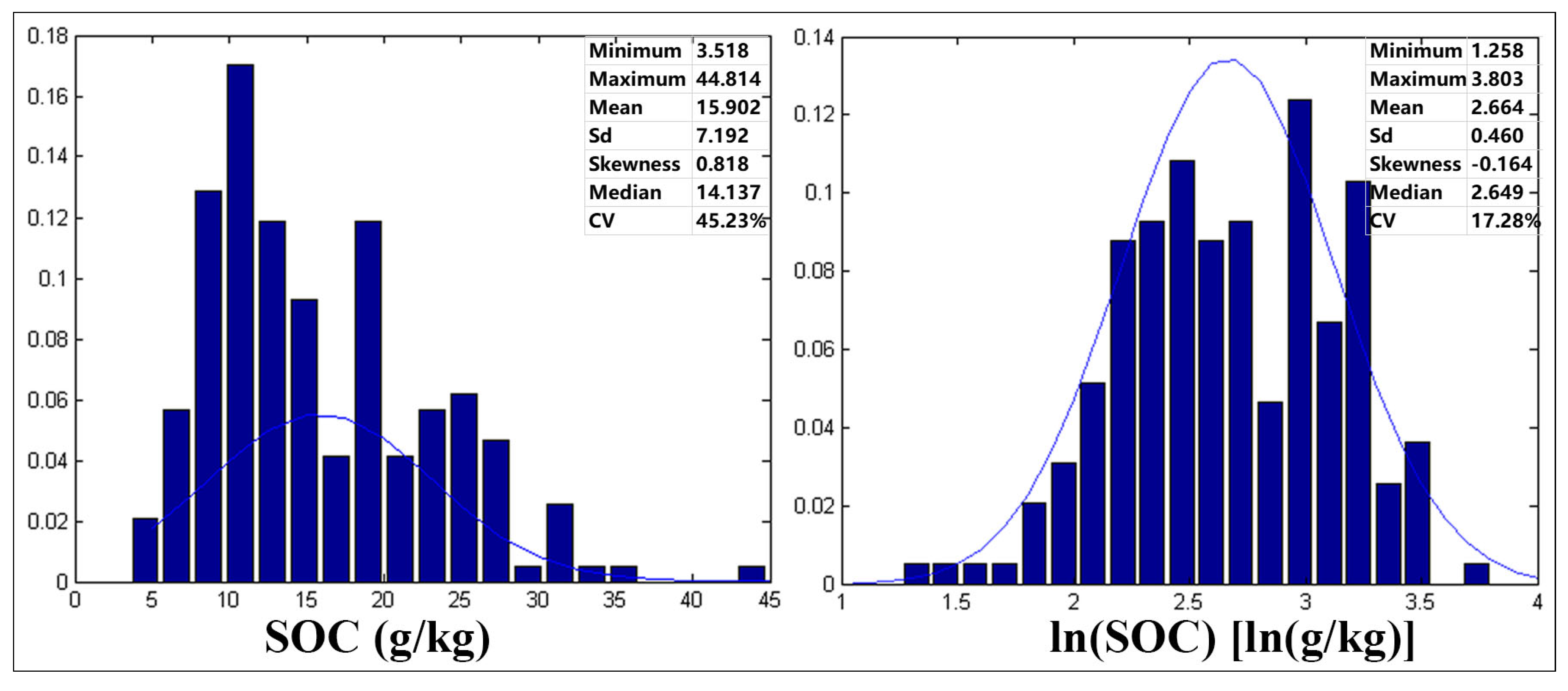
3.1. Descriptive Statistics of SOC Content

Table 2 summarizes the basic statistics of SOC content. The SOC content varied from 3.518–44.814 g/kg. After division, the mean SOC value of the calibration set was close to that of the total dataset, and the coefficient of variation (CV) of the calibration set was at moderate levels. However, the SOC content of the calibration data did not pass through the Kolmogorov–Smirnov (K–S) test. The natural logarithm was used to transform the SOC in the calibration set to fit the normal distribution required by SLR analysis and OK. Figure 3 shows the histograms and basic statistics of SOC content and transferred ln (SOC) content.

3.2. Correlation between SOC and Environmental Variables

Pearson correlation analysis and ANOVA were used to screen out the covariates that were significantly related to ln (SOC) (p < 0.05), which would be used in the regression analysis. Pearson correlation analysis was used to explore the relationship between ln (SOC) and continuous variables (e.g., elevation and slope). Table 3 shows that ln (SOC) was positively correlated with Dis_Lake, NDI, WB, and IC but negatively correlated with elevation, slope, and IJI. The absolute correlation coefficient value of the NDI was the highest among the continuous variables.
ANOVA with least significant difference was used to explore the effects of categorical variables on ln (SOC) (e.g., land use and MCI). Table 4 shows no significant difference in ln (SOC) among the different soil types. Significant differences in ln (SOC) were noted between different land uses and MCIs (Table 5). Specifically, the mean ln (SOC) value of the paddy field was significantly higher than that of irrigated land; the mean ln (SOC) value of the field with MCI 1 was higher than that of the field with MCI 2.
A total of nine significant environmental variables, namely elevation, slope, Dis_Lake, land use, MCI, NDI, IJI, WB, and IC, were used for regression analysis to determine the dominant factors of ln (SOC).

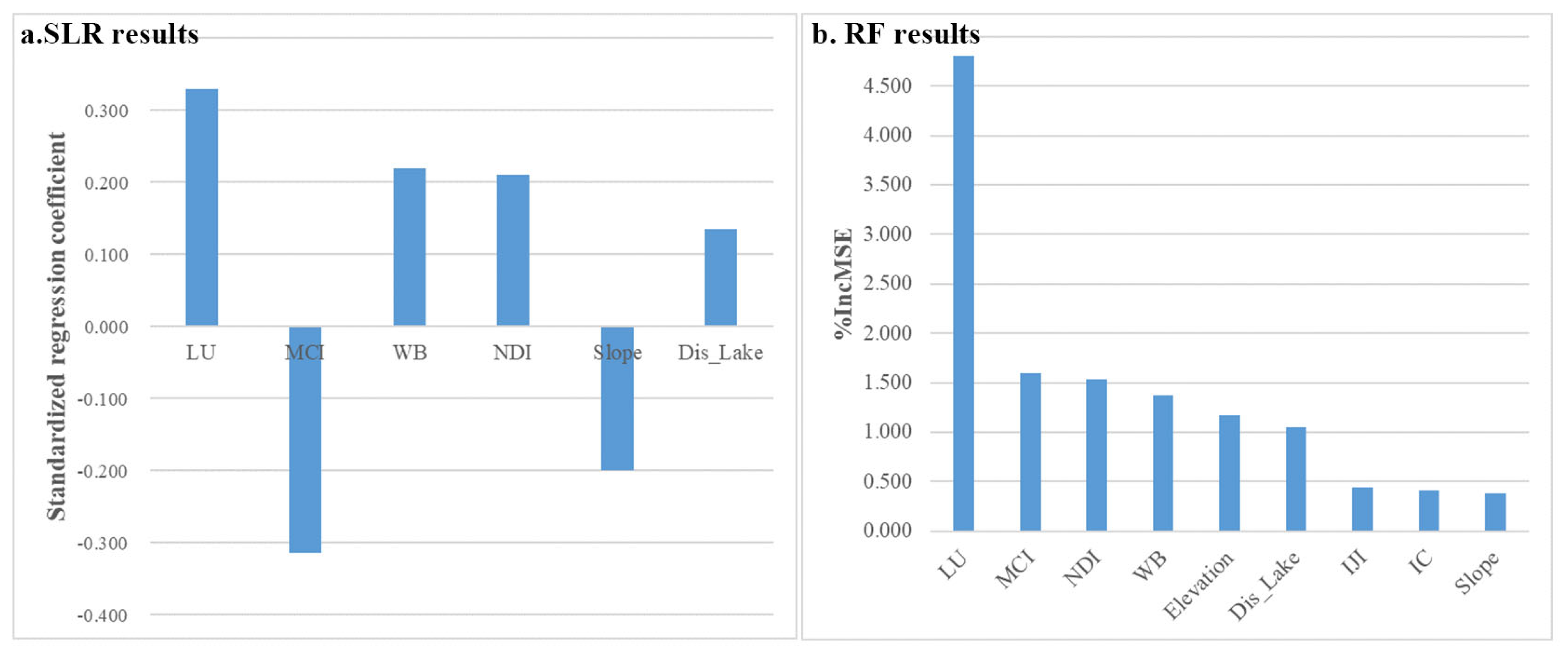
3.3. SLR, RF, and Cubist Model Results

SLR was used to explore the global linear relationship between ln (SOC) and environmental variables (Table 6). The results showed that the integration of natural factors, agricultural activities, and landscape metrics explained 35.4% of the variation in ln (SOC). The coefficients of this regression showed that slope and MCI were negatively related to ln (SOC). The slope increased by 1° or the MCI changed from 1 to 2, and the average decrease in ln (SOC) content was 0.101 and 0.294 ln (g/kg), respectively. The coefficient value of land use was 0.304, indicating that the mean ln (SOC) content of paddy fields was 0.304 ln (g/kg) higher than that of irrigated land. Dis_Lake, NDI, and WB were positively related to ln (SOC). When Dis_Lake increased by 1 km, NDI value increased by 1, and WB increased by 1%, the average increase in ln (SOC) content was 0.033, 0.884, and 0.005 ln(g/kg), respectively.
When parameter “mtry” (i.e., node size) was equal to 2, the RF model had the lowest mean square error value and was used as the final RF prediction model (Figure S1). The RF model combined with the nine covariates explained a 24.6% variation of ln (SOC), which was lower than that of the SLR model. This outcome indicated that the relationships between ln (SOC) and environmental variables were linear rather than non-linear. The standardized coefficients of SLR and %IncMSE index of RF were used to determine the relative importance of the environmental variables (Figure 4). Their results were slightly different, but they all exhibited that land use was the most important indicator of ln (SOC), followed by MCI, WB, and NDI. As a result, agricultural activities play a more important role in SOC variation than natural factors. Land use, MCI, WB, and NDI were the dominant global factors of ln (SOC).
The R2 of the Cubist model was 0.370, which was higher than that of the SLR model. The attribute usage of the Cubist model (Table 7) showed that the relationships between ln (SOC) and environmental variables among different land uses and MCIs varied. NDI was the most frequently used variable in the stratified regression model, followed by WB, slope, Dis_Lake, and IC. IJI and elevation were less frequently used in modeling.
Table 8 summarizes the specific stratification rules and linear regression results for each stratum. The ln (SOC) of paddy field samples was affected by slope, elevation, NDI, IJI, WB, and IC, whereas that of irrigated land samples was affected by Dis_Lake, WB, and IC. In comparison with the coefficients of each variable in the SLR, we found that the ln (SOC) of irrigated land samples was more affected by Dis_Lake, WB, and IC. The ln (SOC) of irrigated land samples was more affected by slope, elevation, IJI, and IC but less affected by NDI and WB. The ln (SOC) with an MCI equal to 2 was only affected by the NDI. The ln (SOC) with MCI equal to 1 was affected by NDI and slope, and the coefficient of NDI in this regression was higher than that in the regression with MCI equal to 2. These results indicated that the relationship between ln (SOC) and environmental variables had stratified heterogeneity, and that the main controlling factors of ln (SOC) in cropping systems were quite varied.
We examined the spatial dependence of different regression model residuals using a semi-variogram model. Based on the principle of the lowest RMSE value, we determined that spherical, exponential, spherical, and Gaussian models were optimal semi-variogram models of calibration data and the residuals of the SLR, RF, and Cubist models, respectively. The ratio of the nugget to sill values of the calibration data and the residuals of the SLR, RF, and Cubist models were 33.49%, 43.75%, 82.05%, and 82.95%, respectively. The ratio of nugget to sill of calibration data was 33.49%, denoting that the spatial dependence of ln (SOC) was medium [65]. The ratio of nugget to sill of the SLR residuals was 43.75%. This phenomenon denoted the medium spatial dependence of the SLR residuals, which violated the residual randomness assumption of the SLR. The ratio of nugget to sill of RF and Cubist was higher than 75%, which denotes the low spatial dependence of RF and Cubist residuals. This phenomenon revealed that RF and Cubist captured the spatial dependence of ln (SOC) better than SLR.

3.4. Evaluation of Prediction Models

The spherical model was used as the theoretical semi-variogram model of OK, and the nugget, partial sill, and range values of the OK model were 0.072, 0.143, and 180 m, respectively. The SLR and RF models were used directly for ln (SOC) estimation. In particular, the Cubist model can combine several neighboring regression residuals (0–9) in the prediction. The results (Figure S2) showed that the Cubist model that integrated with 9 neighboring regression residuals had the lowest mean square error and was used as the final Cubist prediction model. After obtaining ln (SOC) prediction values, these values were back-transformed to obtain SOC content.
The prediction accuracy of the OK, SLR, RF, and Cubist models was evaluated via RMSE, MAE, R2 and LCCC (Table 9). The results showed that the OK model performed poorly, and its prediction R2 was only 0.002. The SLR outperformed the OK model, and the RF outperformed the SLR. The Cubist model was the optimal prediction model with the lowest RMSE and MAE and the highest R2 and LCCC. In comparison with other models, the Cubist model exhibited great improvement in precision and accuracy.

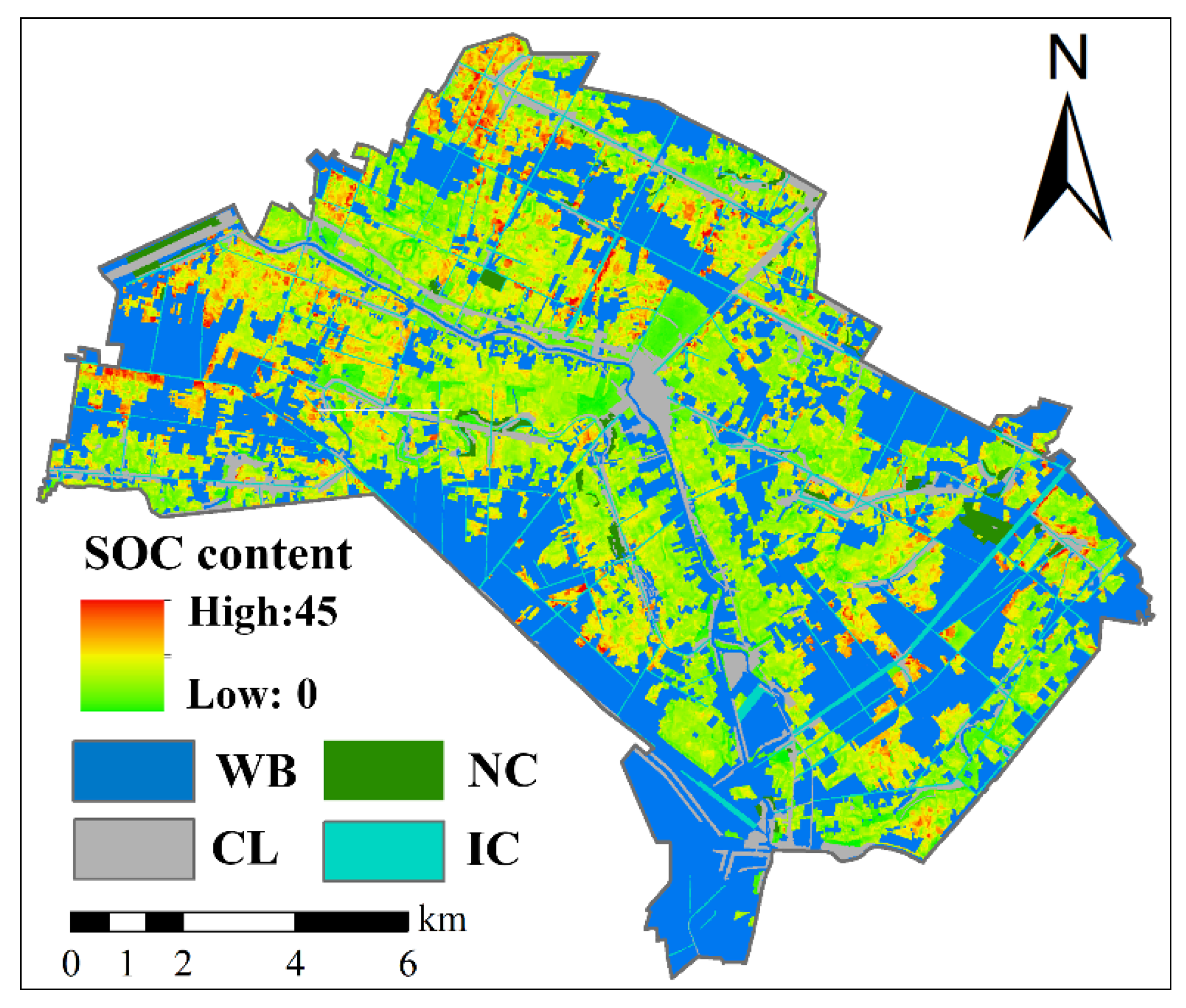
3.5. Spatial Distribution of SOC Content

Figure 5 displays the spatial distribution of SOC content predicted by the Cubist model (optimal prediction model). The SOC map exhibited abundant details and emphasized the sudden changes in SOC among different land uses and MCIs. We found that SOC along the northwest–southeast and northeast–southwest directions showed a trend of first decreasing and then increasing; that is, SOC showed a trend of high outside and low inside in the study area. Specifically, the SOC content was high in the north, west, and southeast of the study area. Combined with the spatial distribution of environmental variables (Figure 2), we found that the high SOC content areas planted single rice (i.e., paddy field and MCI equal to 1). Moreover, these areas had a high density of irrigated canals and water bodies and low and flat terrain, which was conducive to SOC accumulation. The SOC around the central town was low, which might be because the area implemented dry crop rotation (i.e., irrigated land and MCI equal to 2). Moreover, the region was characterized by high terrain and a low amount of straw return and density of water bodies and irrigated canals. These conditions resulted in low SOC input and high SOC loss, which were not conducive to SOC accumulation. In sum, the spatial distribution of SOC content was mainly controlled by land use and MCI and was affected by the amount of straw return, terrain factors, and landscape pattern.

4. Discussion

4.1. Relationship between SOC and Environmental Variables

The results of the SLR, RF, and Cubist models showed that the variation in SOC was related to terrain factors, agricultural activities, and landscape patterns. The latter two play a more important role in controlling SOC variation than natural factors.
Terrain factors influence soil moisture, soil erosion, and deposition by affecting runoff as well as soil temperature by affecting solar radiation intensity, thus directly and indirectly affecting the spatial distribution of SOC [66,67,68,69]. Particularly after long-term cultivation, the soil and water conservation capacity of farmland soil is weakened, and soil erosion is prone to occur [70,71]. The soil is carried along the slope with runoff from high places and deposited in low-lying areas. As a result, the SOC content in the low-lying area is often higher than that at the top of the slope [72,73,74]. Moreover, terrain affects the spatial distribution of SOC by influencing farmers’ decision making on farmland land use types. In the study area, farmers often choose low-lying farmland as a paddy field to facilitate water storage. Irrigated land is often located near rural residential areas where the terrain is relatively high. Given that the mean value of ln (SOC) in paddy fields is significantly higher than that in irrigated land, this terrain-based land use decision strategy intensifies the difference in SOC content between high- and low-lying areas. Therefore, slope and elevation showed a significant relation with ln (SOC), even in such low-relief agricultural areas.
Agricultural activities affect the spatial distribution of SOC by controlling the input of soil carbon and the decomposition rate of SOC [13,75]. A proper cropping and management system is conducive to farmland carbon fixation; otherwise, it leads to SOC loss [76,77,78,79]. In comparison with irrigated land, paddy fields have a higher input of stubble, a higher proportion of large aggregates, and weaker soil respiration caused by flooding environment [80]. As such, paddy fields are more conducive to carbon sequestration. In this study, we found that the ln (SOC) content of paddy fields was significantly higher than that of irrigated lands, which was consistent with the findings of most previous studies [15,81,82,83,84]. MCI reflects tillage intensity and thus becomes an important indicator of SOC variation. For conventional tillage, the increase in tillage intensity accelerates the decomposition of large aggregates in the soil, causing SOC to be directly exposed to the air [70,71]. This increases the mineralization rate of SOC and is not conducive to SOC sequestration in farmland soil. The results of this study confirmed that winter fallow was more conducive to SOC accumulation than rotation with winter wheat.
Straw return has a positive effect on SOC sequestration [85,86,87]. On the one hand, the decomposition of crop residuals provides SOM, N, P, and K to the soil and thus improves soil fertility. On the other hand, the crop residuals form humus under the action of microorganisms, which enhances soil cementation and facilitates the formation of soil macro-aggregates. Straw return can also reduce bulk density, increase soil porosity, improve soil physical structure, and enhance soil and water conservation capacity [85,86,88,89]. As a result, the amount of straw return is often positively correlated with SOC content. In this study, NDI also showed a significantly positive relation with ln (SOC), and its importance was second only to land use and MCI, highlighting the significance of straw return to farmland carbon sequestration.
In this study, landscape metrics were confirmed to be effective indicators of SOC. The IJI was negatively correlated with ln (SOC), which indicated that farmland fragmentation was not conducive to carbon sequestration. WB and IC were significantly positively related to ln (SOC). This phenomenon is probably because the high percentages of water bodies and irrigated canals ensure that local farmlands can be better irrigated, which promotes vegetation growth and thus increases the input of carbon into the soil [90,91,92].
The aforementioned results revealed that terrain factors continued to affect SOC spatial distribution, even in low-relief areas. Human activities, including agricultural activities and landscape patterns, were global dominant factors of SOC variation.

4.2. Stratified Heterogeneous Relationship between SOC and Environmental Variables

The fitting R2 of the Cubist model was higher than that of the global regression model (i.e., SLR and RF), highlighting the consideration of stratified heterogeneous relationships between SOC and environmental variables. The stratification rules show that the relationship between SOC and environmental variables varies with different cropping systems.
The dominant factors of SOC in paddy fields and irrigated fields differed. The SOC of irrigated land was mainly affected by Dis_Lake, WB, and IC, and these covariates were associated with water and irrigation. The SOC of paddy fields was affected by various variables, including elevation, slope, NDI, IJI, WB, and IC. Comparing the absolute values of the coefficients of these variables in the two regressions, we found that the irrigated land sample was more affected by irrigation-related factors. This phenomenon may be because the soil moisture of irrigated land is low, so the increase in soil moisture has a more obvious effect on the decrease in soil temperature and the growth of crops [92,93,94]. However, in paddy fields, SOC is not sensitive to subtle changes in soil moisture owing to the long-term flooding environment [80,95,96]. Therefore, irrigation-related factors have a greater impact on the SOC of irrigated lands. These findings indicate that special attention should be paid to the irrigation of irrigated land.
The relationship between SOC and NDI varies under different MCIs. Specifically, the coefficient of NDI was much larger when MCI was equal to 1 than when MCI was equal to 2, indicating that straw return played a less important role in SOC accumulation when rotating with winter wheat. This may be because the amount of stubble in various summer crops is quite different, which makes a big difference in the amount of stubble in different fields [97,98]. If rotating with winter wheat, then the amount of wheat straw returned from different fields had little difference. Straw return had a greater influence on the spatial variation of SOC when MCI = 1. These findings highlight the importance of straw return on carbon sequestration, especially when only summer crops are planted.

4.3. Comparison of Model Performance

The model evaluation results showed that the OK model performed poorly in SOC estimation. This may be because the spatial distribution of SOC is non-stationary owing to the influence of various natural and human activities, which violates the intrinsic assumption of the OK model [55,99,100]. Moreover, the average distance of the sampling points is 687 m, which is larger than the range of SOC (i.e., 180 m), resulting in a moderate spatial dependence of SOC (nugget-to-sill ratio is 33.46%) [101]. In summary, the spatial non-stationarity and limited spatial dependence of SOC were the reasons for poor prediction accuracy of OK.
The SLR, RF, and The Cubist models outperformed the OK model. Given that the validity of regression models relies highly on the choice of environmental variables, these results demonstrate the effectiveness of agricultural activities and landscape metrics in SOC mapping. The Cubist model outperformed the SLR and RF models, which emphasized the improvement of SOC estimation by considering stratified heterogeneous relationships. Several studies have found that the prediction accuracy of regressions can be improved by adding residuals interpolated by the OK model [102,103,104,105]. However, in this study, we did not use such a strategy because of the low spatial dependence of the regression residuals.

4.4. Limitations and Future Work

In this study, natural factors, agricultural activities, and landscape metrics could explain the 37.0% variation in ln (SOC), in which agricultural activities played more important roles. Other agricultural activities, such as tillage methods [70,71] and fertilization [106,107], may further enhance the explanatory power of the Cubist model. However, obtaining the spatial distribution of tillage methods and fertilization is difficult using current optical remote sensing technology. Their impact on the spatial variation of farmland SOC and their application in SOC mapping need to be further explored.
This study provided a framework to explore the influencing factors of farmland soil properties in plains and to determine the dominant factors of farmland SOC on a regional scale. However, the influencing factors of SOC may vary with the expansion of the study area. For example, natural factors, such as climate and soil type, may play more important roles on a larger scale. The dominant factors of farmland SOC on a large scale should be investigated.

5. Conclusions

This research explored the global and stratified dominant factors of farmland SOC in plains and estimated the spatial distribution of SOC using SLR, RF, and Cubist models. The land use types, MCI, NDI, and WB were the global dominant factors of SOC, indicating that paddy field, low cropping intensity, straw return, and sufficient irrigation facilities are conducive to farmland SOC accumulation. The dominant factors of SOC vary in different cropping systems. Compared with the SOC of paddy fields, the SOC of irrigated land was more affected by irrigation-related factors. The effect of straw return on SOC was diverse under different cropping intensities. These findings reveal the stratified heterogeneous relationship between SOC and covariates and highlight the importance of farmland zoning management. Cubist model outperformed other models, which demonstrated its effectiveness in explaining the SOC variation and SOC mapping in low-relief farmlands.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/rs14153575/s1, Figure S1: Mean square error changes with the increase in mtry in the random forest model. Figure S2: Mean square error changes with the increase in neighbors in the Cubist model.

Author Contributions

Conceptualization, Z.W. and Y.C.; methodology, Z.W. and Z.Y.; software, Y.Z.; validation, Z.W., Y.Z. and Y.H.; formal analysis, Z.W.; investigation, Z.W. and Y.C.; resources, Z.W. and Y.C.; data curation, Z.Y.; writing—original draft preparation, Z.W.; writing—review and editing, Y.C., Z.Y. and Y.Z.; visualization, Z.Y. and Y.H.; supervision, Y.C. and Z.Y.; project administration, Y.C.; funding acquisition, Y.C. All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by the Key R&D projects in Hubei Province (Grant No. 2021BCA220).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Yang, L.; He, X.; Shen, F.; Zhou, C.; Zhu, A.X.; Gao, B.; Chen, Z.; Li, M. Improving prediction of soil organic carbon content in croplands using phenological parameters extracted from NDVI time series data. Soil Tillage Res. 2020, 196, 104465. [Google Scholar] [CrossRef]
  2. Schulze, R.E.; Schutte, S. Mapping soil organic carbon at a terrain unit resolution across South Africa. Geoderma 2020, 373, 114447. [Google Scholar] [CrossRef]
  3. Minasny, B.; Malone, B.P.; McBratney, A.B.; Angers, D.A.; Arrouays, D.; Chambers, A.; Chaplot, V.; Chen, Z.-S.; Cheng, K.; Das, B.S.; et al. Soil carbon 4 per mille. Geoderma 2017, 292, 59–86. [Google Scholar] [CrossRef]
  4. Ni, H.; Liu, C.; Sun, B.; Liang, Y. Response of global farmland soil organic carbon to nitrogen application over time depends on soil type. Geoderma 2022, 406, 115542. [Google Scholar] [CrossRef]
  5. Niu, X.; Liu, C.; Jia, X.; Zhu, J. Changing soil organic carbon with land use and management practices in a thousand-year cultivation region. Agric. Ecosyst. Environ. 2021, 322, 107639. [Google Scholar] [CrossRef]
  6. Qiu, T.; Andrus, R.; Aravena, M.-C.; Ascoli, D.; Bergeron, Y.; Berretti, R.; Berveiller, D.; Bogdziewicz, M.; Boivin, T.; Bonal, R.; et al. Limits to reproduction and seed size-number trade-offs that shape forest dominance and future recovery. Nat. Commun. 2022, 13, 2381. [Google Scholar] [CrossRef] [PubMed]
  7. Davidson, E.A.; Janssens, I.A. Temperature sensitivity of soil carbon decomposition and feedbacks to climate change. Nature 2006, 440, 165–173. [Google Scholar] [CrossRef] [PubMed]
  8. Tian, H.; Zhang, J.; Zhu, L.; Qin, J.; Liu, M.; Shi, J.; Li, G. Revealing the scale- and location-specific relationship between soil organic carbon and environmental factors in China’s north-south transition zone. Geoderma 2022, 409, 115600. [Google Scholar] [CrossRef]
  9. Adingo, S.; Yu, J.-R.; Liu, X.; Jing, S.; Li, X.; Zhang, X. Land-use change influence soil quality parameters at an ecologically fragile area of YongDeng County of Gansu Province, China. Peerj 2021, 9, e12246. [Google Scholar] [CrossRef]
  10. Nijbroek, R.; Piikki, K.; Soderstrom, M.; Kempen, B.; Turner, K.G.; Hengari, S.; Mutua, J. Soil Organic Carbon Baselines for Land Degradation Neutrality: Map Accuracy and Cost Tradeoffs with Respect to Complexity in Otjozondjupa, Namibia. Sustainability 2018, 10, 1610. [Google Scholar] [CrossRef] [Green Version]
  11. Suleymanov, A.; Abakumov, E.; Suleymanov, R.; Gabbasova, I.; Komissarov, M. The Soil Nutrient Digital Mapping for Precision Agriculture Cases in the Trans-Ural Steppe Zone of Russia Using Topographic Attributes. Isprs Int. J. Geo-Inf. 2021, 10, 243. [Google Scholar] [CrossRef]
  12. Minasny, B.; McBratney, A.B. Digital soil mapping: A brief history and some lessons. Geoderma 2016, 264, 301–311. [Google Scholar] [CrossRef]
  13. Dong, W.; Wu, T.; Luo, J.; Sun, Y.; Xia, L. Land parcel-based digital soil mapping of soil nutrient properties in an alluvial-diluvia plain agricultural area in China. Geoderma 2019, 340, 234–248. [Google Scholar] [CrossRef]
  14. Wu, Z.; Liu, Y.; Han, Y.; Zhou, J.; Liu, J.; Wu, J. Mapping farmland soil organic carbon density in plains with combined cropping system extracted from NDVI time-series data. Sci. Total Environ. 2021, 754, 142120. [Google Scholar] [CrossRef]
  15. Liu, Y.; Guo, L.; Jiang, Q.; Zhang, H.; Chen, Y. Comparing geospatial techniques to predict SOC stocks. Soil Tillage Res. 2015, 148, 46–58. [Google Scholar] [CrossRef]
  16. Zhang, X.; Lu, S.; Wang, C.; Zhang, A.; Wang, X. Optimization of tillage rotation and fertilization increased the soil organic carbon pool and crop yield in a semiarid region. Land Degrad. Dev. 2021, 32, 5241–5252. [Google Scholar] [CrossRef]
  17. Wu, Z.H.; Wang, B.Z.; Huang, J.L.; An, Z.H.; Jiang, P.; Chen, Y.Y.; Liu, Y.F. Estimating soil organic carbon density in plains using landscape metric-based regression Kriging model. Soil Tillage Res. 2019, 195, 104381. [Google Scholar] [CrossRef]
  18. Zhang, Y.; Guo, L.; Chen, Y.; Shi, T.; Luo, M.; Ju, Q.; Zhang, H.; Wang, S. Prediction of soil organic carbon based on landsat 8 monthly NDVI data for the Jianghan Plain in Hubei Province, China. Remote Sens. 2019, 11, 1683. [Google Scholar] [CrossRef] [Green Version]
  19. Yang, L.; Song, M.; Zhu, A.X.; Qin, C.; Zhou, C.; Qi, F.; Li, X.; Chen, Z.; Gao, B. Predicting soil organic carbon content in croplands using crop rotation and Fourier transform decomposed variables. Geoderma 2019, 340, 289–302. [Google Scholar] [CrossRef]
  20. Yang, L.; Cai, Y.; Zhang, L.; Guo, M.; Li, A.; Zhou, C. A deep learning method to predict soil organic carbon content at a regional scale using satellite-based phenology variables. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102428. [Google Scholar] [CrossRef]
  21. He, X.; Yang, L.; Li, A.; Zhang, L.; Shen, F.; Cai, Y.; Zhou, C. Soil organic carbon prediction using phenological parameters and remote sensing variables generated from Sentinel-2 images. CATENA 2021, 205, 105442. [Google Scholar] [CrossRef]
  22. Dvorakova, K.; Shi, P.; Limbourg, Q.; van Wesemael, B. Soil organic carbon mapping from remote sensing: The effect of crop residues. Remote Sens. 2020, 12, 1913. [Google Scholar] [CrossRef]
  23. Jiang, H.; Rusuli, Y.; Amuti, T.; He, Q. Quantitative assessment of soil salinity using multi-source remote sensing data based on the support vector machine and artificial neural network. Int. J. Remote Sens. 2019, 40, 284–306. [Google Scholar] [CrossRef]
  24. Nguyen, K.A.; Chen, W.; Lin, B.-S.; Seeboonruang, U. Comparison of Ensemble Machine Learning Methods for Soil Erosion Pin Measurements. Isprs. Int. J. Geo-Inf. 2021, 10, 42. [Google Scholar] [CrossRef]
  25. Mishra, U.; Gautam, S.; Riley, W.J.; Hoffman, F.M. Ensemble Machine Learning Approach Improves Predicted Spatial Variation of Surface Soil Organic Carbon Stocks in Data-Limited Northern Circumpolar Region. Front. Big Data 2020, 3, 528441. [Google Scholar] [CrossRef] [PubMed]
  26. Hounkpatin, K.O.L.; Bossa, A.Y.; Yira, Y.; Igue, M.A.; Sinsin, B.A. Assessment of the soil fertility status in Benin (West Africa)-Digital soil mapping using machine learning. Geoderma Reg. 2022, 28, e00444. [Google Scholar] [CrossRef]
  27. Zhao, D.; Wang, J.; Zhao, X.; Triantafilis, J. Clay content mapping and uncertainty estimation using weighted model averaging. Catena 2022, 209, 105791. [Google Scholar] [CrossRef]
  28. Estevez, V.; Beucher, A.; Mattback, S.; Boman, A.; Auri, J.; Bjork, K.-M.; Osterholm, P. Machine learning techniques for acid sulfate soil mapping in southeastern Finland. Geoderma 2022, 406, 115446. [Google Scholar] [CrossRef]
  29. Zhong, C.; Yang, Z.; Hu, B.; Zhang, X.; Hou, Q.; Xia, X.; Yu, T. Soil organic carbon and the response to climate change in Hebei Plains. Res. Agric. Mod. 2016, 37, 809–816. [Google Scholar]
  30. Takoutsing, B.; Weber, J.C.; Rodriguez Martin, J.A.; Shepherd, K.; Aynekulu, E.; Sila, A. An assessment of the variation of soil properties with landscape attributes in the highlands of Cameroon. Land Degrad. Dev. 2018, 29, 2496–2505. [Google Scholar] [CrossRef]
  31. Bhardwaj, A.K.; Mishra, V.K.; Singh, A.K.; Arora, S.; Srivastava, S.; Singh, Y.P.; Sharma, D.K. Soil salinity and land use-land cover interactions with soil carbon in a salt-affected irrigation canal command of Indo-Gangetic plain. Catena 2019, 180, 392–400. [Google Scholar] [CrossRef]
  32. Alidoust, E.; Afyuni, M.; Hajabbasi, M.A.; Mosaddeghi, M.R. Soil carbon sequestration potential as affected by soil physical and climatic factors under different land uses in a semiarid region. Catena 2018, 171, 62–71. [Google Scholar] [CrossRef]
  33. Yang, S.H.; Zhang, H.T.; Zhang, C.R.; Li, W.D.; Guo, L.; Chen, J.Y. Predicting soil organic matter content in a plain-to-hill transition belt using geographically weighted regression with stratification. Arch. Agron. Soil Sci. 2019, 65, 1745–1757. [Google Scholar] [CrossRef]
  34. Zhou, S. Analysis of Influencing Factors and Prediction of Soil Organic Carbon at Agricultural Landscape in Hilly Area. Master’s Thesis, Southwest University, Chongqing, China, 2016. [Google Scholar]
  35. Quinlan, J.R. Combining Instance-Based and Model-Based Learning. In Proceedings of the Tenth International Conference on International Conference on Machine Learning, Amherst, MA, USA, 27–29 June 1993. [Google Scholar]
  36. Kuhn, M.; Quinlan, R. Cubist: Rule- And Instance-Based Regression Modeling. 2020. Available online: https://cran.r-project.org/web/packages/Cubist/vignettes/cubist.html (accessed on 1 October 2020).
  37. Fathololoumi, S.; Vaezi, A.R.; Alavipanah, S.K.; Ghorbani, A.; Saurette, D.; Biswas, A. Improved digital soil mapping with multitemporal remotely sensed satellite data fusion: A case study in Iran. Sci. Total Environ. 2020, 721, 137703. [Google Scholar] [CrossRef]
  38. Fathololoumi, S.; Vaezi, A.R.; Alavipanah, S.K.; Ghorbani, A.; Saurette, D.; Biswas, A. Effect of multi-temporal satellite images on soil moisture prediction using a digital soil mapping approach. Geoderma 2021, 385, 114901. [Google Scholar] [CrossRef]
  39. Silva, E.B.; Giasson, E.; Dotto, A.C.; ten Caten, A.; Melo Dematte, J.A.; Bacic, I.L.Z.; da Veiga, M. A Regional Legacy Soil Dataset for Prediction of Sand and Clay Content with Vis-Nir-Swir, in Southern Brazil. Rev. Bras. De. Cienc. Do. Solo 2019, 43, 1–20. [Google Scholar] [CrossRef] [Green Version]
  40. dos Santos Teixeira, A.F.; Procopio Pelegrino, M.H.; Faria, W.M.; Godinho Silva, S.H.; Marcolino Goncalves, M.G.; Acerbi Junior, F.W.; Gomide, L.R.; Padua Junior, A.L.; de Souza, I.A.; Chakraborty, S.; et al. Tropical soil pH and sorption complex prediction via portable X-ray fluorescence spectrometry. Geoderma 2020, 361, 114132. [Google Scholar] [CrossRef]
  41. Nelson, D.W.; Sommers, L.E. A rapid and accurate procedure for estimation of organic carbon in soils. Proc. Indiana Acad. Sci. 1974, 84, 456–462. [Google Scholar]
  42. Minasny, B.; McBratney, A.B.; Wadoux, A.M.J.C.; Akoeb, E.N.; Sabrina, T. Precocious 19th century soil carbon science. Geoderma Reg. 2020, 22, e00306. [Google Scholar] [CrossRef]
  43. FAO/IIASA/ISRIC/ISSCAS/JRC. Harmonized World Soil Database (Version 1.2). Available online: http://www.fao.org/home/en/ (accessed on 1 October 2020).
  44. CAS. ASTER DEM. Available online: http://www.gscloud.cn (accessed on 1 September 2019).
  45. Mulla, D.J. Twenty five years of remote sensing in precision agriculture: Key advances and remaining knowledge gaps. Biosyst. Eng. 2013, 114, 358–371. [Google Scholar] [CrossRef]
  46. Yang, R.; Luo, X.; Xu, Q.; Zhang, X.; Wu, J. Measuring the Impact of the Multiple Cropping Index of Cultivated Land during Continuous and Rapid Rise of Urbanization in China: A Study from 2000 to 2015. Land 2021, 10, 491. [Google Scholar] [CrossRef]
  47. Liang, S.Z.; Ma, W.D.; Sui, X.Y.; Yao, H.M.; Li, H.Z.; Liu, T.; Hou, X.H.; Wang, M. Extracting the Spatiotemporal Pattern of Cropping Systems From NDVI Time Series Using a Combination of the Spline and HANTS Algorithms: A Case Study for Shandong Province. Can. J. Remote Sens. 2017, 43, 1–15. [Google Scholar] [CrossRef]
  48. Pan, J.; Chen, Y.; Zhang, Y.; Chen, M.; Shailaja, F.; Luan, B.; Wang, F.; Meng, D.; Liu, Y.; Jiao, L.; et al. Spatial-temporal dynamics of grain yield and the potential driving factors at the county level in China. J. Clean. Prod. 2020, 255, 120312. [Google Scholar] [CrossRef]
  49. Mcnairn, H.; Boisvert, J.B.; Major, D.J.; Gwyn, Q.H.J.; Brown, R.J.; Smith, A.M. Identification of Agricultural Tillage Practices from C-Band Radar Backscatter. Can. J. Remote Sens. 1996, 22, 154–162. [Google Scholar] [CrossRef]
  50. Huang, J.-Y.; Liu, Z.; Wan, W.; Liu, Z.-Y.; Wang, J.-Y.; Wang, S. Remote sensing retrieval of maize residue cover on soil heterogeneous background. Ying Yong Sheng Tai Xue Bao J. Appl. Ecol. 2020, 31, 474–482. [Google Scholar] [CrossRef]
  51. Memon, M.S.; Jun, Z.; Sun, C.; Jiang, C.; Xu, W.; Hu, Q.; Yang, H.; Ji, C. Assessment of Wheat Straw Cover and Yield Performance in a Rice-Wheat Cropping System by Using Landsat Satellite Data. Sustainability 2019, 11, 5369. [Google Scholar] [CrossRef] [Green Version]
  52. Zheng, B.; Campbell, J.B.; Beurs, K.M.D. Remote sensing of crop residue cover using multi-temporal Landsat imagery. Remote Sens. Environ. 2012, 117, 177–183. [Google Scholar] [CrossRef]
  53. Mcgarigal, K. FRAGSTATS: Spatial Pattern Analysis Program for Categorical Maps. Computer Software Program Produced by the Authors at the University of Massachuse-tts, Amherst. 2002. Available online: Www.umass.edu/landeco/research/fragstats/fragstats.html (accessed on 1 October 2020).
  54. Matheron, G. The Intrinsic Random Functions and Their Applications. Adv. Appl. Probab. 1973, 5, 439–468. [Google Scholar] [CrossRef] [Green Version]
  55. Webster, R. Geostatistics for Environmental Scientists; John Wiley & Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
  56. Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
  57. Forkuor, G.; Hounkpatin, O.K.L.; Welp, G.; Thiel, M. High Resolution Mapping of Soil Properties Using Remote Sensing Variables in South-Western Burkina Faso: A Comparison of Machine Learning and Multiple Linear Regression Models. PLoS ONE 2017, 12, e0170478. [Google Scholar] [CrossRef]
  58. Pittman, R.; Hu, B.; Webster, K. Improvement of soil property mapping in the Great Clay Belt of northern Ontario using multi-source remotely sensed data. Geoderma 2021, 381, 114761. [Google Scholar] [CrossRef]
  59. Quinlan, J.R. Combining Instance-Based and Model-Based Learning; Morgan Kaufmann: Burlington, MA, USA, 1993. [Google Scholar]
  60. Worland, S.C.; Farmer, W.H.; Kiang, J.E. Improving predictions of hydrological low-flow indices in ungaged basins using machine learning. Environ. Model. Softw. 2018, 101, 169–182. [Google Scholar] [CrossRef]
  61. Kibler, D.F.; Aha, D.W.; Albert, M.K. Instancebased Prediction of Real-valued Attributes. Comput. Intell. 1989, 5, 51–57. [Google Scholar] [CrossRef] [Green Version]
  62. Lin, I.K. A note on the concordance correlation coefficient. Biometrics 2000, 56, 324–325. [Google Scholar]
  63. Lin, I.K. A concordance correlation coefficient to evaluate reproducibility. Biometrics 1989, 45, 255–268. [Google Scholar] [CrossRef]
  64. Mcbride, G.B. A Proposal for Strength-of-Agreement Criteria for Lin’s Concordance Correlation Coefficient; National Institute of Water & Atmospheric Research Ltd.: Auckland, New Zealand, 2005. [Google Scholar]
  65. Wilding, L.P. Spatial variability: Its documentation, accommodation and implication to soil survey. In Proceedings of the Soil Spatial Variability, Las Vegas, NV, USA, 30 November–1 December 1984. [Google Scholar]
  66. Sun, W.; Zhu, H.; Guo, S. Soil organic carbon as a function of land use and topography on the Loess Plateau of China. Ecol. Eng. 2015, 83, 249–257. [Google Scholar] [CrossRef]
  67. Schwanghart, W.; Jarmer, T. Linking spatial patterns of soil organic carbon to topography—A case study from south-eastern Spain. Geomorphology 2011, 126, 252–263. [Google Scholar] [CrossRef]
  68. Mohseni, N.; Salar, Y.S. Terrain indices control the quality of soil total carbon stock within water erosion-prone environments. Ecohydrol. Hydrobiol. 2021, 21, 46–54. [Google Scholar] [CrossRef]
  69. Wisniewski, P.; Maerker, M. Comparison of Topsoil Organic Carbon Stocks on Slopes under Soil-Protecting Forests in Relation to the Adjacent Agricultural Slopes. Forests 2021, 12, 390. [Google Scholar] [CrossRef]
  70. Man, M.; Wagner-Riddle, C.; Dunfield, K.E.; Deen, B.; Simpson, M.J. Long-term crop rotation and different tillage practices alter soil organic matter composition and degradation. Soil Tillage Res. 2021, 209, 104960. [Google Scholar] [CrossRef]
  71. Topa, D.; Cara, I.G.; Jitareanu, G. Long term impact of different tillage systems on carbon pools and stocks, soil bulk density, aggregation and nutrients: A field meta-analysis. Catena 2021, 199, 105102. [Google Scholar] [CrossRef]
  72. Bameri, A.; Khormalii, F.; Kiani, F.; Dehghani, A.A. Spatial variability of soil organic carbon in different hillslope positions in Toshan area, Golestan Province, Iran: Geostatistical approaches. J. Mt. Sci. 2015, 12, 1422–1433. [Google Scholar] [CrossRef]
  73. Kheir, R.B.; Greve, M.H.; Bocher, P.K.; Greve, M.B.; Larsen, R.; McCloy, K. Predictive mapping of soil organic carbon in wet cultivated lands using classification-tree based models: The case study of Denmark. J. Environ. Manag. 2010, 91, 1150–1160. [Google Scholar] [CrossRef] [PubMed]
  74. Gaspar, L.; Mabit, L.; Lizaga, I.; Navas, A. Lateral mobilization of soil carbon induced by runoff along karstic slopes. J. Environ. Manag. 2020, 260, 110091. [Google Scholar] [CrossRef] [PubMed]
  75. Abbas, F.; Hammad, H.M.; Ishaq, W.; Farooque, A.A.; Bakhat, H.F.; Zia, Z.; Fahad, S.; Farhad, W.; Cerda, A. A review of soil carbon dynamics resulting from agricultural practices. J. Environ. Manag. 2020, 268, 110319. [Google Scholar] [CrossRef]
  76. Tao, F.; Palosuo, T.; Valkama, E.; Makipaa, R. Cropland soils in China have a large potential for carbon sequestration based It on literature survey. Soil Tillage Res. 2019, 186, 70–78. [Google Scholar] [CrossRef]
  77. Guo, N.; Shi, X.; Zhao, Y.; Xu, S.; Wang, M.; Zhang, G.; Wu, J.; Huang, B.; Kong, C. Environmental and anthropogenic factors driving changes in paddy soil organic matter: A case study in the middle and lower Yangtze River Plain of China. Pedosphere 2017, 27, 926–937. [Google Scholar] [CrossRef]
  78. Blonska, E.; Lasota, J.; Vasconcelos da Silva, G.R.; Vanguelova, E.; Ashwood, F.; Tibbett, M.; Watts, K.; Lukac, M. Soil organic matter stabilization and carbon-cycling enzyme activity are affected by land management. Ann. For. Res. 2020, 63, 71–85. [Google Scholar] [CrossRef]
  79. Zeng, Y.; Fang, N.; Shi, Z. Effects of human activities on soil organic carbon redistribution at an agricultural watershed scale on the Chinese Loess Plateau. Agric. Ecosyst. Environ. 2020, 303, 107112. [Google Scholar] [CrossRef]
  80. Qin, Z.; Yang, X.; Song, Z.; Peng, B.; Van Zwieten, L.; Yu, C.; Wu, S.; Mohammad, M.; Wang, H. Vertical distributions of organic carbon fractions under paddy and forest soils derived from black shales: Implications for potential of long-term carbon storage. Catena 2021, 198, 105056. [Google Scholar] [CrossRef]
  81. Jafarian, Z.; Kavian, A. Effects of Land-Use Change on Soil Organic Carbon and Nitrogen. Commun. Soil Sci. Plant Anal. 2013, 44, 339–346. [Google Scholar] [CrossRef]
  82. Li, X.; Zhang, H.; Sun, M.; Xu, N.; Sun, G.; Zhao, M. Land use change from upland to paddy field in Mollisols drives soil aggregation and associated microbial communities. Appl. Soil Ecol. 2020, 146, 103351. [Google Scholar] [CrossRef]
  83. Guo, L.; Zhao, C.; Zhang, H.; Chen, Y.; Linderman, M.; Zhang, Q.; Liu, Y. Comparisons of spatial and non-spatial models for predicting soil carbon content based on visible and near-infrared spectral technology. Geoderma 2017, 285, 280–292. [Google Scholar] [CrossRef]
  84. Mao, D.H.; Wang, Z.M.; Li, L.; Miao, Z.H.; Ma, W.H.; Song, C.C.; Ren, C.Y.; Jia, M.M. Soil organic carbon in the Sanjiang Plain of China: Storage, distribution and controlling factors. Biogeosciences 2015, 12, 1635–1645. [Google Scholar] [CrossRef] [Green Version]
  85. Hu, N.; Shi, H.; Wang, B.; Gu, Z.; Zhu, L. Effects of different wheat straw returning modes on soil organic carbon sequestration in a rice-wheat rotation. Can. J. Soil Sci. 2019, 99, 25–35. [Google Scholar] [CrossRef]
  86. Jin, Z.; Shah, T.; Zhang, L.; Liu, H.; Peng, S.; Nie, L. Effect of straw returning on soil organic carbon in rice-wheat rotation system: A review. Food Energy Secur. 2020, 9, e200. [Google Scholar] [CrossRef] [Green Version]
  87. Zou, H.; Ye, X.; Li, J.; Lu, J.; Fan, Q.; Yu, N.; Zhang, Y.; Dang, X.; Zhang, Y. Effects of Straw Return in Deep Soils with Urea Addition on the Soil Organic Carbon Fractions in a Semi-Arid Temperate Cornfield. PLoS ONE 2016, 11, e0153214. [Google Scholar] [CrossRef]
  88. Liu, J.; Jing, F.; Jiang, G.; Liu, J. Effects of Straw Incorporation on Soil Organic Carbon Density and the Carbon Pool Management Index under Long-Term Continuous Cotton. Commun. Soil Sci. Plant Anal. 2017, 48, 412–422. [Google Scholar] [CrossRef]
  89. Wang, H.; Wang, X.-D.; Tian, X.-H. Effect of straw-returning on the storage and distribution of different active fractions of soil organic carbon. Ying Yong Sheng Tai Xue Bao J. Appl. Ecol. 2014, 25, 3491–3498. [Google Scholar]
  90. Li, Z.; Xu, X.; Pan, G.; Smith, P.; Cheng, K. Irrigation regime affected SOC content rather than plow layer thickness of rice paddies: A county level survey from a river basin in lower Yangtze valley, China. Agric. Water Manag. 2016, 172, 31–39. [Google Scholar] [CrossRef]
  91. Trost, B.; Prochnow, A.; Drastig, K.; Meyer-Aurich, A.; Ellmer, F.; Baumecker, M. Irrigation, soil organic carbon and N2O emissions. A review. Agron. Sustain. Dev. 2013, 33, 733–749. [Google Scholar] [CrossRef] [Green Version]
  92. Hu, Y.; Lu, Y.; Edmonds, J.; Liu, C.; Zhang, Q.; Zheng, C. Irrigation alters source-composition characteristics of groundwater dissolved organic matter in a large arid river basin, Northwestern China. Sci. Total Environ. 2021, 767, 144372. [Google Scholar] [CrossRef]
  93. Zhang, Y.J.; Guo, S.L.; Zhao, M.; Du, L.L.; Li, R.J.; Jiang, J.S.; Wang, R.; Li, N.N. Soil moisture influence on the interannual variation in temperature sensitivity of soil organic carbon mineralization in the Loess Plateau. Biogeosciences 2015, 12, 3655–3664. [Google Scholar] [CrossRef] [Green Version]
  94. Thomas, A.; Cosby, B.J.; Henrys, P.; Emmett, B. Patterns and trends of topsoil carbon in the UK: Complex interactions of land use change, climate and pollution. Sci. Total Environ. 2020, 729, 138330. [Google Scholar] [CrossRef] [PubMed]
  95. Ma, Y.; Xu, J.; Wei, Q.; Yang, S.; Liao, L.; Chen, S.; Liao, Q. Organic carbon content and its liable components in paddy soil under water-saving irrigation. Plant Soil Environ. 2017, 63, 125–130. [Google Scholar] [CrossRef]
  96. Yang, S.; Liu, X.; Liu, X.; Xu, J. Effect of water management on soil respiration and NEE of paddy fields in Southeast China. Paddy Water Environ. 2017, 15, 787–796. [Google Scholar] [CrossRef]
  97. Chen, S.; Xu, C.; Yan, J.; Zhang, X.; Zhang, X.; Wang, D. The influence of the type of crop residue on soil organic carbon fractions: An 11-year field study of rice-based cropping systems in southeast China. Agric. Ecosyst. Environ. 2016, 223, 261–269. [Google Scholar] [CrossRef]
  98. Jarecki, M.K.; Lal, R. Crop management for soil carbon sequestration. Crit. Rev. Plant Sci. 2003, 22, 471–502. [Google Scholar] [CrossRef]
  99. Tziachris, P.; Aschonitis, V.; Chatzistathis, T.; Papadopoulou, M.; Doukas, I.D. Comparing Machine Learning Models and Hybrid Geostatistical Methods Using Environmental and Soil Covariates for Soil pH Prediction. Isprs Int. J. Geo-Inf. 2020, 9, 276. [Google Scholar] [CrossRef] [Green Version]
  100. Hengl, T.; Heuvelink, G.B.; Stein, A. A generic framework for spatial prediction of soil variables based on regression-kriging. Geoderma 2004, 120, 75–93. [Google Scholar] [CrossRef] [Green Version]
  101. Cambardella, C.A.; Moorman, T.B.; Novak, J.M.; Parkin, T.B.; Karlen, D.L.; Turco, R.F.; Konopka, A.E. Field-Scale Variability of Soil Properties in Central Iowa Soils. Soil Sci. Soc. Am. J. 1994, 58, 1501–1511. [Google Scholar] [CrossRef]
  102. Tziachris, P.; Aschonitis, V.; Chatzistathis, T.; Papadopoulou, M. Assessment of spatial hybrid methods for predicting soil organic matter using DEM derivatives and soil parameters. Catena 2019, 174, 206–216. [Google Scholar] [CrossRef]
  103. Wang, L.; Wu, W.; Liu, H.-B. Digital mapping of topsoil pH by random forest with residual kriging (RFRK) in a hilly region. Soil Res. 2019, 57, 387–396. [Google Scholar] [CrossRef]
  104. Guo, P.T.; Li, M.F.; Luo, W.; Tang, Q.F.; Liu, Z.W.; Lin, Z.M. Digital mapping of soil organic matter for rubber plantation at regional scale: An application of random forest plus residuals kriging approach. Geoderma 2015, 237, 49–59. [Google Scholar] [CrossRef]
  105. Matinfar, H.R.; Maghsodi, Z.; Mousavi, S.R.; Rahmani, A. Evaluation and Prediction of Topsoil organic carbon using Machine learning and hybrid models at a Field-scale. Catena 2021, 202, 105258. [Google Scholar] [CrossRef]
  106. Guo, Z.; Han, J.; Li, J.; Xu, Y.; Wang, X. Effects of long-term fertilization on soil organic carbon mineralization and microbial community structure. PLoS ONE 2019, 14, e0211163. [Google Scholar] [CrossRef] [Green Version]
  107. Huang, S.; Chen, J.; Ma, X.; Guo, W.; Yang, L.; Chen, Y.A.; Huang, C. Short-term effects of different fertilization measures on water-stable aggregates and carbon and nitrogen of tea garden soil. In E3S Web of Conferences, Proceedings of the 2020 2nd International Conference on Water Resources and Environmental Engineering, Shanghai, China, 23–24 October 2020; Xiaosheng, Q., Amahmid, O., Eds.; EDP Sciences: Les Ulis, France, 2020; Volume 199. [Google Scholar]
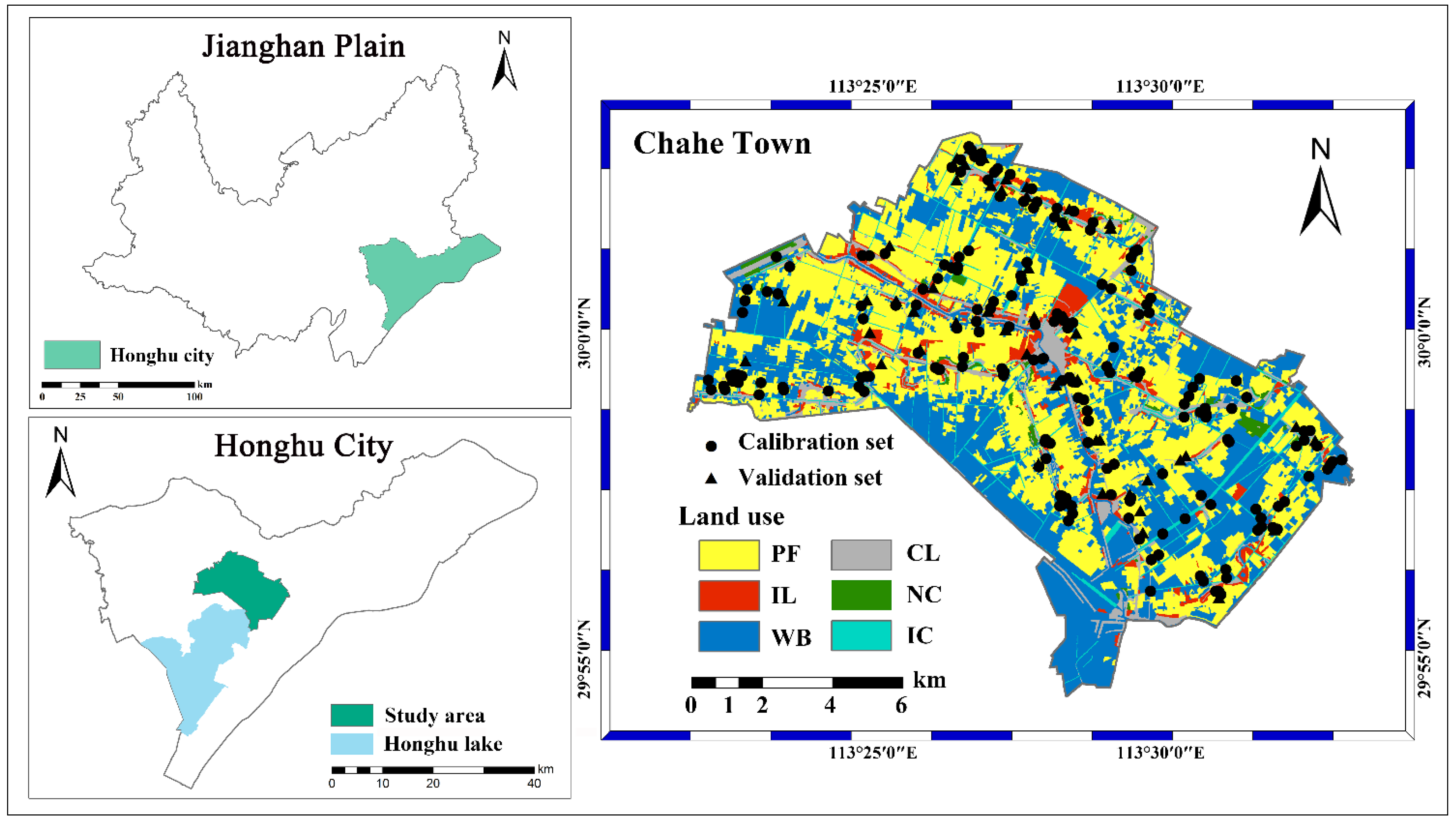
Remotesensing 14 03575 g001 550
Figure 1. Location of the study area and spatial distribution of the soil samples. PF, IL, WB, NC, CL, and IC: paddy field, irrigated land, water bodies, natural cover, construction land, and irrigated canals, respectively.
Figure 1. Location of the study area and spatial distribution of the soil samples. PF, IL, WB, NC, CL, and IC: paddy field, irrigated land, water bodies, natural cover, construction land, and irrigated canals, respectively.
Remotesensing 14 03575 g001
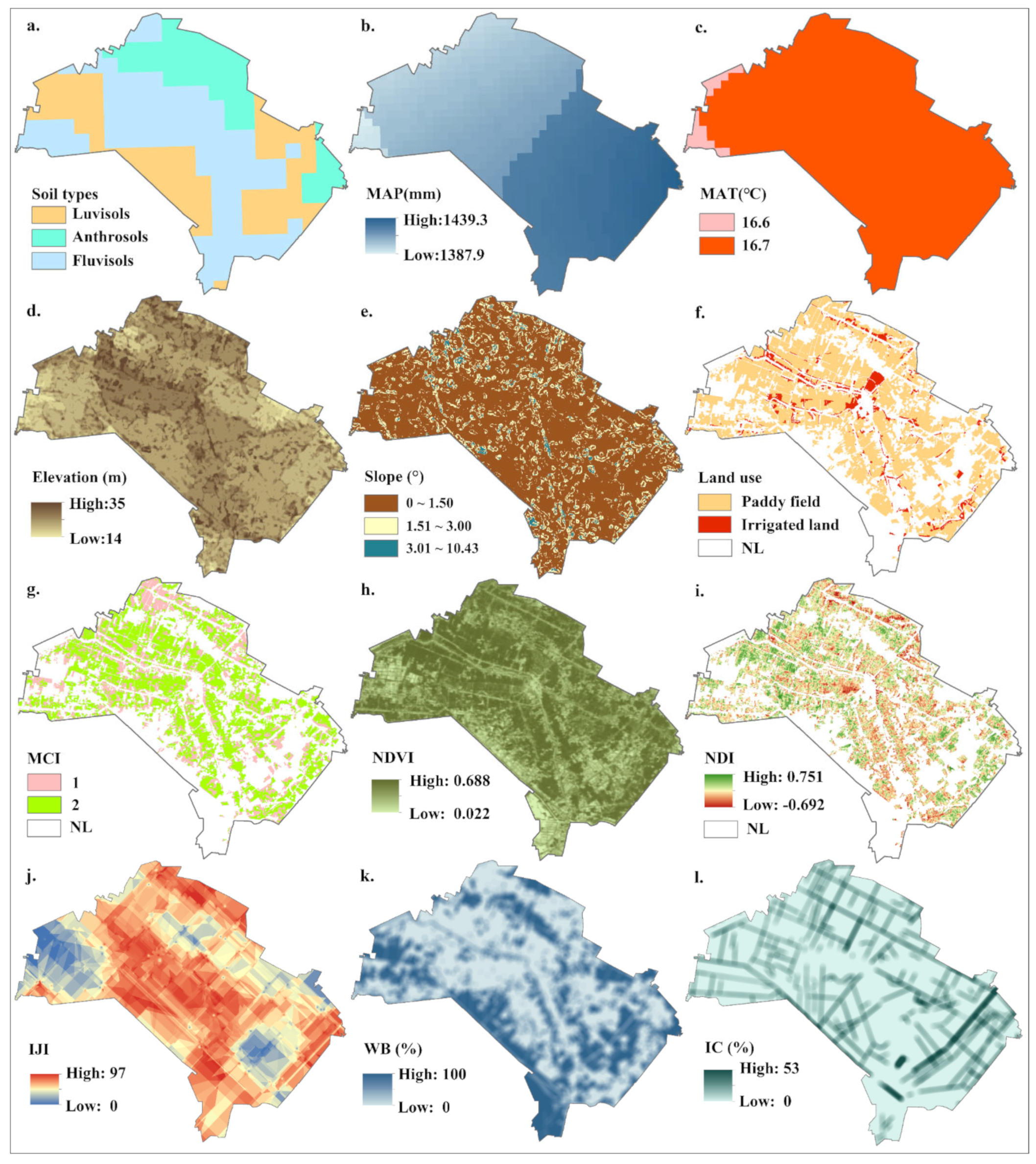
Remotesensing 14 03575 g002 550
Figure 2. Spatial distribution of environmental variables, including soil types (a), MAP (b), MAT (c), elevation (d), slope (e), land use (f), MCI (g), NDVI (h), NDI (i), IJI (j), WB (k), and IC (l). MAP and MAT: mean annual precipitation and temperature; MCI: multiple cropping index; NDVI: normalized difference vegetation index; NDI: normalized difference index; IJI: interspersion and juxtaposition index; WB and IC: percentage of water bodies and irrigated canals.
Figure 2. Spatial distribution of environmental variables, including soil types (a), MAP (b), MAT (c), elevation (d), slope (e), land use (f), MCI (g), NDVI (h), NDI (i), IJI (j), WB (k), and IC (l). MAP and MAT: mean annual precipitation and temperature; MCI: multiple cropping index; NDVI: normalized difference vegetation index; NDI: normalized difference index; IJI: interspersion and juxtaposition index; WB and IC: percentage of water bodies and irrigated canals.
Remotesensing 14 03575 g002
Remotesensing 14 03575 g003 550
Figure 3. Histograms and basic statistics of raw SOC content and transferred ln (SOC) content.
Figure 3. Histograms and basic statistics of raw SOC content and transferred ln (SOC) content.
Remotesensing 14 03575 g003
Remotesensing 14 03575 g004 550
Figure 4. Relative importance of environmental variables obtained by (a) SLR and (b) RF models. LU: land use; MCI: multiple cropping index; NDI: normalized difference index; Dis_Lake: distance from the lake; IJI: interspersion and juxtaposition index; WB and IC: percentage of water bodies and irrigated canals.
Figure 4. Relative importance of environmental variables obtained by (a) SLR and (b) RF models. LU: land use; MCI: multiple cropping index; NDI: normalized difference index; Dis_Lake: distance from the lake; IJI: interspersion and juxtaposition index; WB and IC: percentage of water bodies and irrigated canals.
Remotesensing 14 03575 g004
Remotesensing 14 03575 g005 550
Figure 5. Spatial distribution of SOC content estimated by the Cubist model. WB, NC, CL, and IC: water bodies, natural cover, construction land, and irrigated canals, respectively.
Figure 5. Spatial distribution of SOC content estimated by the Cubist model. WB, NC, CL, and IC: water bodies, natural cover, construction land, and irrigated canals, respectively.
Remotesensing 14 03575 g005
Table
Table 1. Potential influencing factors of SOC content.
Table 1. Potential influencing factors of SOC content.
AspectsEnvironmental FactorsData Source and ResolutionLinks
Natural factorsSoil typesHarmonized World Soil Database, 1 kmhttp://www.fao.org/home/en/,
accessed on 1 October 2020
MAP and MATChinese Resource and Environment Science and Data Center, 500 mhttp://www.resdc.cn/, accessed on 1 October 2020
Elevation, SlopeASTER DEM, 30 mhttp://www.gscloud.cn, accessed on 1 September 2019
Dis_LakeBased on a land use map-
Agricultural activitiesLand useHubei Provincial Department of Land and Resources, 10 mNot open
MCIHJ-1A/1B images, 30 mhttp://218.247.138.119:7777/DSSPlatform/index.html, accessed on 1 September 2019
NDVI
NDILandsat 8 images, 30 mhttp://www.gscloud.cn, accessed on 1 October 2020
Landscape metricsIJI, COHESION, LSI, WB and ICBased on a land use mapnot open
MAP and MAT: mean annual precipitation and temperature; Dis_Lake: distance from the lake; NDVI: normalized difference vegetation index; NDI: normalized difference index; IJI: interspersion and juxtaposition index; LSI: landscape shape index; WB and IC: percentage of water bodies and irrigated canals.
Table
Table 2. Descriptive statistics of SOC (g/kg).
Table 2. Descriptive statistics of SOC (g/kg).
Sample SetNumberMinimumMaximumMeanSdSkewnessCV (%)
Total dataset2423.51844.81415.9107.1020.76844.64
Calibration set1943.51844.81415.9027.1920.81845.23
Validation set485.50631.28215.9416.8000.54142.66
Sd: standard deviation; CV: coefficient of the variation.
Table
Table 3. Correlation coefficient between ln (SOC) and environmental variables.
Table 3. Correlation coefficient between ln (SOC) and environmental variables.
MAPMATElevationSlopeDis_LakeNDVI
ln(SOC)0.055−0.041−0.172 *−0.224 *0.152 *0.013
NDIIJICOHESIONLSIWBIC
ln(SOC)0.241 *−0.161 *0.0320.0860.145 *0.130 *
* statistically significant.
Table
Table 4. Least significant difference test in ANOVA with mean values of SOC among different soil types.
Table 4. Least significant difference test in ANOVA with mean values of SOC among different soil types.
Soil TypesNumberMean [ln(g/kg)]LSD Test
Luvisols402.754a
Anthrosols502.723a
Fluvisols1042.602a
F = 2.14, p > 0.05.
Table
Table 5. Least significant difference test in ANOVA with mean values of SOC among different land use and MCI.
Table 5. Least significant difference test in ANOVA with mean values of SOC among different land use and MCI.
Land UseNumberMean [ln(g/kg)]LSD ResultMCINumberMean [ln(g/kg)]LSD Result
Paddy field902.851a1772.824a
Irrigated land1042.503b21172.559b
F = 31.83, p < 0.05, F = 16.60, p < 0.05.
Table
Table 6. Relationship between ln (SOC) and environmental variables via the SLR model.
Table 6. Relationship between ln (SOC) and environmental variables via the SLR model.
SLR ResultR2
Ln (SOC) = −0.101 × Slope + 0.033 × Dis_Lake + 0.304 × LU − 0.294 × MCI + 0.844 × NDI + 0.005 × WB + 2.5190.354
SLR: stepwise linear regression; LU: land use, paddy fields was set as 1 and irrigated land was set as 0; MCI: multiple cropping index; NDI: normalized difference index; Dis_Lake: distance from the lake; WB: percentage of water bodies.
Table
Table 7. Attribute usages of the Cubist model.
Table 7. Attribute usages of the Cubist model.
VariablesCondsModel
LU50%
MCI8%
NDI 54%
WB 50%
Slope 50%
Dis_Lake 49%
IC 49%
IJI 23%
Elevation 22%
Conds and Model: the percentage of times a variable is used for conditions or in linear regression models; LU: land use; MCI: multiple cropping index; NDI: normalized difference index; Dis_Lake: distance from the lake; IJI: interspersion and juxtaposition index; WB and IC: percentage of water bodies and irrigated canals.
Table
Table 8. Stratification rules and linear regressions of the Cubist model.
Table 8. Stratification rules and linear regressions of the Cubist model.
Stratification RulesLinear Regressions
Rule 1, N = 90LU = paddy fieldln (SOC) = −0.245 × Slope − 0.056 × Elevation + 0.230 × NDI − 0.010 × IJI + 0.001 × WB + 0.035 × IC + 2.387
Rule 2, N = 104LU = irrigated landln (SOC) = 0.115 × Dis_Lake + 0.014 × WB + 0.034 × IC + 1.095
Rule 3, N = 77MCI = 1ln (SOC) = −0.134 × Slope + 2.2 × NDI + 2.400
Rule 4, N = 117MCI = 2ln (SOC) = 0.460 × NDI + 2.345
LU: land use; MCI: multiple cropping index; NDI: normalized difference index; Dis_Lake: distance from the lake; IJI: interspersion and juxtaposition index; WB and IC: percentage of water bodies and irrigated canals.
Table
Table 9. Comparison of the accuracy of the OK, SLR, RF, and Cubist models.
Table 9. Comparison of the accuracy of the OK, SLR, RF, and Cubist models.
OKSLRRFCubist
MAE5.9524.8954.6543.859
RMSE7.1206.1365.8444.894
R20.0020.2050.3010.474
LCCC0.0230.3970.4100.626
OK: ordinary Kriging; SLR: stepwise linear regression; RF: random forest.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Wu, Z.; Chen, Y.; Yang, Z.; Zhu, Y.; Han, Y. Mapping Soil Organic Carbon in Low-Relief Farmlands Based on Stratified Heterogeneous Relationship. Remote Sens. 2022, 14, 3575. https://doi.org/10.3390/rs14153575

AMA Style

Wu Z, Chen Y, Yang Z, Zhu Y, Han Y. Mapping Soil Organic Carbon in Low-Relief Farmlands Based on Stratified Heterogeneous Relationship. Remote Sensing. 2022; 14(15):3575. https://doi.org/10.3390/rs14153575

Chicago/Turabian Style

Wu, Zihao, Yiyun Chen, Zhen Yang, Yuanli Zhu, and Yiran Han. 2022. "Mapping Soil Organic Carbon in Low-Relief Farmlands Based on Stratified Heterogeneous Relationship" Remote Sensing 14, no. 15: 3575. https://doi.org/10.3390/rs14153575

APA Style

Wu, Z., Chen, Y., Yang, Z., Zhu, Y., & Han, Y. (2022). Mapping Soil Organic Carbon in Low-Relief Farmlands Based on Stratified Heterogeneous Relationship. Remote Sensing, 14(15), 3575. https://doi.org/10.3390/rs14153575

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop