Investigating Suppression of Cloud Return with a Novel Optical Configuration of a Doppler Lidar
Abstract
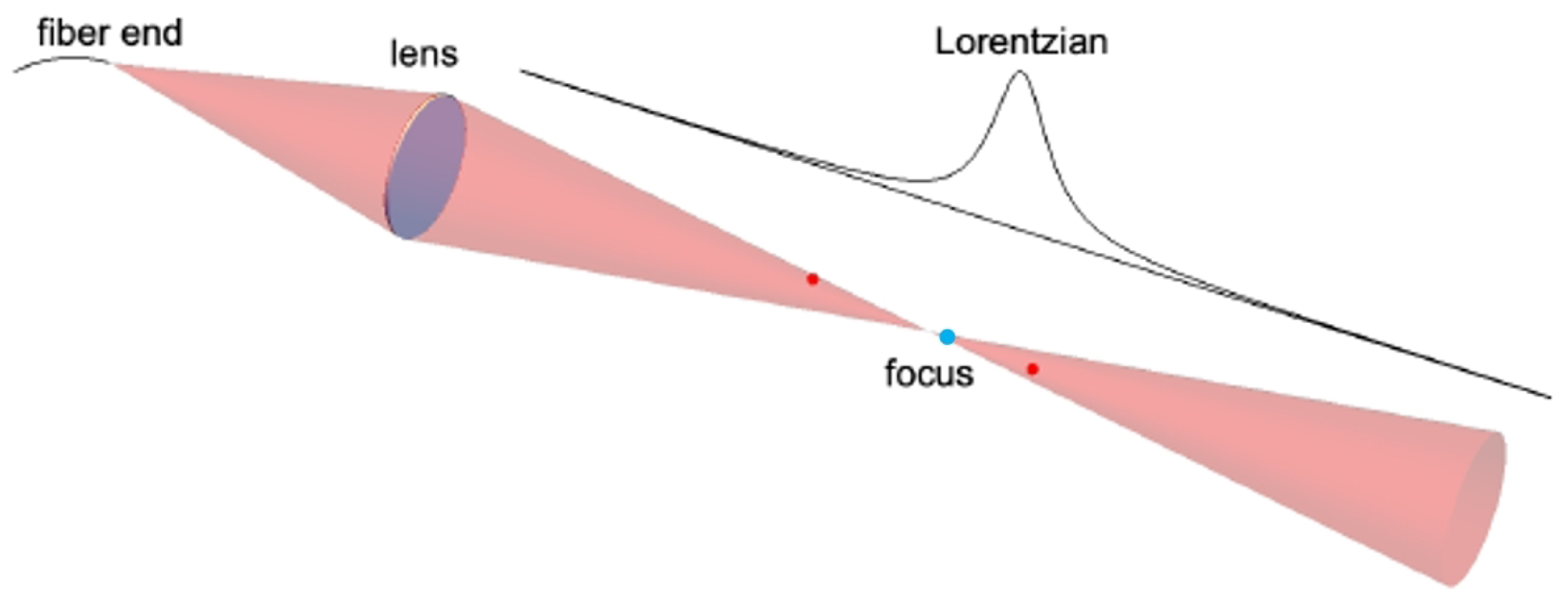
1. Introduction
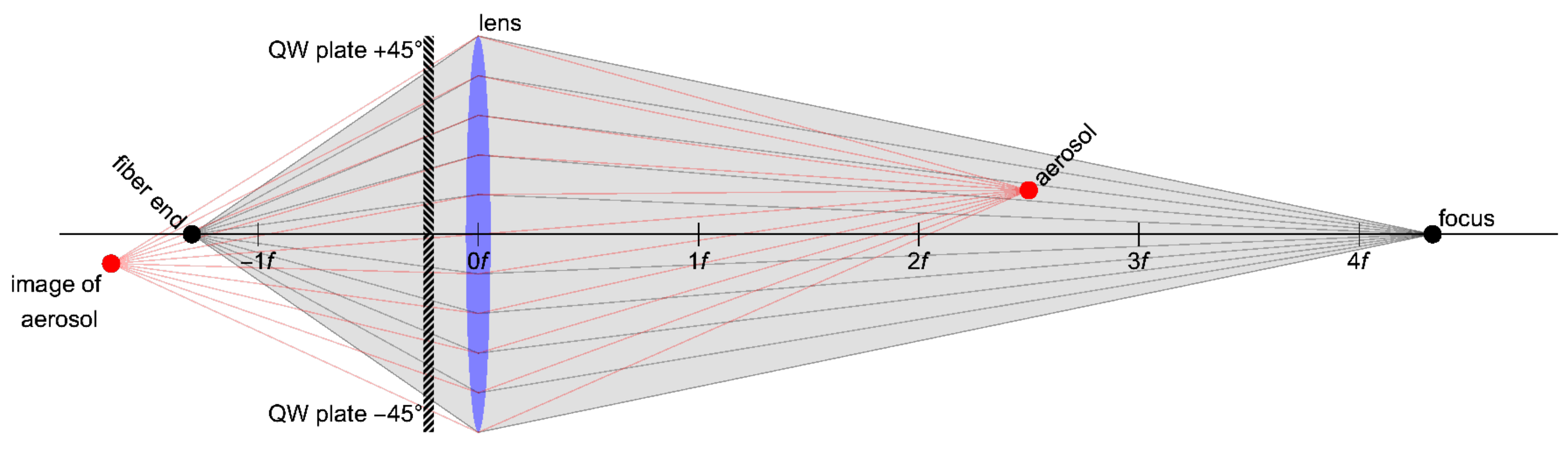
2. Novel Design with Two Quarter-Wave Plates
3. Hermite–Gaussian Modes
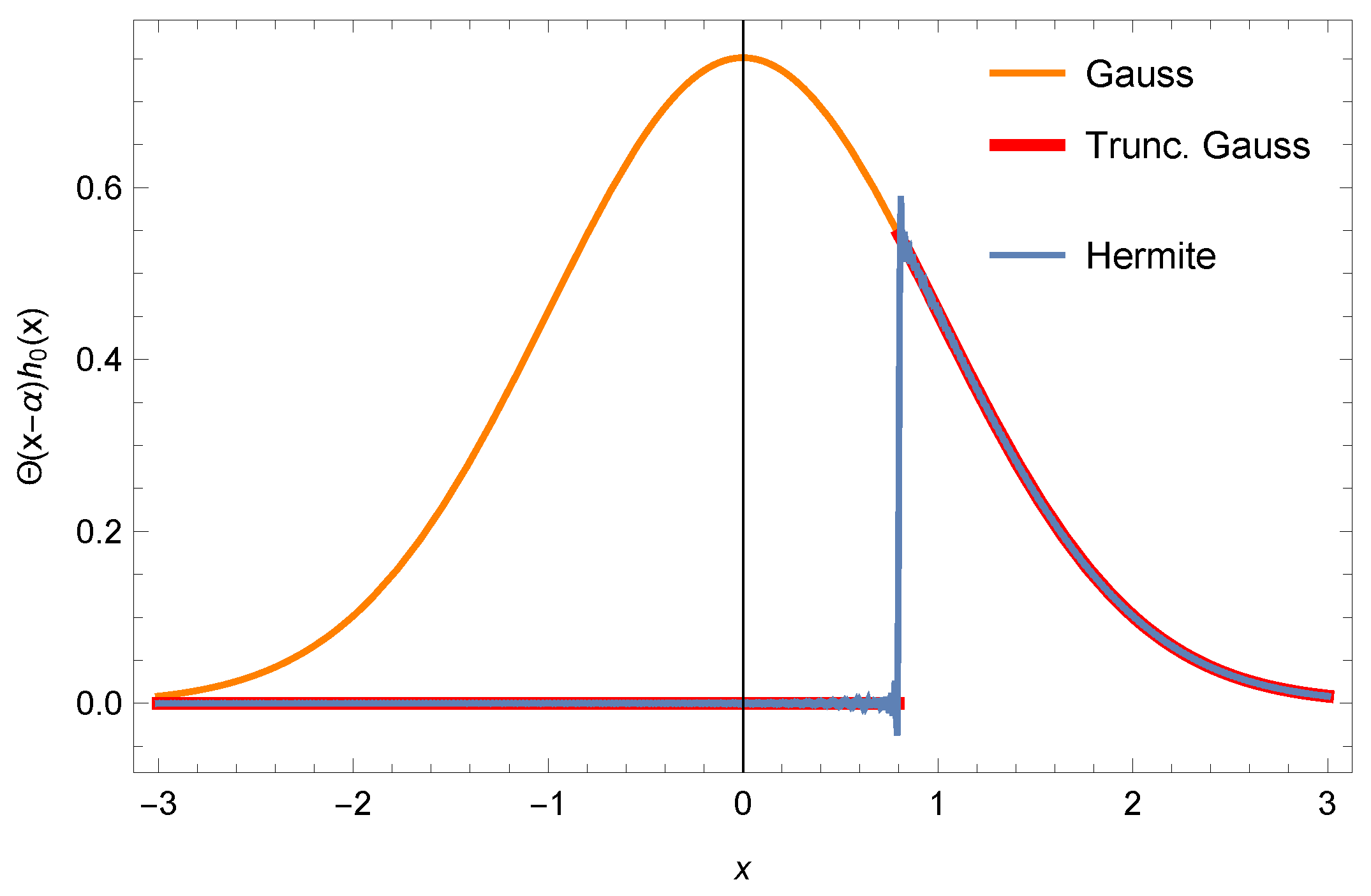
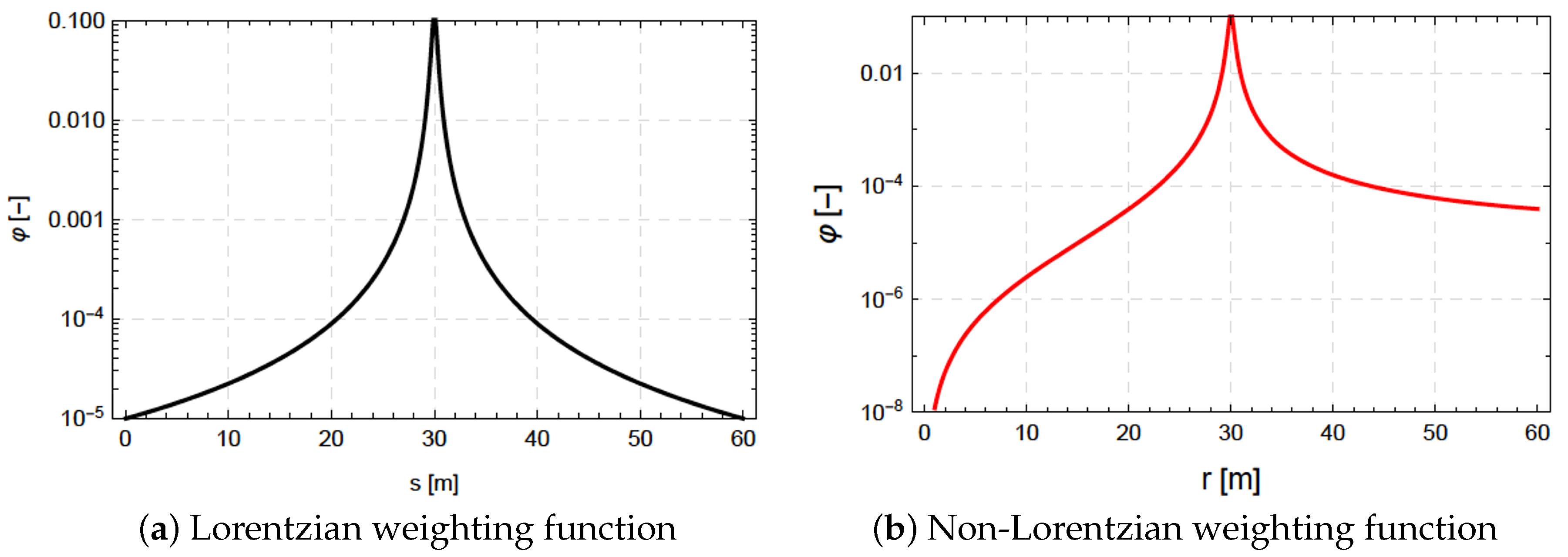
3.1. Half Gaussian Function
3.2. Truncated Gaussian Beam
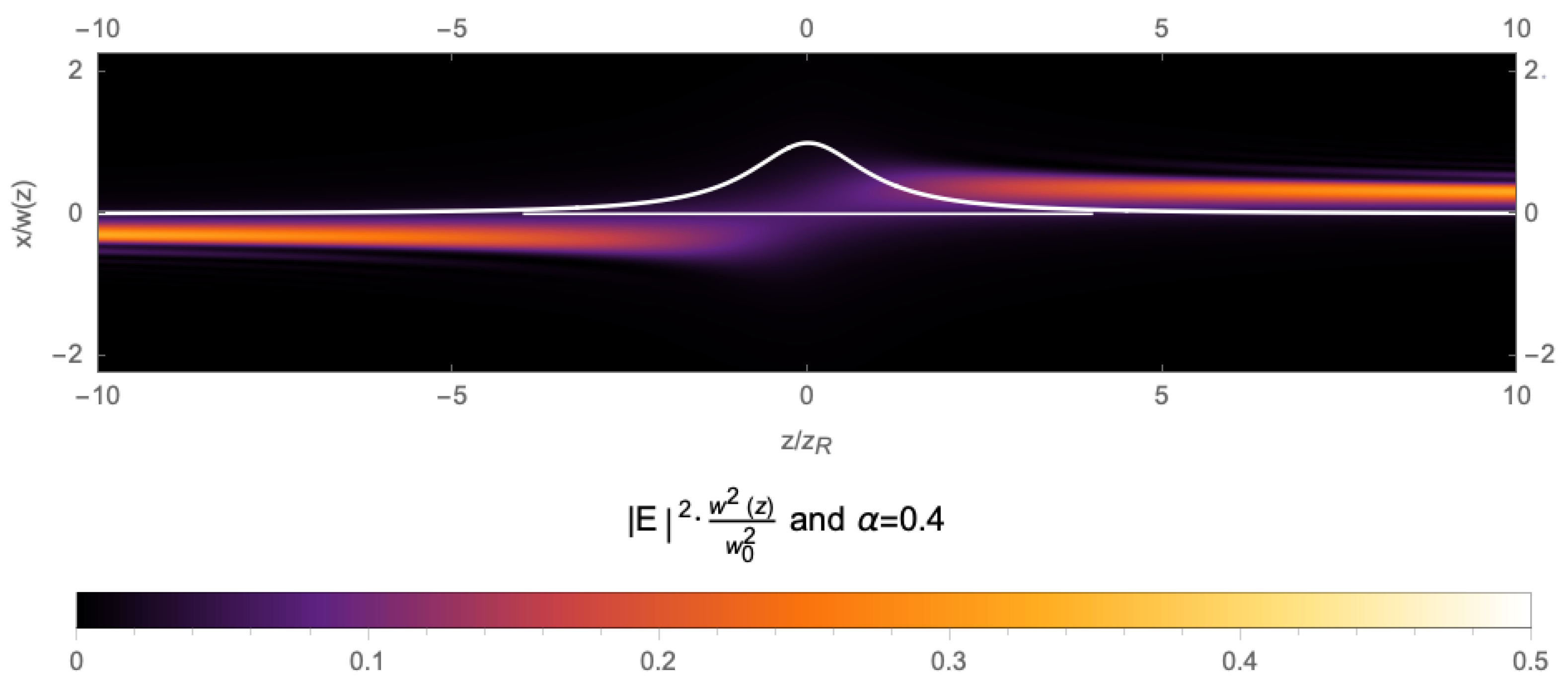
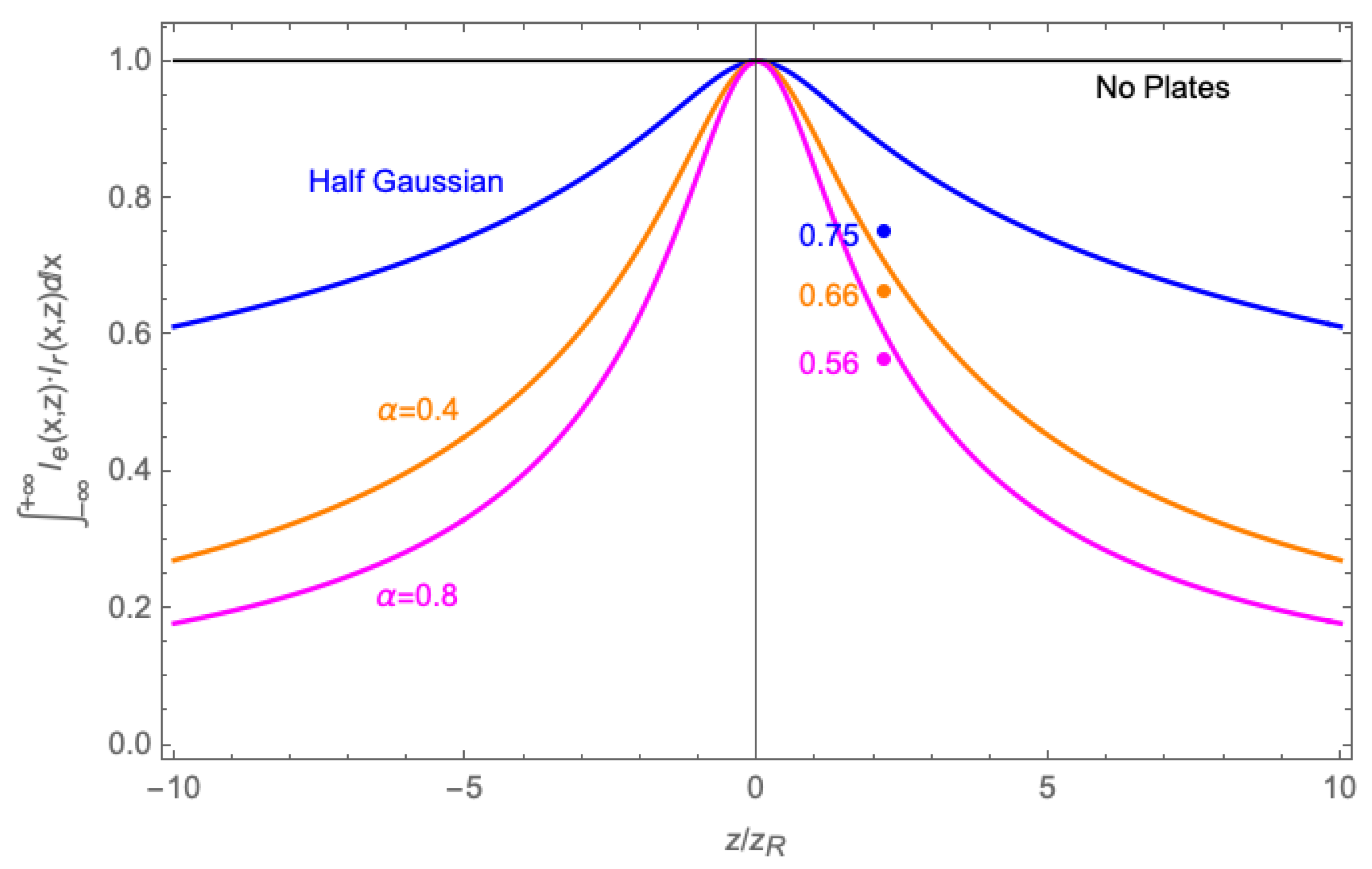
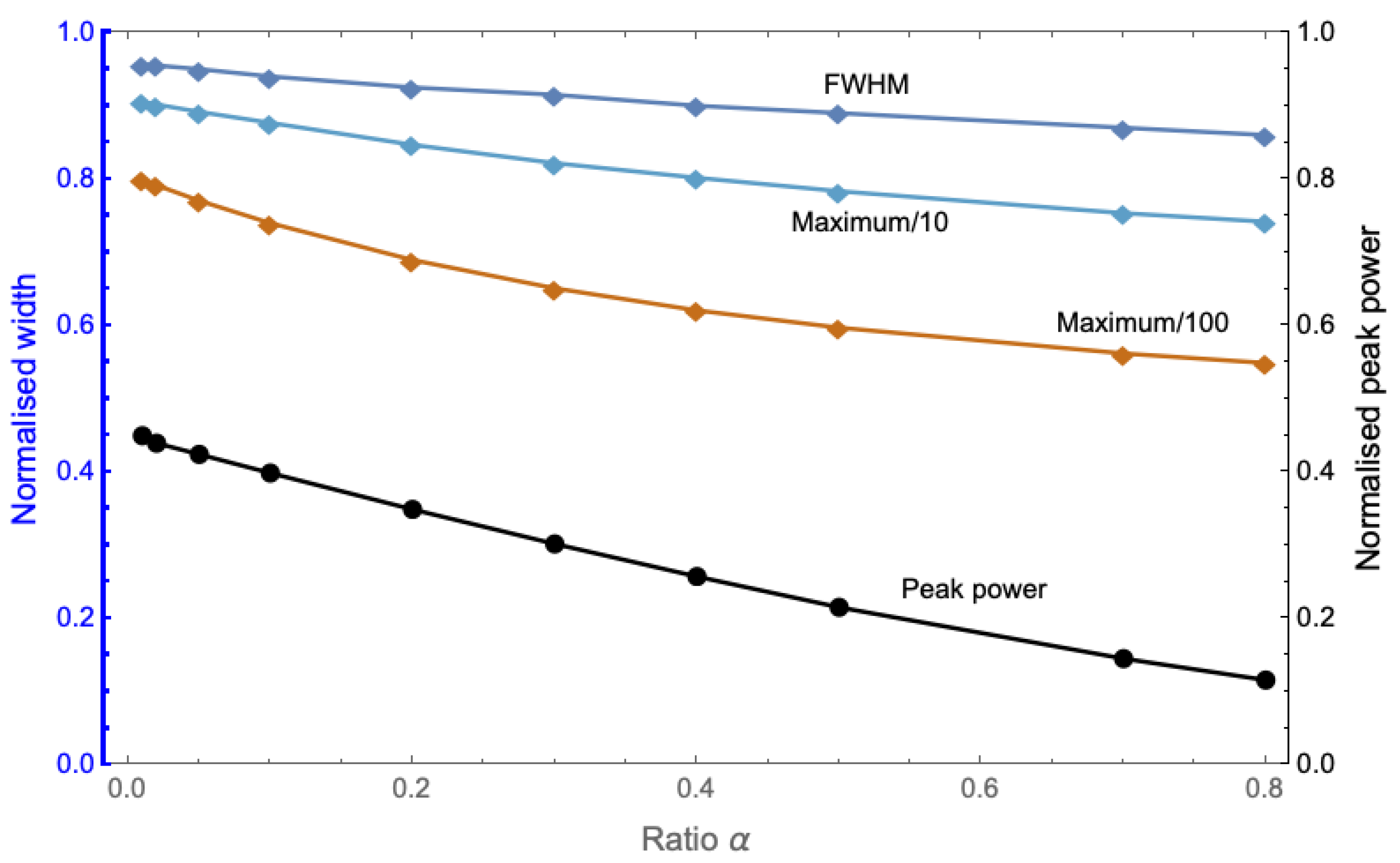
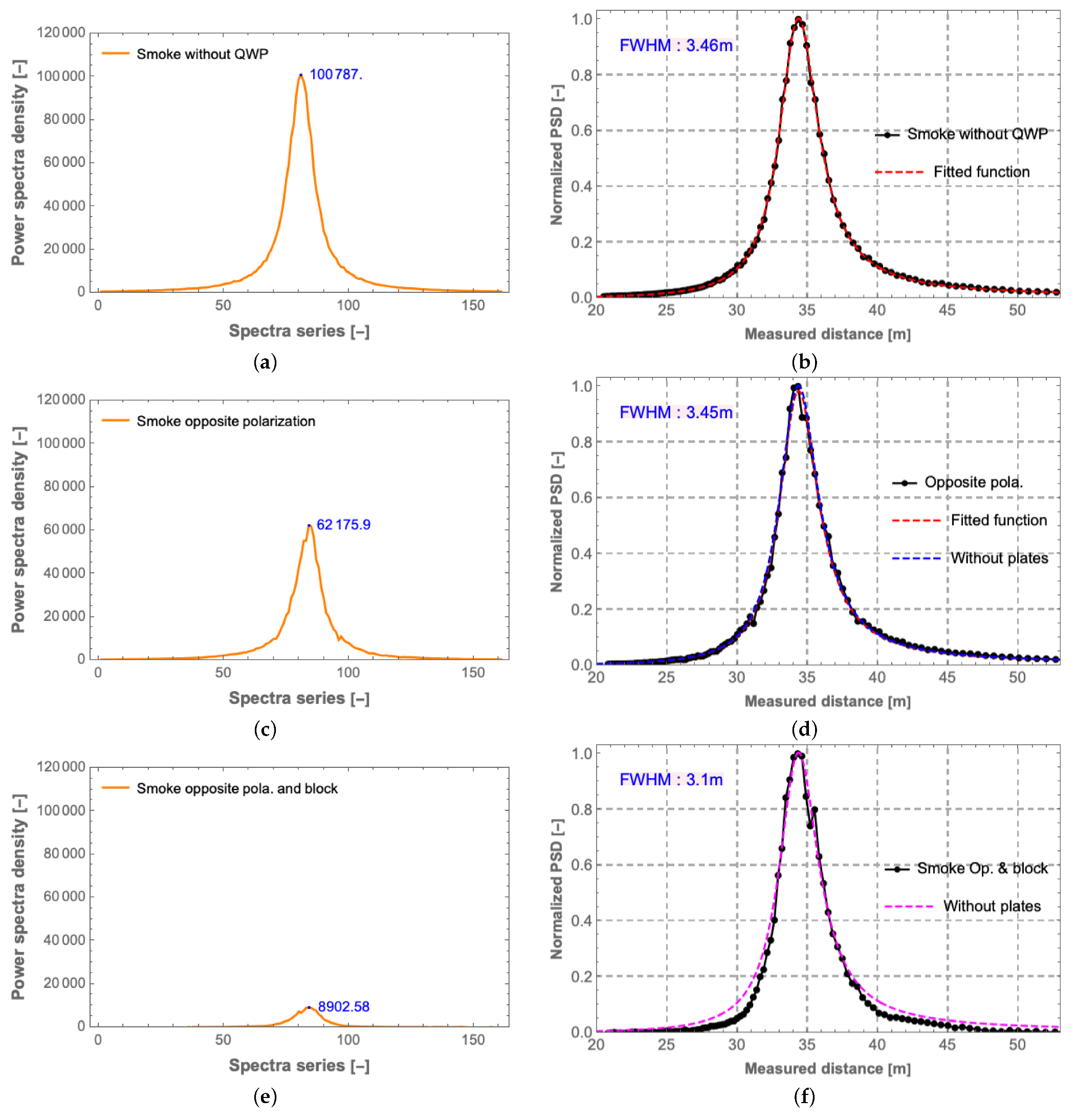
4. Experiment and Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| cw | Continuous-Wave |
| FWHM | the Full-Width at Half-Maximum |
| LOS | Line-of-Sight |
| IQ | In-phase/Quadrature-phase |
| LO | Local Oscillator |
| IF | Intermediate Frequency |
References
- Köpp, F.; Rahm, S.; Smalikho, I.; Dolfi, A.; Cariou, J.P.; Harris, M.; Young, R.I. Comparison of wake-vortex parameters measured by pulsed and continuous-wave lidars. J. Aircr. 2005, 42, 916–923. [Google Scholar] [CrossRef]
- Spuler, S.M.; Richter, D.; Spowart, M.P.; Rieken, K. Optical fiber-based laser remote sensor for airborne measurement of wind velocity and turbulence. Appl. Opt. 2011, 50, 842–851. [Google Scholar] [CrossRef] [PubMed]
- Rodrigo, P.J.; Iversen, T.F.; Hu, Q.; Pedersen, C. Diode laser lidar wind velocity sensor using a liquid-crystal retarder for non-mechanical beam-steering. Opt. Express 2014, 22, 26674–26679. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Simley, E.; Pao, L.Y. A longitudinal spatial coherence model for wind evolution based on large-eddy simulation. In Proceedings of the 2015 American Control Conference (ACC), Chicago, IL, USA, 1–3 July 2015; pp. 3708–3714. [Google Scholar]
- Wei, T.; Xia, H.; Yue, B.; Wu, Y.; Liu, Q. Remote sensing of raindrop size distribution using the coherent Doppler lidar. Opt. Express 2021, 29, 17246–17257. [Google Scholar] [CrossRef] [PubMed]
- Abari, C.F.; Pedersen, A.T.; Dellwik, E.; Mann, J. Performance evaluation of an all-fiber image-reject homodyne coherent Doppler wind lidar. Atmos. Meas. Tech. 2015, 8, 4145–4153. [Google Scholar] [CrossRef]
- Sathe, A.; Mann, J. A review of turbulence measurements using ground-based wind lidars. Atmos. Meas. Tech. 2013, 6, 3147–3167. [Google Scholar] [CrossRef]
- ZX Lidars. The History of ZX Wind LIDARS. Available online: https://www.zxlidars.com/wind-lidar-history/ (accessed on 15 June 2022).
- Harris, M.; Bryce, D.J.; Coffey, A.S.; Smith, D.A.; Birkemeyer, J.; Knopf, U. Advance measurement of gusts by laser anemometry. J. Wind. Eng. Ind. Aerodyn. 2007, 95, 1637–1647. [Google Scholar] [CrossRef]
- Held, D.P.; Mann, J. Lidar estimation of rotor-effective wind speed–an experimental comparison. Wind. Energy Sci. 2019, 4, 421–438. [Google Scholar] [CrossRef]
- Howard, A.Q., Jr.; Naini, T. Four Methods for LIDAR Retrieval of Microscale Wind Fields. Remote Sens. 2012, 4, 2329–2355. [Google Scholar] [CrossRef]
- Held, D.P.; Mann, J. Comparison of methods to derive radial wind speed from a continuous-wave coherent lidar Doppler spectrum. Atmos. Meas. Tech. 2018, 11, 6339–6350. [Google Scholar] [CrossRef]
- Liu, Z.; Barlow, J.F.; Chan, P.W.; Fung, J.C.H.; Li, Y.; Ren, C.; Mak, H.W.L.; Ng, E. A review of progress and applications of pulsed Doppler wind LiDARs. Remotesensing 2019, 11, 2522. [Google Scholar] [CrossRef]
- Kawabata, H.; Kikushima, Y.; Kogaki, T. Wind Profile and Power Performance Measurements Using a Nine-beam Nacelle Lidar. Am. J. Mech. Eng. 2018, 6, 75–82. [Google Scholar] [CrossRef]
- Shin, D.; Ko, K. Application of the nacelle transfer function by a nacelle-mounted light detection and ranging system to wind turbine power performance measurement. Energies 2019, 12, 1087. [Google Scholar] [CrossRef]
- Bingöl, F.; Mann, J.; Larsen, G.C. Light detection and ranging measurements of wake dynamics part I: One-dimensional scanning. Wind. Energy Int. J. Prog. Appl. Wind. Power Convers. Technol. 2010, 13, 51–61. [Google Scholar] [CrossRef]
- Trujillo, J.J.; Bingöl, F.; Larsen, G.C.; Mann, J.; Kühn, M. Light detection and ranging measurements of wake dynamics. Part II: Two-dimensional scanning. Wind Energy 2011, 14, 61–75. [Google Scholar] [CrossRef]
- Annoni, J.; Fleming, P.; Scholbrock, A.; Roadman, J.; Dana, S.; Adcock, C.; Porte-Agel, F.; Raach, S.; Haizmann, F.; Schlipf, D. Analysis of control-oriented wake modeling tools using lidar field results. Wind Energy Sci. 2018, 3, 819–831. [Google Scholar] [CrossRef]
- Scholbrock, A.; Fleming, P.; Schlipf, D.; Wright, A.; Johnson, K.; Wang, N. Lidar-enhanced wind turbine control: Past, present, and future. In Proceedings of the 2016 American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016; pp. 1399–1406. [Google Scholar]
- Dimitrov, N.; Borraccino, A.; Peña, A.; Natarajan, A.; Mann, J. Wind turbine load validation using lidar-based wind retrievals. Wind Energy 2019, 22, 1512–1533. [Google Scholar] [CrossRef]
- Conti, D.; Pettas, V.; Dimitrov, N.; Peña, A. Wind turbine load validation in wakes using wind field reconstruction techniques and nacelle lidar wind retrievals. Wind Energy Sci. 2021, 6, 841–866. [Google Scholar] [CrossRef]
- Peña, A.; Mann, J.; Dimitrov, N. Turbulence characterization from a forward-looking nacelle lidar. Wind Energy Sci. 2017, 2, 133–152. [Google Scholar] [CrossRef]
- Vasiljević, N.; L.M. Palma, J.M.; Angelou, N.; Carlos Matos, J.; Menke, R.; Lea, G.; Mann, J.; Courtney, M.; Frölen Ribeiro, L.; M.G.C. Gomes, V.M. Perdigão 2015: Methodology for atmospheric multi-Doppler lidar experiments. Atmos. Meas. Tech. 2017, 10, 3463–3483. [Google Scholar] [CrossRef]
- Hofsäß, M.; Clifton, A.; Cheng, P.W. Reducing the uncertainty of Lidar measurements in complex terrain using a linear model approach. Remote Sens. 2018, 10, 1465. [Google Scholar] [CrossRef]
- Peña, A.; Hasager, C.; Badger, M.; Barthelmie, R.; Bingöl, F.; Cariou, J.P.; Emeis, S.; Frandsen, S.; Harris, M.; Karagali, I.; et al. Remote Sensing for Wind Energy; Number 0084(EN) in DTU Wind Energy E; DTU Wind Energy: Roskilde, Denmark, 2015. [Google Scholar]
- Mikkelsen, T. On mean wind and turbulence profile measurements from ground-based wind lidars: Limitations in time and space resolution with continuous wave and pulsed lidar systems. In Proceedings of the European Wind Energy Conference and Exhibition, Marseille, France, 16–19 March 2009; Volume 6, pp. 4123–4132. [Google Scholar]
- Harris, M.; Constant, G.; Ward, C. Continuous-wave bistatic laser Doppler wind sensor. Appl. Opt. 2001, 40, 1501–1506. [Google Scholar] [CrossRef]
- Mauder, M.; Eggert, M.; Gutsmuths, C.; Oertel, S.; Wilhelm, P.; Voelksch, I.; Wanner, L.; Tambke, J.; Bogoev, I. Comparison of turbulence measurements by a CSAT3B sonic anemometer and a high-resolution bistatic Doppler lidar. Atmos. Meas. Tech. 2020, 13, 969–983. [Google Scholar] [CrossRef]
- Brinkmeyer, E.; Waterholter, T. Continuous wave synthetic low-coherence wind sensing Lidar: Motionless measurement system with subsequent numerical range scanning. Opt. Express 2013, 21, 1872–1897. [Google Scholar] [CrossRef]
- Abari, C.F.; Pedersen, A.T.; Mann, J. An all-fiber image-reject homodyne coherent Doppler wind lidar. Opt. Express 2014, 22, 25880–25894. [Google Scholar] [CrossRef]
- DeLange, O. Optical heterodyne detection. IEEE Spectr. 1968, 5, 77–85. [Google Scholar] [CrossRef]
- Jacobs, S. Optical heterodyne (coherent) detection. Am. J. Phys. 1988, 56, 235–245. [Google Scholar] [CrossRef]
- Castagner, J.L.; Jones, A.R. A double Gaussian beam method for the determination of particle size, direction and velocity. Part. Part. Syst. Charact. Meas. Descr. Part. Prop. Behav. Powders Other Disperse Syst. 2004, 21, 5–14. [Google Scholar] [CrossRef]
- Volpp, J.; Laskin, A.; Laskin, V.; Ostrun, A. Refractive multi-focus optics for material processing. Int. Congr. Appl. Lasers Electro-Opt. 2016, 2016, 1402. [Google Scholar] [CrossRef]
- WedgedFiberEnd. Micro-Lensed Optical Fibers by WTTechnology. Available online: https://www.wttechnology.com/lensed%20fibers_v5.pdf (accessed on 15 June 2022).
- Saleh, B.E.; Teich, M.C. Fundamentals of Photonics; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Szeg, G. Orthogonal Polynomials; American Mathematical Society: Providence, RI, USA, 1939; Volume 23. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions; Dover Publications: Mineola, NY, USA, 1972. [Google Scholar]
- Bunck, B.F. A fast algorithm for evaluation of normalized Hermite functions. BIT Numer. Math. 2009, 49, 281–295. [Google Scholar] [CrossRef]
- Cleanroom Management International. Smooth Smoke Generator. Available online: https://www.cmitest.com/produits/smoke-generator-air-trace/ (accessed on 15 June 2022).






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, L.; Mann, J.; Sjöholm, M. Investigating Suppression of Cloud Return with a Novel Optical Configuration of a Doppler Lidar. Remote Sens. 2022, 14, 3576. https://doi.org/10.3390/rs14153576
Jin L, Mann J, Sjöholm M. Investigating Suppression of Cloud Return with a Novel Optical Configuration of a Doppler Lidar. Remote Sensing. 2022; 14(15):3576. https://doi.org/10.3390/rs14153576
Chicago/Turabian StyleJin, Liqin, Jakob Mann, and Mikael Sjöholm. 2022. "Investigating Suppression of Cloud Return with a Novel Optical Configuration of a Doppler Lidar" Remote Sensing 14, no. 15: 3576. https://doi.org/10.3390/rs14153576
APA StyleJin, L., Mann, J., & Sjöholm, M. (2022). Investigating Suppression of Cloud Return with a Novel Optical Configuration of a Doppler Lidar. Remote Sensing, 14(15), 3576. https://doi.org/10.3390/rs14153576






