Bayesian Sea Ice Detection Algorithm for CFOSAT
Abstract
:1. Introduction
2. Algorithm Description and Adaptation
2.1. The Bayesian Sea Ice Detection Algorithm for QuikSCAT
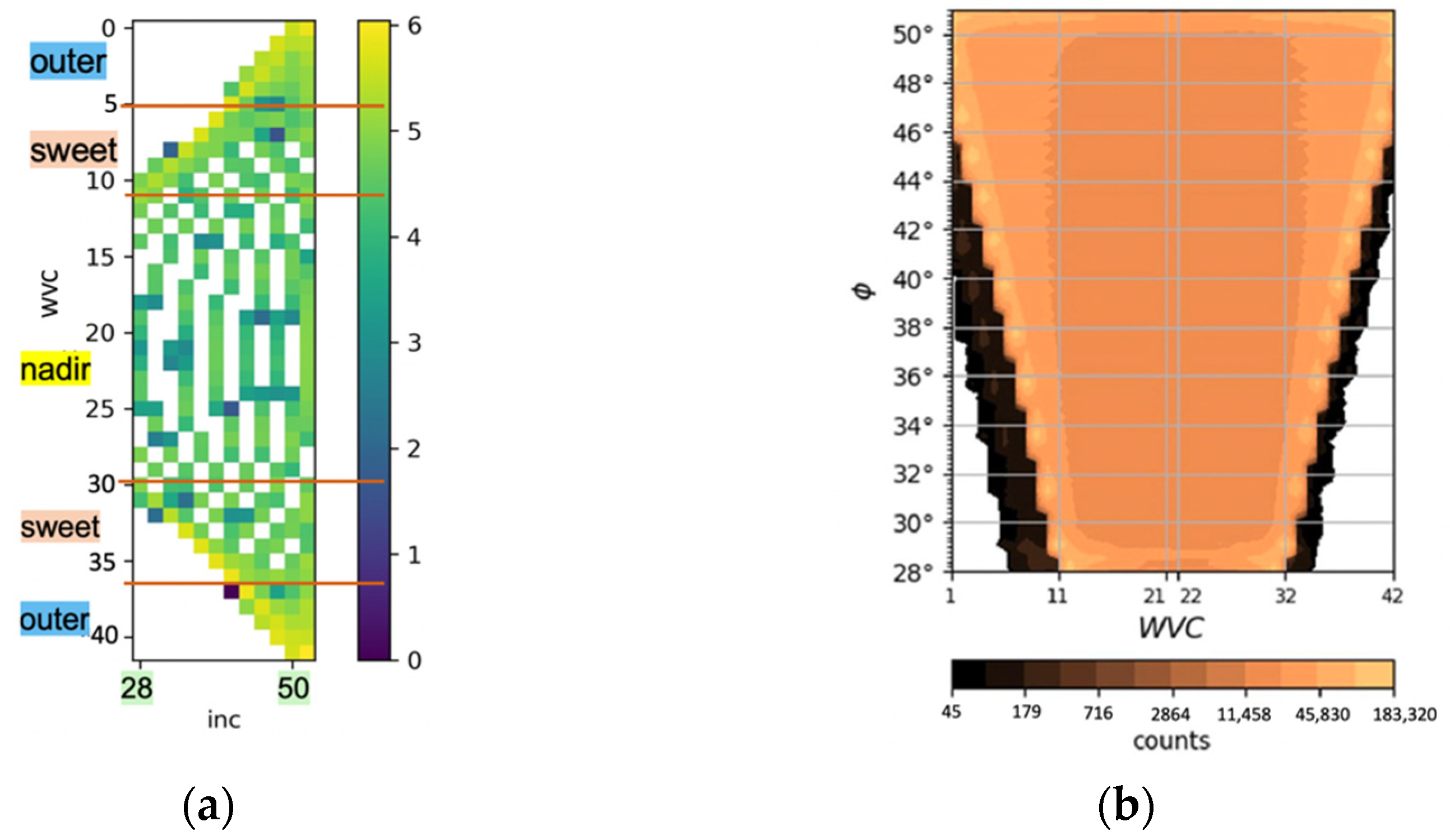
2.2. The Adapted Bayesian Ice Detection for CSCAT
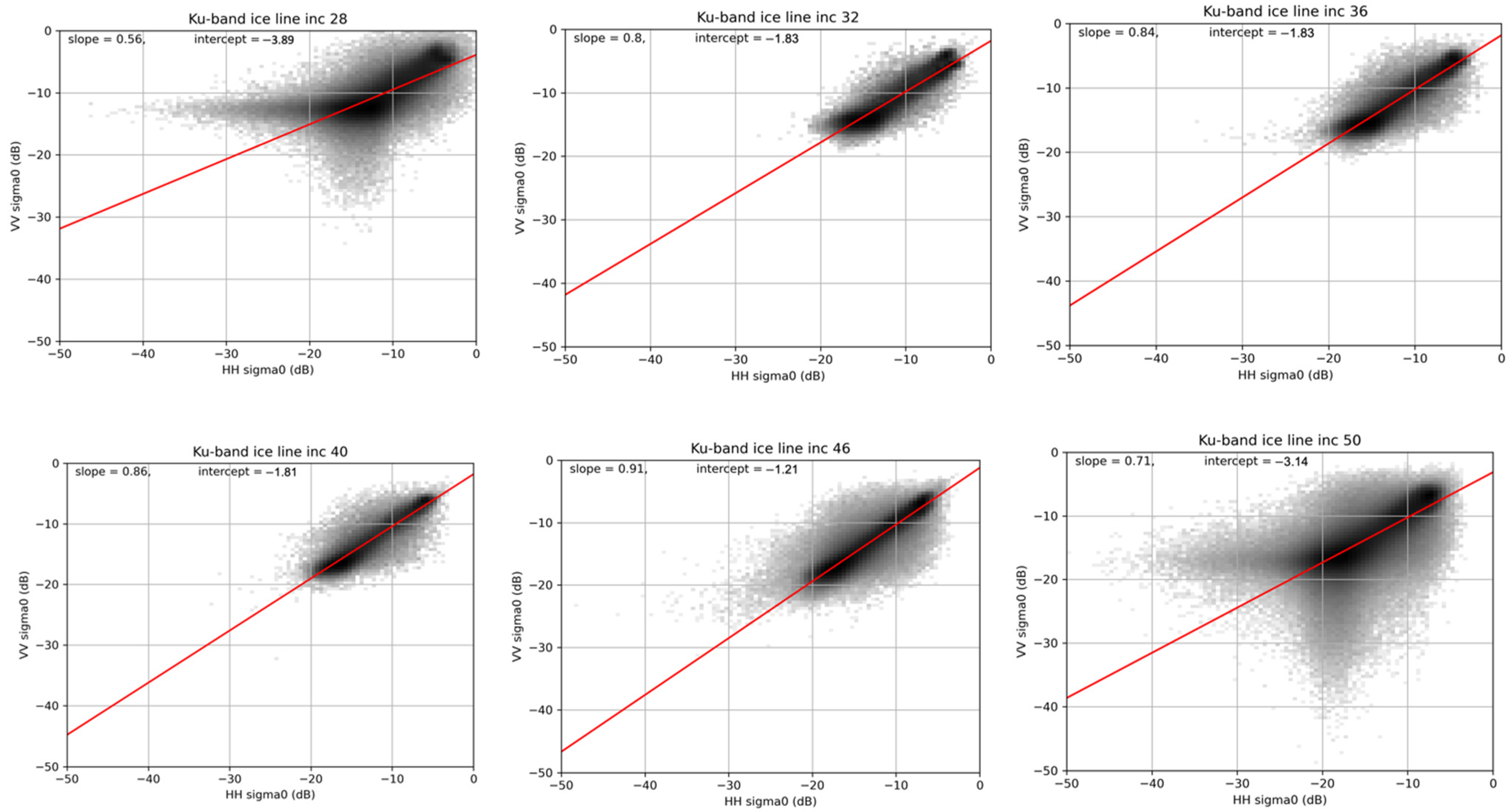
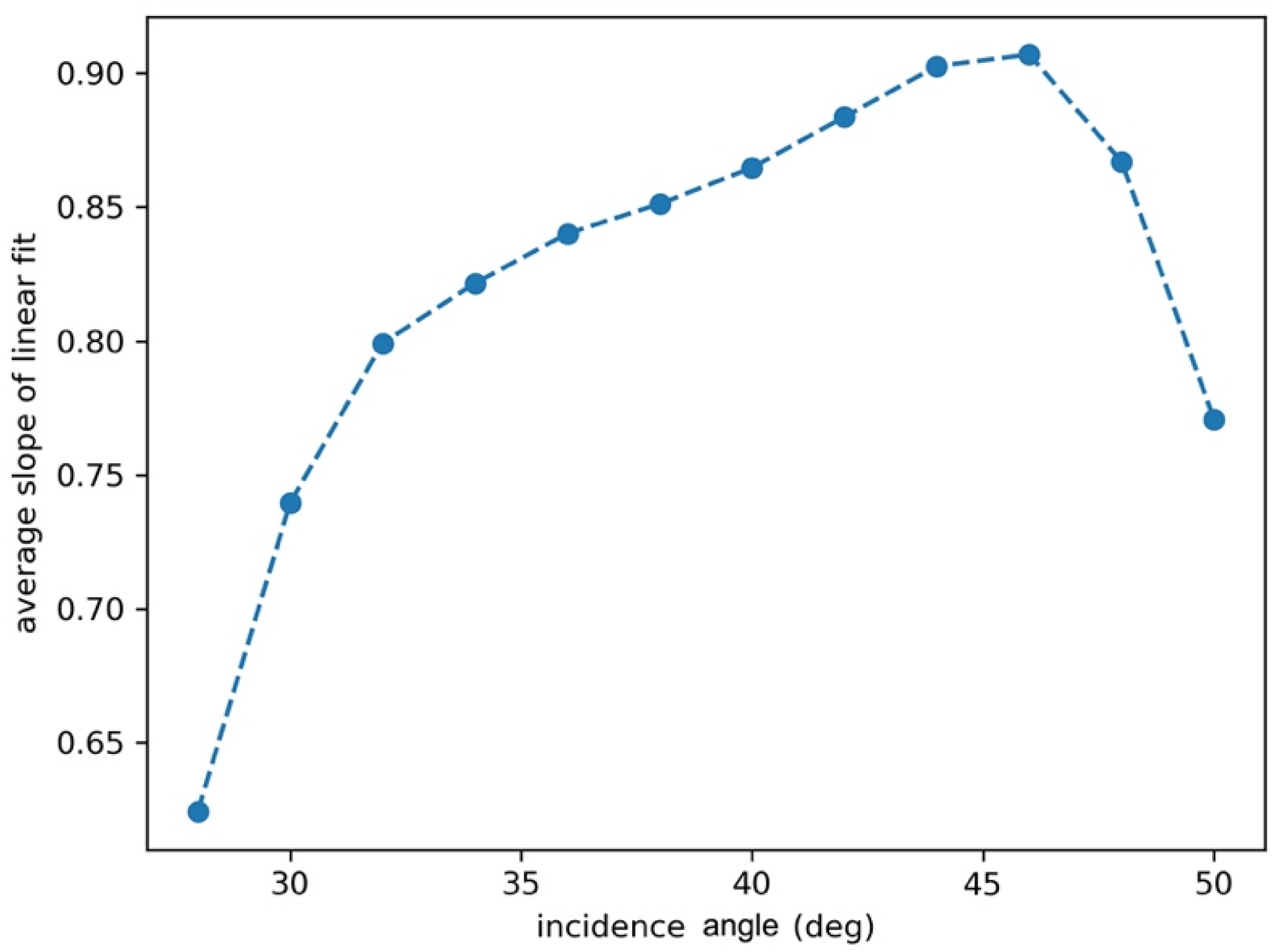
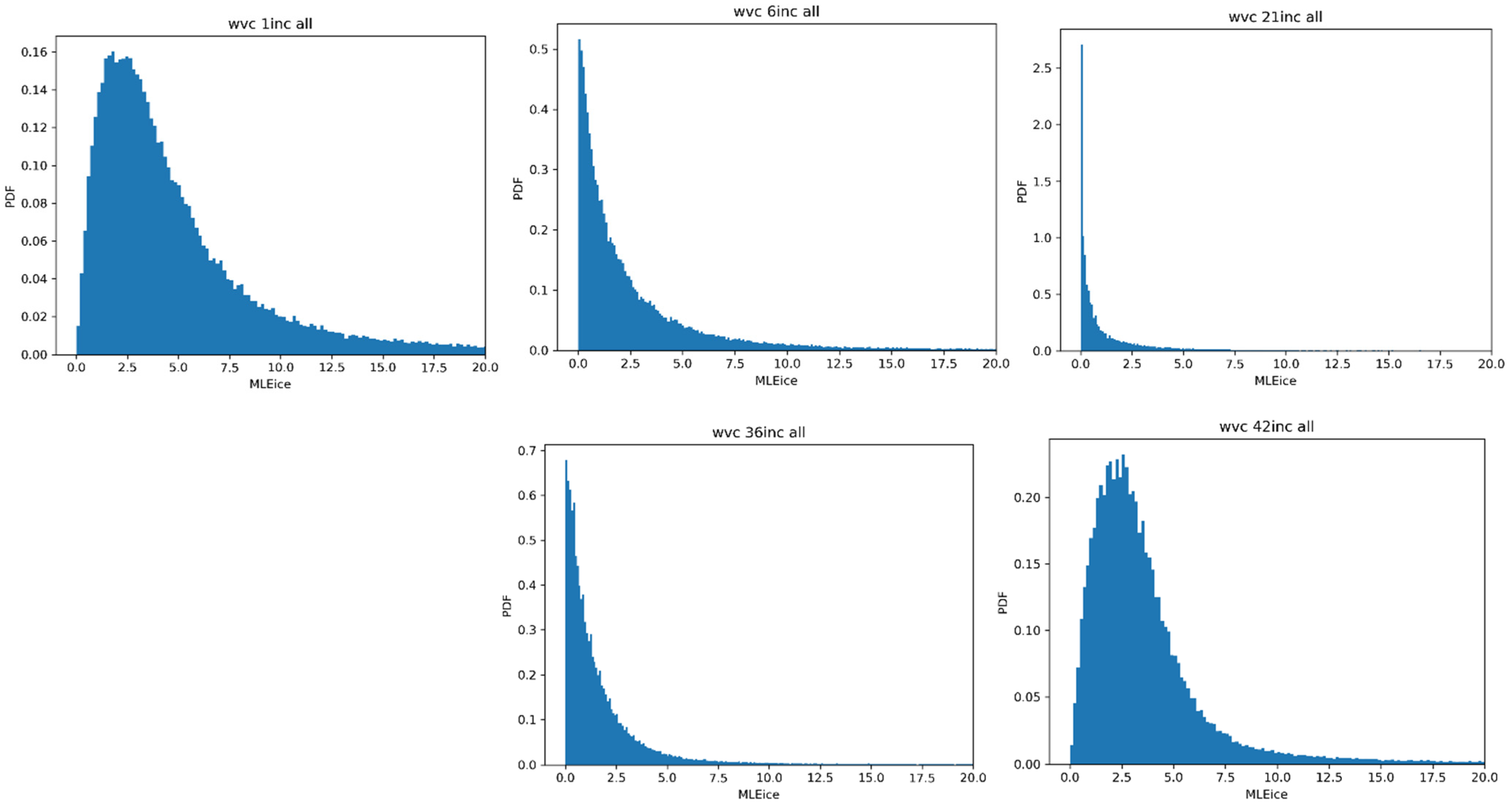
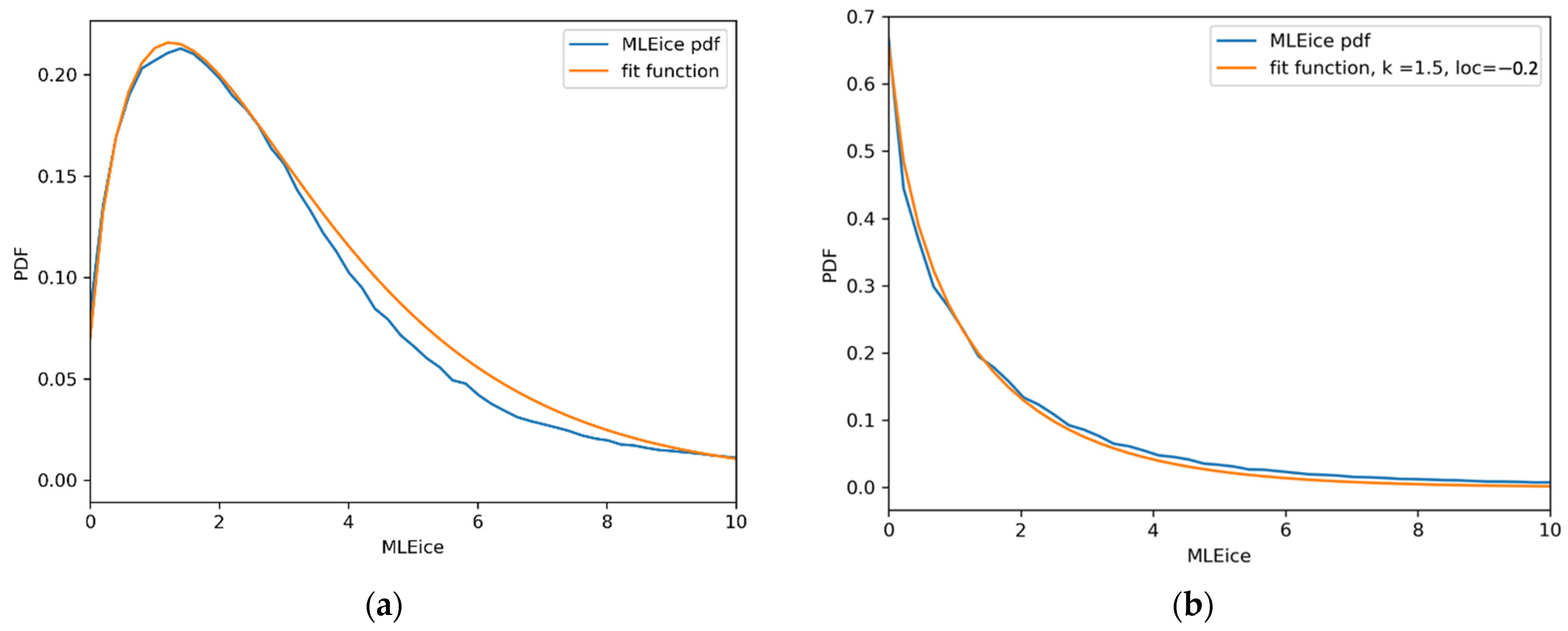
2.2.1. Probability Distribution of
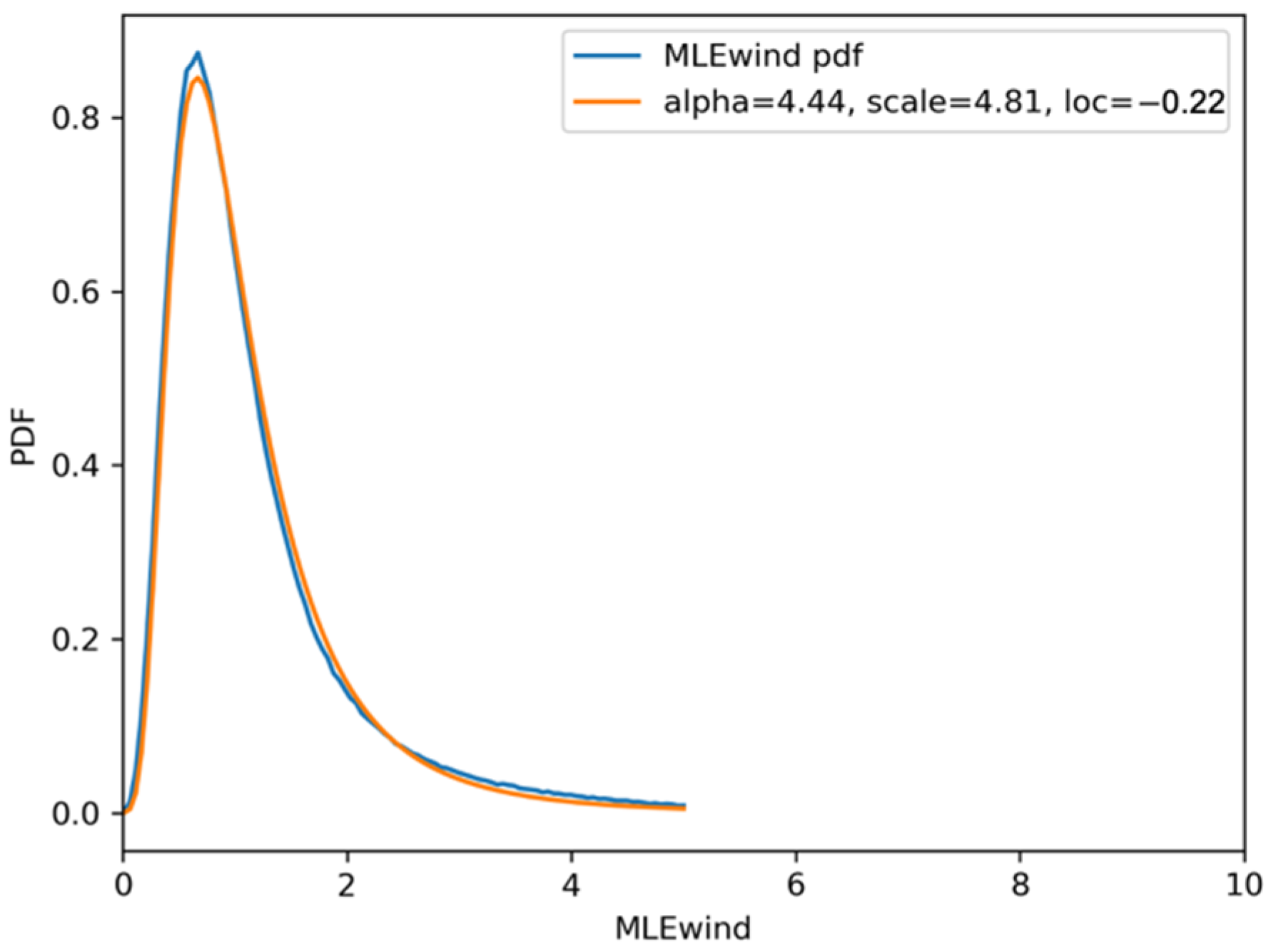
2.2.2. Probability Distribution of
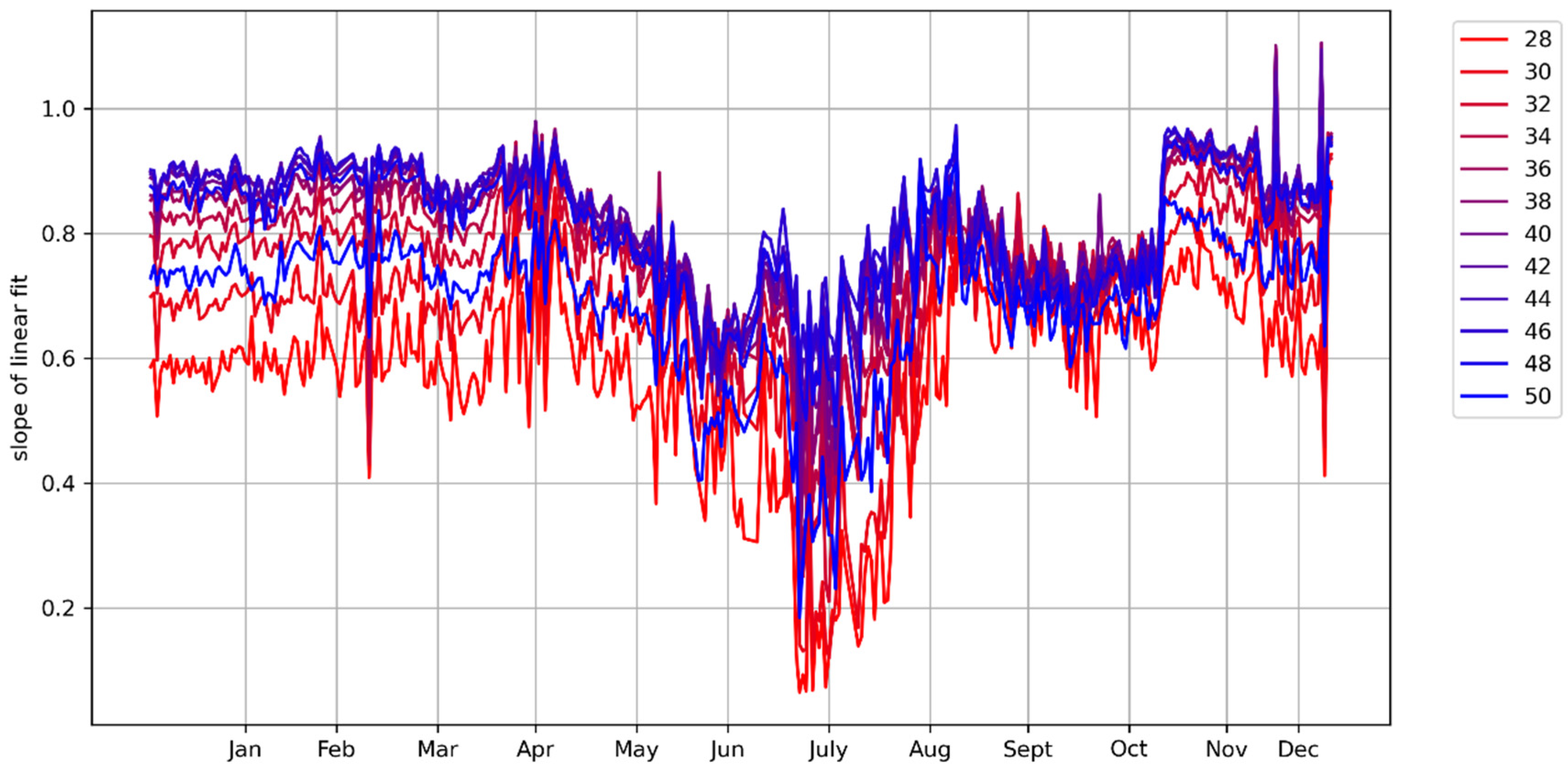
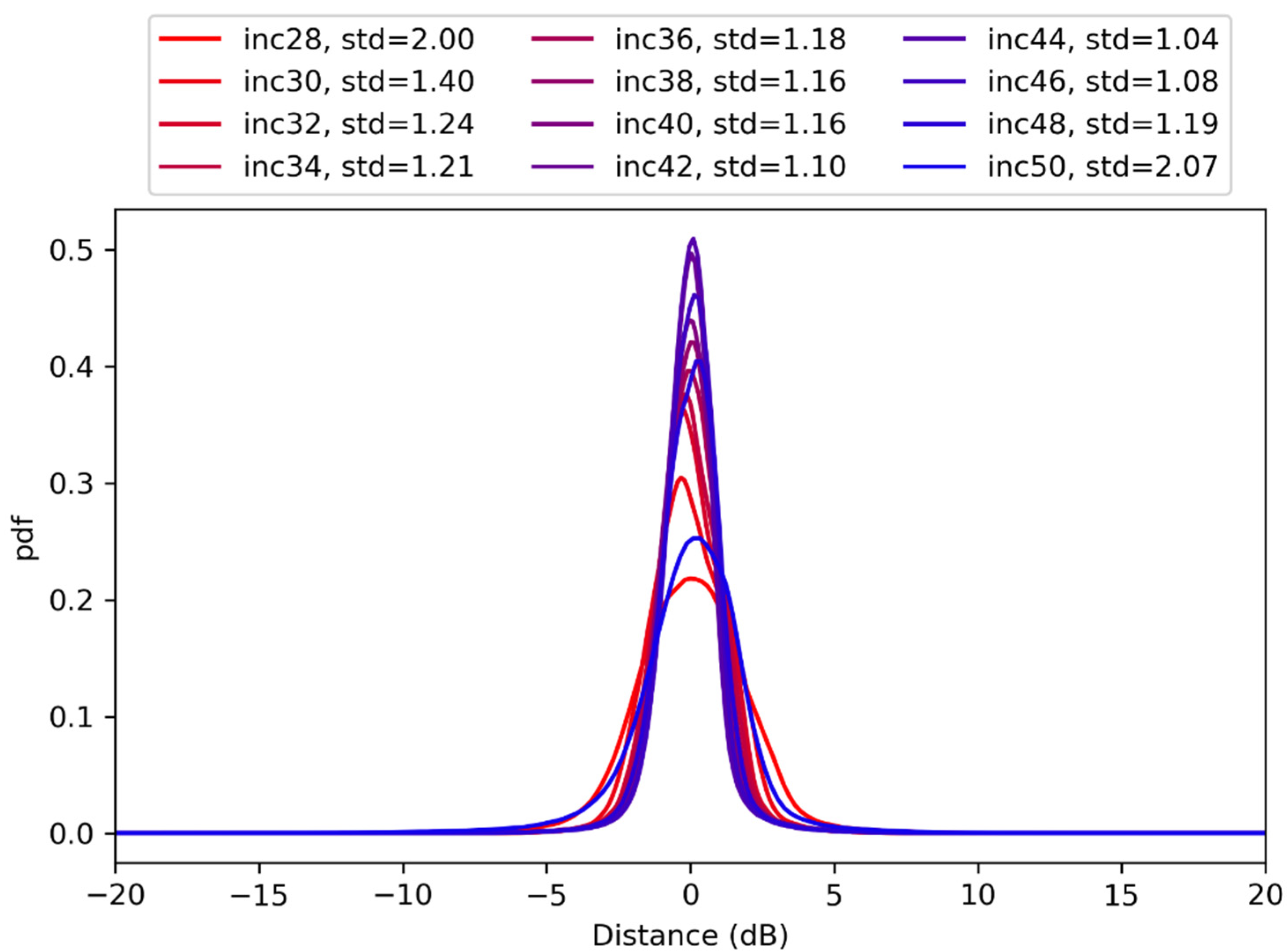
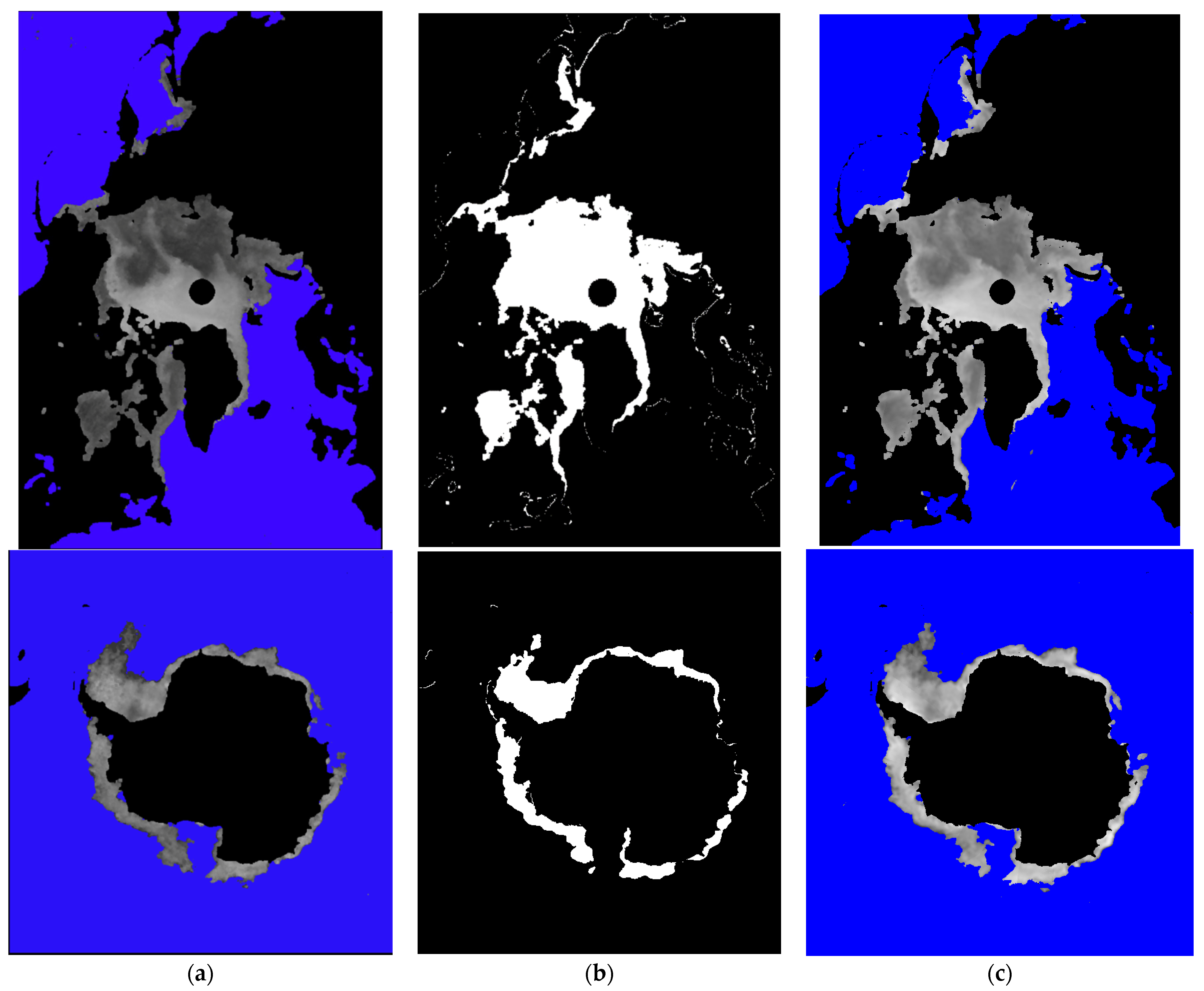
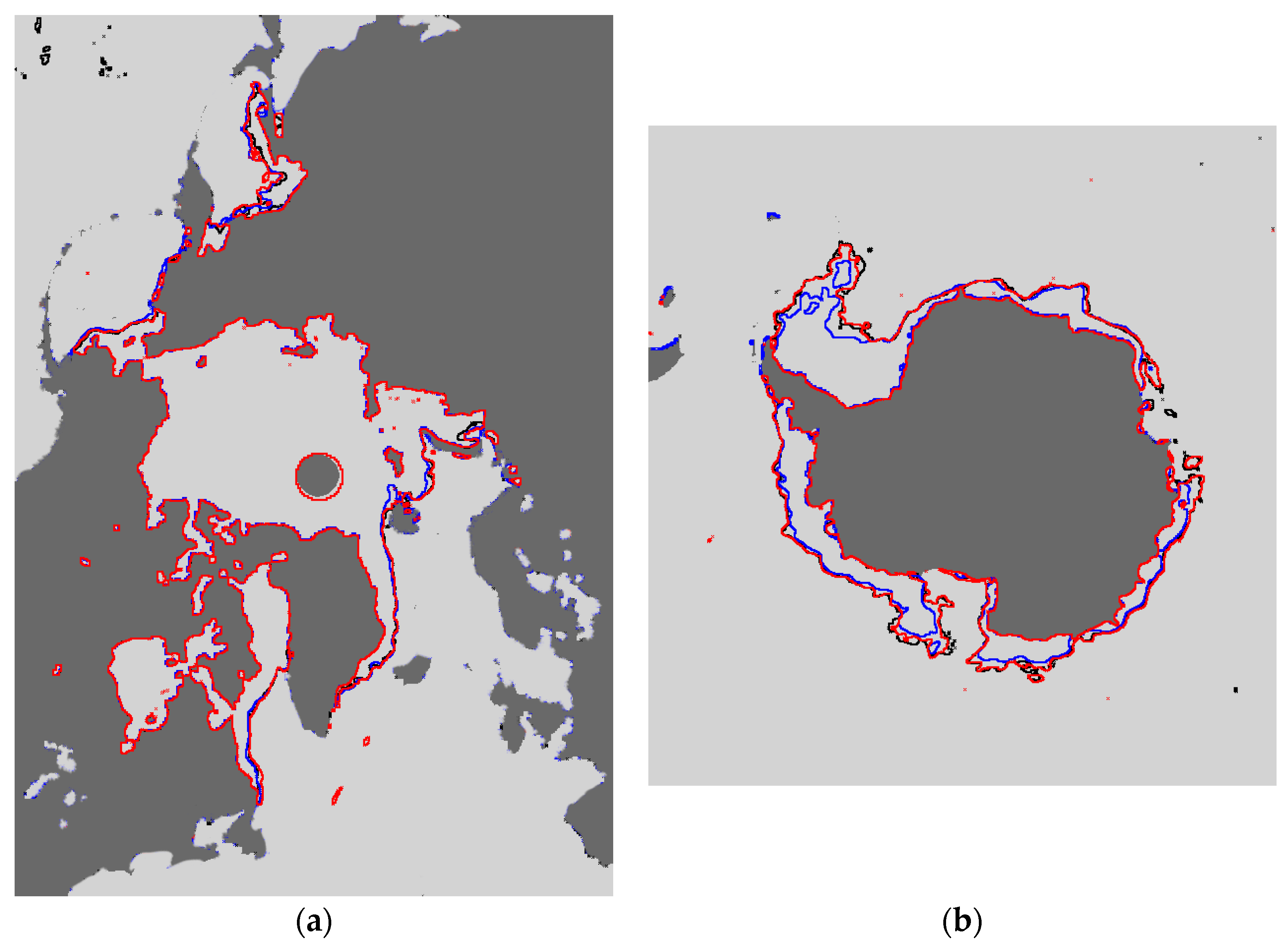
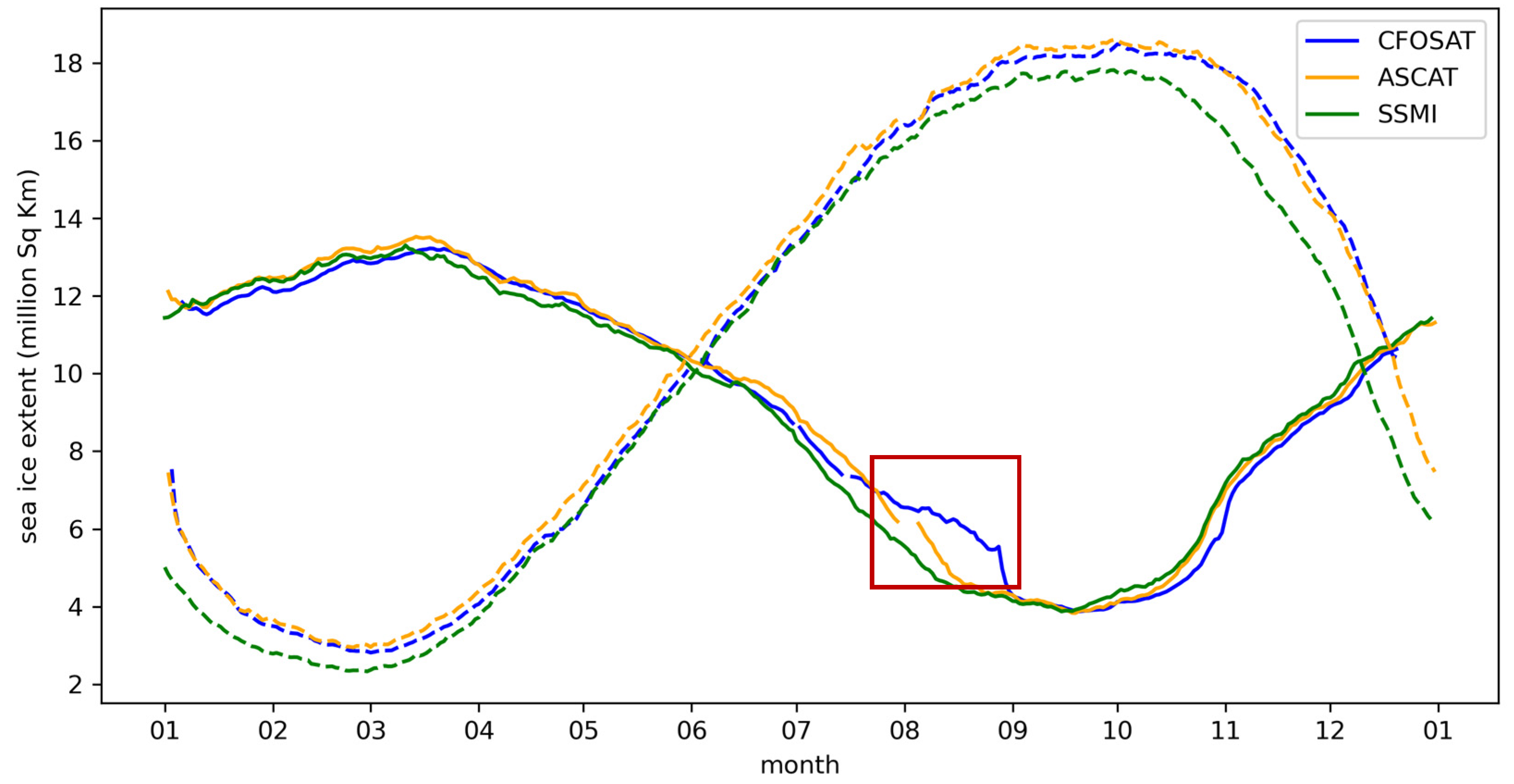
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Comiso, J.C.; Parkinson, C.L.; Gersten, R.; Stock, L. Accelerated decline in the Arctic sea ice cover. Geophys. Res. Lett. 2008, 35, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Stroeve, J.C.; Serreze, M.C.; Holland, M.M.; Kay, J.E.; Malanik, J.; Barrett, A.P. The Arctic’s rapidly shrinking sea ice cover: A research synthesis. Clim. Change 2012, 110, 1005–1027. [Google Scholar] [CrossRef] [Green Version]
- Stroeve, J.; Notz, D. Changing state of Arctic sea ice across all seasons. Environ. Res. Lett. 2018, 13, 103001. [Google Scholar] [CrossRef]
- Parkinson, C.L. A 40-y record reveals gradual Antarctic sea ice increases followed by decreases at rates far exceeding the rates seen in the Arctic. Proc. Natl. Acad. Sci. USA 2019, 116, 14414–14423. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cavalieri, D.J.; Parkinson, C.L.; Gloersen, P.; Comiso, J.C.; Zwally, H.J. Deriving long-term time series of sea ice cover from satellite passive-microwave multisensor data sets. J. Geophys. Res. Ocean. 1999, 104, 15803–15814. [Google Scholar] [CrossRef]
- Haarpaintner, J.; Tonboe, R.T.; Long, D.G.; Van Woert, M.L. Automatic detection and validity of the sea-ice edge: An application of enhanced-resolution QuikScat/SeaWinds data. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1433–1443. [Google Scholar] [CrossRef]
- Anderson, H.S.; Long, D.G. Sea ice mapping method for SeaWinds. IEEE Trans. Geosci. Remote Sens. 2005, 43, 647–657. [Google Scholar] [CrossRef] [Green Version]
- Haarpaintner, J.; Spreen, G. Use of enhanced-resolution QuikSCAT/SeaWinds data for operational ice services and climate research: Sea ice edge, type, concentration, and drift. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3131–3137. [Google Scholar] [CrossRef]
- Belmonte Rivas, M.; Stoffelen, A. New bayesian algorithm for sea ice detection with QuikSCAT. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1894–1901. [Google Scholar] [CrossRef]
- Stoffelen, A.; Verspeek, J.; Haan, S. De C-Band Sea Ice Model. In 2004 Envisat & ERS Symposium; Lacoste, H., Ouwehand, L., Eds.; European Space Agency: Paris, France, 2005; Volume ESA SP-572, p. 143.1. [Google Scholar]
- Belmonte Rivas, M.; Verspeek, J.; Verhoef, A.; Stoffelen, A. Bayesian sea ice detection with the advanced scatterometer ASCAT. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2649–2657. [Google Scholar] [CrossRef]
- Otosaka, I.; Rivas, M.B.; Stoffelen, A. Bayesian sea ice detection with the ERS scatterometer and sea ice backscatter model at C-band. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2248–2254. [Google Scholar] [CrossRef]
- Belmonte Rivas, M.; Otosaka, I.; Stoffelen, A.; Verhoef, A. A scatterometer record of sea ice extents and backscatter: 1992–2016. Cryosphere 2018, 12, 2941–2953. [Google Scholar] [CrossRef] [Green Version]
- Markus, T.; Cavalieri, D.J. An Enhancement of the NASA Team Sea Ice Algorithm. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1387–1398. [Google Scholar] [CrossRef] [Green Version]
- Cavalieri, D.J.; Markus, T.; Hall, D.K.; Ivanoff, A.; Glick, E. Assessment of AMSR-E antarctic winter sea-ice concentrations using aqua MODIS. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3331–3339. [Google Scholar] [CrossRef]
- Meier, W.N.; Stroeve, J. Comparison of sea-ice extent and ice-edge location estimates from passive microwave and enhanced-resolution scatterometer data. Ann. Glaciol. 2008, 48, 65–70. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Stoffelen, A.; Verhoef, A. A Generalized Simulation Capability for Rotating Beam Scatterometers. Atmos. Meas. Tech. 2019, 12, 3573–3594. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Lin, W.; Dong, X.; Lang, S.; Yun, R.; Zhu, D.; Zhang, K.; Sun, C.; Mu, B.; Ma, J.; et al. First Results from the Rotating Fan Beam Scatterometer Onboard CFOSAT. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8793–8806. [Google Scholar] [CrossRef]
- Li, Z.; Stoffelen, A.; Verhoef, A.; Verspeek, J. Numerical Weather Prediction Ocean Calibration for the Chinese-French Oceanography Satellite Wind Scatterometer and Wind Retrieval Evaluation. Earth Sp. Sci. 2021, 8, e2020EA001606. [Google Scholar] [CrossRef]
- Zhang, P.; Hu, X.; Lu, Q.; Zhu, A.; Lin, M.; Sun, L.; Chen, L.; Xu, N. FY-3E: The First Operational Meteorological Satellite Mission in an Early Morning Orbit. Adv. Atmos. Sci. 2022, 39, 1–8. [Google Scholar] [CrossRef]
- Remund, Q.P.; Long, D.G. Sea ice extent mapping using Ku band scatterometer data. J. Geophys. Res. Ocean. 1999, 104, 11515–11527. [Google Scholar] [CrossRef] [Green Version]
- Liu, L.; Dong, X.; Lin, W.; Lang, S.; Wang, L. Polar Sea Ice Detection with the CFOSAT Scatterometer. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 5645–5648. [Google Scholar] [CrossRef]
- Stoffelen, A.; Portabella, M. On Bayesian Scatterometer Wind Inversion. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1523–1533. [Google Scholar] [CrossRef]
- Cavalieri, D.J.; Parkinson, C.L.; Gloersen, P.; Zwally, H.J. Sea Ice Concentrations from Nimbus-7 SMMR and DMSP SSM/I-SSMIS Passive Microwave Data, Version 1; [NSIDC-0051]; National Snow & Ice Data Center: Boulder, CO, USA, 1996. [Google Scholar]

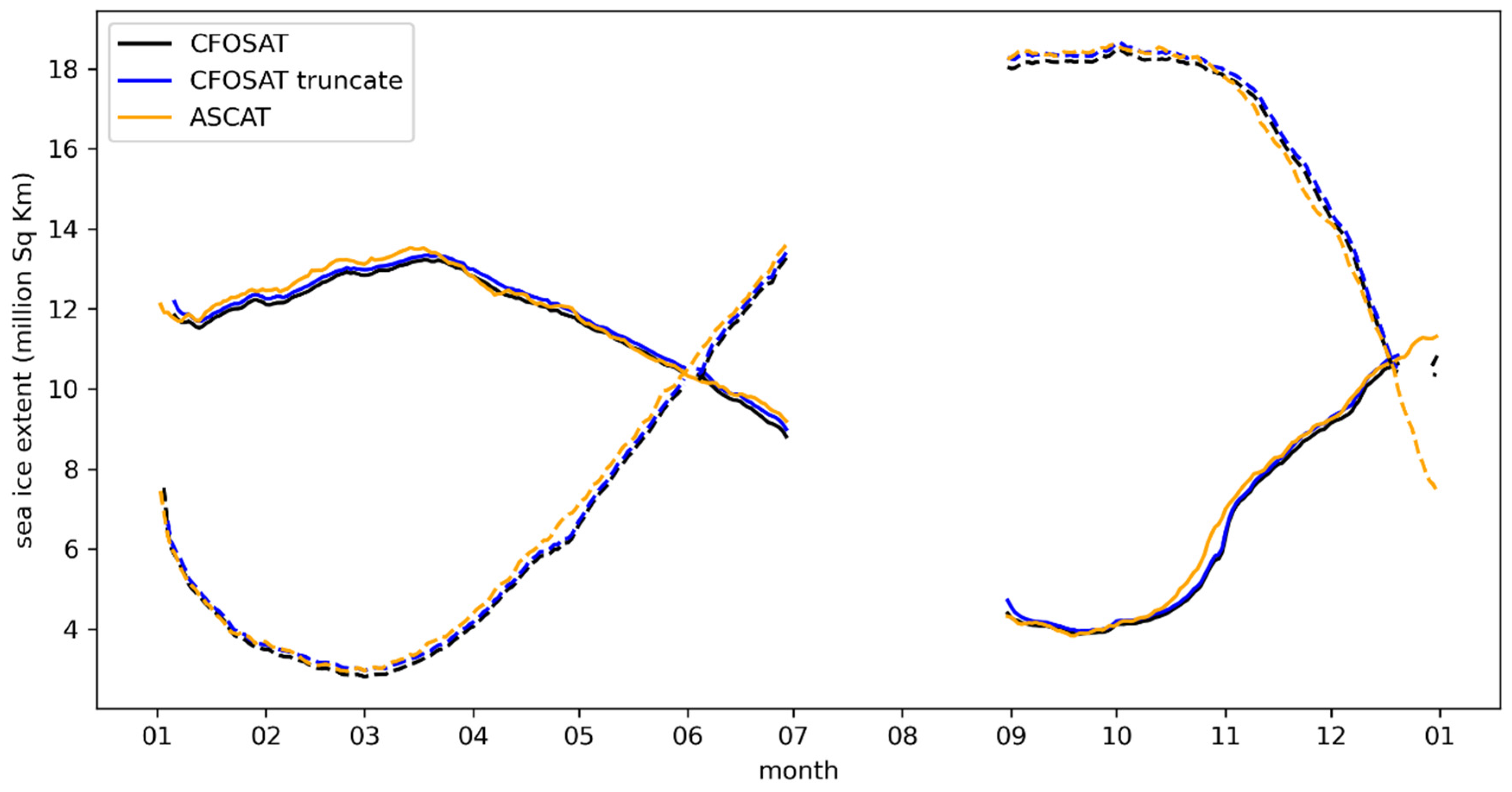
| Average Sea Ice Extent Difference Compared to ASCAT Sea Ice Extent | All_Inc | Truncated_Inc | Exclude_Inc |
|---|---|---|---|
| Arctic (million km2) | 0.18 | 0.05 | 0.13 |
| Antarctic (million km2) | 0.13 | 0.01 | 0.08 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Verhoef, A.; Stoffelen, A. Bayesian Sea Ice Detection Algorithm for CFOSAT. Remote Sens. 2022, 14, 3569. https://doi.org/10.3390/rs14153569
Li Z, Verhoef A, Stoffelen A. Bayesian Sea Ice Detection Algorithm for CFOSAT. Remote Sensing. 2022; 14(15):3569. https://doi.org/10.3390/rs14153569
Chicago/Turabian StyleLi, Zhen, Anton Verhoef, and Ad Stoffelen. 2022. "Bayesian Sea Ice Detection Algorithm for CFOSAT" Remote Sensing 14, no. 15: 3569. https://doi.org/10.3390/rs14153569
APA StyleLi, Z., Verhoef, A., & Stoffelen, A. (2022). Bayesian Sea Ice Detection Algorithm for CFOSAT. Remote Sensing, 14(15), 3569. https://doi.org/10.3390/rs14153569






