High-Resolution Regional Digital Elevation Models and Derived Products from MESSENGER MDIS Images
Abstract
:1. Introduction
2. Data Sources
2.1. Mercury Dual Imaging System (MDIS)
2.2. Mercury Laser Altimeter (MLA)
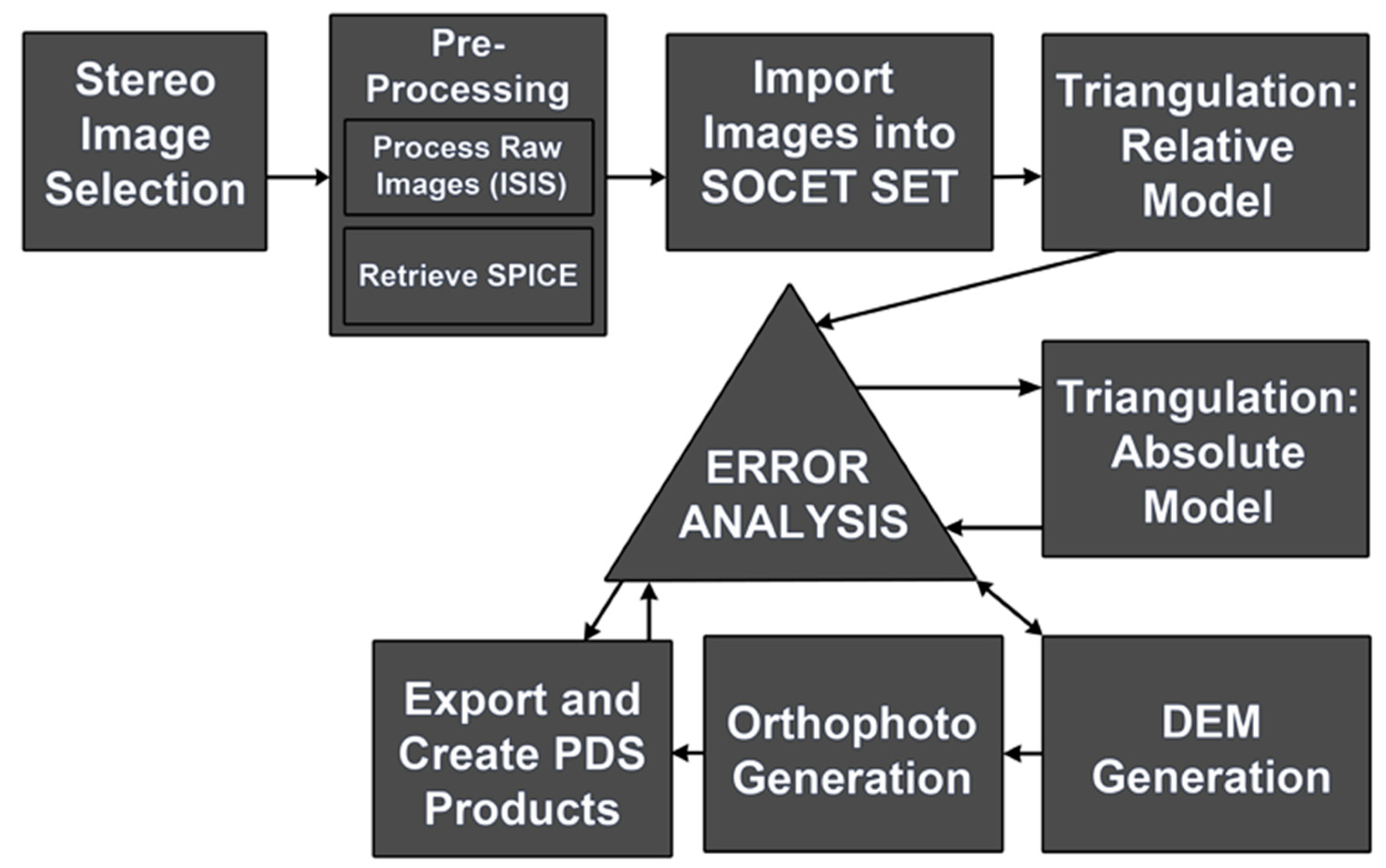
3. Methodology
3.1. Stereo Image Selection
3.2. Image Pre-Processing
3.3. Relative Orientation
3.4. Absolute Orientation
3.5. DEM Extraction
3.6. Orthophoto Generation
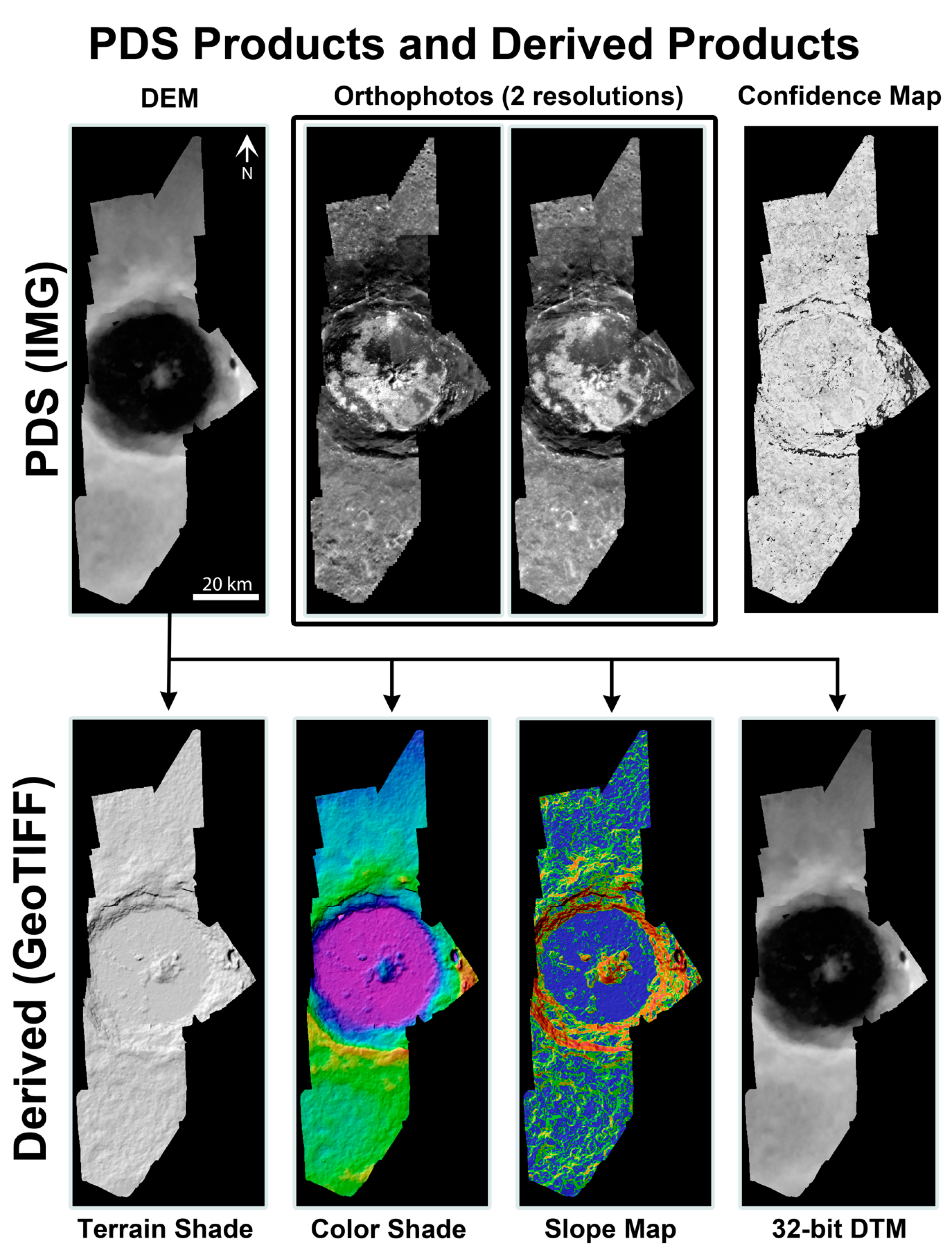
3.7. Planetary Data System (PDS) Products and Derived Products
4. Results: Uncertainty Analysis
4.1. Relative Linear Error
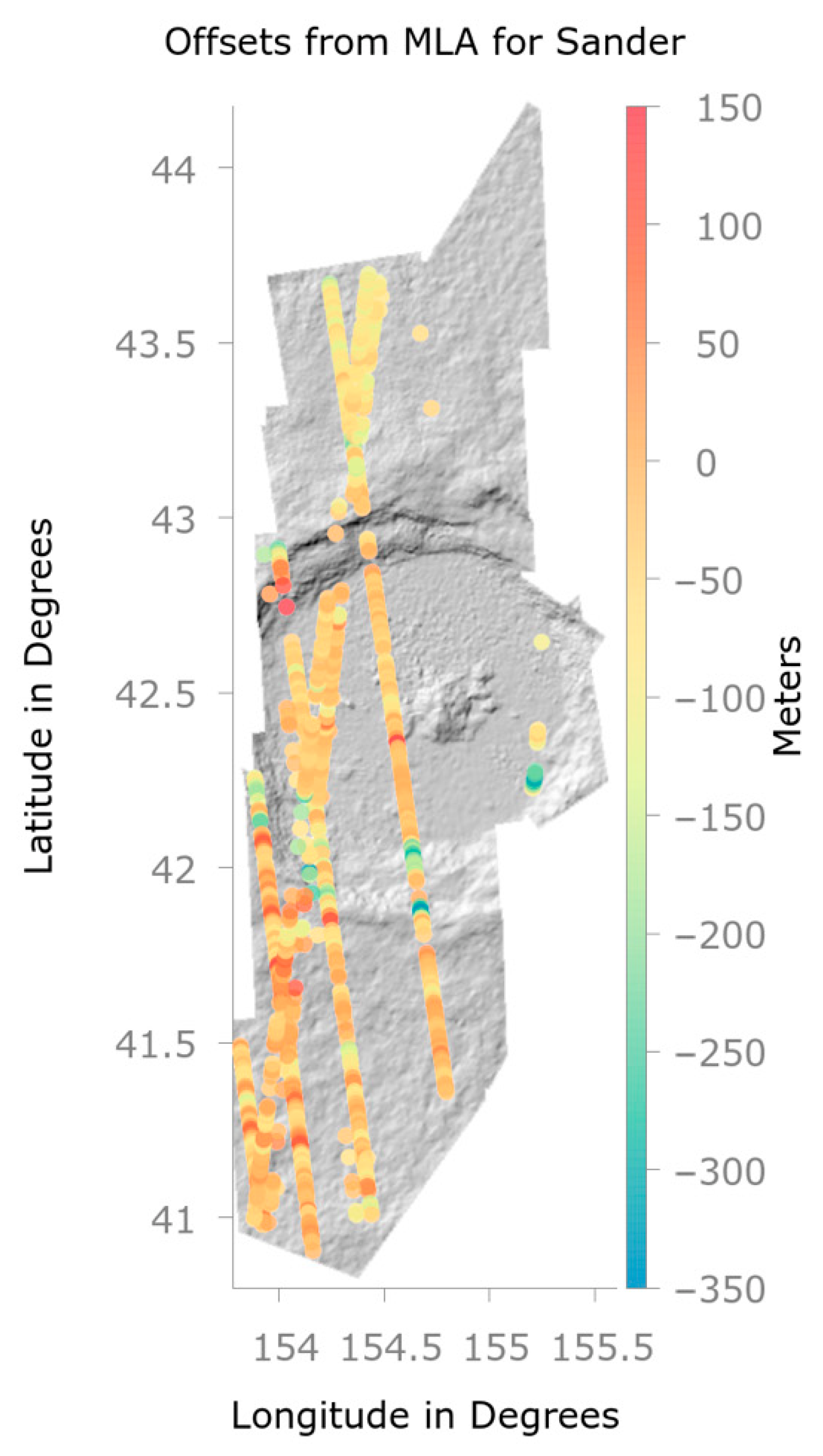
4.2. Offsets from MLA
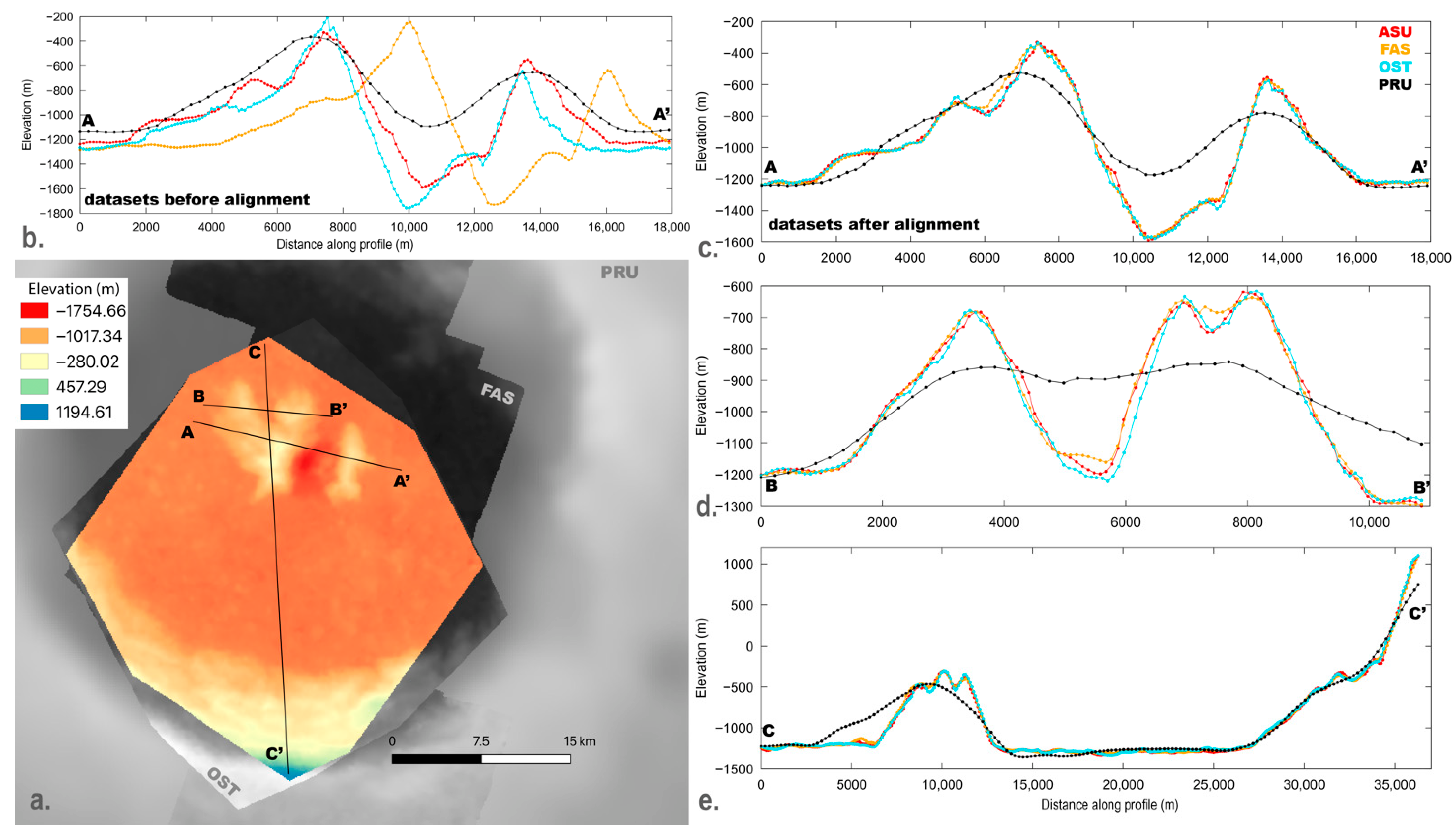
4.3. Comparison to Other Regional Topographic Products
5. Discussion: Scientific Application
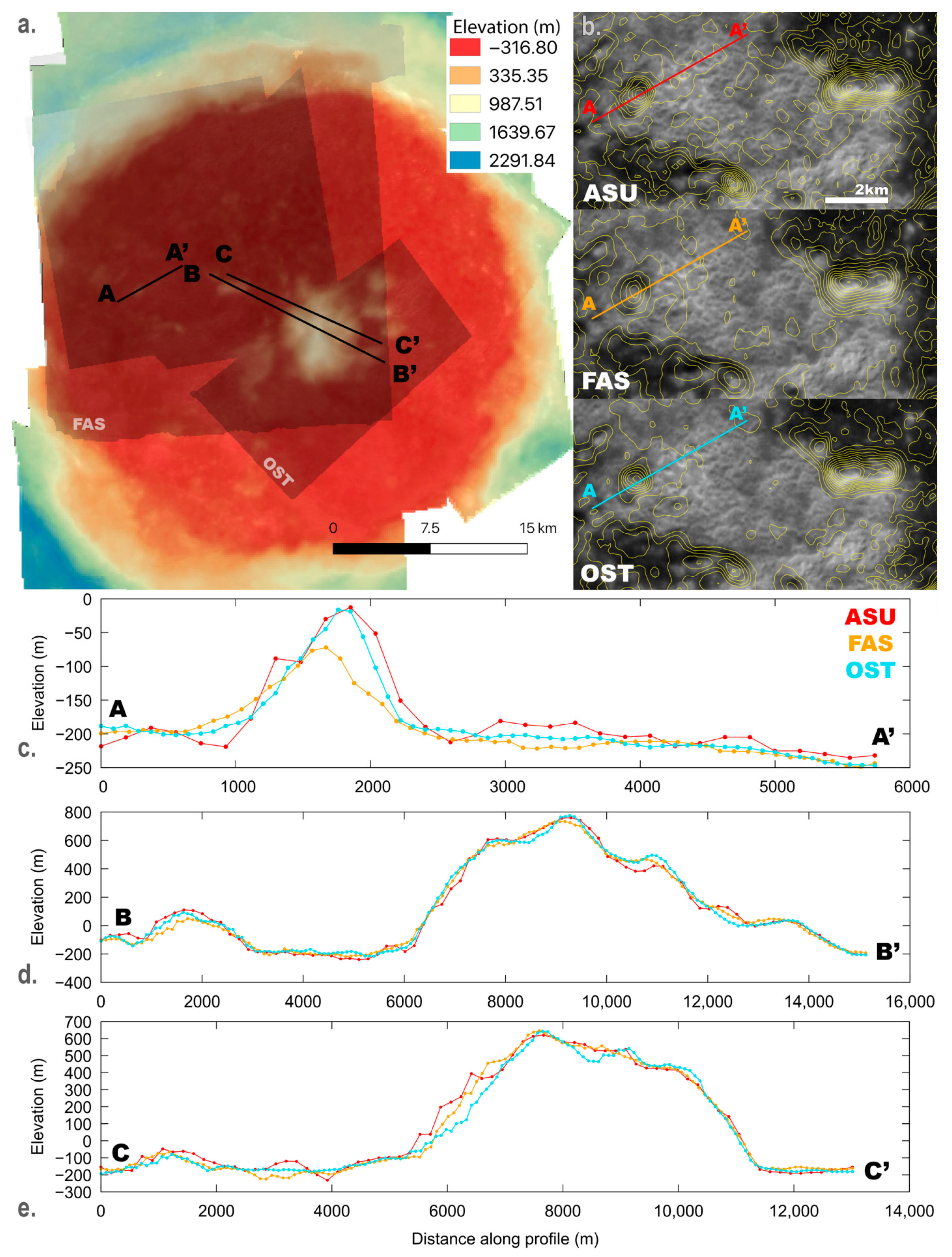
5.1. Anomalous High-Reflectance Regions in Kertész and Sander Craters
5.2. Formation Hypotheses
5.3. Findings: Kertész Crater
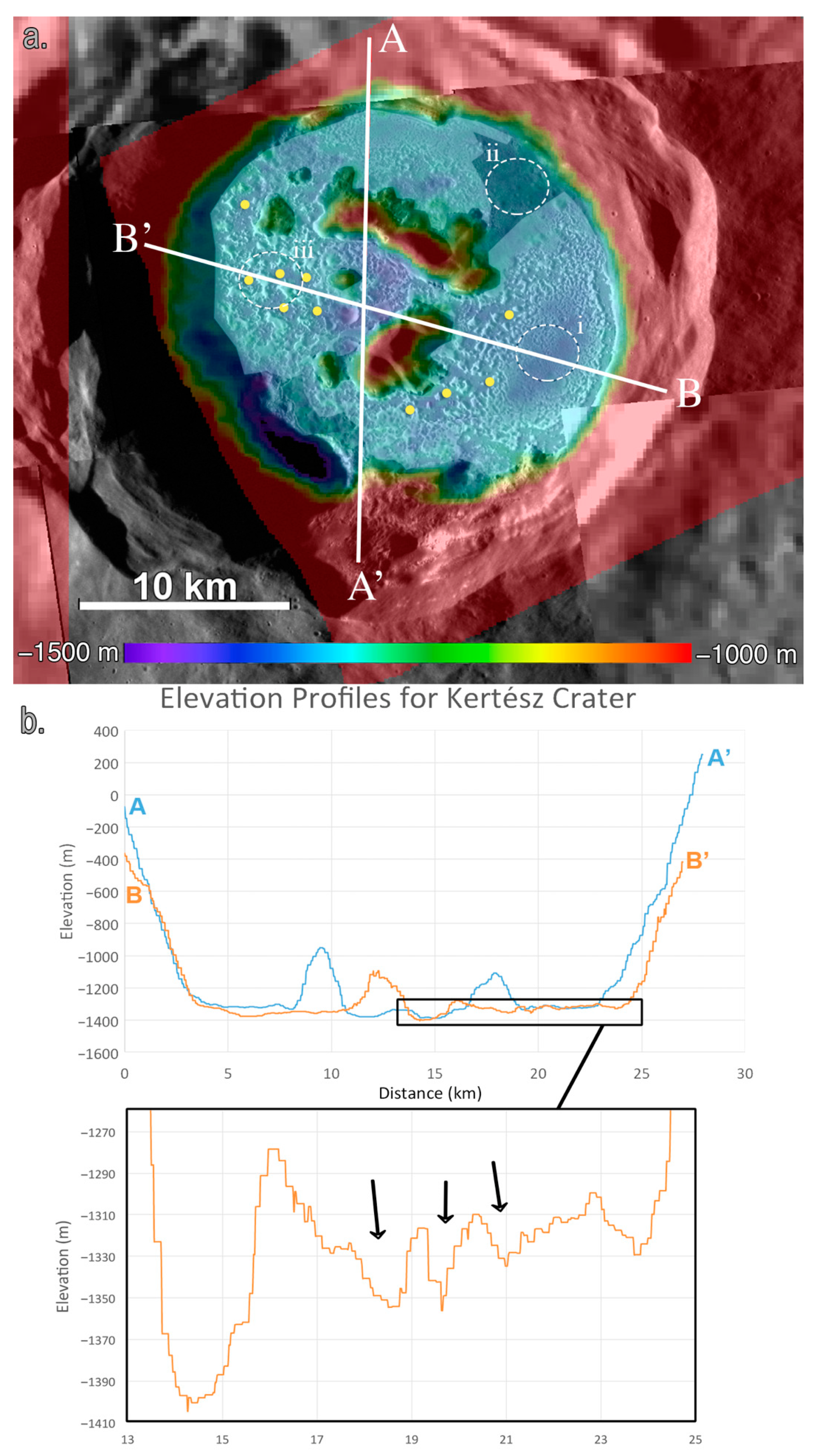
5.4. Findings: Sander Crater
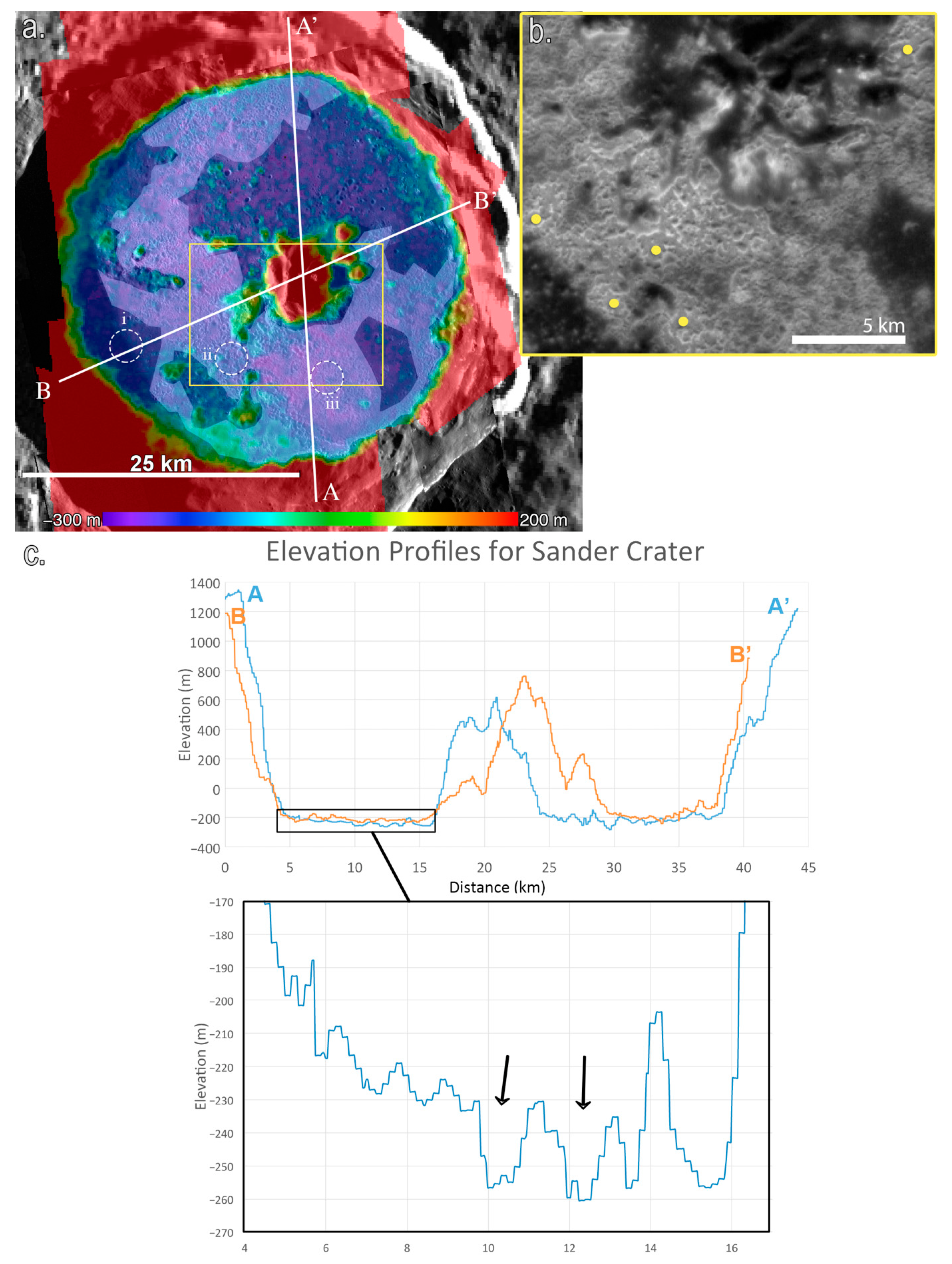
5.5. Findings: Raditladi Basin
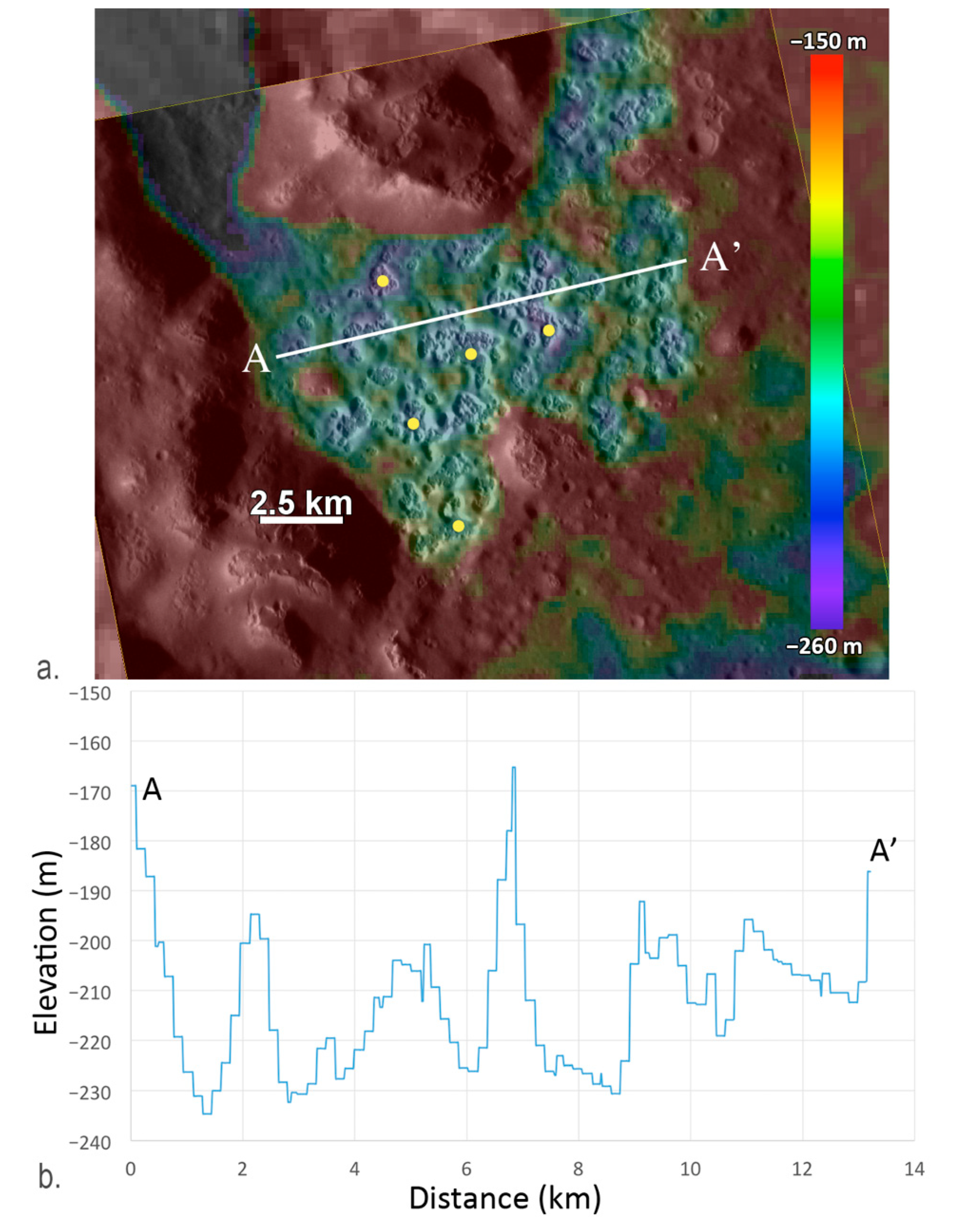
5.6. Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Site | DEM Name | Image 1 | Image 2 | Pixel Scale (m) | Relative Linear Error (m) |
| Vent in Catullus Crater | CATLS01 | EN1020925599M | EN1020925715M | 84 | 83.56 |
| Cunningham Crater | CNGHM01 | EN0215633679M | EN1012716022M | 78 | 48.97 |
| ‘‘ | CNGHM02 | EN0215633679M | EN1012716026M | 78 | 48.00 |
| ‘‘ | CNGHM03 | EN0215633673M | EN1025248438M | 105 | 53.67 |
| ‘‘ | CNGHM04 | EN0215633679M | EN1025248438M | 105 | 53.28 |
| ‘‘ | CNGHM05 | EN0215633673M | EN1012716026M | 78 | 48.51 |
| ‘‘ | CNGHM06 | EN0215633679M | EN1025248434M | 102 | 52.89 |
| ‘‘ | CNGHM07 | EN0215633685M | EN1025248434M | 102 | 52.64 |
| ‘‘ | CNGHM08 | EN1010038716M | EN1012716018M | 78 | 82.29 |
| ‘‘ | CNGHM09 | EN1010038716M | EN1012716022M | 78 | 84.69 |
| ‘‘ | CNGHMMS | - | - | 105 | 84.69 |
| Degas Crater | DEGAS01 | EN1008944217M | EN1024240075M | 97 | 69.26 |
| Scarp in NW Rembrandt Basin | HYNEK01 | EN1015859904M | EN1015861167M | 500 | 383.01 |
| Kertész Crater | KERTS01 | EN1010096377M | EN1025335005M | 120 | 71.46 |
| ‘‘ | KERTS02 | EN1010096377M | EN1010096528M | 120 | 97.34 |
| ‘‘ | KERTSMS | - | - | 120 | 97.34 |
| Kuiper Crater | KUIPR01 | EN0223659984M | EN1002982634M | 270 | 160.37 |
| Paramour Rupes | PARMR01 | EN1045386684M | EN1045387902M | 450 | 256.82 |
| ‘‘ | PARMR02 | EN1045386684M | EN1045387906M | 432 | 256.94 |
| ‘‘ | PARMR03 | EN1045386688M | EN1045387906M | 432 | 260.93 |
| ‘‘ | PARMRMS | - | - | 450 | 260.93 |
| Raditladi Basin | RADIT01 | EN1015425730M | EN1015426008M | 180 | 134.99 |
| ‘‘ | RADIT02 | EN1015425734M | EN1015426008M | 180 | 136.62 |
| ‘‘ | RADIT03 | EN1015425734M | EN1015426012M | 180 | 134.74 |
| ‘‘ | RADITMS | - | - | 180 | 136.62 |
| Sander Crater | SANDR01 | EN1012745010M | EN0218289182M | 105 | 31.95 |
| ‘‘ | SANDR02 | EN1012745010M | EN0218289189M | 103 | 31.11 |
| ‘‘ | SANDR03 | EN1012745010M | EN0217906385M | 160 | 56.26 |
| ‘‘ | SANDR04 | EN1012745010M | EN0233476482M | 92 | 21.43 |
| ‘‘ | SANDR05 | EN1010125026M | EN0217906385M | 160 | 45.96 |
| ‘‘ | SANDR06 | EN1012745056M | EN1010125151M | 88 | 66.78 |
| ‘‘ | SANDR07 | EN1012745056M | EN0218289182M | 105 | 37.46 |
| ‘‘ | SANDR08 | EN1012745056M | EN0218289189M | 103 | 36.23 |
| ‘‘ | SANDR09 | EN1012745056M | EN0217906385M | 160 | 56.36 |
| ‘‘ | SANDR10 | EN1012745056M | EN0233476482M | 92 | 23.73 |
| ‘‘ | SANDR11 | EN1010125151M | EN0217906385M | 160 | 50.19 |
| ‘‘ | SANDR12 | EN1010125151M | EN1010067392M | 88 | 67.22 |
| ‘‘ | SANDR13 | EN1010125151M | EN1010067396M | 88 | 69.59 |
| ‘‘ | SANDR14 | EN0218289168M | EN0217906381M | 162 | 40.46 |
| ‘‘ | SANDR15 | EN0218289175M | EN0217906381M | 162 | 39.96 |
| ‘‘ | SANDR16 | EN0218289175M | EN0217906385M | 160 | 40.05 |
| ‘‘ | SANDR17 | EN0218289175M | EN1012773887M | 107 | 44.74 |
| ‘‘ | SANDR18 | EN0218289182M | EN0217906385M | 160 | 39.62 |
| ‘‘ | SANDR19 | EN0218289182M | EN1012773893M | 105 | 44.19 |
| ‘‘ | SANDR20 | EN0218289189M | EN0217906385M | 160 | 39.11 |
| ‘‘ | SANDR21 | EN0218289189M | EN0217906389M | 157 | 39.09 |
| ‘‘ | SANDR22 | EN0218289189M | EN1012773893M | 103 | 42.36 |
| ‘‘ | SANDR23 | EN0218289189M | EN1012773899M | 103 | 43.55 |
| ‘‘ | SANDR24 | EN0218289189M | EN1012773904M | 103 | 44.59 |
| ‘‘ | SANDR25 | EN0218289196M | EN0217906389M | 157 | 38.6 |
| ‘‘ | SANDR26 | EN0218289196M | EN1012773904M | 101 | 42.77 |
| ‘‘ | SANDR27 | EN0217906381M | EN1012773887M | 162 | 48.77 |
| ‘‘ | SANDR28 | EN0217906385M | EN1010067392M | 160 | 54.88 |
| ‘‘ | SANDR29 | EN0217906385M | EN1012773887M | 160 | 48.64 |
| ‘‘ | SANDR30 | EN0217906385M | EN1012773893M | 160 | 48.35 |
| ‘‘ | SANDR31 | EN0233476482M | EN1012773887M | 92 | 25.61 |
| ‘‘ | SANDR32 | EN0233476482M | EN1012773893M | 92 | 26.36 |
| ‘‘ | SANDR33 | EN0233476482M | EN1012773899M | 92 | 27.14 |
| ‘‘ | SANDR34 | EN0233476487M | EN1012773899M | 91 | 26.22 |
| ‘‘ | SANDR35 | EN0233476487M | EN1012773904M | 91 | 26.99 |
| ‘‘ | SANDR36 | EN0233476492M | EN1012773904M | 90 | 26.11 |
| ‘‘ | SANDRMS | - | - | 162 | 69.59 |
Appendix B

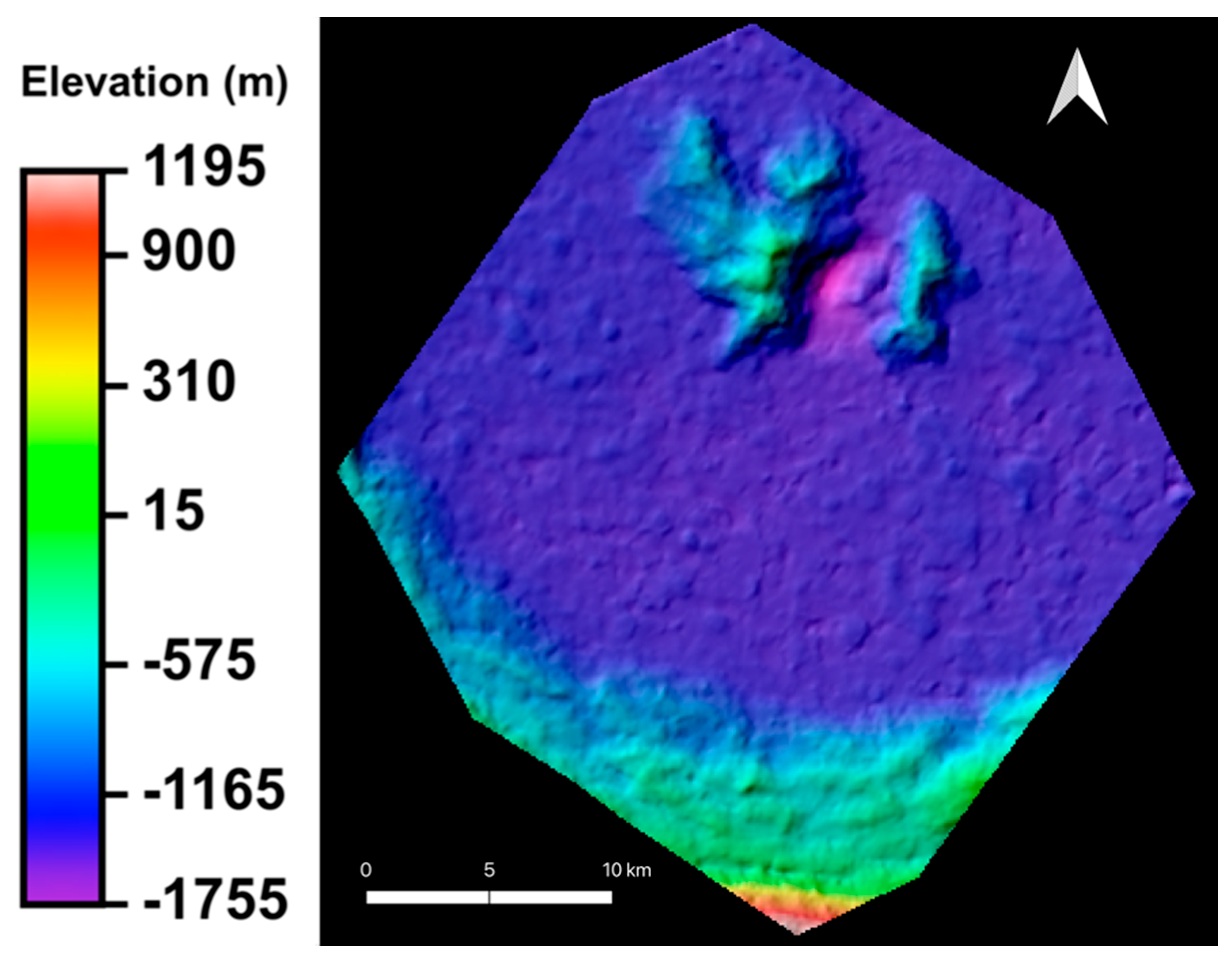

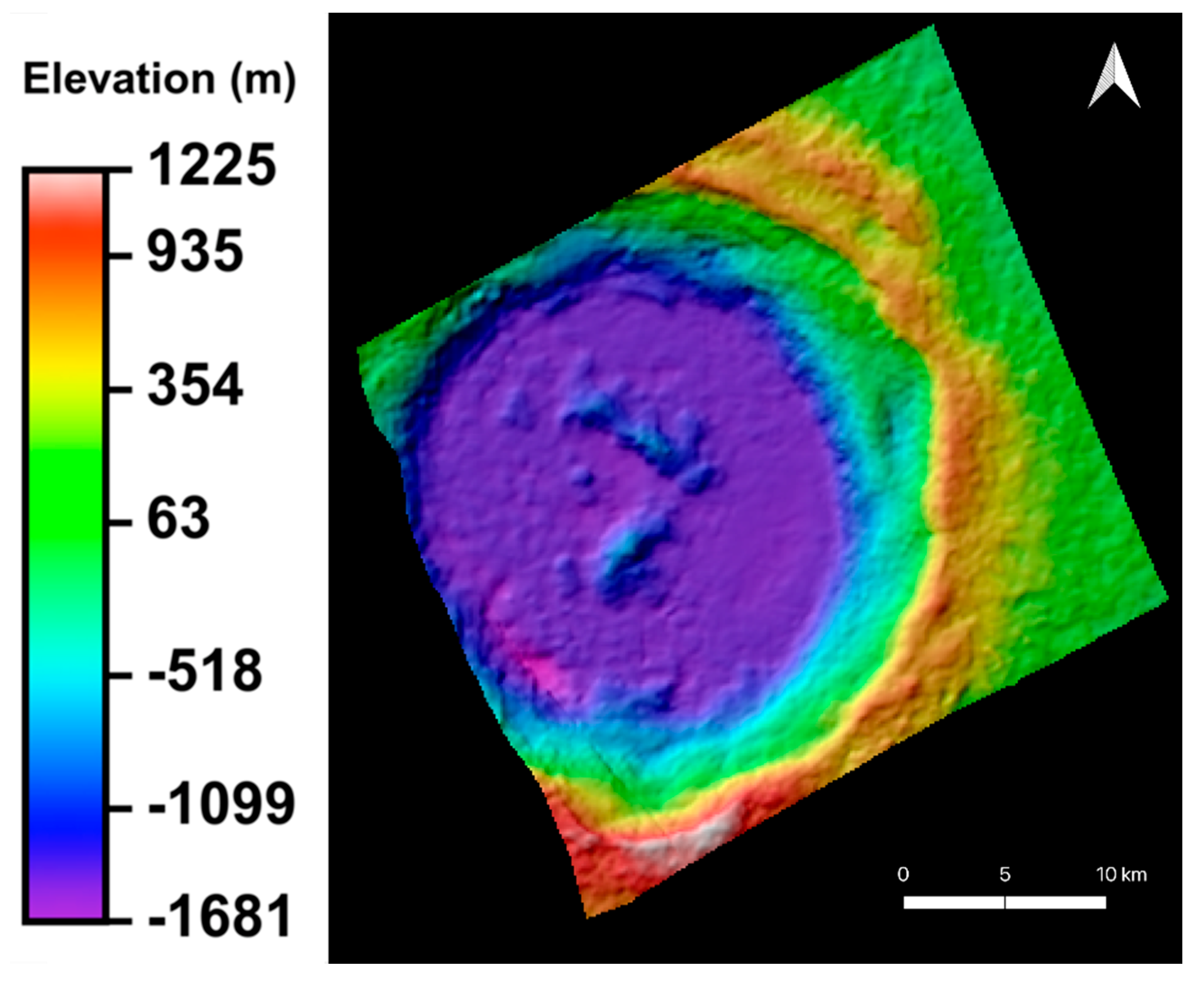



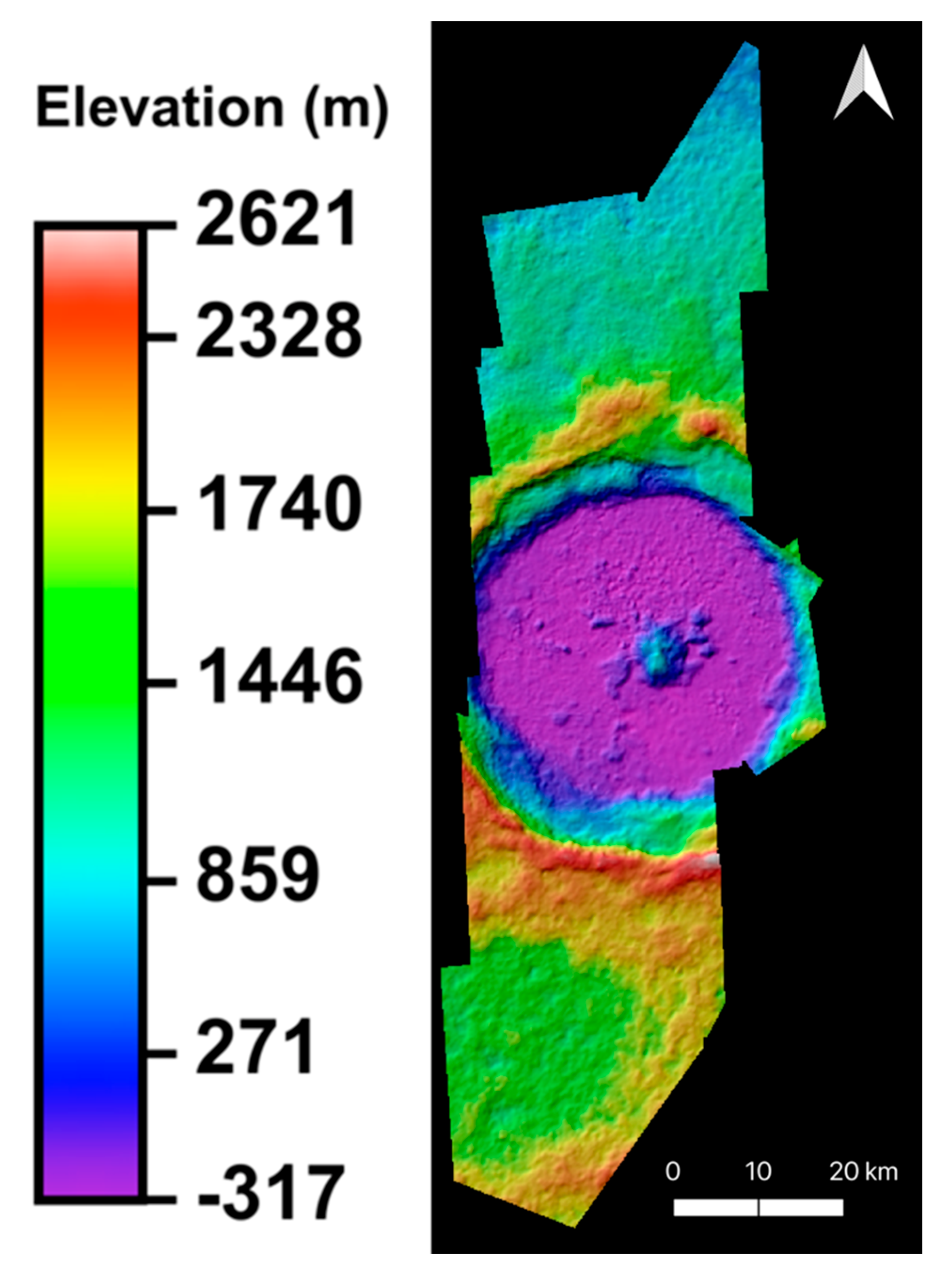
Appendix C

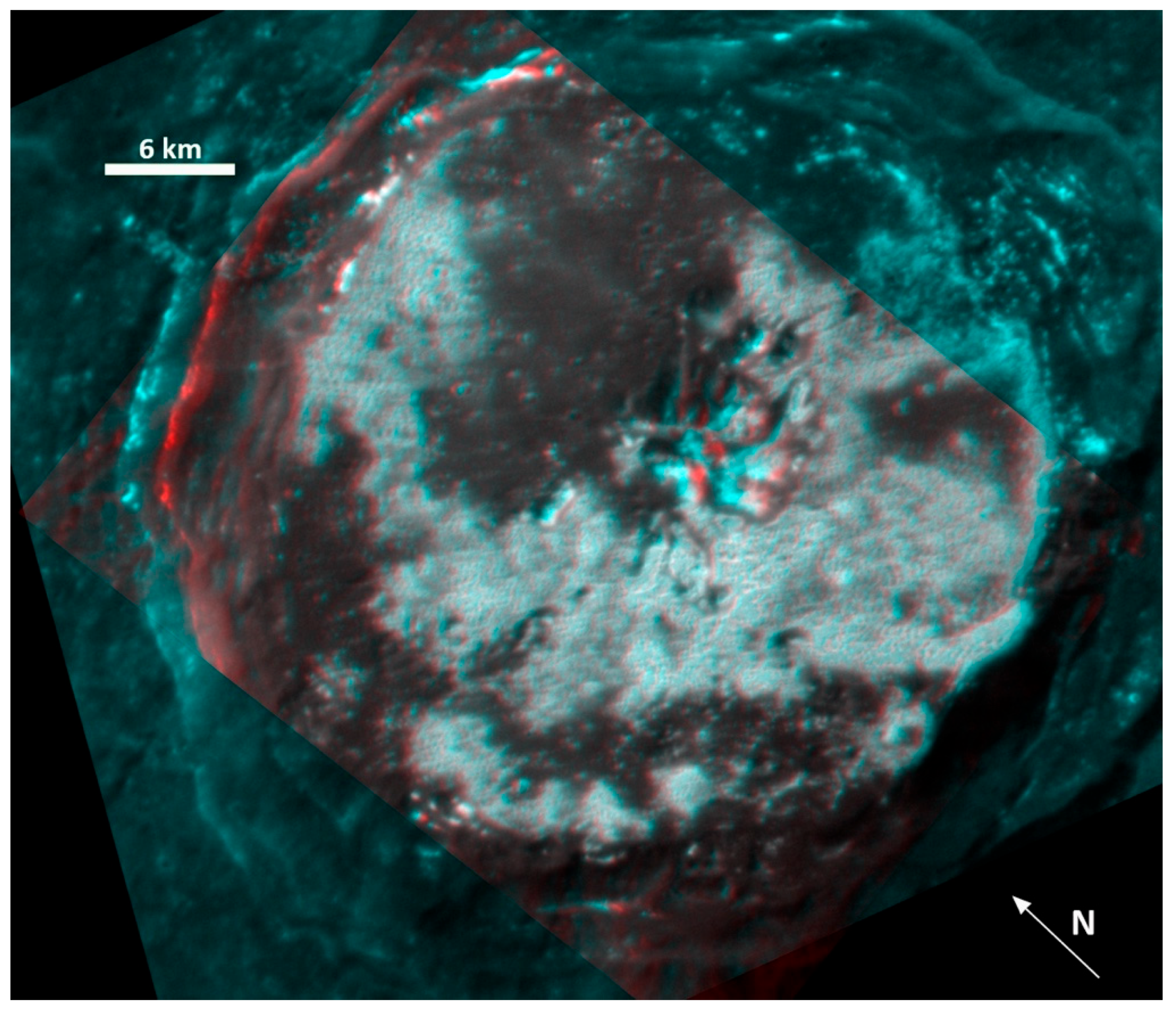

References
- Hawkins, S.E., III; Boldt, J.D.; Darlington, E.H.; Espiritu, R.; Gold, R.E.; Gotwols, B.; Grey, M.P.; Hash, C.D.; Hayes, J.R.; Jaskulek, S.E.; et al. The Mercury Dual Imaging System on the MESSENGER Spacecraft. Space Sci. Rev. 2007, 131, 247–338. [Google Scholar] [CrossRef]
- Hawkins, S.E., III; Murchie, S.L.; Becker, K.J.; Selby, C.M.; Turner, F.S.; Noble, M.W.; Chabot, N.L.; Choo, T.H.; Darlington, E.H.; Denevi, B.W.; et al. In-flight performance of MESSENGER’s Mercury Dual Imaging System. SPIE Opt. Eng. Appl. 2009, 7441, 74410Z. [Google Scholar] [CrossRef]
- Chabot, N.L.; Denevi, B.W.; Murchie, S.L.; Hash, C.D.; Ernst, C.M.; Blewett, D.T.; Nair, H.; Laslo, N.R.; Solomon, S.C. Mapping Mercury: Global imaging strategy and products from the MESSENGER mission. In Proceedings of the 47th Annual Lunar and Planetary Science Conference, The Woodlands, TX, USA, 21–25 May 2016. Abstract #1256. [Google Scholar]
- Moessner, D.P.; McAdams, J.V. Design, implementation, and outcome of MESSENGER’s trajectory from launch to impact. In Proceedings of the Astrodynamics Specialist Conference, American Astronautical Society (AAS 15-608), Vail, CO, USA, 9–13 August 2015. [Google Scholar]
- Sun, X.; Neumann, G.A. Calibration of the Mercury Laser Altimeter on the MESSENGER Spacecraft. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2860–2874. [Google Scholar] [CrossRef]
- Solomon, S.C.; Anderson, B.J. The MESSENGER Mission: Science and Implementation Overview. In Mercury: The View after MESSENGER; Cambridge University Press: Cambridge, UK, 2018; pp. 1–29. [Google Scholar] [CrossRef]
- Bedini, P.D.; Solomon, S.C.; Finnegan, E.J.; Calloway, A.B.; Ensor, S.L.; McNutt, R.L.; Anderson, B.J.; Prockter, L.M. MESSENGER at Mercury: A mid-term report. Acta Astronaut. 2012, 81, 369–379. [Google Scholar] [CrossRef]
- Blewett, D.T.; Chabot, N.L.; Denevi, B.W.; Ernst, C.M.; Head, J.W.; Izenberg, N.R.; Murchie, S.L.; Solomon, S.C.; Nittler, L.R.; McCoy, T.J.; et al. Hollows on Mercury: MESSENGER Evidence for Geologically Recent Volatile-Related Activity. Science 2011, 333, 1856–1859. [Google Scholar] [CrossRef] [Green Version]
- Thomas, R.J.; Rothery, D.A.; Conway, S.J.; Anand, M. Hollows on Mercury: Materials and mechanisms involved in their formation. Icarus 2014, 229, 221–235. [Google Scholar] [CrossRef] [Green Version]
- Blewett, D.T.; Ernst, C.M.; Murchie, S.L.; Vilas, F. Mercury’s Hollows. In Mercury: The View after MESSENGER; Cambridge University Press: Cambridge, UK, 2018; pp. 324–345. [Google Scholar] [CrossRef]
- Cavanaugh, J.F.; Smith, J.C.; Sun, X.; Bartels, A.E.; Ramos-Izquierdo, L.; Krebs, D.J.; McGarry, J.F.; Trunzo, R.; Novo-Gradac, A.M.; Britt, J.L.; et al. The Mercury Laser Altimeter Instrument for the MESSENGER Mission. Space Sci. Rev. 2007, 131, 451–479. [Google Scholar] [CrossRef] [Green Version]
- Solomon, S.C.; McNutt, R.L.; Gold, R.E.; Domingue, D.L. MESSENGER Mission Overview. Space Sci. Rev. 2007, 131, 3–39. [Google Scholar] [CrossRef]
- MESSENGER MLA Team. MESSENGER MLA Calibrated (CDR/RDR) Data Bundle, Version 1. 2018. Available online: https://doi.org/10.17189/1518580 (accessed on 20 July 2022).
- Zuber, M.T.; Smith, D.E.; Phillips, R.J.; Solomon, S.C.; Neumann, G.A.; Hauck, S.A., II; Peale, S.J.; Barnouin, O.S.; Head, J.W.; Johnson, C.L.; et al. Topography of the Northern Hemisphere of Mercury from MESSENGER Laser Altimetry. Science 2012, 336, 217–220. [Google Scholar] [CrossRef] [Green Version]
- MESSENGER MLA Team. MESSENGER MLA CDR/RDR Data Set Description, Version 1. Lidvid urn:nasa:pds:mess_mla_calibrated:document:mess_mla_cdr_rdr_ds::1.0. 2018. Available online: https://pds-geosciences.wustl.edu/messenger/mess-e_v_h-mla-3_4-cdr_rdr-data-v1/messmla_2001/document/mess_mla_cdr_rdr_ds.txt (accessed on 14 July 2022).
- Anderson, J.A.; Sides, S.C.; Soltesz, D.L.; Sucharski, T.L.; Becker, K.J. Modernization of the Integrated Software for Imagers and Spectrometers. In Proceedings of the 35th Lunar and Planetary Science Conference, Houston, TX, USA, 15 March 2004. Abstract #2039. [Google Scholar]
- Keszthelyi, L.; Becker, T.; Sides, S.; Barrett, J.; Cook, D.; Lambright, S.; Lee, E.; Milazzo, M.; Oyama, K.; Richie, J.; et al. Support and future vision for the Integrated Software for Imagers and Spectrometers. In Proceedings of the 44th Lunar and Planetary Science Conference, The Woodlands, TX, USA, 6–8 March 2013. Abstract #2546. [Google Scholar]
- Adoram-Kershner, L.; Berry, K.; Lee, K.; Laura, J.; Mapel, J.; Paquette, A.; Rodriguez, K.; Sanders, A.; Sides, S.; Weller, L.; et al. USGS Astrogeology/ISIS3: ISIS3.10.1 Public Release. 2020. Available online: https://zenodo.org/record/3697255 (accessed on 20 July 2022).
- Miller, S.B.; Walker, A.S. Further developments of Leica digital photogrammetric systems by Helava. ACSM/ASPRS Annu. Conv. Expo. 1993, 3, 256–263. [Google Scholar]
- Miller, S.B.; Walker, A.S. Die Entwicklung der digitalen photogrammetrischen Systeme von Leica und Helava. Z. Photogramm. Fernerkund. 1995, 63, 4–16. [Google Scholar]
- Henriksen, M.R.; Manheim, M.R.; Burns, K.N.; Seymour, P.; Speyerer, E.J.; Deran, A.; Boyd, A.K.; Howington-Kraus, E.; Rosiek, M.R.; Archinal, B.A.; et al. Extracting accurate and precise topography from LROC Narrow Angle Camera stereo observations. Icarus 2017, 283, 122–137. [Google Scholar] [CrossRef]
- Kirk, R.L.; Howington-Kraus, E.; Rosiek, M.R.; Anderson, J.A.; Archinal, B.A.; Becker, K.J.; Cook, D.A.; Galuszka, D.M.; Geissler, P.E.; Hare, T.; et al. Ultrahigh resolution topographic mapping of Mars with MRO HiRISE stereo images: Meter-scale slopes of candidate Phoenix landing sites. J. Geophys. Res. Planets 2008, 113. [Google Scholar] [CrossRef]
- Sutton, S.S.; Chojnacki, M.; McEwen, A.S.; Kirk, R.L.; Dundas, C.M.; Schaefer, E.I.; Conway, S.J.; Diniega, S.; Portyankina, G.; Landis, M.E.; et al. Revealing Active Mars with HiRISE Digital Terrain Models. Remote Sens. 2022, 14, 2403. [Google Scholar] [CrossRef]
- Fassett, C.I. Ames stereo pipeline-derived digital terrain models of Mercury from MESSENGER stereo imaging. Planet. Space Sci. 2016, 134, 19–28. [Google Scholar] [CrossRef] [Green Version]
- Ostrach, L.R.; Dundas, C.M. Topographic assessment of hollows on Mercury: Distinguishing among formation hypotheses. In Proceedings of the Lunar and Planetary Science Conference XLVIII, The Woodlands, TX, USA, 20–24 March 2017. Abstract #1656. [Google Scholar]
- Tenthoff, M.; Wohlfarth, K.; Wöhler, C. High Resolution Digital Terrain Models of Mercury. Remote Sens. 2020, 12, 3989. [Google Scholar] [CrossRef]
- Weirich, J.R.; Domingue, D.L.; Palmer, E.E.; Rodriguez, A. High-Resolution Topography and Photometric Data Cubes for Mercury and the Moon. In Proceedings of the Lunar and Planetary Science Conference LIII, The Woodlands, TX, USA, 7–11 March 2022. Abstract #1115. [Google Scholar]
- Preusker, F.; Stark, A.; Oberst, J.; Matz, K.-D.; Gwinner, K.; Roatsch, T.; Watters, T.R. Toward high-resolution global topography of Mercury from MESSENGER orbital stereo imaging: A prototype model for the H6 (Kuiper) quadrangle. Planet. Space Sci. 2017, 142, 26–37. [Google Scholar] [CrossRef] [Green Version]
- Becker, K.; Robinson, M.; Pruesker, F. MESSENGER MDIS DEM V1.0, NASA Planetary Data System. 2015. Available online: https://doi.org/10.17189/1520282 (accessed on 20 July 2022).
- Becker, K.J.; Archinal, B.A.; Hare, T.H.; Kirk, R.L.; Howington-Kraus, E.; Robinson, M.S.; Rosiek, M.R. Criteria for automated identification of stereo image pairs. In Proceedings of the Lunar and Planetary Science Conference XLVI, The Woodlands, TX, USA, 16–20 March 2015. Abstract #2703. [Google Scholar]
- McAdams, J.V.; Bryan, C.G.; Bushman, S.S.; Calloway, A.B.; Carranza, E.; Flanigan, S.H.; Kirk, M.N.; Korth, H.; Moessner, D.P.; O’Shaughnessy, D.J.; et al. Engineering MESSENGER’s grand finale at Mercury—The low-altitude hover campaign. In Proceedings of the Astrodynamics Specialist Conference, American Astronautical Society (AAS 15-634), Vail, CO, USA, 9–11 August 2015. [Google Scholar]
- Becker, K.J.; Edmundson, K.; Weller, L.; Isbell, C.; Bowman-Cisneros, E.; Speyerer, E.; Henriksen, M.; Preusker, F.; Ensor, S.; Reid, M.; et al. MESSENGER Digital Elevation Model Software Interface Specification, Version 1.6. 2017. Available online: https://pdsimage2.wr.usgs.gov/archive/mess-h-mdis-5-dem-elevation-v1.0/MESSDEM_1001/DOCUMENT/MSGR_DEM_SIS.PDF (accessed on 20 July 2022).
- Forstner, W.; Wrobel, B.; Paderes, F.; Fraser, C.S.; Dolloff, J.; Mikhail, E.M.; Rujikietgumjorn, W. Analytical photogrammetric operations. In Manual of Photogrammetry, 6th ed.; McGlone, J.C., Ed.; American Society for Photogrammetry and Remote Sensing: Bethesda, MD, USA, 2013; pp. 785–955. [Google Scholar]
- BAE Systems. SOCET SET User’s Manual; Version 5.6; BAE Systems. 2011. Available online: https://www.geospatialexploitationproducts.com/content/ (accessed on 20 July 2022).
- BAE Systems. Next-Generation Automatic Terrain Extraction (NGATE). White Paper. 2007. Available online: https://www.geospatialexploitationproducts.com/wp-content/uploads/2016/01/wp_ngate.pdf (accessed on 20 July 2022).
- Zhang, B. Towards a higher level automation in softcopy photogrammetry: NGATE and LIDAR processing in SOCET SET. In Proceedings of the GeoCue Corporation 2nd Annual Technical Exchange Conference, Nashville, TN, USA, 26–27 September 2006. [Google Scholar]
- Miller, S. Photogrammetric products. In Manual of Photogrammetry, 6th ed.; McGlone, J.C., Ed.; American Society for Photogrammetry and Remote Sensing: Bethesda, MD, USA, 2013; pp. 1009–1043. [Google Scholar]
- Warmerdam, F. The Geospatial Data Abstraction Library. In Open Source Approaches in Spatial Data Handling; Hall, G.B., Leahy, M.G., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 87–104. [Google Scholar] [CrossRef]
- Burns, K.N.; Speyerer, E.J.; Robinson, M.S.; Tran, T.; Rosiek, M.R.; Archinal, B.A.; Howington-Kraus, E.; the LROC Science Team. Digital Elevation Models and Derived Products from LROC NAC stereo observations. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 39, 483–488. [Google Scholar] [CrossRef] [Green Version]
- Beyer, R.A.; Alexandrov, O.; McMichael, S. The Ames Stereo Pipeline: NASA’s Open Source Software for Deriving and Processing Terrain Data. Earth Space Sci. 2018, 5, 537–548. [Google Scholar] [CrossRef]
- QGIS.org. QGIS Geographic Information System. QGIS Association. 2022. Available online: http://www.qgis.org (accessed on 6 June 2022).
- Jurgiel, B.; Verchere, P.; Tourigny, E.; Becerra, J. Profile Tool, v4.1.7. PANOimagen S. L. Available online: https://github.com/PANOimagen/profiletool (accessed on 20 July 2022).
- Bland, M.T.; Kirk, R.L.; Galuszka, D.M.; Mayer, D.P.; Beyer, R.A.; Fergason, R.L. How Well Do We Know Europa’s Topography? An Evaluation of the Variability in Digital Terrain Models of Europa. Remote Sens. 2021, 13, 5097. [Google Scholar] [CrossRef]
- Blewett, D.T.; Vaughan, W.M.; Xiao, Z.; Chabot, N.L.; Denevi, B.W.; Ernst, C.M.; Helbert, J.; D’Amore, M.; Maturilli, A.; Head, J.W.; et al. Mercury’s hollows: Constraints on formation and composition from analysis of geological setting and spectral reflectance. J. Geophys. Res. Planets 2013, 118, 1013–1032. [Google Scholar] [CrossRef] [Green Version]
- Blewett, D.T.; Stadermann, A.C.; Susorney, H.C.; Ernst, C.M.; Xiao, Z.; Chabot, N.L.; Denevi, B.W.; Murchie, S.L.; McCubbin, F.M.; Kinczyk, M.J.; et al. Analysis of MESSENGER high-resolution images of Mercury’s hollows and implications for hollow formation. J. Geophys. Res. Planets 2016, 121, 1798–1813. [Google Scholar] [CrossRef]
- Vaughan, W.M.; Helbert, J.; Blewett, D.T.; Head, J.W.; Murchie, S.L.; Gwinner, K.; McCoy, T.J.; Solomon, S.C. Hollow-forming layers in impact craters on Mercury: Massive sulfide or chloride deposits formed by impact melt differentiation? In Proceedings of the Lunar and Planetary Science Conference XLIII, The Woodlands, TX, USA, 7–11 March 2022. Abstract #1187. [Google Scholar]
- Phillips, M.S.; Moersch, J.E.; Viviano, C.E.; Emery, J.P. The lifecycle of hollows on Mercury: An evaluation of candidate volatile phases and a novel model of formation. Icarus 2021, 359, 114306. [Google Scholar] [CrossRef]
- Benkhoff, J.; Murakami, G.; Baumjohann, W.; Besse, S.; Bunce, E.; Casale, M.; Cremosese, G.; Glassmeier, K.-H.; Hayakawa, H.; Heyner, D.; et al. BepiColombo—Mission Overview and Science Goals. Space Sci. Rev. 2021, 217, 90. [Google Scholar] [CrossRef]
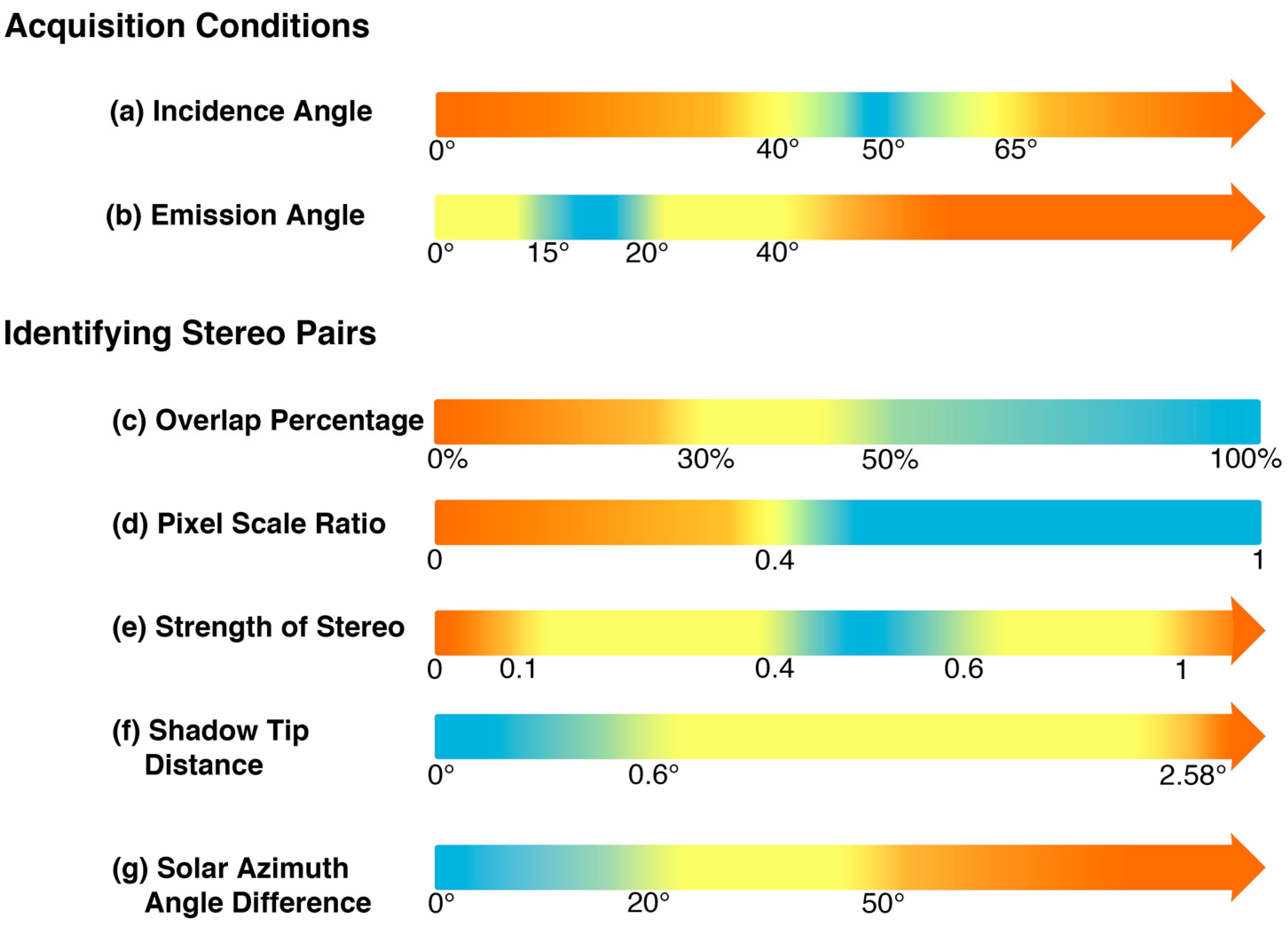



| Acquisition Conditions | Identifying Stereo Pairs | ||||||
|---|---|---|---|---|---|---|---|
| Incidence Angle (°) | Emission Angle (°) | Overlap Percentage | Pixel Scale Ratio | Strength of Stereo | Shadow Tip Distance (°) | Solar Az. Angle Diff. (°) | |
| Minimum | 30 | 1 | 0.45 | 0.40 | 0.37 | 0.00 | 0.00 |
| Maximum | 64 | 50 | 100 | 0.99 | 1.39 | 0.02 | 32.65 |
| Average | 45 | 26 | 56.86 | 0.66 | 0.80 | 0.15 | 8.99 |
| Median | 44 | 32 | 51.81 | 0.68 | 0.72 | 0.11 | 6.60 |
| MST Parameters | Values |
|---|---|
| Camera ΔX | 100 m |
| Camera ΔY | 100 m |
| Camera ΔZ | 10 m |
| Attitude ΔOmega * | 0.1° |
| Attitude Δphi * | 0.1° |
| Attitude Δkappa * | 0.1° |
| Site Name | # of Stereo Pairs | Center Latitude, Longitude (°N, °E) | DEM Mosaic Pixel Scale (m) | Relative Linear (Vertical) Error (m) | # of MLA Points for Comparison | MLA Mean (Vertical) Offset (m) | MLA Standard Deviation (m) |
|---|---|---|---|---|---|---|---|
| Catullus Crater * | 1 | 21.88°, 292.5° | 84 | 84 | 777 | −255 | 188 |
| Cunningham Crater | 9 | 30.40°, 157.0° | 105 | 85 | 127 | 2 | 58 |
| Degas Crater | 1 | 36.86°, 232.6° | 97 | 70 | 125 | −1 | 109 |
| Scarp in NW Rembrandt Basin | 1 | −31.16°, 82.5° | 500 | 383 | - | - | - |
| Kertész Crater | 2 | 31.45°, 146.3° | 120 | 98 | 27 | −9 | 51 |
| Kuiper Crater | 1 | −11.3°, 329.1° | 270 | 161 | - | - | - |
| Paramour Rupes * | 3 | −5.07°, 145.1° | 450 | 261 | 138 | −5 | 185 |
| Raditladi Hollows | 3 | 15.20°, 120.2° | 180 | 137 | 154 | −44 | 52 |
| Sander Crater | 36 | 42.50°, 154.7° | 162 | 70 | 756 | −44 | 65 |
| Dataset | Method | Resolution Range (m/px) | Number of DEMs | ASU Site (# DEMs from Dataset That Overlap) |
|---|---|---|---|---|
| Manheim et al. (this study) (“ASU”) | SOCET SET | 78–500 | 9 mosaics; 57 individual DEMs | - |
| Fassett [24] (“FAS”) | Ames Stereo Pipeline | 45–245 | 96 | Catullus (2), Degas (1), Raditladi (3), Sander (1) |
| Ostrach and Dundas [25] (“OST”) | SOCET SET | 25–120 | 11 | Degas (1), Sander (1), Kertész (2) |
| Preusker et al. [28] (“PRU”) | Custom stereophotogrammetry | 222 | 4 quadrangles | Catullus (1), Degas (1), Kuiper (1) |
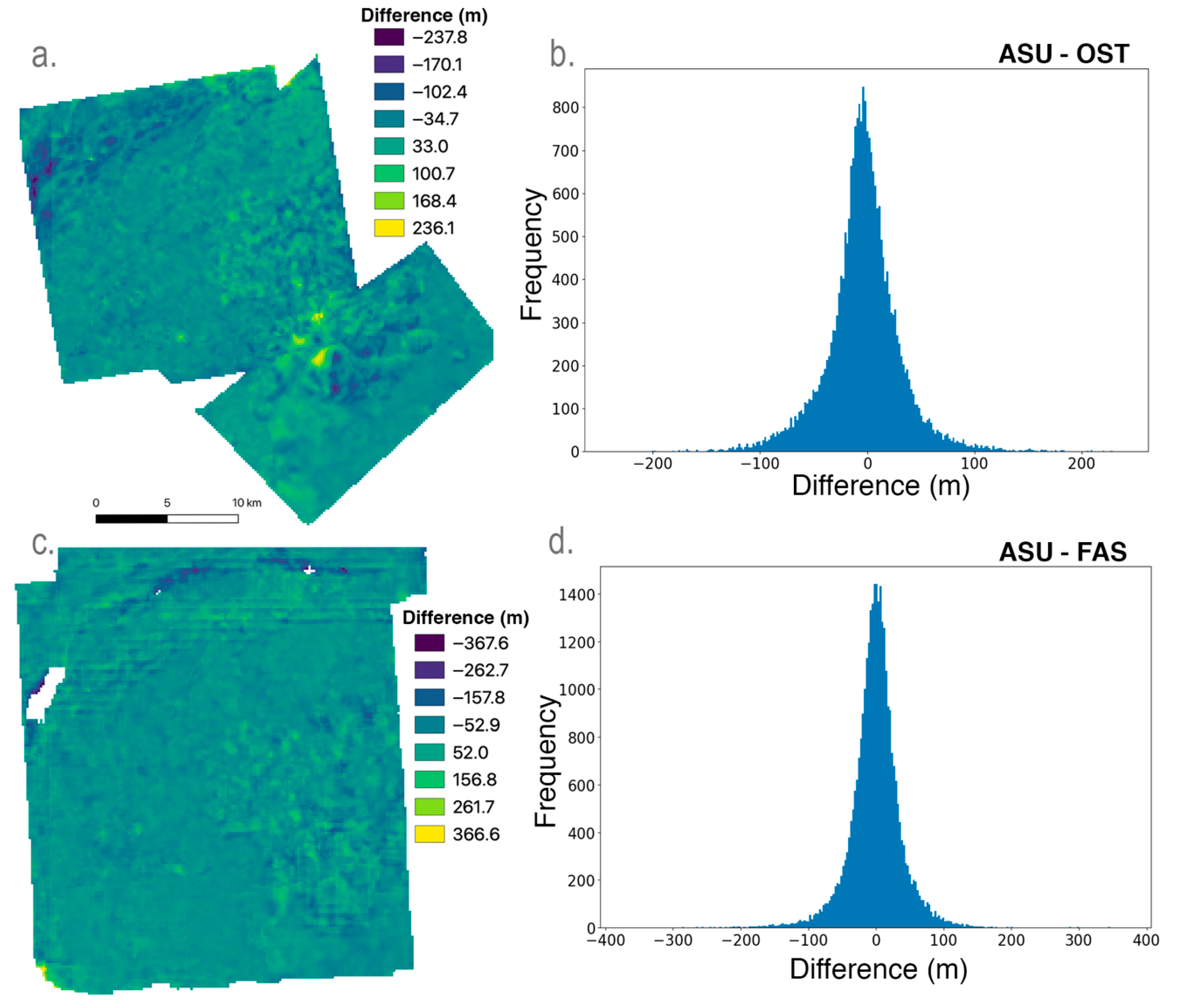
| ASU DEM | Subtracted DEM | Standard Deviation | Mean Diff. (m) | Std Dev. of Abs. Diff. | Mean Abs. Diff. | Minimum (m) | Maximum (m) |
|---|---|---|---|---|---|---|---|
| Catullus | FAS a | 39.97 | 2.31 | 29.51 | 27.06 | −417.34 | 284.83 |
| Catullus | FAS b | 62.27 | −0.06 | 50.61 | 36.29 | −873.00 | 352.96 |
| Catullus | PRU | 56.83 | −6.71 | 41.25 | 39.66 | −404.20 | 263.67 |
| Degas | FAS | 17.78 | −0.18 | 13.39 | 11.69 | −161.41 | 123.54 |
| Degas | OST | 19.77 | 0.81 | 14.51 | 13.46 | −207.45 | 185.70 |
| Degas | PRU | 84.62 | −10.45 | 66.54 | 53.31 | −571.25 | 430.98 |
| Kertész | OST c | 20.23 | 0.22 | 14.67 | 13.93 | −193.86 | 201.48 |
| Kertész | OST d | 37.57 | −2.30 | 28.82 | 24.20 | −256.25 | 315.43 |
| Kuiper | DLR | 55.77 | 0.93 | 37.21 | 41.55 | −552.13 | 620.03 |
| Raditladi | FAS e | 85.43 | 19.87 | 59.39 | 64.55 | −397.21 | 559.83 |
| Raditladi | FAS f | 31.30 | 2.46 | 22.49 | 21.90 | −248.57 | 246.98 |
| Raditladi | FAS g | 31.79 | 2.97 | 23.24 | 21.89 | −256.89 | 594.35 |
| Sander | FAS | 38.54 | −0.60 | 28.07 | 26.42 | −367.55 | 366.59 |
| Sander | OST | 35.70 | −3.60 | 25.75 | 24.99 | −237.77 | 236.10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manheim, M.R.; Henriksen, M.R.; Robinson, M.S.; Kerner, H.R.; Karas, B.A.; Becker, K.J.; Chojnacki, M.; Sutton, S.S.; Blewett, D.T. High-Resolution Regional Digital Elevation Models and Derived Products from MESSENGER MDIS Images. Remote Sens. 2022, 14, 3564. https://doi.org/10.3390/rs14153564
Manheim MR, Henriksen MR, Robinson MS, Kerner HR, Karas BA, Becker KJ, Chojnacki M, Sutton SS, Blewett DT. High-Resolution Regional Digital Elevation Models and Derived Products from MESSENGER MDIS Images. Remote Sensing. 2022; 14(15):3564. https://doi.org/10.3390/rs14153564
Chicago/Turabian StyleManheim, Madeleine R., Megan R. Henriksen, Mark S. Robinson, Hannah R. Kerner, Bradley A. Karas, Kris J. Becker, Matthew Chojnacki, Sarah S. Sutton, and David T. Blewett. 2022. "High-Resolution Regional Digital Elevation Models and Derived Products from MESSENGER MDIS Images" Remote Sensing 14, no. 15: 3564. https://doi.org/10.3390/rs14153564
APA StyleManheim, M. R., Henriksen, M. R., Robinson, M. S., Kerner, H. R., Karas, B. A., Becker, K. J., Chojnacki, M., Sutton, S. S., & Blewett, D. T. (2022). High-Resolution Regional Digital Elevation Models and Derived Products from MESSENGER MDIS Images. Remote Sensing, 14(15), 3564. https://doi.org/10.3390/rs14153564






