Deriving River Discharge Using Remotely Sensed Water Surface Characteristics and Satellite Altimetry in the Mississippi River Basin
Abstract
1. Introduction
2. Materials and Methods
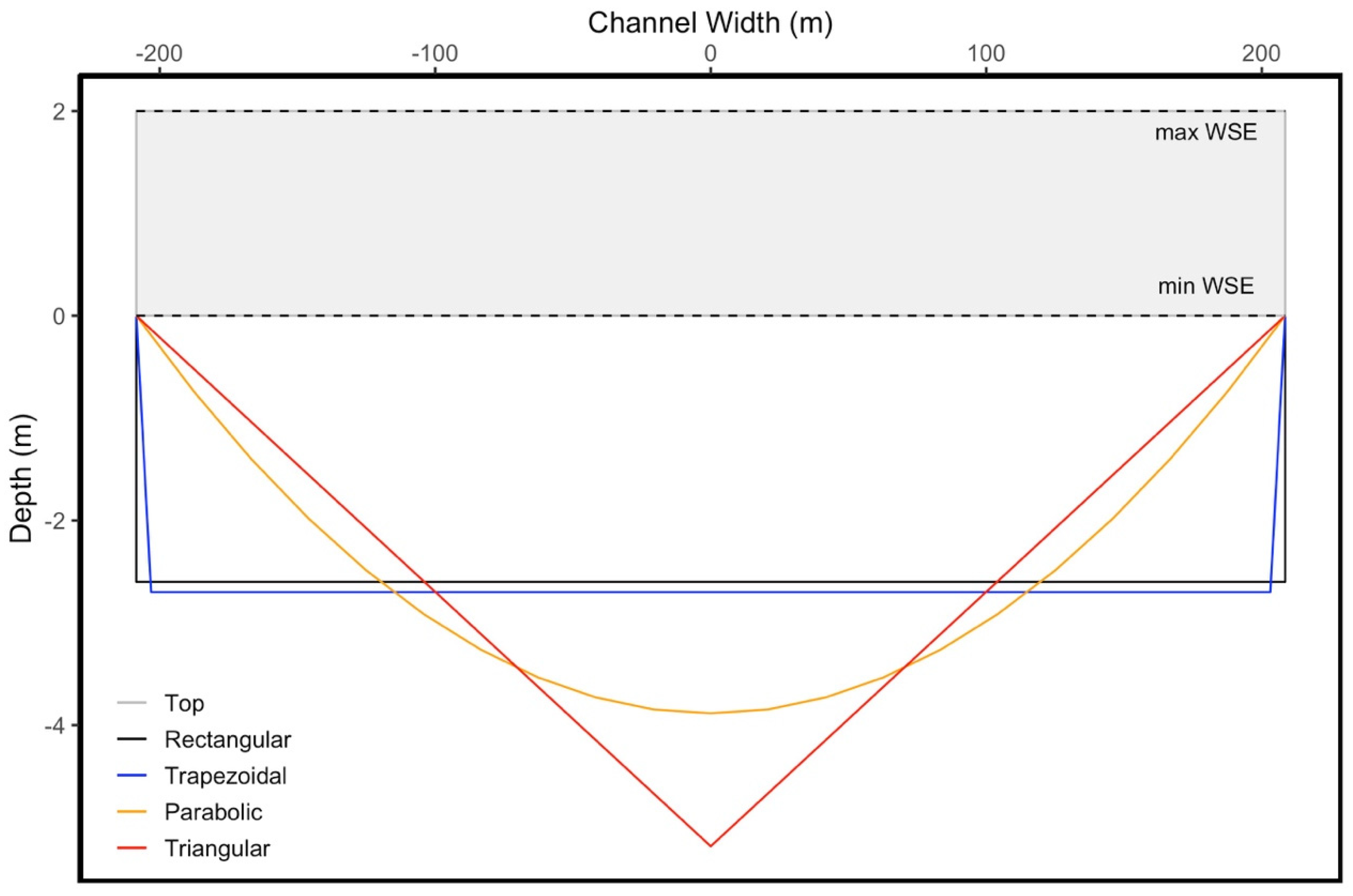
2.1. Estimation of River Discharge
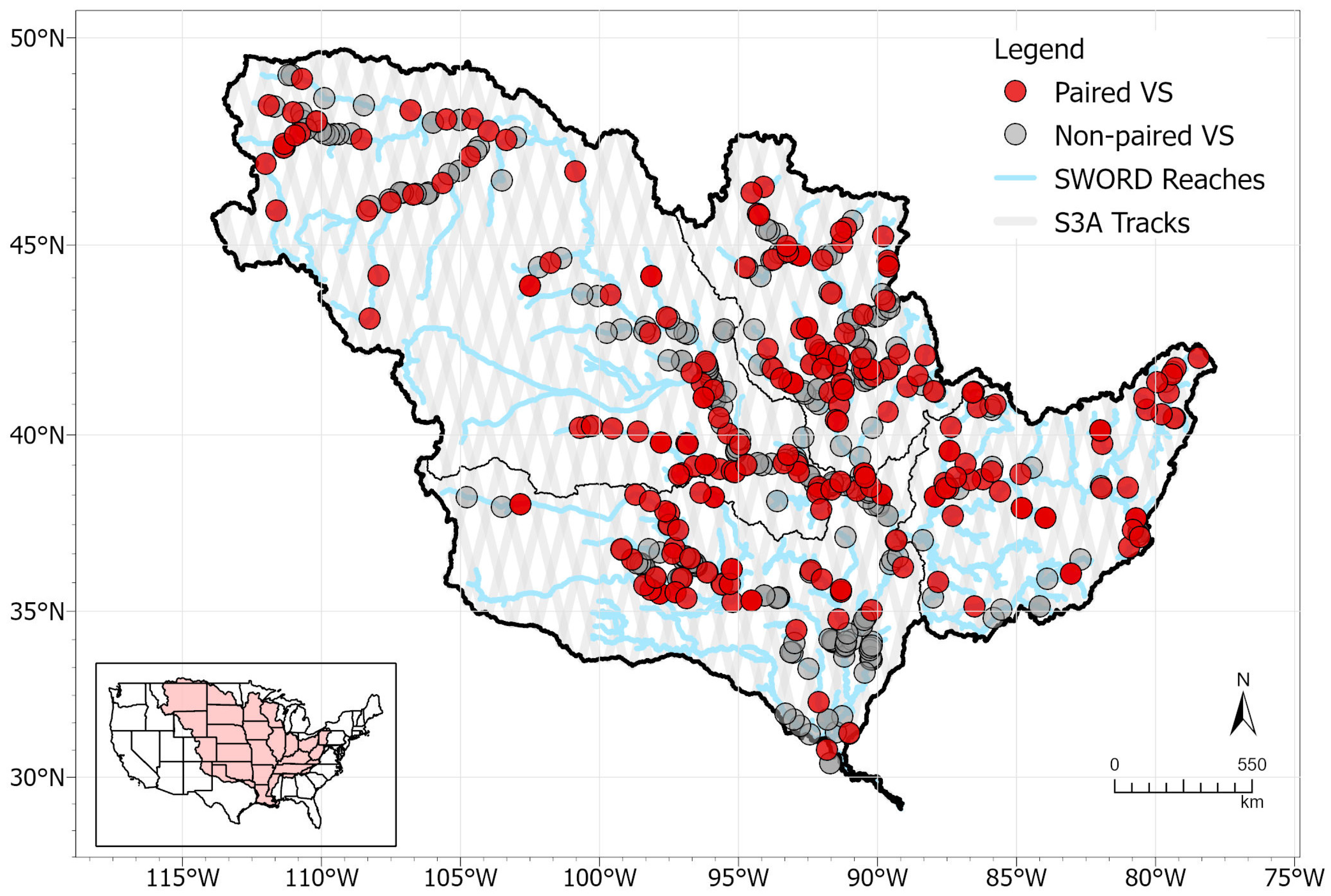
2.2. In Situ Data
2.3. Remote Sensing Data
2.3.1. Satellite Altimetry
2.3.2. SWOT River Database (SWORD)
2.3.3. Global Precipitation Measurement (GPM)
2.3.4. GRACE Total Water Storage Anomalies (TWSA)
2.4. Discharge Estimation and Parameter Optimization
2.5. Assessing the Discharge Method
3. Results
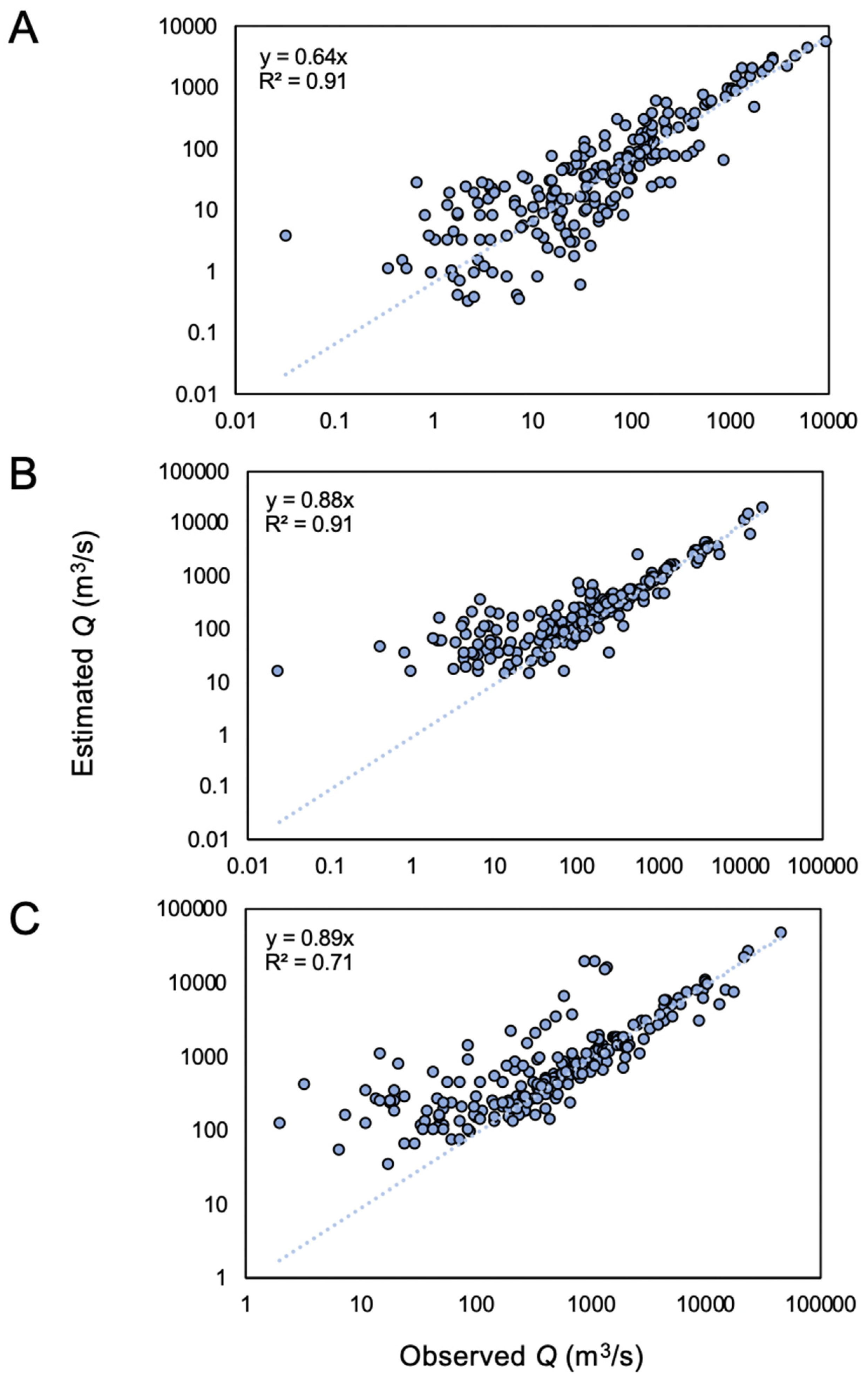
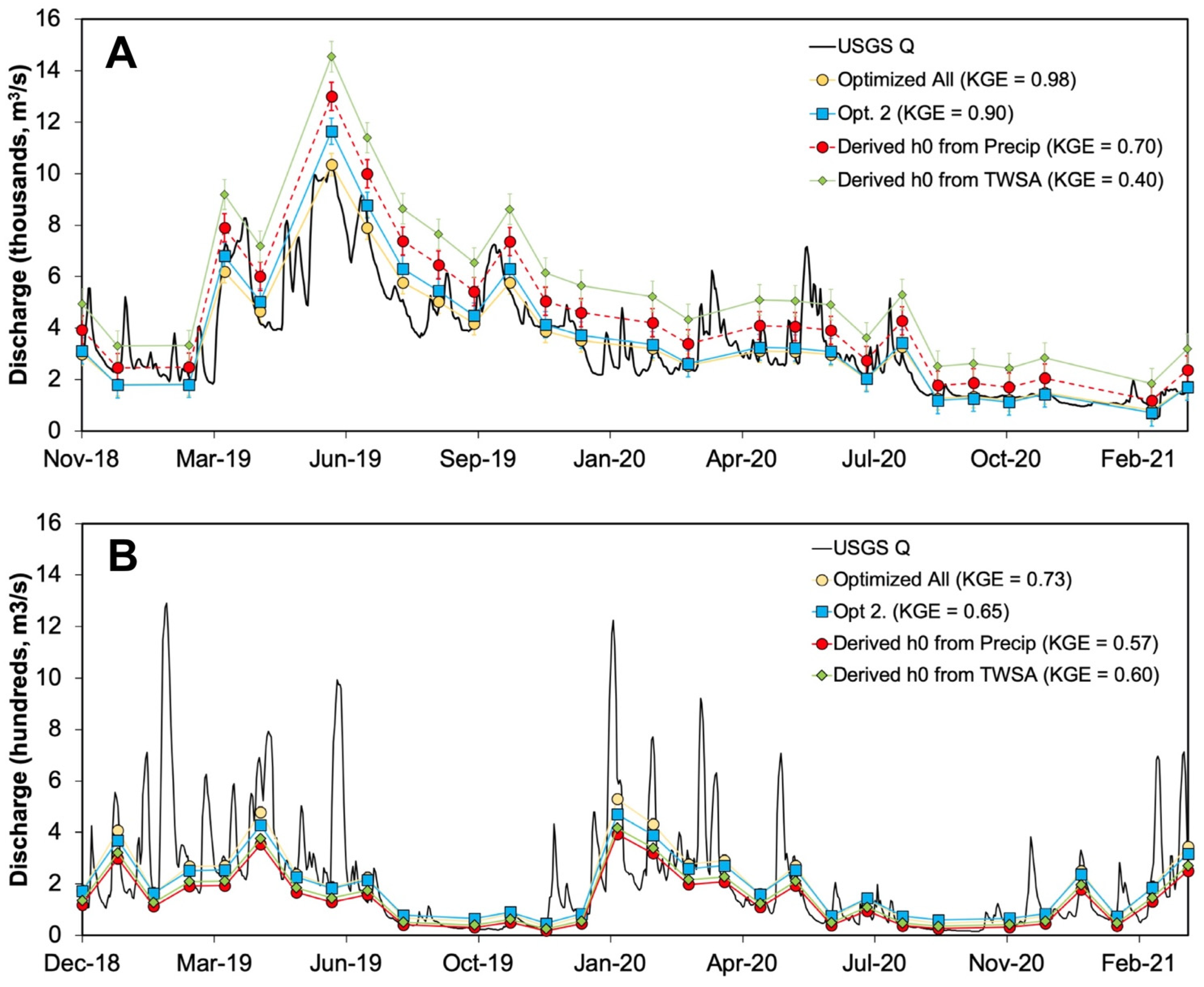
3.1. Results of Estimation Methods
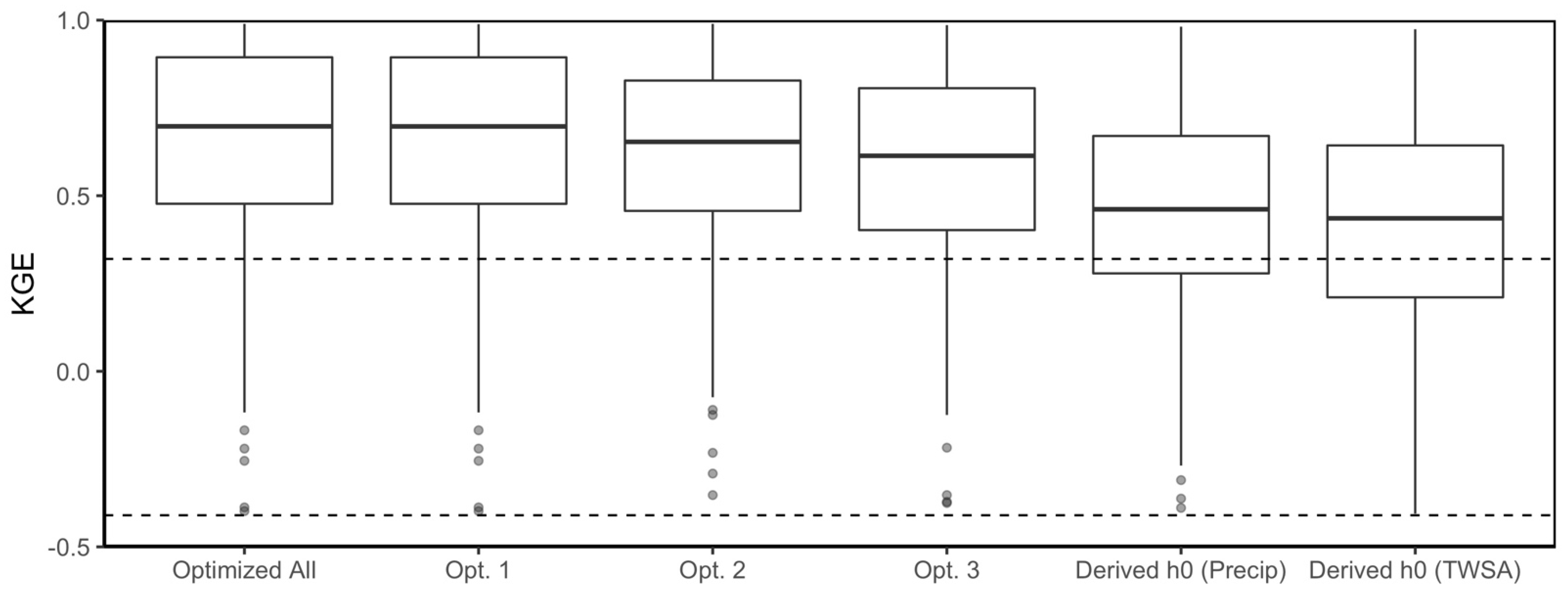
3.2. Performance of Channel Form
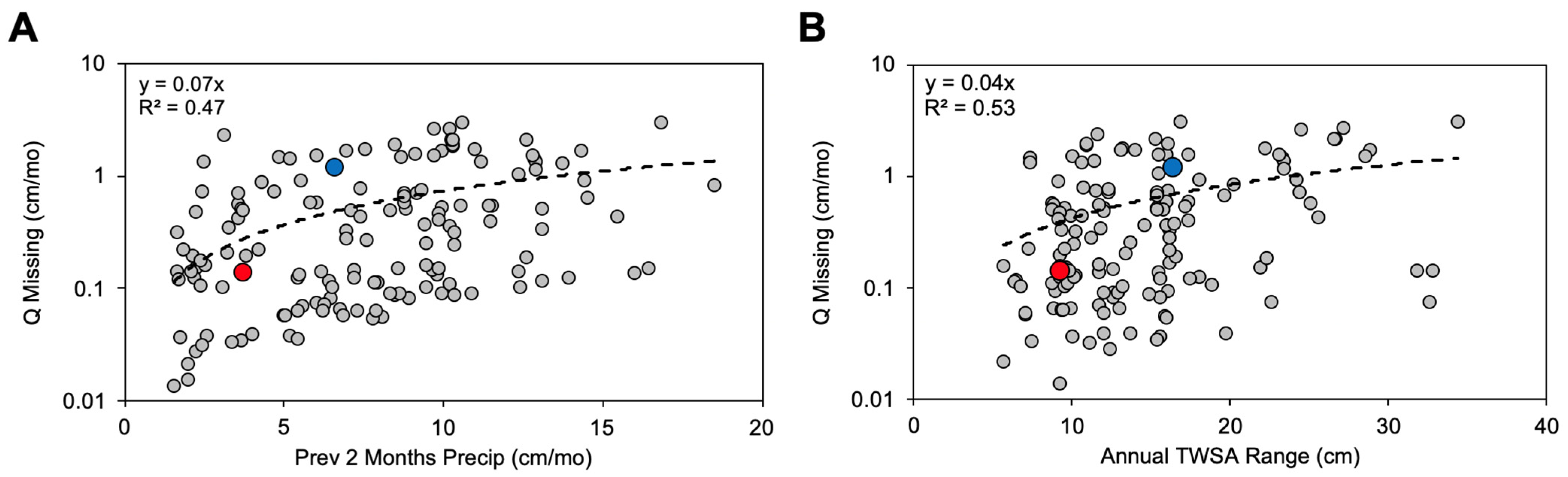
3.3. Using GPM Precipitation and GRACE TWSA for Estimating Q in Ungauged Locations
4. Discussion
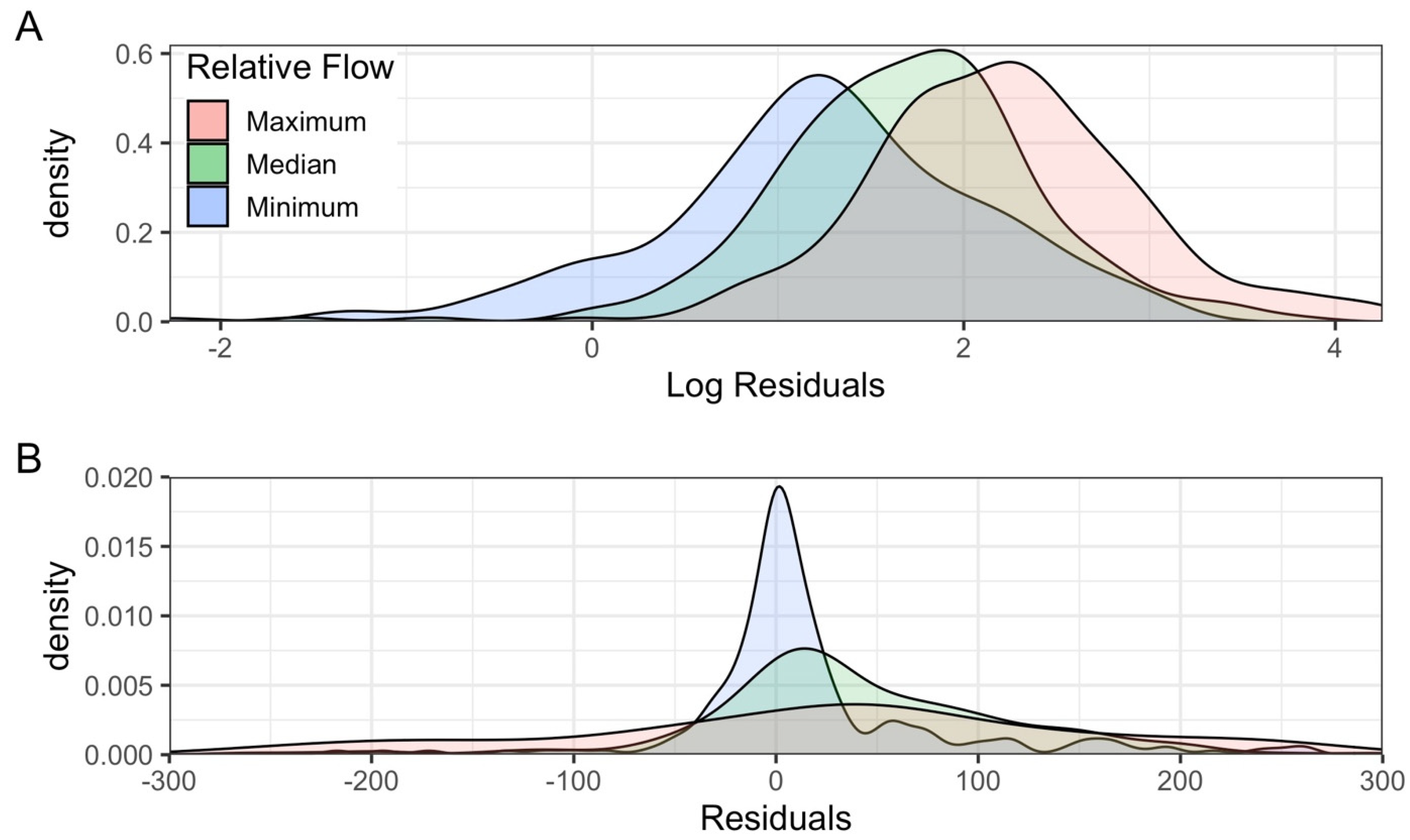
4.1. Sources of Bias in the Calculated Discharge
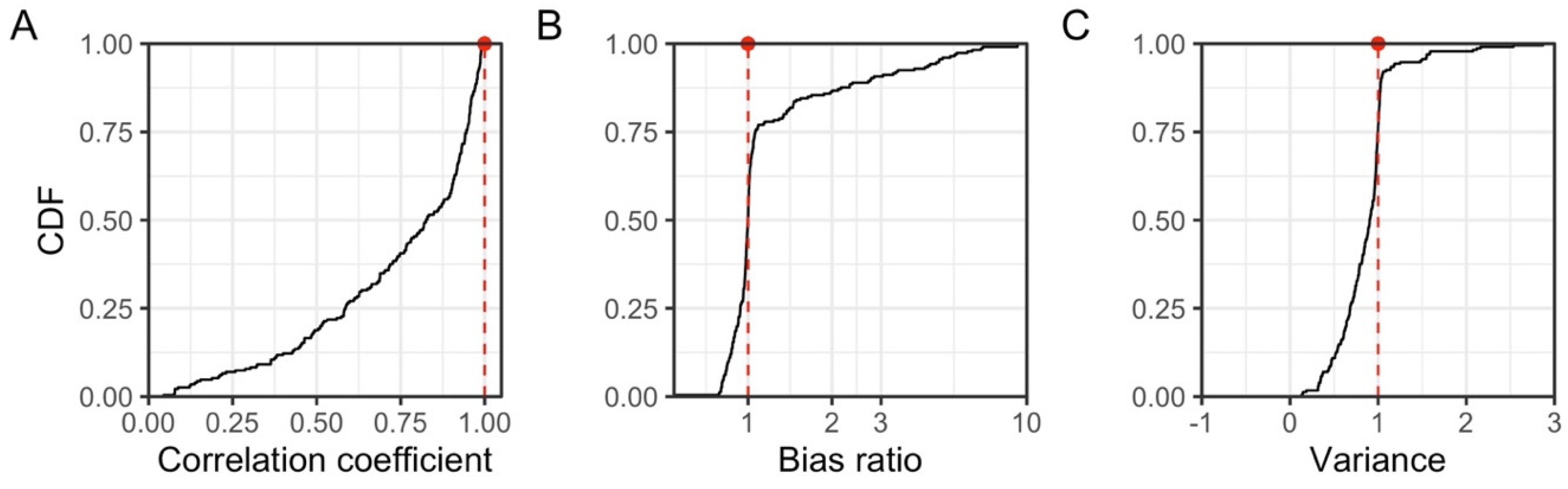
4.2. Uncertainty
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Scherer, D.; Schwatke, C.; Dettmering, D.; Seitz, F. Long-Term Discharge Estimation for the Lower Mississippi River Using Satellite Altimetry and Remote Sensing Images. Remote Sens. 2020, 12, 2693. [Google Scholar] [CrossRef]
- Bjerklie, D.M. Estimating the bankfull velocity and discharge for rivers using remotely sensed river morphology information. J. Hydrol. 2007, 341, 144–155. [Google Scholar] [CrossRef]
- Nickles, C.; Beighley, E.; Feng, D. The Applicability of SWOT’s Non-Uniform Space–Time Sampling in Hydrologic Model Calibration. Remote Sens. 2020, 12, 3241. [Google Scholar] [CrossRef]
- Pavelsky, T.M.; Durand, M.T.; Andreadis, K.M.; Beighley, E.; Paiva, R.; Allen, G.H.; Miller, Z.F. Assessing the potential global extent of SWOT river discharge observations. J. Hydrol. 2014, 519, 1516–1525. [Google Scholar] [CrossRef]
- Gleason, C.J.; Wada, Y.; Wang, J. A Hybrid of Optical Remote Sensing and Hydrological Modeling Improves Water Balance Estimation. J. Adv. Model. Earth Syst. 2018, 10, 2–17. [Google Scholar] [CrossRef]
- The Global Runoff Data Centre. Koblenz, Germany. Available online: https://www.bafg.de/GRDC/EN/Home/homepage_node.html (accessed on 12 June 2022).
- Maidment, D.R. Open Water Data in Space and Time. JAWRA J. Am. Water Resour. Assoc. 2016, 52, 816–824. [Google Scholar] [CrossRef]
- Boulomytis, V.; Zuffo, A.; Filho, J.G.D.; Alam Imteaz, M. Estimation and calibration of Manning’s roughness coefficients for ungauged watersheds on coastal floodplains. Int. J. River Basin Manag. 2016, 15, 199–206. [Google Scholar] [CrossRef]
- Sneeuw, N.; Lorenz, C.; Devaraju, B.; Tourian, M.J.; Riegger, J.; Kunstmann, H.; Bárdossy, A. Estimating Runoff Using Hydro-Geodetic Approaches. Surv. Geophys. 2014, 35, 1333–1359. [Google Scholar] [CrossRef]
- Zakharova, E.; Nielsen, K.; Kamenev, G.; Kouraev, A. River discharge estimation from radar altimetry: Assessment of satellite performance, river scales and methods. J. Hydrol. 2020, 583, 124561. [Google Scholar] [CrossRef]
- Dixon, B.; Earls, J. Effects of urbanization on streamflow using SWAT with real and simulated meteorological data. Appl. Geogr. 2012, 35, 174–190. [Google Scholar] [CrossRef]
- Faramarzi, M.; Abbaspour, K.C.; Vaghefi, S.A.; Farzaneh, M.R.; Zehnder, A.J.; Srinivasan, R.; Yang, H. Modeling impacts of climate change on freshwater availability in Africa. J. Hydrol. 2013, 480, 85–101. [Google Scholar] [CrossRef]
- Ferreira, V.G.; Gong, Z.; He, X.; Zhang, Y.; Andam-Akorful, S.A. Estimating total discharge in the yangtze river basin using satellite-based observations. Remote Sens. 2013, 5, 3415–3430. [Google Scholar] [CrossRef]
- Tourian, M.J.; Sneeuw, N.; Bárdossy, A. A quantile function approach to discharge estimation from satellite altimetry (ENVISAT). Water Resour. Res. 2013, 49, 4174–4186. [Google Scholar] [CrossRef]
- Tourian, M.J.; Schwatke, C.; Sneeuw, N. River discharge estimation at daily resolution from satellite altimetry over an entire river basin. J. Hydrol. 2017, 546, 230–247. [Google Scholar] [CrossRef]
- Tourian, M.J.; Elmi, O.; Mohammadnejad, A.; Sneeuw, N. Estimating River Depth from SWOT-Type Observables Obtained by Satellite Altimetry and Imagery. Water 2017, 9, 753. [Google Scholar] [CrossRef]
- Abdalla, S.; Kolahchi, A.A.; Ablain, M.; Adusumilli, S.; Bhowmick, S.A.; Alou-Font, E.; Amarouche, L.; Andersen, O.B.; Antich, H.; Aouf, L.; et al. Altimetry for the future: Building on 25 years of progress. Adv. Space Res. 2021, 68, 319–363. [Google Scholar] [CrossRef]
- Revel, M.; Ikeshima, D.; Yamazaki, D.; Kanae, S. A Framework for Estimating Global-Scale River Discharge by Assimilating Satellite Altimetry. Water Resour. Res. 2021, 57. [Google Scholar] [CrossRef]
- Fekete, B.M.; Vörösmarty, C.J. The Current Status of Global River Discharge Monitoring and Potential New Technologies Complementing Traditional Discharge Measurements; Predict. Ungauged Basins PUB Kick-off (Proceedings PUB Kick-off Meet. held Bras. Novemb. 2002), IAHS Publ. no. 309. November 2007, pp. 129–136. Available online: https://www.researchgate.net/profile/Balazs-Fekete-5/publication/228607122_The_current_status_of_global_river_discharge_monitoring_and_potential_new_technologies_complementing_traditional_discharge_measurements/links/00b7d521cca70a8c3d000000/The-current-status-of-global-river-discharge-monitoring-and-potential-new-technologies-complementing-traditional-discharge-measurements.pdf (accessed on 20 July 2022).
- Lamine, B.; Ferreira, V.; Yang, Y.; Ndehedehe, C.; He, X. Estimation of the Niger River cross-section and discharge from remotely-sensed products. J. Hydrol. Reg. Stud. 2021, 36, 100862. [Google Scholar] [CrossRef]
- Bjerklie, D.M.; Birkett, C.M.; Jones, J.W.; Carabajal, C.; Rover, J.; Fulton, J.; Garambois, P.-A. Satellite remote sensing estimation of river discharge: Application to the Yukon River Alaska. J. Hydrol. 2018, 561, 1000–1018. [Google Scholar] [CrossRef]
- Biancamaria, S.; Lettenmaier, D.P.; Pavelsky, T.M. The SWOT Mission and Its Capabilities for Land Hydrology. Surv. Geophys. 2016, 37, 307–337. [Google Scholar] [CrossRef]
- Te Chow, V. Open Channel Hydraulics; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Kim, D.; Yu, H.; Lee, H.; Beighley, E.; Durand, M.; Alsdorf, D.E.; Hwang, E. Ensemble learning regression for estimating river discharges using satellite altimetry data: Central Congo River as a Test-bed. Remote Sens. Environ. 2018, 221, 741–755. [Google Scholar] [CrossRef]
- Das, B.C. Modeling of most efficient channel form: A quantitative approach. Model. Earth Syst. Environ. 2015, 1, 1–9. [Google Scholar] [CrossRef][Green Version]
- Bjerklie, D.M.; Fulton, J.W.; Dingman, S.L.; Canova, M.G.; Minear, J.T.; Moramarco, T. Fundamental Hydraulics of Cross Sections in Natural Rivers: Preliminary Analysis of a Large Data Set of Acoustic Doppler Flow Measurements. Water Resour. Res. 2020, 56. [Google Scholar] [CrossRef]
- Altenau, E.H.; Pavelsky, T.M.; Durand, M.T.; Yang, X.; Frasson, R.P.D.M.; Bendezu, L. The Surface Water and Ocean Topography (SWOT) Mission River Database (SWORD): A Global River Network for Satellite Data Products. Water Resour. Res. 2021, 57. [Google Scholar] [CrossRef]
- Zhang, X.; Jiang, L.; Kittel, C.M.M.; Yao, Z.; Nielsen, K.; Liu, Z.; Wang, R.; Liu, J.; Andersen, O.B.; Bauer-Gottwein, P. On the Performance of Sentinel-3 Altimetry Over New Reservoirs: Approaches to Determine Onboard A Priori Elevation. Geophys. Res. Lett. 2020, 47. [Google Scholar] [CrossRef]
- Allen, G.H.; Pavelsky, T.M. Global extent of rivers and streams. Science 2018, 361, 585–588. [Google Scholar] [CrossRef] [PubMed]
- Yamazaki, D.; Ikeshima, D.; Sosa, J.; Bates, P.D.; Allen, G.H.; Pavelsky, T.M. MERIT Hydro: A High-Resolution Global Hydrography Map Based on Latest Topography Dataset. Water Resour. Res. 2019, 55, 5053–5073. [Google Scholar] [CrossRef]
- Skofronick-Jackson, G.; Kirschbaum, D.; Petersen, W.; Huffman, G.; Kidd, C.; Stocker, E.; Kakar, R. The Global Precipitation Measurement (GPM) mission’s scientific achievements and societal contributions: Reviewing four years of advanced rain and snow observations. Q. J. R. Meteorol. Soc. 2018, 144, 27–48. [Google Scholar] [CrossRef]
- Huffman, J.; Stocker, G.J.; Bolvin, E.F.; Nelkin, D.T.; Tan, E.J. GPM IMERG Final Precipitation L3 1 month 0.1 degree × 0.1 degree V06,” Greenbelt, MD, Goddard Earth Sciences Data and Information Services Center (GES DISC). 2019. Available online: https://catalog.data.gov/dataset/gpm-imerg-final-precipitation-l3-1-month-0-1-degree-x-0-1-degree-v06-gpm-3imergm-at-ges-di (accessed on 20 July 2022).
- Macedo, H.E.; Beighley, R.E.; David, C.H.; Reager, J.T. Using GRACE in a streamflow recession to determine drainable water storage in the Mississippi River basin. Hydrol. Earth Syst. Sci. 2019, 23, 3269–3277. [Google Scholar] [CrossRef]
- Sun, A.Y.; Scanlon, B.R.; AghaKouchak, A.; Zhang, Z. Using GRACE Satellite Gravimetry for Assessing Large-Scale Hydrologic Extremes. Remote Sens. 2017, 9, 1287. [Google Scholar] [CrossRef]
- Knoben, W.J.M.; Freer, J.E.; Woods, R.A. Technical note: Inherent benchmark or not? Comparing Nash–Sutcliffe and Kling–Gupta efficiency scores. Hydrol. Earth Syst. Sci. 2019, 23, 4323–4331. [Google Scholar] [CrossRef]
- Nickles, C.; Beighley, E.; Zhao, Y.; Durand, M.; David, C.; Lee, H. How Does the Unique Space-Time Sampling of the SWOT Mission Influence River Discharge Series Characteristics? Geophys. Res. Lett. 2019, 46, 8154–8161. [Google Scholar] [CrossRef]
- Maritan, A.; Rinaldo, A.; Rigon, R.; Giacometti, A.; Rodríguez-Iturbe, I. Scaling laws for river networks. Phys. Rev. E 1996, 53, 1510–1515. [Google Scholar] [CrossRef]
- Tavakoly, A.A.; Snow, A.D.; David, C.H.; Follum, M.L.; Maidment, D.R.; Yang, Z.-L. Continental-Scale River Flow Modeling of the Mississippi River Basin Using High-Resolution NHDPlus Dataset. JAWRA J. Am. Water Resour. Assoc. 2016, 53, 258–279. [Google Scholar] [CrossRef]
- Grannemann, N.G.; Sharp, J.M. Alluvial hydrogeology of the lower Missouri River valley. J. Hydrol. 1979, 40, 85–99. [Google Scholar] [CrossRef]
- Lin, P.; Pan, M.; Beck, H.E.; Yang, Y.; Yamazaki, D.; Frasson, R.; David, C.H.; Durand, M.; Pavelsky, T.M.; Allen, G.H.; et al. Global Reconstruction of Naturalized River Flows at 2.94 Million Reaches. Water Resour. Res. 2019, 55, 6499–6516. [Google Scholar] [CrossRef]
- Harrigan, S.; Zsoter, E.; Alfieri, L.; Prudhomme, C.; Salamon, P.; Wetterhall, F.; Barnard, C.; Hannah Cloke, H.; Pappenberger, F. GloFAS-ERA5 operational global river discharge reanalysis 1979–Present. Earth Syst. Sci. Data 2020, 12, 2043–2060. [Google Scholar] [CrossRef]
- Hydroweb Product User Manual: Timeseries Specified by LEGOS and Computed by CLS on Behalf of CNES. 2021. Available online: https://www.theia-land.fr/wp-content/uploads/2021/06/Handbook_Hydroweb-V2.1.pdf (accessed on 20 July 2022).
- Bjerklie, D.M.; Dingman, S.L.; Vorosmarty, C.J.; Bolster, C.H.; Congalton, R.G. Evaluating the potential for measuring river discharge from space. J. Hydrol. 2003, 278, 17–38. [Google Scholar] [CrossRef]
- Simeonov, J.A.; Holland, K.T.; Anderson, S.P. River Discharge and Bathymetry Estimation from Inversion of Surface Currents and Water Surface Elevation Observations. J. Atmospheric Ocean. Technol. 2019, 36, 69–86. [Google Scholar] [CrossRef]
- Larnier, K.; Monnier, J.; Garambois, P.-A.; Verley, J. River discharge and bathymetry estimation from SWOT altimetry measurements. Inverse Probl. Sci. Eng. 2020, 29, 759–789. [Google Scholar] [CrossRef]

| Method | Optimized Parameters | Constant Parameters |
|---|---|---|
| Optimized All | shape, n, h0 | - |
| Opt. 1 | n, h0 | shape |
| Opt. 2 | shape, h0 | n |
| Opt. 3 | h0 | shape, n |
| Derived h0 (GPM precip.) | h0 | shape, n |
| Derived h0 (GRACE TWSA) | h0 | shape, n |
| Method | KGE > −0.41 | KGE > 0.32 |
|---|---|---|
| Optimized All | 87 | 71 |
| Opt. 1 | 87 | 71 |
| Opt. 2 | 75 | 63 |
| Opt. 3 | 73 | 60 |
| Derived h0 (GPM precip.) | 66 | 47 |
| Derived h0 (GRACE TWSA) | 65 | 42 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gehring, J.; Duvvuri, B.; Beighley, E. Deriving River Discharge Using Remotely Sensed Water Surface Characteristics and Satellite Altimetry in the Mississippi River Basin. Remote Sens. 2022, 14, 3541. https://doi.org/10.3390/rs14153541
Gehring J, Duvvuri B, Beighley E. Deriving River Discharge Using Remotely Sensed Water Surface Characteristics and Satellite Altimetry in the Mississippi River Basin. Remote Sensing. 2022; 14(15):3541. https://doi.org/10.3390/rs14153541
Chicago/Turabian StyleGehring, Jaclyn, Bhavya Duvvuri, and Edward Beighley. 2022. "Deriving River Discharge Using Remotely Sensed Water Surface Characteristics and Satellite Altimetry in the Mississippi River Basin" Remote Sensing 14, no. 15: 3541. https://doi.org/10.3390/rs14153541
APA StyleGehring, J., Duvvuri, B., & Beighley, E. (2022). Deriving River Discharge Using Remotely Sensed Water Surface Characteristics and Satellite Altimetry in the Mississippi River Basin. Remote Sensing, 14(15), 3541. https://doi.org/10.3390/rs14153541







