Reflective Tomography Lidar Image Reconstruction for Long Distance Non-Cooperative Target

Abstract

In the long-distance space target detection, the technique of laser reflection tomography (LRT) shows great power and attracts more attention for further study and real use. However, space targets are often non-cooperative, and normally a 360° complete view of reflection projections cannot be obtained. Therefore, this article firstly introduces an improved LRT system design with more advanced laser equipment for long-distance non-cooperative detection to ensure the high quality of the lidar beam and the lidar projection data. Then, the LRT image reconstruction is proposed and focused on the laser image reconstruction method utilizing the total variation (TV) minimization approach based on the sparse algebraic reconstruction technique (ART) model, in order to reconstruct the laser image in a sparse or incomplete view of projections. At last, comparative experiments with the system are performed to validate the advantages of this method with the LRT system. In both near and far field experiments, the effectiveness and superiority of the proposed method are verified for different types of projection data through comparison to typical methods.

1. Introduction

With the rapid development of aerospace science and technology, space target detection and identification have become a hot topic. Reflective tomography lidar can overcome the resolution limitation with little influence from the external environment, especially for targets in the dark background, such as space satellites and debris, which has been proved to be a new lidar system with long distance and high resolution.

Developed from computed tomography (CT), the concept of laser reflective tomography (LRT) was firstly introduced in 1988 by Parker et al. [1] and then some reflection tomography lidar imaging experiments were carried out. In recent years, the research of lidar imaging technology has come into a new stage [2]. Lidar obtains the laser echo projection data at different angles and reconstructs the image of the target by image reconstruction algorithms. For non-cooperative space target detection, the optical imaging system makes it difficult to obtain the detailed information of the target in a long distance due to the limitation of receiver aperture. However, the spatial resolution of lidar imaging based on the reflection tomography is independent of the range and receiver aperture, only related to the pulse width, bandwidth, and noise. On the basis of the improvement of the lidar experimental system, the theory of LRT was further developed, and many efforts have been made to complete the non-cooperative space target detection. Jin conducted reflection tomography lidar imaging by pulse detection to obtain the image of the conical object in the laboratory environment and experiment preliminarily on the LRT imaging with the incomplete view of the projection data [3,4,5]. Zhang determined the limiting conditions of the sampling interval and sampling angle for laser reflective tomography imaging in sensing targets with typical shapes [6,7]. Hu applied LRT to plane target centroid detection for the first time and proposed a method for calculating centroid distance using multi-angle echo data [8]. However, to obtain accurate imaging of non-cooperative space targets in incomplete angles, breakthroughs should be made in both the system design and the laser image reconstruction method, which is also the focus of this article.

Radon-Fourier [3,9] transform is the basic tomographic algorithm, but its accuracy is low, and the reconstructed image has obvious artifacts. Therefore, the FBP algorithm [10,11,12,13] has become the most commonly used algorithm for laser reflection tomography. However, in the space environment, almost all space targets are non-cooperative targets, which significantly affects the result of the FBP algorithm. Hence, it is not acceptable under such circumstances. R. Gordon [14] first proposed the ART to reconstruct the image by solving the linear equations. Considering the projection matrix is huge and cannot be solved directly, the reconstructed image is generally obtained by iterative approximation [15]. ART breaks through the limitation of the viewing angle and can roughly reconstruct the image in the sparse viewing angle. Then, ART is applied to LRT, which can be solved by the iterative method combined with prior knowledge [16]. At the same time, in order to solve the problem of the complex and time-consuming iterative process caused by the huge measurement matrix, the relative method is also utilized [17]. However, the implementation of ART is complicated, and the reconstructed image quality is not high enough and is sensitive to noise. Therefore, it is necessary to improve ART algorithm.

For non-cooperative targets in space, image reconstruction from a small number of observations is at the heart of the problem, which reminds us of the sparse recovery technique. Many prior works in other domains have been performed to improve the source reconstruction quality. In the medical CT image restoration field, Liu et al. proposed a total variation-strokes-projection onto the convex sets (TVS-POCS) reconstruction method to preserve consistencies and eliminate the patchy artifacts [18]. Non-local total variation (NLTV) minimization combined with reweighted L1-norm was conducted by Kim et al. for compressed sensing CT reconstruction [19]. The referable method can also be found in electron tomography, where Goris et al. applied the TV reconstruction technique [20]. Zhang et al. applied the sparse recovery iterative minimization method in ship classification to estimate the high-resolution range profiles of ships [21]. Rostami et al. resolved the imitation in the sensor networks by using diffusive compressed sensing and sparse recovery under the heat equation constraint [22]. Inspired by these excellent prior works, this article introduces the TV sparse reconstruction approach to a more advanced LRT imaging system to detect long distance non-cooperative targets in space, for better performance in resolution maintenance and artifact elimination of the lidar imaging. Furthermore, regarding the angle limitation in the space non-cooperative target detection due to orbits of the target and the transceiver, LRT imaging utilizing the TV sparse approach especially shows its dominance in high-quality image reconstruction of the space target with a sparse or incomplete view of projections.

The rest of the article is organized as follows. In Section 2, the LRT model and the experimental system set up by us are presented. In Section 3, the framework of LRT for real data is introduced, and then the TV sparse reconstruction with the ART model approach is presented for laser image reconstruction, in order to improve the anti-noise ability and reduce the artifacts of the image reconstructed by an incomplete view of projections. Experiments are performed in both the near-field and far-field environments to validate the effectiveness of the proposed method in Section 4, and real data in more complicated environments is also experimented with and discussed in Section 5. Finally, the conclusion is given in Section 6.

2. LRT Model and Experimental Design

2.1. Laser Reflection Tomography Model

The LRT imaging technology detects the multi-view one-dimensional echo signal of the target viz. projections from different angles. Then, the 2-D contour image of the target is reconstructed by image reconstruction techniques.

The LRT imaging model is shown in Figure 1. The $rov$ coordinate system is obtained by a rotation $\theta$ of the $xoy$ coordinate system, which expresses the relationship between the $(x,y)$ coordinate and the $(r,v)$ coordinate. The emitted laser beam covers the entire target $g(x,y)$ surface along the detection direction, and Radon transform is performed to obtain the reflection projection $p_r(r,\theta )$ of the target at angle $\theta$ [8]:

$$p_r(r,\theta )={\displaystyle {\int }_{L_{r,\theta }}g(x,y)}dv={\displaystyle {\int }_{L_{r,\theta }}g(r\cos \theta -v\sin \theta ,r\sin \theta +v\cos \theta )dv}$$

(1)

The integration path $L_{r,\theta }$ is perpendicular to the illumination direction, and the polar diameter $r=x\cos \theta +y\sin \theta$, $v$ is the integration path. In laser reflection tomography, the laser cannot penetrate the target, so the reflection coefficient is 0 outside the surface, i.e.,

$$g(x,y)=0,(x,y)\notin D$$

(2)

where $D$ is the target surface point set.

2.2. Experimental System

The laser reflection tomography system is implemented at the preset test environment. Figure 2a shows the actual photograph of the laser transmitter system. As shown in Figure 2b, the scene of the laser reflection tomography experimental platform includes the laser transmitter, the turntable and wireless remote receiving module, and one target. In the experiment, the laser pulse width is 100 ps, the bandwidth is 10 GHz, and the laser beam completely covers the target. The target is placed on the turntable, which is 1 m above the ground.

While transmitting the laser, the turntable rotates at a uniform angular speed of 25° per second to ensure that the laser frequency and the received echo frequency match the uniform speed of the target.

The detailed schematic diagram of the LRT experimental system is shown in Figure 3. The LRT radar prototype is composed of four parts, including the transmitting part, the receiving part, the data acquisition part, and the data processing part. The transmitting part is composed of a microchip laser, two reflectors, one beam splitter, and one expander system whereas the receiving part is composed of a receiving telescope and a 7.5 GHz avalanche photodiode (APD) detection module, along with a 15 GHz bandwidth Pin light detection module on the other side of the splitter. A laser pulse high-speed data acquisition module with a bandwidth of 4.25 GHz and a sampling rate of 50 GSPS is employed in the data acquisition part and the data processing part is controlled by the industrial personal computer and is able to complete real-time data processing [6].

3. LRT Image Reconstruction

3.1. LRT Data Processing Framework

Via the LRT experimental system mentioned in Section 2, we are able to conduct the LRT experiment, where we transmit the laser toward the intended target and obtain reflection projection data from laser echo. Then, it is necessary to process the echo data to reconstruct the image of the target. The flow chart of the image reconstruction by projection data is shown in Figure 4:

The first step is the registration of projection data. In the outfield experiment environment, the atmospheric turbulence and the jitter of the target and the platform leads to the inconsistency of the rotation center position of the projection data collected over different angles. The image reconstruction based on the misaligned projection data causes dislocation and distortion in the imaging results, which can seriously affect the identification of the contour of the target. Phase retrieval and feature tracking techniques are commonly used for registration [23,24].

The second step is the projection data conversion. The difference between LRT and computed tomography (CT) imaging is that LRT is based on the reflection coefficient of the object surface, whereas CT imaging is based on the internal transmission coefficient [25]. Therefore, the reflection projection data needs to be preprocessed where it is converted into transmission data, which can greatly reduce the difficulty of image reconstruction. Then, the relationship between them can be expressed as

$$p(r,\theta +{90}^{\circ })=p_r(r,\theta )+{[p_r(r,\theta +{180}^{\circ })]}^T$$

(3)

where $\theta (0\le \theta \le {179}^{\circ })$ is the incident angle, $p_r(r,\theta )$ is $0-{179}^{\circ }$ reflection projection data, $p_r(r,\theta +{180}^{\circ })$ is ${180}^{\circ }-{359}^{\circ }$ projection data, $p_r(r,\theta +{90}^{\circ })$ denotes the transmission projection data, and T means the symmetric transformation.

The last step, which obtains the cross-section information of an object by measuring the projection of the object in different viewing angles, is tomography. It is undoubtedly the most important throughout the process. With the emergence and development of lidar, tomography algorithm is introduced, which improves the accuracy and efficiency of laser imaging technology. At present, the commonly used classical algorithms include iRadon transform [3], FBP [10,11,12,13], and ART [14]. However, the iRadon transform algorithm can only restore the image roughly, which is far from the ideal imaging result. The FBP algorithm requires complete projection data; otherwise, there will be serious artifacts and distortions, resulting in the reconstructed image quality unable to be guaranteed. However, in practice, it is difficult to sample 360° projections of the target due to the clutter interference, insufficient data, or missing data. On the other hand, although ART can reconstruct the image from incomplete projection data, it is too sensitive to noise and is complex to implement, so the effectiveness and timeliness of the ART cannot be guaranteed at the same time.

Therefore, aiming at solving the problem of large artifacts, low anti-noise performance of the ART and incomplete projections limitations of the FBP algorithm, we utilize the gradient sparse characteristics of the laser reconstructed image, add the regularization term of the imaging model, and combine the ART with the TV sparse reconstruction approach for the LRT technique, which is discussed in detail in the remainder of this section.

3.2. Tomographic Imaging of Lidar Projection Data

3.2.1. ART for Lidar Image Reconstruction

ART reconstructs the image of the target by solving linear equations as Equation (4). Considering the projection measurement matrix is huge and cannot be solved directly, the reconstructed image is generally obtained by iterative approximation. The iterative method first discretizes the continuous image $u(x,y)$. The whole image is divided into $N=n\times n$ pixels, the width of which is $\delta$, and the gray value of each pixel is a constant value. Thus, the image can be represented by an n-dimensional matrix $u=[u_1,u_2,\dots .u_N]$. Assuming that the projection data obtained by M-ray projection is represented by a matrix $p=[p_1,p_2,\dots ,p_M]$, the process of image reconstruction is equivalent to solving the gray value of each pixel in the image according to the received projection data, i.e., the essence of iterative reconstruction is to solve the linear equations:

$$\{\begin{array}{l}{\omega }_{11}{u}_1+{\omega }_{12}{u}_2+\dots +{\omega }_{1N}{u}_N=p_1\\ {\omega }_{21}{u}_1+{\omega }_{22}{u}_2+\dots +{\omega }_{2N}{u}_N=p_2\\ \dots \\ {\omega }_{31}{u}_1+{\omega }_{32}{u}_2+\dots +{\omega }_{3N}{u}_N=p_M\end{array}$$

(4)

$$p_i={\displaystyle \sum _{j=1}^N{p}_{ij}={\displaystyle \sum _{j=1}^N{\omega }_{ij}{u}_j,i=1,2,\dots ,M}}$$

(5)

where ${\omega }_{i,j}$ is the weight factor, which represents the weight of the jth pixel on the ith projection value of the image passed by the ray, i.e., the crossing length of the ray and each pixel grid. Equation (5) can also be expressed by matrix:

$$p=Au$$

(6)

Practically, it is very difficult to directly solve the equations. Hence, Kaczmarz relaxation method [15] is generally used to solve the problem. For the ith set of projection data, the iterative equation of ART is:

$$u_j^{k+1}=u_j^k+{\lambda }_1\frac{p_i-{\displaystyle {\sum }_{j=1}^N{\omega }_{in}{u}_n^k}}{{\omega }_{in}^2},i=1,2,\dots ,N$$

(7)

where $i$ is the projection sequence number, $j$ is the pixel sequence number, $k$ is the number of iterations, and ${\lambda }_1$ denotes the relaxation factor. After traversing all grids, an iterative process is completed.

3.2.2. Sparse Reconstruction with ART Model

Based on the traditional ART, considering that most of the reconstructed images of laser reflection tomography have sparse characteristics, or have sparse representation under certain transform bases, the sparse reconstruction method is proposed for the image reconstruction [15]. The image $u$ itself is sparse or the representation of the image under certain transformation bases is sparse, i.e., there exists a matrix $\psi$ when the equation $u=\psi \alpha$ holds, where $\alpha$ is sparse and $\psi$ is a sparse transformation matrix. In this way, the original ART model (4) is transformed to

$$p=Au=A\psi \alpha =B\alpha$$

(8)

where $B=A\psi$. Then, $\alpha$ is reconstructed from the observation value $p$ and matrix $B$, and the original image is reconstructed by $u=\psi \alpha$.

Hence, the image recovery problem based on compressed sensing is transformed to an $L_0$ norm minimization problem, and the norm $L_1$ is used to replace the norm $L_0$, making it a convex optimization problem, which is convenient to solve. The equation can be expressed as:

$$\underset{\alpha }{\min }{\Vert \alpha \Vert }_1,\begin{array}{ccc}& s.t.& \begin{array}{cc}& p=B\alpha \end{array}\end{array}$$

(9)

where ${\Vert \cdot \Vert }_i(i=0,1,2)$ represents the $i$ norm. Common sparse model solving methods include basic pursuit (BP), orthogonal matching pursuit (OMP), etc. The principle of the BP algorithm is to constantly find the smaller norm $L_1$ of $\alpha$ to explain the projection data $p$. By constant iteration to find a sufficient sparse signal (a signal with a sufficiently small norm $L_1$) that meets the condition, it can be considered that the most appropriate solution of the equation is found. For linear equations $p=B\alpha$, if we take each column in the matrix as a variable, OMP can select the variables most correlated with the current residual in each iteration process. These selected variables can form a subspace of the matrix $B$, and each residual is obtained by calculating the difference of $p$ with the orthogonal projection of $p$ on the subspace.

In other words, because there are many zero elements in $\alpha$, $p$ should belong to a subspace of $Span(B)$, which refers to the column vector space of $B$. Furthermore, the subspace of $Span(B)$ can be represented as $Span(B_{sub})$. Note that the subspace $B_{sub}$ is composed of some columns of $B$, and $\alpha$ corresponds with these columns which are recorded as ${\alpha }_{sub}$. If $B_{sub}$ can be figured out, the following optimization problems can be solved:

$$\arg {\min }_{x_{sub}}{\Vert B_{sub}{\alpha }_{sub}-p\Vert }_2$$

(10)

Then, the linear regression is applied to obtain ${\alpha }_{sub}={(B_{sub}^T{B}_{sub})}^{-1}{B}_{sub}^{T}p$. Thus, $\alpha$ is obtained (for the other elements it is zero). The efficiency of the OMP algorithm is greatly improved compared with BP algorithm, but the determination of sparsity fluctuates greatly in different situations, resulting in low image quality. Therefore, this article adopts the idea of sparse reconstruction, combined with the TV regularization approach to reconstruct the image.

3.2.3. TV Sparse Reconstruction with ART Model

In this article, considering that the laser reconstructed image has gradient sparse characteristics, an image reconstruction method based on the TV minimization approach is proposed. At the same time, in order to reduce the image reconstruction error, ART is used to obtain the initial iterative image of TV. Compressed sensing theory points out that most images can be sparse represented by appropriate transforms, such as DCT, FFT, wavelet transform, and so on [15]. In this article, the sparse transformation matrix is measured by total variation. Furthermore, the regularization of the image model is added to achieve the sparse representation of the image. The total variation of an image is defined as the square of the sum of discrete gradients of pixels in two dimensional directions of the image, which is represented as:

$$\mathrm{TV}(u)={\displaystyle {\sum }_{i,j}\left|\nabla u_{i,j}\right|}=\sqrt{{\left|u(x+1,y)-u(x,y)\right|}^2+{\left|u(x,y+1)-u(x,y)\right|}^2}$$

(11)

For the ART model $p=Au$, the TV sparse regularization model based on TV minimization is established as follows:

$$\underset{u}{\min }{\Vert Au-p\Vert }_2^2+{\lambda }_2{\Vert \mathrm{TV}(u)\Vert }_1$$

(12)

where ${\lambda }_2$ is the regularization parameter. Update the image with ART, and then iterate with the gradient descent method to minimize TV. The iterative equation is:

$$u_{i,j}^{k+1}=u_{i,j}^k-\alpha \frac{\partial \mathrm{TV}(u_{i,j}^k)}{\partial u_{i,j}^k}$$

(13)

where $u_{i,j}^{k+1}$ is the last iterated image, $k$ is the number of iterations, $\partial$ is the gradient, and $\alpha$ is the step of gradient descent. By updating the image alternatively using ART algorithm and TV minimization, steps of the TV sparse reconstruction with ART model are described in Algorithm 1.

Algorithm 1: Implementation of TV sparse reconstruction with ART model.

Given $p,A,N$, maxiter, $\alpha$

Initialization: $u_0=0$

for k = 1,2,3... maxiter   do

ART Updating:

for j = 1,2,3..., N     do

$u_j^k=u_j^{k-1}+\lambda \frac{p_i-{\displaystyle {\sum }_{j=1}^N{\omega }_{in}{u}_n^{k-1}}}{{\displaystyle {\sum }_{n=1}^N{\omega }_{in}^2}}{\omega }_{ij}$

$u_j^k=\{\begin{array}{c}{u}_j^k\begin{array}{cc}& \end{array}{u}_j^k\ge 0\\ 0_{}^{}\begin{array}{cc}& \end{array}{u}_j^k<0\end{array}$

end

TV Minimization:

$t^{k-1}=u^k$

$v=\partial {\Vert t^{k-1}\Vert }_{TV}/\partial t^{k-1}$

$t^k=t^{k-1}-\alpha \cdot v$

$u^k=t^k$

$k=k+1$

End

4. Experiments

In this section, the outfield experiments are carried out on the detection target as shown in Figure 5 under the condition of both near-field and far-field. The detection target, which is made of retroreflective material, is composed of three squares, 4 cm on the side, and the included angle between each two is 135°. The laser transmitter is located around 30 m away from the detection target in the near-field and 1 km away in the far-field. Furthermore, the two sets of the echo data are all collected every 1° of target rotation, and 360 groups of echo data can be collected by the turntable rotating for one turn under both conditions.

4.1. Near-Field Experiment

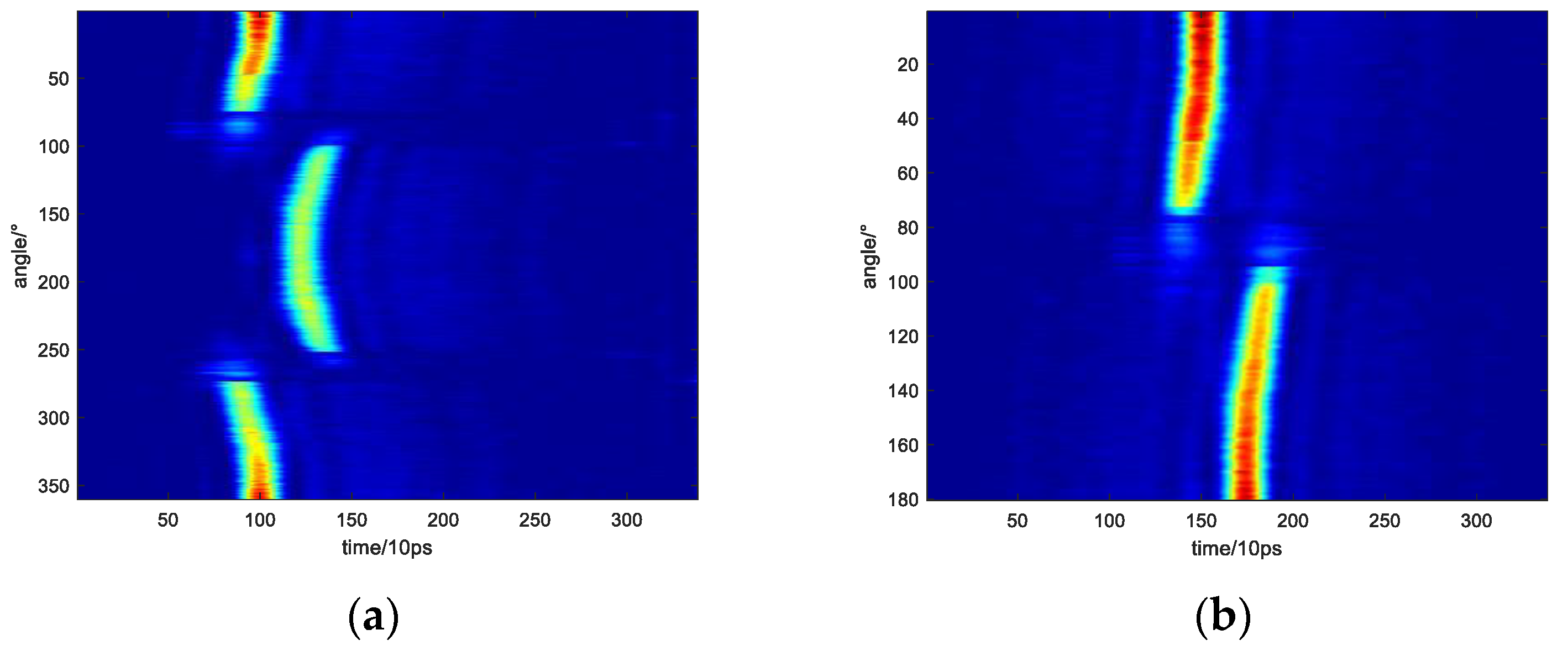
Figure 6a shows the laser reflection projection data after registration in the near-field experiment. A small amount of negative data is caused by the negative noise of the detector, so the negative value in the echo is eliminated. Then, the projection data are converted according to Equation (3), as shown in Figure 6b.

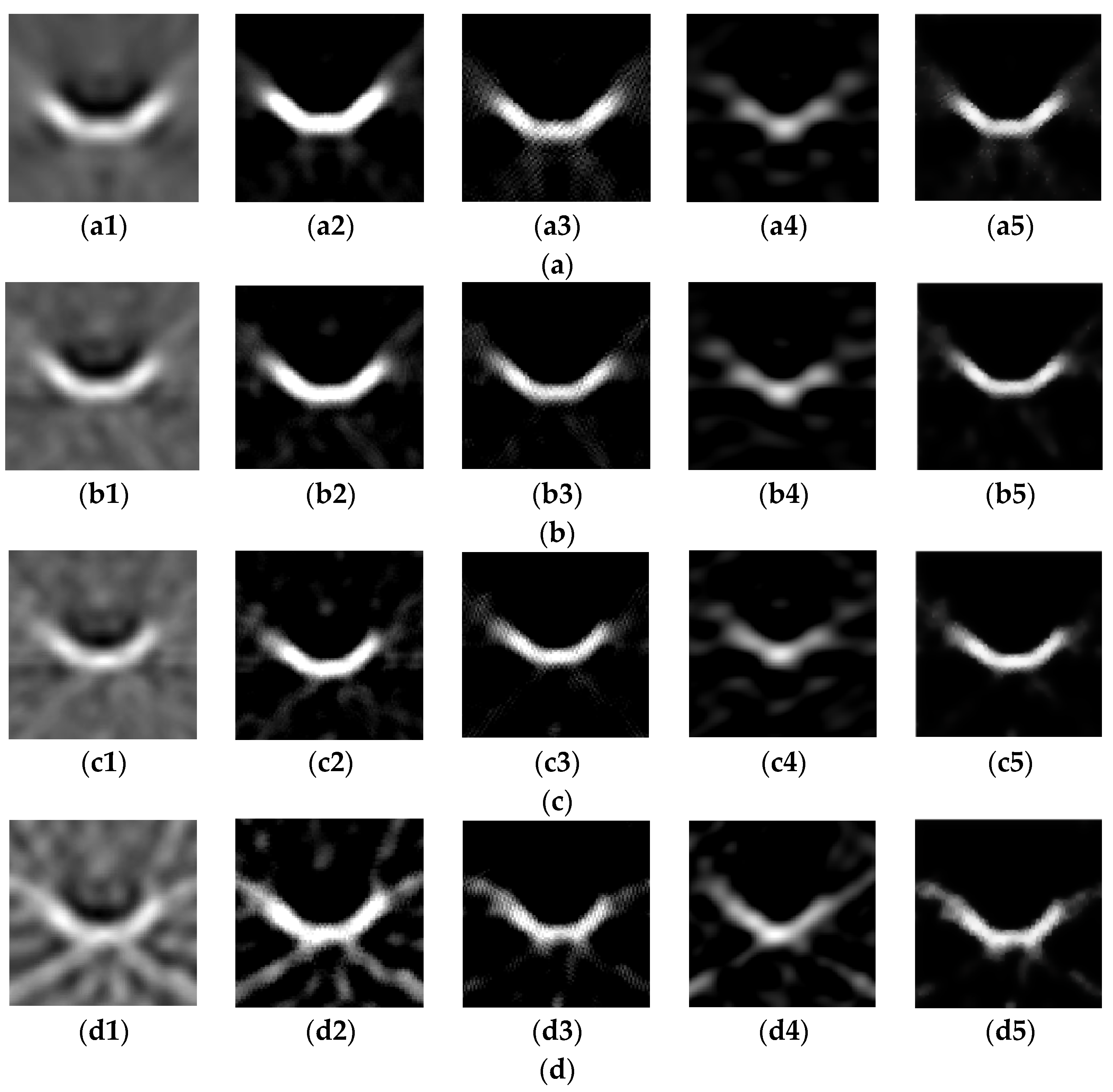
For the projection data in the near-field experiment, the proposed TV sparse imaging reconstruction method in Section 3.2 is performed compared with FBP [10,11,12,13], ART [14], and sparse ART with a complete view of projections and uniformly sampled projections in 5°, 10°, and 20° viewing intervals. The results are shown in Figure 7. In Figure 7a, the iRadon [3,9] results are illustrated just to show the target contour according to the definition in Equation (1), as mentioned in Section 3.1. In Figure 7(a4), for sparse ART with OMP algorithm mentioned in Section 3.2.2, because of using discrete Fourier transform as a sparse basis, it cannot make good use of the gradient sparse features of laser image, leading to obvious deviation between the reconstructed contour and the original target. Then, for Figure 7(a2,a3,a5), the target contour is very clear after imaging with all three approaches. In Figure 7(a5), the resolution of the reconstructed image is significantly improved by using the proposed algorithm compared to Figure 7(a2). Comparing Figure 7(a5) with Figure 7(a3), there are artifacts in the image reconstructed by the traditional ART, which are mostly eliminated in the result of the proposed method. Therefore, in the case of the complete angle, the proposed algorithm greatly improves the resolution of the reconstructed image and reduces the image artifacts.

Next, experiments are carried out at projections with viewing intervals of 5°, 10°, and 20°, respectively. In the near-field experiment, according to the Nyquist sampling theorem, the maximum projection angle sampling interval required to completely reconstruct the detected target laser image within the range of 360° is calculated as about 9°. In Figure 7b, the sampling rate still meets the Nyquist sampling law, and the reconstruction result shows little difference from Figure 7a. When the viewing interval of the projection data is 10° and 20°, the sampling does not meet the Nyquist sampling law. It can be noticed in Figure 7c,d, with the increase in sampling angle interval, that the artifacts in the reconstructed image by iRadon and FBP algorithm increase significantly, which seriously affects the identification of the target contour. However, in the three results related to the ART in Figure 7(c3–c5) and Figure 7(d3–d5), the artifacts are in good condition. At the same time, the imaging resolution of the proposed algorithm is better than the traditional ART and sparse ART with the OMP algorithm. Comparing Figure 7(d5) with Figure 7(a5,b5,c5), with the increase in the sparsity of the angle, the image resolution is generally consistent with that in the complete angle. Furthermore, the artifact is in good condition and the image edge is smooth as well, which greatly reduces the requirements for the detection angle of non-conforming targets and provides convenience for high-efficiency and high-precision laser image reconstruction of non-conforming targets.

For quantitative assessment, information entropy (IE), no-reference signal-to-noise ratio (NRSNR), and variance (Var) are introduced to evaluate the imaging results by using different approaches. IE is defined as follows [26,27]:

$$IE=-{\displaystyle \sum p_i\ln p_i}$$

(14)

where $p_i$ is the probability that the pixel value in the image is $i$. According to Shannon’s information theory, larger entropy indicates more information. That is, the image is clearer with larger IE in LRT reconstruction.

SNR is the proportion of signal to noise and reflects the influence of the noise to signal or image. Here, the NRSNR is adopted to measure the denoising and artifact elimination effect of different reconstruction algorithms. Furthermore, the NRSNR is represented as follows [28]:

$$NRSNR=10{\log }_{10}\frac{255\times 255}{K}(dB)$$

(15)

$$K=\frac{G}{M\times N}$$

(16)

where $K$ is the noise level of the image, $G={\displaystyle \sum (g(x,y)-TH)}$ is the noise distribution, $g(x,y)$ is the pixel value of the image, $TH$ is a set threshold, and $M$ and $N$ are the size of the image. The impact of the noise is smaller when the NRSNR value is higher, which indicates that the quality of the image is better. In this article, NRSNR is utilized to evaluate the anti-noise performance of different algorithms particularly.

Var reflects the contrast ratio of the image [26], and the definition of Var is:

$$Var={\displaystyle {\sum }_y{\displaystyle {\sum }_x\left|g(x,y)-\mu \right|}}$$

(17)

where $g(x,y)$ is the pixel value of the image at coordinates $(x,y)$ and $\mu$ is the mean pixel value of the whole image. In other words, it is easier to distinguish different objects when the Var is higher.

Based on the metrics mentioned above, all the reconstructed results in Figure 7 are measured by IE, SNR, and Var as illustrated in

Table 1. Comparison of the metric values of the results by using different algorithms.

	IE				NRSNR (dB)				Var
	FBP	ART	OMP	TV-ART	FBP	ART	OMP	TV-ART	FBP	ART	OMP	TV-ART
complete view	5.1485	6.2253	6.1133	9.6305	1.5081	2.0758	2.6317	3.2437	0.0463	0.2478	0.1318	0.3428
5° intervals	5.2353	5.2453	6.197	9.6313	1.5746	1.9728	2.3742	3.1592	0.0470	0.0423	0.0881	0.1572
10° intervals	5.3875	5.1411	6.0973	9.6319	1.7853	1.8311	2.4937	3.4724	0.0481	0.109	0.0649	0.1776
20° intervals	5.4357	4.6286	5.7298	9.6313	1.9615	1.574	2.623	3.2858	0.0461	0.0618	0.031	0.0912

. As shown in Table 1, the IE value of the TV sparse reconstruction method is the highest and maintains well at different sampling intervals, which indicates that the reconstructed image of the proposed method better reflects the feature of the target. Meanwhile, the SNR value and Var value of the proposed method are also better than the other algorithms at different sampling intervals, which further proves the effectiveness of the TV sparse reconstruction method in LRT.

Then, we test the anti-noise performance of the proposed algorithm and explore if it still works under non-uniformly sampled projection data. Adding Gaussian noise to the projection data at complete view angles and 10° intervals, the images reconstructed by iRadon and FBP algorithm are destroyed by the noise in Figure 8b, yet the proposed algorithm shows excellent performance in denoising regardless of the angle in Figure 8(b5). It also performs better than the traditional ART not only in denoising ability but also in edge preservation. In addition, experiments are conducted in random sampling at 10° intervals, as shown in Figure 8c. The result of the proposed algorithm in Figure 8(c5) is superior to other algorithms in artifact elimination and the image can also be generally well reconstructed under the influence of random sampling. For better analysis, all the reconstructed results are evaluated by IE, NRSNR, and Var, illustrated in

Table 2. Comparison of anti-noise and random sampled results with the three metrics.

	IE				NRSNR (dB)				Var
	FBP	ART	OMP	TV-ART	FBP	ART	OMP	TV-ART	FBP	ART	OMP	TV-ART
complete view with noise	5.3208	5.4121	6.1208	9.6315	1.9989	1.9855	1.6487	2.2245	0.0298	0.0563	0.1359	0.2552
10° intervals with noise	5.4262	4.6257	6.1078	9.6305	2.0265	1.6557	1.3547	2.5897	0.0137	0.0379	0.0641	0.1966
10° intervals random sample	5.2839	4.7442	6.5712	9.6314	2.0345	1.5427	1.3827	2.3098	0.0418	0.0375	0.0651	0.0982

. It can be concluded from Table 2 that whether the projection data are added with noise or non-uniformly sampled, the IE and Var of the proposed method are still better than that of the other three. It also can be noted that the NRSNR of the reconstructed image using the proposed method is 2.2245 and 2.5897 in complete views and 10° intervals, respectively, almost 30% higher than that of the FBP, ART, and OMP approaches, which highlights the anti-noise performance of the TV sparse reconstruction method with incomplete views of projection data.

Finally, the proposed algorithm is tested under 0–60°, 90°, 120°, and 150° views of projections. Among the results, the image can be roughly reconstructed under the 150° view of projections, as shown in Figure 9c, and Figure 9(c5) shows that the resolution under the proposed algorithm is significantly better. When the viewing angle is less than 120° as Figure 9a,b, it is hard to recognize the contour of the image. To assess the LRT reconstruction performance under a limited range of projections, the correlation coefficient (CC) [29] is employed to measure the similarity between the reconstructed images with the complete viewing angles and images with the incomplete viewing angles by using the same algorithm. Furthermore, the CC is defined as follows:

$$\mathrm{C}\mathrm{C}=\frac{cov(A,B)}{\sqrt{var(A)var(B)}}$$

(18)

here $A$ and $B$ are the two compared images, $cov(A,B)$ is the covariance between $A$ and $B$, and $var(A)$ is the variance of $A$. The CC value is between 0 and 1, where the closer the CC value is to 1, the more similar the two images are. Therefore, the reconstruction images in incomplete sampled views can be effectively evaluated as long as the CC value is calculated between these images and the image with full sampled views.

From

Table 3. CC values of different algorithms with incomplete views of projection.

	CC
	FBP	ART	OMP	TV-ART
0–60° sampled	0.4443	0.5061	0.4562	0.5380
0–90° sampled	0.4934	0.4848	0.5178	0.5789
0–120° sampled	0.6348	0.6538	0.6048	0.6919
0–150° sampled	0.8480	0.8612	0.6916	0.9319

, it is obvious that the reconstructed images under the 0–150° view of projections in Figure 9d are all the most similar to the images under the complete view of projections in Figure 7a, as Figure 9d has more viewing angles compared to 0–60°, 90°, and 120° viewing projections. By using the proposed method, the CC values between the LRT images under the limited range of projections and the images under the complete view of projections are all the highest, which validates the superiority of the method compared to other algorithms when dealing with the case of incomplete viewing angles.

4.2. Far-Field Experiment

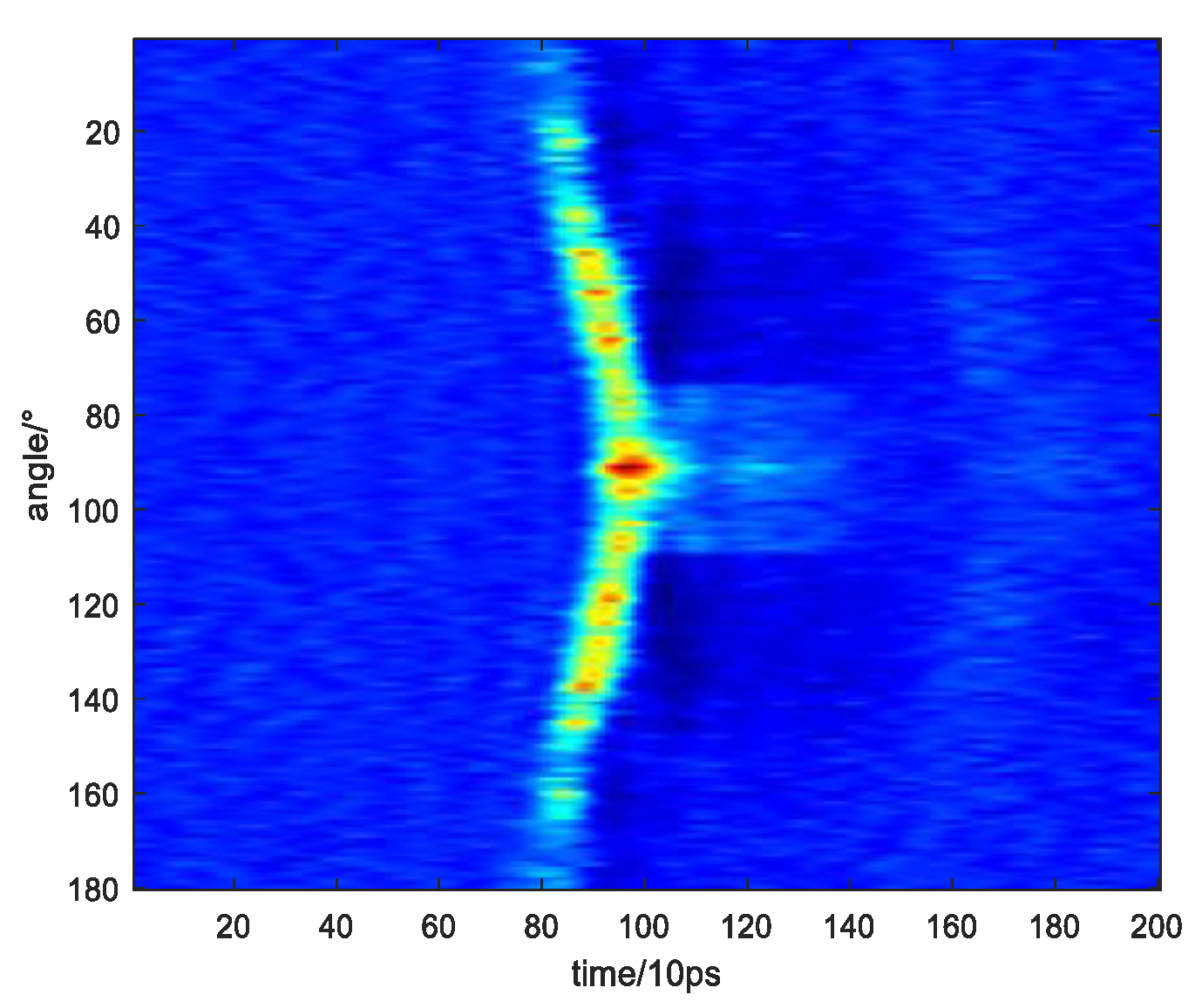
After meliorating the optical system in the laser transmitter and using a more advanced module, the far-field experiment is performed on the same detection target as shown in Figure 5. After preprocessing the projection data, Figure 10 shows the converted projection data of the far-field experiment. It is obvious that the quality of the projection data is significantly improved in that the echo data hardly fluctuate and their continuity is maintained well.

Similarly, for the projection data in the improved far-field experiment, the proposed imaging reconstruction algorithm is performed compared to iRadon, FBP, and ART with the complete view of projections and uniformly sampled projections in 5°, 10°, and 20° viewing intervals. The results are shown in Figure 11.

As shown in Figure 11, the reconstruction result is significantly optimized and the contour of the detection target is well embodied, which indicates that the new optical system has a great impact on the experiment. From the images in Figure 11a, the included angle between each two squares can be clearly seen, overmatching the imaging results of the near-field experiment. However, it is also obvious that there are more artifacts in this experiment due to the influence of interference in the long distance.

The reconstruction effect of different algorithms resembles the result in the near-field experiment. The proposed TV sparse reconstruction with the ART algorithm shows a better effect under the circumstance of both complete view sampling and sparse sampling, which further proves the high precision of the algorithm.

Table 4. IE, NRSNR, and Var value of different algorithms in far-field experiment.

	IE				NRSNR (dB)				Var
	FBP	ART	OMP	TV-ART	FBP	ART	OMP	TV-ART	FBP	ART	OMP	TV-ART
complete view	4.5046	2.2764	3.9911	9.6317	4.251	1.5794	3.3193	5.7955	0.0781	0.0101	0.0563	0.1015
5° intervals	4.4616	1.9777	4.0875	9.6308	3.734	1.4916	4.0301	4.6043	0.0933	0.0187	0.0227	0.098
10° intervals	4.6289	1.764	4.4602	9.6312	3.3437	1.4779	3.9256	4.5962	0.0526	0.039	0.0545	0.0559
20° intervals	4.5152	1.7045	4.6932	9.6316	4.1645	1.5371	3.8309	4.7132	0.0319	0.0446	0.0452	0.0503

analyzes the IE, NRSNR, and Var of four approaches in far-field experiments. It can be clearly seen that the IE, NRSNR, and Var of the proposed method are still better than that of FBP, ART, and OMP. Take the results in 20° intervals as an example; the IE, NRSNR, and Var of the proposed method are 9.6316, 4.7132, and 0.0503, respectively, improved by about 160%, 50%, and 25% compared to that of other approaches. As a result, the effectiveness of the proposed TV sparse reconstruction with the ART algorithm in sparse views is again verified by the far-field experiment.

Figure 12 shows the second far-field experimental imaging results and then the same conclusion can be drawn as near-field experiments. In Figure 12a,b, it can be clearly seen that the proposed method reconstructs the contour of the target well and performs better in denoising than the FBP and ART algorithms. In Figure 12c, the reconstruction effect of random sampling is not ideal, but the proposed method generally restores the contour of the target, which proves to be effective in random sampling as well. As shown in

Table 5. IE, NRSNR, and Var value of anti-noise and random sampled results.

	IE				NRSNR (dB)				Var
	FBP	ART	OMP	TV-ART	FBP	ART	OMP	TV-ART	FBP	ART	OMP	TV-ART
complete view with noise	5.0696	2.1788	4.0617	9.6315	6.978	2.1002	4.8256	11.8431	0.0084	0.0086	0.0164	0.01672
10° intervals with noise	5.154	1.9383	4.2768	9.6314	7.3181	1.974	5.2402	9.1245	0.0022	0.0044	0.0553	0.0479
10° intervals random sample	4.373	1.8787	4.491	9.6313	4.9049	1.8302	2.4533	6.9627	0.0219	0.005	0.0297	0.0411

, the proposed method is still the best among the four algorithms, whether the projection data are added with noise or non-uniformly sampled, which proves the reliability of the proposed method once again. Furthermore, the NRSNR of the reconstructed image using the proposed method is also the highest, proving that the TV sparse reconstruction method possesses the character of working well when dealing with noise.

Finally, the proposed algorithm is tested under 0–60°, 90°, 120°, and 150° views of projections with new far-field data. When the viewing angle is less than 120° as in Figure 13a,b, it is still hard to recognize the contour of the image. However, in this experiment, the image can be reconstructed well under the 150° view of projections as shown in Figure 13c, which is superior to the near-field results. Further, Figure 13(c5) shows that the quality of the reconstructed image using proposed algorithm in 150° view of projections can reach the same level as in complete angles. Correspondingly,

Table 6. CC values of different algorithms with incomplete views of projection.

	CC
	FBP	ART	OMP	TV-ART
0–60° sampled	0.3978	0.3687	0.1975	0.4913
0–90° sampled	0.471	0.4134	0.3701	0.4925
0–120° sampled	0.4353	0.4269	0.4066	0.4727
0–150° sampled	0.7586	0.7499	0.6805	0.7979

analyzes the similarity between Figure 13a–d and Figure 11a in the form of CC. Furthermore, the superiority of the LRT TV-ART method is obvious according to the quantitative comparison in Table 6.

5. Discussion

In Section 4, both near-field and far-field experiments are performed and IE, NRSNR, Var, and CC are employed as the quantitative validation to validate the proposed method with nature data. As a result, the proposed method shows its superiority in the sparse or limited view of projections and better noise-suppressing ability compared to iRadon, FBP, ART, and OMP approaches.

However, though near and far-field experiments verify the effectiveness of the TV sparse reconstruction with the ART model method, there are still some limitations. Now we can focus on another far-field experiment. In this far-field experiment, atmospheric turbulence is relatively serious. In addition, the jitter of the platform brings more noise to the nature data and poor illumination makes it harder to achieve a high quality image.

In this far-field experiment, the distance between the laser transmitter and the detection target is 1 km. The echo data are collected every 2° of target rotation and 180 groups of echo data can be collected. The detection target is a triangular prism. The cross section of the triangular prism is an isosceles triangle, with a short side of 11 cm and a long side of 15 cm. Figure 14a shows the far-field target. Figure 14b shows the laser reflection projection data after registration in the far-field experiment. In Figure 14b, the echo data are influenced significantly, and it can be obviously noticed that the noise destroys the continuity of the echo data and the echo fluctuates violently, which is different from echo data in the near-field environment. Similarly, the projection data in the far-field experiment is preprocessed to obtain the converted projection data in complete viewing angles, as shown in Figure 14c.

Then, for the projection data in the far-field experiment, the proposed imaging reconstruction algorithm is performed compared to iRadon, FBP, and ART with a complete view of projections and uniformly sampled projections in 5°, 10°, and 20° viewing intervals. The results are shown in Figure 15. The far-field experiment is also performed. In Figure 15a, for the projection data in the complete angle, all algorithms can generally reconstruct the target and the reconstructed contour of the target in Figure 15(a4) is clearer than others. However, compared with Figure 7a, it can be noticed that the reconstructed image is disturbed and has more artifacts because of the serious noise. Then, when the Nyquist sampling law is satisfied, Figure 15b shows that the reconstruction result of each algorithm is basically consistent with that under complete projections, respectively. With the increase in viewing intervals in Figure 15c,d, the projection sampling does not meet the Nyquist sampling law. In this condition, the artifact of image reconstruction results of iRadon and FBP algorithm increases significantly, which is not suitable for projection data reconstruction at a sparse angle. Moreover, the proposed TV sparse ART method obviously shows its advantages in artifact elimination and anti-noise performance, as displayed in Figure 15(c4,d4). Although the far-field experiment is affected by atmospheric turbulence and jitter of the target and platform, the proposed TV sparse ART method still maintains the image contour resolution of the detected target under sparse angle projection data due to its good anti-noise performance and artifact elimination.

To conclude, the TV sparse reconstruction method shows its great potential in LRT of the space target, where better performance under a sparse or limited view of projections along with the better ability of anti-noise and artifact elimination make it surpass traditional approaches in the quality of image reconstruction. However, though in most cases the image of the target can be generally restored, some improvements still need to be made, especially in more complex environments. Our future work will focus on the system design to promote its applicability and improve the algorithm to achieve the balance between the noise suppression and reconstructed image quality.

6. Conclusions

In this article, the tomography model of laser reflection projection data is introduced, and the designed LRT experimental system is shown. Then, aiming at solving the problem of high-resolution image reconstruction of long-distance non-cooperative target detection under the sparse or incomplete view of reflection projections, a laser image reconstruction approach viz. TV sparse reconstruction with ART model is proposed for lidar imaging of LRT. Considering that the ART model can be formed into the sparse reconstruction model, this article uses ART to reconstruct the initial image, and then utilizes the TV model and the gradient descent algorithm to reduce the total variation of the iterative image and improve its quality. Finally, the near-field and far-field experiments are performed, and comparisons are made between different algorithms to verify the effectiveness and universality of the proposed method. The experimental result illuminates that the proposed LRT imaging using TV sparse reconstruction with the ART model greatly maintains the resolution of the reconstructed image and improves the artifact elimination ability and the anti-noise performance, which is of major significance to the long-distance space non-cooperative target detection. Furthermore, the proposed method also shows its superiority under random sampling and limited viewing angles, which should be still improved while dealing with the far-field target. Furthermore, the experiments also show the weakness of the LRT system in that the reconstruction results are badly influenced when interferences exist, such as wind or vibration. Therefore, more improvement should be made in both the LRT system and the algorithm to strengthen its reliability and accuracy in our future work.