Quantifying the Influences of Driving Factors on Land Surface Temperature during 2003–2018 in China Using Convergent Cross Mapping Method
Abstract
:1. Introduction
2. Materials and Methods
2.1. Satellite Products
2.2. ESA-CCI Soil Moisture Data
2.3. ERA5-Land and CRU Data
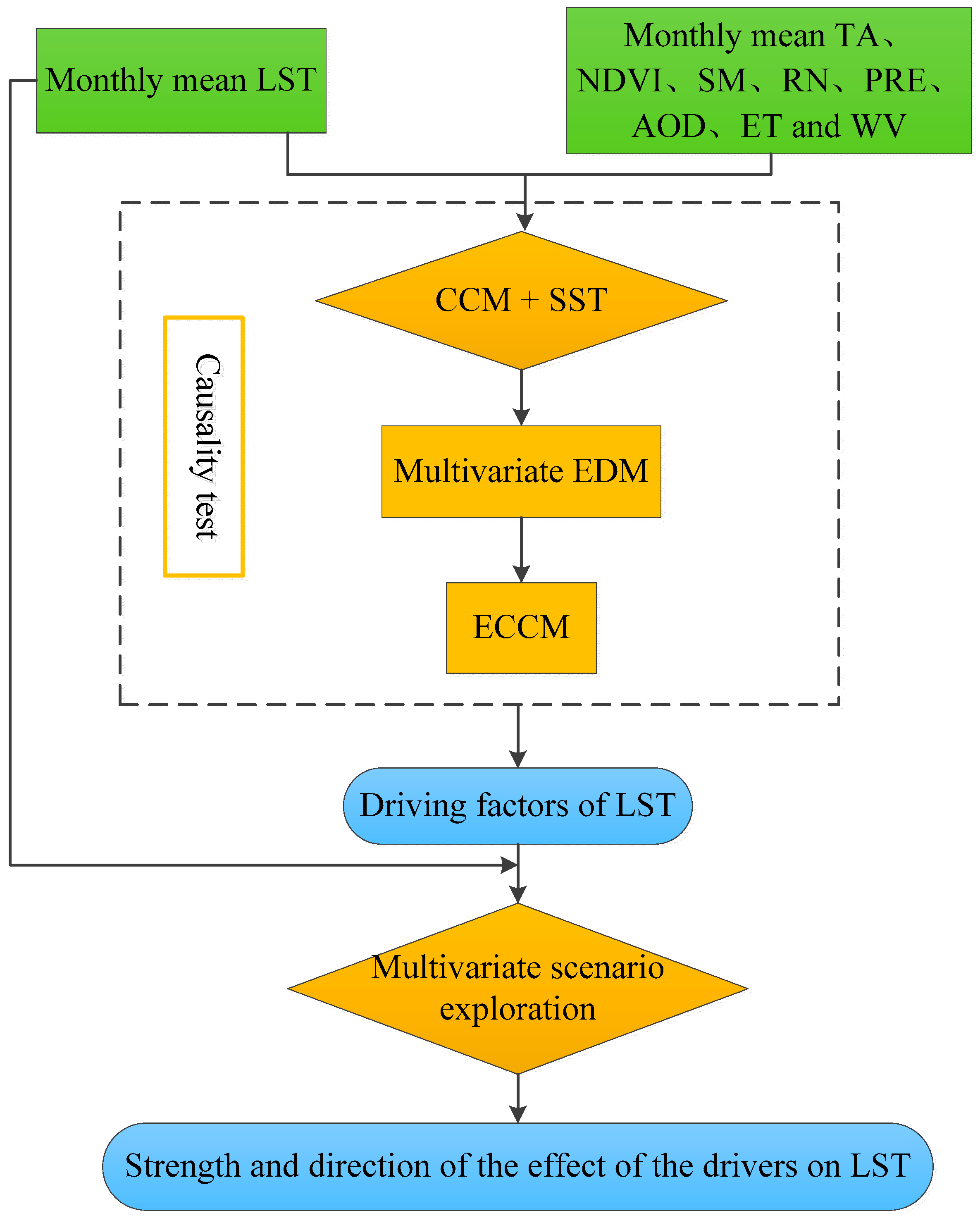
3. Method
3.1. CCM
3.2. SST
3.3. Multivariate EDM
3.4. ECCM
3.5. Multivariate Scenario Exploration
4. Results
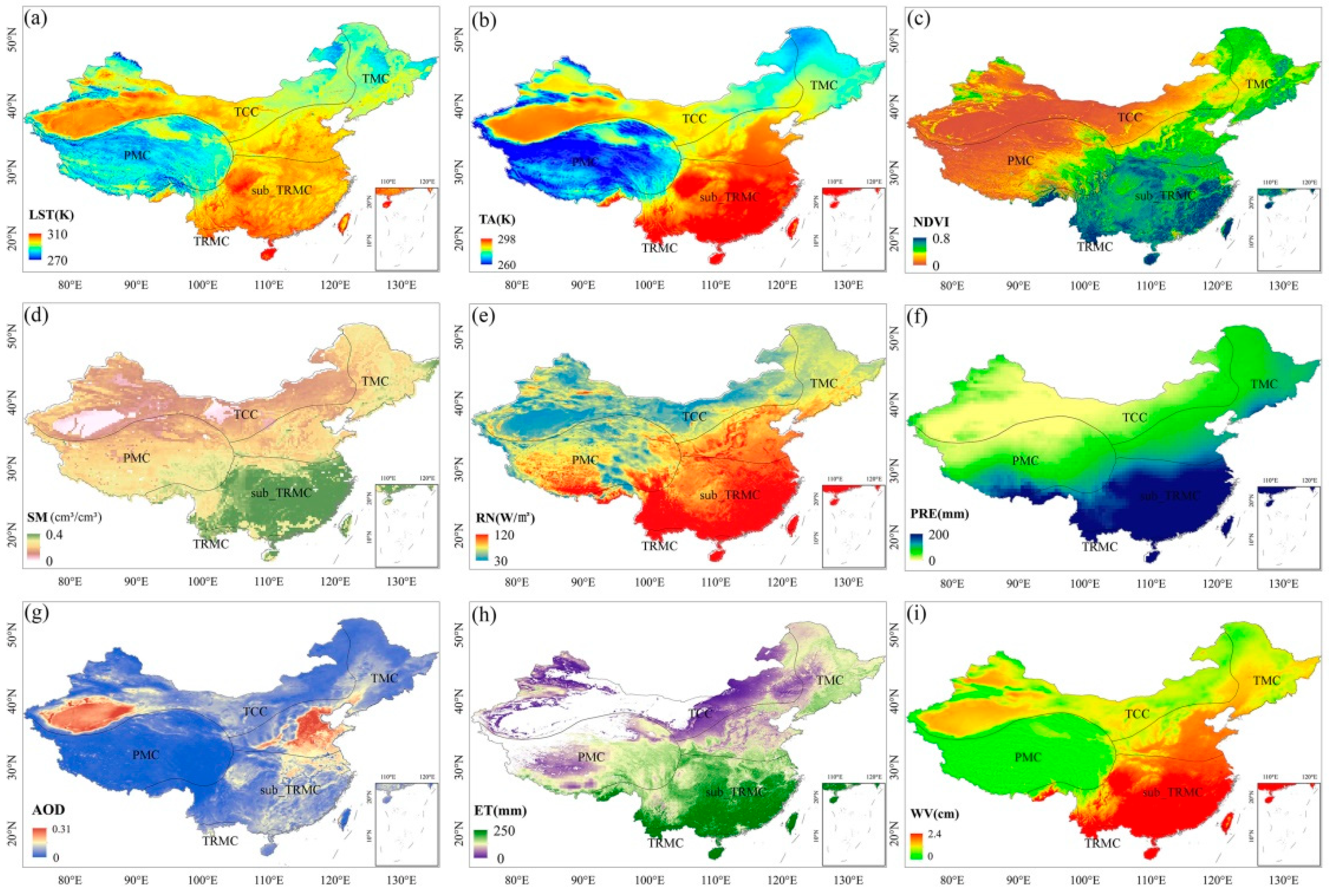
4.1. Spatial Pattern of LST and Environmental Factors
4.2. Causality Detection Process between LST and Environmental Factors
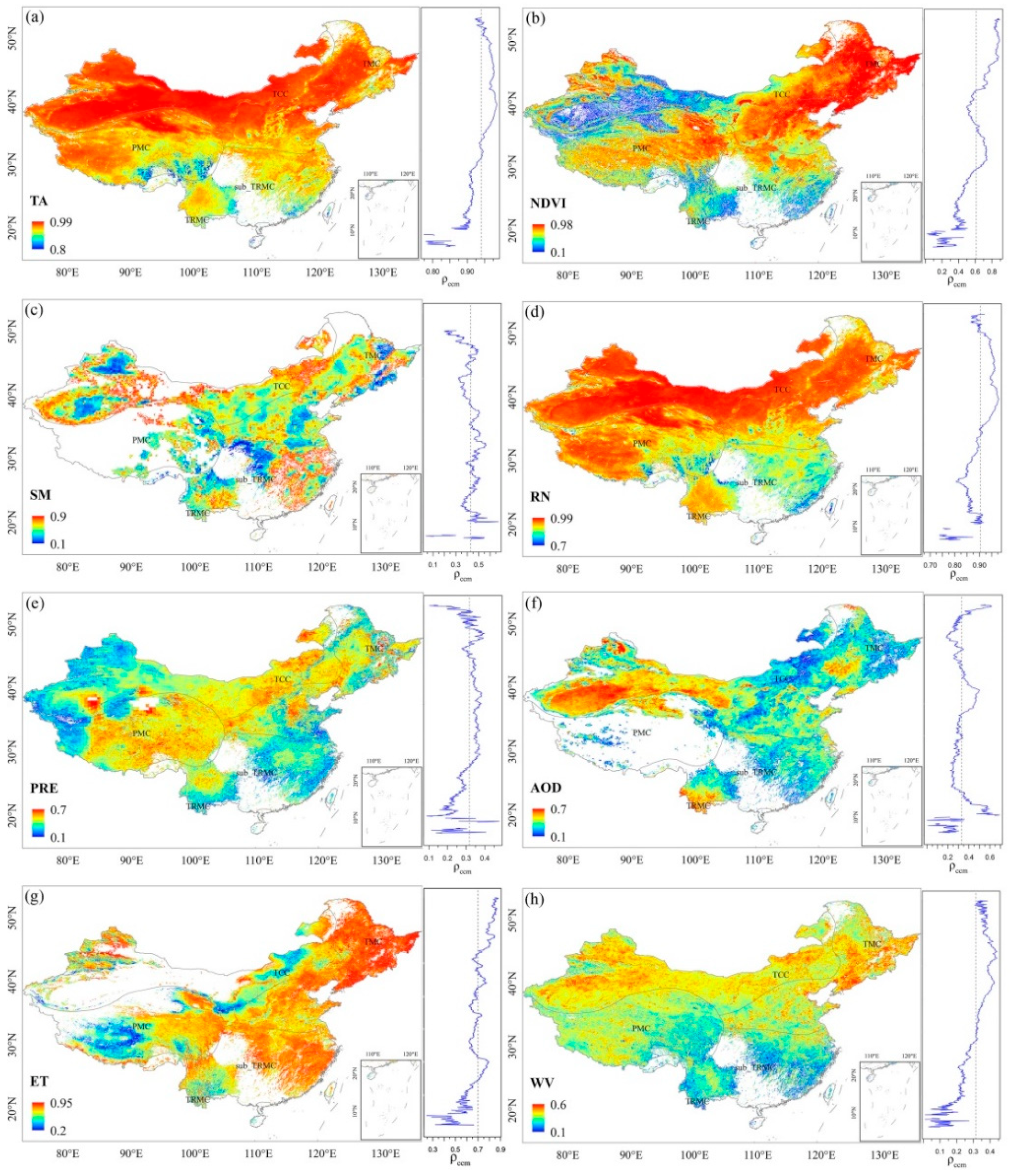
4.3. Result of CCM and SST Tests of China
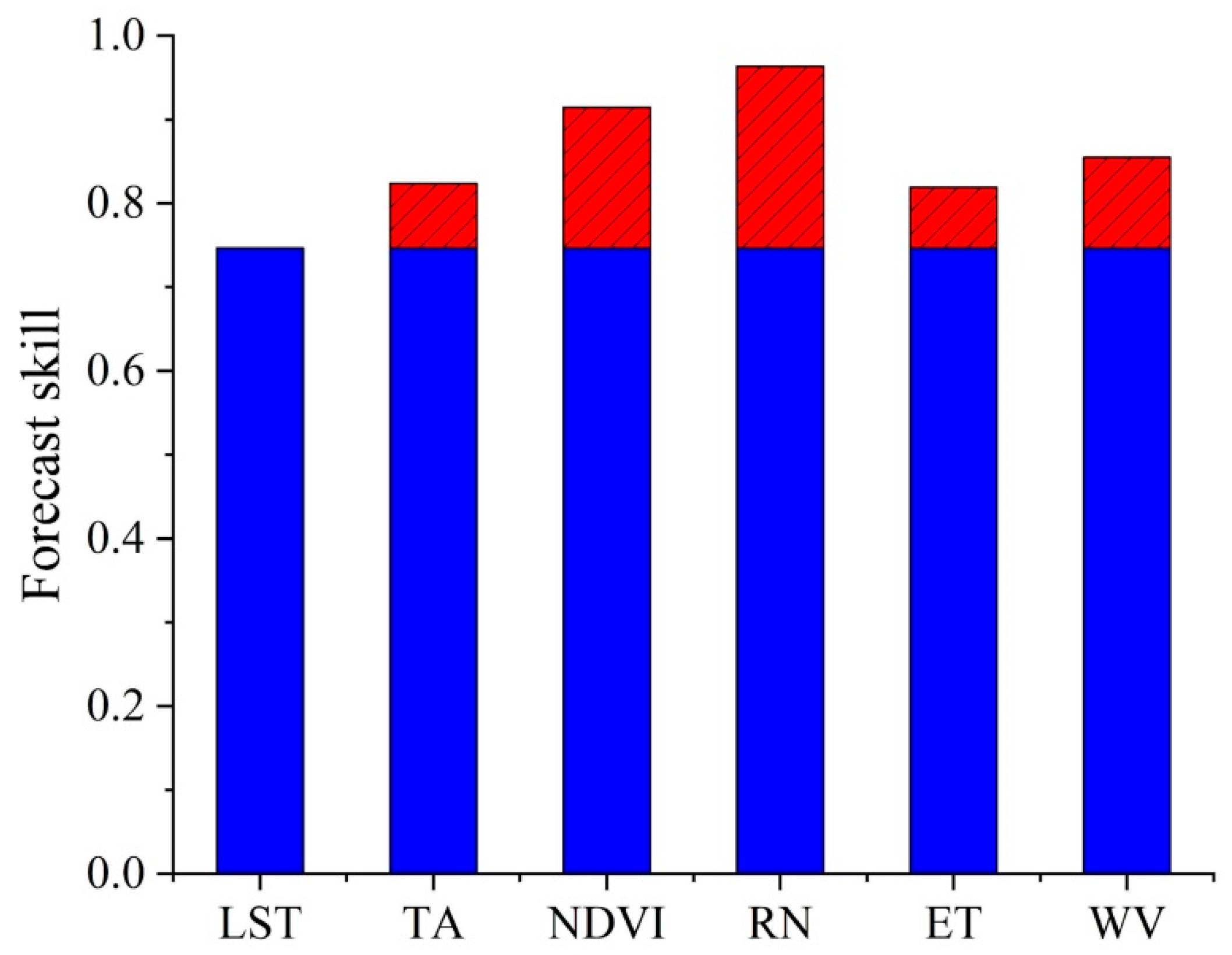
4.4. Pseudo-Causality Detection by Multivariate EDM
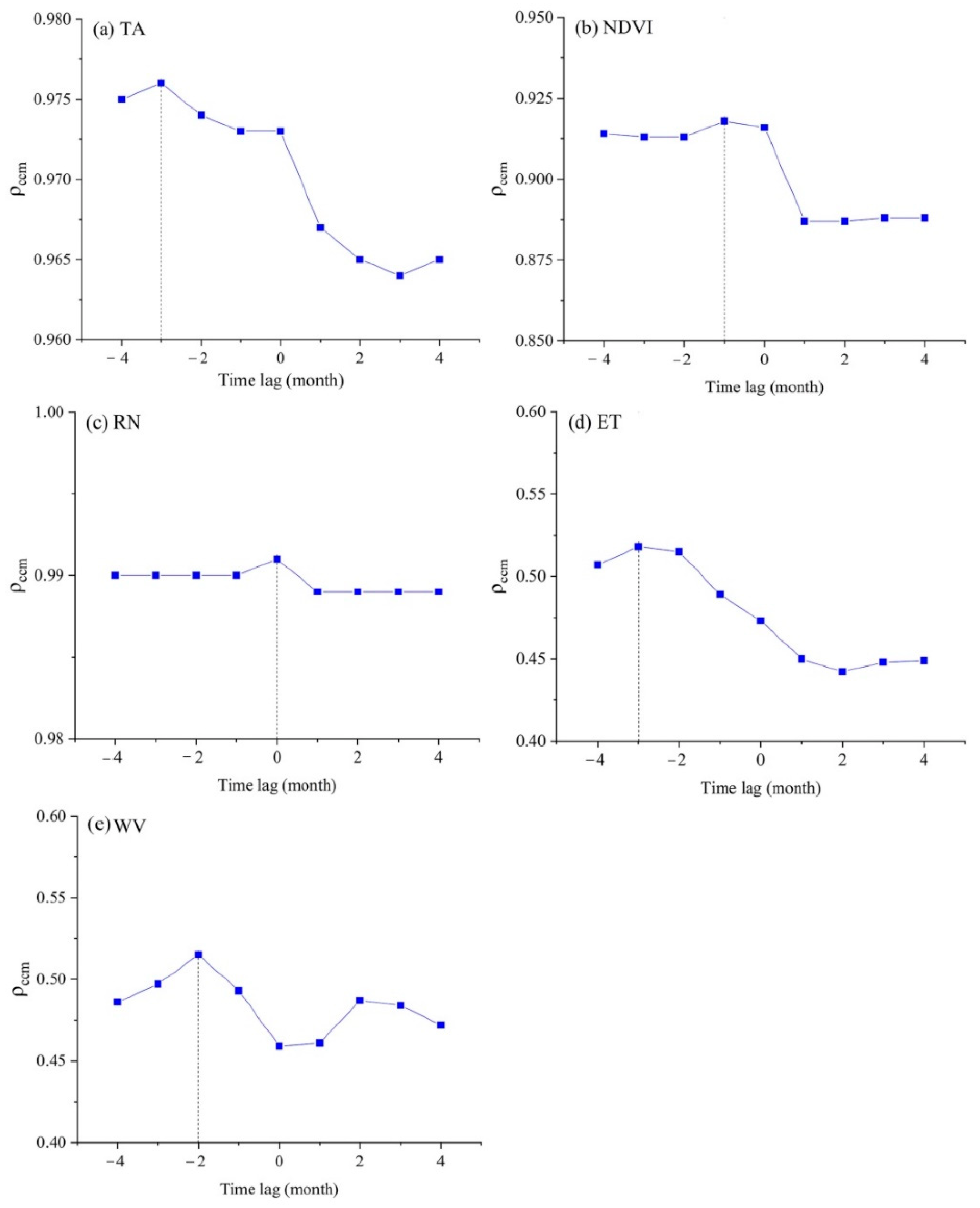
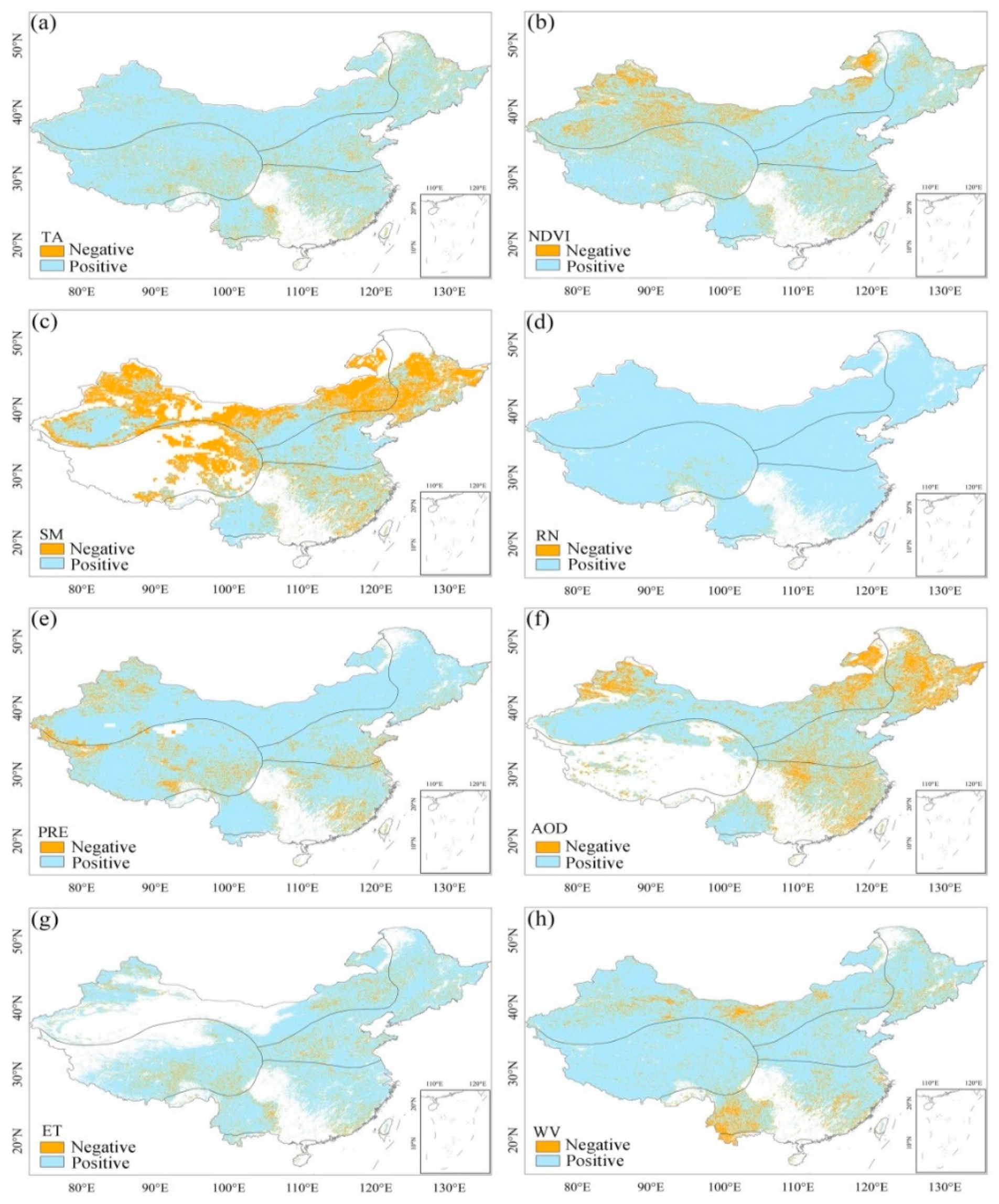
4.5. Pseudo-Causality Detection by ECCM
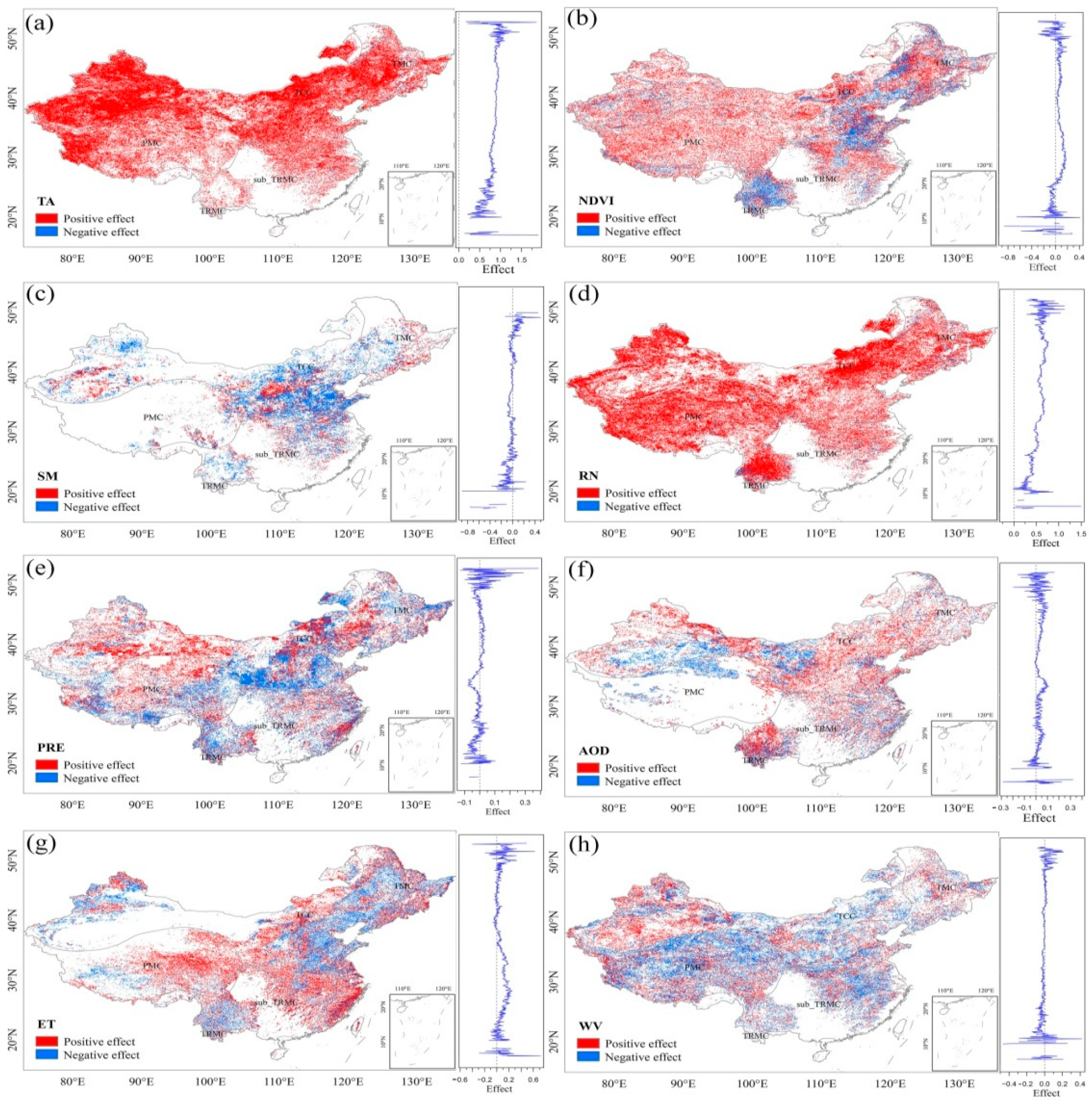
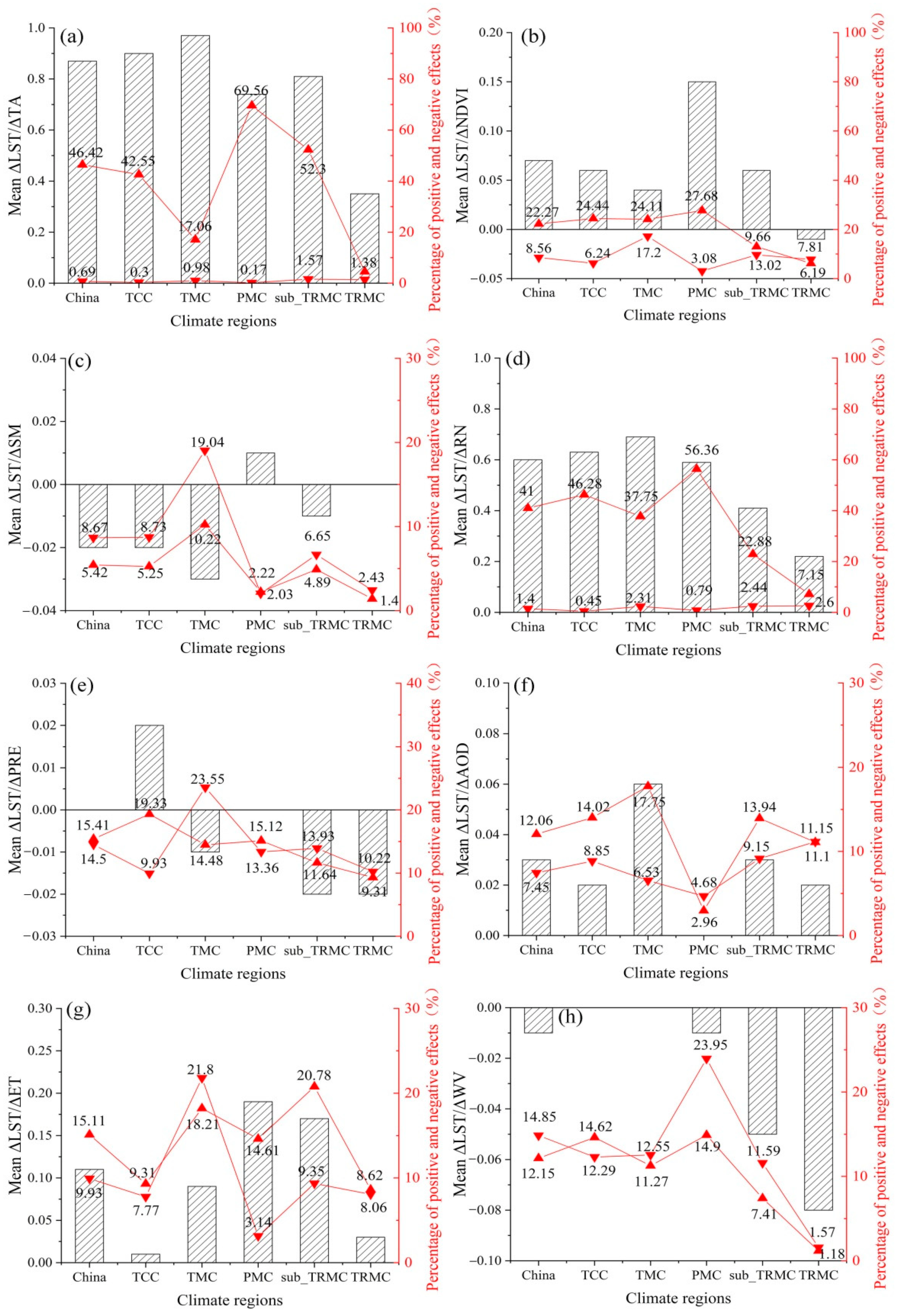
4.6. Effect of Driving Factors on LST
5. Discussion
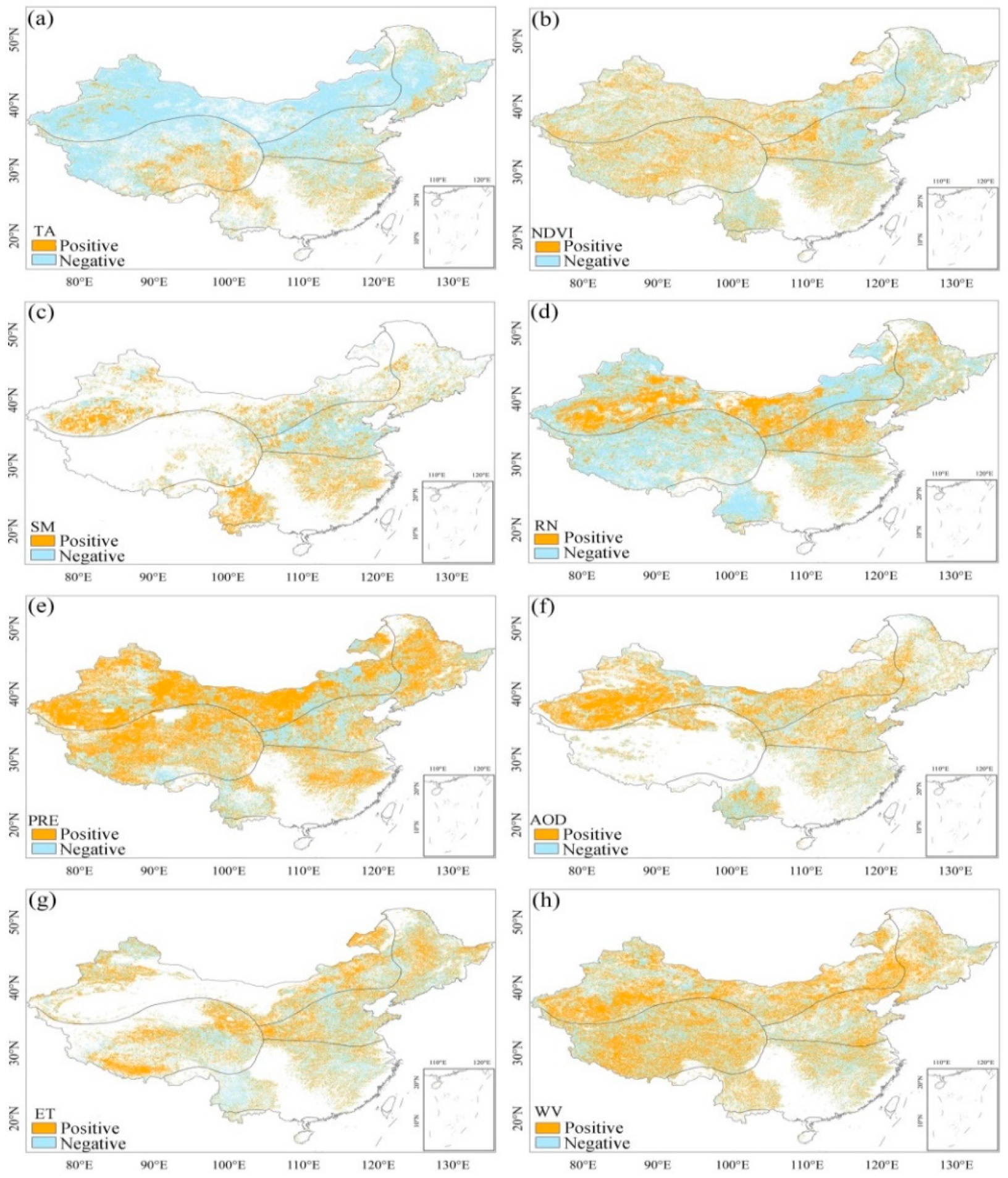
5.1. Type of Causal Relationship between LST and Drivers
5.2. Bidirectional Causality between LST and Drivers
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- GCOS. GCOS 2016 Implementation Plan; World Meteorological Agency (WMO): Marrakesh, Morocco, 2016; Available online: https://library.wmo.int/doc_num.php?explnum_id=3417 (accessed on 10 November 2020).
- Sun, Z.; Wang, Q.; Batkhishig, O.; Ouyang, Z. Relationship between evapotranspiration and land surface temperature under energy- and water-limited conditions in dry and cold climates. Adv. Meteorol. 2016, 2016, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Aguilar-Lome, J.; Espinoza-Villar, R.; Espinoza, J.; Rojas-Acuña, J.; Willems, B.; Leyva-Molina, W. Elevation-dependent warming of land surface temperatures in the Andes assessed using MODIS LST time series (2000–2017). Int. J. Appl. Earth Obs. Geoinf. 2019, 77, 119–128. [Google Scholar] [CrossRef]
- Abera, T.; Heiskanen, J.; Maeda, E.; Pellikka, P. Land surface temperature trend and its drivers in East Africa. J. Geophys. Res. Atmos. 2020, 125, 23. [Google Scholar] [CrossRef]
- Wu, H.; Li, Z.; Yu, X.; Zeng, Q.; Lin, J.; Chen, Y.; Ai, S.; Guo, P.; Lin, H. Empirical dynamic modeling reveals climatic drivers in dynamics of bacillary dysentery epidemics in China. Environ. Res. Lett. 2020, 15, 124054. [Google Scholar] [CrossRef]
- Yang, J.; Ren, J.; Sun, D.; Xiao, X.; Xia, J.; Jin, C.; Li, X. Understanding land surface temperature impact factors based on local climate zones. Sustain. Cities Soc. 2021, 69, 102818. [Google Scholar] [CrossRef]
- Guo, G.; Wu, Z.; Xiao, R.; Chen, Y.; Liu, X.; Zhang, X. Impacts of urban biophysical composition on land surface temperature in urban heat island clusters. Landsc. Urban Plan. 2015, 135, 1–10. [Google Scholar] [CrossRef]
- Luyssaert, S.; Jammet, M.; Stoy, P.; Estel, S.; Pongratz, J.; Ceschia, E.; Churkina, G.; Don, A.; Erb, K.; Ferlicoq, M.; et al. Land management and land-cover change have impacts of similar magnitude on surface temperature. Nat. Clim. Change 2014, 4, 389–393. [Google Scholar] [CrossRef] [Green Version]
- Peng, S.; Piao, S.; Zeng, Z.; Ciais, P.; Zhou, L.; Li, L.; Myneni, R.; Yin, Y.; Zeng, H. Afforestation in China cools local land surface temperature. Proc. Natl. Acad. Sci. USA 2014, 111, 2915–2919. [Google Scholar] [CrossRef] [Green Version]
- Deng, Y.; Wang, S.; Bai, X.; Tian, Y.; Wu, L.; Xiao, J.; Chen, F.; Qian, Q. Relationship among land surface temperature and LUCC, NDVI in typical karst area. Sci. Rep. 2018, 8, 641. [Google Scholar] [CrossRef]
- Yu, Y.; Duan, S.; Li, Z.; Chang, S.; Xing, Z.; Leng, P.; Gao, M. Interannual spatiotemporal variations of land surface temperature in China from 2003 to 2018. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 1783–1795. [Google Scholar] [CrossRef]
- Zhou, D.; Xiao, J.; Frolking, S.; Liu, S.; Zhang, L.; Cui, Y.; Zhou, G. Croplands intensify regional and global warming according to satellite observations. Remote Sens. Environ. 2021, 264, 112585. [Google Scholar] [CrossRef]
- Wu, X.; Wang, L.; Yao, R.; Luo, M.; Li, X. Identifying the dominant driving factors of heat waves in the North China Plain. Atmos. Res. 2021, 252, 105458. [Google Scholar] [CrossRef]
- Peng, W.; Zhou, J.; Wen, L.; Xue, S.; Dong, L. Land surface temperature and its impact factors in Western Sichuan Plateau, China. Geocarto Int. 2016, 32, 919–934. [Google Scholar] [CrossRef]
- Zhao, H.; Ren, Z.; Tan, J. The spatial patterns of land surface temperature and its impact factors: Spatial non-stationarity and scale effects based on a Geographically-Weighted Regression Model. Sustainability 2018, 10, 2242. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Samat, A.; Abuduwaili, J.; Ge, Y. Quantifying the influences of land surface parameters on LST variations based on GeoDetector model in Syr Darya Basin, Central Asia. J. Arid Environ. 2021, 186, 104415. [Google Scholar] [CrossRef]
- Sugihara, G.; May, R.; Ye, H.; Hsieh, C.; Deyle, E.; Fogarty, M.; Munch, S. Detecting causality in complex ecosystems. Science 2012, 338, 496–500. [Google Scholar] [CrossRef]
- Chen, Z.; Zhuang, Y.; Xie, X.; Chen, D.; Cheng, N.; Yang, L.; Li, R. Understanding long-term variations of meteorological influences on ground ozone concentrations in Beijing During 2006–2016. Environ. Pollut. 2019, 245, 29–37. [Google Scholar] [CrossRef]
- Clark, A.; Ye, H.; Isbell, F.; Deyle, E.; Cowles, J.; Tilman, G.; Sugihara, G. Spatial convergent cross mapping to detect causal relationships from short time series. Ecology 2015, 96, 1174–1181. [Google Scholar] [CrossRef]
- Deyle, E.; Maher, M.; Hernandez, R.; Basu, S.; Sugihara, G. Global environmental drivers of influenza. Proc. Natl. Acad. Sci. USA 2016, 113, 13081–13086. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Yang, J.; Chen, Y.; De Maeyer, P.; Li, Z.; Duan, W. Detecting the causal effect of soil moisture on precipitation using Convergent Cross Mapping. Sci. Rep. 2018, 8, 12171. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, F.; Cao, Y.; Yuan, X.; Yang, C. Improved CCM for variable causality detection in complex systems. Control. Eng. Pract. 2019, 83, 67–82. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, D.; Zhao, C.; Kwan, M.; Cai, J.; Zhuang, Y.; Zhao, B.; Wang, X.; Chen, B.; Yang, J.; et al. Influence of meteorological conditions on PM2.5 concentrations across China: A review of methodology and mechanism. Environ. Int. 2020, 139, 105558. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Li, R.; Chen, D.; Zhuang, Y.; Gao, B.; Yang, L.; Li, M. Understanding the causal influence of major meteorological factors on ground ozone concentrations across China. J. Clean. Prod. 2020, 242, 118498. [Google Scholar] [CrossRef]
- Barraquand, F.; Picoche, C.; Detto, M.; Hartig, F. Inferring species interactions using Granger causality and convergent cross mapping. Theor. Ecol. 2020, 14, 87–105. [Google Scholar] [CrossRef]
- Granger, C. Investigating Causal Relations by Econometric Models and Cross-spectral Methods. Econometrica 1969, 37, 424. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, T.; Fu, B. A measure of spatial stratified heterogeneity. Ecol. Indic. 2016, 67, 250–256. [Google Scholar] [CrossRef]
- Liu, H.; Lei, M.; Zhang, N.; Du, G. The causal nexus between energy consumption, carbon emissions and economic growth: New evidence from China, India and G7 countries using convergent cross mapping. PLoS ONE 2019, 14, e0217319. [Google Scholar] [CrossRef]
- Ye, H.; Deyle, E.R.; Gilarranz, L.J.; Sugihara, G. Distinguishing time-delayed causal interactions using convergent cross mapping. Sci. Rep. 2015, 5, 14750. [Google Scholar] [CrossRef] [Green Version]
- Deyle, E.R.; Fogarty, M.; Hsieh, C.-H.; Kaufman, L.; MacCall, A.D.; Munch, S.B.; Perretti, C.T.; Ye, H.; Sugihara, G. Predicting climate effects on Pacific sardine. Proc. Natl. Acad. Sci. USA 2013, 110, 6430–6435. [Google Scholar] [CrossRef] [Green Version]
- Heskamp, L.; Abeelen, A.S.M.-V.D.; Lagro, J.; Claassen, J.A. Convergent cross mapping: A promising technique for cerebral autoregulation estimation. Int. J. Clin. Neurosci. Ment. Health 2014, 1, S20. [Google Scholar] [CrossRef] [Green Version]
- Luo, L.; Cheng, F.; Qiu, T.; Zhao, J. Refined convergent cross-mapping for disturbance propagation analysis of chemical processes. Comput. Chem. Eng. 2017, 106, 1–16. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Y.; Qin, S.; Wu, B.; Wu, X.; Zhu, Y.; Shao, Y.; Gao, Y.; Jin, Q.; Lai, Z. Effects of seasonal variability of climatic factors on vegetation coverage across drylands in northern China. Land Degrad. Dev. 2018, 29, 1782–1791. [Google Scholar] [CrossRef]
- Wang, J.-Y.; Kuo, T.-C.; Hsieh, C.-H. Causal effects of population dynamics and environmental changes on spatial variability of marine fishes. Nat. Commun. 2020, 11, 2635. [Google Scholar] [CrossRef] [PubMed]
- Wan, Z.; Li, Z.-L. A physics-based algorithm for retrieving land-surface emissivity and temperature from EOS/MODIS data. IEEE Trans. Geosci. Remote. Sens. 1997, 35, 980–996. [Google Scholar] [CrossRef]
- Wan, Z.; Zhang, Y.; Zhang, Q.; Li, Z.L. Validation of the land-surface temperature products retrieved from Terra Moderate Resolution Imaging Spectroradiometer data. Remote Sens. Environ. 2002, 83, 163–180. [Google Scholar] [CrossRef]
- Wan, Z.; Li, Z. Radiance-based validation of the V5 MODIS land-surface temperature product. Int. J. Remote Sens. 2008, 29, 5373–5395. [Google Scholar] [CrossRef]
- Wan, Z.; Li, Z.-L. MODIS land surface temperature and emissivity. In Land Remote Sensing and Global Environmental Change; Springer: Berlin/Heidelberg, Germany, 2010; pp. 563–577. [Google Scholar]
- Carlson, T.N.; Ripley, D.A. On the relation between NDVI, fractional vegetation cover, and leaf area index. Remote Sens. Environ. 1997, 62, 241–252. [Google Scholar] [CrossRef]
- Chen, Y.; Xia, J.; Liang, S.; Feng, J.; Fisher, J.B.; Li, X.; Li, X.; Liu, S.; Ma, Z.; Miyata, A.; et al. Comparison of satellite-based evapotranspiration models over terrestrial ecosystems in China. Remote Sens. Environ. 2014, 140, 279–293. [Google Scholar] [CrossRef]
- Dorigo, W.; Wagner, W.; Albergel, C.; Albrecht, F.; Balsamo, G.; Brocca, L.; Chung, D.; Ertl, M.; Forkel, M.; Gruber, A.; et al. ESA CCI Soil Moisture for improved Earth system understanding: State-of-the art and future directions. Remote Sens. Environ. 2017, 203, 185–215. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Dorigo, W.A.; Parinussa, R.M.; De Jeu, R.A.M.; Wagner, W.; McCabe, M.F.; Evans, J.P.; Van Dijk, A.I.J.M. Trend-preserving blending of passive and active microwave soil moisture retrievals. Remote Sens. Environ. 2012, 123, 280–297. [Google Scholar] [CrossRef]
- An, R.; Zhang, L.; Wang, Z.; Quaye-Ballard, J.A.; You, J.; Shen, X.; Gao, W.; Huang, L.; Zhao, Y.; Ke, Z. Validation of the ESA CCI soil moisture product in China. Int. J. Appl. Earth Obs. Geoinf. 2016, 48, 28–36. [Google Scholar] [CrossRef]
- Albergel, C.; Dorigo, W.; Reichle, R.H.; Balsamo, G.; De Rosnay, P.; Munoz-Sabater, J.; Isaksen, L.; De Jeu, R.; Wagner, W. Skill and Global Trend Analysis of Soil Moisture from Reanalyses and Microwave Remote Sensing. J. Hydrometeorol. 2013, 14, 1259–1277. [Google Scholar] [CrossRef]
- Harris, I.; Osborn, T.J.; Jones, P.; Lister, D. Version 4 of the CRU TS monthly high-resolution gridded multivariate climate dataset. Sci. Data 2020, 7, 109. [Google Scholar] [CrossRef] [Green Version]
- Sugihara, G.; May, R.M. Nonlinear forecasting as a way of distinguishing chaos from measurement error in time series. Nature 1990, 344, 734–741. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Method; Charless Griffin: London, UK, 1975. [Google Scholar]
- Sugihara, G.; Deyle, E.R.; Ye, H. Reply to Baskerville and Cobey: Misconceptions about causation with synchrony and seasonal drivers. Proc. Natl. Acad. Sci. USA 2017, 114, E2272–E2274. [Google Scholar] [CrossRef] [Green Version]
- Deyle, E.R.; May, R.M.; Munch, S.B.; Sugihara, G. Tracking and forecasting ecosystem interactions in real time. Proc. R. Soc. B Boil. Sci. 2016, 283, 20152258. [Google Scholar] [CrossRef]
- Yue, S.; Pilon, P.; Cavadias, G. Power of the Mann–Kendall and Spearman’s rho tests for detecting monotonic trends in hydrological series. J. Hydrol. 2002, 259, 254–271. [Google Scholar] [CrossRef]
- Amiri, R.; Weng, Q.; Alimohammadi, A.; Alavipanah, S.K. Spatial–temporal dynamics of land surface temperature in relation to fractional vegetation cover and land use/cover in the Tabriz urban area, Iran. Remote Sens. Environ. 2009, 113, 2606–2617. [Google Scholar] [CrossRef]
- Gallo, K.; Hale, R.; Tarpley, D.; Yu, Y. Evaluation of the Relationship between Air and Land Surface Temperature under Clear- and Cloudy-Sky Conditions. J. Appl. Meteorol. Clim. 2011, 50, 767–775. [Google Scholar] [CrossRef]
- Cao, J.; Zhou, W.; Zheng, Z.; Ren, T.; Wang, W. Within-city spatial and temporal heterogeneity of air temperature and its relationship with land surface temperature. Landsc. Urban Plan. 2021, 206, 103979. [Google Scholar] [CrossRef]
- Karnieli, A.; Agam, N.; Pinker, R.T.; Anderson, M.; Imhoff, M.L.; Gutman, G.G.; Panov, N.; Goldberg, A. Use of NDVI and Land Surface Temperature for Drought Assessment: Merits and Limitations. J. Clim. 2010, 23, 618–633. [Google Scholar] [CrossRef]
- Mutiibwa, D.; Strachan, S.; Albright, T. Land Surface Temperature and Surface Air Temperature in Complex Terrain. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4762–4774. [Google Scholar] [CrossRef]
- Myhre, G.; Myhre, C.E.L.; Samset, B.H.; Storelvmo, T. Aerosols and their relation to global climate and climate sensitivity. Nat. Educ. Knowl. 2013, 4, 7. [Google Scholar] [CrossRef]







| Data | Product | Spatial Resolution | Temporal Resolution |
|---|---|---|---|
| Land Surface Temperature | MYD11C3 | 0.05° (~5.6 km) | Monthly |
| Normalized Difference Vegetation Index | MYD13C2 | 500 m (0.5 km) | 8-day |
| Aerosol Optical Depth | MYD04_L2 | 10 km | Daily |
| Net Evapotranspiration | MYD16A2 | 500 m (0.5 km) | 8-day |
| Water Vapor | MYD05_L2 | 5 km | Daily |
| Soil Moisture | ESA-CCI | 0.25° (28 km) | Daily |
| Air Temperature | ERA5-Land | 0.1° (11.2 km) | Monthly |
| Surface Net Solar Radiation | ERA5-Land | 0.1° (11.2 km) | Monthly |
| Surface Net Thermal Radiation | ERA5-Land | 0.1° (11.2 km) | Monthly |
| Precipitation | CRU | 0.5° (56 km) | Monthly |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Y.; Shang, G.; Duan, S.; Yu, W.; Labed, J.; Li, Z. Quantifying the Influences of Driving Factors on Land Surface Temperature during 2003–2018 in China Using Convergent Cross Mapping Method. Remote Sens. 2022, 14, 3280. https://doi.org/10.3390/rs14143280
Yu Y, Shang G, Duan S, Yu W, Labed J, Li Z. Quantifying the Influences of Driving Factors on Land Surface Temperature during 2003–2018 in China Using Convergent Cross Mapping Method. Remote Sensing. 2022; 14(14):3280. https://doi.org/10.3390/rs14143280
Chicago/Turabian StyleYu, Yanru, Guofei Shang, Sibo Duan, Wenping Yu, Jélila Labed, and Zhaoliang Li. 2022. "Quantifying the Influences of Driving Factors on Land Surface Temperature during 2003–2018 in China Using Convergent Cross Mapping Method" Remote Sensing 14, no. 14: 3280. https://doi.org/10.3390/rs14143280
APA StyleYu, Y., Shang, G., Duan, S., Yu, W., Labed, J., & Li, Z. (2022). Quantifying the Influences of Driving Factors on Land Surface Temperature during 2003–2018 in China Using Convergent Cross Mapping Method. Remote Sensing, 14(14), 3280. https://doi.org/10.3390/rs14143280






