Abstract
Due to the difference in surface reflectivity, the laser measurement waveform data recorded in full waveform have a saturation phenomenon. When the signal is saturated, the echo waveform produces peak clipping and pulse spreading, which seriously restrict the accuracy of laser measurement results and the usability of data. Therefore, we conducted a ranging investigation on the “peak clipping” phenomenon of the saturated waveform and found a nonlinear time delay in the range, which is between the two extreme cases of saturated “dead time” and Gaussian fitting peak time as pulse signal reception time. Subsequently, based on the consistent relationship between the geometric characteristics of the high- and low-gain channels of the space-borne laser altimeter, we constructed a laser waveform saturation compensation model, namely, the laser pulse flight time delay compensation and the laser waveform peak intensity compensation, and carried out the data saturation compensation and validation with the dual-channel measurement data from the GaoFen-7 (GF-7) satellite. The experimental results showed that the saturation compensation model (SCM) proposed in this paper could restore the features of the saturated waveform signal and effectively improve the accuracy of the laser ranging. The accuracy of the laser waveform fitting result after saturation compensation improved from 0.7 ns (0.11 m) to 0.14 ns (0.02 m), which greatly improved the usability of the saturated laser measurement waveform data.
1. Introduction
Space-borne laser altimeter is an active remote sensing measurement equipment that can accurately and quickly obtain three-dimensional surface information. In 2003, the ICESat satellite launched by the National Aeronautics and Space Administration (NASA) carried the first Earth observation laser altimeter system, the Geoscience Laser Altimeter System (GLAS) [1], and related research has played an important role in polar ice elevation measurement, monitoring changes in sea ice thickness, forest biomass estimation, global elevation control point acquisition, etc. [2,3,4,5,6]. As laser altimetry has shown better development potential and application prospects in three-dimensional space exploration, other countries have developed more laser altimeters to enhance their laser exploration capabilities [7,8,9].
In 2016, China launched the ZiYuan3-02 (ZY3-02) satellite which carried the first domestic experimental laser altimetry payload and successfully obtained laser altimetry data, laying an important technical foundation for the rapid development of satellite laser altimetry in China [10,11]. GaoFen-7 (GF-7) satellite was launched successfully on 3 November 2019, which carried a set of laser altimeter systems to meet the 1:10,000 scale stereo mapping [12,13,14]. In 2020, ZiYuan3-03 (ZY3-03) was launched one after another, and its laser altimeter was upgraded to an operational payload based on the experimental payload of the ZY3-02 satellite [15,16]. Unlike the ZY3-02/03 satellite, the GF-7 satellite platform was equipped with a full-waveform laser altimeter. The space-borne laser altimeter that records the full waveform can not only obtain more abundant surface height information but also obtain the geometric and physical features of ground objects using waveform inversion technology [17,18]. Notably, the full-waveform data improve the practicability of the space-borne laser altimeter and the waveform quality, which is important for the accuracy of laser altimetry and ground feature inversion.
Due to the variation of the Earth’s surface reflectivity, scattering angle, and atmospheric conditions, the echo signal collected by the laser altimeter has an extensive linear dynamic range. To accommodate the return pulse with a wide range of signal power, the upper and lower limits are preset when designing a space-borne laser altimeter, but under high signal conditions (such as high energy, high reflectivity, and clear sky), the two-way atmospheric transmission and surface reflectivity can exceed expectations to the point where the peak power of the return pulse sometimes exceeds the linear dynamic range of the receiver, resulting in saturation of the remote sensing signal [19,20]. This saturation phenomenon is common in satellite remote sensing data, such as DMSP-OLS nighttime light data and synthetic aperture radar (SAR) data, and usually, a specific gain function relationship model is used to correct the saturation data [21,22]. Concerning the saturation data of space-borne lidar, the Sun team used a spare laser detector to establish the saturation correction model in the laboratory and conduct ranging correction. The saturation correction model was improved by comparing the GLAS elevation compensation value and the GPS measurement value [23,24,25,26].
The calculated ranging information could yield a longer laser pulse time of flight by applying a method based on a linear receiver to process the laser saturation waveform. A dual-channel with high and low gain was designed for the GF-7 space-borne laser altimetry system to effectively deal with the laser saturation waveform problem. In this paper, we proposed to construct the SCM for laser waveform data to recover the energy characteristics and geometric measurement accuracy of the laser saturation waveform for the consistent relationship between the high- and low-gain channels of the space-borne laser altimetry. In Section 2, we describe the technical performance and system structure of the GF-7 laser altimeter system. In Section 3, we introduce the main methodological process of laser waveform saturation compensation, including signal saturation identification, the feature parameter extraction method, and the construction method of the SCM. Then in Section 4, we conduct experiments and analyses and perform range accuracy verification and waveform feature recovery. Section 5 mainly discusses the applicability and error analysis of the method. Finally, Section 6 summarizes the conclusions of this study.
2. The GF-7 Laser Altimeter System
The GF-7 space-borne laser altimeter system is equipped with four lasers (two main components and two backups), two footprint cameras, and one optical axis surveillance camera. The main technical performance parameters [12] of the laser are listed in Table 1.

Table 1.
Main technical performance parameters of the laser.
The GF-7 space-borne laser altimeter system adopts a dual-beam synchronous Earth observation system. Each laser beam has two independent transceiver channels, and each channel contains three complete parts: a laser transmitter, a full-waveform receiver, and a footprint camera. The transmitting channel consists of two independent lasers and a transmitting lens. The receiving channel shares the receiving telescope. After the laser echo of the two channels passes through the receiving telescope, it enters the corresponding full-waveform receiver and footprint camera [27]. The structure of the laser altimeter is shown in Figure 1.
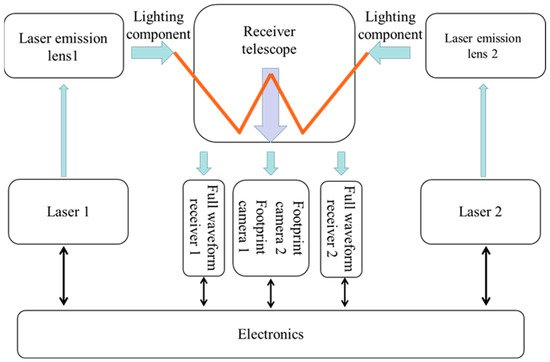
Figure 1.
Structural diagram of the GF-7 laser altimeter [28].
3. Methods
Aiming for the dual-channel structural characteristics of the GF-7 laser altimeter system, this paper proposes a laser waveform signal saturation compensation algorithm as shown in Figure 2 with the following main steps:
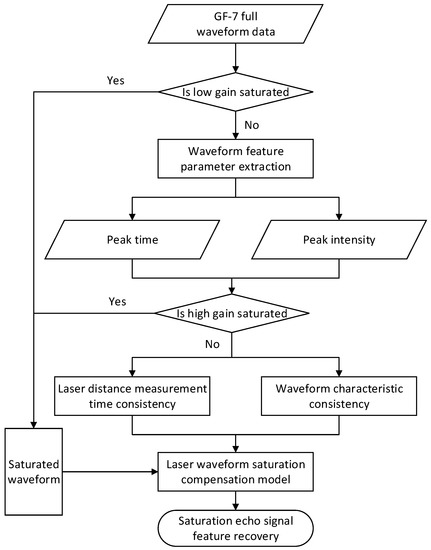
Figure 2.
Flow chart of the laser waveform signal saturation compensation algorithm.
- Filtering waveform data. Two sets of data were selected from the GF-7 full-waveform data. One set of data showed no saturation in both high- and low-gain channels; in the other set of data, there was saturation in the high-gain channel and no saturation in the low-gain channel.
- Waveform pre-processing. The laser altimetry full-waveform data were waveform decomposed to obtain single-peak echo data; then, the valid waveform was filtered out using the threshold denoising method.
- Extraction of laser waveform characteristic parameters. The Gaussian fitting of valid waveform data involved using the least square method iteration to extract the peak time and peak intensity parameters.
- Construction of the laser waveform saturation compensation model. Based on the consistency of laser ranging time and waveform features between the high- and low-gain channels of the space-borne laser altimeter, the laser waveform compensation model was constructed, namely, laser pulse flight delay compensation and laser waveform peak intensity compensation.
- Recovery of saturated waveform characteristic parameters. The SCM was used to compensate for the features of the saturated waveform and then recover the energy characteristics and geometric measurement accuracy of the laser saturated waveform.
3.1. Signal Saturation Identification
After the satellite is in orbit, the return pulse energy exceeds the linear dynamic range of the receiver with changes in laser emission energy, environmental conditions, and surface reflectivity. This saturation usually occurs on snow and ice, smooth paved floors in cities and towns, and other areas with high reflectivity [29].
In the design of the waveform sampling circuit of the GF-7 laser, to avoid damage to equipment caused by excessive signal strength, the detector assembly adopts the protection mechanism of high- and low-gain amplifiers. When the signal power exceeds the effective quantification range of the receiver’s linear dynamic change, the signal peak is truncated by the detector, and the “peak clipping” phenomenon with three or more consecutive identical voltage value occurs; that is, “signal saturation” occurs, as shown in Figure 3. When the receiver is saturated, the echo waveform produces flat peaks and pulse broadening, thus prolonging the pulse time of flight and affecting the ranging accuracy.
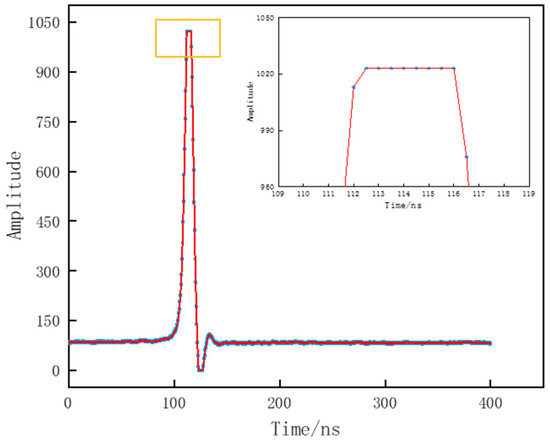
Figure 3.
GF-7 space-borne laser altimeter echo data (flat peak).
The ICESat/GLAS laser altimetry system adopts a single gain channel with a linear dynamic effect of 8 bits and an effective quantization range of 0–255 for the echo waveform signal values [25]. The GF-7 space-borne laser altimeter system detector and ICESat/GLAS detector are both linear detectors but the GF-7 laser receiver uses a linear dynamic sampling range with 10-bit quantization, and the effective quantization range of the echo waveform signal value is 0–1023 [30]. Obviously, the quantization range of the GF-7 laser receiver has been improved, but for the larger dynamic range of the echo signal, there is still saturation of the echo signal.
3.2. Extraction of Laser Waveform Characteristic Parameters
The waveform data of the GF-7 laser altimeter include the transmitting waveform and echo waveform, and the sampling frequency was 2 GHz. The transmitted waveform adopts a Gaussian basis mode, and the echo waveform can be expressed as the superposition of the Gaussian signal and noise. The single-peak echo signal can be expressed by the following Gaussian distribution function [31]:
where is the peak, is the corresponding time of the peak, is the root mean square pulse width, and is the waveform noise value.
The full-waveform laser altimeter mainly uses the flight time measurement method to achieve range, as shown in Formula (2). The peak method is used to determine the transmitting signal time and the receiving time of the echo signal; that is, the laser ranging value is calculated by calculating the peak time of the transmitting wave and the echo.
where is the speed of light, is the time of receiving the signal for the system, and is the time of transmitting the signal for the system.
Owing to the influence of the equipment itself and the measurement environment, there is some noise in the signal detected by the laser receiving system. Background noise has a very important influence on the extraction of the waveform characteristic parameters. Threshold denoising is used to pre-process the original waveform data of the space-borne laser, and the effective waveform can be screened out. The average and mean square deviation of 100 sampling values were used to estimate the threshold of background noise. Sampling point data greater than the background noise threshold are effective data. The calculation formulas for background noise mean, , and the mean square deviation, , are as follows:
where is the sample value of each n frames before and after the echo data, is the number of waveform sampling points used to calculate the background noise parameters, and is the waveform intensity value.
In the satellite on-orbit operation, the quantization error of the space-borne laser analog waveform signal is generated after digital processing, which makes the emission and echo appear as multiple maximum values in some cases or prevents the peak point from being the real waveform peak point, resulting in random errors in laser ranging. Therefore, to improve the ranging accuracy, the least square method is used to iteratively perform Gaussian fitting for the effective waveform, and then the waveform characteristic parameters are extracted [32].
By fitting a single-peak laser signal with a Gaussian function, characteristic parameters such as peak time, peak intensity, and pulse width can be obtained [33]. Figure 4 shows an example of extracting some characteristic parameters of the laser echo waveform.
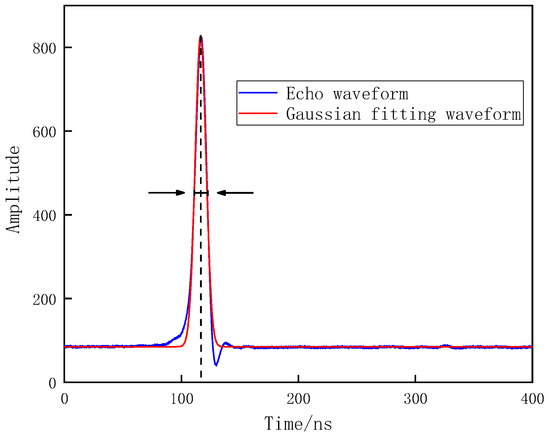
Figure 4.
Parameter extraction of the laser echo waveform.
3.3. Saturated Compensation Model
The GF-7 laser altimeter records the echo waveform data through high-gain and low-gain channels, as shown in Figure 5.
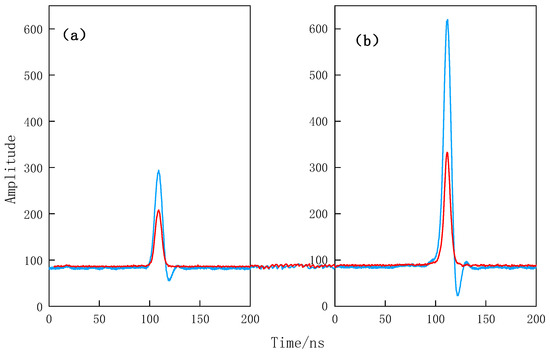
Figure 5.
Schematic diagram of high- and low-gain comparison of laser emission waveform (a) and echo waveform (b). The blue solid line is the high-gain waveform and the red solid line is the low-gain waveform.
Compared with low-gain data, high-gain data are more prone to saturation in strong reflection echo signals; although low gain is not easy to saturate, some effective signals are easily submerged by noise when the local surface reflectivity is low. When the signal of the high-gain channel is saturated and the signal of the low-gain channel is not saturated, there is a deviation in the ranging value obtained by Gaussian fitting after processing the high- and low-gain waveforms, as shown in Figure 6. Because the high- and low-gain channels obtain the ranging information of the same pulse, the low-gain pulse time of flight (TOF) can be used to correct the signal receiving time of the high-gain saturated echo.
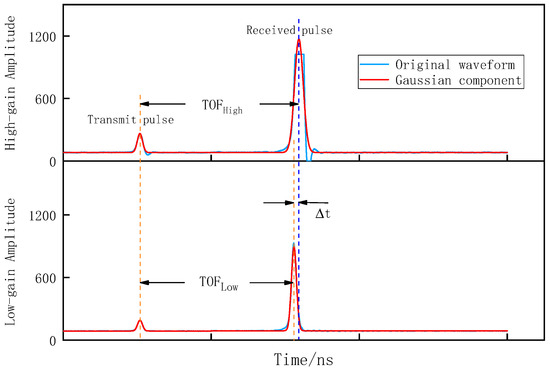
Figure 6.
Schematic diagram of the deviation of the Gaussian fitting results in high gain (saturated) and low gain (unsaturated). TOF is the pulse flight time and Δt is the ranging difference.
When the saturation is too high and the waveform amplitude is too large, the broadening of the echo pulse changes with saturation. The peak time obtained using the Gaussian model is used to preliminarily locate the saturated echo reception time, which is denoted as t1, and then based on the dual-channel ranging consistency assuming that the pulse crossing times are equal, the saturated echo reception time t2 is solved using the Gaussian parameters of the low-gain waveform corresponding to the saturated waveform and the Gaussian parameters of its transmitting waveform, after which the difference between the two is compared to establish a functional model between the saturation and deviation values of the echo receiving time. Using this model, the error values corresponding to different saturation levels are calculated and used to correct the echo receiving time of the saturated waveform, namely,
where is the receiving time for corrected laser signals and is a Gaussian fitting peak time parameter for saturated echo. The specific process is shown in Figure 7.
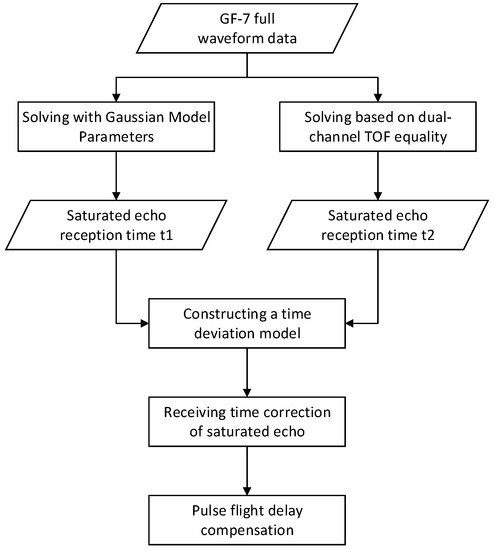
Figure 7.
Flow diagram of the laser pulse delay compensation process.
According to the working mode of GF-7 laser ranging, it is known that the dual gain channels obtain the ranging information of the same pulse, and therefore, the pulse time of flight obtained by high and low gain are equal and the waveform intensity values of the two channels collected by the digitizer are linearly correlated. The regression model is established by using the peak intensity parameters of the high- and low-gain unsaturated data, which is applied to the saturated waveform to compensate for the high gain using its corresponding low-gain echo peak intensity. Finally, the features of the saturated echo signal are restored based on the receiving time compensation model and peak intensity regression model of the saturated echo.
4. Experiments and Analysis
4.1. Experimental Data
In the experiment, one-track laser data taken by the GF-7 satellite in December 2019 were selected. The terrain of the experimental area includes mountains, towns, water, and farmland, as shown in Figure 8. The experimental data were divided into two groups: in the first group, the laser waveform data did not appear saturated in both high- and low-gain channels; in the second group of data, the laser waveform was saturated in the high-gain channel and there was no saturation in the low-gain channel. Two groups of experimental data were used to verify the time delay compensation and waveform characteristic parameter recovery of the laser saturation waveform.
Figure 8.
Schematic diagram of typical saturated data acquisition location.
The experiment was divided into two main parts. First was the pulse time of flight delay compensation experiment, which used the full-waveform data of the GF-7 laser altimeter to verify the time delay phenomenon of the saturated waveform, and the ranging deviation model, which was established to compensate for the receiving time of the saturated echo. Second was the saturated waveform characteristic parameter recovery experiment, which used GF-7 unsaturated high- and low-gain waveform data of the same laser beam to establish a peak intensity regression model and the low-gain peak intensity parameters corresponding to the saturated waveform to compensate for the high gain. Then, the features of the saturated waveform signal were recovered by combining the pulse time delay compensation of the saturated echo in Experiment 1.
4.2. Experiment 1: Laser Pulse Flight Delay Compensation
The signal saturation of the laser detector showed a “peak clipping” phenomenon in the waveform feature but there was a time delay in the photoelectronic response of the detector, which is usually called the saturation “dead time” [34]. We assumed that the saturated echo waveform did not record the signal beyond the threshold strength, and then the laser ranging from one was calculated according to the waveform characteristic parameters. We also assumed that the receiving time of the saturated echo signal was the “dead time,” that is, the laser detector only generated one digital number (DN) value when detecting one or more electrons. The “dead time” signal was eliminated and the waveform parameters were calculated to obtain the laser ranging value of two.
In the experiment, high- and low-gain waveform data with different saturations were selected. Based on the ranging value of the low-gain channel laser waveform, the errors ranging from one and two were counted and the ranging deviation value of the high-gain saturation waveform was obtained, as shown in Figure 9.
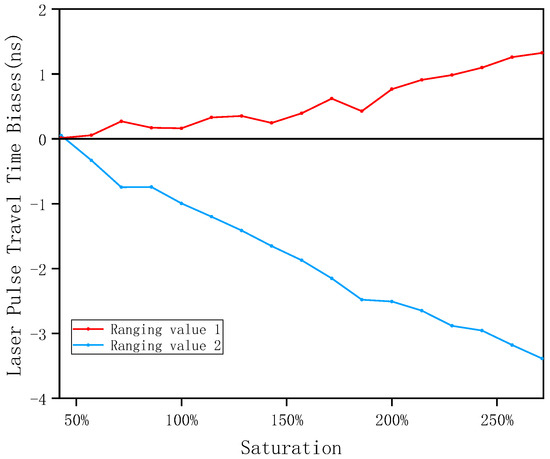
Figure 9.
Ranging means deviation of high and low gain with different saturation.
Taking the peak time after eliminating saturated “dead time” as the receiving time of saturated echo signal, the ranging accuracy was 0.322 m. Taking the Gaussian fitting peak time as the receiving time of the saturated echo signal, the ranging accuracy reached 0.106 m. By comparing the pulse time of flight of the two algorithms in Figure 9, it could be found that the “peak clipping” phenomenon of the saturated waveform had a nonlinear time delay in the range.
In this experiment, a data set (including 30 sets of high- and low-gain full-waveform data) of dual-channel unsaturated waveforms with different waveform parameters of the same laser beam of the GF-7 space-borne laser altimeter was randomly selected for Gaussian fitting, and the corresponding waveform characteristic parameters (i.e., peak time and peak intensity parameters) were extracted. First, the consistency of the GF-7 dual-channel ranging was verified according to the extracted transmitting wave and echo peak time parameters. The verification results showed that the measurement distances of the two channels with high and low gain were equal within the systematic error range, as shown in Figure 10; the determination coefficient was one, and the residual plots are shown in Figure 11.
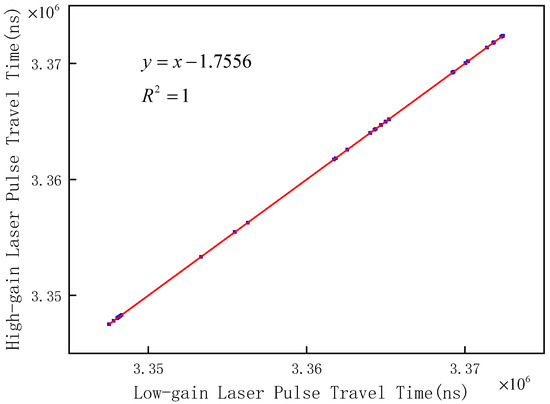
Figure 10.
Fitting results of the high- and low-gain time of flight.
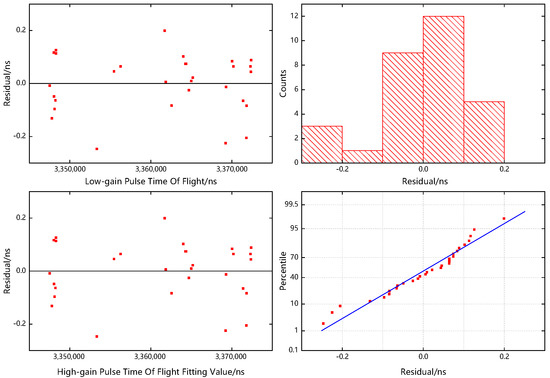
Figure 11.
Residual plots of the high- and low-gain TOF fitting, which are composed of the residual plot with the independent variable as abscissa (upper left), the residual plot with the fitted value of the dependent variable as abscissa (lower left), the histogram of the residuals (upper right), and the normal probability plot of the residuals (lower right).
The experiment calculated the low-gain channel laser pulse time of flight corresponding to the high-gain saturated waveform and used it as the laser pulse time of flight of the high-gain saturated waveform. The peak time parameter of the high-gain transmit waveform was added to calculate the receiving time of the high-gain saturated echo.
Since the “peak clipping” phenomenon of the saturated waveform had a nonlinear time delay in ranging, the ranging deviation changed with the change in saturation. We selected 51 groups of sample data with different saturations (saturation range 0–300%). By comparing the difference between the Gaussian fitting peak time of the saturated echo and the receiving time of the echo signal based on the dual-channel consistency solution, a functional relationship model between the deviation value and saturation was established. As shown in Figure 12, the goodness of fit of the model was 0.895, and the residual figure is shown in Figure 13.
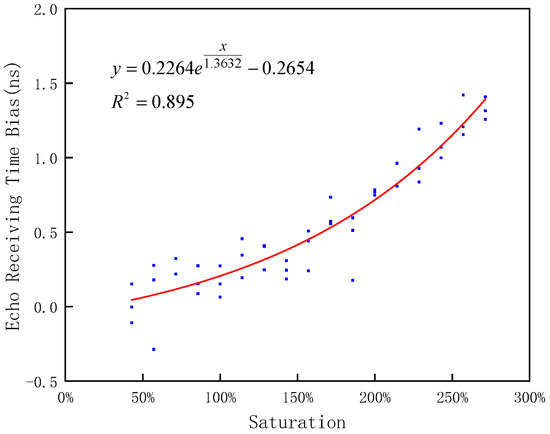
Figure 12.
The variation of the laser signal receiving time deviation with saturation.
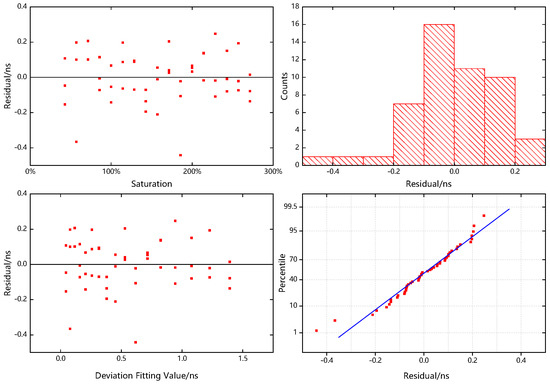
Figure 13.
Residual plots of the laser signal reception time deviation model, which are composed of the residual plot with the independent variable as abscissa (upper left), the residual plot with the fitted value of the dependent variable as abscissa (lower left), the histogram of the residuals (upper right), and the normal probability plot of the residuals (lower right).
The accuracy of the laser ranging value calculated by eliminating the saturated “dead time” was 0.322 m (2.15 ns), and the accuracy of the laser ranging value calculated directly from the waveform characteristic parameters was 0.106 m (0.7 ns). While the laser ranging value was calculated after the pulse time of flight delay compensation, the ranging accuracy was the highest, up to 0.021 m (0.14 ns). The compensation algorithm could effectively improve the range accuracy of the saturated laser pulse.
4.3. Experiment 2: Recovery of Characteristic Parameters of Saturated Waveform
The GF-7 laser dual-gain channel obtains the echo signal of the same pulse, and as a result, the peak intensity of the dual-channel wave is linearly correlated with the effective quantification range of the detector. A data set (containing 50 sets of full waveforms with unsaturated both high and low gain) was randomly selected as a sample for the experiment. By regression analysis of the peak intensity of the dual-channel unsaturated waveform, the fitting results of the peak intensity of the high- and low-gain echoes were obtained as shown in Figure 14, and the goodness of fit of the model was 0.992, with its residual plots shown in Figure 15. Using this linear regression model to compensate for the saturated waveform data of the high-gain channel, the peak intensity parameter of the high-gain saturated echo could be obtained.
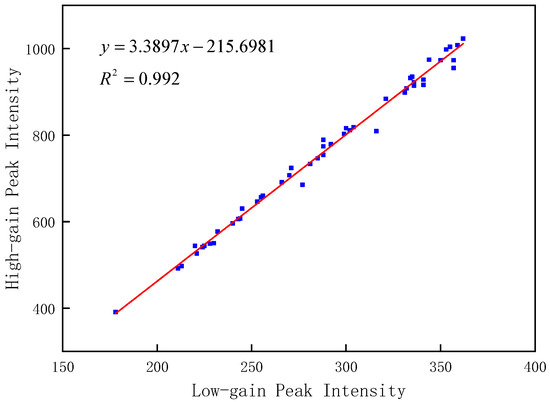
Figure 14.
Fitting results of the high- and low-gain peak intensity regression model.
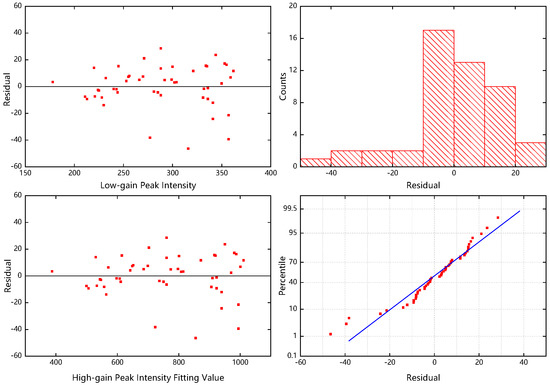
Figure 15.
Residual plots of the fitted high- and low-gain peak intensity regression model, which are composed of the residual plot with the independent variable as abscissa (upper left), the residual plot with the fitted value of the dependent variable as abscissa (lower left), the histogram of the residuals (upper right), and the normal probability plot of the residuals (lower right). The units of coordinate axes are arbitrary.
The unsaturated data sets of the same size from other tracks were selected experimentally, and the peak intensity solved from the laser measurements was used as the reference base to verify the calibration accuracy of the high-low gain peak intensity regression model in this article. Through the correlation analysis of the high- and low-gain peak intensity of the unsaturated data sets from two different tracks, it could be determined that the regression model was linear and had a consistent slope within a certain confidence interval (see the top of Figure 16). The regression model and the other tracks’ low-gain data were used to predict the relative high-gain peak intensity, and the peak intensity solved from the other tracks’ laser measurements were used as checkpoints to determine the relative correction error of the regression model. The experimental results showed that the relative correction accuracy of the model reached 98.2%, and its relative correction accuracy error distribution is shown at the bottom of Figure 16.
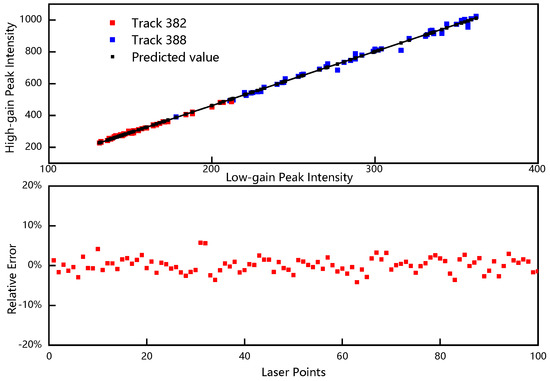
Figure 16.
The correlation analysis of the high- and low-gain peak intensity is shown at the top of the graph, where the red points are the measured values for track 382, the blue points are the measured values for track 388, and the black points are the predicted values calculated by the regression model. The relative correction error of the peak intensity of the laser waveform for the unsaturated data set is shown at the bottom of the figure.
Based on the saturated echo receiving time compensation model and peak intensity regression model, we compensated the original saturated waveform and obtained the echo pulse signals with different saturations, as shown in Figure 17.
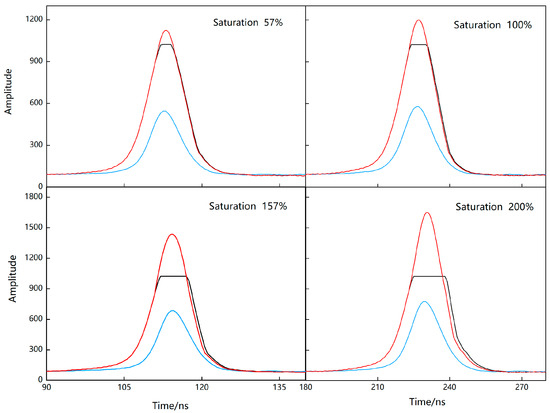
Figure 17.
Laser pulse saturation echo compensation results. The black solid line is the high-gain saturated echo, the blue solid line is the low-gain unsaturated echo, and the red solid line is the high-gain echo after saturation compensation.
5. Discussion
According to the operating mode of the space-borne laser altimeter, it is known that the different gain channels acquire the same pulse ranging information, and ideally, they have a linear correlation between the different gain channels. However, due to the laser pulse being affected by its own performance, clouds, atmosphere, ground features, and other factors in the process of propagation, the recorded echo signal is inevitably mixed with different degrees of noise, and in the process of data processing, some random noise values of the high- and low-gain waveforms as well as the accuracy of the waveform fitting can cause small errors in the ranging results. Therefore, during the verification of the GF-7 dual-channel ranging consistency, there was a phenomenon of high linear consistency without perfect linearity, and the fitting accuracy was almost 100 percent. In the subsequent experiments, we ignored these small errors and evaluated the accuracy of the compensation results based on consistent high- and low-gain ranging.
The method proposed in this paper is a waveform saturation compensation model constructed based on the consistency of geometric characteristics of the high- and low-gain channels of a space-borne laser altimeter. For the case of high-gain saturation and low-gain unsaturation, we could obtain the functional relationship between saturation and distance deviation according to the model (shown in Figure 12) to perform ranging compensation on the saturated waveform and then combine it with the peak intensity regression model to achieve the feature recovery of the saturated signals. However, for the case where both high- and low-gain waveforms are saturated, we could only compensate the ranging of laser waveforms with different gains by saturation, and feature recovery was not possible. In addition, the method is also relevant in single-channel space-borne laser altimeters such as the Chinese Terrestrial Ecosystem and Carbon Inventory Satellite (TECI-Satellite) which will be launched in the latter half of 2022.
6. Conclusions
In this study, the full-waveform data of the GF-7 space-borne laser altimeter were taken as the experimental object. Focusing on the issue of saturation of laser measurement waveform data recorded by a full waveform, the study uncovered a method for recovering the features of a saturated waveform signal. Based on the SCM, the echo pulse receiving time of the saturated waveform was corrected to improve the ranging accuracy of the saturated waveform data. The following conclusions were drawn:
- Based on the dual-channel ranging consistency, it was found that the laser saturation waveform had a nonlinear delay in calculating the pulse flight time.
- The pulse delay compensation model could be used to correct the range distance of the GF-7 space-borne laser altimeter saturated data and improve the ranging accuracy of saturated data. The ranging accuracy after correction by the SCM could be improved from 0.7 ns (0.11 m) to 0.14 ns (0.02 m).
- The compensation method proposed in this paper could effectively restore the features of saturated waveform signals, which is of great significance in the study of global elevation control point acquisition, forest parameter inversion, biomass estimation, and polar ice cover monitoring.
Author Contributions
X.F. and S.L. proposed the methodology and wrote the manuscript. S.L. contributed to improving the methodology and is the corresponding author. H.P. helped edit and improve the manuscript. Q.Y. contributed to methodological testing. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the project of the National Natural Science Foundation of China (No. 41901400 and 41971418), the project of the Natural Science Foundation of Hunan Province, China (grant No. 2020JJ1003 and grant No. 2022JJ30254), the project of the Scientific Research Fund of Hunan Provincial Education Department (grant No. 20C0800 and grant No. 19C0744), and the Gaofen Satellite Remote Sensing Surveying and Mapping Application Demonstration System (Phase II) of China (grant No. 42-Y30B04-9001-19/21).
Data Availability Statement
The data are not publicly available due to restrictions of privacy.
Acknowledgments
The authors would like to thank the Land Satellite Remote Sensing Application Center for providing the GF-7 satellite data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Schutz, B.E.; Zwally, H.J.; Shuman, C.A.; Hancock, D.; DiMarzio, J.P. Overview of the ICESat mission. Geophys. Res. Lett. 2005, 32, L21S01. [Google Scholar] [CrossRef] [Green Version]
- Zwally, H.J.; Schutz, B.; Abdalati, W.; Abshire, J.; Bentley, C.; Brenner, A.; Bufton, J.; Dezio, J.; Hancock, D.; Harding, D. ICESat’s laser measurements of polar ice, atmosphere, ocean, and land. J. Geodyn. 2002, 34, 405–445. [Google Scholar] [CrossRef] [Green Version]
- Zwally, H.J.; Yi, D.; Kwok, R.; Zhao, Y. ICESat measurements of sea ice freeboard and estimates of sea ice thickness in the Weddell Sea. J. Geophys. Res. Oceans 2008, 113, C02S15. [Google Scholar] [CrossRef] [Green Version]
- Tian, J.; Wang, L.; Li, X.; Yin, D.; Gong, H.; Nie, S.; Shi, C.; Zhong, R.; Liu, X.; Xu, R. Canopy height layering biomass estimation model (CHL-BEM) with full-waveform LiDAR. Remote Sens. 2019, 11, 1446. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Huang, H.; Gong, P.; Liu, C.; Li, C.; Li, W. Forest canopy height extraction in rugged areas with ICESAT/GLAS data. IEEE Trans. Geosci. Remote Sens. 2013, 52, 4650–4657. [Google Scholar] [CrossRef]
- Atwood, D.K.; Guritz, R.M.; Muskett, R.R.; Lingle, C.S.; Sauber, J.M.; Freymueller, J.T. DEM control in arctic Alaska with ICESat laser altimetry. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3710–3720. [Google Scholar] [CrossRef]
- Araki, H.; Tazawa, S.; Noda, H.; Ishihara, Y.; Goossens, S.; Sasaki, S.; Kawano, N.; Kamiya, I.; Otake, H.; Oberst, J.; et al. Lunar Global Shape and Polar Topography Derived from Kaguya-LALT Laser Altimetry. Science 2009, 323, 897–900. [Google Scholar] [CrossRef]
- Kamalakar, J.A.; Prasad, A.S.L.; Bhaskar, K.V.S.; Selvaraj, P.; Venkateswaran, R.; Kalyani, K.; Goswami, A.; Raja, V. Lunar Laser Ranging Instrument (LLRI): A tool for the study of topography and gravitational field of the Moon. Curr. Sci. 2009, 96, 512–516. [Google Scholar]
- Tong, X.H.; Li, L.Y.; Liu, S.J.; Xu, Y.S.; Ye, Z.; Jin, Y.M.; Wang, F.X.; Xie, H. Detection and estimation of ZY-3 three-line array caused by attitude oscillation. ISPRS-J. Photogramm. Remote Sens. 2015, 101, 291–309. [Google Scholar] [CrossRef]
- Guoyuan, L.; Xinming, T. Analysis and validation of ZY-3 02 satellite laser altimetry data. Acta Geod. Cartogr. Sin. 2017, 46, 1939. [Google Scholar]
- Li, G.; Tang, X.; Gao, X.; Wang, X.; Fan, W.; Chen, J.; Mo, F. Integration of ZY3-02 satellite laser altimetry data and stereo images for high-accuracy mapping. Photogramm. Eng. Remote Sens. 2018, 84, 569–578. [Google Scholar] [CrossRef]
- Xie, J.; Huang, G.; Liu, R.; Zhao, C.; Dai, J.; Jin, T.; Mo, F.; Zhen, Y.; Xi, S.; Tang, H. Design and data processing of China’s first spaceborne laser altimeter system for earth observation: GaoFen-7. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1034–1044. [Google Scholar] [CrossRef]
- Li, G.; Guo, J.; Tang, X.; Ye, F.; Zuo, Z.; Liu, Z.; Chen, J.; Xue, Y. Preliminary quality analysis of GF-7 satellite laser altimeter full waveform data. Int. Arch. Photogramm. Remote Sens. 2020, 43, 129–134. [Google Scholar] [CrossRef]
- Tang, X.; Xie, J.; Liu, R.; Huang, G.; Zhao, C.; Zhen, Y.; Tang, H.; Dou, X. Overview of the GF-7 laser altimeter system mission. Earth Space Sci. 2020, 7, e2019EA000777. [Google Scholar] [CrossRef]
- Tang, X.; Gao, X.; Cao, H.; Mo, F.; Wang, Z.; Xu, W.; Zhu, G.; Yue, Q.; Hu, F.; Zhu, H. The China ZY3-03 Mission: Surveying and mapping technology for high-resolution remote sensing satellites. IEEE Geosci. Remote Sens. Mag. 2020, 8, 8–17. [Google Scholar] [CrossRef]
- Xie, J.; Liu, R.; Mei, Y.; Liu, W.; Pan, J. Preliminary Pointing Bias Calibration of ZY3-03 Laser Altimeter. J. Geodes. Geo. Sci. 2021, 4, 91. [Google Scholar]
- Wang, X.; Cheng, X.; Gong, P.; Huang, H.; Li, Z.; Li, X. Earth science applications of ICESat/GLAS: A review. Int. J. Remote Sens. 2011, 32, 8837–8864. [Google Scholar] [CrossRef]
- Chen, Q. Retrieving vegetation height of forests and woodlands over mountainous areas in the Pacific Coast region using satellite laser altimetry. Remote Sens. Environ. 2010, 114, 1610–1627. [Google Scholar] [CrossRef]
- Fricker, H.; Borsa, A.; Minster, B.; Carabajal, C.; Quinn, K.; Bills, B. Assessment of ICESat performance at the salar de Uyuni, Bolivia. Geophys. Res. Lett. 2005, 32, L21S06. [Google Scholar] [CrossRef] [Green Version]
- Abshire, J.B.; Sun, X.; Riris, H.; Sirota, J.M.; McGarry, J.F.; Palm, S.; Yi, D.; Liiva, P. Geoscience laser altimeter system (GLAS) on the ICESat mission: On-orbit measurement performance. Geophys. Res. Lett. 2005, 32, L21S02. [Google Scholar] [CrossRef] [Green Version]
- Letu, H.; Hara, M.; Tana, G.; Nishio, F. A saturated light correction method for DMSP/OLS nighttime satellite imagery. IEEE Trans. Geosci. Remote Sens. 2011, 50, 389–396. [Google Scholar] [CrossRef]
- Mei, Z.; Zhi-min, Z.; Yun-kai, D. Research on the Saturated Raw Data Correction Method for SAR Application. J. Electron. Inf. Technol. 2007, 29, 2114–2116. [Google Scholar]
- Sun, X.; Abshire, J.; Yi, D. Geoscience Laser Altimeter System-Characteristics and Performance of the Altimeter Receiver. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 8–12 December 2003; p. C32A-0432. [Google Scholar]
- Sun, X.; Abshire, J.; Yi, D.; Fricker, H. ICESat receiver signal dynamic range assessment and correction of range bias due to saturation. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 12–16 December 2005; p. C34A-07. [Google Scholar]
- Sun, X.; Abshire, J.B.; Borsa, A.A.; Fricker, H.A.; Yi, D.; DiMarzio, J.P.; Paolo, F.S.; Brunt, K.M.; Harding, D.J.; Neumann, G.A. ICESAT/GLAS altimetry measurements: Received signal dynamic range and saturation correction. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5440–5454. [Google Scholar] [CrossRef] [PubMed]
- ICESat/GLAS Data: Description of Past Data Releases. Available online: http://nsidc.org/data/icesat/past_releases.html (accessed on 27 June 2022).
- Xie, H.; Li, B.; Tong, X.; Zhang, X.; He, T.; Dai, J.; Huang, G.; Zhang, Z.; Liu, S. A Planimetric Location Method for Laser Footprints of the Chinese Gaofen-7 Satellite Using Laser Spot Center Detection and Image Matching to Stereo Image Product. IEEE Trans. Geosci. Remote Sens. 2021, 59, 9758–9771. [Google Scholar] [CrossRef]
- Aiyan, G.; Dai Jun, Z.C. Design and on-orbit validation of GF-7 satellite laser altimeter. Spacecr. Eng. 2020, 39, 43–48. [Google Scholar]
- Borsa, A.A.; Fricker, H.A.; Brunt, K.M. A terrestrial validation of ICESat elevation measurements and implications for global reanalyses. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6946–6959. [Google Scholar] [CrossRef]
- Zhiqiang, Z.; Xinming, T.; Guoyuan, L.; Song, L. Adaptive Gaussian filtering of the full waveform of GF-7 satellite laser altimeter. Infrared Laser Eng. 2020, 49, 20200251. [Google Scholar] [CrossRef]
- Wagner, W.; Ullrich, A.; Ducic, V.; Melzer, T.; Studnicka, N. Gaussian decomposition and calibration of a novel small-footprint full-waveform digitising airborne laser scanner. ISPRS-J. Photogramm. Remote Sens. 2006, 60, 100–112. [Google Scholar] [CrossRef]
- Zhang, Z.; Xie, H.; Tong, X.; Zhang, H.; Tang, H.; Li, B.; Wu, D.; Hao, X.; Liu, S.; Xu, X. A Combined Deconvolution and Gaussian Decomposition Approach for Overlapped Peak Position Extraction From Large-Footprint Satellite Laser Altimeter Waveforms. IEEE J. Sel. Top. App. Earth Obs. Remote Sens. 2020, 13, 2286–2303. [Google Scholar] [CrossRef]
- Wang, Y.; Ni, W.; Sun, G.; Chi, H.; Zhang, Z.; Guo, Z. Slope-adaptive waveform metrics of large footprint lidar for estimation of forest aboveground biomass. Remote Sens. Environ. 2019, 224, 386–400. [Google Scholar] [CrossRef]
- Ke, H.; Song, L.; Yue, M.; Xin, T.; Hui, Z.; Zhi-Yu, Z. Theoretical model and correction method of range walk error for single-photon laser ranging. Acta Phys. Sin. 2018, 67, 221401. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).