Abstract
This paper investigates the direction-of-arrival (DOA) estimation-based target localization problem using an array radar under complex multipath propagation scenarios. Prevalent methods may suffer from performance degradation due to the deterministic signal model mismatch, especially when the exact knowledge of a propagation environment is unavailable. To cope with this problem, we first establish an improved signal model of multipath propagation for low-angle target localization scenarios, where the dynamic nature of convoluted interferences induced by complex terrain reflections is taken into account. Subsequently, an iterative implementation-based target localization algorithm with the improved propagation model is proposed to eliminate the detrimental effect of coherent interferences on target localization performance. Compared to existing works, the proposed algorithm can maintain satisfactory estimation performance in terms of target location parameters, even in severe multipath interference conditions, where the decorrelation preprocessing and accurate knowledge about the multipath propagation environment are not required. Both simulation and experimental results demonstrate the effectiveness of the proposed propagation model and localization algorithm.
1. Introduction
Target localization is a fundamental task of great importance, arising in various radar applications such as tracking targets of interest [1,2,3]. However, one of the challenges for an array radar system to achieve accurate height measurement of low-angle targets is the presence of complex reflections from the Earth’s ground surface, i.e., multipath propagation, resulting in severe estimation error in terms of target location parameters [4,5,6,7]. The difficulty of solving this problem lies in the fact that target signals are corrupted by spatially and temporally convoluted ground reflections. In such a scenario, classical DOA estimation-based target localization methods suffer from the influence of coherent multipath interferences, resulting in localization performance degradation, especially when the exact prior knowledge of the practical propagation environment is unavailable.
During the last few decades, the target localization problem has been investigated from different aspects (see, for example, [8,9,10,11,12] and references therein). High-resolution subspace-based algorithms, such as the multiple signal classification (MUSIC) algorithm [8], have been developed to achieve satisfactory target localization performance, where the additional preprocessing with spatial smoothing (SS) technique [9] is commonly employed to compensate for the rank deficiency of the signal covariance matrix, such as arising in a multipath propagation scenario. However, such preprocessing will reduce a radar system’s degrees of freedom, resulting in angular resolution deterioration. While another group of maximum likelihood (ML) algorithms can be directly employed in the presence of multipath interferences due to the lower sensitivity to coherent signal effects [13,14,15], this kind of approach would need to address the nonlinear optimization problem, resulting in high computational complexity [16]. To ameliorate this issue, the alternating projection (AP) technique is employed to accelerate ML [17]. Moreover, the refined maximum likelihood (RML) method [12] is also investigated to achieve satisfactory estimates of target location parameters with low computational load by exploring the exact knowledge of the multipath propagation environment. However, this method may encounter a severe performance deterioration due to the model mismatch under rugged topography conditions.
It is worth mentioning that existing methods, such as the RML algorithm, commonly rely on an implicit assumption of multipath propagation within the signal model. This assumption calls for the ground surface to be flat, resulting in a deterministic signal model that incorporates the time-invariant propagation relationship between a target and its single reflecting path. While this simplified model can be employed in the scenario involving a smooth ground surface, it may produce localization performance degradation in practice due to the dynamic distribution of complex terrain reflections [18,19,20]. Unlike target localization methods employing the deterministic signal model, the compressive sensing-based algorithm can achieve satisfactory estimation performance of target location parameters by exploiting the low-rank property [18,19]. However, the performance of such algorithms may degrade when the rank-1 constraint is not satisfied. In addition, the model uncertainty induced by convoluted ground reflections is also not taken into consideration. Accurate localization for targets of interest is crucial for modern radar systems under a multipath interference scenario when the exact knowledge of the propagation environment is unavailable. Therefore, it is significant and urgent to address the abovementioned problems.
In this paper, we aim to improve the estimation accuracy of target location parameters under a complex multipath interference scenario. By considering the uncertainty of exact prior information pertaining to the propagation environment in practical applications, an improved multipath propagation model is first established for low-angle target localization scenarios, where the impractical constraint imposed by the deterministic propagation model is avoided. In addition, such a formulation enhances the accuracy and robustness of modeling dynamic multipath effects induced by practical terrain reflections. Based on the improved multipath propagation model, the target localization problem is reformulated as recovering the sparse spectrum of spatial signals by employing an overcomplete representation framework for radar observations. An iterative implementation-based target localization algorithm is then proposed to interpret accurate target location parameters by jointly optimizing an adaptive filter bank and a parameterized sparse coefficient vector. Finally, the model uncertainty induced by dynamic terrain reflections is taken into account to improve the target localization performance. Compared to prevalent approaches, the proposed algorithm can effectively ameliorate the influence of multipath interferences without the need of spatial smoothing preprocessing and exact knowledge of multipath propagation scenarios, such as the initialization of path detection and multipath channel parameters. Moreover, target location parameters can be achieved from convoluted multipath interferences with improved estimation accuracy.
This paper is organized as follows. Section 2 formulates the improved signal model of multipath propagation under a low-angle target localization environment. The proposed target localization algorithm is presented in Section 3. Section 4 demonstrates the performance of the proposed propagation model and localization algorithm via both simulation and experimental results under various scenarios. Finally, conclusions are given in Section 5.
2. Multipath Propagation Signal Model
Figure 1 illustrates the improved multipath propagation model under the scenario involving convoluted ground reflections. Due to the multipath propagation phenomenon, an M-channel isotropic array radar system is impinged by distinct paths from K narrowband targets located in the far-field at directions , where the target index . We first define as the path index, with being the number of reflecting paths corresponding to the propagation of the kth target signal such that the ith reflecting path originates from direction . Points , , and in Figure 1 denote the location of the bottom sensor of the array radar, the ith reflecting position for the kth target, and the kth target, respectively. Variables and are, respectively, the height of the bottom sensor and the height of the kth target. In addition, and denote the distance between the radar position and the kth target and the distance between the radar position and the ith image of the kth target, respectively. Variables and denote the vertical distance from the kth target to its ith reflecting surface and the grazing angle of the ith reflecting path corresponding to the kth target, respectively.
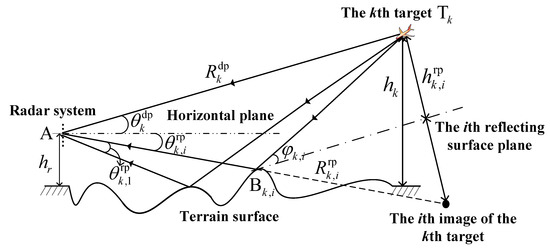
Figure 1.
The improved multipath propagation model for a low-angle target localization scenario, where the dash-dotted line denotes the ith reflecting surface plane corresponding to the kth target.
It is worth highlighting that, for the kth target, multipath reflections with the ith reflecting ground surface will generate four propagation paths during the radar’s transmission and reception processes, which is shown in Table 1. As reported in [21], the transmitted signal that propagates through the direct and reflecting paths should simultaneously illuminate the kth target and perform a coherent superposition. We assume that the superposition signal at the kth target is
where , , , and denote the signal power, the complex envelope, the carrier frequency of the transmitted signal, and the phase term, respectively. According to the reciprocal theorem, the signal received by the mth channel can be expressed as
where is the scattering coefficient of the kth target, denotes the specular reflection coefficient of the ith reflecting path corresponding to the kth target, and are, respectively, time delays of the direct path and the ith reflecting path corresponding to the kth target with respect to the mth sensor, and is the additive Gaussian white noise of the mth sensor.

Table 1.
Multipath propagation of the kth target with its ith reflecting path.
By selecting a reference antenna sensor, time delays and can be, respectively, written as
and
where denotes the time delay caused by the distance from the kth target to the reference antenna sensor, with c being the light speed; denotes the time difference induced by the length difference between the direct path and the ith reflecting path corresponding to the kth target; and are relative time delays measured at directions and , respectively. Since the transmitted waveform is narrowband, we have
Substituting Equations (3)–(5) into Equation (2) results in
where and , with denoting the wavelength.
After demodulation and A/D conversion, signals received by the array radar can be expressed via an vector
where and denote array steering vectors towards directions and , respectively, , with L being the number of available snapshots, and with denoting the transpose operator.
Equation (7) can be rewritten in matrix form as
where , is the array manifold matrix defined as
with , and the vector
with for the direct-path component of the kth target.
It is important to note that the channel parameter in Equation (2) reveals the physical interaction between the ith reflecting signal and the corresponding area of the illuminated ground surface. In general, is defined as the ratio of the electric field phasor of the kth target’s ith reflecting signal to that of the kth target’s direct-path signal, which can be decomposed by [22]
where , , and denote, respectively, the Fresnel reflection coefficient, the divergence factor, and the specular scattering factor for the ith multipath corresponding to the kth target. In particular, expressions of for vertical and horizontal polarizations, which are determined by the radar polarization mode, the ith reflecting path’s grazing angle corresponding to the kth target, and the radar wavelength, are, respectively, given as [23,24]
and
In Equations (12) and (13), the variable denotes the complex dielectric constant defined as , where denotes the relative dielectric constant, denotes the conductivity of the ground surface corresponding to the ith reflecting path of the kth target, and the constant . The variable is employed due to the curvature of the Earth’s surface [25]. It is worth mentioning that the proposed propagation model can be easily extended to take into account the spherical Earth model, while the effect of the Earth’s curvature is not discussed in this paper. In addition, models the reduction effect induced by the roughness of the illuminated ground surface [26], which is expressed by
where , with being the standard deviation of height distribution for the illuminated terrain surface. Given the knowledge of array observations , the key objective is to achieve accurate location parameters and for targets of interest from the complex multipath interference environment.
3. Methodology of Target Localization
3.1. Overcomplete Representation Framework
To exploit the sparse characteristic of incident signals in the spatial domain, we start to reformulate the array observation vector in Equation (8) as a parameterized version via employing the overcomplete representation [27,28,29,30,31,32]. This reformulation allows for the transformation of estimating target location parameters into the problem of achieving the sparse (parameterized) spatial spectrum of incident path signals. Specifically, let denote the set of potential locations for spatial paths; an overcomplete dictionary can be constructed by collecting steering vectors for each element of such that
where denotes a sampling grid set covering , and is the number of predefined directions. We note that is independent of since is predefined. With reference to the dictionary , Equation (8) is rewritten as
where is the parameterized coefficient vector holding potential spatial signals over the sampling grid set . It can be inferred from (8) and (16) that the gth element of is
When a sufficient sampling quantization is employed, should, in theory, be a zero vector except for non-zero elements corresponding to spatial paths. It is important to highlight that the overcomplete representation of array observation in Equation (16) reformulates the target localization problem as obtaining parameterized coefficient vectors , from which target location parameters can be extracted. To this end, we aim to jointly optimize an adaptive filter bank and the parameterized sparse coefficient vector.
3.2. Iterative Implementation-Based Target Location Parameter Extraction
With reference to Equation (16), the estimate of the adaptive filter bank can be obtained by minimizing the constrained minimum mean-square error (MMSE) problem [33,34]
where , , and are, respectively, the expectation operator, the , and the conjugate transpose. In Equation (18), is a closed set defined as
where denotes the auto-covariance of , denotes the trace of a matrix, and is employed to bound the variance of .
For an arbitrary matrix , the -weighted norm of is defined by
where is an positive definite matrix. In particular, the -weighted projection of an arbitrary matrix onto a closed set is defined by
According to Theorem 2 stated in [35], the matrix that minimizes the constrained MMSE problem in Equation (18) can be achieved by
In Equation (22), is the unconstrained MMSE estimator given by
where is the Moore–Penrose pseudo-inverse of and is the cross-covariance matrix of and . By utilizing the Lagrange multiplier, the solution to (22) can be achieved by , where denotes the largest value for which holds.
Substituting (16) in (23) yields
where denotes the noise correlation matrix, which can be generally estimated by
where denotes the number of time samples during an observation interval in which no target signal response is present.
While the diagonal elements of the correlation matrix reveal the spatial power distribution of incident path signals, such information, in general, cannot be determined a priori. To address this issue, we employ an iterative implementation strategy [36,37] such that the initialization of the parameterized vector can be achieved via
We define as the iteration index, with Q being the maximum iteration number. Let and , being the estimated adaptive filter bank and parameterized vector in the qth iteration, respectively. With reference to Equations (24) and (26), the estimate of in the th iteration can be achieved by
In Equation (27), , where ⊙ and denote the Hadamard product and the identity matrix of size , respectively. The Hadamard product operation is employed based on the fact that the temporal correlation is a statistical measurement over time and joint optimization essentially operates on each snapshot independently, or, at best, combines the independent estimations of spatial power distribution via noncoherent integration [38]. Given , the estimated parameterized vector in the th iteration can then be determined via
It is worth highlighting that the iterative application between (27) and (28) provides a stepwise refinement of the spatial resolution until only the locations of incident paths are preserved. During interim iterations, however, the estimated power distribution of spatial paths over components of the determined parameterized coefficient vector in Equation (28) produces an intrinsic scale factor that may be very small, which will detrimentally affect the power estimate of spatial paths and thus decrease the estimation accuracy of location parameters. To ameliorate this issue, the energy normalization operation at each iteration is employed to guarantee component estimates of the parameterized coefficient vector, where the recovered signal possesses the same energy as the actual received signal. With reference to Equation (28), the th energy estimate of the recovered signal can be achieved by
Therefore, the estimate in Equation(28) can then be modified as the energy-normalized version such that
where denotes the energy of the received signal.
3.3. Model Uncertainty Enhancement
While perfect knowledge of the overcomplete dictionary in Equation (16) is generally assumed, such an assumption may not be valid in practice due to the convoluted terrain reflection, resulting in model uncertainties. This limitation motivates us to take into account the modeling error for the iterative implementation method to enhance the target localization performance in practical applications. To this end, the signal model in Equation (16) is generalized as
where the vector incorporates unknown modeling errors. The mth element of can be expressed as , with denoting the deviation that characterizes the modeling error effect in the mth sensor. We assume that the distribution of modeling errors is i.i.d. for each sensor with mean-zero and variance of . In addition, modeling errors are assumed to be independent with the target signal and direction. Therefore, Equation (31) can be rewritten as
where
with denoting the all-one column vector of size .
Substituting (32) in (23) results in
With reference to Equations (30), (32), and (34), the th estimate of in Equation (27) can be modified as
where
By utilizing Equation (35), the th estimate of the parameterized vector in the presence of model uncertainty can be achieved by
We note that Equations (35)–(38) serve as the core of the iterative implementation-based target localization algorithm, where the integration of time samples and the model uncertainty are considered. The above process is repeated until a stable power distribution of spatial signals is obtained or a predefined maximum iteration number is reached, and the final estimate can then be achieved. Elements within , therefore, reveal the estimate of energy distribution corresponding to the spatial signals. Let be the set of indices g that generate peaks to the following function
where
and is the gth element of . Therefore, the DOA estimate set can be achieved by .
It is important to note that the kth target direction estimate denoted by can be identified from based on the geometry relationship between the direct and reflecting paths corresponding to the kth target [18]. With reference to the geometrical relationship in the improved multipath propagation model shown in Section 2, the kth target height can then be achieved by
For clarity, the procedure for extracting target location parameters of the proposed algorithm is summarized in Algorithm 1.
| Algorithm 1: The proposed target height estimation algorithm |
 |
4. Results
4.1. Simulation Results with Synthetic Data
We verify the performance of the proposed algorithm via simulation results, where an uniform linear array (ULA) radar of 20 isotropic antenna sensors spaced a half-wavelength apart is employed. To assess the performance of different algorithms, comparisons under various scenarios are conducted with some baseline algorithms, including the RML algorithm [12], the AP-ML algorithm [17], the SS-MUSIC algorithm [9], the rank-1 constraint-based method [18], and the OMP algorithm [32]. The estimation performance of target location parameters is evaluated via the root mean-square error (RMSE), defined by
and
where denotes the predefined number of Monte Carlo trials; and are, respectively, the DOA and height estimates of the kth target in the pth simulation trial.
We first validate the localization performance of the respective algorithms under a multipath propagation scenario, where a single target of interest with two coherent interference paths is considered. The parameter list used for this simulation setup is shown in Table 2. It is worth mentioning that the exact knowledge of the multipath propagation scenario is unknown beforehand. In Figure 2, we present the RMSE result of the respective algorithms versus the input signal-to-noise ratio (SNR). We can note that a severe performance degradation occurs for the RMLE algorithm due to the mismatch of the classical two-ray signal model, even under high SNR conditions. This result explains why the deterministic propagation model-based methods cannot achieve satisfactory localization performance in practical applications. We can also note from Figure 2 that the estimation accuracy obtained by the SS-MUSIC algorithm is worse than that obtained by the AP-ML algorithm, the OMP algorithm, the rank-1 constraint-based method, and the proposed algorithm when SNR is larger than dB. This is because the decorrelation preprocessing employed in the SS-MUSIC approach decreases the angular resolution. In addition, the rank-1 constraint-based method, the OMP algorithm, and the AP-ML approach show similar performance, while the proposed algorithm exceeds the other five algorithms. These results indicate that the proposed algorithm can obtain satisfactory estimation performance for target location parameters under the coherent multipath environment considered in this simulation, where the requirement for exact knowledge of the propagation scenario can be avoided.

Table 2.
Parameter list for the first simulation.
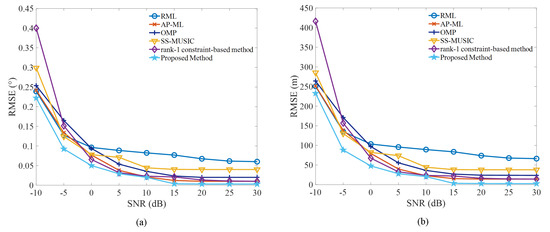
Figure 2.
Comparison of RMSE results in terms of target location parameter estimates versus input SNR under the scenario involving a single target and two coherent interference paths. (a) The estimate result of target direction. (b) The estimate result of target height.
In the second simulation, we consider a more generalized scenario to evaluate the parameter estimation performance of the proposed algorithm, where two targets with three coherent reflection interferences are employed. Parameters utilized in this simulation are shown in Table 3. Similarly, the exact knowledge of the propagation environment is also unknown for this simulation. We compare the estimation performance of the proposed algorithm and baseline algorithms; RMSE results of target location parameters versus input SNRs for targets with different height values are shown in Figure 3a,b and Figure 3c,d, respectively.

Table 3.
Parameter list for the second simulation.
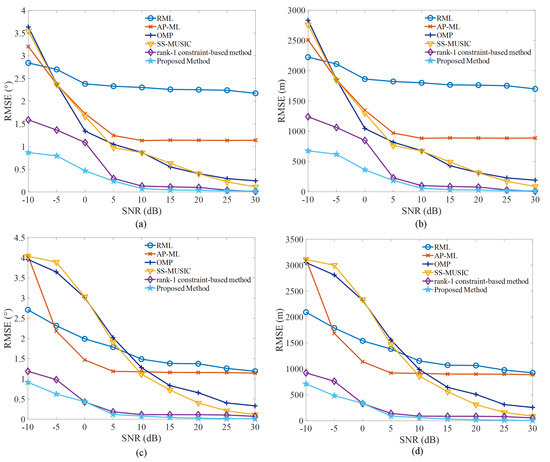
Figure 3.
Comparison of RMSE results in terms of target location parameter estimates under the multipath environment involving two targets with three coherent interference paths. (a) Direction estimate of the target with km. (b) Height estimate of the target with km. (c) Direction estimate for the target with km. (d) Height estimate for the second target with km.
We can note from Figure 3 that both the RML and the AP-ML algorithms suffer from a severe impact induced by ground interference in this scenario. As a result, it is difficult for them to achieve effective target localization performance even under high SNR conditions. Furthermore, the OMP and the SS-MUSIC algorithms are also influenced by the detrimental effect contributed by the complex propagation environment, especially for the low SNR conditions. On the contrary, it is worth highlighting that the localization performance achieved by the proposed algorithm is better than that achieved by other comparison algorithms under the same SNR condition. These results indicate that the proposed algorithm can achieve satisfactory estimation performance for target location parameters under the considered multipath interference scenario.
4.2. Experimental Results with Real Measured Data
We show experimental results derived from real measured datasets to demonstrate the effectiveness of the proposed algorithm in a realistic target localization scenario involving multipath propagation. The utilized dataset was collected by an experimental 8-channel array radar, where the adjacent sensors were separated by half a wavelength. It is important to note that the employed array radar was located in a rugged terrain environment, where the ground surface reflection would generate convoluted multipath interferences. In particular, the original radar observation data were processed by several preprocessing operations, including the pulse compression (PC), the moving target indication (MTI), and the constant false alarm detection (CFAD), to detect and track the target. The true values of target direction and distance relative to the radar position across the observation time, which were achieved by the global position system (GPS), are shown in Figure 4 and Figure 5, respectively. It can be observed that, during the observation period, the direction and distance of the target vary from to and km to km, respectively.
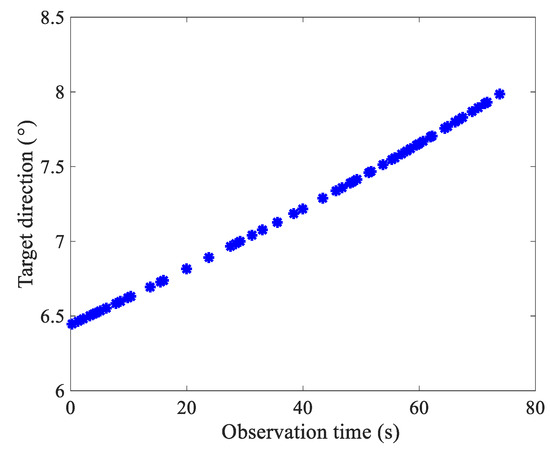
Figure 4.
The ground truth of target direction recorded by the global position system across the observation time.
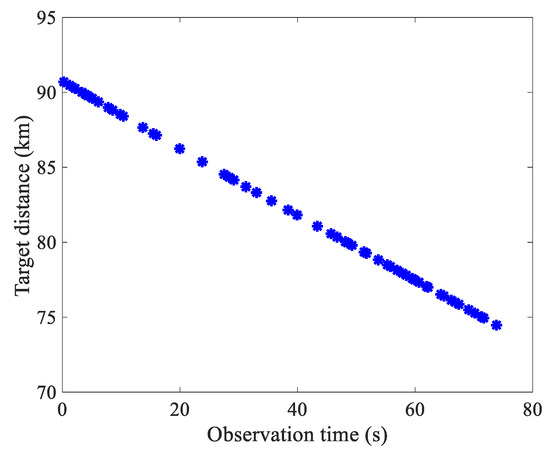
Figure 5.
The ground truth of target distance recorded by the global position system across the observation time.
The processed results of target direction and height obtained by the respective algorithms are given in Figure 6. We can note that the RML algorithm, the AP-ML algorithm, the OMP algorithm, the SS-MUSIC algorithm, and the rank-1 constraint-based method are influenced to varying degrees by convoluted reflection interferences for most of the observation time. The result reveals that these four algorithms produce more significant estimation fluctuations than the proposed algorithm. As a result, they cannot accurately estimate target location parameters in this realistic environment. In contrast, the proposed algorithm outperforms the baseline algorithms and can achieve relatively satisfactory target angle and height estimates. In addition, a comparison result of the average running time for different methods at one observation time index is shown in Table 4. These experiments were implemented using 64-bit MATLAB R2021b on a Windows 11 system computer with a 2.3-GHz Intel Core i7 CPU and 16 GB memory. The result in Table 4 shows that the proposed algorithm achieves a significant estimation performance improvement with slightly more computation time compared to the RML algorithm or the SS-MUSIC algorithm.
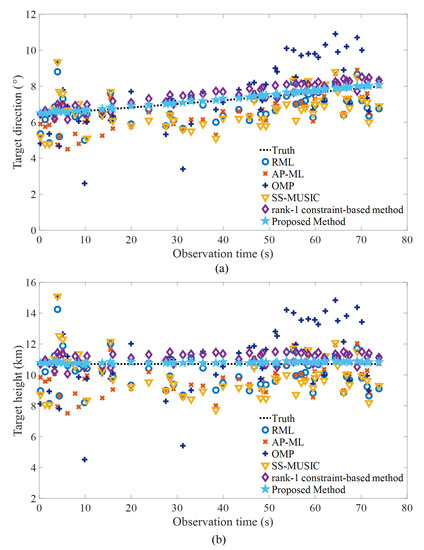
Figure 6.
Estimation results of target location parameter across the observation time. (a) Target direction estimates achieved by different algorithms. (b) Target height estimates achieved by different algorithms.

Table 4.
Average running times of different algorithms.
To validate the robustness performance in terms of the location parameter estimation of the proposed algorithm, Figure 7 shows the statistical result for target height estimates of the respective algorithms under different threshold values. We note that the proposed algorithm can achieve better estimation performance than the other four baseline algorithms at most threshold value points; it can consistently estimate the target location parameter. In particular, estimation percentages of the RML algorithm, the AP-ML algorithm, the OMP algorithm, the SS-MUSIC algorithm, and the rank-1 constraint-based method are, respectively, , , , , and when the threshold value is equal to 150 m. On the contrary, the proposed algorithm achieves a estimation percentage at the same threshold value. The results in Figure 6 and Figure 7 indicate that the proposed algorithm can significantly improve the parameter estimation accuracy in the realistic multipath propagation environment.
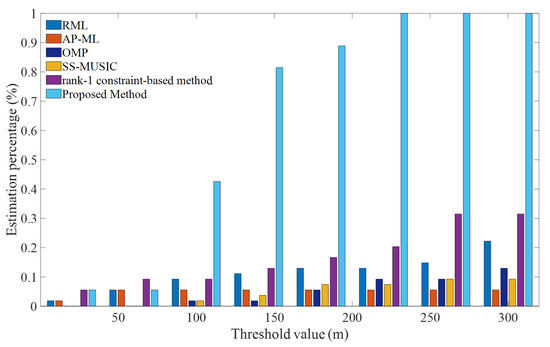
Figure 7.
Statistical result of the estimation percentage in terms of target height across different threshold values.
5. Conclusions
We studied the DOA estimation-based target localization problem under complex multipath effects without the exact knowledge of the propagation environment. First, an improved multipath propagation model for target localization under multipath propagation scenarios was established, where the impractical assumption within the classical deterministic propagation model has been avoided. Therefore, the accuracy and generalization ability of the propagation signal model related to the array observation can be improved. Then, after analyzing the propagation mechanism of the multipath channel parameter, the iterative implementation-based target localization algorithm was proposed to alleviate the detrimental effect of the convoluted coherent interference due to multipath propagation on target location parameter estimates. It has been shown by simulation and experimental results that the proposed algorithm can achieve satisfactory estimation performance for target location parameters compared with other baseline methods.
Author Contributions
Y.L. conducted the literature review and wrote the paper. H.L. supervised the overall project. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China under Grant 62192714.
Data Availability Statement
The data presented in this study are available on request from the author.
Acknowledgments
The authors would like to thank the reviewers for their time and effort.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yang, R.; Bar-Shalom, Y.; Ng, G.W. Altitude estimation using multipath with a two-dimensional radar over spherical earth. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 770–782. [Google Scholar] [CrossRef]
- Bosse, E.; Turner, R.M.; Lecours, M. Tracking swerling fluctuating targets at low altitude over the sea. IEEE Trans. Aerosp. Electron. Syst. 2002, 27, 806–822. [Google Scholar] [CrossRef]
- Liu, Y.B.; Wang, C.Y.; Gong, J.; Tan, M.; Chen, G. Robust suppression of deceptive jamming with VHF-FDA-MIMO radar under multipath effects. Remote Sens. 2022, 14, 942. [Google Scholar] [CrossRef]
- Naseri, H.; Koivunen, V. Cooperative simultaneous localization and mapping by exploiting multipath propagation. IEEE Trans. Signal Process. 2017, 65, 200–211. [Google Scholar] [CrossRef]
- Liu, F.; Wang, J.; Sun, C.; Du, R. Spatial differencing method for DOA estimation under the coexistence of both uncorrelated and coherent signals. IEEE Trans. Antennas Propag. 2012, 60, 2052–2062. [Google Scholar] [CrossRef]
- Zhao, J.; Tian, Y.; Wen, B.; Tian, Z. Coherent DOA estimation in sea surface observation with direction-finding HF radar. IEEE Trans. Geosci. Remote Sens. 2021, 59, 6651–6661. [Google Scholar] [CrossRef]
- Bourlier, C.; Kubické, G. Ground wave propagation along an inhomogeneous rough surface in the HF band: Millington effect for a flat earth. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1374–1382. [Google Scholar] [CrossRef]
- Schmidt, R.O. A Signal Subspace Approach to Multiple Emitter Location and Spectral Estimation. Ph.D. Dissertation, Stanford University, Stanford, CA, USA, 1981. [Google Scholar]
- Pillai, S.U.; Kwon, B.H. Forward/backward spatial smoothing techniques for coherent signal identification. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 8–15. [Google Scholar] [CrossRef] [Green Version]
- Nielsen, U.; Yan, J.; Gogineni, S.; Dall, J. Direction-of-arrival analysis of airborne ice depth sounder data. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2239–2249. [Google Scholar] [CrossRef] [Green Version]
- Hizal, A.; Koc, S. Mitigating the multipath effects of low angle monopulse tracking by even difference pattern. In Proceedings of the European Radar Conference, Amsterdam, The Netherlands, 31 October–2 November 2012; pp. 290–293. [Google Scholar]
- Lo, T.; Litva, J. Use of a highly deterministic multipath signal model in low-angle tracking. IEE Proc. F-Radar Signal Process. 1991, 2, 163–171. [Google Scholar] [CrossRef]
- Djeddou, M.; Belouchrani, A.; Aouada, S. Maximum likelihood anglefrequency estimation in partially known correlated noise for low-elevation targets. IEEE Trans. Signal Process. 2005, 53, 3057–3064. [Google Scholar] [CrossRef]
- Stoica, P.; Nehorai, A. Performance study of conditional and unconditional direction-of-arrival estimation. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 1783–1795. [Google Scholar] [CrossRef]
- Schweppe, F. Sensor-array data processing for multiple-signal sources. IEEE Trans. Inf. Theory. 1968, 14, 294–305. [Google Scholar] [CrossRef]
- Zhou, Z.; Christensen, M.G.; Jensen, J.R.; So, H.C. Joint DOA and fundamental frequency estimation based on relaxed iterative adaptive approach and optimal filtering. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Vancouver, BC, Canada, 26–31 May 2013; pp. 6812–6816. [Google Scholar]
- Choi, Y.H. Alternating projection for maximum-likelihood source localization using eigendecomposition. IEEE Signal Process. Lett. 1999, 6, 73–75. [Google Scholar] [CrossRef]
- Liu, Y.; Jiu, B.; Xia, X.-G.; Liu, H.; Zhang, L. Height measurement of low-angle target using MIMO radar under multipath interference. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 808–818. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, H.; Wang, L.; Bi, G. Target localization in high-coherence multipath environment based on low-rank decomposition and sparse representation. IEEE Trans. Geosci. Remote Sens. 2020, 58, 6197–6209. [Google Scholar] [CrossRef]
- Trizna, D.B. A model for brewster angle damping and multipath effects on the microwave radar sea echo at low grazing angles. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1232–1244. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, H.; Xia, X.-G.; Zhang, L.; Jiu, B. Projection techniques for altitude estimation over complex multipath condition based VHF radar. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 2362–2375. [Google Scholar] [CrossRef]
- Blair, W.D.; Brandt-pearce, M. Statistic of monopulse measurements of Rayleigh targets in the presence of specular and diffuse multipath. In Proceedings of the IEEE Radar Conference, Atlanta, GA, USA, 1–3 May 2001; pp. 369–375. [Google Scholar]
- Jiang, W.; Zhang, M.; Wei, P.; Nie, D. Spectral decomposition modeling method and its application to EM scattering calculation of large rough surface with SSA method. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2015, 8, 1848–1854. [Google Scholar] [CrossRef]
- Takahashi, R.; Hirata, K.; Maniwa, H. Altitude estimation of low elevation target over the sea for surface based phased array radar. In Proceedings of the IEEE Radar Conference, Arlington, VA, USA, 10–14 May 2010; pp. 123–128. [Google Scholar]
- Watson, G.A.; Mccabe, D.H. Benchmark Problem with a Multisensory Framework for Radar Resource Allocation and Tracking of Highly Maneuvering Targets, Closely-Spaced Targets, and Targets in the Presence of Sea-Surface-Induced Multipath; Technical Report NSWCDD/TR-99/32; Defense Technical Information Center: Fort Belvoir, VA, USA, 1999.
- Northam, D.Y. A Stochastic Simulation of Low Grazing Angle, Forward Scatter, Over-Water Multipath Effects; Technical Report 5658; Naval Research Laboratory: Washington, DC, USA, 1981. [Google Scholar]
- Malioutov, D.; Cetin, M.; Willsky, A. A sparse signal reconstruction perspective for source localization with sensor arrays. IEEE Trans. Signal Process. 2005, 53, 3010–3022. [Google Scholar] [CrossRef] [Green Version]
- Model, D.; Zibulevsky, M. Signal reconstruction in sensor arrays using sparse representations. Signal Process. 2006, 86, 624–638. [Google Scholar] [CrossRef]
- Ma, D.D.; Yuan, Y.; Wang, Q. Hyperspectral anomaly detection via discriminative feature learning with multiple-dictionary sparse representation. Remote Sens. 2018, 10, 745. [Google Scholar] [CrossRef] [Green Version]
- Sun, L.; Cheng, Q.H.; Chen, Z.G. Hyperspectral image super-resolution method based on spectral smoothing prior and tensor tubal row-sparse representation. Remote Sens. 2022, 14, 2142. [Google Scholar] [CrossRef]
- Hyder, M.M.; Mahata, K. Direction-of-arrival estimation using a mixed ℓ2,0 norm approximation. IEEE Trans. Signal Process. 2010, 58, 4646–4655. [Google Scholar] [CrossRef]
- Neira, L.R.; Lowe, D. Optimized orthogonal matching pursuit approach. IEEE Signal Process. Lett. 2002, 9, 137–140. [Google Scholar] [CrossRef] [Green Version]
- Kay, S.M. Fundamentals of Statistical Signal Processing: Estimation Theory; Prentice-Hall: Upper Saddle River, NJ, USA, 1993. [Google Scholar]
- Michaeli, T.; Eldar, Y.C. Minimum MSE estimation with convex constraints. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Honolulu, HI, USA, 16–20 April 2007; pp. 1093–1096. [Google Scholar]
- Michaeli, T.; Eldar, Y. Constrained Linear Minimum MSE Estimation. October 2007. Available online: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.605.1972 (accessed on 1 October 2007).
- Cheng, L.; Wang, K.; Ren, M.; Yan, G. Adaptive filter approach for GPS multipath estimation under correntropy criterion in dynamic multipath environment. IEEE Trans. Signal Process. 2019, 67, 5798–5810. [Google Scholar] [CrossRef]
- Nam, W.; Kong, S. Least-squares-based iterative multipath super-resolution technique. IEEE Trans. Signal Process. 2013, 61, 519–529. [Google Scholar] [CrossRef] [Green Version]
- Blunt, S.D.; Chan, T.; Gerlach, K. A new framework for direction-of-arrival estimation. In Proceedings of the IEEE Sensor Array and Multichannel Signal Processing Workshop, Darmstadt, Germany, 21–23 July 2008; pp. 81–85. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).