Abstract
In a changing environment, changes in terrestrial water storage (TWS) in basins have a significant impact on potential floods and affect flood risk assessment. Therefore, we aimed to study the impact of TWS on potential floods. In this study, we reconstructed the TWS based on precipitation and temperature, evaluated the reconstructed TWS data based on Gravity Recovery and Climate Experiment (GRACE)-TWS data, and analyzed and calculated the flood potential index (FPI) in the Yangtze River Basin (YRB). The related influencing factors were analyzed based on the Global Land Data Assimilation System (GLDAS) data and Granger’s causality test. The main conclusions are as follows: (1) although the GRACE-TWS anomaly (GRACE-TWSA) in the YRB showed an increasing trend for the averaged TWSA over all grids in the whole basin (i.e., 0.31 cm/a, p < 0.05), the variable infiltration capacity-soil moisture anomalies (VIC-SMA) showed a decreasing trend (i.e., −0.048 cm/a, p > 0.05) during April 2002–December 2019; (2) a larger relative contribution of detrended precipitation to FPI was found in the Jialingjiang River Basin (JRB), Wujiang River Basin (WRB), Dongting Lake Rivers Basin (DLRB), YinBin-Yichang reaches (YB-YC), and Yichang-Hukou reaches (YC-HK), while the contribution of detrended TWS to FPI in the Poyang Lake Rivers Basin (PLRB) was larger than that in other basins; and (3) the original and detrended soil moisture (SM) and TWS in the YRB showed a significant positive correlation (p < 0.05), while the significant effect of SM on TWS caused a change in FPI in the YRB and its sub-basins. This study is of great significance for the correct understanding of the FPI and the accurate assessment of flood risk.
1. Introduction
Floods are extremely common and widely occurring disasters that result in great economic loss and life loss in many countries and regions worldwide [1]. A previous study reported that floods caused more than 7 million deaths and property damage of 600 billion US Dollars worldwide during the period 1900–2019 [2]. In recent years, more extreme precipitation has intensified the risk of flood disasters owing to climate change and accelerating urbanization, threatening residents’ safety and properties [3]. For example, China often suffers from many natural disasters, in which flood disasters comprise a major part, impacting two-thirds of the country [4]. Therefore, regional flood risk assessment is a critical issue for natural science and technology [5,6].
Since 1980, remote sensing technology has been widely applied, particularly in environmental science [7], engineering construction [8], planning design [9], and hydrological science [10]. For instance, it is widely used to monitor, map, and forecast hydrological extremes [11]. The Gravity Recovery Climate Experiment (GRACE) has been extensively applied to evaluate terrestrial water storage (TWS) [12,13,14]. TWS derived from GRACE (GRACE-TWS) with a spatial resolution of approximately 300 × 300 km2 and monthly temporal resolution contains information on various forms of surface water (e.g., runoff, snow water equivalent, canopy water storage), soil moisture (SM), and groundwater [11]. Originally, GRACE satellite products were widely applied to study the dynamics of TWS at the global scale or watershed scale in hydrology research [15]. In recent years, GRACE-TWS has also been extensively used to analyze floods [16,17,18]. For instance, Chen et al. (2010) studied abnormal floods in the Amazon basin in 2009 through GRACE-TWS [16]. Moreover, GRACE observation data have been used for research in hydrometeorology related to runoff, groundwater, evapotranspiration, glaciers, and snow cover [19,20,21,22]. In other words, the GRACE satellite fills a gap by directly obtaining information on TWS. However, the data interruption between GRACE and GRACE-Follow On seriously affects the application of GRACE-TWS in hydrology research over longer periods [23]. Therefore, it is helpful to reconstruct the interrupted data between GRACE and GRACE-Follow On for hydrological research based on GRACE data.
The flood potential index (FPI), which has been commonly applied in the evaluation of large-scale potential floods [23,24], provides a favorable index for measuring floods on a monthly scale in certain basins [25]. With GRACE-TWS being at a monthly scale, the FPI derived from GRACE-TWS is also at a monthly scale instead of a daily scale, which usually aims at flood evaluation [11]. The FPI contains information on the watershed from precipitation and TWS, which are applied to explore water about potential water storage [11]. The application of the FPI in large-scale basins greatly enhances the precision of flood estimation [24]. Groundwater plays a dominant role in water supply, accounting for almost 33% of the total withdrawals worldwide [10]. Owing to the great importance of water to the economy and society, groundwater in many aquifers around the world (e.g., US High Plains-the California Central Valley and North China Plain) has been rapidly depleted [26,27]. Furthermore, SM is a dominant factor affecting the amount of groundwater in the hydrological model from the Global Land Data Assimilation System (GLDAS) [27,28]. Therefore, if floods are assessed through the FPI, the role of SM at the regional or watershed scale needs to be taken seriously.
The Yangtze River Basin (YRB), spanning 19 provinces in China, is the third-largest basin in the world, with area of 1.8 million km2 and rich natural resources [27,29]. The basin has a large population and a developed economy that has experienced frequent and severe floods in the past [29]. For example, the occurrence of extreme precipitation led to the floods in 1998, resulting in the inundation of 2.1 million hectares and destruction of 5 million houses, causing an economic loss of 20 billion US Dollars [30]. However, previous studies have mainly paid attention to extremely hydro-meteorological events [31,32], neglecting the impact of groundwater changes on floods and the relationship between TWS and floods. Meanwhile, the YRB Protection Law and the economic belt construction plan in the YRB proposed by the national government have heightened the importance of flood research in the YRB. Therefore, this study attempted the following research: (1) to explore the spatial-temporal features of the FPI in the YRB under the precipitation and GRACE-TWS; (2) to explore the coupling relationship among extreme precipitation, TWS, and runoff; and (3) to analyze the potential drivers of FPI for SM and TWS in the YRB.
2. Study Area
Major parts of the YRB are in the subtropical part of China, spanning from the eastern to western parts of China [10]. The river rises on the Qinghai Tibet Plateau and flows into the East China Sea (Figure 1). Due to the special biodiversity in the YRB, the World Wildlife Fund has listed it as one of the 200 priority ecological areas in the world [10]. Located in the YRB, the world-famous Three Gorges Dam is regarded as playing a significant role in power generation, runoff regulation, and shipping [27,33,34]. The lower YRB mainly has a typical subtropical monsoon climate, in which the annual temperature is between 11.5 °C and 18.4 °C and the annual average precipitation is between 758.9 mm and 1970.4 mm, which causes hot and rainy weather in summer and warm and moist weather in winter [10,27].
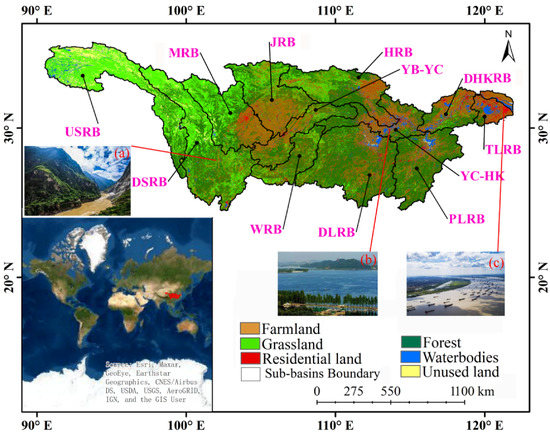
Figure 1.
Study Area and its location in the World [27]. (Sub-figures (a–c) are typical topographic maps of the upper, middle and lower reaches of the YRB, respectively).
This study divides the YRB into 12 sub-basins according to the classification criteria of the Ministry of Water Resources of the People’s Republic of China (e.g., Figure 1 and Table 1). In the past, there have been many flood events in the YRB, causing serious loss to life and property (e.g., Figure 2) [34]. The flood disaster situation in the YRB has been alleviated only by the construction of the Three Gorges Dam [35].

Table 1.
The codes and their related sub-basins in the YRB.

Figure 2.
Floods records and their characteristics in the YRB during April 2002–December 2019. (a–d) are the area (km2) affected by floods, the year of flood disaster, the duration (days) of each flood disaster, and the severity classification of each flood disaster, respectively. The color dots represent the flood locations in the YRB during April 2002–December 2019.).
3. Materials and Methods
3.1. Materials
3.1.1. GRACE Products
In this study, GRACE/GRACE-Follow on Release Level (RL) 06 Mascon Solutions product at a monthly scale and 0.25° spatial resolution were downloaded from the Center for Space Research (http://www2.csr.utexas.edu/grace/, accessed on 1 January 2021) [27]. The time span of product and data related to GRACE are from April 2002 to June 2017, while the data from GRACE-Follow On are from May 2018 to December 2019. CSR global mascon RL06 data can be applied directly without further adjustment of the scale factor, as it is not extensively affected by leakage and measurement errors [36,37]. For some missing short-term monthly data, the linear interpolation method was used. The raw monthly GRACE-TWSA product took the period from January 2004 to December 2009 as a reference [27]. In addition, seasonal and trend items can be obtained through GRACE/GRACE-Follow on RL06 Mascon TWS products.
3.1.2. Variable Infiltration Capacity (VIC)-Runoff/SM
Because SM (i.e., moisture in the layer of 0~1.9 m below the ground surface) plays an important role in the water content underground, both the SM and runoff depth (mm) in the VIC Model from GLDAS were also chosen for extreme runoff analysis (https://earthdata.nasa.gov, accessed on 1 January 2021) [27]. Their time span is from April 2002 to December 2019, and its temporal and spatial resolutions are monthly and 1° latitude × 1° longitude, respectively. There are also many other hydrological variables, such as evaporation and subsurface runoff, in the simulation results of the VIC model [38]. For comparison, SM was also treated by removing the averaged value from January 2004 to December 2009, expanding the spherical harmonic coefficient, truncating the term at order 60, and recombining it into SM (i.e., SMA). Meanwhile, the runoff data for the same period were also used to obtain anomaly values.
3.1.3. Flood Data
The flood data in Excel and Shapefile formats for open access in this study were obtained from the Dartmouth Flood Observation Center (available at http://www.dartmouth.edu/~floods/, accessed on 1 January 2021). The flood start time, flood duration, flood location, flood-affected area, and other related information are included in the compiled data from worldwide satellite observations and weather service reporting [27]. In this study, the information about the floods in the YRB from 2002–2019 can be seen in Figure 2.
3.1.4. Meteorological Data
Meteorological data (i.e., temperature and precipitation) used to reconstruct TWS are 0.5° latitude × 0.5° longitude grid data of daily surface temperature and precipitation in China (V2.0), respectively, sourced from the China Meteorological Administration (available at: http://www.nmic.cn/data, accessed on 1 January 2021) covering the period of January 1961 to the present, were transformed into grid data based on observation data from meteorological stations [27]. In this study, all the grid data were interpolated to 1° latitude × 1° longitude based on the inverse distance weighted (IDW) method to ensure the spatial location of grid data corresponding one by one.
3.2. Method
3.2.1. Reconstruction of TWS between GRACE and GRACE-Follow On
The linear model proposed by Beven (2012) [39] was used to compensate for the missing TWS in some months during the time series of GRACE and GRACE-Follow On. However, the missing data between GRACE and GRACE-Follow On were obtained from the method reported by Humphrey and Gudmundsson (2019) [40] (see Equation (1)):
where P(t), t, τ(t), and TWS(t) are the precipitation on the tth day, daily time vector, residence time of TWS, and TWS on the tth day, respectively.
TWS usually leaves reservoirs, rivers, or lakes by evapotranspiration, so the residence time of TWS has a direct impact on evapotranspiration. Therefore, the residence time of the TWS can be introduced by the method demonstrated by Humphrey and Gudmundsson (2019) [40], as shown in Equation (2):
where a, b, and (t) represent the parameters and the transformation for the daily temperature T(t), respectively.
If the temperature is less than 0 degrees centigrade, the change in temperature does not cause the parameters of this method to be sensitive [40]; the process can be described as follows
where mean (T0) and SD(T0) stands for the average air temperature on the tth day and the standard deviation of air temperature. In this study, the grid data of precipitation and temperature were applied to reconstruct the interruption data between GRACE and GRACE-FO.
In addition, the initial water storage can be expressed as:
The monthly TWS obtained from the daily TWS can be corrected based on the following details:
where anom (), tm, β, and ε are the operator removing the seasonal cycle and linear trend, monthly temporal resolution from averaged daily water storage time series, corrected scaling factor, and error term, respectively. Since many types of GRACE trends are caused by human activities, the trends in the calibrated period should be removed [39]. However, the seasonal and trend items mainly come from GRACE Mascon products based on Equation (7), which can be seen the following:
where A6, A5, A4, A3, A2, and A1 are the constant item, coefficient of a linear item, semi-annual phase, semi-annual amplitude, annual phase, and annual amplitude, respectively. In addition, t0 stands for the referenced time, which is regarded as 1 January 2002. Here, the error of the interpolated TWS was within 5 cm, so the corresponding results can be used to this basin [28]. After the correction, the corresponding seasonal term trends and linear trends are re-added to the series.
3.2.2. Derivation of FPI
The FPI can be acquired from monthly precipitation, GRACE-TWS data according to the method developed by Reager and Famiglietti (2009) [25], and the following steps:
where , S(t − 1), and Smax denote the maximum relative deficit of TWS, the TWS in the previous month, and the maximum storage capacity of the TWS anomaly (TWSA), respectively.
Subsequently, the flood potential amount (FPA) is obtained as Equation (9):
where the positive FPA and Pmon denote the maximum relative deficit of precipitation over TWS when flooding might occur and monthly precipitation, respectively.
In conclusion, the FPI is acquired by the standardized FPA:
All FPIs were less than or equal to 1. The closer the value is to 1, the greater the possibility of flooding [25].
3.2.3. Granger Causality Analysis
Granger put forward the definition of Granger causality in 1969 [41] and expanded it in 1980 [42]. Its definition is based on a complete information set and an occurrence time sequence. It is agreed that j is all the information in the universe up to n period, and Yn is all the information up to n period (t = 1…n), Xn+1 is the value of X in the n + 1 period, and Jn − Yn is all information except Y. The expression that the occurrence of Y affects the occurrence of X is as follows:
where E stands for the conditional distribution expectation. When the statistical variable F is greater than the significant level P, there is an obvious causal relationship between the X and Y time series. When the statistical variable F is less than the significance level P, there is no causal relationship between the X and Y time series. Overall, before conducting the test, de-trending, de-meaning, Augmented Dickey–Fuller (ADF) test, and general regression model prediction are required. It indicates a necessary causal relationship between the couple series when the variability between the predicted data and the observed values passes the test. In this study, the causal relationship between SMA/TWSA and FPI were investigated.
3.2.4. Standardization Method
To generate different hydrological variables in the same standard quantity, precipitation, runoff, and SM were standardized as follows:
where xt, yt, xmin, and xmax are the hydrological variables before and after standardization at period t, and the minimum and maximum values in the time series, respectively.
3.2.5. Calculation of Relative Contribution
In this study, the relative contribution of precipitation and TWS can be predicted to explore the obvious factors of FPI from precipitation and TWS. A standardized multiple linear regression model was established to obtain the relative contribution by taking the time series of precipitation and TWS as independent variables and FPI as dependent variables. For each sub basin in the YRB, this study adopted the averaged standardized precipitation, TWS and FPI time series for multivariate fitting to estimate relative contribution during the period of 2002–2019.
where represents the linear trend of the dependent variable from standardized precipitation and TWS. and denote the linear trend of standardized FPI and relative contribution, respectively.
4. Results
4.1. Characteristic of TWSA in the YRB during April 2002–December 2019
Figure 3 shows the trend of TWSA in the YRB and its sub-basins based on the Mann–Kendall test and Sen’s slope. It was found that the TWSA in the Yichang-Yibin reaches, Wujiang River Basin, Dongting Lake River Basin, Poyang Lake Rivers Basin, and Yichang-Hukou reaches were in surplus; the maximum TWSA was about 5 cm, but a deficit situation was found in the upper reaches of the Jialingjiang River Basin and Hanjiang River Basin, in which the significant decreasing trend was approximately −1 cm (Figure 3b). Moreover, the TWSA in the middle reaches of the YRB showed an obvious increasing trend (p < 0.05) up to 1 cm/year, while those in the upper reaches of JRB and HRB showed an obvious decreasing trend (p < 0.05) of up to −0.5 cm/year (Figure 3b). However, although the GRACE-TWSA in the YRB showed an increasing trend, the VIC-SMA showed a decreasing trend, with the change rates of 0.31 cm/year and −0.048 cm/year, respectively, for the averaged value in the whole basin (Figure 3c). In terms of the uncertainty of the reconstructed TWSA, the uncertainty in the middle and lower reaches of the YRB was significantly higher than those in the upper reaches of the YRB (Figure 3d). Figure 3e shows that the TWS in all sub-basins of the YRB was increasing, and the TWS in the YRB, Minjiang River Basin, Jialingjiang River Basin, Wujiang River Basin, Dongting Lake Rivers Basin, and Yichang-Hukou reaches reached a significant level (p < 0.05).

Figure 3.
Slope of GRACE-TWSA and VIC-SMA in the YRB during April 2002–December 2019. (a–d) are averaged monthly GRACE-TWSA, slope and related points with significant trend, time series of GRACE-TWSA and VIC-SMA, annual slope and significant level, respectively. (e) represents the slope and significant level of TWSA in whole YRB and its sub-basins. The red circle and the blue circle represent significant decrease and significant increase, respectively).
4.2. Derivation of FPI in the YRB
Figure 4 describes the major process of calculating the FPI from the GRACE-TWS in the YRB from April 2002 to December 2019. Figure 4a shows the maximum storage capacity (MSC) of the TWS in the YRB. This explained that the larger MSC was found in the Poyang Lake Rivers Basin, but the smaller MSC was mainly located in the Jialingjiang River Basin. In terms of the normalized storage deficit, while the smaller MSC was seen in the upper reaches of the YRB, the larger MSC was concentrated in the Poyang Lake Rivers Basin, which also signified small and large storage capacities in the upper reaches of the YRB and Poyang Lake Rivers Basin, respectively, in June 2002 (Figure 4b). Figure 4c shows that the FPI in the upper reaches of the YRB, Hanjiang River Basin, and Poyang Lake Rivers Basin was higher than that in other regions, which indicated that these regions were more likely to experience floods during June 2002. However, as shown in Figure 4d, the flood records only showed that there were floods in the Poyang Lake Rivers Basin and Han River Basin, but the relevant records did not appear in the Jialingjiang River Basin during June 2002 when the abundant precipitation was concentrated in the middle and lower reaches of the YRB rather than in the upper reaches [43].
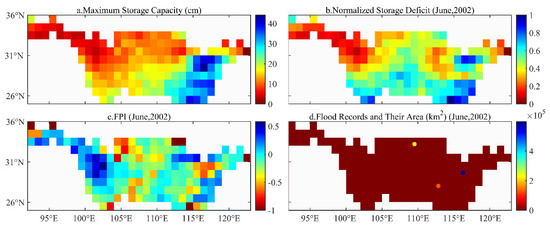
Figure 4.
Examples involved in calculating the FPI in the YRB during April 2002–December 2019. ((a–d) are the MSC (cm), normalized storage deficit in June 2002, FPI in June 2002, and flood records and their area (km2) in June 2002, respectively).
4.3. Impacts of Major Hydrological Factors on the FPI
Figure 5 depicts the relative contributions of precipitation and TWS to the FPI in the YRB from April 2002 to December 2019. It was found that the relative contribution of precipitation to FPI in the Minjiang River Basin, Hanjiang River Basin, and Dongting Lake River Basin was significantly greater than those in other sub-basins (Figure 5a). However, those of TWS in the Poyang Lake Rivers Basin was significantly larger than that in other regions (i.e., 0.58) (Figure 5b); in terms of the detrended precipitation, the larger relative contribution was found in the Jialiangjiang River Basin, Wujiang River Basin, Dongting Lake River Basin, Yibin-Yichang reach, and Yichang-Hukou reaches, while the contribution of detrended TWS to FPI in the Poyang Lake Rivers Basin was larger than that in other basins during April 2002–December 2019 (Figure 5c,d). Except for Poyang Lake Rivers Basin, the relative contribution of original and detrended precipitation to FPI in all other sub-basins was greater than that of TWS and detrended TWS (Figure 5e,f).

Figure 5.
Relative contribution from original and de-trended precipitation and TWSA to FPI in the YRB and its sub-basins during April 2002–December 2019.
4.4. Relationship between Extremely Monthly Runoff and Other Major Monthly Hydrological Factors
The driving factors of extreme runoff (i.e., the monthly runoff was ranked from smallest to largest, and if the specific runoff was at a value above the three-quarter percentile, it was identified as Runoff ≥ 75%.) from the VIC model in each grid of the YRB were analyzed (e.g., Figure 6). First, the runoff, precipitation, and TWSA were standardized from small to large, and then the precipitation and TWSA under different cases were extracted at the periods of extreme runoff (i.e., Runoff ≥ 75%). When the runoff was greater than, or, in extreme cases, the precipitation was greater than or equal to 75%, the precipitation and TWSA were greater than or equal to 75% (i.e., Case 1); when the runoff was greater than or equal to 75%, the precipitation was greater than or equal to 75%, but the TWSA was less than 75% (i.e., Case 2); when the runoff was greater than or equal to 75%, the precipitation was less than 75%, but the TWSA was greater than or equal to 75% (i.e., Case 3). When the runoff was greater than or equal to 75%, both the precipitation and TWSA were less than 75% (i.e., Case 4). For Case 1, the eligible grids were mainly distributed in the Hanjiang River Basin and Yichang-Hukou reach, respectively (Figure 6a); for Case 2, the eligible grids were mainly concentrated in the Poyang Lake Rivers Basin, Wujiang River Basin, and Minjiang River Basin, respectively (Figure 6b); in Case 3, the eligible points were mainly located in the Wujiang River Basin, Dongting Lake Rivers Basin, and Minjiang River Basin, respectively (Figure 6c); and in Case 4, the eligible grids were mainly located in the Hanjiang River Basin and Jialingjiang River Basin (Figure 6d). In summary, the extreme runoff in the Minjiang River Basin was 100% consistent with Case 1, followed by the Hanjiang River Basin and the main stream below Hukou; the extreme runoff in the Poyang Lake Rivers Basin and the upstream of Jinshajiang-Shigu were mainly consistent with Case 2; the extreme runoff in Dongting Lake Rivers Basin and the Hanjiang River Basin were mainly consistent with Case 3, and it is worth noting that there were few extreme runoff basins in line with Case 4 (Figure 6e).

Figure 6.
Percentage of extreme runoff (i.e., runoff ≥ 75%) falling in these four kinds of Case for the combination between precipitation and TWSA in the YRB and its sub-basins during April 2002–December 2019.
To further explore the relationship between runoff, TWSA, precipitation, and FPI, all the differences between the runoff and precipitation percentiles were compared with zero. We studied the events when the other mainly hydrological factors (precipitation, TWSA, runoff, and FPI) were higher or lower than the median when the runoff percentile exceeded the precipitation percentile (i.e., Figure 7). It was found that there were a few grid points of other main hydrological elements that were greater than or equal to the median, and they were mainly located in the upstream of Jinshajiang-Shigu and downstream of Jinshajiang-Shigu when the runoff percentile exceeded or equaled the precipitation percentile (i.e., Figure 7a–d). On the contrary, the grid points of other main hydrological elements less than the median were rich and mainly concentrated in the middle and lower reaches of the YRB when runoff exceeded or equaled the precipitation (i.e., Figure 7e–h). The grid points of other main hydrological factors greater than or equal to the median were few and were mainly concentrated in the Jialingjiang River Basin when the runoff was less than the precipitation (i.e., Figure 7i–l). In contrast, the grid points of other main hydrological factors less than the median were almost in the YRB when the runoff was less than the precipitation (i.e., Figure 7m–p).

Figure 7.
Different cases for the percentile of runoff, precipitation, FPI and TWSA compared to 50% for the positive and negative value of runoff minus precipitation in the YRB during April 2002–December 2019.
Furthermore, we studied the relationship among runoff, precipitation, TWSA, and FPI in the whole YRB and its sub-basins (Figure 8). The grids were mainly located in the Poyang Lake Rivers basin, upstream of Jinshajiang-Shigu-downstream of Jinshajiang-Shigu, Dongting Lake River Basin, Jialingjiang River Basin, and Minjiang River Basin when the average runoff was greater than the average precipitation, and the main hydrological factors were greater than the median (Figure 8a). When runoff was greater than precipitation and other major hydrological factors were less than or equal to the median, it was performed in all sub-basins, and TWS occupied a dominant position in all sub-basins (Figure 8b). However, the main hydrological factors in the grids larger than the median were majorly located in the Hanjiang River basin and Jialingjiang River Basin when the runoff was less than the precipitation (Figure 8c). The grid points of other main hydrological factors less than the median were reflected in all sub-basins of the YRB, among which TWS was the most obvious, followed by the FPI when the runoff was less than the precipitation (Figure 8d).

Figure 8.
Different cases for the percentile of runoff, precipitation, FPI and TWSA compared to 50% for the positive and negative value of runoff minus precipitation in the YRB during April 2002–December 2019. ((a–d) are the cases for the percentile of runoff minus precipitation no less than 0 and factors no less than 50, the percentile of runoff minus precipitation no less than 0 and factors less than 50, the percentile of runoff minus precipitation less than 0 and factors no less than 50, and the percentile of runoff minus precipitation less than 0 and factors less than 50, respectively).
4.5. Impacts of SM on TWSA in the YRB
The SM anomalies from the VIC using the SM were estimated, and the relative contributions of SM and precipitation on GRACE-TWSA were evaluated from April 2002 to December 2019 (Figure 9). It was found that the contribution of precipitation to TWSA in the middle and lower reaches of the YRB was significantly greater than that of the SMA, and the relative contribution of SMA to TWSA in the upper reaches of the YRB was significantly greater than that of the precipitation for the original precipitation and SMA (Figure 9a,b). However, the change in relative contribution in spatial distribution was not obvious, but there were some differences in some grids for detrended precipitation and SMA (Figure 9c,d). The relative contribution of precipitation to GRACE-TWSA in the upstream of Jinshajiang-Shigu Wujiang River Basin, Dongting Lake Rivers Basin, and Yichang-Hukou reaches was significantly higher than that of SMA, whereas, in the downstream of Jinshajiang-Shigu, Yibin-Yichang Reaches, Jialingjiang River Basin, Hanjiang River Basin, Poyang Lake Rivers Basin, and Minjiang River Basin, the relative contribution of SMA to GRACE-TWSA was significantly higher than that of precipitation (Figure 9e,f). Among all the sub-basins, precipitation in the Wujiang River Basin had the largest contribution to the TWSA, which was close to 1 (Figure 9e,f).

Figure 9.
Relative contribution of original and de-trended precipitation and VIC-SMA on GRACE-TWSA in the YRB during April 2002–December 2019.
The relationship between the VIC-SMA and GRACE-TWSA in the YRB and its sub-basins was analyzed from April 2002 to December 2019 (Figure 10). SMA and TWSA in all sub-basins showed a significant positive correlation (p < 0.05), including the original time series and detrended time series. For the original time series, the correlation coefficient of SMA and TWSA in the downstream of Jinshajiang-Shigu was the highest, reaching 0.89 (Figure 10c) and the lowest, 0.25, in the Wujiang River Basin (Figure 10f); however, Figure 11 shows the relationship between SMA and FPI in the YRB; the strongest correlation was found in the Poyang Lake Rive basin, which reached 0.78, as shown in Figure 11l); the poorest correlation was explored in the Taihu Lake River Basin, which was approximately 0.45 (Figure 11m). Therefore, due to the close correlation between the TWSA and SMA, the change in SM can lead to significant changes in the TWSA and FPI.

Figure 10.
Kernel plot between standard GRACE-TWSA and VIC-GWSA in the sub-basins of YRB during April 2002–December 2019.
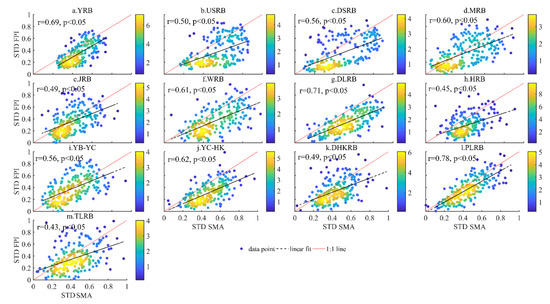
Figure 11.
Kernel plot between standard FPI and VIC-SMA in the sub-basins of YRB during April 2002–December 2019.
Moreover, the Granger causality test was also used to study the causal relationship between SMA and TWSA/FPI (Table 2 and Table 3). The results showed that, except for upstream of Jinshajiang-Shigu-downstream of Jinshajiang-Shigu and Hanjiang River Basin, SMA in most sub-basins of the YRB was increasing, and except for Yichang-Hukou reaches, the causality between the SMA and TWSA was obvious (p < 0.05) in the whole YRB and other sub-basins at multiple lag times (Table 2), and there was a significant relationship between SMA and FPI in the YRB on different lag time scales (Table 3). In conclusion, our study found that the significant effect of SMA on TWSA affected the change in FPI in the YRB.

Table 2.
Granger’s Causality test between VIC-SMA and GRACE-TWSA in the YRB and its sub-basins at the lags of 1–6 months.

Table 3.
Granger’s Causality test between SMA and FPI in the YRB and its sub-basins at the lags of 1–6 months.
5. Discussion
5.1. Why Do TWSA and SMA Increase in the YRB and Its Most Sub-Basins?
For the average of the whole YRB, the TWSA and SMA show an increasing trend [10,28]. However, trends in the TWSA and SMA are affected by many factors, including climate change, land use and cover change, and human activities [10,44]. The increasing trend of different types of precipitation in the YRB is closely related to the changing trend of groundwater, which indicates that the precipitation in the YRB plays a critical role in groundwater reserves, as the impact of climate change on groundwater can be reflected by the change in precipitation [45]. In addition, the water-retaining design of the dam intercepts a large amount of runoff, thus increasing the TWSA in the middle and upper reaches of the YRB [10,29]. Although the runoff regulated by the dam reduces the runoff in the flood season of the middle and lower reaches, it also increases the land water storage in the dry season of the middle and lower reaches [44].
Perhaps because trends in land use and vegetation in recent decades have led to increased groundwater storage in China [10,30]. In details, the great floods in the YRB in 1998 reminded humans of the importance of ecological conservation [45]. Subsequently, nationwide ecological conservation and afforestation programs began to be implemented and the vegetation cover in China increased significantly in the following decades, while the increase in organic matter due to more vegetation litter increased precipitation infiltration into the soil to some extent, which in turn led to an increase in groundwater storage [10,46]. As a typical region in the subtropical monsoon zone, its soils do not have a thick envelope and are more prone to saturated runoff rather than hyper-infiltrated runoff after heavy precipitation [10,47]. Therefore, TWS and SM were considered as the major factors of floods in the middle reaches of YRB.
5.2. Why Is the Spatial Distribution of Higher Flood Frequency Areas Inconsistent with Smaller MSC?
From the above study, it can be seen that the smaller MSC was mainly concentrated in the upper reaches of the YRB, while the higher flood frequency was mainly concentrated in the middle and lower reaches of the YRB. As the flood information confirms, the recent flood events with longer duration and higher intensity were mainly concentrated in the middle and lower reaches of the YRB (see Figure 2), which was also consistent with the result of Xiong et al. [47]. Despite the larger FPI in the upper Yangtze River, there were no significant flood events for the Mountainous terrain with large altitude differences. However, there were flood events in the middle and lower Yangtze River, which were more consistent with the FPI in the middle and lower reaches, which was related to the plains terrain and water storage deficit in the local region [10]. In addition, for the YRB in the monsoon region, in which the floods were closely related to precipitation, many stations with significant (p < 0.05) increases in precipitation extremes were concentrated in the middle and lower reaches of the YRB during 1961–2019 [29]. Meanwhile, the change in the teleconnection index (i.e., Niño 3.4 index) affected the change in precipitation to a certain extent, which may cause flood events [33]. For example, Xiao et al. (2017) reported that precipitation extremes were prone to decrease in the central part of China for the annual positive ENSO but increased in the eastern part of China in the following year [46]. Moreover, Miao et al. (2019) also pointed out that when the current year was in the El Niño stage, the frequency of rainy days and extreme precipitation events in Southeast China was higher in the following year [47]. The physical mechanism of ENSO precipitation dependence is related to the modulation effect of ENSO on a large-scale circulation model [29,33,48]. In addition, other teleconnection indices (e.g., North Atlantic Oscillation, Atlantic Multi-decadal Oscillation, and Pacific Decadal Oscillation) could also affect precipitation in the YRB [49,50]. In addition, from the perspective of topography and geographical location, the middle-lower reaches of the YRB were close to the coast, resulting in a strong Pacific monsoon and relatively abundant average annual precipitation, while the upper reaches of the YRB were far away from the Pacific Ocean, leading to a relatively weak Pacific monsoon and low average annual precipitation [51]. The middle-upper reaches of the YRB have higher altitude, more undulating terrain, and deep valleys, resulting in unobstructed and easy runoff. In contrast, the low terrain was distributed in the middle-lower reaches of the YRB, suffering from slow runoff velocity and poor drainage, which are more likely to cause floods [33,46].
6. Conclusions
This study reconstructed the TWSA based on precipitation and temperature, evaluated the reconstructed TWSA data based on GRACE-TWSA data, analyzed and calculated the FPI in the YRB based on the reconstructed TWSA, and analyzed the related influencing factors of FPI based on the GLDAS data and Granger’s causality test. The main conclusions are as follows.
- (1)
- The TWSA in the middle reaches of the YRB showed an obvious increasing trend (p < 0.05), while those in the upper reaches of the Jialingjiang River Basin and Hanjiang River Basin showed an obvious decreasing trend (p < 0.05). However, although the GRACE-TWSA in the YRB showed an increasing trend for the averaged TWSA over all grids in the whole basin, the VIC-SMA showed a decreasing trend (p < 0.05).
- (2)
- The relative contribution of precipitation to FPI in the Minjiang River Basin, Hanjiang River Basin, and Dongting Lake River Basin was significantly greater than that in other sub-basins; however, the contribution of TWSA to Poyang Lake Rivers Basin was significantly larger than that in other regions, and the larger relative contribution of detrended precipitation of FPI was found in the Jialingjiang River Basin, Wujiang River Basin, Dongting Lake River Basin, Yibin-Yichang, and Yichang-Hukou, while the contribution of detrended TWSA to FPI in the Poyang Lake Rivers Basin was larger than that in other basins during April 2002–December 2019.
- (3)
- The contribution of precipitation to the TWSA in the middle-lower reaches of the YRB was significantly greater than that of the SMA, and the relative contribution of the original SMA to TWSA in the upper reaches of the YRB was significantly greater than that of the original precipitation, and the original and detrended SMA and TWSA in the YRB showed a significant positive correlation (p < 0.05), while the significant effect of SM on TWS affected the change in FPI in the YRB and most of its sub-basins.
Author Contributions
Conceptualization, P.Y. and X.Z.; methodology, W.W.; software, Y.Z.; validation, X.L.; formal analysis, X.Z.; investigation, W.W.; resources, P.Y.; data curation, P.Y. and S.Z.; writing—original draft preparation, P.Y.; writing—review and editing, P.Y.; visualization, X.L.; supervision, N.C.; project administration, J.X.; funding acquisition, P.Y. All authors have read and agreed to the published version of the manuscript.
Funding
The research is supported by the National Nature Science Foundation of China (No. 42171047), Open Research Fund of State Key Laboratory of Simulation and Regulation of Water Cycle in River Basin (China Institute of Water Resources and Hydropower Research) (IWHR-SKL-202217), and Open Fund of National Engineering Research Center for Geographic Information System, China University of Geosciences (2021KFJJ01).
Data Availability Statement
While the meteorological data were downloaded from China Meteorological Administration (available at: http://www.nmic.cn/data/detail/dataCode) (accessed on 1 January 2021), GRACE data and product were sourced from the University of Texas at Austin (available at: http://www2.csr.utexas.edu/grace) (accessed on 1 January 2021).
Acknowledgments
We thank the China Meteorological Administration and the University of Texas at Austin for providing us with valuable and informative data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Stefanidis, S.; Stathis, D. Assessment of flood hazard based on natural and anthropogenic factors using analytic hierarchy process (AHP). Nat. Hazards. 2013, 68, 569–585. [Google Scholar] [CrossRef]
- EM-DAT Disaster PProfiles, The OFDA/CRED International Disaster Database. 2020. Available online: http://www.emdat.be/database (accessed on 28 December 2020).
- Wu, C.H.; Huang, G.R.; Yu, H.J. Prediction of extreme floods based on CMIP5 climate models: A case study in the Beijiang River basin, South China. Hydrol. Earth Syst. Sci. 2015, 19, 1385–1399. [Google Scholar] [CrossRef] [Green Version]
- Lai, C.; Chen, X.; Chen, X.; Wang, Z.; Wu, X.; Zhao, S. A fuzzy comprehensive evaluation model for flood risk based on the combination weight of game theory. Nat. Hazards. 2015, 77, 1243–1259. [Google Scholar] [CrossRef]
- Wang, Z.L.; Lai, C.G.; Chen, X.H.; Yang, B.; Zhao, S.W.; Bai, X.Y. Flood hazard risk assessment model based on random forest. J. Hydrol. 2015, 527, 1130–1141. [Google Scholar] [CrossRef]
- Sperotto, A.; Torresan, S.; Gallina, V.; Coppola, E.; Crittoa, A.; Marcomini, A. A multidisciplinary approach to evaluate pluvial floods risk under changing climate: The case study of the municipality of Venice (Italy). Sci. Total Environ. 2016, 562, 1031–1043. [Google Scholar] [CrossRef]
- Gacia, E.; Soto, D.X.; Roig, R.; Catalan, J. Phragmites australis as a dual indicator (air and sediment) of trace metal pollution in wetlands—The key case of Flix reservoir (Ebro River). Sci. Total Environ. 2020, 765, 142789. [Google Scholar] [CrossRef]
- Long, J.L.; Li, H.; Wang, Z.Y.; Wang, B.; Xu, Y.J. Three decadal morphodynamic evolution of a large channel bar in the middle Yangtze River: Influence of natural and anthropogenic interferences. Catena 2021, 199, 105128. [Google Scholar] [CrossRef]
- Dijk, D.V.; Shoaie, S.; Leeuwen, T.V.; Veraverbeke, S. Spectral signature analysis of false positive burned area detection from agricultural harvests using Sentinel-2 data. Int. J. Appl. Earth Obs. 2021, 97, 102296. [Google Scholar]
- Liu, X.M.; Liu, C.; Brutsaert, W. Mutual consistency of groundwater storage changes derived from GRACE and from baseflow recessions in the Central Yangtze River basin. J. Geophys. Res. 2020, 125, e2019JD031467. [Google Scholar] [CrossRef]
- Shah, D.; Mishra, V. Strong influence of changes in terrestrial water storage on flood potential in India. J. Geophys. Res. 2021, 126, e2020JD033566. [Google Scholar] [CrossRef]
- Asoka, A.; Wada, Y.; Fishman, R.; Mishra, V. Strong linkage between precipitation intensity and monsoon season groundwater recharge in India. Geophys. Res. Lett. 2018, 45, 5536–5544. [Google Scholar] [CrossRef] [Green Version]
- Asoka, A.; Mishra, V. Anthropogenic and climate contributions on the changes in terrestrial water storage in India. J. Geophys. Res. 2020, 125, e2020JD032470. [Google Scholar] [CrossRef]
- Tapley, B.D.; Bettadpur, S.; Ries, J.C.; Thompson, P.F.; Watkins, M.M. GRACE measurements of mass variability in the earth system. Science 2004, 305, 503–505. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wahr, J.; Swenson, S.; Velicogna, I. Accuracy of GRACE mass estimates. Geophys. Res. Lett. 2006, 33, L06401. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D. The 2009 exceptional Amazon flood and interannual terrestrial water storage change observed by GRACE. Water Resources Res. 2010, 46, W12526. [Google Scholar] [CrossRef] [Green Version]
- Reager, J.T.; Thomas, B.F.; Famiglietti, J.S. River basin flood potential inferred using GRACE gravity observations at several months lead time. Nat. Geosci. 2014, 7, 588–592. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Zhang, Z.; Save, H.; Wiese, D.N.; Landerer, F.W.; Long, D.; Longuevergne, L.; Chen, J. Global evaluation of new GRACE mascons products for hydrologic applications. Water Resour. Res. 2016, 52, 9412–9429. [Google Scholar] [CrossRef]
- Boronina, A.; Ramillien, G.L. Application of AVHRR imagery and GRACE measurements for calculation of actual evapotranspiration over the Quaternary aquifer (Lake Chad basin) and validation. J. Hydrol. 2008, 348, 98–109. [Google Scholar] [CrossRef]
- Rodell, M.; Velicogna, I.; Famiglietti, J.S. Satellite-based estimates of groundwater depletion in India. Nature 2009, 460, 999–1002. [Google Scholar] [CrossRef] [Green Version]
- Strassberg, G.; Scanlon, B.R.; Chambers, D. Evaluation of groundwater storage monitoring with the GRACE satellite: Case study of the High Plains aquifer, central United States. Water Resour. Res. 2009, 45, W05410. [Google Scholar] [CrossRef] [Green Version]
- Syed, T.H.; Famiglietti, J.S.; Chambers, D.P. GRACE-based estimates of terrestrial freshwater discharge from basin to continental scales. J. Hydrometeorol. 2009, 10, 22–40. [Google Scholar] [CrossRef]
- Long, D.; Shen, Y.; Sun, A.; Hong, Y.; Longuevergne, L.; Yang, Y.T.; Li, B.; Chen, L. Drought and flood monitoring for a large karst plateau in Southwest China using extended GRACE data. Remote Sens. Environ. 2014, 155, 145–160. [Google Scholar] [CrossRef]
- Zhang, Q.; Gu, X.; Singh, V.P.; Shi, P.; Luo, M. Timing of floods in southeastern China: Seasonal properties and potential causes. J. Hydrol. 2017, 552, 732–744. [Google Scholar] [CrossRef]
- Reager, J.T.; Famiglietti, J.S. Global terrestrial water storage capacity and flood potential using GRACE. Geophys. Res. Lett. 2009, 36, L23402. [Google Scholar] [CrossRef] [Green Version]
- Famiglietti, J.S. The global groundwater crisis. Nat. Clim. Change 2014, 4, 945–948. [Google Scholar] [CrossRef]
- Yang, P.; Xia, J.; Luo, X.G.; Meng, L.S.; Zhang, S.Q.; Cai, W.; Wang, W.Y. Impacts of climate change-related flood events in the Yangtze River Basin based on multi-source data. Atmos. Res. 2021, 263, 105819. [Google Scholar] [CrossRef]
- Zhong, Y.; Zhong, M.; Mao, Y.; Ji, B. Evaluation of evapotranspiration for exorheic catchments of China during the GRACE Era: From a water balance perspective. Remote Sens. 2020, 12, 511. [Google Scholar] [CrossRef] [Green Version]
- Li, B.Y.; Chen, N.C.; Wang, W.; Wang, C.; Schmitt, R.J.P.; Lin, A.; Daily, G.C. Eco-environmental impacts of dams in the Yangtze River Basin, China. Sci. Total Environ. 2021, 774, 145743. [Google Scholar] [CrossRef]
- Piao, S.; Yin, G.; Tan, J.; Cheng, L.; Huang, M.; Li, Y.; Liu, R.; Mao, J.; Myneni, R.B.; Peng, S.; et al. Detection and attribution of vegetation greening trend in China over the last 30 years. Glob. Change Biol. 2015, 21, 1601–1609. [Google Scholar] [CrossRef]
- Chen, J.; Wu, X.; Finlayson, B.L.; Webber, M.; Wei, T.; Li, M.; Chen, Z. Variability and trend in the hydrology of the Yangtze River, China: Annual precipitation and runoff. J. Hydrol. 2014, 513, 403–412. [Google Scholar] [CrossRef]
- Lü, M.; Wu, S.J.; Chen, J.; Chen, C.; Wen, Z.; Huang, Y. Changes in extreme precipitation in the Yangtze River basin and its association with global mean temperature and ENSO. Int. J. Climatol. 2018, 38, 1989–2005. [Google Scholar] [CrossRef]
- Li, X.; Zhang, K.; Gu, P.; Feng, H.T.; Cheng, B.C. Changes in precipitation extremes in the Yangtze River basin during 1960–2019 and the association with global warming, ENSO, and local effects. Sci. Total Environ. 2021, 760, 144244. [Google Scholar] [CrossRef] [PubMed]
- Fu, B.J.; Wu, B.F.; Lü, Y.H.; Xu, Z.H.; Cao, J.H.; Niu, D. Three Gorges Project: Efforts and challenges for the environment. Prog. Phys. Geog. 2010, 34, 741–754. [Google Scholar] [CrossRef]
- Zheng, L.; Xu, J.; Wang, D.; Xu, G.; Tan, Z.; Xu, L.; Wang, X. Acceleration of vegetation dynamics in hydrologically connected wetlands caused by Dam operation. Hydrol. Processes 2021, 35, e14026. [Google Scholar] [CrossRef]
- Save, H. CSR GRACE RL06 Mascon Solutions (Vol. 1.); Texas Data Repository Data Verse; University of Texas: Austin, TX, USA, 2019. [Google Scholar] [CrossRef]
- Save, H.; Bettadpur, S.; Tapley, B.D. High-resolution CSR GRACE RL05 mascons. J. Geophys. Res. 2016, 121, 7547–7569. [Google Scholar] [CrossRef]
- Beaudoing, H.; Rodell, M. NASA/GSFC/HSL, GLDAS VIC Land Surface Model L4 3 Hourly 1.0 × 1.0 Degree V2.0; Goddard Earth Sciences Data and Information Services Center (GES DISC): Greenbelt, MD, USA, 2020. [Google Scholar]
- Beven, K.J. Rainfall-Runoff Modelling: The Primer, 2nd ed.; John Wiley & Sons: Chichester, UK, 2012. [Google Scholar]
- Humphrey, V.; Gudmundsson, L. GRACE-REC: A reconstruction of climate-driven water storage changes over the last century. Earth Syst. Sci. Data 2019, 11, 1153–1170. [Google Scholar] [CrossRef] [Green Version]
- Granger, C.W.J. Investigating Causal Relations by Econometric Models and Cross-spectral Methods. Econometrica 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Granger, C.W.J. Testing for causality: A personal viewpoint. J. Econ. Dynam. Control. 1980, 2, 329–352. [Google Scholar] [CrossRef]
- Lai, C.; Shao, Q.X.; Chen, X.H.; Wang, Z.L.; Zhou, X.W.; Yang, B.; Zhang, L.L. Flood risk zoning using a rule mining based on ant colony algorithm. J. Hydrol. 2016, 542, 268–280. [Google Scholar] [CrossRef]
- Feng, W.; Zhong, M.; Lemoine, J.M.; Biancale, R.; Hsu, H.T.; Xia, J. Evaluation of groundwater depletion in North China using the Gravity Recovery and Climate Experiment (GRACE) data and ground-based measurements. Water Resour. Res. 2013, 49, 2110–2118. [Google Scholar] [CrossRef]
- Wei, X.; Sun, G.; Liu, S.; Jiang, H.; Zhou, G.; Dai, L. The forest-streamflow relationship in China: A 40-year retrospect. J. Am. Water Resour. As. 2008, 44, 1076–1085. [Google Scholar] [CrossRef] [Green Version]
- Xiao, M.; Zhang, Q.; Singh, V.P. Spatiotemporal variations of extreme precipitation regimes during 1961–2010 and possible teleconnections with climate indices across China. Int. J. Climatol. 2017, 37, 468–479. [Google Scholar] [CrossRef]
- Miao, C.; Duan, Q.; Sun, Q.; Lei, X.; Li, H. Non-uniform changes in different categories of precipitation intensity across China and the associated large-scale circulations. Environ. Res. Lett. 2019, 14, 025004. [Google Scholar] [CrossRef]
- Xiong, J.H.; Yin, J.B.; Guo, S.L.; Xiong, F.; Li, N. Integrated flood potential index for flood monitoring in the GRACE era. J. Hydrol. 2021, 603, 127115. [Google Scholar] [CrossRef]
- Sun, Z.; Zhu, X.; Pan, Y.; Zhang, J. Assessing terrestrial water storage and flood potential using GRACE data in the Yangtze River basin, China. Remote Sens. 2017, 9, 1011. [Google Scholar] [CrossRef] [Green Version]
- Cheng, Q.; Gao, L.; Zuo, X.; Zhong, F. Statistical analyses of spatial and temporal variabilities in total, daytime, and nighttime precipitation indices and of extreme dry/wet association with large-scale circulations of Southwest China, 1961–2016. Atmos. Res. 2019, 219, 166–182. [Google Scholar] [CrossRef]
- Gao, T.; Zhang, Q.; Luo, M. Intensifying effects of El Niño events on winter precipitation extremes in southeastern China. Clim. Dynam. 2020, 54, 631–648. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).