Deep Learning-Based Super-Resolution Reconstruction and Algorithm Acceleration of Mars Hyperspectral CRISM Data
Abstract
:1. Introduction
2. Materials
2.1. Data Description
2.2. Dataset Creation
2.2.1. Data Pre-Processing
2.2.2. Data Cropping
3. Method
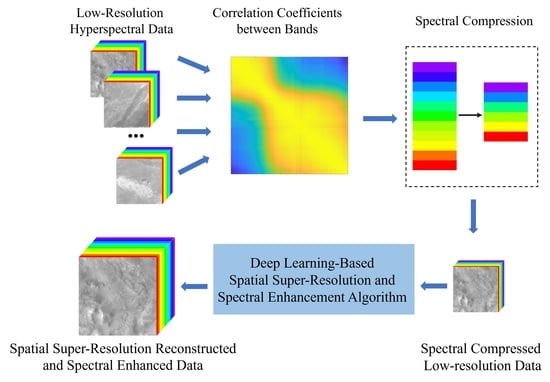
3.1. Hyperspectral Image SR Algorithm
3.2. Data Compression Algorithms
3.2.1. Spectral Compression
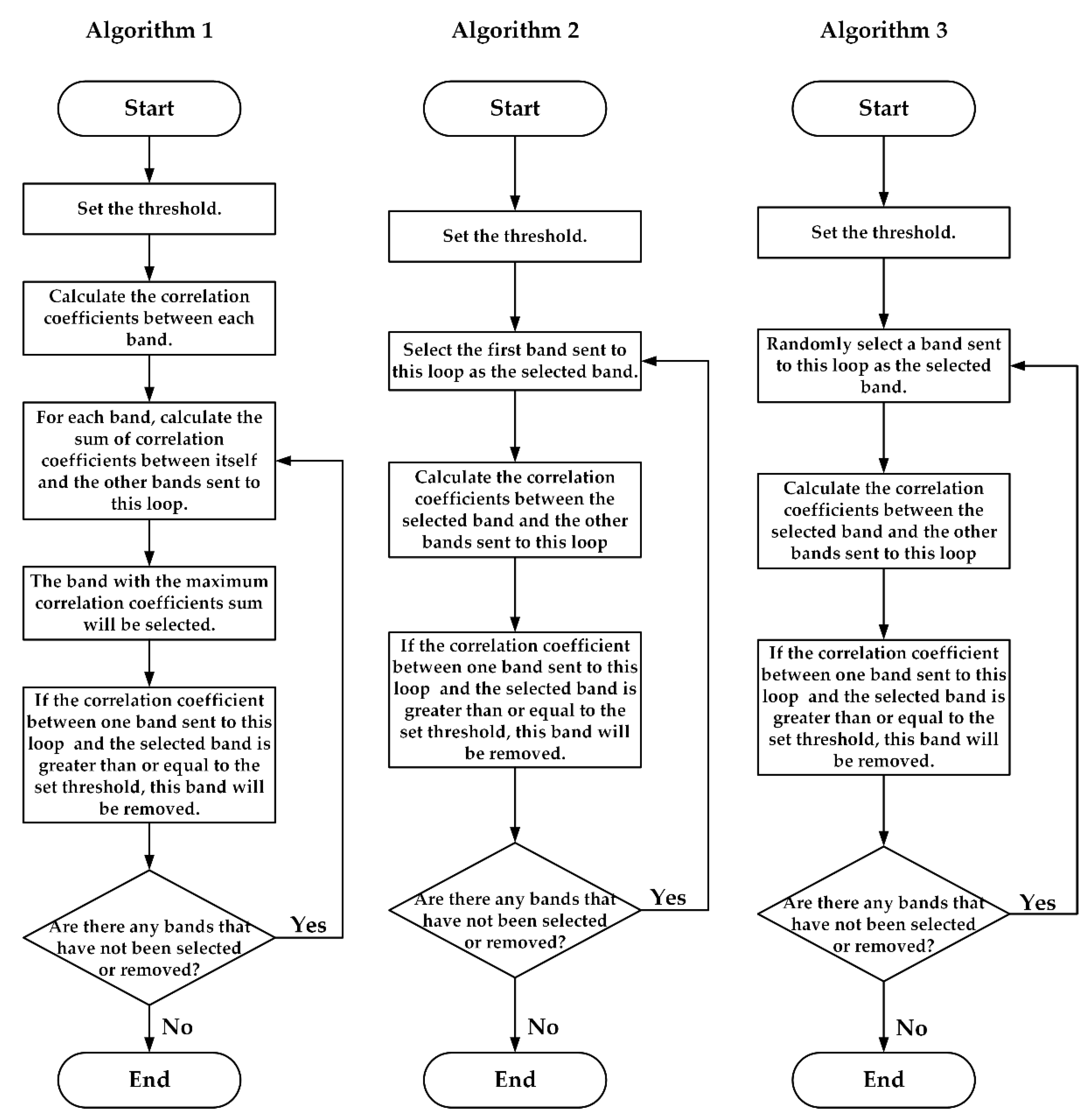
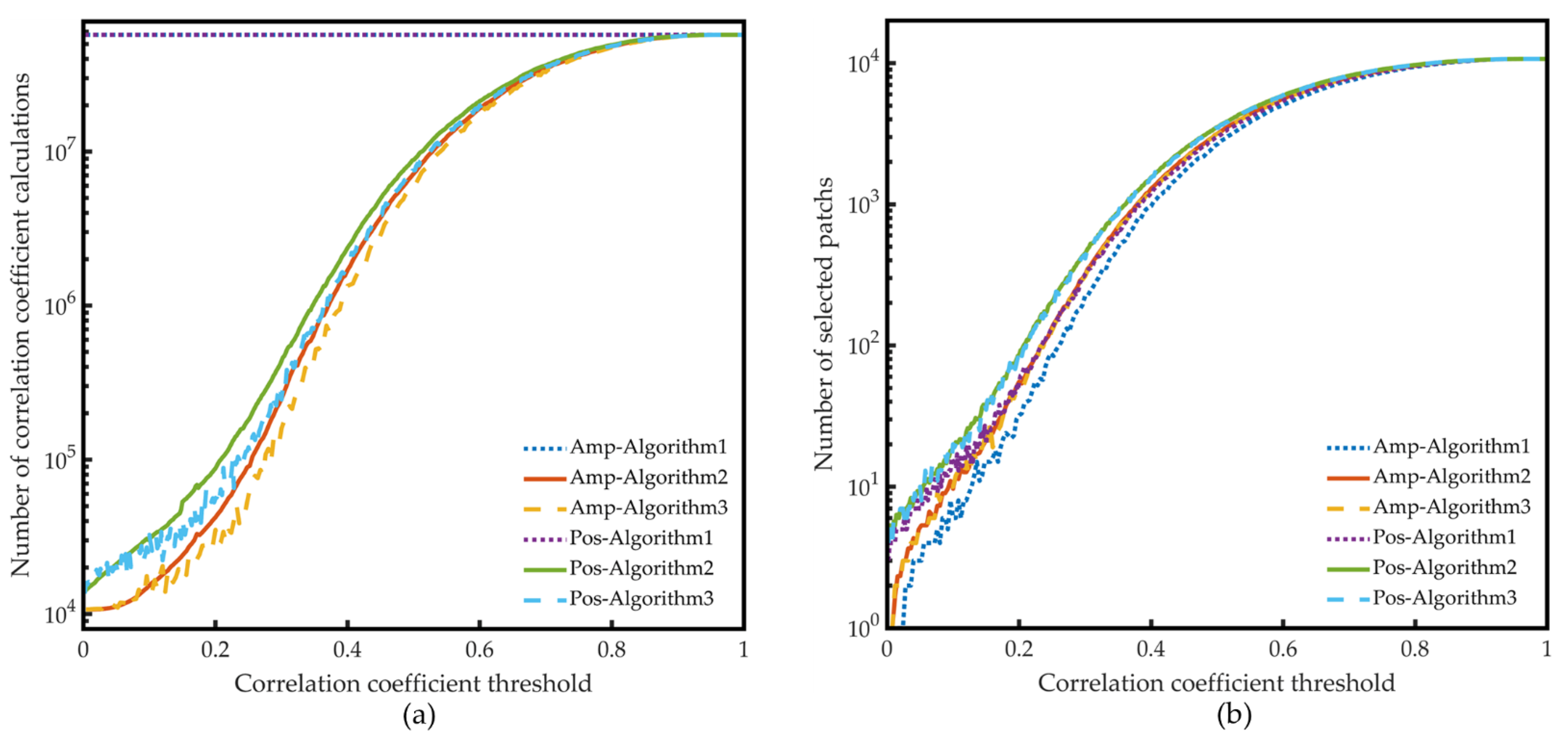
- Compression Algorithms Based on Data Selection
- 2.
- Compression Algorithm Based on PCA
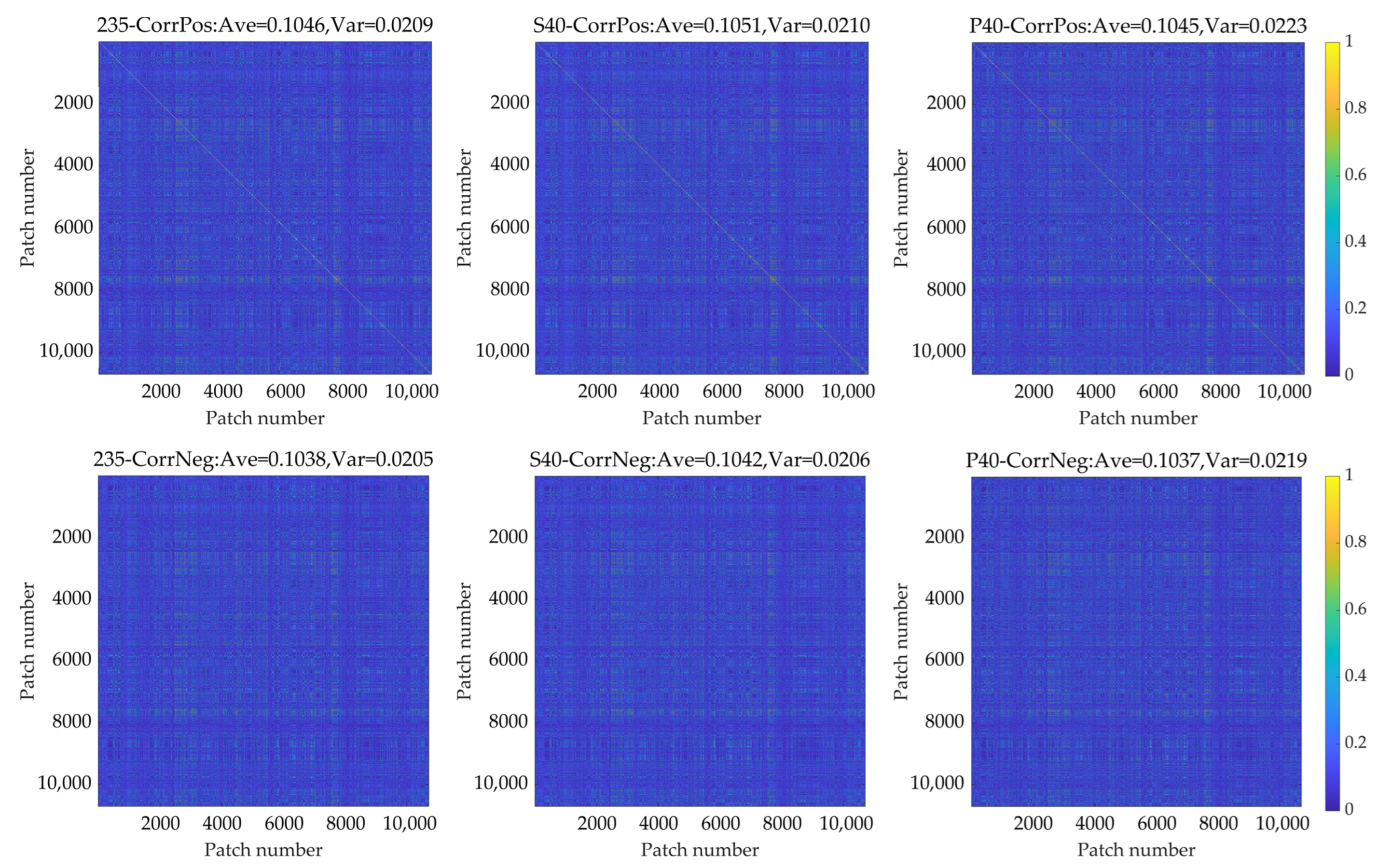
3.2.2. Spatial Compression
4. Results
4.1. Spectral Compression
4.1.1. Compression Algorithms Based on Data Selection
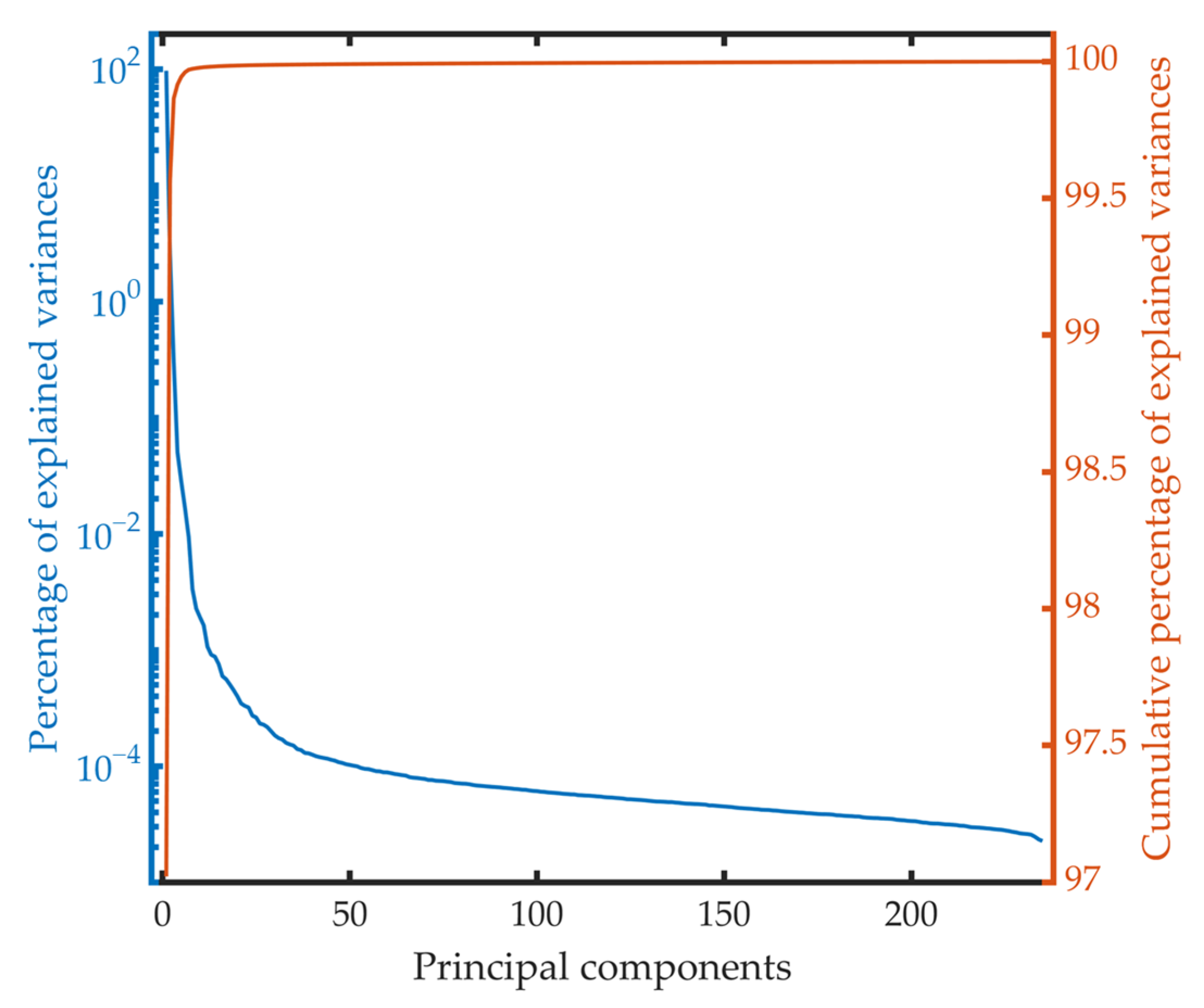
4.1.2. Compression Algorithm Based on PCA
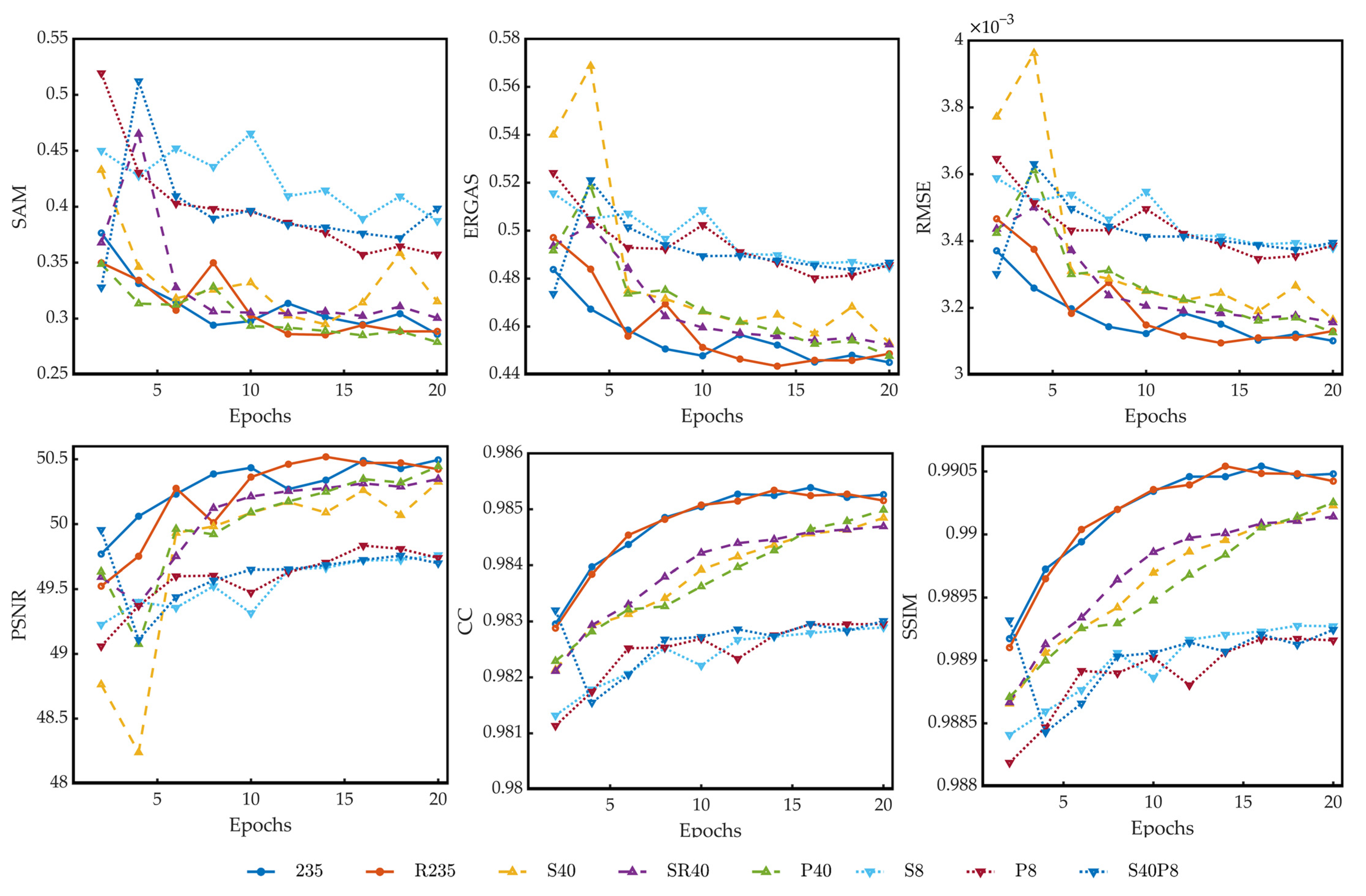
4.2. Comparision of Models Trained on Different Compressed Datasets
- 235: the original dataset with 235 bands;
- S40: dataset with 40 bands constructed by using compression algorithm based on data selection;
- P40: dataset with 40 principal components constructed by using compression algorithm based on PCA;
- S8: dataset with eight bands constructed by using compression algorithm based on data selection;
- P8: dataset with 8 principal components constructed by using compression algorithm based on PCA;
- S40P8: dataset with eight principal components constructed by using compression algorithm based on PCA on dataset S40;
- R235: dataset with 235 bands constructed by reordering the bands of dataset 235;
- SR40: dataset with 40 bands constructed by reordering the bands of dataset S40.
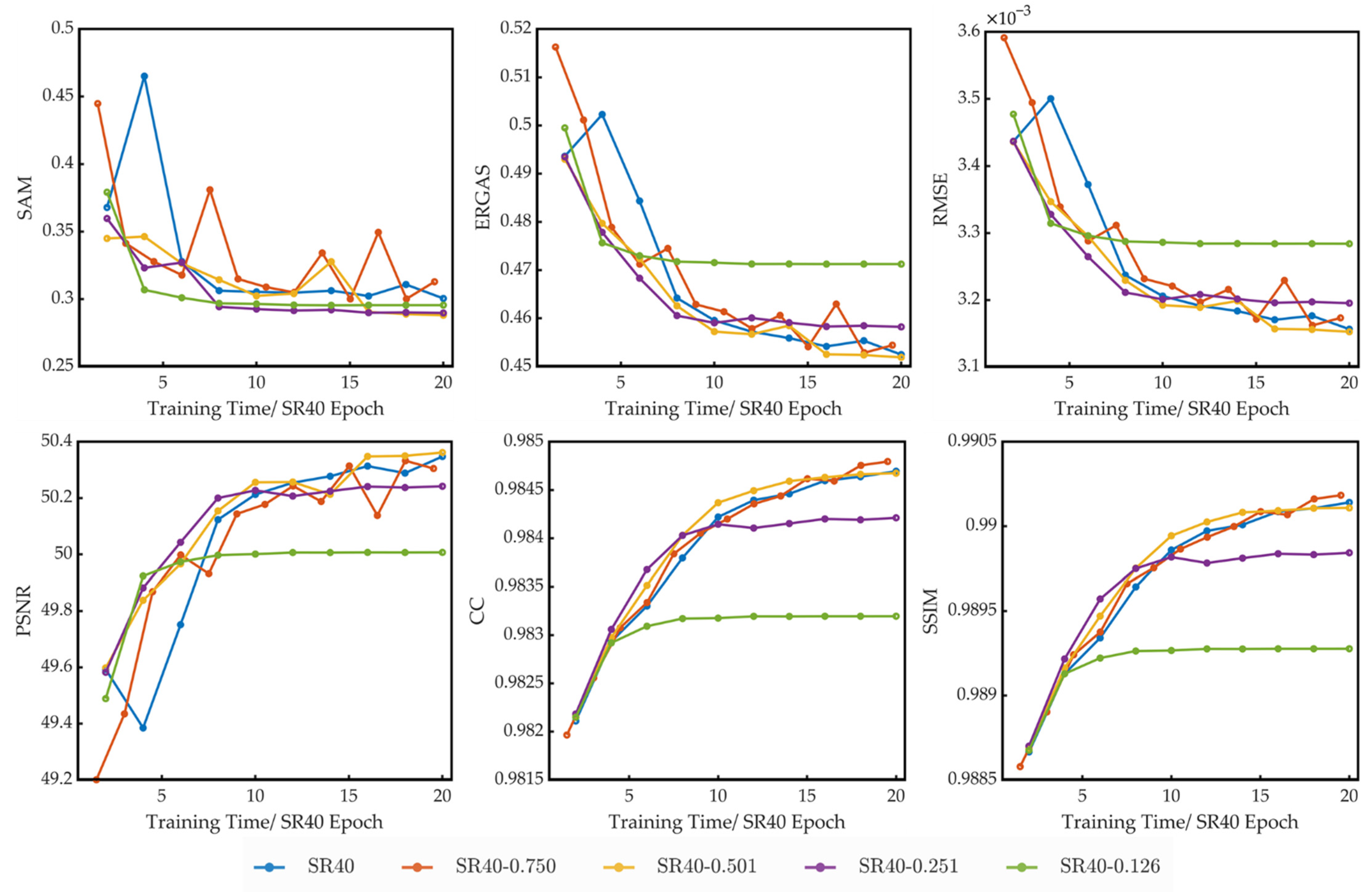
4.3. Spatial Compression
5. Discussion
5.1. Spectral Compression
5.2. Spatial Compression
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Index | Product ID | Index | Product ID | Index | Product ID |
|---|---|---|---|---|---|
| 1 | frt0000a8ce_07_if166l_trr3 | 20 | frt000165f7_07_if166l_trr3 | 39 | frt000093be_07_if166l_trr3 |
| 2 | frt0000a09c_07_if166l_trr3 | 21 | frt0000634b_07_if163l_trr3 | 40 | frt000095fe_07_if166l_trr3 |
| 3 | frt0000a33c_07_if164l_trr3 | 22 | frt0001756e_07_if164l_trr3 | 41 | frt000097e2_07_if166l_trr3 |
| 4 | frt0000a063_07_if165l_trr3 | 23 | frt00008144_07_if164l_trr3 | 42 | frt000135db_07_if166l_trr3 |
| 5 | frt0000a425_07_if166l_trr3 | 24 | frt00009824_07_if164l_trr3 | 43 | frt000174f4_07_if166l_trr3 |
| 6 | frt0000a546_07_if165l_trr3 | 25 | frt00003bfb_07_if166l_trr3 | 44 | frt000199c7_07_if166l_trr3 |
| 7 | frt0000aa03_07_if166l_trr3 | 26 | frt00003e12_07_if166l_trr3 | 45 | frt000251c0_07_if165l_trr3 |
| 8 | frt0000abcb_07_if166l_trr3 | 27 | frt00003fb9_07_if166l_trr3 | 46 | frt0000406b_07_if165l_trr3 |
| 9 | frt0000ada4_07_if168l_trr3 | 28 | frt00005a3e_07_if165l_trr3 | 47 | frt0000979c_07_if165l_trr3 |
| 10 | frt0000bda8_07_if165l_trr3 | 29 | frt00009d31_07_if164l_trr3 | 48 | frt0001642e_07_if166l_trr3 |
| 11 | frt0000a106_07_if163l_trr3 | 30 | frt00013d3b_07_if165l_trr3 | 49 | frt0001821c_07_if166l_trr3 |
| 12 | frt0000a377_07_if165l_trr3 | 31 | frt00016a73_07_if166l_trr3 | 50 | frt00003584_07_if166l_trr3 |
| 13 | frt0001b615_07_if166l_trr3 | 32 | frt00018dca_07_if166l_trr3 | 51 | frt00009971_07_if166l_trr3 |
| 14 | frt00004af7_07_if164l_trr3 | 33 | frt00019daa_07_if165l_trr3 | 52 | frt00017103_07_if165l_trr3 |
| 15 | frt00008c90_07_if163l_trr3 | 34 | frt00024c1a_07_if165l_trr3 | 53 | frt00018781_07_if165l_trr3 |
| 16 | frt000028ba_07_if165l_trr3 | 35 | frt000047a3_07_if166l_trr3 | 54 | frt00019538_07_if166l_trr3 |
| 17 | frt000035db_07_if164l_trr3 | 36 | frt000048b2_07_if165l_trr3 | 55 | frt00023565_07_if166l_trr3 |
| 18 | frt000128d0_07_if165l_trr3 | 37 | frt000050f2_07_if165l_trr3 | 56 | frt00023728_07_if166l_trr3 |
| 19 | frt000161ef_07_if167l_trr3 | 38 | frt000064d9_07_if166l_trr3 | 57 | frt000088d0_07_if166l_trr3 |
Appendix B
Appendix C
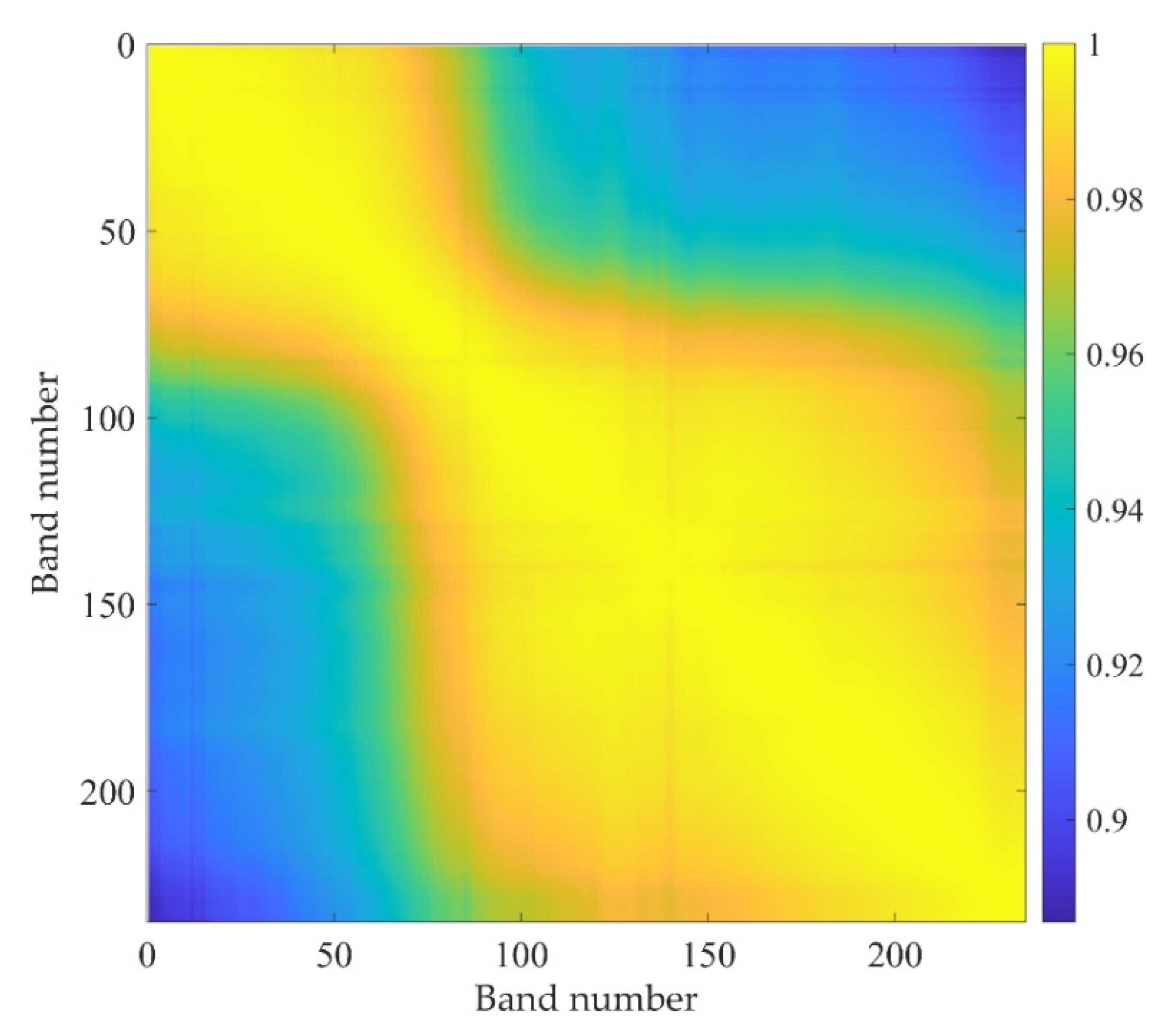
| Band Number | 1 | 34 | 67 | 100 | 133 | 166 | 199 | 232 |
|---|---|---|---|---|---|---|---|---|
| 1 | 1.0000 | 0.9960 | 0.9841 | 0.9413 | 0.9248 | 0.9119 | 0.9061 | 0.8889 |
| 34 | 0.9960 | 1.0000 | 0.9926 | 0.9529 | 0.9373 | 0.9286 | 0.9244 | 0.9107 |
| 67 | 0.9841 | 0.9926 | 1.0000 | 0.9803 | 0.9686 | 0.9623 | 0.9571 | 0.9431 |
| 100 | 0.9413 | 0.9529 | 0.9803 | 1.0000 | 0.9956 | 0.9939 | 0.9863 | 0.9698 |
| 133 | 0.9248 | 0.9373 | 0.9686 | 0.9956 | 1.0000 | 0.9968 | 0.9918 | 0.9780 |
| 166 | 0.9119 | 0.9286 | 0.9623 | 0.9939 | 0.9968 | 1.0000 | 0.9967 | 0.9848 |
| 199 | 0.9061 | 0.9244 | 0.9571 | 0.9863 | 0.9918 | 0.9967 | 1.0000 | 0.9942 |
| 232 | 0.8889 | 0.9107 | 0.9431 | 0.9698 | 0.9780 | 0.9848 | 0.9942 | 1.0000 |


Appendix D

| CorrPos | Patch 1 | Patch 2 | Patch 3 | Patch 4 | CorrNeg | Patch 1 | Patch 2 | Patch 3 | Patch 4 |
| Patch 1 | 1.00 | 0.95 | 0.00 | 0.00 | Patch 1 | 0.00 | 0.00 | 0.95 | 0.96 |
| Patch 2 | 0.95 | 1.00 | 0.00 | 0.00 | Patch 2 | 0.00 | 0.00 | 0.92 | 0.96 |
| Patch 3 | 0.00 | 0.00 | 1.00 | 0.92 | Patch 3 | 0.95 | 0.92 | 0.00 | 0.00 |
| Patch 4 | 0.00 | 0.00 | 0.92 | 1.00 | Patch 4 | 0.96 | 0.96 | 0.00 | 0.00 |
| CorrPos | Patch 5 | Patch 6 | Patch 7 | Patch 8 | CorrNeg | Patch 5 | Patch 6 | Patch 7 | Patch 8 |
| Patch 5 | 1.00 | 0.00 | 0.00 | 0.00 | Patch 5 | 0.00 | 0.00 | 0.08 | 0.44 |
| Patch 6 | 0.00 | 1.00 | 0.00 | 0.00 | Patch 6 | 0.00 | 0.00 | 0.04 | 0.13 |
| Patch 7 | 0.00 | 0.00 | 1.00 | 0.00 | Patch 7 | 0.08 | 0.04 | 0.00 | 0.00 |
| Patch 8 | 0.00 | 0.00 | 0.00 | 1.00 | Patch 8 | 0.44 | 0.13 | 0.00 | 0.00 |

References
- Schmidt, R.; Credland, J.D.; Chicarro, A.; Moulinier, P. ESA’s Mars Express mission—Europe on its way to Mars. ESA Bulletin. Bull. ASE. Eur. Space Agency 1999, 98, 56–66. [Google Scholar]
- Chapman, C.R.; Pollack, J.B.; Sagan, C. An analysis of the Mariner 4 photography of Mars; Smithsonian Institution Astrophysical Observatory: Cambridge, MA, USA, 1968. [Google Scholar]
- Howell, E.; Stein, V. Mars Missions: A Brief History. Available online: https://www.space.com/13558-historic-mars-missions.html (accessed on 22 June 2022).
- Ehlmann, B.; Anderson, F.; Andrews-Hanna, J.; Catling, D.; Christensen, P.; Cohen, B.; Dressing, C.; Edwards, C.; Elkins-Tanton, L.; Farley, K. The sustainability of habitability on terrestrial planets: Insights, questions, and needed measurements from Mars for understanding the evolution of Earth-like worlds. J. Geophys. Res. Planets 2016, 121, 1927–1961. [Google Scholar] [CrossRef]
- Farmer, J. Thermophiles, early biosphere evolution, and the origin of life on Earth: Implications for the exobiological exploration of Mars. J. Geophys. Res. Planets 1998, 103, 28457–28461. [Google Scholar] [CrossRef]
- Grotzinger, J.; Beaty, D.; Dromart, G.; Gupta, S.; Harris, M.; Hurowitz, J.; Kocurek, G.; McLennan, S.; Milliken, R.; Ori, G.G. Mars Sedimentary Geology: Key Concepts and Outstanding Questions; Mary Ann Liebert, Inc.: New Rochelle, NY, USA, 2011. [Google Scholar]
- McKay, C.P.; Stoker, C.R. The early environment and its evolution on Mars: Implication for life. Rev. Geophys. 1989, 27, 189–214. [Google Scholar] [CrossRef] [Green Version]
- Poulet, F.; Bibring, J.-P.; Mustard, J.; Gendrin, A.; Mangold, N.; Langevin, Y.; Arvidson, R.; Gondet, B.; Gomez, C. Phyllosilicates on Mars and implications for early Martian climate. Nature 2005, 438, 623–627. [Google Scholar] [CrossRef]
- Read, P.; Lewis, S.; Mulholland, D. The physics of Martian weather and climate: A review. Rep. Prog. Phys. 2015, 78, 125901. [Google Scholar] [CrossRef] [Green Version]
- Christensen, E.J. Martian topography derived from occultation, radar, spectral, and optical measurements. J. Geophys. Res. 1975, 80, 2909–2913. [Google Scholar] [CrossRef]
- Zuber, M.T.; Solomon, S.C.; Phillips, R.J.; Smith, D.E.; Tyler, G.L.; Aharonson, O.; Balmino, G.; Banerdt, W.B.; Head, J.W.; Johnson, C.L. Internal structure and early thermal evolution of Mars from Mars Global Surveyor topography and gravity. Science 2000, 287, 1788–1793. [Google Scholar] [CrossRef] [Green Version]
- Bibring, J.P.; Erard, S. The Martian surface composition. Space Sci. Rev. 2001, 96, 293–316. [Google Scholar] [CrossRef]
- Bandfield, J.L.; Hamilton, V.E.; Christensen, P.R. A global view of Martian surface compositions from MGS-TES. Science 2000, 287, 1626–1630. [Google Scholar] [CrossRef] [Green Version]
- Richardson, M.I.; Mischna, M.A. Long-term evolution of transient liquid water on Mars. J. Geophys. Res. Planets 2005, 110, E03003. [Google Scholar] [CrossRef] [Green Version]
- Clifford, S.M.; Lasue, J.; Heggy, E.; Boisson, J.; McGovern, P.; Max, M.D. Depth of the Martian cryosphere: Revised estimates and implications for the existence and detection of subpermafrost groundwater. J. Geophys. Res. Planets 2010, 115, E07001. [Google Scholar] [CrossRef]
- Rogers, A.D.; Hamilton, V.E. Compositional provinces of Mars from statistical analyses of TES, GRS, OMEGA and CRISM data. J. Geophys. Res. Planets 2015, 120, 62–91. [Google Scholar] [CrossRef]
- Zou, Y.; Zhu, Y.; Bai, Y.; Wang, L.; Jia, Y.; Shen, W.; Fan, Y.; Liu, Y.; Wang, C.; Zhang, A. Scientific objectives and payloads of Tianwen-1, China’s first Mars exploration mission. Adv. Space Res. 2021, 67, 812–823. [Google Scholar] [CrossRef]
- Nawar, S.; Buddenbaum, H.; Hill, J.; Kozak, J. Modeling and mapping of soil salinity with reflectance spectroscopy and landsat data using two quantitative methods (PLSR and MARS). Remote Sens. 2014, 6, 10813–10834. [Google Scholar] [CrossRef] [Green Version]
- Thomas, M.; Walter, M.R. Application of hyperspectral infrared analysis of hydrothermal alteration on Earth and Mars. Astrobiology 2002, 2, 335–351. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Du, B.; Zhong, Y. Hybrid detectors based on selective endmembers. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2633–2646. [Google Scholar] [CrossRef]
- Zhou, F.; Yang, W.; Liao, Q. Interpolation-based image super-resolution using multisurface fitting. IEEE Trans. Image Process. 2012, 21, 3312–3318. [Google Scholar] [CrossRef]
- Rajan, D.; Chaudhuri, S. Generalized interpolation and its application in super-resolution imaging. Image Vis. Comput. 2001, 19, 957–969. [Google Scholar] [CrossRef]
- Park, S.C.; Park, M.K.; Kang, M.G. Super-resolution image reconstruction: A technical overview. IEEE Signal Process. Mag. 2003, 20, 21–36. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Cui, R.; Li, B.; Song, R.; Li, Y.; Du, Q. Hyperspectral Image Super-Resolution with 1D–2D Attentional Convolutional Neural Network. Remote Sens. 2019, 11, 2859. [Google Scholar] [CrossRef] [Green Version]
- Zou, C.; Huang, X. Hyperspectral image super-resolution combining with deep learning and spectral unmixing. Signal Process. Image Commun. 2020, 84, 115833. [Google Scholar] [CrossRef]
- Wang, Q.; Li, Q.; Li, X. Hyperspectral Image Superresolution Using Spectrum and Feature Context. IEEE Trans. Ind. Electron. 2021, 68, 11276–11285. [Google Scholar] [CrossRef]
- Ha, V.K.; Ren, J.; Xu, X.; Zhao, S.; Xie, G.; Vargas, V.M. Deep Learning Based Single Image Super-Resolution: A Survey. In Proceedings of the International Conference on Brain Inspired Cognitive Systems, Xi’an, China, 7–8 July 2018; pp. 106–119. [Google Scholar]
- Ma, W.; Pan, Z.; Yuan, F.; Lei, B. Super-Resolution of Remote Sensing Images via a Dense Residual Generative Adversarial Network. Remote Sens. 2019, 11, 2578. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Liu, S.; Wang, Z. A general framework for image fusion based on multi-scale transform and sparse representation. Inf. Fusion 2015, 24, 147–164. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Learning a Deep Convolutional Network for Image Super-Resolution. In Proceedings of the European Conference on Computer Vision (ECCV), Zurich, Switzerland, 6–12 September 2014. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Kim, J.; Lee, J.K.; Lee, K.M. Accurate Image Super-Resolution Using Very Deep Convolutional Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1646–1654. [Google Scholar]
- Hu, J.; Li, Y.; Xie, W. Hyperspectral Image Super-Resolution by Spectral Difference Learning and Spatial Error Correction. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1825–1829. [Google Scholar] [CrossRef]
- Zheng, K.; Gao, L.; Zhang, B.; Cui, X. Multi-Losses Function Based Convolution Neural Network for Single Hyperspectral Image SuperResolutio. In Proceedings of the 2018 Fifth International Workshop on Earth Observation and Remote Sensing Applications (EORSA), Xi’an, China, 18–20 June 2018; pp. 1–4. [Google Scholar]
- Li, Y.; Zhang, L.; Ding, C.; Wei, W.; Zhang, Y. Single Hyperspectral Image Super-resolution with Grouped Deep Recursive Residual Network. In Proceedings of the 2018 IEEE Fourth International Conference on Multimedia Big Data (BigMM), Xi’an, China, 13–16 September 2018; pp. 1–4. [Google Scholar]
- Liu, W.; Lee, J. An Efficient Residual Learning Neural Network for Hyperspectral Image Super resolution. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1240–1253. [Google Scholar] [CrossRef]
- Jiang, J.; Sun, H.; Liu, X.; Ma, J. Learning spatial-spectral prior for super-resolution of hyperspectral imagery. IEEE Trans. Comput. Imaging 2020, 6, 1082–1096. [Google Scholar] [CrossRef]
- Murchie, S. Compact Reconnaissance Imaging Spectrometer for Mars (CRISM) on Mars Reconnaissance Orbiter (MRO). J. Geophys. Res. Atmos. 2007, 112, E05S03. [Google Scholar] [CrossRef]
- Morgan, M.; Seelos, F.; Murchie, S. The CRISM Analysis Toolkit (CAT): Overview and Recent Updates. In Proceedings of the Third Planetary Data Workshop and the Planetary Geologic Mappers Annual Meeting, Flagstaff, Arizona, 12–15 June 2017; p. 7121. [Google Scholar]
- Amador, E.S.; Bandfield, J.L.; Thomas, N.H. A search for minerals associated with serpentinization across Mars using CRISM spectral data. Icarus 2018, 311, 113–134. [Google Scholar] [CrossRef]
- Tian, L.; Fan, C.; Ming, Y.; Jin, Y. Stacked PCA network (SPCANet): An Effective Deep Learning for Face Recognition. In Proceedings of the 2015 IEEE International Conference on Digital Signal Processing (DSP), Singapore, 21–24 July 2015; pp. 1039–1043. [Google Scholar]
- Valpola, H. From Neural PCA to Deep Unsupervised Learning. In Advances in Independent Component Analysis and Learning Machines; Elsevier: Amsterdam, The Netherlands, 2015; pp. 143–171. [Google Scholar]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep learning-based classification of hyperspectral data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Jolliffe, I. Pincipal Component Analysis; Springer: Berlin/Heidelberg, Germany, 2002; Volume 25, p. 513. [Google Scholar]
- Yuhas, R.H.; Goetz, A.F.; Boardman, J.W. Discrimination Among Semi-Arid Landscape Endmembers Using the Spectral Angle Mapper (SAM) Algorithm. In Proceedings of the JPL, Summaries of the Third Annual JPL Airborne Geoscience Workshop, Volume 1: AVIRIS Workshop, Pasadena, CA, USA, 1–5 June 1992; pp. 147–149. [Google Scholar]
- Wald, L. Data Fusion: Definitions and Architectures: Fusion of Images of Different Spatial Resolutions; Presses des MINES: Paris, France, 2002. [Google Scholar]
- Loncan, L.; De Almeida, L.B.; Bioucas-Dias, J.M.; Briottet, X.; Chanussot, J.; Dobigeon, N.; Fabre, S.; Liao, W.; Licciardi, G.A.; Simoes, M. Hyperspectral pansharpening: A review. IEEE Geosci. Remote Sens. Mag. 2015, 3, 27–46. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed] [Green Version]





| Spectrometer | Satellite | Launch Time | Spatial Resolution | Spectral Resolution | Wavelength Range | Number of Bands |
|---|---|---|---|---|---|---|
| TES | Mars Global Surveyor | 1996 | 3 × 6 km | 10 cm−1/20 cm−1 | 5.8–50 μm | 148/296 |
| OMEGA | ESA’s Mars Express | 2003 | 0.3–4.8 km | 7–20 nm | 0.36–5.1 μm | 352 |
| CRISM | Mars Reconnaissance Orbiter | 2005 | 18–200 m | 6.55 nm | 0.36–3.92 μm | 544/72 |
| MMS | Tianwen-1 Mission | 2020 | 265 m–3.2 km | 6/12/20 nm | 0.45–3.4 μm | 576/72 |
| CorrTh | Algorithm 1 | Algorithm 2 | Algorithm 3-1 | Algorithm 3-2 | Algorithm 3-3 | Algorithm 3 | Algorithm 3/2 | Algorithm 3/1 |
|---|---|---|---|---|---|---|---|---|
| 0.9970 | 27,495 | 1382 | 877 | 853 | 866 | 865.33 | 62.61% | 3.15% |
| 0.9980 | 27,495 | 1955 | 994 | 1164 | 1061 | 1073.00 | 54.88% | 3.90% |
| 0.9990 | 27,495 | 3341 | 1728 | 1732 | 1888 | 1782.67 | 53.36% | 6.48% |
| 0.9996 | 27,495 | 7263 | 3616 | 3656 | 3494 | 3588.67 | 49.41% | 13.05% |
| CorrTh | Algorithm 1 | Algorithm 2 | Algorithm 3-1 | Algorithm 3-2 | Algorithm 3-3 | Algorithm 3 | Algorithm 3/2 | Algorithm 3/1 |
|---|---|---|---|---|---|---|---|---|
| 0.9970 | 8 | 11 | 9 | 9 | 9 | 9.00 | 81.82% | 112.50% |
| 0.9980 | 11 | 15 | 11 | 12 | 11 | 11.33 | 75.56% | 103.03% |
| 0.9990 | 19 | 27 | 21 | 21 | 23 | 21.67 | 80.25% | 114.04% |
| 0.9996 | 40 | 58 | 47 | 49 | 47 | 47.67 | 82.18% | 119.17% |
| Spectral Feature Number | Training Time | SR Reconstruction Time |
|---|---|---|
| 235 | ~910 min | ~109 ms |
| 40 | ~276 min | ~25 ms |
| 8 | ~187 min | ~7 ms |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, M.; Chen, S. Deep Learning-Based Super-Resolution Reconstruction and Algorithm Acceleration of Mars Hyperspectral CRISM Data. Remote Sens. 2022, 14, 3062. https://doi.org/10.3390/rs14133062
Sun M, Chen S. Deep Learning-Based Super-Resolution Reconstruction and Algorithm Acceleration of Mars Hyperspectral CRISM Data. Remote Sensing. 2022; 14(13):3062. https://doi.org/10.3390/rs14133062
Chicago/Turabian StyleSun, Mingbo, and Shengbo Chen. 2022. "Deep Learning-Based Super-Resolution Reconstruction and Algorithm Acceleration of Mars Hyperspectral CRISM Data" Remote Sensing 14, no. 13: 3062. https://doi.org/10.3390/rs14133062
APA StyleSun, M., & Chen, S. (2022). Deep Learning-Based Super-Resolution Reconstruction and Algorithm Acceleration of Mars Hyperspectral CRISM Data. Remote Sensing, 14(13), 3062. https://doi.org/10.3390/rs14133062