Segmentation of PMSE Data Using Random Forests
Abstract
:1. Introduction
2. Theory
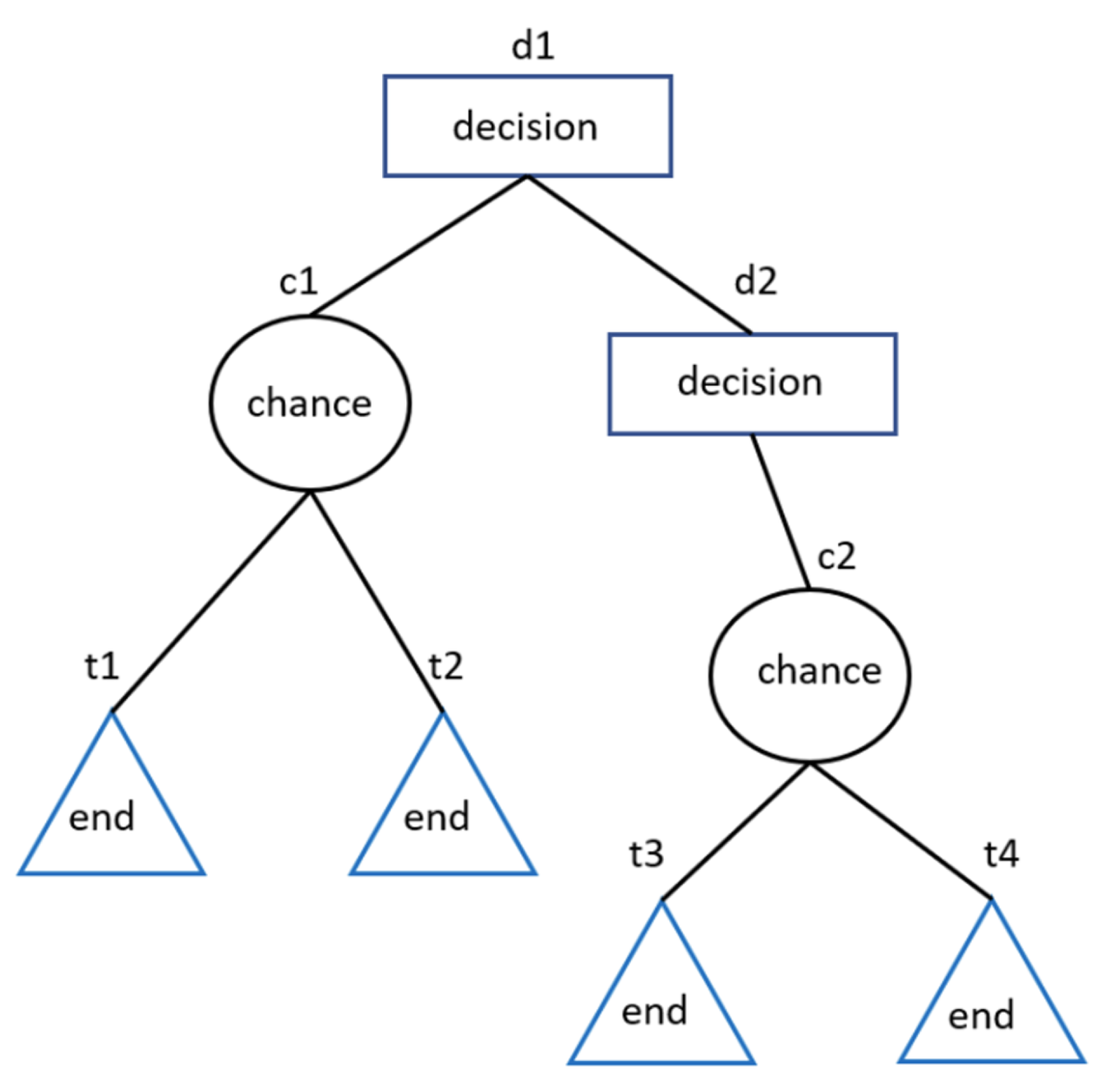
2.1. Random Forests
2.2. Weighted-Down Technique
2.3. Metrics for Evaluation of Performance
2.3.1. Classification Error
2.3.2. Logarithmic Loss
2.3.3. Area under ROC Curve (AUC)
3. Method
3.1. Dataset
3.2. Labeling
3.3. Labels with Reduced Weighting
3.4. Random Forests Application
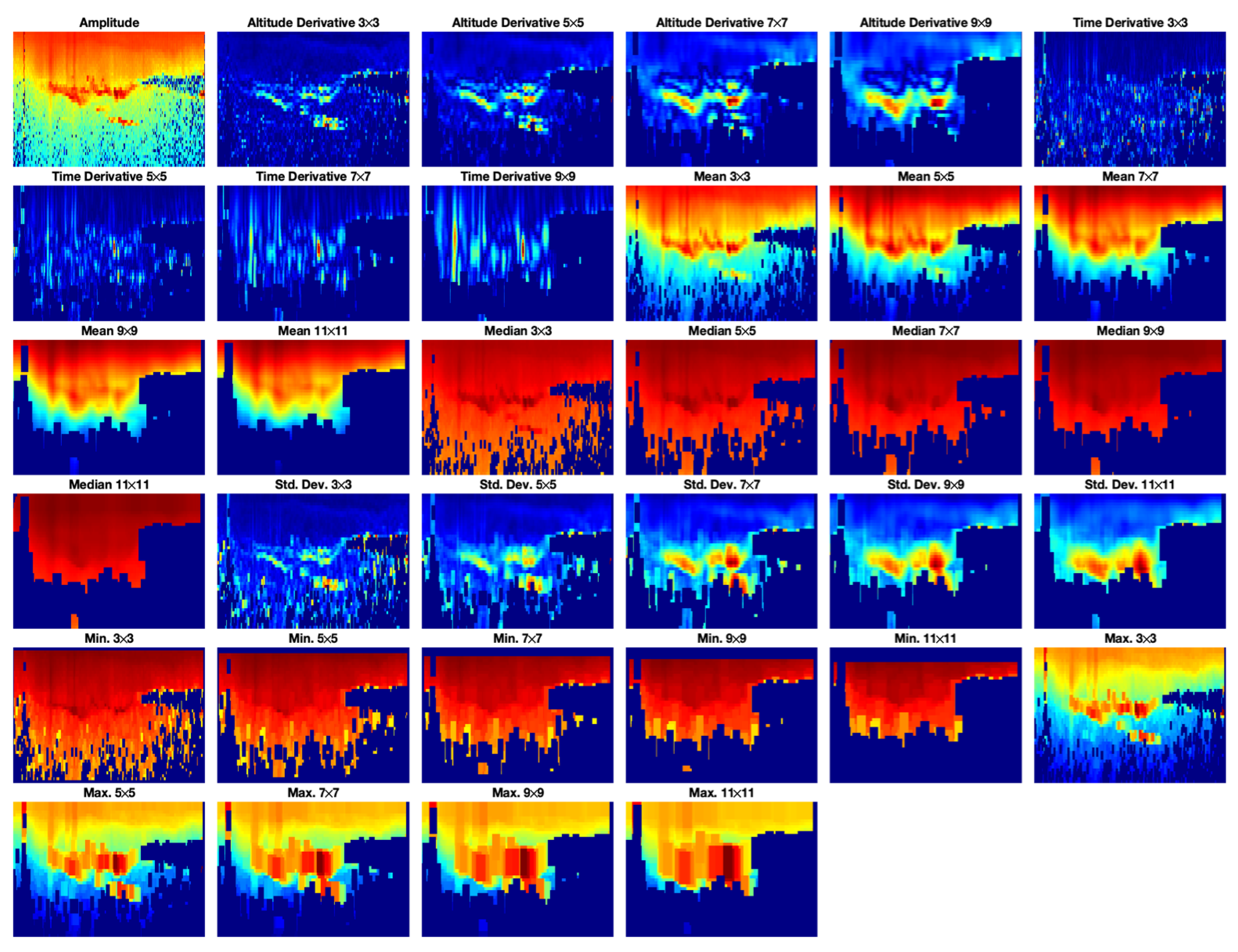
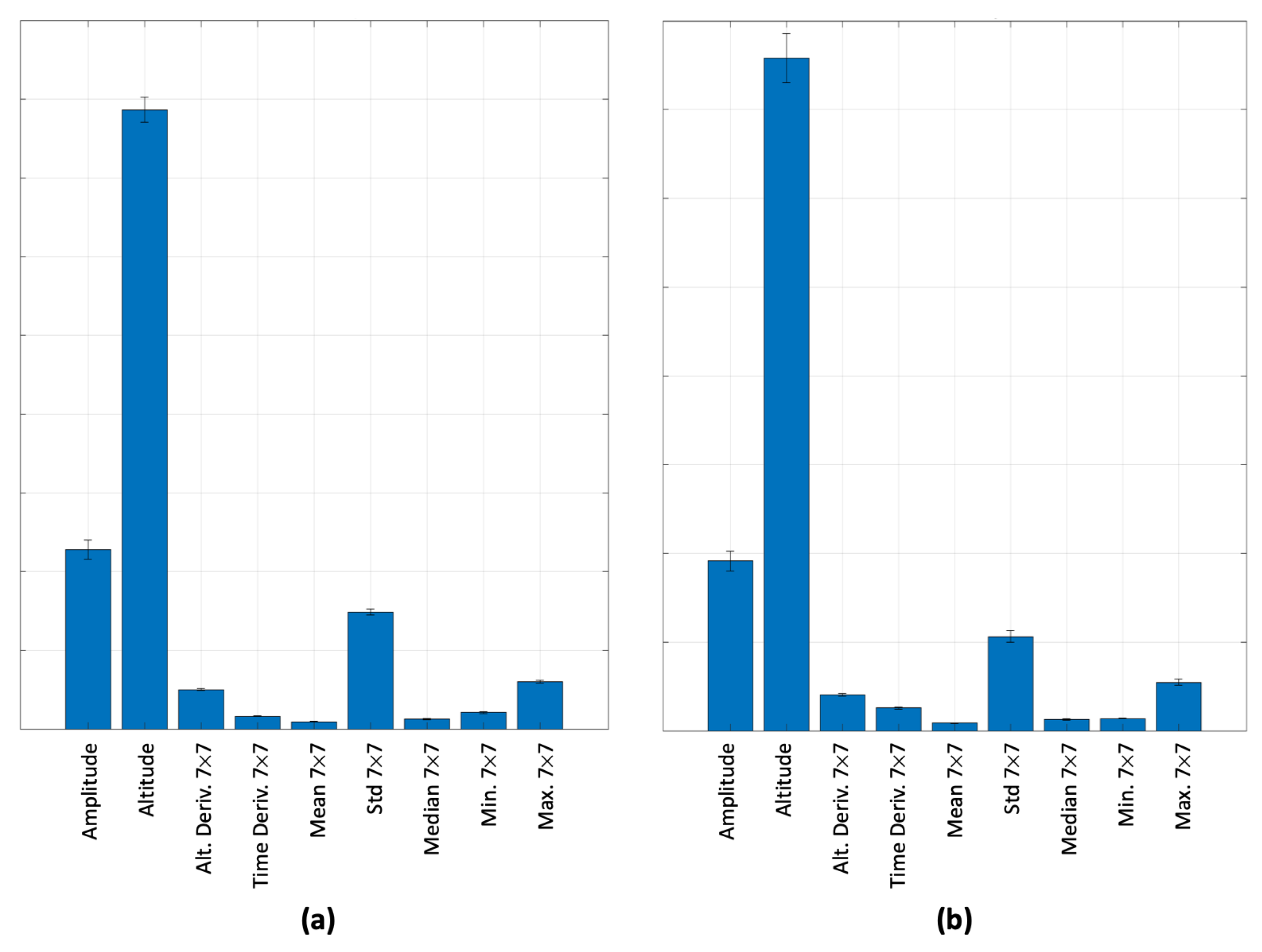
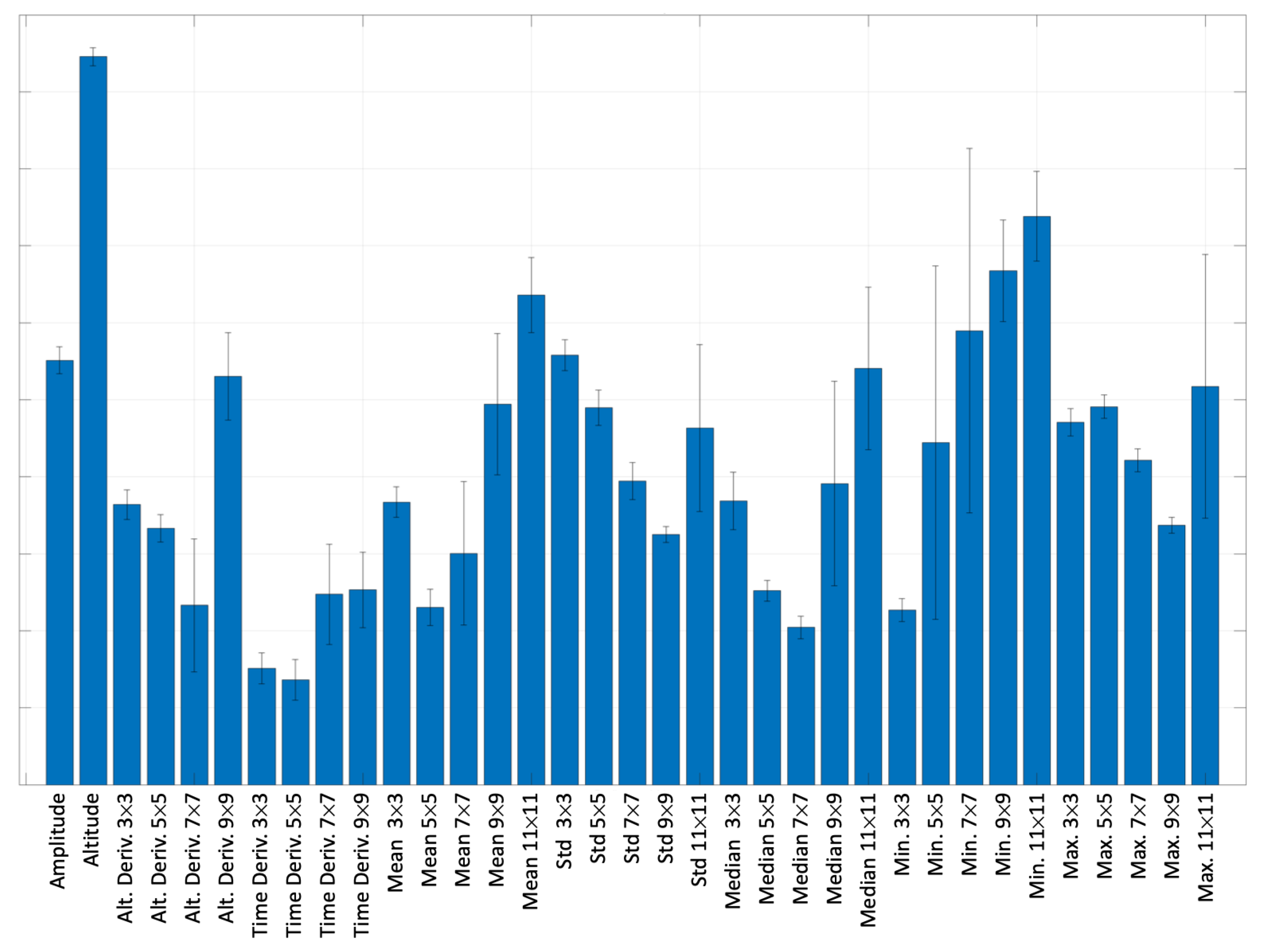
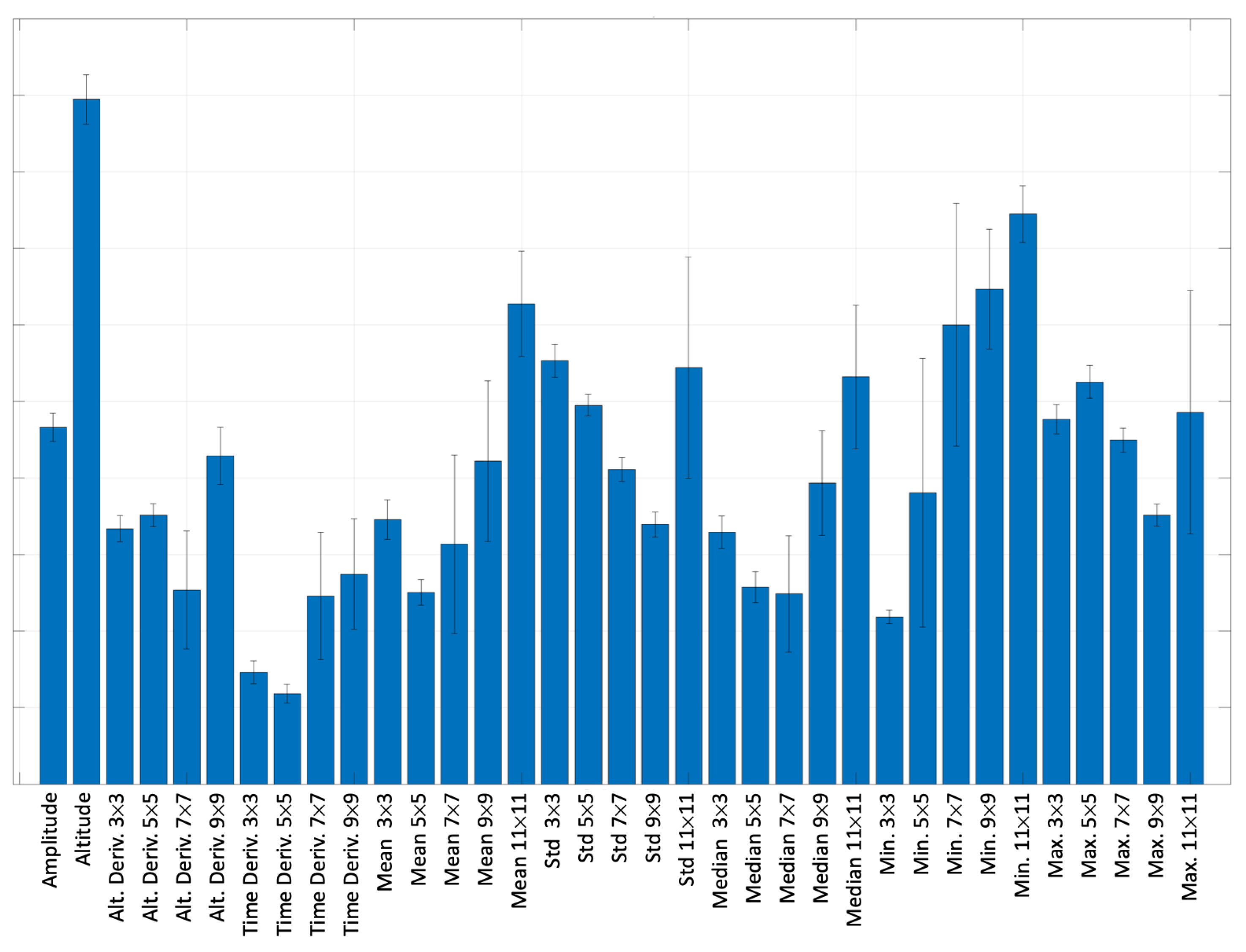
3.5. Feature Extraction
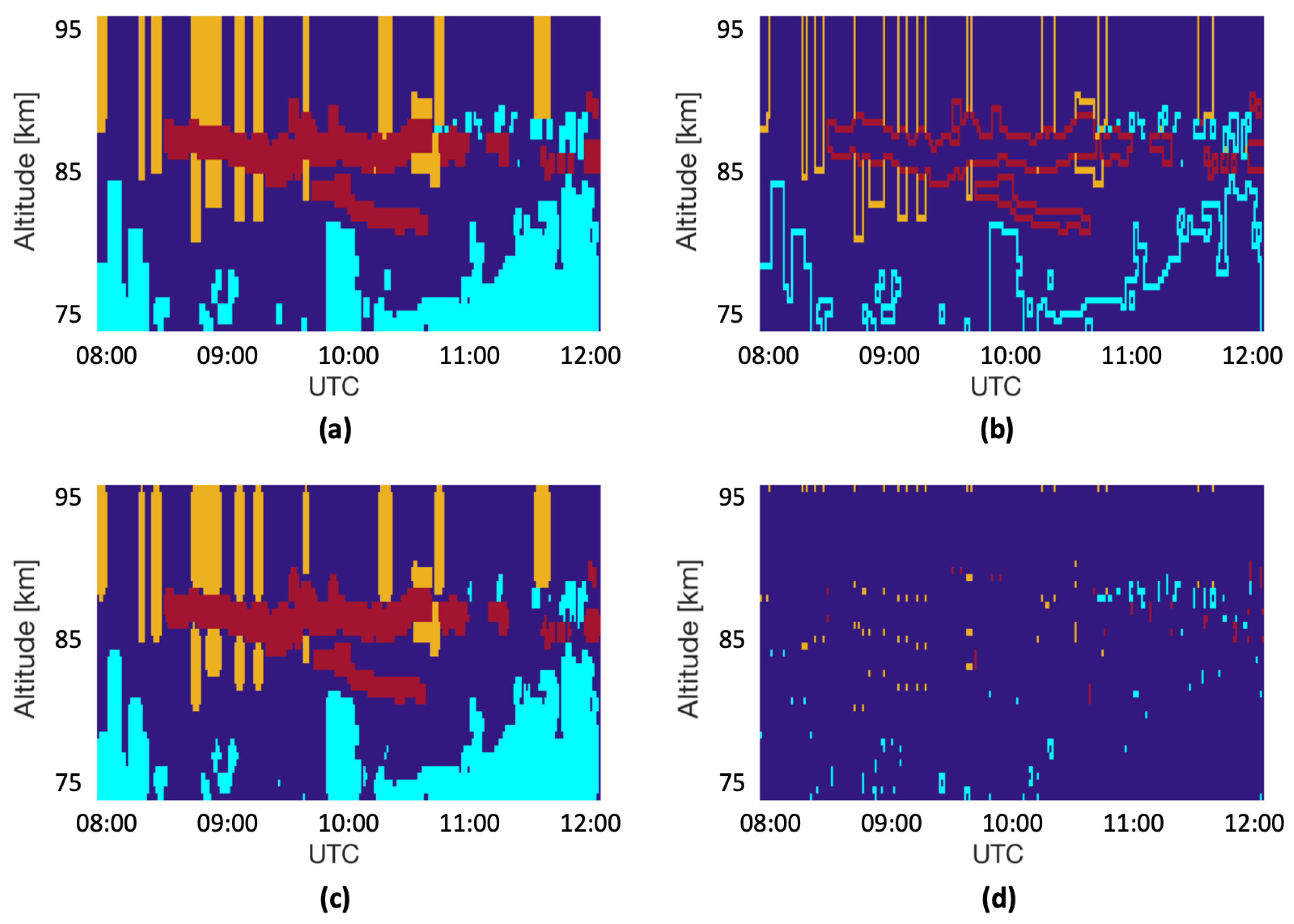
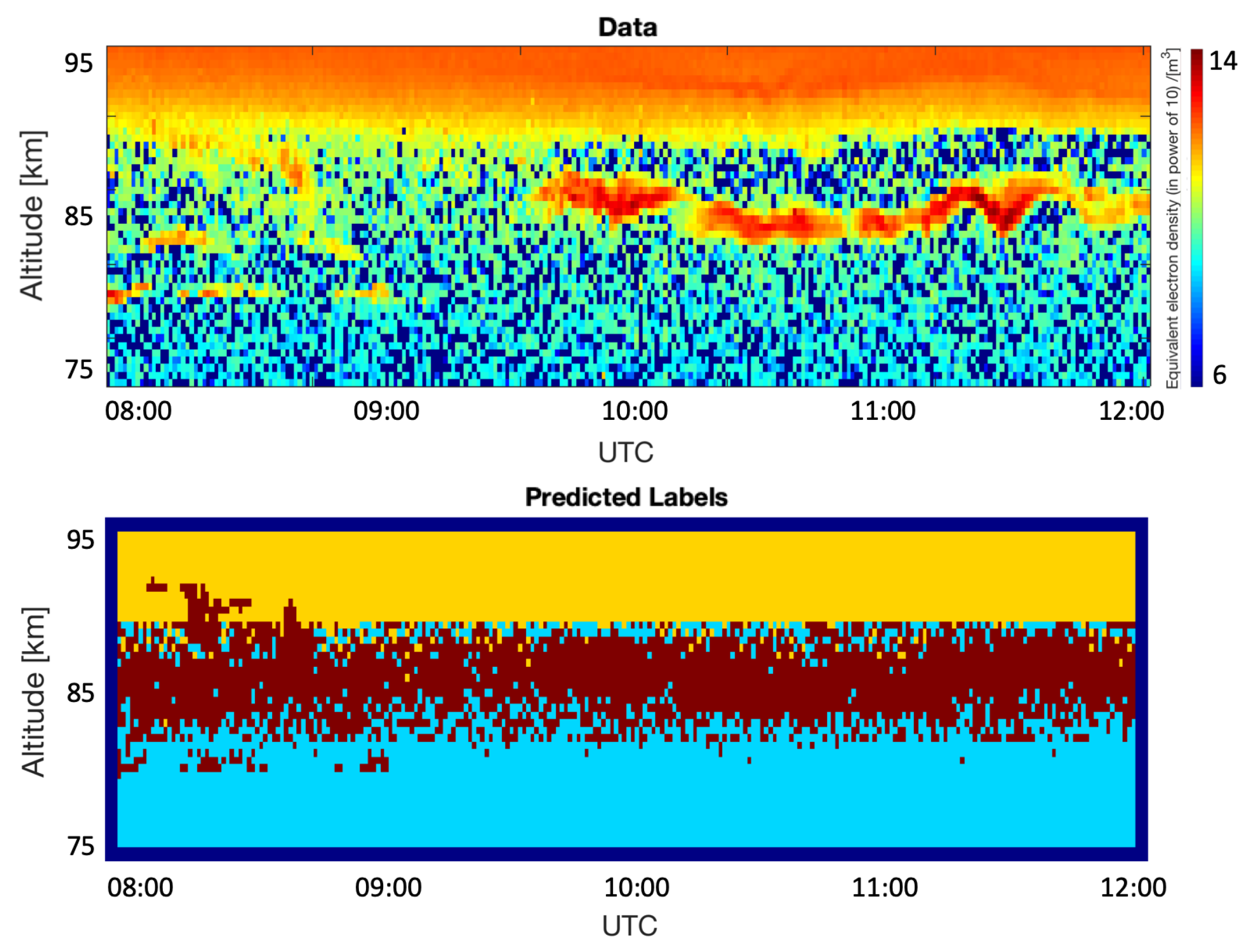
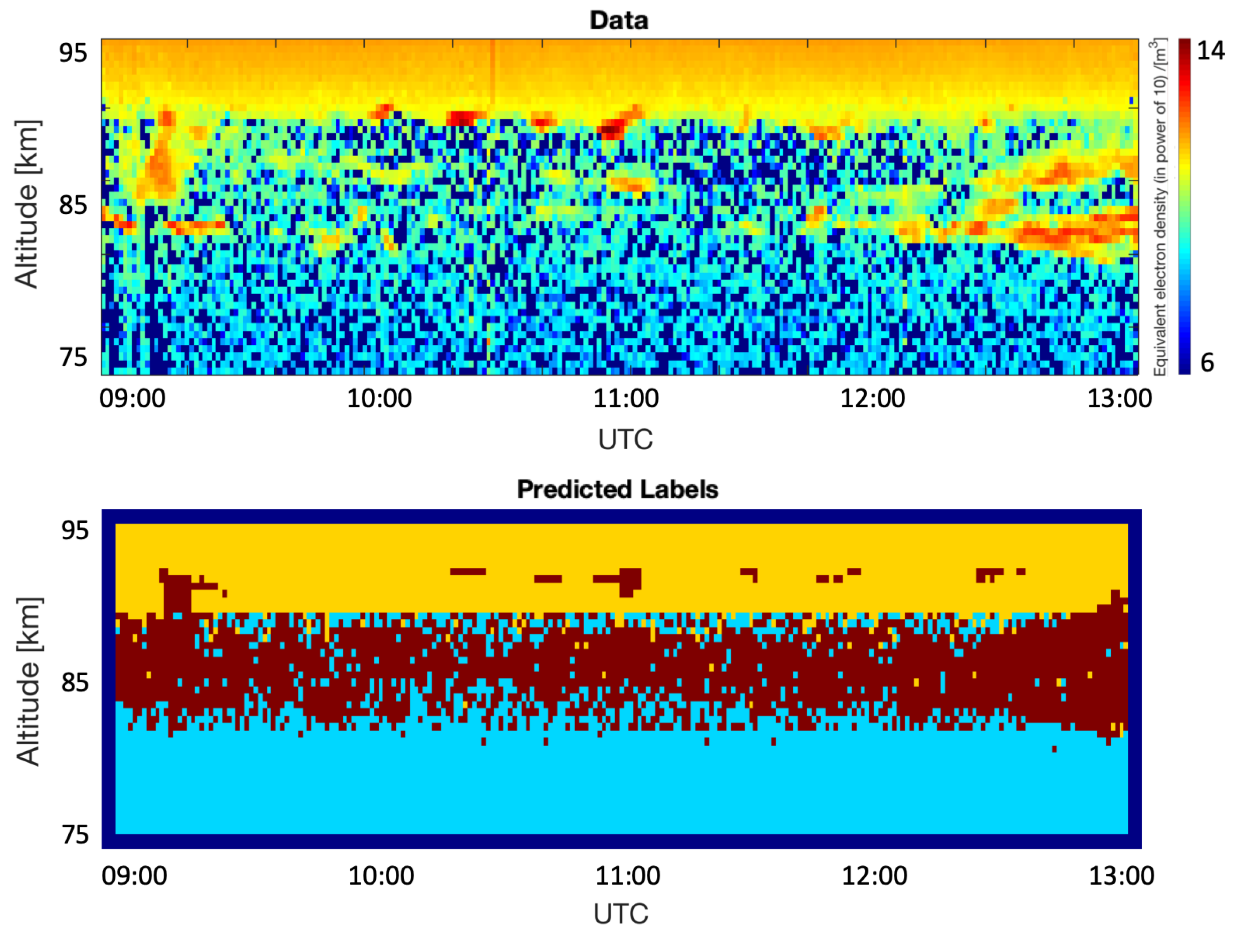
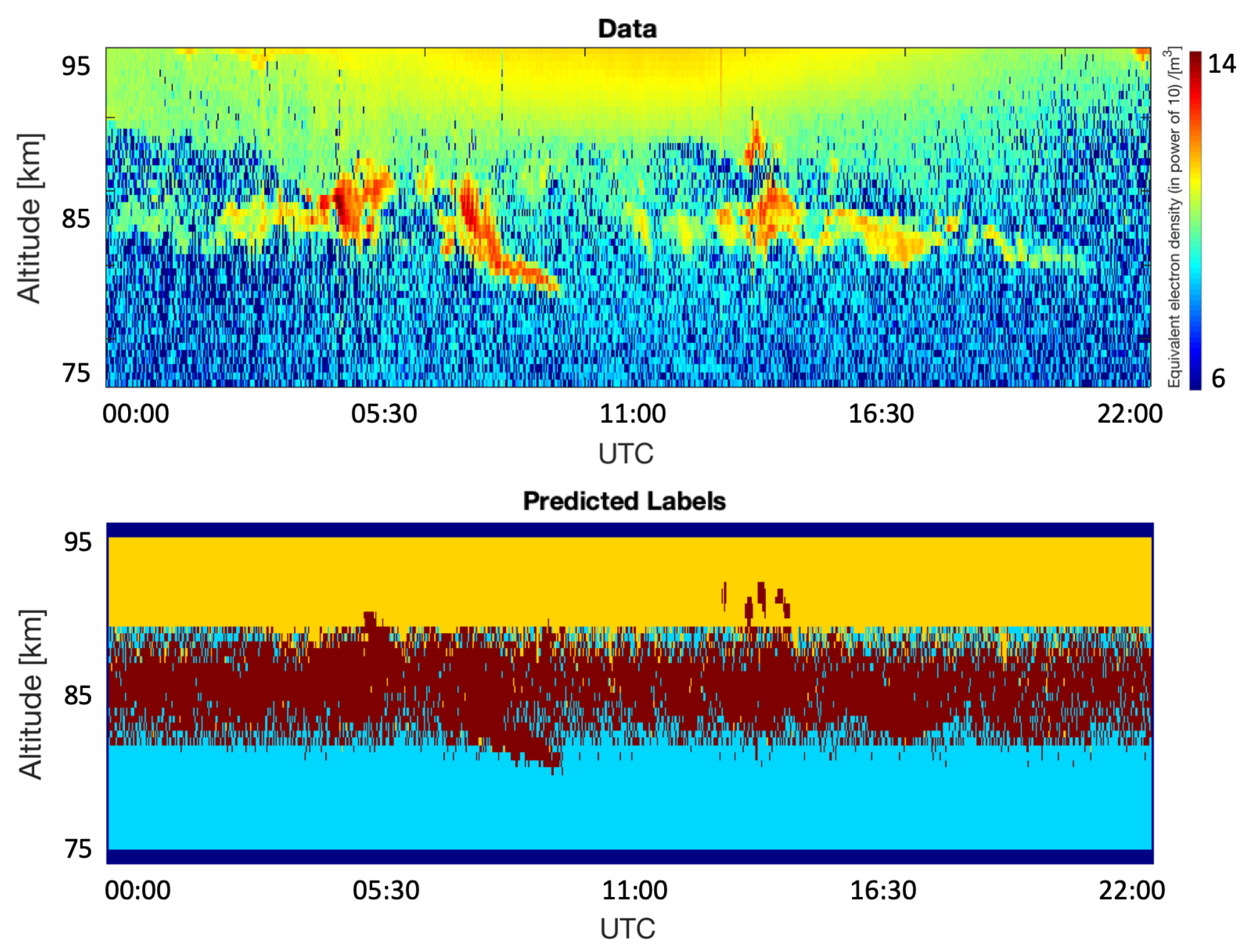
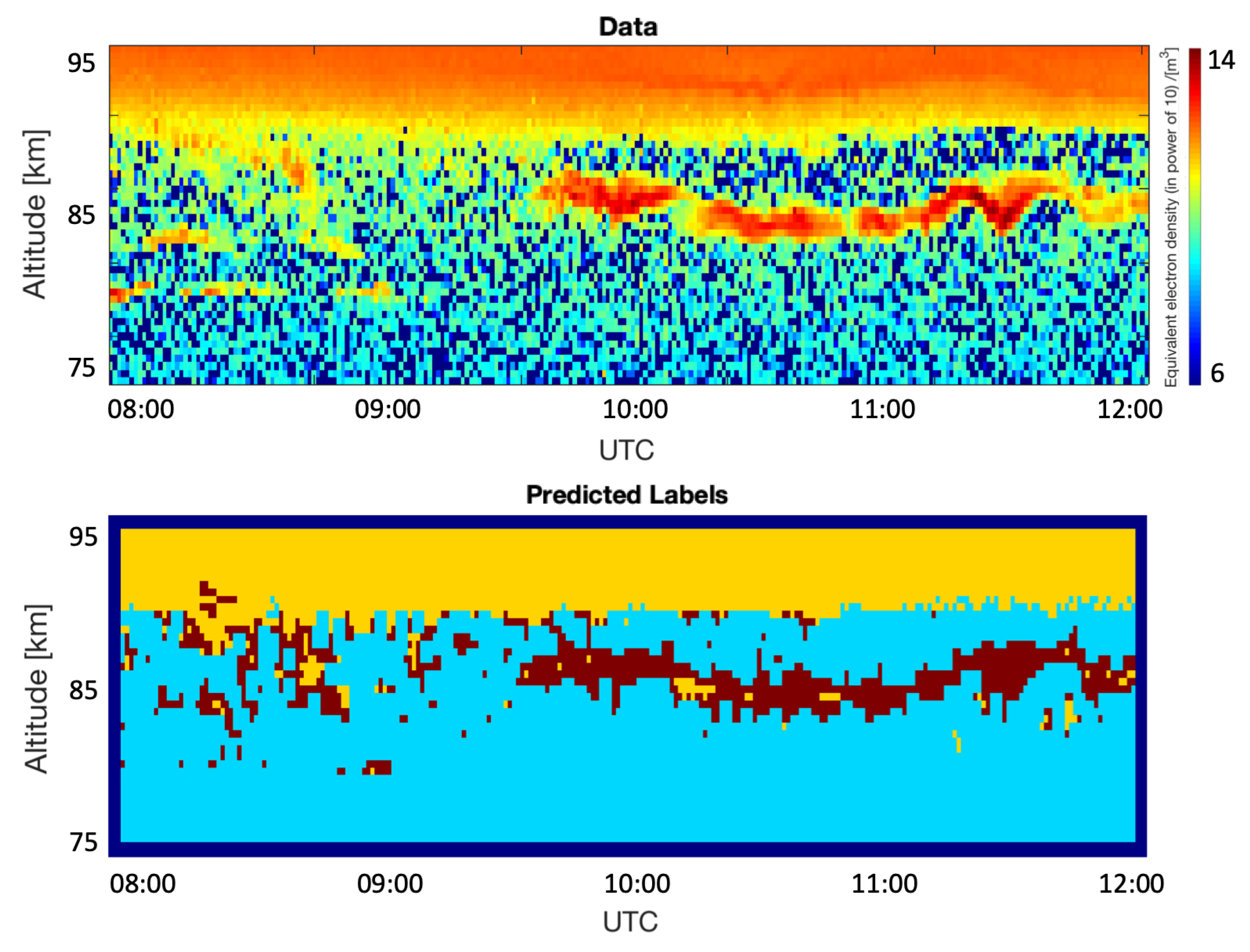
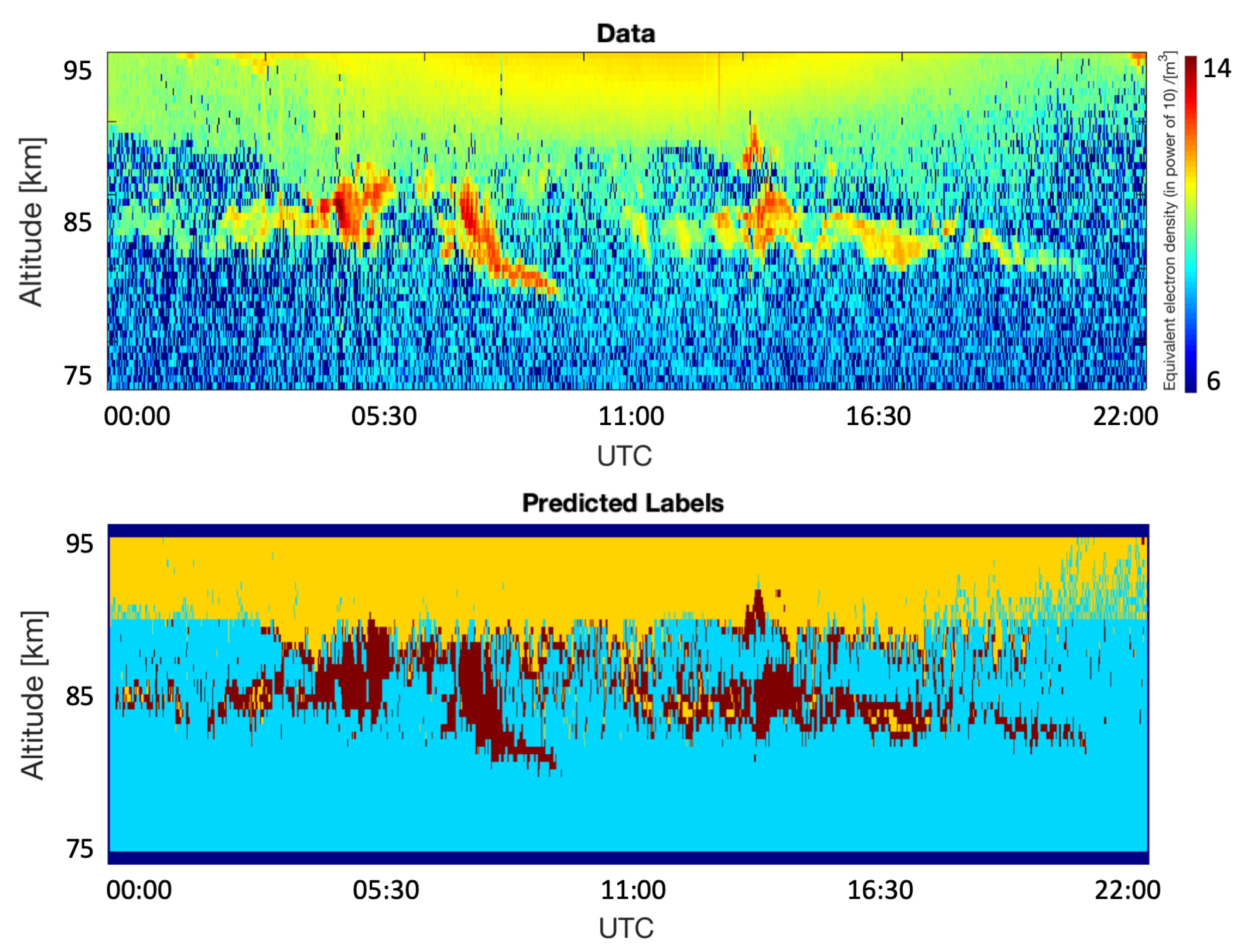
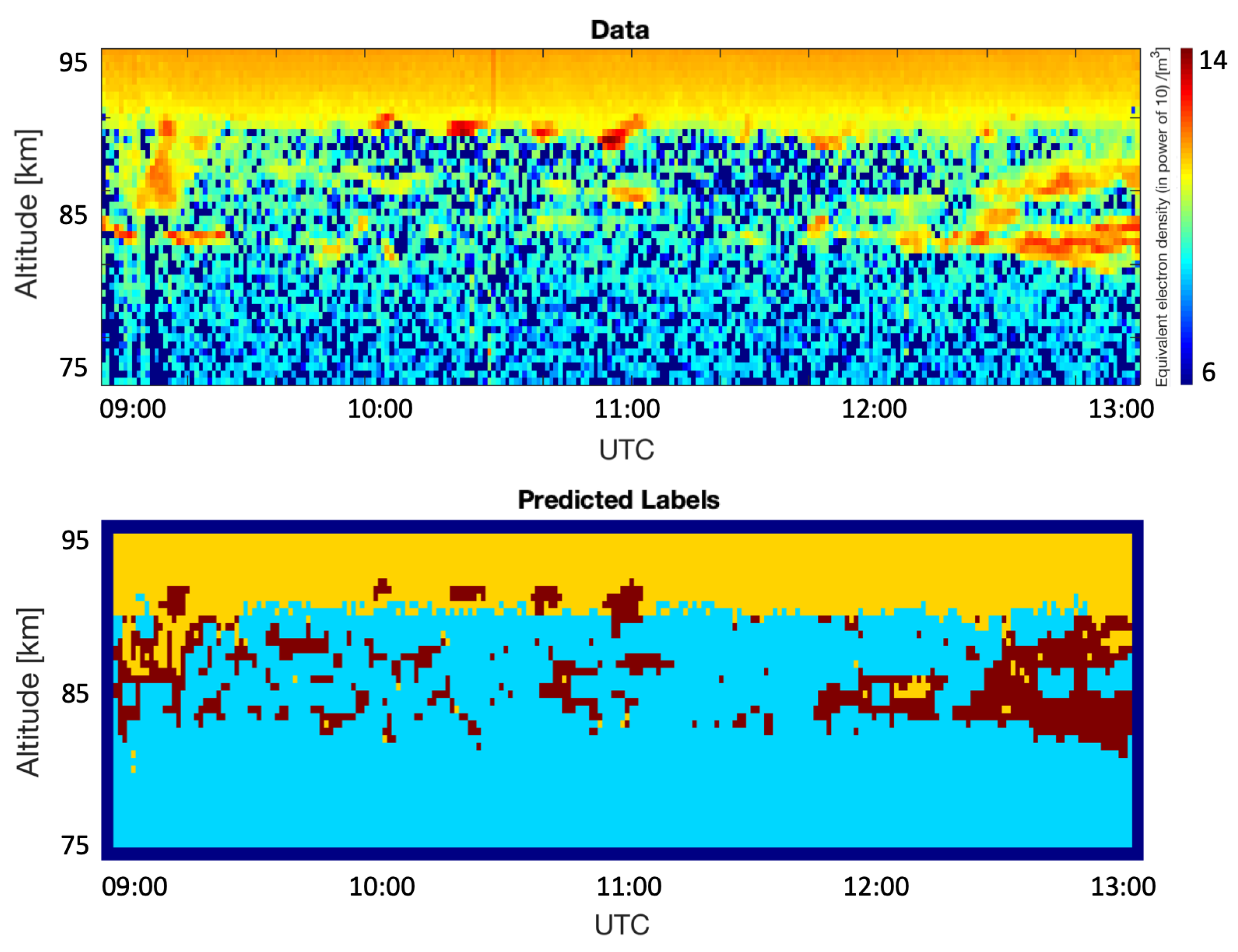
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Latteck, R.; Renkwitz, T.; Chau, J.L. Two decades of long-term observations of polar mesospheric echoes at 69°N. J. Atmos. Sol.-Terr. Phys. 2021, 216, 105576. [Google Scholar] [CrossRef]
- Cho, J.Y.N.; Röttger, J. An updated review of polar mesosphere summer echoes: Observation, theory, and their relationship to noctilucent clouds and subvisible aerosols. J. Geophys. Res. Atmos. 1997, 102, 2001–2020. [Google Scholar] [CrossRef] [Green Version]
- Rapp, M.; Lübken, F.J. Polar mesosphere summer echoes (PMSE): Review of observations and current understanding. Atmos. Chem. Phys. 2004, 4, 2601–2633. [Google Scholar] [CrossRef] [Green Version]
- Avaste, O. Noctilucent clouds. J. Atmos. Terr. Phys. 1993, 55, 133–143. [Google Scholar] [CrossRef]
- Gadsden, M. A secular change in noctilucent cloud occurrence. J. Atmos. Terr. Phys. 1990, 52, 247–251. [Google Scholar] [CrossRef]
- Almeida, M.; Zhuang, Y.; Ding, W.; Crouter, S.E.; Chen, P. Mitigating Class-Boundary Label Uncertainty to Reduce Both Model Bias and Variance. ACM Trans. Knowl. Discov. Data 2021, 15, 27. [Google Scholar] [CrossRef]
- Mann, I.; Häggström, I.; Tjulin, A.; Rostami, S.; Anyairo, C.C.; Dalin, P. First wind shear observation in PMSE with the tristatic EISCAT VHF radar. J. Geophys. Res. Space Phys. 2016, 121, 11271–11281. [Google Scholar] [CrossRef]
- Ecklund, W.L.; Balsley, B.B. Long-term observations of the Arctic mesosphere with the MST radar at Poker Flat, Alaska. J. Geophys. Res. Space Phys. 1981, 86, 7775–7780. [Google Scholar] [CrossRef]
- Hoppe, U.P.; Hall, C.; Röttger, J. First observations of summer polar mesospheric backscatter with a 224 MHz radar. Geophys. Res. Lett. 1988, 15, 28–31. [Google Scholar] [CrossRef]
- Hocking, W.; Rüster, R.; Czechowsky, P. Absolute reflectivities and aspect sensitivities of VHF radio wave scatterers measured with the SOUSY radar. J. Atmos. Terr. Phys. 1986, 48, 131–144. [Google Scholar] [CrossRef]
- Kaminski, B.; Jakubczyk, M.; Przemyslaw, S. A framework for sensitivity analysis of decision trees. Cent. Eur. J. Oper. Res. 2018, 26, 135–159. [Google Scholar] [CrossRef] [PubMed]
- Quinlan, J.R. Induction of Decision Trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef] [Green Version]
- Quinlan, J.R. C4.5: Programs for Machine Learning; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1993. [Google Scholar]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: New York, NY, USA, 2013. [Google Scholar]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Chapman and Hall/CRC: Monterey, CA, USA, 1984. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning: With Applications in R; Springer Publishing Company, Incorporated: New York, NY, USA, 2014. [Google Scholar]
- Cutler, A.; Cutler, D.R.; Stevens, J.R. Random Forests. In Ensemble Machine Learning: Methods and Applications; Zhang, C., Ma, Y., Eds.; Springer: Boston, MA, USA, 2012; pp. 157–175. [Google Scholar] [CrossRef]
- Probst, P.; Wright, M.N.; Boulesteix, A.L. Hyperparameters and tuning strategies for random forest. WIREs Data Min. Knowl. Discov. 2019, 9, e1301. [Google Scholar] [CrossRef] [Green Version]
- Grömping, U. Variable Importance Assessment in Regression: Linear Regression versus Random Forest. Am. Stat. 2009, 63, 308–319. [Google Scholar] [CrossRef]
- Karpievitch, Y.V.; Hill, E.G.; Leclerc, A.P.; Dabney, A.R.; Almeida, J.S. An Introspective Comparison of Random Forest-Based Classifiers for the Analysis of Cluster-Correlated Data by Way of RF++. PLoS ONE 2009, 4, e7087. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Tyralis, H.; Papacharalampous, G.; Langousis, A. A Brief Review of Random Forests for Water Scientists and Practitioners and Their Recent History in Water Resources. Water 2019, 11, 910. [Google Scholar] [CrossRef] [Green Version]
- Ristin, M.; Guillaumin, M.; Gall, J.; Van Gool, L. Incremental Learning of Random Forests for Large-Scale Image Classification. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 490–503. [Google Scholar] [CrossRef]
- Gall, J.; Razavi, N.; Van Gool, L. An Introduction to Random Forests for Multi-class Object Detection. In Outdoor and Large-Scale Real-World Scene Analysis; Dellaert, F., Frahm, J.M., Pollefeys, M., Leal-Taixé, L., Rosenhahn, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 243–263. [Google Scholar]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Mahapatra, D. Analyzing Training Information From Random Forests for Improved Image Segmentation. IEEE Trans. Image Process. 2014, 23, 1504–1512. [Google Scholar] [CrossRef]
- Probst, P.; Boulesteix, A.L. To Tune or Not to Tune the Number of Trees in Random Forest. J. Mach. Learn. Res. 2017, 18, 6673–6690. [Google Scholar]
- MathWorks. Available online: https://se.mathworks.com/help/stats/compactclassificationensemble.loss.html (accessed on 8 July 2021).
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Jozwicki, D.; Sharma, P.; Mann, I. Investigation of Polar Mesospheric Summer Echoes Using Linear Discriminant Analysis. Remote Sens. 2021, 13, 522. [Google Scholar] [CrossRef]
- Lehtinen, M.S.; Huuskonen, A. General incoherent scatter analysis and GUISDAP. J. Atmos. Terr. Phys. 1996, 58, 435–452. [Google Scholar] [CrossRef]
- Doug Morris, R.R. Sobel gradient kernels (3 × 3, 5 × 5, 7 × 7, 9 × 9). Available online: https://imagej.nih.gov/nih-image/download/user-macros/slowsobel.macro (accessed on 11 May 2021).



| Dates | Start Time in UTC | End Time in UTC |
|---|---|---|
| (dd:mm:yyyy) | (hh:mm:ss) | (hh:mm:ss) |
| 28 June 2008 | 07:58:33 | 08:36:18 |
| 30 June 2008 | 07:59:38 | 12:07:30 |
| 02 July 2008 | 10:24:30 | 11:59:02 |
| 10 June 2009 | 09:03:42 | 11:56:09 |
| 14 July 2009 | 08:19:33 | 11:33:15 |
| 16 July 2009 | 08:47:30 | 10:06:26 |
| 17 July 2009 | 07:49:44 | 11:59:30 |
| 30 July 2009 | 12:15:29 | 15:59:08 |
| 06 July 2010 | 07:00:30 | 23:59:30 |
| 07 July 2010 | 00:00:30 | 21:59:27 |
| 08 July 2010 | 09:00:42 | 12:59:03 |
| 09 July 2010 | 09:00:24 | 12:59:09 |
| 01 June 2011 | 08:34:31 | 10:02:07 |
| 08 June 2011 | 07:23:50 | 13:01:07 |
| 09 June 2011 | 08:01:45 | 12:59:26 |
| 12 June 2012 | 07:13:31 | 23:59:28 |
| 29 June 2012 | 10:21:57 | 10:30:04 |
| 11 July 2012 | 07:54:57 | 13:09:40 |
| 13 June 2013 | 07:12:33 | 08:59:26 |
| 28 June 2013 | 07:02:43 | 12:58:28 |
| 12 July 2013 | 00:00:28 | 21:58:28 |
| 27 July 2013 | 08:56:36 | 13:05:14 |
| 27 June 2014 | 09:03:48 | 12:59:38 |
| 01 July 2014 | 09:00:36 | 13:00:24 |
| 22 July 2014 | 22:26:33 | 23:59:28 |
| 23 July 2014 | 00:00:28 | 09:26:28 |
| 10 August 2015 | 09:14:40 | 16:12:28 |
| 12 August 2015 | 20:04:40 | 23:59:28 |
| 13 August 2015 | 00:00:28 | 01:59:26 |
| 20 August 2015 | 00:00:28 | 01:59:26 |
| Logarithmic Error | Logarithmic Error OOB | Classification Error | Classification Error OOB | AUC Ion. Back. | AUC Noise | AUC PMSE | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Filter Size | mtry | Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std |
| 3 × 3 | 3 | 0.39468 | 0.00115 | 0.39455 | 0.00112 | 0.10498 | 0.00018 | 0.10926 | 0.00058 | 0.98396 | 0.00041 | 0.98103 | 0.00039 | 0.97001 | 0.00035 |
| 3 × 3 | 6 | 0.37179 | 0.00093 | 0.37093 | 0.00095 | 0.11519 | 0.00096 | 0.11285 | 0.00223 | 0.98883 | 0.00020 | 0.98663 | 0.00013 | 0.97768 | 0.00017 |
| 3 × 3 | 9 | 0.37161 | 0.00004 | 0.37035 | 0.00003 | 0.13725 | 0.00035 | 0.13305 | 0.00016 | 0.98667 | 0.00005 | 0.96972 | 0.00005 | 0.96404 | 0.00009 |
| 5 × 5 | 3 | 0.41333 | 0.00176 | 0.41349 | 0.00171 | 0.12525 | 0.00424 | 0.12593 | 0.00332 | 0.98593 | 0.00033 | 0.97600 | 0.00035 | 0.96480 | 0.00079 |
| 5 × 5 | 6 | 0.38747 | 0.00062 | 0.38795 | 0.00059 | 0.11493 | 0.00062 | 0.11739 | 0.00042 | 0.98933 | 0.00009 | 0.98159 | 0.00057 | 0.97461 | 0.00010 |
| 5 × 5 | 9 | 0.36193 | 0.00011 | 0.36262 | 0.00013 | 0.11379 | 0.00026 | 0.11519 | 0.00011 | 0.98901 | 0.00012 | 0.98134 | 0.00018 | 0.97612 | 0.00033 |
| 7 × 7 | 3 | 0.42243 | 0.00114 | 0.42247 | 0.00114 | 0.12452 | 0.00366 | 0.12899 | 0.00226 | 0.98280 | 0.00025 | 0.97158 | 0.00029 | 0.96459 | 0.00121 |
| 7 × 7 | 6 | 0.39271 | 0.00126 | 0.39313 | 0.00128 | 0.11445 | 0.00099 | 0.11632 | 0.00052 | 0.98836 | 0.00014 | 0.98084 | 0.00022 | 0.97499 | 0.00013 |
| 7 × 7 | 9 | 0.36027 | 0.00005 | 0.36120 | 0.00006 | 0.10833 | 0.00076 | 0.11041 | 0.00042 | 0.98652 | 0.00008 | 0.98213 | 0.00005 | 0.97406 | 0.00008 |
| 9 × 9 | 3 | 0.42842 | 0.00069 | 0.42829 | 0.00070 | 0.14273 | 0.00432 | 0.13902 | 0.00356 | 0.98083 | 0.00033 | 0.96983 | 0.00027 | 0.95969 | 0.00123 |
| 9 × 9 | 6 | 0.38914 | 0.00147 | 0.38861 | 0.00150 | 0.12105 | 0.00097 | 0.11740 | 0.00070 | 0.98594 | 0.00020 | 0.98062 | 0.00057 | 0.97007 | 0.00010 |
| 9 × 9 | 9 | 0.36235 | 0.00004 | 0.36162 | 0.00005 | 0.11938 | 0.00031 | 0.11632 | 0.00026 | 0.98276 | 0.00022 | 0.97944 | 0.00012 | 0.96780 | 0.00010 |
| 11 × 11 | 3 | 0.42290 | 0.00061 | 0.42310 | 0.00064 | 0.12776 | 0.00066 | 0.12760 | 0.00057 | 0.98121 | 0.00029 | 0.97027 | 0.00042 | 0.96548 | 0.00061 |
| 11 × 11 | 6 | 0.37492 | 0.00113 | 0.37509 | 0.00118 | 0.11085 | 0.00025 | 0.10928 | 0.00042 | 0.98337 | 0.00053 | 0.98262 | 0.00028 | 0.97105 | 0.00051 |
| 11 × 11 | 9 | 0.36253 | 0.00003 | 0.36265 | 0.00005 | 0.11887 | 0.00065 | 0.11831 | 0.00046 | 0.98089 | 0.00016 | 0.97877 | 0.00008 | 0.96882 | 0.00009 |
| All Sizes | 5 | 0.43433 | 0.00164 | 0.43477 | 0.00165 | 0.13891 | 0.01048 | 0.13772 | 0.00575 | 0.98039 | 0.00056 | 0.97096 | 0.00076 | 0.95898 | 0.00072 |
| All Sizes | 10 | 0.41768 | 0.00102 | 0.41817 | 0.00101 | 0.10884 | 0.00035 | 0.11096 | 0.00079 | 0.98535 | 0.00008 | 0.97749 | 0.00077 | 0.96591 | 0.00058 |
| All Sizes | 15 | 0.40385 | 0.00124 | 0.40429 | 0.00122 | 0.11200 | 0.00479 | 0.10980 | 0.00438 | 0.98752 | 0.00014 | 0.98091 | 0.00016 | 0.96857 | 0.00042 |
| All Sizes | 20 | 0.39397 | 0.00142 | 0.39433 | 0.00142 | 0.12100 | 0.00198 | 0.11975 | 0.00159 | 0.98850 | 0.00021 | 0.98234 | 0.00017 | 0.97017 | 0.00019 |
| All Sizes | 25 | 0.38476 | 0.00107 | 0.38505 | 0.00108 | 0.12963 | 0.00031 | 0.12798 | 0.00038 | 0.98852 | 0.00008 | 0.98334 | 0.00012 | 0.97092 | 0.00005 |
| All Sizes | 30 | 0.37788 | 0.00076 | 0.37810 | 0.00077 | 0.12929 | 0.00015 | 0.12834 | 0.00004 | 0.98817 | 0.00011 | 0.98329 | 0.00014 | 0.97074 | 0.00042 |
| All Sizes | 35 | 0.37096 | 0.00004 | 0.37113 | 0.00007 | 0.12963 | 0.00018 | 0.12967 | 0.00055 | 0.98651 | 0.00014 | 0.97192 | 0.00016 | 0.96238 | 0.00096 |
| Logarithmic Error | Logarithmic Error OOB | Classification Error | Classification Error OOB | AUC Ion. Back. | AUC Noise | AUC PMSE | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Filter Size | mtry | Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std |
| 3 × 3 | 3 | 0.38950 | 0.00162 | 0.38927 | 0.00162 | 0.09828 | 0.00050 | 0.09697 | 0.00054 | 0.98806 | 0.00039 | 0.98300 | 0.00093 | 0.97536 | 0.00047 |
| 3 × 3 | 6 | 0.36683 | 0.00040 | 0.36659 | 0.00039 | 0.10360 | 0.00182 | 0.10437 | 0.00153 | 0.99176 | 0.00016 | 0.98826 | 0.00015 | 0.98212 | 0.00009 |
| 3 × 3 | 9 | 0.36459 | 0.00004 | 0.36427 | 0.00007 | 0.11532 | 0.00022 | 0.11578 | 0.00041 | 0.99063 | 0.00006 | 0.97384 | 0.00008 | 0.97110 | 0.00024 |
| 5 × 5 | 3 | 0.41009 | 0.00097 | 0.40947 | 0.00101 | 0.10974 | 0.00501 | 0.10625 | 0.00234 | 0.98778 | 0.00034 | 0.97695 | 0.00019 | 0.97437 | 0.00089 |
| 5 × 5 | 6 | 0.38508 | 0.00056 | 0.38407 | 0.00060 | 0.10504 | 0.00023 | 0.10131 | 0.00043 | 0.99152 | 0.00004 | 0.98119 | 0.00087 | 0.98128 | 0.00058 |
| 5 × 5 | 9 | 0.36253 | 0.00018 | 0.36111 | 0.00016 | 0.10598 | 0.00023 | 0.10088 | 0.00035 | 0.99095 | 0.00009 | 0.97723 | 0.00026 | 0.97715 | 0.00036 |
| 7 × 7 | 3 | 0.41946 | 0.00203 | 0.42020 | 0.00200 | 0.11242 | 0.00602 | 0.11725 | 0.00443 | 0.98662 | 0.00047 | 0.97677 | 0.00038 | 0.97086 | 0.00129 |
| 7 × 7 | 6 | 0.38950 | 0.00128 | 0.39053 | 0.00126 | 0.10166 | 0.00063 | 0.10692 | 0.00086 | 0.99168 | 0.00010 | 0.98475 | 0.00013 | 0.97987 | 0.00014 |
| 7 × 7 | 9 | 0.35469 | 0.00007 | 0.35640 | 0.00008 | 0.09460 | 0.00039 | 0.10087 | 0.00040 | 0.98998 | 0.00002 | 0.98615 | 0.00006 | 0.97921 | 0.00068 |
| 9 × 9 | 3 | 0.42364 | 0.00314 | 0.42302 | 0.00314 | 0.11726 | 0.00428 | 0.11962 | 0.00382 | 0.98395 | 0.00041 | 0.97341 | 0.00063 | 0.96720 | 0.00155 |
| 9 × 9 | 6 | 0.38314 | 0.00176 | 0.38282 | 0.00173 | 0.10587 | 0.00037 | 0.10529 | 0.00046 | 0.98849 | 0.00033 | 0.98271 | 0.00028 | 0.97598 | 0.00030 |
| 9 × 9 | 9 | 0.35714 | 0.00002 | 0.35719 | 0.00002 | 0.10516 | 0.00026 | 0.10440 | 0.00031 | 0.98648 | 0.00013 | 0.98298 | 0.00012 | 0.97465 | 0.00010 |
| 11 × 11 | 3 | 0.41998 | 0.00261 | 0.41864 | 0.00259 | 0.11798 | 0.00039 | 0.11496 | 0.00037 | 0.98394 | 0.00048 | 0.97410 | 0.00019 | 0.96995 | 0.00030 |
| 11 × 11 | 6 | 0.37212 | 0.00042 | 0.37113 | 0.00042 | 0.09978 | 0.00030 | 0.09628 | 0.00007 | 0.98557 | 0.00026 | 0.98462 | 0.00010 | 0.97410 | 0.00010 |
| 11 × 11 | 9 | 0.35753 | 0.00004 | 0.35661 | 0.00002 | 0.10448 | 0.00025 | 0.10290 | 0.00031 | 0.98402 | 0.00008 | 0.98029 | 0.00005 | 0.97274 | 0.00007 |
| All Sizes | 5 | 0.43022 | 0.00128 | 0.43013 | 0.00129 | 0.12580 | 0.01500 | 0.12236 | 0.00691 | 0.98521 | 0.00048 | 0.97142 | 0.00144 | 0.96726 | 0.00061 |
| All Sizes | 10 | 0.41479 | 0.00193 | 0.41452 | 0.00195 | 0.10435 | 0.00043 | 0.10037 | 0.00059 | 0.98886 | 0.00012 | 0.97768 | 0.00084 | 0.97209 | 0.00045 |
| All Sizes | 15 | 0.40186 | 0.00152 | 0.40145 | 0.00156 | 0.10167 | 0.00621 | 0.09960 | 0.00439 | 0.99041 | 0.00025 | 0.98078 | 0.00013 | 0.97444 | 0.00032 |
| All Sizes | 20 | 0.39105 | 0.00107 | 0.39054 | 0.00106 | 0.11213 | 0.00276 | 0.10939 | 0.00199 | 0.99138 | 0.00015 | 0.98215 | 0.00007 | 0.97609 | 0.00015 |
| All Sizes | 25 | 0.38112 | 0.00227 | 0.38047 | 0.00232 | 0.11830 | 0.00013 | 0.11614 | 0.00013 | 0.99157 | 0.00007 | 0.98331 | 0.00009 | 0.97686 | 0.00021 |
| All Sizes | 30 | 0.37277 | 0.00038 | 0.37199 | 0.00041 | 0.11913 | 0.00015 | 0.11693 | 0.00028 | 0.99121 | 0.00007 | 0.98287 | 0.00022 | 0.97694 | 0.00041 |
| All Sizes | 35 | 0.36581 | 0.00003 | 0.36490 | 0.00003 | 0.11985 | 0.00008 | 0.11747 | 0.00011 | 0.98922 | 0.00016 | 0.97259 | 0.00018 | 0.96867 | 0.00028 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jozwicki, D.; Sharma, P.; Mann, I.; Hoppe, U.-P. Segmentation of PMSE Data Using Random Forests. Remote Sens. 2022, 14, 2976. https://doi.org/10.3390/rs14132976
Jozwicki D, Sharma P, Mann I, Hoppe U-P. Segmentation of PMSE Data Using Random Forests. Remote Sensing. 2022; 14(13):2976. https://doi.org/10.3390/rs14132976
Chicago/Turabian StyleJozwicki, Dorota, Puneet Sharma, Ingrid Mann, and Ulf-Peter Hoppe. 2022. "Segmentation of PMSE Data Using Random Forests" Remote Sensing 14, no. 13: 2976. https://doi.org/10.3390/rs14132976
APA StyleJozwicki, D., Sharma, P., Mann, I., & Hoppe, U.-P. (2022). Segmentation of PMSE Data Using Random Forests. Remote Sensing, 14(13), 2976. https://doi.org/10.3390/rs14132976







