Features of Winter Stratosphere Small-Scale Disturbance during Sudden Stratospheric Warmings
Abstract
:1. Introduction
1.1. Winter Circumpolar Vortex and a Jet Stream
1.2. Internal Gravity Waves in a Jet Stream
2. Data and Analysis Methods
3. Results
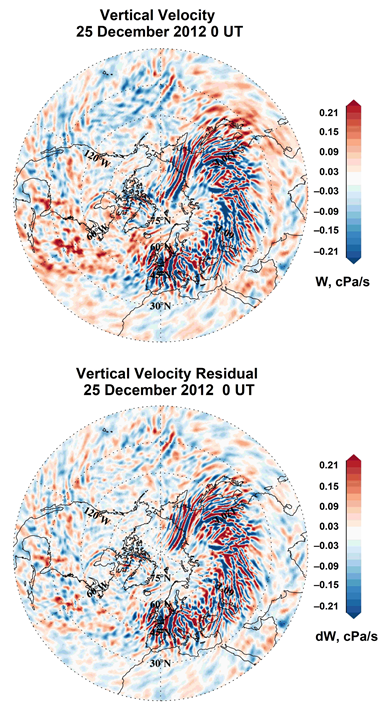
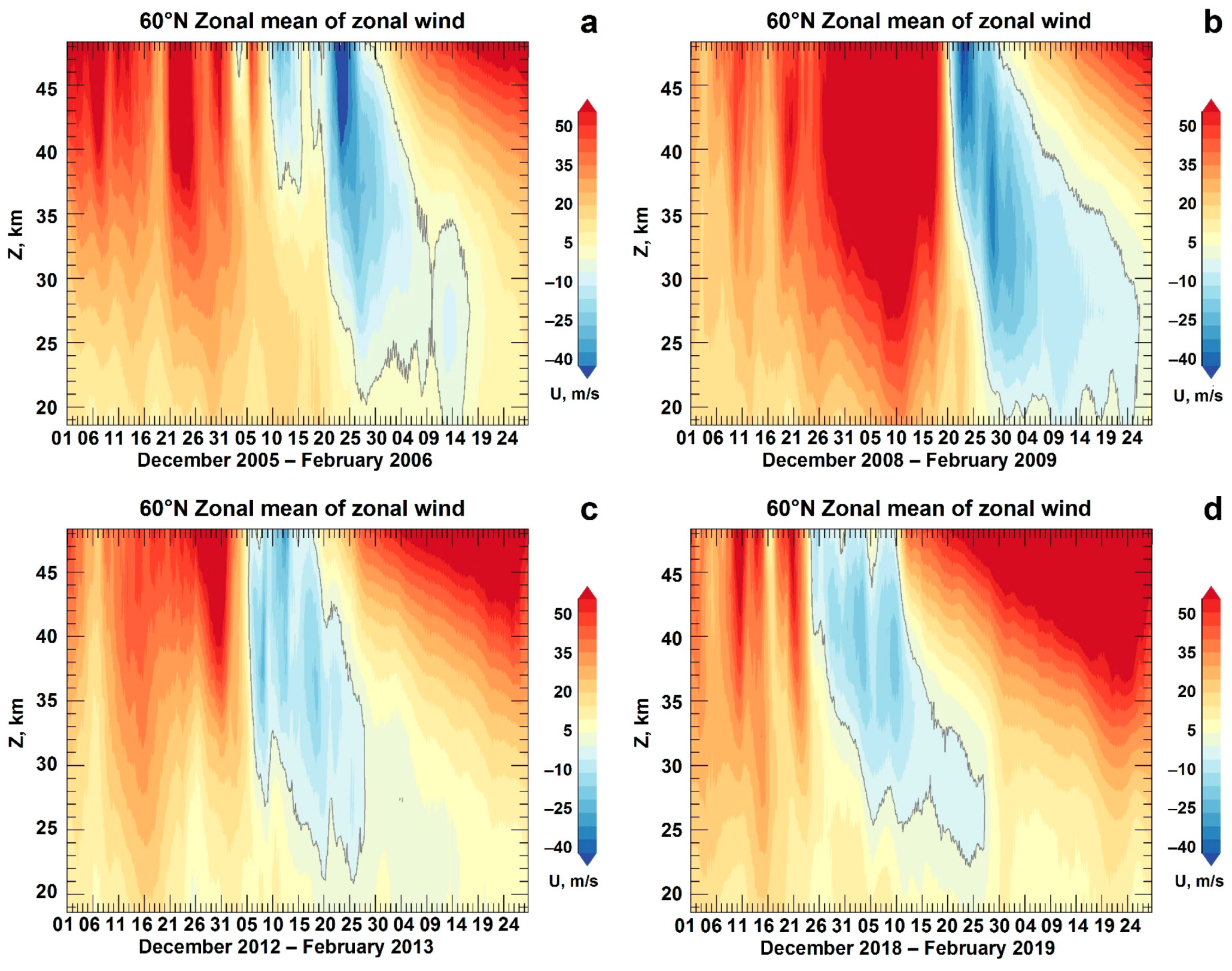
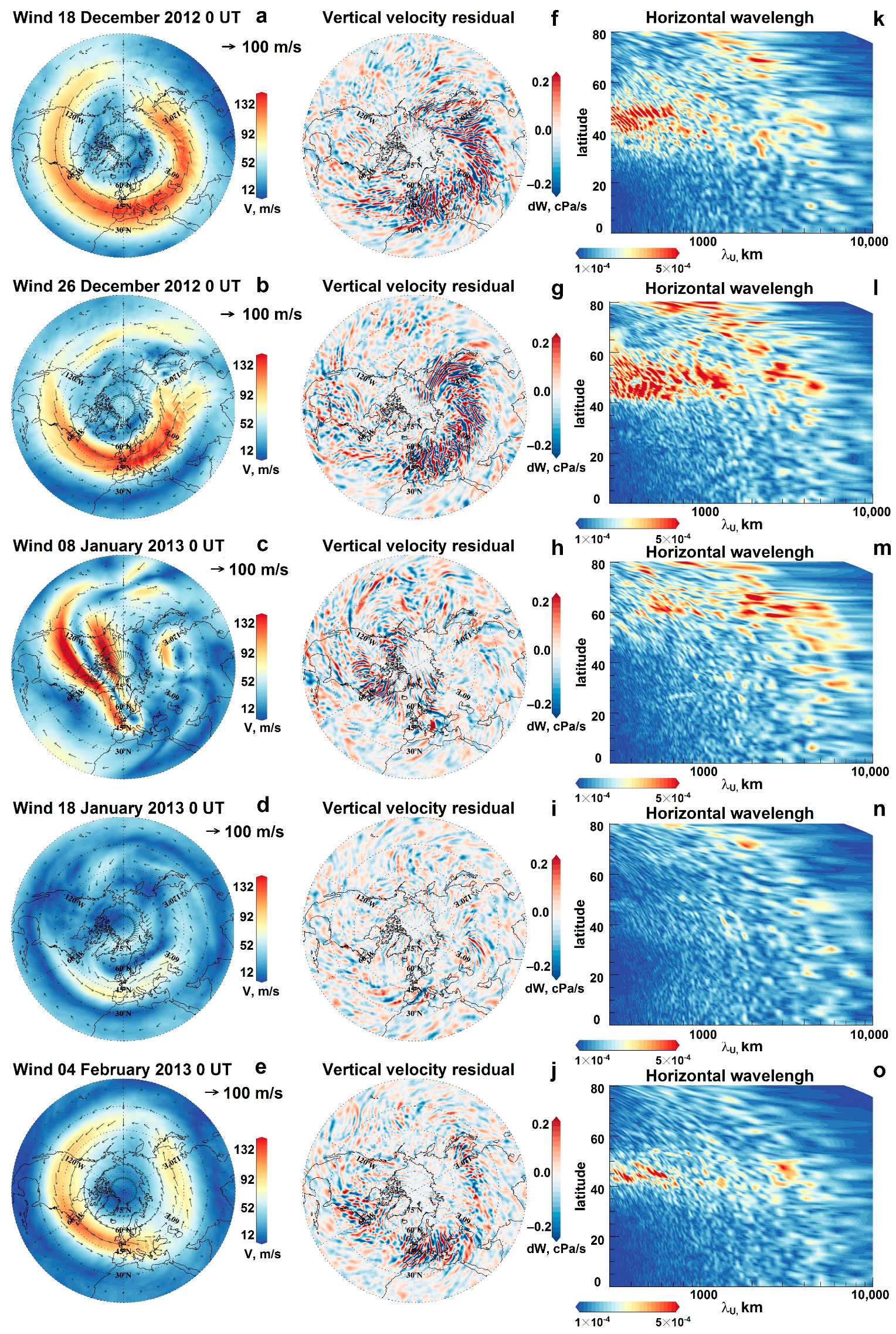
3.1. IGW Dynamics at Different SSW Stages
3.2. Estimates of Basic Parameters of the Observed Waves
3.3. Statistical Estimates of the Observed Effect
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Coy, L.; Nash, E.R.; Newman, P.A. Meteorology of the polar vortex: Spring 1997. Geophys. Res. Lett. 1997, 24, 2693–2696. [Google Scholar] [CrossRef]
- Newman, P.A.; Schoeberl, M.R. Middle atmosphere: Polar vortex. In Encyclopedia of Atmospheric Sciences; Holton, J.R., Pyle, J., Curry, J.A., Eds.; Academic Press: San Diego, CA, USA, 2003; pp. 1321–1328. [Google Scholar]
- Waugh, D.W.; Polvani, L.M. Stratospheric polar vortices. In The Stratosphere: Dynamics, Transport, and Chemistry; Polvani, L.M., Sobel, A.H., Waugh, D.W., Eds.; Geophysical Monograph Series; American Geophysical Union: Washington, DC, USA, 2010; Volume 190, pp. 43–57. [Google Scholar] [CrossRef]
- Schoeberl, M.R.; Hartmann, D.L. The dynamics of the stratospheric polar vortex and its relation to springtime ozone depletions. Science 1991, 251, 46–52. [Google Scholar] [CrossRef]
- Karpetchko, A.; Kyrö, E.; Knudsen, B.M. Arctic and Antarctic polar vortices 1957–2002 as seen from the ERA-40 reanalyses. J. Geophys. Res. 2005, 110, D21109. [Google Scholar] [CrossRef]
- Hamilton, K. Dynamical coupling of the lower and middle atmosphere: Historical background to current research. J. Atmos. Sol.-Terr. Phys. 1999, 61, 73–84. [Google Scholar] [CrossRef]
- Labitzke, K.G.; van Loon, H. The Stratosphere: Phenomena, History, and Relevance; Springer: New York, NY, USA, 1999; 179p. [Google Scholar]
- Sun, L.; Robinson, W.A. Downward influence of stratospheric final warming events in an idealized model. Geophys. Res. Lett. 2009, 36, L03819. [Google Scholar] [CrossRef]
- Baldwin, M.P.; Dunkerton, T.J. Stratospheric harbingers of anomalous weather regimes. Science 2001, 294, 581–584. [Google Scholar] [CrossRef]
- Kushner, P.J. Annular modes of the troposphere and stratosphere. In The Stratosphere: Dynamics, Transport, and Chemistry; Polvani, L.M., Sobel, A.H., Waugh, D.W., Eds.; Geophysical Monograph Series; American Geophysical Union: Washington, DC, USA, 2010; Volume 190, pp. 59–91. [Google Scholar] [CrossRef]
- Pogoreltsev, A.I.; Aniskina, O.G.; Ermakova, T.S.; Savenkova, E.N.; Chen, W.; Wei, K. Interannual and intraseasonal variability of stratospheric dynamics and stratosphere-troposphere coupling during northern winter. J. Atmos. Sol.-Terr. Phys. 2015, 136, 187–200. [Google Scholar] [CrossRef]
- Waugh, D.W.; Sobel, A.H.; Polvani, L.M. What is the polar vortex and how does it influence weather? Bull. Am. Meteorol. Soc. 2017, 98, 37–44. [Google Scholar] [CrossRef]
- Schoeberl, M.R. Stratospheric warmings: Observations and theory. J. Geophys. Res. Space Phys. 1978, 16, 521–538. [Google Scholar] [CrossRef]
- Baldwin, M.P.; Holton, J.R. Climatology of the stratospheric polar vortex and planetary wave breaking. J. Atmos. Sci. 1988, 45, 1123–1142. [Google Scholar] [CrossRef]
- Abatzoglou, J.T.; Magnusdottir, G. Wave breaking along the stratospheric polar vortex as seen in ERA-40 data. Geophys. Res. Lett. 2007, 34, L08812. [Google Scholar] [CrossRef]
- Kim, B.M.; Son, S.W.; Min, S.K.; Jeong, J.H.; Kim, S.J.; Zhang, X.; Shim, T.; Yoon, J.H. Weakening of the stratospheric polar vortex by Arctic sea-ice loss. Nat. Commun. 2014, 5, 4646. [Google Scholar] [CrossRef]
- Zhang, J.; Tian, W.; Chipperfield, M.P.; Xie, F.; Huang, J. Persistent shift of the Arctic polar vortex towards the Eurasian continent in recent decades. Nat. Clim. Chang. 2016, 6, 1094–1099. [Google Scholar] [CrossRef]
- Seviour, W.J. Weakening and shift of the Arctic stratospheric polar vortex: Internal variability or forced response? Geophys. Res. Lett. 2017, 44, 3365–3373. [Google Scholar] [CrossRef]
- Labitzke, K. Temperature changes in the mesosphere and stratosphere connected with circulation changes in winter. J. Atmos. Sci. 1972, 29, 756–766. [Google Scholar] [CrossRef]
- Stan, C.; Straus, D.M. Stratospheric predictability and sudden stratospheric warming events. J. Geophys. Res. Atmos. 2009, 114, D12103. [Google Scholar] [CrossRef]
- Matsuno, T. A dynamical model of the stratospheric sudden warming. J. Atmos. Sci. 1971, 28, 1479–1494. [Google Scholar] [CrossRef]
- Scott, R.K.; Polvani, L.M. Internal Variability of the Winter Stratosphere. Part I: Time-Independent Forcing. J. Atmos. Sci. 2006, 63, 2758–2776. [Google Scholar] [CrossRef]
- Pogoreltsev, A.I.; Vlasov, A.A.; Fröhlich, K.; Jacobi, C. Planetary waves in coupling the lower and upper atmosphere. J. Atmos. Sol.-Terr. Phys. 2007, 69, 2083–2101. [Google Scholar] [CrossRef]
- Charlton, A.J.; Polvani, L.M. A new look at stratospheric sudden warmings. Part I: Climatology and modeling benchmarks. J. Clim. 2007, 20, 449–469. [Google Scholar] [CrossRef]
- Whiteway, J.A.; Duck, T.J.; Donovan, D.P.; Bird, J.C.; Pal, S.R.; Carswell, A.I. Measurements of gravity wave activity within and around the Arctic stratospheric vortex. Geophys. Res. Lett. 1997, 24, 1387–1390. [Google Scholar] [CrossRef]
- Gerrard, A.J.; Bhattacharya, Y.; Thayer, J.P. Observations of in-situ generated gravity waves during a stratospheric temperature enhancement (STE) event. Atmos. Chem. Phys. 2011, 11, 11913–11917. [Google Scholar] [CrossRef]
- Frissell, N.A.; Baker, J.B.H.; Ruohoniemi, J.M.; Greenwald, R.A.; Gerrard, A.J.; Miller, E.S.; West, M.L. Sources and characteristics of medium-scale traveling ionospheric disturbances observed by high-frequency radars in the North American sector. J. Geophys. Res. Space Phys. 2016, 121, 3722–3739. [Google Scholar] [CrossRef]
- Liu, X.; Yue, J.; Xu, J.; Garcia, R.R.; Russell, J.M., III; Mlynczak, M.; Wu, D.L.; Nakamura, T. Variations of global gravity waves derived from 14 years of SABER temperature observations. J. Geophys. Res. Atmos. 2017, 122, 6231–6249. [Google Scholar] [CrossRef]
- Wu, D.L.; Waters, J.W. Satellite observations of atmospheric variances: A possible indication of gravity waves. Geophys. Res. Lett. 1996, 23, 3631–3634. [Google Scholar] [CrossRef]
- Jiang, J.H.; Eckermann, S.D.; Wu, D.L.; Hocke, K.; Wang, B.; Ma, J.; Zhang, Y. Seasonal variation of gravity wave sources from satellite observation. Adv. Space Res. 2005, 35, 1925–1932. [Google Scholar] [CrossRef]
- Jiang, J.H.; Wu, D.L.; Wang, D.-Y. Interannual variation of gravity waves in the Arctic and Antarctic winter middle atmosphere. Adv. Space Res. 2006, 38, 2418–2423. [Google Scholar] [CrossRef]
- Wilson, R.; Chanin, M.-L.; Hauchecorne, A. Gravity waves in the middle atmosphere observed by Rayleigh lidar. Part 2. Climatology. J. Geophys. Res. 1991, 96, 5169–5183. [Google Scholar] [CrossRef]
- Yamashita, C.; Liu, H.-L.; Chu, X. Gravity wave variations during the 2009 stratospheric sudden warming as revealed by ECMWF-T799 and observations. Geophys. Res. Lett. 2010, 37, L22806. [Google Scholar] [CrossRef]
- Schoon, L.; Zülicke, C. A novel method for the extraction of local gravity wave parameters from gridded three-dimensional data: Description, validation, and application. Atmos. Chem. Phys. 2018, 18, 6971–6983. [Google Scholar] [CrossRef]
- Shpynev, B.G.; Churilov, S.M.; Chernigovskaya, M.A. Generation of waves by jet-stream instabilities in winter polar stratosphere/mesosphere. J. Atmos. Sol.-Terr. Phys. 2015, 136, 201–215. [Google Scholar] [CrossRef]
- Shpynev, B.G.; Khabituev, D.S.; Chernigovskaya, M.A.; Zorkal’tseva, O.S. Role of winter jet stream in the middle atmosphere energy balance. J. Atmos. Sol.-Terr. Phys. 2019, 188, 1–10. [Google Scholar] [CrossRef]
- Vadas, S.L. Horizontal and vertical propagation of gravity waves in thermosphere from lower atmospheric and thermospheric sources. J. Geophys. Res. 2007, 112, A06305. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. QJR Meteorol Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Shpynev, B.G.; Chernigovskaya, M.A.; Khabituev, D.S. Spectral characteristics of atmospheric waves generated by winter stratospheric jet stream in the Northern Hemisphere. Sovrem. Probl. Distantsionnogo Zondirovaniya Zemli Kosm. 2016, 13, 120–131. [Google Scholar] [CrossRef]
- Hines, C.O. Internal atmospheric gravity waves at ionospheric heights. Can. J. Phys. 1960, 38, 1441–1481. [Google Scholar] [CrossRef]
- Gossard, E.E.; Hooke, W.H. Waves in the Atmosphere: Atmospheric Infrasound and Gravity Waves: Their Generation and Propagation, Developments in Atmospheric Science; Elsevier Scientific Pub. Co.: Amsterdam, The Netherlands; New York, NY, USA, 1975; Volume 2, 456p. [Google Scholar]
- Kaifler, B.; Lübken, F.-J.; Höffner, J.; Morris, R.J.; Viehl, T.P. Lidar observations of gravity wave activity in the middle atmosphere over Davis (69°S, 78°E), Antarctica. J. Geophys. Res. Atmos. 2015, 120, 4506–4521. [Google Scholar] [CrossRef]
- Liu, H.-L.; Yudin, V.A.; Roble, R.G. Day-to-day ionospheric variability due to lower atmosphere perturbations. Geophys. Res. Lett. 2013, 40, 665–670. [Google Scholar] [CrossRef]
- Medvedeva, I.; Ratovsky, K. Studying atmospheric and ionospheric variabilities fromlong-termspectrometric and radio sounding measurements. J. Geophys. Res. Space Phys. 2015, 120, 5151–5159. [Google Scholar] [CrossRef]
- Yasyukevich, A.; Medvedeva, I.; Sivtseva, V.; Chernigovskaya, M.; Ammosov, P.; Gavrilyeva, G. Strong Interrelation between the Short-Term Variability in the Ionosphere, Upper Mesosphere, and Winter Polar Stratosphere. Remote Sens. 2020, 12, 1588. [Google Scholar] [CrossRef]
- Yiğit, E.; Medvedev, A.S. Internal waves coupling processes in Earth’s atmosphere. Adv. Space Res. 2015, 55, 983–1003. [Google Scholar] [CrossRef]
- Chernigovskaya, M.A.; Shpynev, B.G.; Ratovsky, K.G. Meteorological effects of ionospheric disturbances from vertical radio sounding data. J. Atmos. Sol.-Terr. Phys. 2015, 136, 235–243. [Google Scholar] [CrossRef]
- Chernigovskaya, M.A.; Shpynev, B.G.; Ratovsky, K.G.; Belinskaya, A.Y.; Stepanov, A.E.; Bychkov, V.V.; Grigorieva, S.A.; Panchenko, V.A.; Korenkova, N.A.; Mielich, J. Ionospheric Response to Winter Stratosphere/Lower Mesosphere Jet stream in the Northern Hemisphere as Derived from Vertical Radio Sounding Data. J. Atmos. Sol.-Terr. Phys. 2018, 180, 126–136. [Google Scholar] [CrossRef]
- Lukianova, R.; Kozlovsky, A.; Shalimov, S.; Ulich, T.; Lester, M. Thermal and dynamical perturbations in the winter polar mesosphere-lower thermosphere region associated with sudden stratospheric warmings under conditions of low solar activity. J. Geophys. Res. Space Phys. 2015, 120, 5226–5240. [Google Scholar] [CrossRef]
- Nayak, C.; Yigit, E. Variation of small-scale gravity wave activity in the ionosphere during the major sudden stratospheric warming event of 2009. J. Geophys. Res. Space Phys. 2019, 124, 470–488. [Google Scholar] [CrossRef]
- Vasilyev, R.V.; Artamonov, M.F.; Beletsky, A.B.; Zorkaltseva, O.S.; Komarova, E.S.; Medvedeva, I.V.; Mikhalev, A.V.; Podlesny, S.V.; Ratovsky, K.G.; Syrenova, T.E.; et al. Scientific goals of optical instruments of the National Heliogeophysical Complex. Sol.-Terr. Phys. 2020, 6, 84–97. [Google Scholar] [CrossRef]
- Yasyukevich, A.S. Features of short-period variability of total electron content at high and middle latitudes. Sol.-Terr. Phys. 2021, 7, 71–78. [Google Scholar] [CrossRef]

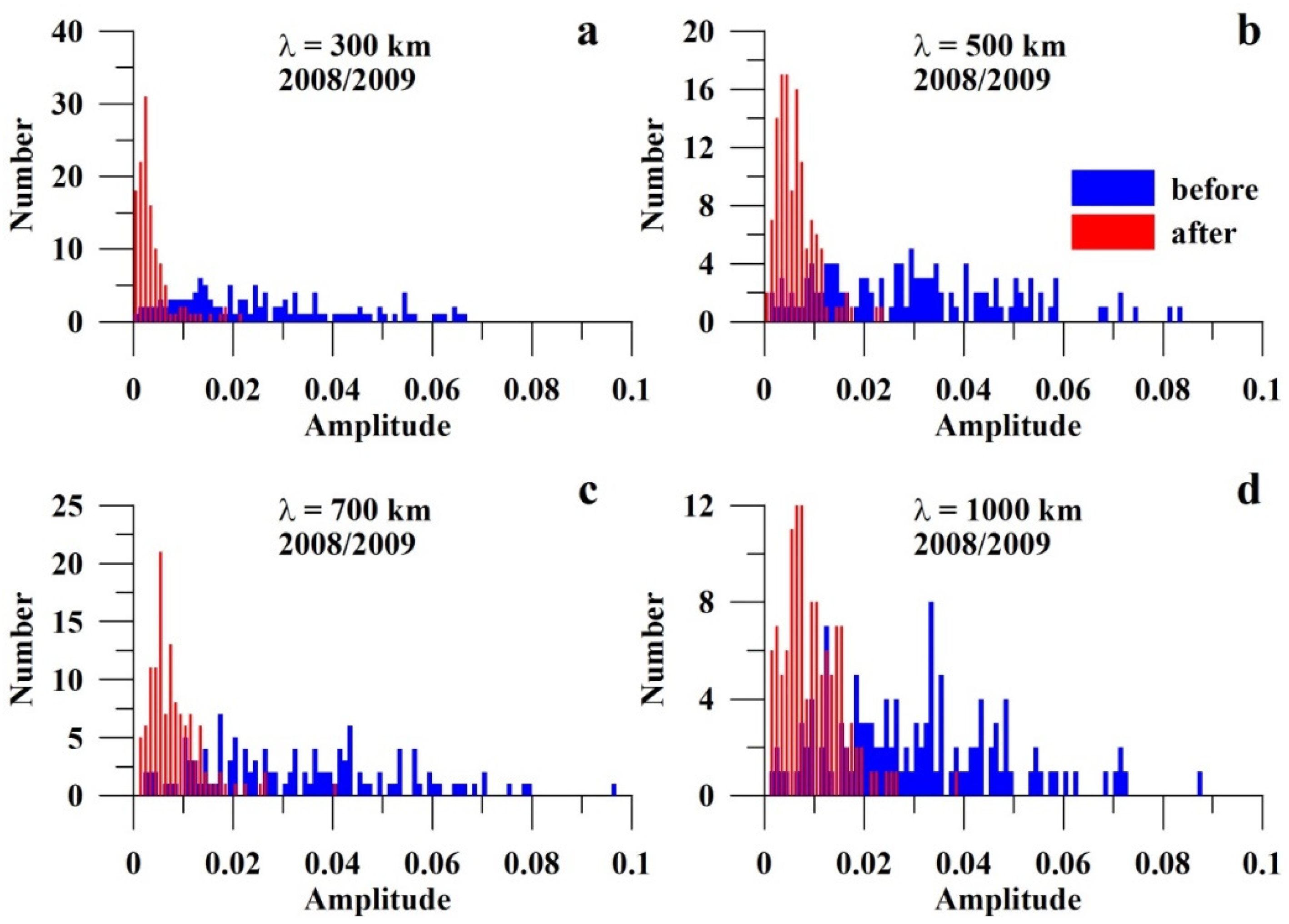
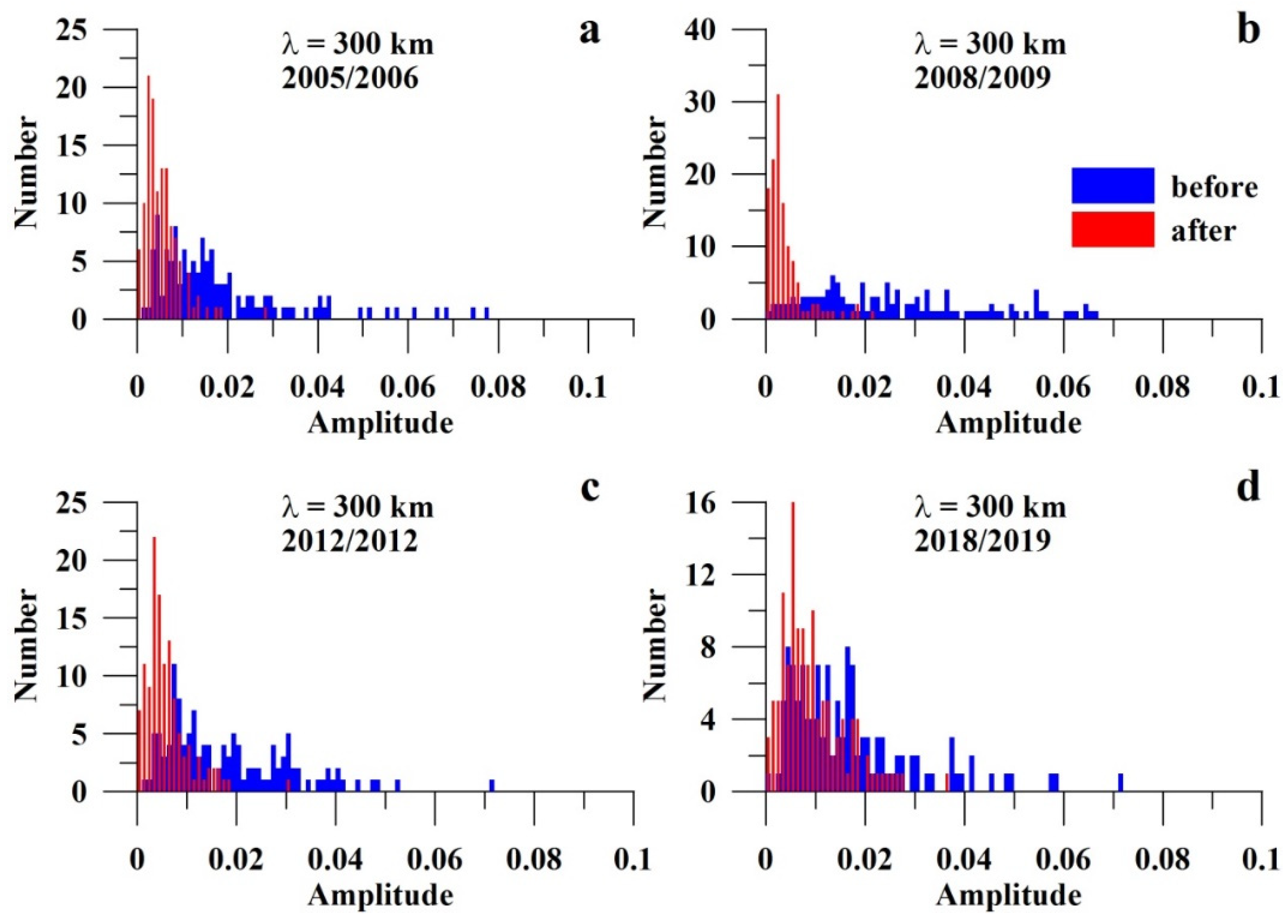
| λU, km | 2005/2006 | 2008/2009 | 2012/2013 | 2018/2019 |
|---|---|---|---|---|
| 300 | 3.25 (p = 7.2 × 10−16) | 6.73 (p = 6.9 × 10−26) | 3.05 (p = 3.7 × 10−19) | 1.81 (p = 9.9 × 10−9) |
| 500 | 2.57 (p = 5.7 × 10−15) | 2.81 (p = 1.8 × 10−28) | 2.34 (p = 1.4 × 10−15) | 1.75 (p = 1.0 × 10−9) |
| 700 | 2.37 (p = 8.6 × 10−18) | 3.98 (p = 4.5 × 10−28) | 1.86 (p = 5.8 × 10−11) | 1.82 (p = 5.8 × 10−14) |
| 1000 | 2.53 (p = 8.8 × 10−18) | 3.16 (p = 1.0 × 10−22) | 1.85 (p = 2.1 × 10−13) | 1.86 (p = 4.4 × 10−14) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yasyukevich, A.S.; Chernigovskaya, M.A.; Shpynev, B.G.; Khabituev, D.S.; Yasyukevich, Y.V. Features of Winter Stratosphere Small-Scale Disturbance during Sudden Stratospheric Warmings. Remote Sens. 2022, 14, 2798. https://doi.org/10.3390/rs14122798
Yasyukevich AS, Chernigovskaya MA, Shpynev BG, Khabituev DS, Yasyukevich YV. Features of Winter Stratosphere Small-Scale Disturbance during Sudden Stratospheric Warmings. Remote Sensing. 2022; 14(12):2798. https://doi.org/10.3390/rs14122798
Chicago/Turabian StyleYasyukevich, Anna S., Marina A. Chernigovskaya, Boris G. Shpynev, Denis S. Khabituev, and Yury V. Yasyukevich. 2022. "Features of Winter Stratosphere Small-Scale Disturbance during Sudden Stratospheric Warmings" Remote Sensing 14, no. 12: 2798. https://doi.org/10.3390/rs14122798
APA StyleYasyukevich, A. S., Chernigovskaya, M. A., Shpynev, B. G., Khabituev, D. S., & Yasyukevich, Y. V. (2022). Features of Winter Stratosphere Small-Scale Disturbance during Sudden Stratospheric Warmings. Remote Sensing, 14(12), 2798. https://doi.org/10.3390/rs14122798







