Adaptive Unsupervised-Shadow-Detection Approach for Remote-Sensing Image Based on Multichannel Features

Abstract

Shadow detection is an essential research topic in the remote-sensing domain, as the presence of shadow causes the loss of ground-object information in real areas. It is hard to define specific threshold values for the identification of shadow areas with the existing unsupervised approaches due to the complexity of remote-sensing scenes. In this study, an adaptive unsupervised-shadow-detection method based on multichannel features is proposed, which can adaptively distinguish shadow in different scenes. First, new multichannel features were designed in the hue, saturation, and intensity color space, and the shadow properties of high hue, high saturation, and low intensity were considered to solve the insufficient feature-extraction problem of shadows. Then, a dynamic local adaptive particle swarm optimization was proposed to calculate the segmentation thresholds for shadows in an adaptive manner. Finally, experiments performed on the Aerial Imagery dataset for Shadow Detection (AISD) demonstrated the superior performance of the proposed approach in comparison with traditional unsupervised shadow-detection and state-of-the-art deep-learning methods. The experimental results show that the proposed approach can detect the shadow areas in remote-sensing images more accurately and efficiently, with the F index being 82.70% on the testing images. Thus, the proposed approach has better application potential in scenarios without a large number of labeled samples.

1. Introduction

Shadow in remote-sensing images is formed when direct light is totally or partially blocked by ground objects [1,2,3]. Although shadow information can be used to estimate the direction of light sources or the height of buildings [4,5,6], the existence of shadow leads to a partial loss of radiometric information in the blocked areas. Recently, high-resolution and super-resolution remote-sensing images have been applied widely [7]. The shadow makes image interpretation (e.g., object detection and classification) difficult or impossible [8,9,10], and especially in high-resolution remote-sensing images. Therefore, the extraction of shadow regions in high-resolution remote-sensing images is an essential step for subsequent image processing. The accuracy of shadow detection has an important effect on applications, such as classification, object detection, and change detection.

The existing shadow-detection methods for remote-sensing images can be divided into two categories: unsupervised shadow detection and supervised shadow detection. Unsupervised shadow detection refers to detecting shadow regions through certain features of shadow, without training samples. The main idea of these methods is to obtain the parameters on the characteristics, such as spectral differences [11,12,13] and geometric features [14,15,16], and they are usually assisted by the prior position, height, camera calibration parameters, and orientation knowledge about scenes and sensors. The disadvantage of these methods is that the parameters that are related to scenes are hard to obtain, such as the spectrum, intensity, color temperature, camera correction parameters, and geometric characteristics of ground objects (height, angle, etc.). For example, Tian [17] propose a tricolor attenuation model to extract shadow areas, but the parameters of the tricolor attenuation model need knowledge about the spectral power distribution of daylight and skylight. However, it is difficult to detect the shadow due to the lack of illumination information in various scenes. Nakajima [11] uses airborne laser scanner data to export the digital surface model for the purpose of simulating the shadow. However, in many cases, the digital surface model of remote-sensing images is hard to obtain. Therefore, a particular method that performs well in one situation may give a poor performance in other situations due to the change in these parameters. The supervised learning methods, as the name implies, rely on many labeled shadow samples. Deep-learning methods, which can learn the complex nonlinear characteristics of training data, have been widely used for the shadow detection of remote-sensing images in recent years [18,19,20,21,22]. Although these methods can achieve a high shadow-detection accuracy, few labeled shadow samples are used in many situations in practice and labeling the shadow samples often requires a large amount of labor costs.

An adaptive unsupervised shadow-detection method for remote-sensing images was developed in this study to improve the generalization ability of shadow-detection models and to degrade the dependence on labeled samples.

Specifically, the main contributions of this study can be summarized as follows:

• Multichannel features are designed on the basis of the hue, saturation, and intensity (HSI) space. The designed multichannel corresponds to the visible spectral bands (400–700 nm) for aerial images. The shadow characteristics of low intensity, high hue, and high saturation are considered to capture the shadow characteristics comprehensively;
• A dynamic local adaptive particle-swarm-optimization (DLA-PSO) algorithm is proposed to calculate the threshold for determining shadow regions adaptively. The main idea of DLA-PSO is to select the optimal segmentation threshold for multi-channel features.

The structure of this paper is organized as follows. Section 2 reviews the related traditional unsupervised methods and the state-of-the-art deep-learning methods for the shadow detection of remote-sensing images. Section 3 describes the proposed shadow-detection method in detail. Section 4 verifies the rationality of the channel design and the robustness of DLA-PSO qualitatively and quantitatively. Section 5 discusses the parameter settings, advantages, and limitations of the proposed model. Section 6 provides the conclusions.

2. Related Work

A variety of shadow-detection methods have been proposed in the past decades. In accordance with the need of labeled shadow samples, these methods can be roughly divided into two categories: unsupervised shadow detection and supervised shadow detection.

2.1. Unsupervised Shadow Detection

Unsupervised shadow detection does not require a large amount of prior knowledge and labeled samples. Unsupervised shadow detection can be divided into model-based and property-based methods. The model-based methods require the prior position, height, and orientation knowledge of the scenes and sensors when detecting shadow regions [1,23]. Zhu developed a cloud shadow-detection method [24]. In their study, the illuminating angle and view angle of the sensor are used together to predict shadow locations. Lee detected the shadowed objects by considering the direction of the shadow area toward the regions of light sources [25]. However, model-based methods are limited because acquiring accurate related geometrical parameters is difficult. The property-based methods distinguish between shadow and nonshadow regions by considering properties such as the geometric and spectral characteristics (e.g., the intensity). Compared with model-based methods, the property-based methods require minimal previous information. The property-based methods have been widely used in the existing literature due to the simplicity of the principle and application.

For the property-based methods, two crucial issues (namely, the selection of the shadow property in the color space and the determination of suitable thresholds) should be solved carefully to identify shaded regions. Color can be represented in different 3D spaces (e.g., red, green, blue (RGB) HSI, hue saturation value (HSV), and C1C2C3 color space), and one color space can be converted into another through a mathematical transformation. Each color space has special properties and may be suitable for a specific scenario. Yang proposes a normalized blue channel on the basis of the characteristics of the high blue value of shadow regions in the RGB color space [26]. In the normalized blue channel, the shadow regions are mainly concentrated in the high-pixel part, but the blue ground objects have high-pixel value. The main disadvantage of the RGB color space is due to its insufficient ability to distinguish between similar colors. Tsai introduced a spectral ratio of hue to intensity (SRHI) to detect shadow in the HSI chromaticity space [27]. However, such a method cannot distinguish shadow from ground objects with high hue values (e.g., dark blue or dark green). The C1C2C3 color space is widely used and is considered the best nonlinear variation for shadow detection [28]. The selection of the color space affects the shadow-detection performance. Tsai compared the effectiveness of shadow detection in different color spaces and found that the best shadow-detection performance is the HSI color space [27]. Some researchers have tried to detect shadows by combining multiple color spaces (e.g., the RGB and HSI) to utilize the spectral properties of shadows [29]. Previous studies have proven that three different indices for shadow detection based on the HSI color space produce more accurate results than using the HSI color space only. In summary, the principle and application of property-based methods are simple and require minimal information about the illumination conditions and geometric scenes. The selection of a suitable color space and shadow features is helpful to promote the detection accuracy.

The thresholds in property-based methods can be calculated in a global or local manner. The global thresholds can be determined by using the histogram bimodal method [29], Otsu method [30], and maximum entropy method [31]. The idea of the histogram bimodal method is to treat the valley of the gray histogram as the threshold value. However, the gray distribution of an image does not necessarily fit the bimodal, and the determined threshold cannot describe the shaded regions accurately. The maximum entropy method calculates the threshold by maximizing the information entropy of foreground and background images. The Otsu method determines the optimal threshold by maximizing the interclass variance. However, the global threshold cannot ensure the performance of shadow detection due to the color diversity of ground objects. Commonly used local-threshold-selection methods include the seeded-region-growing and max-flow/min-cut algorithms [32]. The former merges the adjacent pixels with the same attribute to separate the connected region, and the latter minimizes the energy function of the network by constructing a graph cut network. The general idea of these methods is to calculate the threshold of shadows by considering the similarity of neighboring pixels in the local regions of the remote-sensing image. However, the local-threshold-selection methods are often trapped in the local-optimum problem, without considering the characteristic of the whole image.

2.2. Supervised Shadow Detection

Shadow detection can be achieved with the assistance of machine learning or artificial intelligence. The supervised-shadow-detection method can effectively identify the shaded areas by learning features from considerable training data. Lorenzi detected a shadow region from very high-resolution satellite images by using support vector machine [33]. Yuan developed a shadow-region classifier by combining the logistic-regression and conditional-random-field models [34]. Recently, the deep-learning technique has been applied to shadow detection. Deep-learning models, such as convolutional neural networks (CNNs) and graph convolutional networks (GCNs), have shown superiority in semantic segmentation or object recognition [35,36]. Shadow detection from high-resolution remote-sensing images can be regarded as a semantic-segmentation problem. Ronneberger verified the effectiveness of the U-Net network in shadow detection [37]. Badrinarayanan proposed a Segnet framework [38]. The advantage of Segnet is that the decoder performs nonlinear upsampling on its low-resolution input feature, so as to perform semantic segmentation on the target object in the image. Lei designed a recursive-attention-residual (RAR) module and bidirectional feature pyramid network on the basis of a CNN and proposed a BDRAR algorithm to enhance the detected shadow details [39].

Although the supervised-shadow-detection methods can often achieve better accuracy, the model training process depends heavily on labeled samples. On the one hand, ensuring sufficient training samples is difficult for every scenario. On the other hand, labeling the training samples is related to a large amount of labor costs. Thus, the supervised-shadow-detection method is limited in some application scenarios, and especially in small-sample situations.

2.3. Critical Analysis of Existing Work

In summary, the supervised and unsupervised approaches have their advantages and disadvantages. Although the supervised approaches (including the deep-learning model) can achieve a high shadow-detection accuracy, there are few open datasets for the remote-sensing field in practice, which leads to a serious impact on the performance of shadow detection. Labeling the shadow samples on the basis of satellite images (such as DOTA [40], INRIA aerial datasets [41], etc.) often requires a large amount of labor costs. Luo [2] has publicly released the first Aerial Image dataset for Shadow Detection (AISD). This dataset is aerial orthorectified color imagery with a spatial resolution of 0.3 m, covering five major regions of the world. Moreover, due to the complexity of remote-sensing object types and geometric structures, shadow areas are often scattered in various regions of remote-sensing images with irregular shapes, making it difficult for mainstream deep-learning methods to distinguish complex and diverse features. In addition, the color characteristics of sunlit areas with weak illumination are similar to those shadow areas that are in the process of extracting nonlinear features, which will also cause false detection. The unsupervised approach requires minimal training samples and can be applied to a wide range of applications. However, capturing the shadow characteristics comprehensively and determining the segment threshold for shadow in an adaptive manner considering the diverse characteristics of complex ground objects is difficult. Thus, objects with similar spectral properties are misjudged. For example, the high-hue (green, red) ground objects in nonshadow areas are detected as shadowed areas due to the small difference between the hue and brightness values. Therefore, the development of an unsupervised-shadow-detection approach that can capture the shadow characteristics comprehensively and calculate the shadow threshold adaptively is necessary.

3. Method

3.1. Research Framework

An adaptive unsupervised-shadow-detection method based on multichannel features is described. First, aerial images in the RGB color space should be converted into the HSI color space because the HSI color space is more consistent with visual characteristics [42]. Considering that Gaussian noise may be produced due to the poor optical elements or high temperature of the sensor in the process of image acquisition, a Gaussian filter is applied after the conversion to remove the Gaussian noise in each channel. The main approach is roughly divided into three parts, as follows: (1) the design of multiple channels to capture shadow characteristics comprehensively; (2) the determination of the segment threshold for each channel on the basis of an optimization method, named DLA-PSO; and (3) regional optimization by applying mathematical morphology. The overview of the research framework is presented in Figure 1.

3.2. Conversion from RGB to HSI Color Space

Firstly, the RGB image should be converted into the HSI color space, which is composed of hue (H), saturation (S), and intensity (I) channels, due to the superiority of the HSI color space in discriminating similar colors. The conversion can be achieved via the following formulas [42]:

$$\mathrm{I}=\frac{1}{3}\left(R+G+B \right)$$

(1)

$$\mathrm{S}=1-\frac{3}{R+G+B}\min \left(R, G, B\right)$$

(2)

$$\mathrm{H}=\{\begin{array}{c}\theta , B\le G\\ 360-\theta , B>G\end{array}$$

(3)

$$\mathsf{\theta }=\mathrm{arcos}\frac{\left(R-G\right)+\left(G-B\right)}{2\sqrt{{\left(R-B\right)}^2+\left(R-B\right)\left(G-B\right)}}$$

(4)

Gaussian noise exists in each component channel, and the presence of Gaussian noise affects shadow recognition and threshold selection [43]. Therefore, Gaussian filtering can be used to eliminate the noise in the image. Usually, a 2D Gaussian function can be used to remove noise, which is expressed as follows:

$$h_g\left(n_1, n_2, \delta \right)=\frac{1}{2\pi {\delta }^2}{e}^{\frac{-\left(n_1^2+n_2^2\right)}{2{\delta }^2}}$$

(5)

$$h\left(n_1, n_2\right)=\frac{h_g\left(n_1, n_2, \delta \right)}{{{\displaystyle \sum }}_{n_1}{{\displaystyle \sum }}_{n_2}{h}_g}$$

(6)

where $n_{1 }\mathrm{and} n_2$ are the ordinates of pixels, and $\delta$ is the standard deviation of the normal distribution. The size of the $\delta$ determines the smooth effect of the image, and the default value for the $\delta$ is usually 0.5 [43]. The output ($h\left(n_1, n_2\right)$) is the weighted average of the adjacent pixel points around.

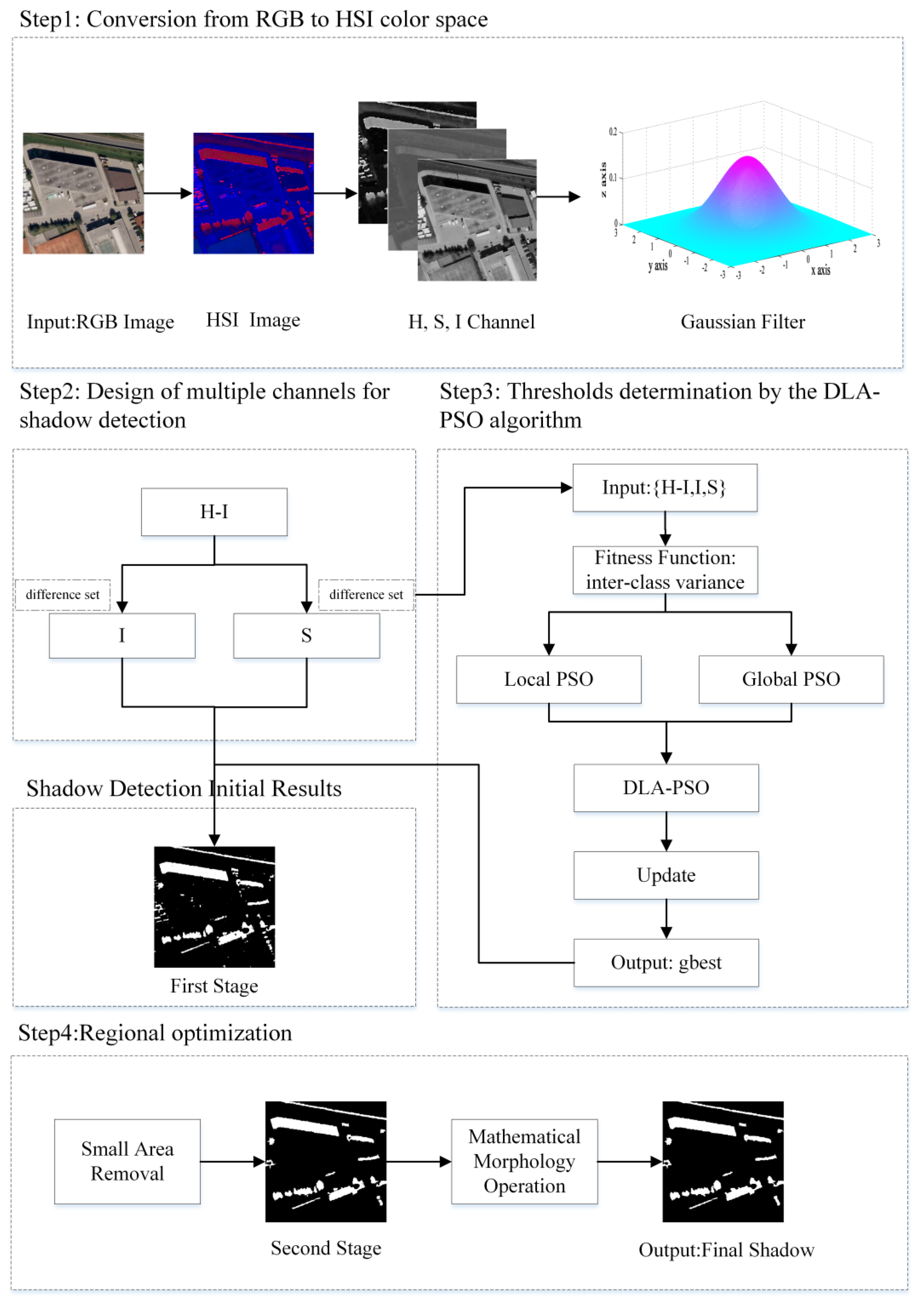
3.3. Design of Multiple Channels for Shadow Detection

In this paper, the design of multiple channels considers both the properties of shadow and the interference of special remote-sensing features on shadow detection. The design of shadow channels should reflect the characteristics of the shadow region in the HSI color space. Shadow areas are caused by objects blocking the sun’s light; thus, they have low intensity [44]. The saturation in the shadow region is high due to the influence of atmospheric Rayleigh scattering. The Phong illumination model shows that the shaded areas often have high hue values [45].

Figure 2 shows the grayscale maps of multiple channels for the same image in shadow detection. Figure 2a,b illustrates the original image and the true labeled shaded region, and Figure 2c displays the grayscale map for the H channel. As observed in Figure 2c, the areas with high hue (lawns, football fields, etc.) cannot be distinguished from real shadow areas through the hue channel. The intensity value of these high-hue areas is higher than the shadow areas, as shown in the I channel in Figure 2f. On the basis of the characteristics of the shadow areas (i.e., high hue and low brightness), a new channel (namely, the H-I channel) is designed in this study. The rationality of the H-I channel depends on its ability to strengthen the difference between the H and I channels and distinguish the objects with high hue (lawns, football fields, etc.) and the shadow regions from the image. The value of the shadow areas through the H-I channel are higher than the high-hue objects in the nonshadow region, which appears white in Figure 2d and can be easily separated. Dark objects (e.g., black roof or gray roads) with high hue and low intensity are found in the nonshadow areas. They are easily mistaken for shadows through the H-I channel. Therefore, a saturation channel is considered. These dark objects in nonshadow areas (i.e., the misjudged shadows) are usually less saturated and are brighter than real shadow areas. Therefore, the shadow regions detected through the H-I channel are further refined by using the low-saturation and high-intensity constraints. Specifically, the initial shadow-detection results are first obtained through the H-I channel. The initial detected shadow regions are processed in the saturation and intensity channels. The intersection regions of the detected regions in different channels are treated as the final shadow regions. Accurate shadow-detection results can be realized through the designed detection channels and framework. The ground truth in this paper is actually a shadow mask provided by manual annotation in the AISD dataset. Due to large number of shadows with various types and shapes in the selected aerial images, the shadow masks were carefully annotated by Luo et al. [2]. In recent years, the AISD dataset has been widely used for evaluating shadow-detection performance [2,46]. As shown in Figure 2g, the detected shadow is consistent with the ground truth.

3.4. Threshold Determination Using the DLA-PSO Algorithm

Another issue is how to select the optimal thresholds for each channel (i.e., H-I, S, and I channels) adaptively and accurately. In this study, a DLA-PSO is proposed on the basis of the traditional OTSU algorithm and PSO. PSO is a classical intelligent optimization algorithm that has been widely used in image registration [47,48,49] and image segmentation [50,51,52]. The advantages of the PSO algorithm include simplicity, fewer parameters, and fast convergence [53]. The determination of thresholds in shadow detection can be calculated by using the PSO algorithm. In the PSO algorithm, an optimization function needs to be set to judge the fitness of the particle before and after the movement. On the basis of the fitness function, the individual optimal value ($pbes{t}_i$) of the particle (i) and the global optimal value ($gbest$) can be found. Shadow detection, itself, is a pixel-level image binary classification task, and the interclass-variance formula is a method to divide the image into foreground and background according to the gray characteristics of the image. In terms of shadow detection, the threshold of each channel needs to use the formula of interclass variance as the evaluation standard. The maximum interclass variance means the minimum misclassification probability. Given a particle swarm of the size (n) $Q=\left\{X_1,X_2,\dots ,X_n\right\}$, the velocity of each particle is randomly set as $V=\left\{v_1,v_2,\dots ,v_n\right\}$. The optimal threshold for shadow detection can be obtained by maximizing the interclass variance, which can be calculated as:

$$g=w_0{\left({\mu }_0-\mu \right)}^2+w_1{\left({\mu }_1-\mu \right)}^2$$

(7)

where $g$ represents the interclass variance, $w_0$ represents the proportion of shadow pixels in the overall image, and $w_1$ represents the proportion of nonshadow pixels in the overall image. ${\mu }_0$ represents the average gray value in the shadow image, and ${\mu }_1$ represents the average gray value in the nonshadow image. $\mu$ represents the average gray value of the whole image, which can be expressed as $\mu =w_0{\mu }_0+w_1{\mu }_1$. Thus, the simplified formula of interclass variance can be obtained as:

$$g=w_0{w}_1{\left({\mu }_0-{\mu }_1\right)}^2$$

(8)

To solve the local-optimal problem for the classical PSO algorithm, a DLA-PSO algorithm is proposed in this study. For the k-th iteration, the PSO algorithm changes the velocity and position of the particle in accordance with the velocity-update and position-update formula of the particle (i), which can be expressed as:

$$v_i^k=w{v}_i^{k-1}+c_1{r}_1\left(pbes{t}_i-X_i^{k-1}\right)+c_2{r}_2\left(gbes{t}^{k-1}-X_i^{k-1}\right)$$

(9)

$$X_i^k=X_i^{k-1}+v_i^{k-1}$$

(10)

where $c_1$ and $c_2$ are the learning factors, which are usually set to 2. $r_1$ and $r_2$ are random factors between 0 and 1, which are used to enhance the performance of the PSO algorithm [53,54,55]. In Formula (9), the inertia weight (w) determines the prior knowledge’s influence on the current velocity and affects the convergence speed of the algorithm. When w is set too small, it means that the historical speed has too little influence on the current velocity, so that the particle moves in the local range, resulting in the local optimal solution. However, if w is too large, it means that the historical speed has heavy influence, so that the particles move in a wide range in the later period, which will lead to nonconvergence. A large w should be specified at the initial stage so that particles can find the optimal value domain as soon as possible. To avoid the situation of local optimization, a small w should be given at the later stage so that a stable search speed can be maintained to accurately search the optimal threshold within the optimal value domain. This process is performed to balance the global search speed and local optimization effect. For this reason, a dynamic inertia weight ($w$) is introduced, which is calculated as:

$$w=w_{max}-\frac{\left(w_{max}-w_{min}\right)·k}{Ma{x}_{iteration}}$$

(11)

The dynamic inertia weight changes with the number of iterations (k), total number of iterations ($Ma{x}_{iteration}$), maximum weight ($w_{max}$), and minimum weight ($w_{min}$). The $w_{max}$ is set to 0.95, and the $w_{min}$ is set to 0.4 [56].

In this study, it can be found, from Formula (9), that the classical PSO algorithm adjusts the particle velocity by the individual optimal position ($pbes{t}_i$) and the global optimal position ($gbes{t}^{k-1}$). When the value of $gbes{t}^{k-1}-X_i^{k-1}$ is too large, the convergence rate of the particle is fast in the early stage, resulting in the local-optimal condition. However, when the value of $pbes{t}_i-X_i^{k-1}$ is too large, nonconvergence will occur in the late searching period under the constraint of a lack of global information. In order to alleviate the contradiction, neighborhood particles are considered, and the current iteration and the maximum iteration are combined to design the β value. Therefore, global PSO and local PSO are combined to define the velocity-updating formula:

$$v_i^{k-1}=\left(1-\beta \right)·GlobalPS{O}_i+\beta ·LocalPS{O}_i$$

(12)

$$GlobalPS{O}_i=w{v}_i^{k-1}+c_1{r}_1\left(pbes{t}_i-X_i^{k-1}\right)+c_2{r}_2\left(gbes{t}^{k-1}-X_i^{k-1}\right)$$

(13)

$$LocalPS{O}_i=w{v}_i^{k-1}+c_1{r}_1\left(pbes{t}_i-X_i^{k-1}\right)+c_3{r}_3\left(pbes{t}_{i+1}-X_i^{k-1}\right)$$

(14)

$$\beta =\frac{k}{Ma{x}_{iteration}}$$

(15)

$$X_i^k=X_i^{k-1}+v_i^{k-1}$$

(16)

where Formula (13) represents the velocity updating on the basis of the global PSO, and Formula (14) represents the velocity updating on the basis of the optimization of particles in the local neighborhood.

The particle-velocity-update formula ($v_i^{k-1}$) is divided into four parts: $w{v}_i^{k-1}$ is the product of the particle velocity in the k − 1 evolution and the dynamic inertia weight, which is regarded as the prior knowledge part of the particle (i); $pbes{t}_i-X_i^{k-1}$ is the local perception part, which is the optimal distance between the current position of the particle (i) and its own individual, and reflects the self-cognition of the particle (i) itself; $gbes{t}^{k-1}-X_i^{k-1}$ is the global perception part, which is the distance between the global optimal position and the current position of the particle, and it reflects the global cognition of the particle (i); $pbes{t}_{i+1}-X_i^{k-1}$ is the neighborhood perception part, which is the distance between the neighborhood particle and the current position of the particle, and it reflects the communication and information sharing between the particle (i) and its companions. Thus, at the beginning of iteration, $gbes{t}^{k-1}$ is more suitable for searching the approximate range of optimal thresholds. At the same time, the existence of nearby particles can also limit the local-optimal problem caused by excessive velocity. In addition, more consideration is given to the influence of adjacent particles and current particles in the late search process, so that the optimal threshold can be accurately found within the rough range determined in the early stage to avoid the problem of nonconvergence. The framework of the DLA-PSO algorithm is illustrated in Algorithm 1.

Algorithm 1: Framework of the DLA-PSO algorithm

Input: Designed channels (H-I, I, S); n, Max_iteration; Output:$\mathit{gbest}$

Initialization: c1 = 2, c2 = 2, ${\mathrm{w}}_{max}=0.95$,${\mathrm{w}}_{end}=0.4$; r1, r2 = rand ();$v_0$ = 2; while (k < Max_iteration), do; Calculate the fitness function according to Otsu algorithm; $pbes{t}_i^k=w_0{w}_1{\left({\mu }_0-{\mu }_1\right)}^2$; Set the optimal particle value $pbes{t}_i^k$ and $gbes{t}^k$ in the k-th iteration; $pbes{t}_i^k=\left\{ pbes{t}_1^k,pbes{t}_2^k,\dots ,pbes{t}_n^k\right\}$; $gbes{t}^k=\max \left(pbes{t}_i^k\right)$ for i = 1 to n, do; if ($g\left(pbes{t}_i^k\right)>g\left(pbes{t}_i\right)$), then; $pbes{t}_i=pbes{t}_i^k$; if ($g\left(gbes{t}^k\right)>g\left(gbest\right)$), then; $gbest=gbes{t}^k$; Update ${\mathrm{X}}_{\mathrm{i}}^{\mathrm{k}}$ and ${\mathrm{v}}_{\mathrm{DLA}-\mathrm{PSO}}^{\mathrm{k}-1}$; $v_{DLA-PSO}^{k-1}=\left(1-\beta \right)·GlobalPS{O}_i+\beta ·LocalPS{O}_i$; $X_i^k=X_i^{k-1}+v_{DLA-PSO}^{k-1}$; $\mathit{k}\leftarrow \mathit{k}+\mathbf{1}$; return$\mathit{gbest}.$

3.5. Regional Optimization

The initial shadow-detection results can be obtained by using the proposed DLA-PSO algorithm. However, small low-brightness objects (e.g., the black vehicles on the road) in nonshadow areas or bright ground objects (e.g., white vehicles) in shadow regions are often misjudged. Two types of regional optimization are adopted in the proposed approach to further improve the shadow-detection precision. The connected regions in the shadow-segmentation results are calculated to select the low-brightness objects in the nonshadow area. To eliminate small low-brightness objects (e.g., the black vehicles on the road) in the nonshadow area, a spatial lower limit for the area of small objects should be given. In this paper, the spatial lower limit is set according to the spatial resolution of the experimental datasets and the size of vehicles in real life. The spatial resolution of the AISD dataset is 0.3 m, meaning that one pixel grid in the image represents an actual area of 0.09 square meters. In real life, the length of a vehicle is about 4–6 m, and the width is about 2 m. Thus, it can be calculated that a car occupies about 90–130 pixels in the AISD dataset. Therefore, the spatial lower limit is set as 130 for regional optimization. Meanwhile, bright ground objects in shadow (e.g., white vehicles) are often mistaken for sunlit areas. Due to the small size of the white vehicles in the remote-sensing image, it will appear as small holes in the detected shaded area, as shown in Figure 3d. The closure operation of mathematical morphology is applied to the detected shadow areas to fill these holes.

Mathematical morphology is widely used in image processing, and especially in edge extraction and image segmentation [57]. Two basic operations in mathematical morphology are the corrosion operation and the expansion operation. Small holes can be filled by using the closed operation, which is expansion followed by corrosion and is expressed as:

$$A\oplus V=\left\{\sigma |{\widehat{V}}_{\sigma }{\displaystyle \cap }A\ne \varnothing \right\}$$

(17)

$$A\odot V=\left\{\sigma |{\left(V\right)}_{\sigma }\subseteq A\right\}$$

(18)

$$A•V=\left(A\oplus V\right)\odot V$$

(19)

Formulas (17)–(19) represent the expansion, corrosion, and closure operations, respectively. The expansion enlarges the boundary of the target set (A) and corrosion shrinks the boundary of the target set (A). By definition, the closure operation of mathematical morphology can fill small holes and eliminate small, narrow cracks and voids while keeping the shapes and positions of objects unchanged. Therefore, the closure operation of mathematical morphology is adopted to eliminate the small holes in the detected shadow that are caused by bright small objects in the shadow area, as illustrated in Figure 3e.

4. Experiment

The indices of the accuracy, precision, recall, and F-measure are introduced to make the comparison reliable and to evaluate these methods quantitatively, which are formulated as:

$$ACC=\frac{TP+TN}{TP+TN+FP+FN}$$

(20)

$$Precision=\frac{TP}{TP+FP}$$

(21)

$$Recall=\frac{TP}{TP+FN}$$

(22)

$$F_{Measure}=\frac{2·Precision·Recall}{Precision+Recall}$$

(23)

where TP and TN refer to the parts that are properly checked as shadow and nonshadow. FP represents the missing shadow, and FN represents the part that is mistakenly checked as a shaded area. ACC is adopted as the accuracy metric, and $F_{Measure}$ represents an aggregative indicator that considers precision and recall, ranging from 0 to 1.

4.1. Rationality of Channel Design

This section first discusses the rationality of the channel design on shadow detection. A remote-sensing image of Innsbruck is adopted as the original image in Figure 4a. Hue, saturation, and intensity serve as single-channel detection in the HSI color space in Figure 4b–d. However, the characteristics of the single channel ignore the important shadow attributes of other channels. For example, in Figure 4d, only the intensity of shadows is considered and, as a result, the playground with low intensity is mistaken as shadow. Shadow detection is often interfered with by high-hue ground objects (grass, etc.), which are of high hue and high intensity in the illumination area but of high hue and low intensity in the shadow area. As shown in

Table 1. Comparative evaluation for designed channels.

	Single Channel				Multiple Channels
	H	S	I	H-I	Nonordered HSI	DLA-PSO
Precision	0.6596	0.4966	0.3373	0.9158	0.9862	0.9393
Recall	0.9563	0.7063	0.9911	0.9404	0.6816	0.9379
F	0.7807	0.5832	0.5033	0.9279	0.8061	0.9386

, the F value of the single channel (hue, saturation, and intensity) is less than 0.8, resulting in a poor comprehensive detection performance. Therefore, the rationality of the H-I channel depends on its ability to strengthen the difference between the H and I channels and distinguish the objects with high hue (lawns, football fields, etc.) and the shadow regions from the image, as shown in Figure 4e. As can be seen from Figure 4c,d, some ground objects with low intensity and high saturation in the sunlit area will also cause interference in shadow detection, and so shadow detection that combines the saturation channel and intensity is considered to obtain better results. After determining the designed channels, the order of the H-I, S, and I channels should be considered in the next step. Figure 4f shows the shadow-detection results of a nonordered HSI channel design. As shown in Table 1, the F value of the nonordered HSI channel is 0.8061. Although a nonordered design can detect most of the shadow regions, the boundary of the shadow areas is blurred and irregular. The proposed DLA-PSO, based on multichannel features, has an F value of 0.9386, as shown in Figure 4g and Table 1. The channel design of the DLA-PSO method can achieve a more accurate shadow-detection result by comparing the performances of a single channel and multiple channels.

4.2. Robust Evaluation of DLA-PSO

In this part, the robustness of the proposed approach is evaluated on public remote-sensing datasets. The popular AISD public remote-sensing dataset is used as the benchmark to compare the performances of different shadow-detection methods. The data include 514 remote-sensing images with spatial resolutions of 0.3 m, covering five different cities (namely, Austin, Vienna, Innsbruck, Chicago, and Tyrol). The AISD datasets can be obtained from https://github.com/RSrscoder/AISD, (accessed on 1 March 2022). The remote-sensing images in the AISD dataset only contain RGB bands. However, the proposed method can be extended by adding other bands (e.g., near-infrared band) [58] to detect shadows in future work.

For the shadow-detection methods, the proposed approach is compared with traditional unsupervised methods and the latest deep-learning methods. Traditional methods include the SRHI, normalized-blue (NB), histogram-threshold-detection (HTD), and C1C2C3 space detection (C1C2C3) methods. This study selects three representative deep-learning algorithms (namely, the U-Net, Segnet, and BDRAR methods). The U-net model adopts an encoder–decoder structure and a jump-connection design so as to retain more image details and achieve good effects in shadow detection [37,59,60]. Compared with U-net, the Segnet model restores the feature graph to high resolution in the upsampling process, thus preserving the location of the target feature, and finally achieving shadow detection [38,61]. The BDRAR model adds an attention residual module and bidirectional pyramid network on the basis of the CNN framework. This model fully mines the global and local context information in different layers of CNN coding, so that the feature extraction of shadow samples is considered more comprehensively [39].

Considering that each city has different illumination characteristics and urban architectural features, five representative urban images were selected to analyze the performances of different methods qualitatively and quantitatively. Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9a,j serve as the original images and ground truth, respectively.

4.2.1. Comparative Experimental Analysis on Austin Dataset

Figure 5b–e shows the results of the traditional shadow-detection methods. The C1C2C3 method cannot detect most of the shadow regions. Buildings and trees cannot be distinguished from their shadows, as shown in Figure 5e. In Figure 5b,d, the SRHI and HTD methods wrongly detected the dark roofs as shadow areas. Although the NB method can separate roofs from shadow regions, the error caused by the vegetation can still be mistaken for shadows in Figure 6c. From the above analysis, the traditional methods tend to detect the sunlit dark objects as shadow and the shadowed bright objects as nonshadow falsely because they heavily rely on shadow properties.

For deep-learning methods, the U-Net, Segnet, and BDRAR methods can detect most of the shadow regions correctly, without significant errors, but many sunlit objects (vehicles, etc.) are mixed, thereby affecting the accuracy of the U-Net and Segnet methods, as shown in Figure 5f,g. The BDRAR method can achieve better results and can eliminate the error caused by vehicles compared with the U-Net and Segnet methods. However, the boundary features of the shadow areas are blurred and irregular, resulting in some error in the details. Narrow shadows cannot be effectively recognized in the BDRAR method in Figure 5h. This condition is because deep-learning methods lack learning ability on complex ground objects in remote-sensing images. Aiming at shadow in remote-sensing images, the proposed method in this paper considers both the shadow attributes and characteristics of easily confused objects (such as high-hue grassland and high-saturation road), and designs multiple channels, so as to achieve the accurate detection of shadow and better retain the characteristics of the boundary. The DLA-PSO method can precisely detect the shadow regions, avoiding the interference of vegetation, vehicles, and roofs, and it can extract the true shadow boundary clearly and regularly. From the quantitative indicators in

Table 2. Austin shadow-test-evaluation index.

	SRHI	NB	HTD	C1C2C3	U-Net	Segnet	BDRAR	DLA-PSO
Precision	0.5801	0.6687	0.6061	0.3228	0.8046	0.7383	0.9391	0.9646
Recall	0.8623	0.8771	0.9718	0.7739	0.9482	0.9585	0.6903	0.8042
F-Measure	0.6936	0.7589	0.7466	0.4556	0.8705	0.8341	0.7957	0.8771
Accuracy	0.8774	0.9103	0.8938	0.7023	0.9546	0.9386	0.9429	0.9606

, the accuracy of the DLA-PSO method achieves up to 96%, which is higher than the other compared methods. The comprehensive indicator, the F-measure, in the DLA-PSO method performs the best among all methods, with a score of 87.7%. In summary, the shadow results detected by the proposed DLA-PSO method are more consistent with the ground truth in Austin City.

4.2.2. Comparative Experimental Analysis on Vienna Dataset

Although shadow areas can be detected by the traditional methods in Figure 6b–e, some dark roofs are still wrongly detected as shadows, leading to a low accuracy and F value. For deep-learning methods, the detection results of the U-Net and Segnet methods in Figure 6f,g are mixed with additional interferences (dark cars, trees) due to the complex features in Venice. The building outline in the BDRAR method is smooth, without sharp edges or corners, resulting in some detailed error, as shown in Figure 6h. As shown in Figure 6i and

Table 3. Vienna shadow-test-evaluation index.

	SRHI	NB	HTD	C1C2C3	U-Net	Segnet	BDRAR	DLA-PSO
Precision	0.8362	0.8571	0.6852	0.7323	0.865	0.82	0.976	0.9348
Recall	0.7663	0.7708	0.9445	0.7467	0.9072	0.918	0.7512	0.8443
F-Measure	0.7997	0.8116	0.7942	0.7394	0.8865	0.8662	0.849	0.8873
Accuracy	0.9123	0.9183	0.8881	0.8797	0.9464	0.9374	0.9389	0.951

, the proposed DLA-PSO method can detect the shadow area more accurately, with an accuracy of 95.1%. The comprehensive evaluation indicator (F) achieves a score of 0.8873, which is the highest score among all the methods. The proposed DLA-PSO method has excellent results in the shadow detection of Venice City.

4.2.3. Comparative Experimental Analysis on Innsbruck Dataset

As shown in the results in Figure 7b,d,e, the SRHI, HTD, and C1C2C3 methods wrongly detect the dark green roofs as shadow, leading to a low accuracy and F value. U-Net and Segnet mistakenly recognize the sunlit dark roofs in the upper part of the figure as shadow in Figure 7f,g. Although the NB and BDRAR methods can well avoid the interference of sunlit dark ground objects, the F value in

Table 4. Innsbruck shadow-test-evaluation index.

	SRHI	NB	HTD	C1C2C3	U-Net	Segnet	BDRAR	DLA-PSO
Precision	0.4041	0.8775	0.6573	0.4195	0.8282	0.8116	0.9799	0.9036
Recall	0.6552	0.6759	0.9413	0.7335	0.8529	0.8879	0.6104	0.8105
F-Measure	0.4999	0.7636	0.7741	0.5337	0.8403	0.848	0.7522	0.8545
Accuracy	0.7072	0.9065	0.8773	0.7137	0.9276	0.935	0.9102	0.9378

shows that the comprehensive performance of shadow detection is low, and the accuracy is slightly lower than the DLA-PSO method. Compared with deep-learning methods, the proposed DLA-PSO method has a slight improvement in the comprehensive performance of detection, with a score of 85.45%. The shadow-detection accuracy has the highest score: up to 93.78%. The proposed DLA-PSO method has the best effect on remote-sensing shadow detection in Innsbruck City.

4.2.4. Comparative Experimental Analysis on Chicago Dataset

As shown in the results in Figure 8b,d,e, the SRHI, HTD, and C1C2C3 methods detect the dark road surface and lawns in the upper left corner as shadow. The shadow results of the U-Net and Segnet methods mix with additional interferences (sunlit objects), as shown in Figure 8f,g. However, the BDRAR method loses small ground objects in Figure 8h. As observed in Figure 8i and

Table 5. Chicago shadow-test-evaluation index.

	SRHI	NB	HTD	C1C2C3	U-Net	Segnet	BDRAR	DLA-PSO
Precision	0.3937	0.8642	0.5299	0.519	0.6805	0.5894	0.9048	0.9215
Recall	0.8422	0.7043	0.9436	0.6908	0.8841	0.9268	0.6326	0.6837
F-Measure	0.5365	0.7761	0.6787	0.5927	0.7691	0.7205	0.7446	0.7849
Accuracy	0.8075	0.9462	0.8818	0.8744	0.9298	0.9049	0.9426	0.949

, the proposed DLA-PSO method can accurately identify shadow regions, with the highest accuracy (94.9%) and F value (0.7849) among all the methods.

4.2.5. Comparative Experimental Analysis on Tyrol Dataset

As shown in Figure 9b,d,e, the SRHI, HTD, and C1C2C3 methods wrongly recognize lawns as shadow due to the similar spectral ratios between the vegetation and the shadow in the Tyrol dataset. For deep-learning methods, the results of the U-Net and Segnet methods identify small sunlit areas by mistake, thereby greatly reducing the detection accuracy, as shown in Figure 9f,g. The NB and BDRAR methods can detect shadow regions well from the original image. However, the proposed DLA-PSO method has a detection accuracy of 97.31% and an F value of 0.8646, which are higher than other methods, as shown in

Table 6. Tyrol shadow-test-evaluation index.

	SRHI	NB	HTD	C1C2C3	U-Net	Segnet	BDRAR	DLA-PSO
Precision	0.1946	0.9888	0.2479	0.2125	0.8788	0.7646	0.9682	0.9822
Recall	0.7872	0.7298	0.9934	0.7301	0.7176	0.7507	0.7238	0.7721
F-Measure	0.3121	0.8398	0.3968	0.3292	0.7880	0.7576	0.8284	0.8646
Accuracy	0.6146	0.9691	0.6646	0.6696	0.9357	0.9200	0.9667	0.9731

. Therefore, the proposed method has the best detection performance in Tyrol City.

A boxplot for 50 testing images is introduced to show the F-value distributions of the DLA-PSO method and comparative approaches to verify the robustness of the proposed DLA-PSO. A boxplot contains five indicators, which are the minimum, lower quartile, median, upper quartile, and maximum. The advantage of the boxplot is that it excludes the interference of outliers and depicts the dispersion distribution of the data stably. The region between the lower quartile and upper quartile determines the box size. The smaller the region, the more concentrated the F value.

The average shadow-detection F values of different shadow-detection methods are shown in

Table 7. Average shadow-detection F values of different shadow-detection methods.

Index	SRHI	NB	HTD	C1C2C3	U-Net	Segnet	BDRAR	DLA-PSO
F	58.04%	74.52%	64.55%	53.65%	82.35%	78.15%	72.15%	82.70%

. The F values of the SRHI, HTD, and C1C2C3 methods are less than 65%, and those of some of the deep-learning methods, such as U-Net, Segnet, and BDRAR, are above 70%. Deep-learning methods perform better than traditional methods. The F value of the proposed DLA-PSO is 82.70%, which is higher than all the compared methods. Although the average detection F value of DLA-PSO is 0.35% higher than that of the U-Net method, the U-Net method requires training samples in advance, while the proposed method is an adaptive unsupervised-shadow-detection method, which can quickly and accurately identify the shadow area. Most importantly, the average F value in Table 7 needs to be comprehensively analyzed in combination with the box diagram of the F-value distribution in Figure 10. The size of the box and the region between the lower quartile and upper quartile, and between the maximum and minimum of the DLA-PSO method, are the smallest, indicating the strongest robustness of DLA-PSO. The box height of DLA-PSO is the highest, demonstrating superior shadow-detection performance. However, the U-Net method has a larger fluctuation range than the DLA-PSO method, and its lowest value reaches 0.58, indicating the weaker robustness. The above analysis indicates that the DLA-PSO method is robust and excellent in shadow detection.

From the above analysis, the proposed DLA-PSO method is consistent with the real shadow areas. The accuracy and F value of the proposed method are the highest compared with the other methods under five different urban scenes. From the boxplot, the DLA-PSO method performs the best among the compared methods.

4.2.6. Comparative Experimental Analysis on Vegetation Application

In this part, the vegetation images of the Kitsap district and San Francisco are selected to verify the performance of the proposed method for shadow detection in comparison with the existing methods in both qualitative and quantitative ways. The visualization results of the shadow detection on the vegetation images are shown in Figure 11 and Figure 12.

Figure 11b–e and Figure 12b–e show the results of the traditional shadow-detection methods. Vegetation in the same area can show slight color differences due to the light, soil type, vegetation type, and many other factors. Some darker vegetation can be mistaken for shadow, as shown in Figure 11b,d and Figure 12b,d. Secondly, as shadows of vegetation are complex, some small shadows just fall on the light-colored vegetation, resulting in misjudgment, as shown in Figure 11c,e and Figure 12c,e. In conclusion, traditional methods are not effective for vegetation shadow detection. Figure 11f–h and Figure 12f–h show the results of the deep-learning methods for vegetation shadow detection. Compared with traditional methods, the detection accuracy of deep-learning methods is greatly improved. However, the U-Net and Segnet methods also have false detection, as shown in Figure 11f,g and Figure 12f,g. The reason is that these models are not capable of learning irregular shadows of remote-sensing images. The BDRAR model can improve the performance of shadow detection due to the addition of the bidirectional pyramid mechanism. However, some small vegetation shadows will be mistaken as nonshadow in Figure 11h and Figure 12h, which is caused by the insufficient learning ability of these models with regard to small target shadows. The proposed method in this paper can realize the detection of small shadows, and the detected shadows are closer to the real shadows of vegetation visually, as shown in Figure 11i and Figure 12i.

The quantitative results of the vegetation shadow detection in the Kitsap district and San Francisco are shown in

Table 8. Evaluation index for vegetation shadow in Kitsap district.

	SRHI	NB	HTD	C1C2C3	U-Net	Segnet	BDRAR	DLA-PSO
Precision	0.4425	0.9998	0.6055	0.8889	0.7446	0.6962	0.9543	0.8856
Recall	0.6665	0.6905	0.9101	0.3254	0.8824	0.9549	0.7607	0.9664
F-Measure	0.5319	0.8169	0.7272	0.4764	0.8076	0.8053	0.8465	0.9243
Accuracy	0.8241	0.9536	0.8976	0.8931	0.9391	0.9314	0.9613	0.9732

and

Table 9. Evaluation index for vegetation shadow in San Francisco district.

	SRHI	NB	HTD	C1C2C3	U-Net	Segnet	BDRAR	DLA-PSO
Precision	0.5711	0.9436	0.4586	0.5482	0.6997	0.584	0.9323	0.8665
Recall	0.8397	0.447	0.9986	0.488	0.9412	0.9729	0.7208	0.9091
F-Measure	0.6798	0.6066	0.6286	0.5164	0.8026	0.7299	0.813	0.8873
Accuracy	0.9103	0.9342	0.8697	0.899	0.9583	0.9301	0.963	0.9745

. As can be seen from Table 8 and Table 9, the performances of the traditional methods for shadow detection in vegetation application are generally low, with F values lower than 70% in most cases. The performance of the deep-learning method is higher than that of traditional methods in shadow detection. The accuracy of deep-learning methods is above 90%, and the F value is around 80% in most cases. In particular, due to its fine network design, the shadow-detection performance of the BDRAR model is higher than those of the U-Net and Segnet methods, with the F value reaching 84%. The proposed method in this paper has the highest accuracy of 97% and a superior performance, with the F value closing to 90%. Moreover, the shadows detected by the proposed DLA-PSO method are more consistent with the ground truth in vegetation application. In summary, the proposed method has excellent performance in vegetation shadow detection.

5. Discussion

5.1. Parameter Settings

The number of particles and iterations have an influence on the determination of thresholds in the PSO algorithm. For the DLA-PSO algorithm, the positions of particles refer to the possible segmentation values, and the optimal segmentation value denotes the threshold to differentiate the shadow regions from nonshadow regions. Therefore, the reasonable number of particles (i.e., the possible positions of particles) should range between 0 and 255. If the number of particles is small, then the DLA-PSO algorithm may fall into the local optimum and excessive particles may influence the computational efficiency. The max iteration parameter determines the number of particle movements, which determines the computational efficiency, together with the selection of the particle number. In practice, the number of particles and max iteration should be carefully determined by considering the computational efficiency and detection precision. If the number of max iterations is set to 100 and the initial velocity (v0) is 2, then setting the number of particles in the range of from 20 to 30 is reasonable by comparing the precision and efficiency under different parameters.

In this study, the computational efficiency is compared between the DLA-PSO algorithm and the proposed parameters and other methods. Five different urban datasets from AISD were selected as the benchmark, and the results of the average computing time are shown in

Table 10. The comparison of average computing times on different urban datasets.

Time (s)	Austin Dataset	Venice Dataset	Innsbruck Dataset	Chicago Dataset	Tyrol Dataset
DLA-PSO	1.51 s	1.65 s	1.39 s	1.59 s	1.07 s
SRHI	7.9 s	5.41 s	2.3 s	8.45 s	1.73 s
NB	6.4 s	3.92 s	1.85 s	6.23 s	1.48 s
HTD	5.94 s	2.65 s	1.67 s	6.95 s	1.68 s
C1C2C3	7.91 s	5.46 s	3 s	7.15 s	2.26 s
U-Net	5.28 s	4.17 s	4.64 s	4.1 s	2.02 s
Segnet	10.41 s	5.1 s	4.6 s	4.53 s	2.05 s
BDRAR	11.76 s	4.36 s	3.03 s	4.32 s	3.7 s

. As shown in Table 10, the average computing time of the DLA-PSO method is the shortest in all the compared methods, verifying the best computational performance of the proposed DLA-PSO under these parameters.

5.2. Shadow/Nonshadow Contrast Effect

In this section, we show that shadow/nonshadow contrast may affect the performance of shadow detection. Shadow/nonshadow contrast is defined as:

$$R=\frac{I_{shadow}}{I_{sunlit}}$$

(24)

where $I_{shadow}$ and $I_{sunlit}$ represent the average brightness of the shadow and sunlit areas, respectively. The value of R will affect the performance of shadow detection. A large R value means that the difference between shadow and nonshadow is small, which makes shadow detection difficult. This study selects different shadow/nonshadow contrast images from the AISD dataset to explore the relationship between the contrast ratio (R) and the shadow-detection performance (F value). The result is shown in Figure 13.

It can be concluded from Figure 13 that, when the R value is in the range of 0.17~0.51, the F value remains around 0.9, and the shadow-detection performance stays at a high level. However, when R exceeds 0.51, F drops by 20% to around 0.75. In future experiments, the maximum shadow/nonshadow contrast should be set to 0.51, which can ensure the performance of the shadow detection at a high level.

5.3. Advantage and Limitation

In this study, multiple channels (i.e., H-I, S, I) were designed to capture the shadow characteristics comprehensively. The rationality of the H-I channel depends on its ability to strengthen the difference between the H and I channels and distinguish the objects with high hue (lawns, football fields, etc.) and the shadow regions from the image. The influence of the combination order of different channels is studied to improve the performance of shadow detection. The DLA-PSO method is proposed by combining the OTSU and PSO algorithms to calculate the threshold for determining shadow regions adaptively. The experimental results on different urban scenes prove that the proposed approach can achieve a good shadow-detection performance, without a large number of labeled samples. Traditional methods use unsupervised ways to achieve shadow detection, but an adaptive unsupervised method, proposed in this paper, shows a great improvement in shadow detection compared with them. Shadow-detection methods based on the CNN, U-Net, and Segnet frameworks have been highly recommended in recent years. Their advantage lies in the use of the supervised learning method to automatically learn the nonlinear characteristics of training samples so as to achieve a high accuracy of shadow detection. However, the effectiveness of deep-learning models depends on training samples, to a large extent, and the learning ability of shadow details is insufficient. The accuracy of the proposed method in this paper is slightly improved compared with the deep-learning method, but the robustness of the method is higher than the current deep-learning method (as illustrated in Figure 10). In conclusion, the proposed algorithm shows advantages in detection precision and computational efficiency compared with seven mainstream algorithms.

The proposed algorithm has some limitations. The learning factors (i.e., c₁ and c₂ in Formula (9)) in the DLA-PSO method should be manually specified by users. They affect the determination of the step size of the particle (i) to the direction of the $pbes{t}_i$ and the $gbes{t}^{k-1}$ and the performance of the DLA-PSO algorithm. Following common practice, c₁ and c₂ were fixed as constants, and their influence on the shadow-detection results was not investigated. The performance of the proposed algorithm is influenced by the fitness function. In this study, the interclass variance is set as the fitness function of the DLA-PSO algorithm. However, such a fitness function does not guarantee the best shadow detection performance in all situations. In future studies, other fitness functions may be adopted to promote the robustness of the proposed algorithm.

6. Conclusions

In this study, an adaptive unsupervised-shadow-detection approach for remote-sensing images, based on multichannel features, was developed. We designed multiple channels for shadow detection in accordance with the shadow characteristics in the HSI color space. The designed combination of multiple channels can capture the shadow characteristics comprehensively and can eliminate the interferences of high-hue and dark-colored ground objects (e.g., lawns, black roof, and soccer fields) in remote-sensing images. For the optimal threshold selection, a new DLA-PSO method is proposed to find the optimal threshold accurately and quickly. Local regions are optimized through small-area removal and the mathematical morphology operation. The experimental results on different urban scenes show that the proposed approach can detect shadow areas more accurately and efficiently, with the F index being 82.70% in the testing images. Moreover, the proposed method in this study has the highest accuracy of 97% and a superior performance, with the F value closing to 90%. Compared with other traditional and deep-learning methods from the qualitative and quantitative analyses, the superiority and stability of the proposed method in shadow detection are verified. However, the shadow-detection method proposed in this study is mainly based on the visible spectral features of aerial images. In future work, the addition of an infrared spectral band and the redesign of the shadow-detection channels can be considered. Furthermore, future work will focus on the model transferability of the proposed shadow-detection method. Remote-sensing images with different spatial resolutions or complex land-cover types should be applied to verify the robustness of the proposed DLA-PSO method. Shadow removal and image interpretation by incorporating the spectral and spatial information will be the focus of future research.