Calibration of Co-Located Identical PAR Sensors Using Wireless Sensor Networks and Characterization of the In Situ fPAR Variability in a Tropical Dry Forest
Abstract
:1. Introduction
2. Materials and Methods
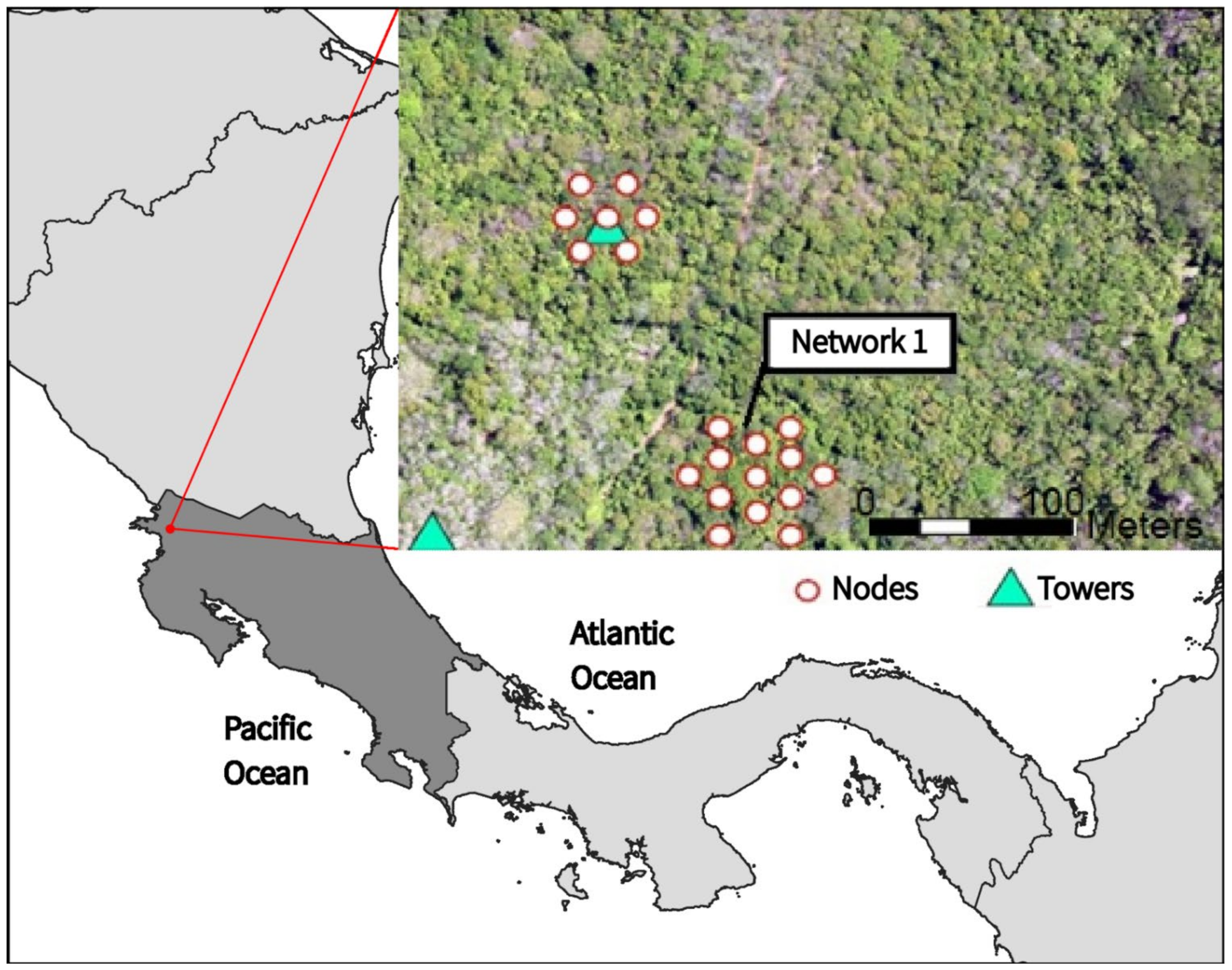
2.1. Study Site
2.2. Instrumentation
2.3. Calibration of PAR Sensors
2.4. Data Processing
2.5. Environemtal Contribution Data Analysis
2.6. Spatial Variability Analysis
3. Results
3.1. Sensor Calibration
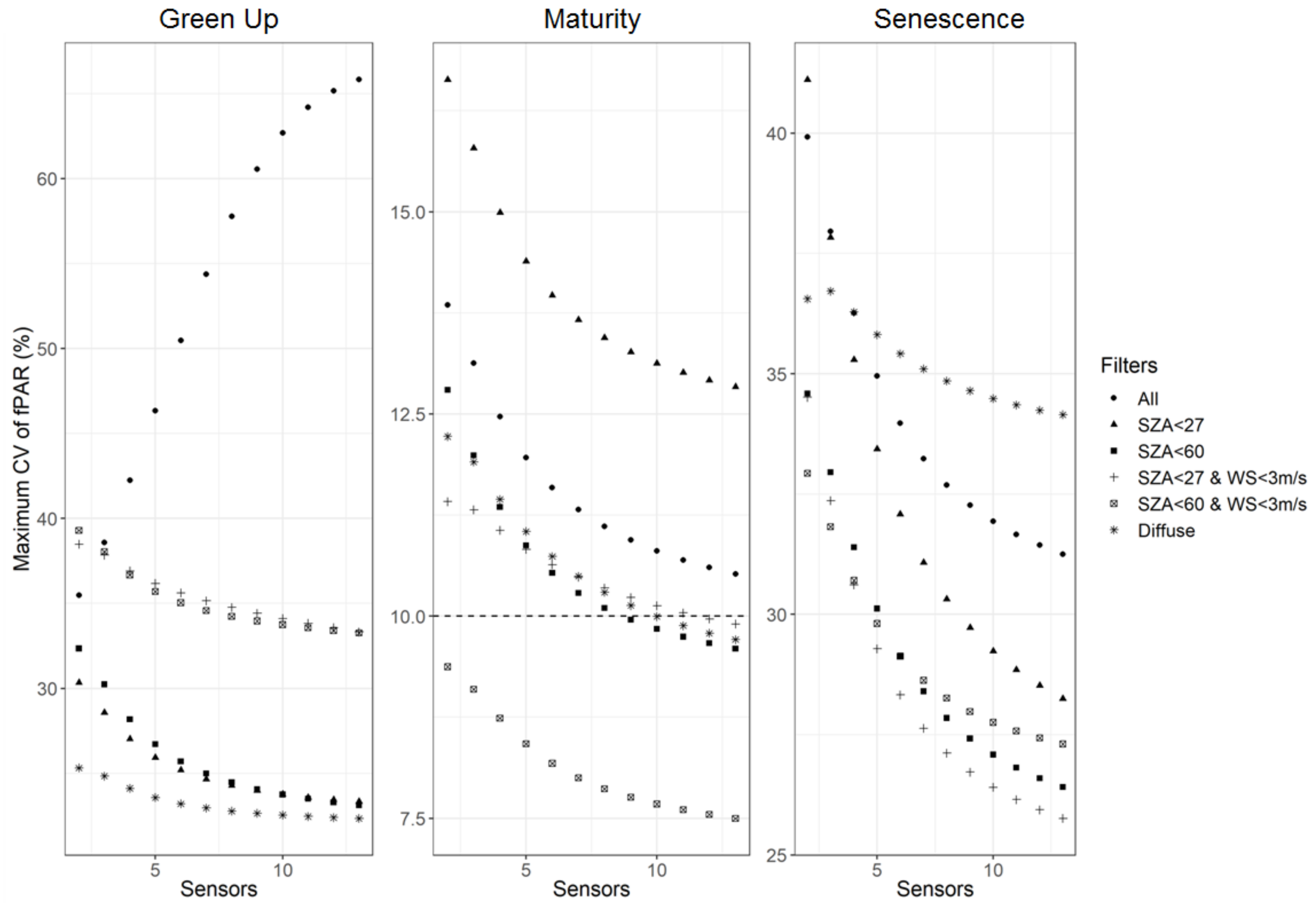
3.2. Spatial Variability Analysis
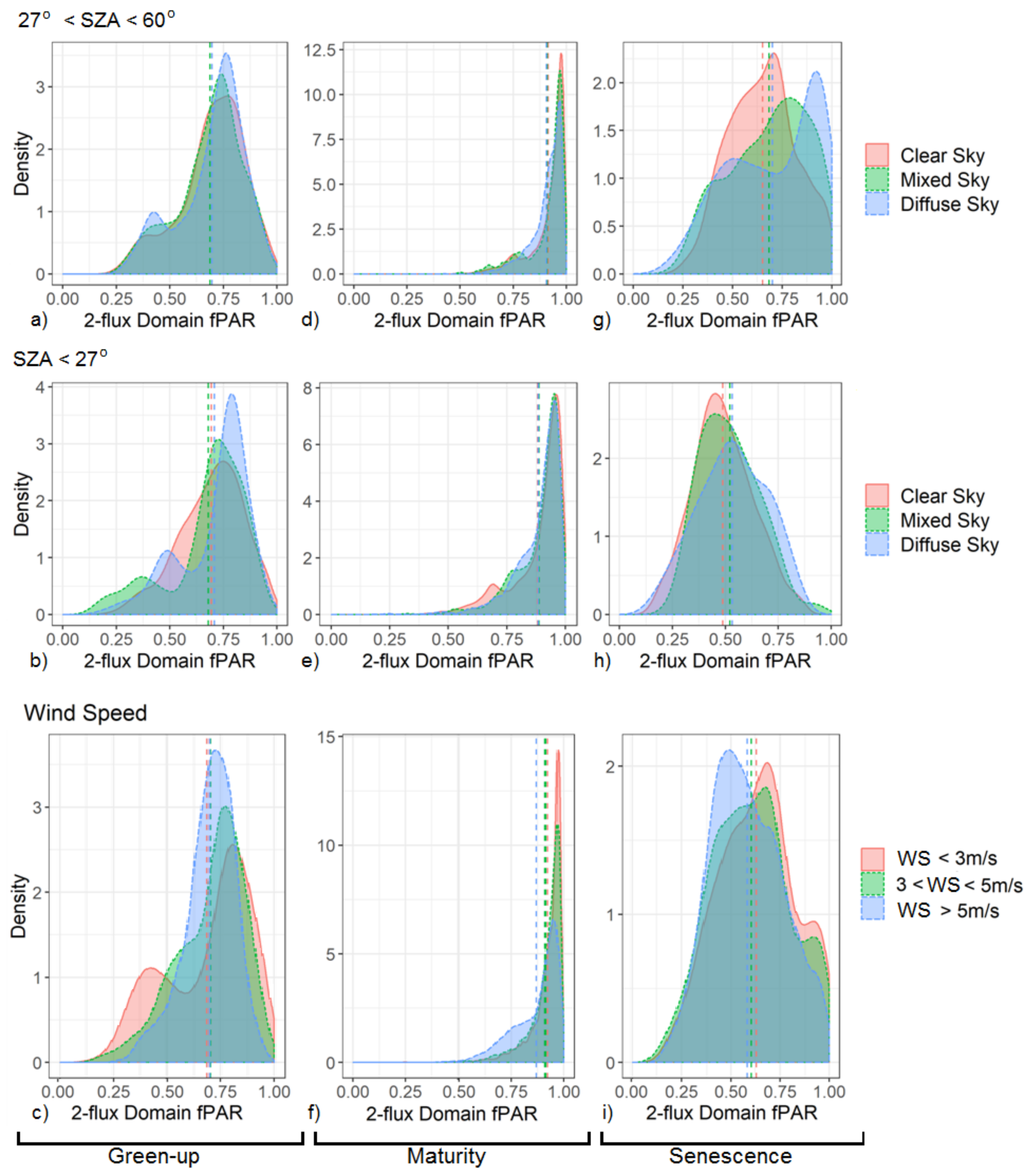
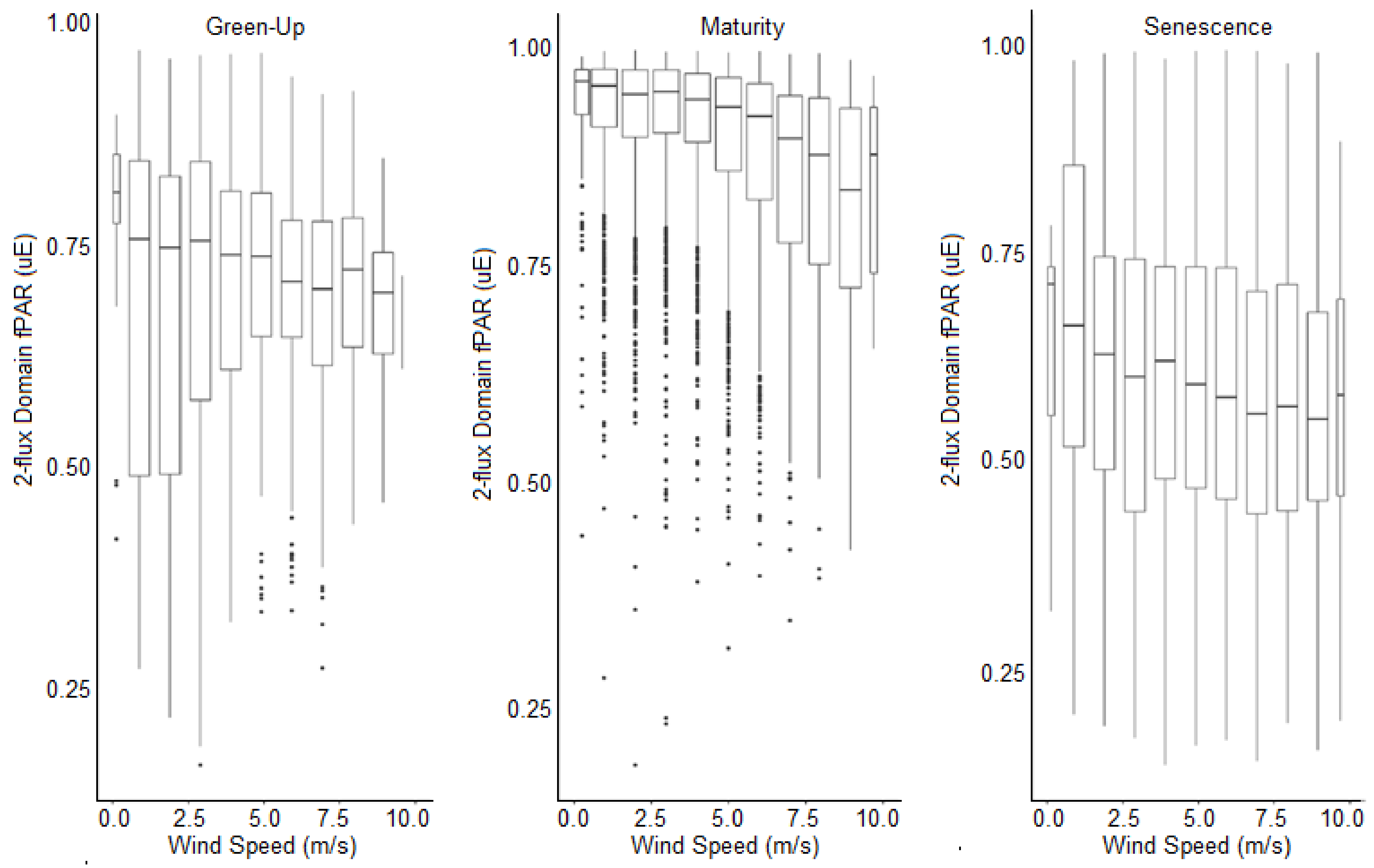
3.3. Variability Due to Environmental Factors by Phenophase
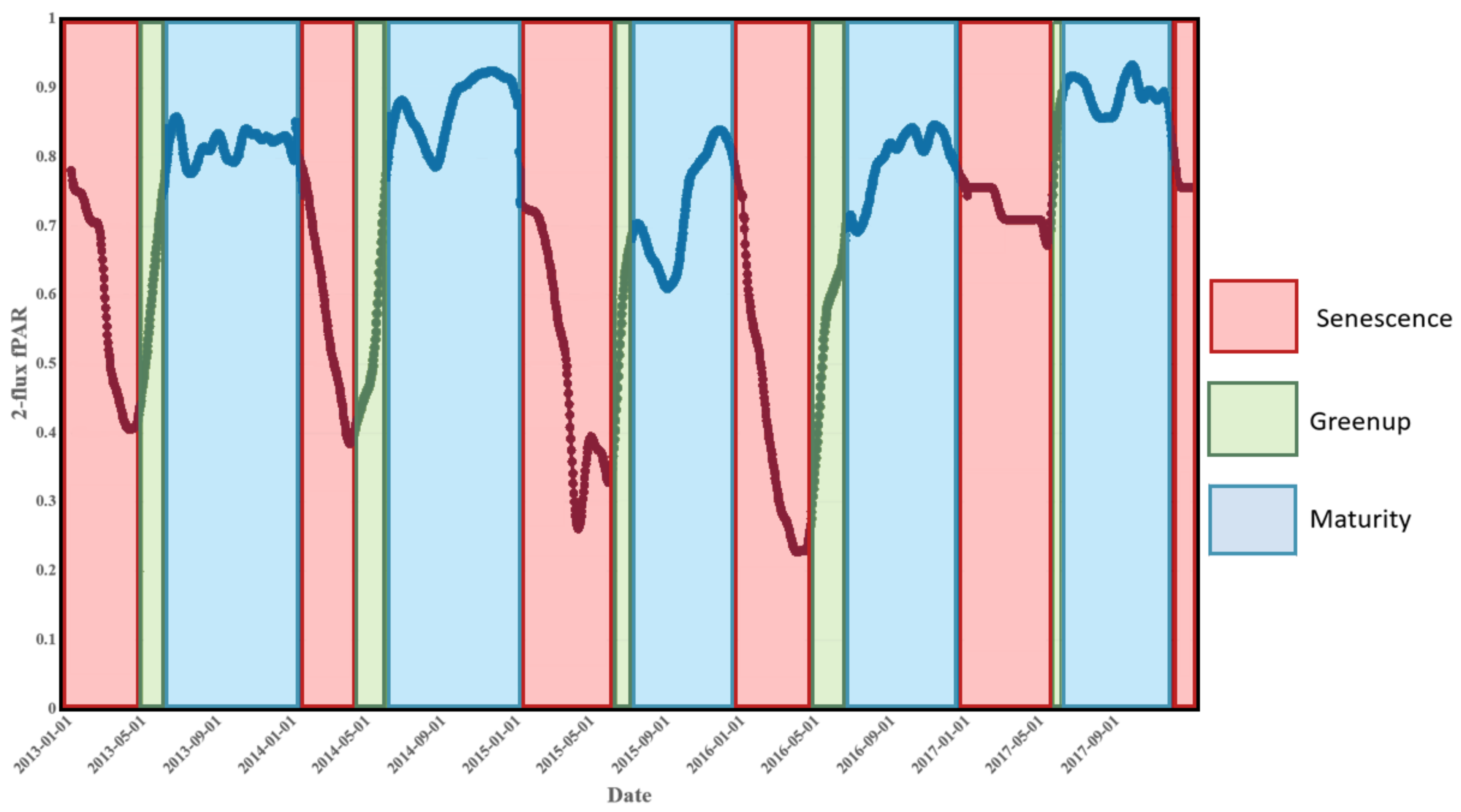
3.3.1. Green-Up
3.3.2. Maturity
3.3.3. Senescence
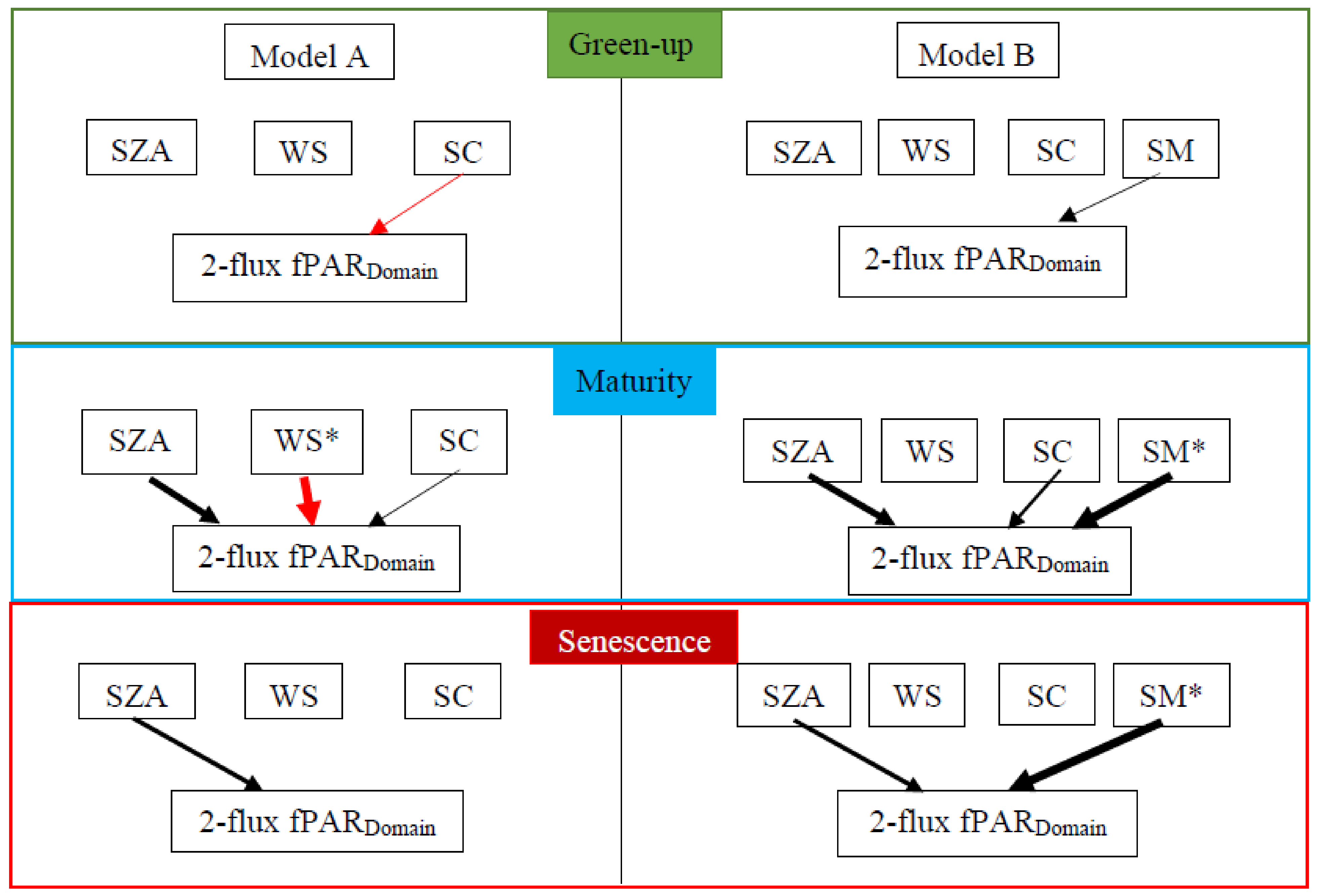
3.4. General Linear Mixed-Effect Models
4. Discussion
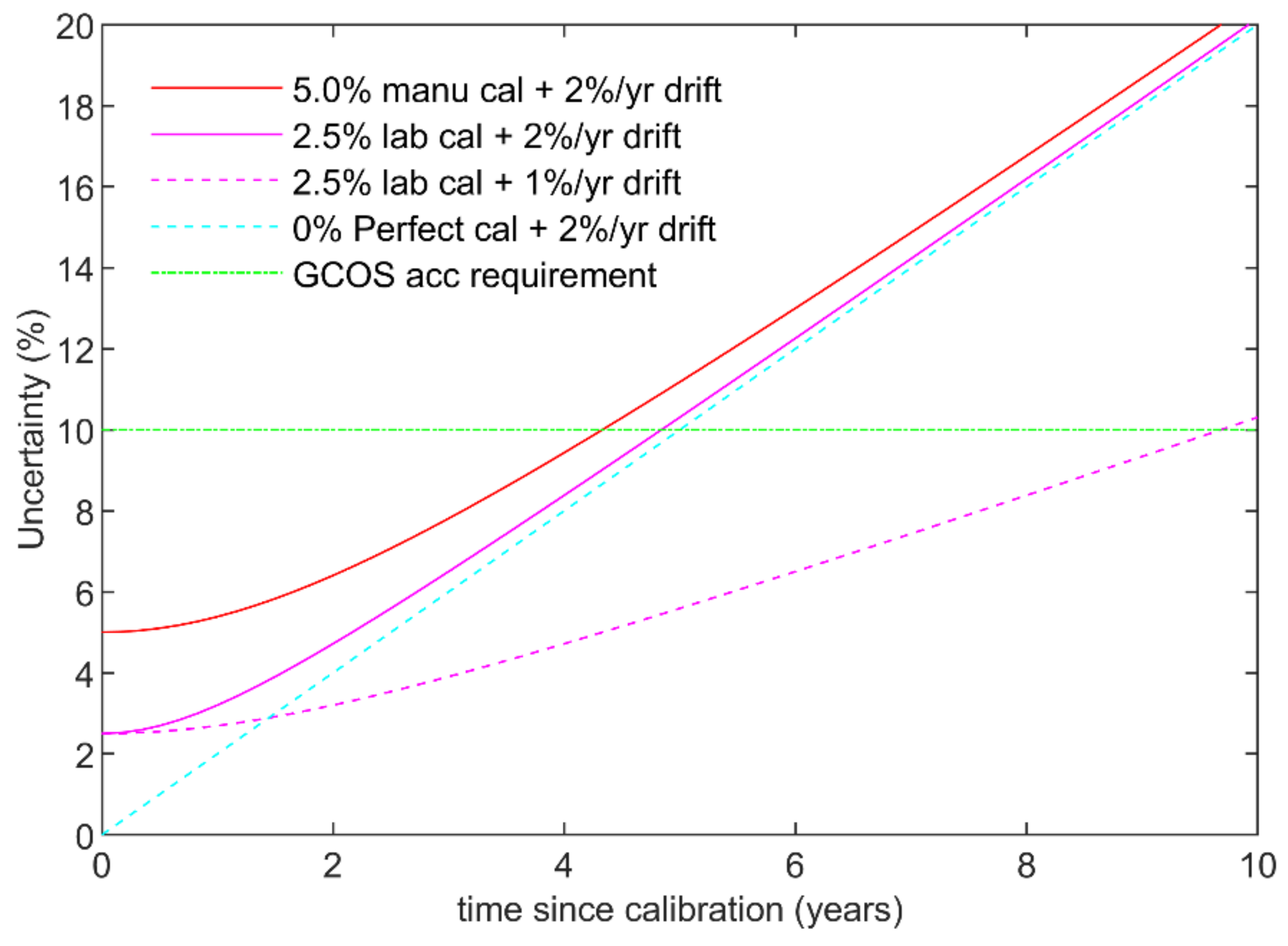
4.1. Calibration Considerations
4.2. Influence of Environmental Conditions on the 2-Flux fPAR GLME
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- McDowell, N.G.; Coops, N.C.; Beck, P.S.A.; Chambers, J.Q.; Gangodagamage, C.; Hicke, J.A.; Huang, C.; Kennedy, R.; Krofcheck, D.J.; Litvak, M.; et al. Global satellite monitoring of climate-induced vegetation disturbances. Trends Plant Sci. 2015, 20, 114–123. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Claverie, M.; Vermote, E.F.; Weiss, M.; Baret, F.; Hagolle, O.; Demarez, V. Validation of coarse spatial resolution LAI and FAPAR time series over cropland in southwest France. Remote Sens. Environ. 2013, 139, 216–230. [Google Scholar] [CrossRef]
- Gower, S.T.; Kucharik, C.J.; Norman, J.M. Direct and Indirect Estimation of Leaf Area Index, fAPAR, and Net Primary Production of Terrestrial Ecosystems. Remote Sens. Environ. 1999, 70, 29–51. [Google Scholar] [CrossRef]
- Myneni, R.; Ramakrishna, R.; Nemani, R.; Running, S. Estimation of global leaf area index and absorbed par using radiative transfer models. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1380–1393. [Google Scholar] [CrossRef] [Green Version]
- Myneni, R.B.; Knyazikhin, Y.; Privette, J.L.; Running, S.W.; Nemani, R.; Zhang, Y.; Tian, Y.; Wang, Y.; Morissette, J.T.; Glassy, J.; et al. MODIS. Leaf Area Index (LAI) And Fraction Of Photosynthetically Active Radiation Absorbed By Vegetation (FPAR) Product. Modis Atbd 1999, Version 4, 130. Available online: http://eospso.gsfc.nasa.gov/atbd/modistables.html (accessed on 1 September 2018).
- Li, W.; Fang, H. Estimation of direct, diffuse, and total FPARs from Landsat surface reflectance data and ground-based estimates over six FLUXNET sites. J. Geophys. Res. Biogeosci. 2015, 120, 96–112. [Google Scholar] [CrossRef]
- Gobron, N.; Pinty, B.; Aussedat, O.; Chen, J.M.; Cohen, W.B.; Fensholt, R.; Gond, V.; Huemmrich, K.F.; Lavergne, T.; Mélin, F.; et al. Evaluation of fraction of absorbed photosynthetically active radiation products for different canopy radiation transfer regimes: Methodology and results using Joint Research Center products derived from SeaWiFS against ground-based estimations. J. Geophys. Res. Earth Surf. 2006, 111, D13. [Google Scholar] [CrossRef]
- Thomas, V.; Finch, D.; McCaughey, J.; Noland, T.; Rich, L.; Treitz, P. Spatial modelling of the fraction of photosynthetically active radiation absorbed by a boreal mixedwood forest using a lidar–hyperspectral approach. Agric. For. Meteorol. 2006, 140, 287–307. [Google Scholar] [CrossRef]
- Chen, J. Canopy architecture and remote sensing of the fraction of photosynthetically active radiation absorbed by boreal conifer forests. IEEE Trans. Geosci. Remote Sens. 1996, 34, 1353–1368. [Google Scholar] [CrossRef]
- Widlowski, J.-L. On the bias of instantaneous FAPAR estimates in open-canopy forests. Agric. For. Meteorol. 2010, 150, 1501–1522. [Google Scholar] [CrossRef]
- Bondeau, A.; Kicklighter, D.W.; Kaduk, J. Model Intercomparison. Comparing global models of terrestrial net primary productivity (NPP): Importance of vegetation structure on seasonal NPP estimates. Glob. Chang. Biol. 1999, 5, 35–45. [Google Scholar] [CrossRef]
- Liu, R.; Sun, J.; Wang, J.; Li, X.; Yang, F.; Chen, P. Study of remote sensing based parameter uncertainty in production efficiency models state key laboratory of resources and environmental information systems. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 3303–3306. [Google Scholar]
- Madani, N.; Kimball, J.S.; Running, S.W. Improving Global Gross Primary Productivity Estimates by Computing Optimum Light Use Efficiencies Using Flux Tower Data. J. Geophys. Res. Biogeosci. 2017, 122, 2939–2951. [Google Scholar] [CrossRef]
- Zhang, R.; Zhou, Y.; Luo, H.; Wang, F.; Wang, S. Estimation and Analysis of Spatiotemporal Dynamics of the Net Primary Productivity Integrating Efficiency Model with Process Model in Karst Area. Remote Sens. 2017, 9, 477. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Q.; Zhao, J.; Zhu, Z.; Zhang, H.; Zhang, Z.; Guo, X.; Bi, Y.; Sun, L. Remotely Sensed Estimation of Net Primary Productivity (NPP) and Its Spatial and Temporal Variations in the Greater Khingan Mountain Region, China. Sustainability 2017, 9, 1213. [Google Scholar] [CrossRef] [Green Version]
- Nightingale, J.; Schaepman-Strub, G.; Nickeson, J. Assessing satellite-derived land product quality for Earth system science applications: Overview of the CEOS LPV sub-group. In Proceedings of the Earth Observation for Land-Atmosphere Interaction Science Conference, Rome, Italy, 3–5 November 2010. [Google Scholar]
- Carrara, A.; Kolari, P.; De Beeck, M.O.; Arriga, N.; Berveiller, D.; Dengel, S.; Ibrom, A.; Merbold, L.; Rebmann, C.; Sabbatini, S.; et al. Radiation measurements at ICOS ecosystem stations. Int. Agrophys. 2018, 32, 589–605. [Google Scholar] [CrossRef]
- D’Odorico, P.; Gonsamo, A.; Pinty, B.; Gobron, N.; Coops, N.; Mendez, E.; Schaepman, M.E. Intercomparison of fraction of absorbed photosynthetically active radiation products derived from satellite data over Europe. Remote Sens. Environ. 2014, 142, 141–154. [Google Scholar] [CrossRef]
- Majasalmi, T.; Stenberg, P.; Rautiainen, M. Comparison of ground and satellite-based methods for estimating stand-level fPAR in a boreal forest. Agric. For. Meteorol. 2017, 232, 422–432. [Google Scholar] [CrossRef]
- Nestola, E.; Sánchez-Zapero, J.; Latorre, C.; Mazzenga, F.; Matteucci, G.; Calfapietra, C.; Camacho, F. Validation of PROBA-V GEOV1 and MODIS C5 & C6 fAPAR Products in a Deciduous Beech Forest Site in Italy. Remote Sens. 2017, 9, 126. [Google Scholar] [CrossRef] [Green Version]
- Senna, M.C.A.; Costa, M.H.; Shimabukuro, Y.E. Fraction of photosynthetically active radiation absorbed by Amazon tropical forest: A comparison of field measurements, modeling, and remote sensing. J. Geophys. Res. Earth Surf. 2005, 110, G01008. [Google Scholar] [CrossRef] [Green Version]
- Stenberg, P.; Mõttus, M.; Rautiainen, M. Photon recollision probability in modelling the radiation regime of canopies—A review. Remote Sens. Environ. 2016, 183, 98–108. [Google Scholar] [CrossRef]
- Van Der Zande, D.; Stuckens, J.; Verstraeten, W.W.; Muys, B.; Coppin, P. Assessment of Light Environment Variability in Broadleaved Forest Canopies Using Terrestrial Laser Scanning. Remote Sens. 2010, 2, 1564–1574. [Google Scholar] [CrossRef] [Green Version]
- Putzenlechner, B.; Marzahn, P.; Kiese, R.; Ludwig, R.; Sanchez-Azofeifa, A. Assessing the variability and uncertainty of two-flux FAPAR measurements in a conifer-dominated forest. Agric. For. Meteorol. 2018, 264, 149–163. [Google Scholar] [CrossRef]
- Steinberg, D.; Goetz, S.; Hyer, E. Validation of MODIS. F/sub PAR/products in boreal forests of Alaska. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1818–1828. [Google Scholar] [CrossRef]
- Li, W.; Weiss, M.; Waldner, F.; Defourny, P.; Demarez, V.; Morin, D.; Hagolle, O.; Baret, F. A Generic Algorithm to Estimate LAI, FAPAR and FCOVER Variables from SPOT4_HRVIR and Landsat Sensors: Evaluation of the Consistency and Comparison with Ground Measurements. Remote Sens. 2015, 7, 15494–15516. [Google Scholar] [CrossRef] [Green Version]
- Fensholt, R.; Sandholt, I.; Rasmussen, M.S. Evaluation of MODIS LAI, fAPAR and the relation between fAPAR and NDVI in a semi-arid environment using in situ measurements. Remote Sens. Environ. 2004, 91, 490–507. [Google Scholar] [CrossRef]
- Pinty, B.; Jung, M.; Kaminski, T.; Lavergne, T.; Mund, M.; Plummer, S.; Thomas, E.; Widlowski, J.-L. Evaluation of the JRC-TIP 0.01° products over a mid-latitude deciduous forest site. Remote Sens. Environ. 2011, 115, 3567–3581. [Google Scholar] [CrossRef]
- Ahl, D.E.; Gower, S.T.; Burrows, S.N.; Shabanov, N.V.; Myneni, R.; Knyazikhin, Y. Monitoring spring canopy phenology of a deciduous broadleaf forest using MODIS. Remote Sens. Environ. 2006, 104, 88–95. [Google Scholar] [CrossRef] [Green Version]
- Pickett-Heaps, C.A.; Canadell, J.G.; Briggs, P.R.; Gobron, N.; Haverd, V.; Paget, M.; Pinty, B.; Raupach, M.R. Evaluation of six satellite-derived Fraction of Absorbed Photosynthetic Active Radiation (FAPAR) products across the Australian continent. Remote Sens. Environ. 2014, 140, 241–256. [Google Scholar] [CrossRef]
- Gu, L.; Baldocchi, D.; Verma, S.B.; Black, T.A.; Vesala, T.; Falge, E.M.; Dowty, P.R. Advantages of diffuse radiation for terrestrial ecosystem productivity. J. Geophys. Res. Earth Surf. 2002, 107, ACL 2-1–ACL 2-23. [Google Scholar] [CrossRef] [Green Version]
- Leuchner, M.; Hertel, C.; Menzel, A. Spatial variability of photosynthetically active radiation in European beech and Norway spruce. Agric. For. Meteorol. 2011, 151, 1226–1232. [Google Scholar] [CrossRef]
- Shabanov, N.; Wang, Y.; Buermann, W.; Dong, J.; Hoffman, S.; Smith, G.; Tian, Y.; Knyazikhin, Y.; Myneni, R. Effect of foliage spatial heterogeneity in the MODIS LAI and FPAR algorithm over broadleaf forests. Remote Sens. Environ. 2003, 85, 410–423. [Google Scholar] [CrossRef] [Green Version]
- Portillo-Quintero, C.; Sánchez-Azofeifa, G. Extent and conservation of tropical dry forests in the Americas. Biol. Conserv. 2010, 143, 144–155. [Google Scholar] [CrossRef]
- Pastorello, G.Z.; Sanchez-Azofeifa, G.A.; Nascimento, M.A. Enviro-Net: A Network of Ground-based Sensors for Tropical Dry Forests in the Americas. Sensors 2011, 11, 6454–6479. [Google Scholar] [CrossRef] [PubMed]
- Rawat, P.; Singh, K.D.; Chaouchi, H.; Bonnin, J.M. Wireless sensor networks: A survey on recent developments and potential synergies. J. Supercomput. 2014, 68, 1–48. [Google Scholar] [CrossRef]
- Sanchez-Azofeifa, A.; Guzmán, J.A.; Campos, C.A.; Castro, S.; Garcia-Millan, V.; Nightingale, J.; Rankine, C. Twenty-first century remote sensing technologies are revolutionizing the study of tropical forests. Biotropica 2017, 49, 604–619. [Google Scholar] [CrossRef]
- S’nchez-Azofeifa, G.A.; Rankine, C.; Santo, M.M.D.E.; Fatland, R.; Garcia, M. Wireless Sensing Networks for Environmental Monitoring: Two Case Studies from Tropical Forests. In Proceedings of the 2011 IEEE Seventh International Conference on eScience, Stockholm, Sweden, 5–8 December 2011; pp. 70–76. [Google Scholar] [CrossRef]
- World Meteorological Organization. Systematic Observation Requirements for Satellite-Based Data Products for Climate 2011 Update Supplemental Details to the Satellite-Based Component of the Implementation Plan; WMO: Geneva, Swizerland, 2011. [Google Scholar]
- Janzen, D.H. Costa Rica’s Area de Conservación Guanacaste: A long march to survival through non-damaging biodevelopment. Biodiversity 2000, 1, 7–20. [Google Scholar] [CrossRef]
- Janzen, D.H.; Hallwachs, W. Biodiversity Conservation History and Future in Costa Rica: The Case of Área de Conservación Guanacaste (ACG). Costa Rican Ecosyst. 2016, 290, 300. [Google Scholar]
- Kalacska, M.; Sanchez-Azofeifa, A.; Calvo-Alvarado, J.C.; Quesada, M.; Rivard, B.; Janzen, D. Species composition, similarity and diversity in three successional stages of a seasonally dry tropical forest. For. Ecol. Manag. 2004, 200, 227–247. [Google Scholar] [CrossRef]
- Sanchez-Azofeifa, G.A.; Kalacska, M.; Quesada, M.; Calvo-Alvarado, J.C.; Nassar, J.M.; Rodriguez, J.P. Need for Integrated Research for a Sustainable Future in Tropical Dry Forests. Conserv. Biol. 2005, 19, 285–286. [Google Scholar] [CrossRef]
- Rankine, C.J. Monitoring Seasonal and Secondary Succession Processes in Deciduous Forests Using Near-Surface Optical Remote Sensing and Wireless Sensor Networks. Ph.D. Thesis, University of Alberta, Edmonton, AB, Canada, 2016; p. 167. [Google Scholar] [CrossRef]
- Younis, M.; Akkaya, K. Strategies and techniques for node placement in wireless sensor networks: A survey. Ad Hoc Netw. 2007, 6, 621–655. [Google Scholar] [CrossRef]
- Quantum Sensor Models SQ-100 and SQ-300 Series (Including S.S. Models); Apogee Instruments Rev: Logan, UT, USA, 2019; 20p.
- Apogee Quantum Sensor Calibration Certificate; Apogee Instruments: Logan, UT, USA, 2019.
- JCGM Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement (Évaluation des Données de Mesure—Guide Pour l’Expression de l’Incertitude de Mesure). 2008. Available online: https://www.bipm.org/documents/20126/2071204/JCGM_100_2008_E.pdf/cb0ef43f-baa5-11cf-3f85-4dcd86f77bd6 (accessed on 1 September 2018).
- Walter, I.A.; Allen, R.; Elliot, R.; Itenfisu, D.; Brown, P.; Jensen, M.E.; Mecham, B.; Howell, T.A.; Snyder, R.; Eching, S.; et al. The asce standardized reference evapotranspiration equation environmental and water resources institute of the American society of civil engineers standardization of reference evapotranspiration task committee. Am. Soc. Civ. Eng. 2002, 1, 1–51. [Google Scholar]
- Lange, M.; Doktor, D. phenex: Auxiliary Functions for Phenological Data Analysis. R Package Version 1.4-5. 2017. Available online: https://cran.r-project.org/web/packages/phenex/index.html (accessed on 1 September 2018).
- Cliff, N. Dominance statistics: Ordinal analyses to answer ordinal questions. Psychol. Bull. 1993, 114, 494. [Google Scholar] [CrossRef]
- Chadwick, R.; Good, P.; Martin, G.; Rowell, D.P. Large rainfall changes consistently projected over substantial areas of tropical land. Nat. Clim. Chang. 2015, 6, 177–181. [Google Scholar] [CrossRef]
- Kalacska, M.; Calvo-Alvarado, J.C.; Sanchez-Azofeifa, G.A. Calibration and assessment of seasonal changes in leaf area index of a tropical dry forest in different stages of succession. Tree Physiol. 2005, 25, 733–744. [Google Scholar] [CrossRef] [Green Version]
- Zelazowski, P.; Malhi, Y.; Huntingford, C.; Sitch, S.; Fisher, J. Changes in the potential distribution of humid tropical forests on a warmer planet. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2011, 369, 137–160. [Google Scholar] [CrossRef]
- Wang, H. Extending the Linear Model with R: Generalized Linear, Mixed Effects and Nonparametric Regression Models Edited by Faraway J. J. Biom. 2006, 62, 1278. [Google Scholar] [CrossRef]
- Majasalmi, T. Estimation of Leaf Area Index and the Fraction of Absorbed Photosynthetically Active Radiation in a Boreal; University of Helsinki: Helsinki, Finland, 2015; ISBN 9789516514638. [Google Scholar]
- Chazdon, R.L.; Fetcher, N. Photosynthetic Light Environments in a Lowland Tropical Rain Forest in Costa Rica. J. Ecol. 1984, 72, 553–564. [Google Scholar] [CrossRef]
- Vierling, L.A.; Wessman, C.A. Photosynthetically active radiation heterogeneity within a monodominant Congolese rain forest canopy. Agric. For. Meteorol. 2000, 103, 265–278. [Google Scholar] [CrossRef]
- Asner, G.P.; Wessman, C.A. Scaling PAR absorption from the leaf to landscape level in spatially heterogeneous ecosystems. Ecol. Model. 1997, 103, 81–97. [Google Scholar] [CrossRef]
- Verhoef, W. Light scattering by leaf layers with application to canopy reflectance modeling: The SAIL model. Remote Sens. Environ. 1984, 16, 125–141. [Google Scholar] [CrossRef] [Green Version]
- Campos, F.A. A Synthesis of Long-Term Environmental Change in Santa Rosa, Costa Rica. In Primate Life Histories, Sex Roles, and Adaptability; Springer: Cham, Switzerland, 2018; pp. 331–358. [Google Scholar] [CrossRef]
- Castillo-Núñez, M.; Sánchez-Azofeifa, G.A.; Croitoru, A.; Rivard, B.; Calvo-Alvarado, J.; Dubayah, R.O. Delineation of secondary succession mechanisms for tropical dry forests using LiDAR. Remote Sens. Environ. 2011, 115, 2217–2231. [Google Scholar] [CrossRef]
- Janzen, D.H. Tropical dry forests. Biodiversity 1988, 15, 130–137. [Google Scholar]
- Sanchez-Azofeifa, G.A.; Quesada, M.; Rodriguez, J.P.; Nassar, J.M.; Stoner, K.E.; Castillo, A.; Garvin, T.; Zent, E.L.; Calvo-Alvarado, J.C.; Kalacska, M.E.; et al. Research Priorities for Neotropical Dry Forests. Biotropica 2005, 37, 477–485. [Google Scholar] [CrossRef]
- Hwang, T.; Gholizadeh, H.; Sims, D.A.; Novick, K.A.; Brzostek, E.R.; Phillips, R.P.; Roman, D.T.; Robeson, S.; Rahman, A.F. Capturing species-level drought responses in a temperate deciduous forest using ratios of photochemical reflectance indices between sunlit and shaded canopies. Remote Sens. Environ. 2017, 199, 350–359. [Google Scholar] [CrossRef]
- Sánchez-Azofeifa, G.A.; Kalácska, M.; Espírito-Santo, M.M.D.; Fernandes, G.W.; Schnitzer, S. Tropical dry forest succession and the contribution of lianas to wood area index (WAI). For. Ecol. Manag. 2009, 258, 941–948. [Google Scholar] [CrossRef]
- Cai, Z.-Q.; Schnitzer, S.A.; Bongers, F. Seasonal differences in leaf-level physiology give lianas a competitive advantage over trees in a tropical seasonal forest. Oecologia 2009, 161, 25–33. [Google Scholar] [CrossRef] [Green Version]

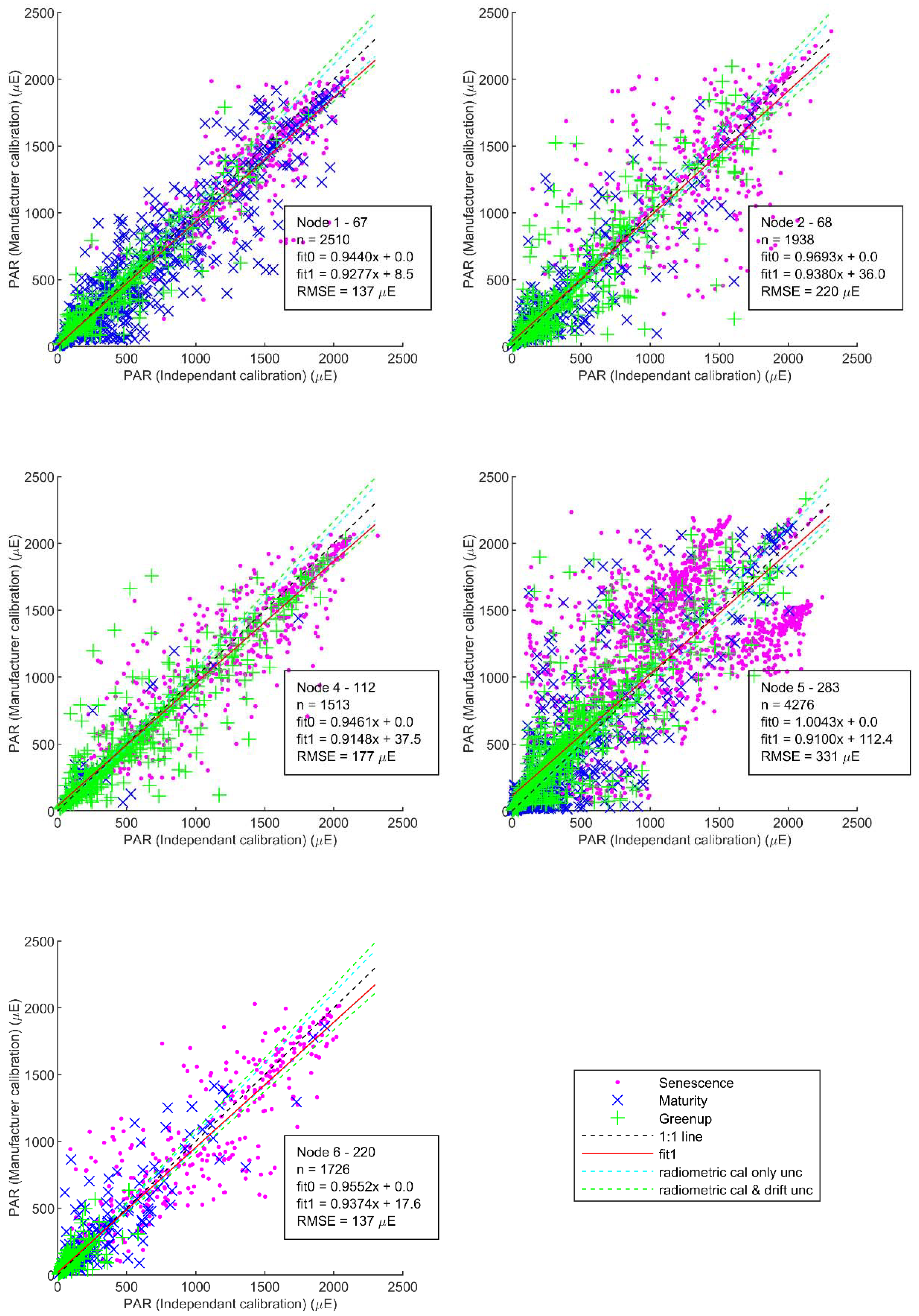
| Node [Sensor #] | Time Series Analysed | Fit0 Gradient | Fit1 Gradient |
|---|---|---|---|
| 1 [#67] | Apr 2015–Nov 2015 | 0.9440 (5.6%) | 0.9277 (7.2%) |
| 2 [#68] | Apr 2015–Nov 2015 | 0.9693 (3.1%) | 0.9380 (6.2%) |
| 4 [#112] | Apr 2015–Apr 2016 | 0.9461 (5.4%) | 0.9148 (8.5%) |
| 5 [#283] | May 2015–Jan 2016 | 1.0043 (−0.4%) | 0.9100 (9.0%) |
| 6 [#220] | May 2015–Mar 2016 | 0.9552 (4.5%) | 0.9374 (6.3%) |
| Uncertainty Contribution | Time Since Installation | Value (k = 1) |
|---|---|---|
| Resident sensor calibration uncertainty umanu cal | - | 5% |
| Resident sensor drift umanu drift | 3 years @ 2% per year | 6% |
| Temporary sensor calibration uncertainty uNPL cal | - | 2.5% |
| Temporary sensor drift uNPL drift | 0.5 years @ 2% per year | 1% |
| Total (as per Equation (2)) | 8.3% |
| Variable (s) | Classification Scheme | Selection Scheme |
|---|---|---|
| Illumination (SZA and SC) | SZA < 27° 27° < SZA < 60° Clear Sky: iPAR > 1100 µE Mixed Sky: 900 µE < iPAR < 1100 µE Diffuse Sky: iPAR < 900 µE | WS < 3 m/s |
| Wind speed (WS) | WS < 3 m/s 3 m/s < WS < 5 m/s WS > 5 m/s | Diffuse sky (iPAR < 900 µE) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sanchez-Azofeifa, A.; Sharp, I.; Green, P.D.; Nightingale, J. Calibration of Co-Located Identical PAR Sensors Using Wireless Sensor Networks and Characterization of the In Situ fPAR Variability in a Tropical Dry Forest. Remote Sens. 2022, 14, 2752. https://doi.org/10.3390/rs14122752
Sanchez-Azofeifa A, Sharp I, Green PD, Nightingale J. Calibration of Co-Located Identical PAR Sensors Using Wireless Sensor Networks and Characterization of the In Situ fPAR Variability in a Tropical Dry Forest. Remote Sensing. 2022; 14(12):2752. https://doi.org/10.3390/rs14122752
Chicago/Turabian StyleSanchez-Azofeifa, Arturo, Iain Sharp, Paul D. Green, and Joanne Nightingale. 2022. "Calibration of Co-Located Identical PAR Sensors Using Wireless Sensor Networks and Characterization of the In Situ fPAR Variability in a Tropical Dry Forest" Remote Sensing 14, no. 12: 2752. https://doi.org/10.3390/rs14122752
APA StyleSanchez-Azofeifa, A., Sharp, I., Green, P. D., & Nightingale, J. (2022). Calibration of Co-Located Identical PAR Sensors Using Wireless Sensor Networks and Characterization of the In Situ fPAR Variability in a Tropical Dry Forest. Remote Sensing, 14(12), 2752. https://doi.org/10.3390/rs14122752







