Abstract
Rainfall is the main factor that induces debris flow. Satellite rainfall products provide a new source of data in terms of debris flow-triggering conditions to overcome the lack of rainfall data coverage from ground-based rainfall gauges in large-scale mountainous regions. In this study, the applicability of four satellite rainfall products (CMORPH, GPM, MSWEP, and PERSIANN) in the Hengduan Mountain region (HMR) was evaluated with reference to ground observation data from 2000 to 2020. The critical rainfall and rainfall thresholds under different rainfall patterns and warning levels that trigger debris flows were analyzed according to the empirical cumulative distribution function (ECDF) and cumulative probability. The results showed that CMORPH (comprehensive indicator score (CI = 0.72) and GPM (CI = 0.70) performed better in the simulation of daily rainfall sequence consistency and extreme rainfall conditions in the study area. CMORPH also had the highest reconstruction rate for correctly capturing rainfall events that triggered debris flows, with a value of 89%. Approximately half of the rainfall patterns that cause debris flows are antecedent-effective-rainfall-dominated. Both intraday-rainfall-dominated and intraday-antecedent-rainfall-balanced patterns were below 30%. There were evident differences in the critical rainfall for different rainfall patterns under the same warning level. By comparing the results of previous studies on rainfall thresholds, it is believed that the results of this study confirm the application of satellite rainfall products; in addition, the calculated rainfall thresholds can provide a reference for the early warning of debris flows in the HMR. In general, this work is of great significance to the prediction and early warning of debris flow hazards.
1. Introduction
Debris flows are significant components of many major natural disasters, causing serious casualties and damage to regional public and private property. Rainfall is generally considered one of the most critical factors in debris flows [1,2,3]. The occurrence of regional rainfall leads to an unstable force balance on hillsides, which increases river erosion and triggers debris flows as the intensity of rainfall increases [4]. Revealing the relationship between rainfall conditions and debris flow is of great significance to the mechanisms of debris flow, disaster prediction, and early warning.
Determining the rainfall conditions of debris flows in the form of rainfall thresholds is a common tool for analyzing the response of debris flows to rainfall [5]. These critical rainfall conditions are described using different parameters [6,7]. The parameters commonly used in earlier studies to describe the critical rainfall conditions of debris flows are rainfall intensity [8,9], rainfall duration [10,11], cumulative rainfall for a given duration [12], daily rainfall, and antecedent rainfall index [13,14]. Guuzzetti et al. [15] conducted an extensive review of the international literature and stated that for defining rainfall thresholds, physically based (process-based, conceptual thresholds) or empirical (historical, statistical thresholds) approaches can be used. Physically based debris flow rainfall threshold models have good performance, but this requires accurate hydrological and geotechnical information [16]. It can be well applied in specific debris flow trenches or on small scales, but it is less feasible on large scales [17]. Based on the rainfall information of the historical debris flow time, the empirical method can be used to determine the rainfall threshold using statistical methods according to the conditions that lead to the occurrence of debris flow; thus, it has been widely used [6,7,9,10,12,13,15,18,19,20,21,22,23,24].
Rainfall gauge observations are typically used to define the rainfall threshold of debris flows. However, in mountainous areas where debris flows are frequent, there is a lack of comprehensive rainfall gauge monitoring networks owing to space limitations. Therefore, it is not possible to use data based on ground stations to comprehensively monitor the time and location of debris flow [20,25]. In the absence of rainfall gauges and the uneven distribution of rainfall data, satellite or radar-measured rainfall product data may be a better choice than an interpolation method with large uncertainties for calculating rainfall [7,26]. In recent years, satellite rainfall products have become viable sources of rainfall data for real-time rainfall field changes. International scholars have also conducted a series of analyses of different areas of satellite rainfall products [27,28,29], applications at different scales [30], and extreme precipitation [31,32,33]. Recently, satellite-based rainfall products have also greatly supported the study of rainfall thresholds for landslides and debris flow. For example, Hong et al. [34] evaluated the potential of a real-time NASA TRMM-based multi-satellite precipitation analysis (TMPA) system. It is a starting point for early warning systems for rainfall-triggered landslides in combination with TRMM. Nikolopoulos et al. [25] presented an intercomparison among satellite-based precipitation products and observed large differences between debris flow event-based rainfall characteristics derived from rainfall gauge and satellite-based estimates, revealing considerable inter-product variability in debris flow-triggering rainfall characteristics. Kirschbaum and Stanley [35] developed a landslide hazard assessment for a situational awareness model based on the Global Precipitation Measurement (GPM) mission precipitation datasets. He et al. [36] defined four groups of rainfall thresholds at different quantile levels of quantile regression for landslides in China based on the satellite precipitation product produced by the National Oceanic and Atmospheric Administration (NOAA) Climate Prediction Center Morphing technique (CMORPH). Jia et al. [37] evaluated the performance of satellite-based rainfall data (CMORPH, TMPA, precipitation estimation from remotely sensed information using artificial neural networks (PERSIANN), and multi-source weighted-ensemble precipitation (MSWEP) for global rainfall-induced landslide warnings. Wang et al. [38] confirmed the ability of the GPM to define rainfall conditions for triggering hydro-morphological processes and acknowledged the potential underestimation and/or bias that characterize any satellite rainfall products.
In the Hengduan Mountain region (HMR), rainfall-induced debris flows are a widespread and persistent hazard owing to diverse debris flow conditioning factors, such as varying climates, complex terrains, and active geological movements [39]. Previous studies have analyzed the rainfall triggering conditions of debris flow gullies (such as Jiangjia Gully, Yunnan [40,41,42,43,44]) and areas with high debris flow susceptibility caused by tectonic movements, such as the Wenchuan earthquake area [45,46,47], Dazhou, Sichuan [48], and the Anning River–Zemu River Fault Zone [49] in the study area. The method for calculating rainfall thresholds also varies with the scale of the study area. Specifically, Zhang et al. [43] presented a physics-based model validated in Jiangjia Gully to derive the intensity–duration (I-D) curve by analyzing the stability of an unsaturated soil mass. Long et al. [41] considered that the density of debris flow is used as the control factor to fit the rainfall threshold curves, and an equation considering the factors of loose solid sources and runoff has been adopted to calculate the density of debris flow in the Jiangjia Gully located in Yunnan Province, China. Guo et al. [40] determined the debris flow-triggering threshold by considering antecedent rainfall collected by nine siphon rain gauges through a case study in Jiangjia Ravine, Yunnan, China. Zhou and Tang [45] presented 11 rainfall events that induced debris flows that occurred between 2008 and 2012 after the Wenchuan earthquake, and data from the Mayiping rainfall gauge were used as the main data source. Guo et al. [47] explored the local I-D relationship based on 252 post-earthquake debris flows and rainfall data for 226 stations collected from the Meteorological Bureau of Sichuan Province. In the study of the rainfall conditions of debris flow in the HMR, rainfall data from gauge stations are the main source of rainfall threshold data for debris flow, and a few studies have directly used satellite rainfall data for application. For example, Liu et al. [39] analyzed the geological and topographical variations in effective rainfall for debris flow occurrence from a large-scale perspective based on TRMM satellite rainfall data. However, there are some uncertainties in the application of satellite rainfall data because of the spatial heterogeneity of extreme rainfall modeling [50], especially in mountainous areas [51]. There is a lack of applicability assessment of satellite rainfall products in the HMR when applied to the analysis of debris flow rainfall conditions. In addition, in terms of rainfall triggering conditions of debris flow, the rainfall events that trigger debris flow are mainly selected for empirical statistical analysis in this area, whereas the influence of different rainfall patterns on debris flow is ignored. However, clarifying the impact of rainfall processes on debris flow initiation and the corresponding critical rainfall conditions associated with different rainfall processes are urgent issues to be considered [49].
This study evaluated the application of four state-of-the-art satellite rainfall products (CMORPH, GPM, MSWEP, and PERSIANN) with higher resolution in HMR by evaluating the consistency of a daily series and extreme precipitation based on daily precipitation data from ground stations from 2000 to 2020. Rainfall patterns were categorized according to the relative contributions of both cumulative effective rainfall and daily rainfall to debris flow occurrence. The critical rainfall conditions and empirical cumulative effective rainfall—rainfall duration (E-D) thresholds of different rainfall patterns were calculated under different warning levels, which were defined according to the empirical cumulative distribution function (ECDF) and cumulative probability. The possibility of their application in debris flow warnings are discussed accordingly.
2. Materials and Methods
2.1. Study Area
The Hengduan Mountain region includes the Hengduan Mountains and adjacent mountainous areas with similar landforms and environments to the Hengduan Mountains, covering an area of 436,300 km2 (Figure 1). It is approximately 1043 km long, stretching from 24.7°N to 34.1°N, and approximately 900 km wide, ranging from 96.6°E to 104.7°E. Affected by geological tectonic movements in the area, the mountains and rivers are juxtaposed, mostly in the near north-south (or north-northwest) orientation. The terrain in this area is highly undulating, with elevations ranging from 351 m to 7417 m, and undulations as high as 1000–2500 m. Due to the influence of the southwest and southeast monsoons, the HMR has a significant monsoon climate, and the average annual precipitation for many years is between 500–2600 mm [39]. The spatial difference in precipitation in different seasons was obvious and affects significant societal risk due to rainfall-induced hazards such as landslides and debris flows.
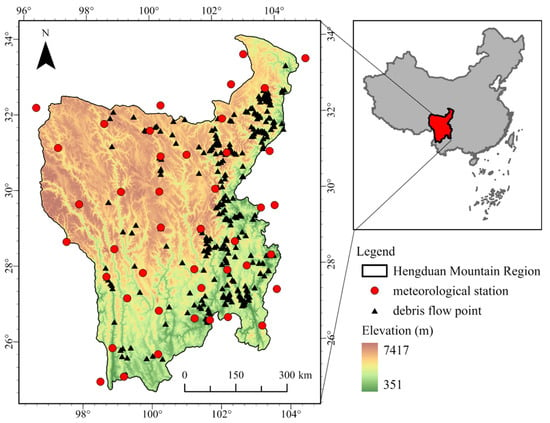
Figure 1.
Map of the Hengduan Mountain region (HMR) showing the distribution of the debris flow points and meteorological stations in the period 2000–2020.
2.2. Data
2.2.1. Debris Flow Catalog
Data for more than 400 debris flow records from 2000 to 2020 were collected from the HMR (Figure 1). Each record is associated with information including the precise location (longitude and latitude) and time of occurrence (day, month, and year) of the debris flow. Related information was obtained from several sources, including reports from authorities (China Ministry of Natural Resources geological disaster danger report) and national, regional, and local media. The occurrence time listed by Beijing was converted to satellite estimates (UTC).
2.2.2. Rainfall Dataset
Rainfall Gauge Data
The daily rainfall for the 43 meteorological stations for the period 2000–2020 was accessed via the China Meteorological Administration website (http://data.cma.cn/ (accessed on 6 January 2021), Figure 1). Daily rainfall was used to evaluate rainfall estimates related to the four satellite-derived rainfall products. In addition, the latent time gap between ground rainfall gauge observations (Beijing time) and satellite estimates (UTC) was re-aligned following the criteria proposed by previous studies [38].
Satellite Rainfall Products
CMORPH, which was developed by the NOAA Climate Prediction Center (CPC) in the United States, uses motion vectors derived from half-hourly interval geostationary satellite IR imagery to propagate relatively high-quality precipitation estimates derived from passive microwave data [52]. CMORPH-CRT is adjusted by matching the PDF of daily CMORPH-RAW against that of the CPC unified daily gauge analysis for each month over land; thus, the CMORPH-CRT data provides a month delay. CMORPH-CRT data with a temporal resolution of 30 min and a spatial resolution of 8 km over the HMR from 2000 to 2020 were selected and obtained from https://ftp.cpc.ncep.noaa.gov/precip/CMORPH_V1.0/CRT/8km-30min/ (accessed on 16 July 2021). In the following analysis, the CMORPH-CRT dataset is referred to as “CMORPH”.
The Integrated Multi-Satellite Retrievals for GPM (IMERG) is a unified U.S. algorithm that provides a multi-satellite precipitation product for the U.S. GPM team [53]. GPM (IMERG) offers three global precipitation products: early, late, and final runs. In the final run, the input precipitation estimates computed from the various satellite passive microwave sensors were intercalibrated to the CORRA product, then “forward/backward morphed” and combined with microwave precipitation-calibrated geo-IR fields and adjusted with the seasonal Global Precipitation Climatology Project (GPCP) Satellite-Gauge (SG) surface precipitation data to provide precipitation estimates on a 0.1° × 0.1° grid over the globe [54]. The current record period is from June 2000 to the present. Therefore, the final run data over HMR from June 2000 to 2020 were selected and were obtained from https://pmm.nasa.gov/data-access/downloads/gpm (accessed on 19 July 2021).
MSWEP is a global precipitation product with a 3-hourly 0.1° resolution available from 1979 to the present in real-time [55]. The product is unique in that it merges gauge, satellite, and reanalysis data to obtain the highest-quality precipitation estimates at every location. MSWEP incorporates daily gauge observations and accounts for gauge reporting times to reduce temporal mismatches between satellite reanalysis estimates and gauge observations. Near real-time estimates are available with a latency of approximately 3 h. MSWEP V2 data over HMR from 2000 to 2020 were selected and can be obtained from http://www.gloh2o.org/mswep/ (accessed on 20 July 2021).
PERSIANN-Cloud Classification System (PERSIANN-CCS) is a real-time global high resolution (0.04° × 0.04°) satellite precipitation product developed by the Center for Hydrometeorology and Remote Sensing at the University of California, Irvine [56]. The PERSIANN-CCS system enables the categorization of cloud patch features based on cloud height, areal extent, and variability of texture estimated from satellite imagery. PERSIANN-CCS provides rainfall data in different time steps (hourly, 3-hourly, 6-hourly, daily, monthly, and yearly) from June 2003 to the present [57]. The rainfall data of HMR from June 2003 to 2020 in a 3-h time step were selected and can be obtained from http://persiann.eng.uci.edu/CHRSdata/PERSIANN-CCS (accessed on 23 July 2021). In the following investigations, “PERSIANN” is used to represent the PERSIANN-CCS dataset.
For fair intercomparison, rainfall datasets were compared with meteorological station observations on a daily scale, and the four satellite rainfall products were carried out in 3 h steps to calculate the debris flow rainfall threshold to ensure consistency with MSWEP data. As satellite rainfall products are all gridded data, the value of the grid whose center is closest to the location of the target point (meteorological station or debris flow point) is selected to reconstruct the rainfall sequence for subsequent analysis. This process is implemented through the “terra” package in the R program.
2.3. Methods
First, the consistency of four satellite rainfall products with ground-based observations was assessed using consistent statistical indicators and extreme rainfall indicators, and a comprehensive evaluation of the rainfall products was conducted using the technique for order preference by similarity to the ideal solution model (TOPSIS). Then, based on the assessment results, the intraday rainfall and antecedent effective rainfall of the debris flow in the HMR were extracted, and the characteristics of the different rainfall patterns leading to the debris flow were analyzed statistically. Finally, the critical rainfall and E-D thresholds of the HMR and different rainfall patterns at different warning levels were calculated by combining the above results.
2.3.1. Evaluation Methods for Satellite Rainfall Products in Daily and Extreme Rainfall
Several widely used statistical indicators were used to analyze the general similarities and differences of the four satellite rainfall product data relative to the meteorological station daily observation data. The detailed formulae are summarized in Table 1.

Table 1.
Definitions and equations of the statistical indicators.
The simulation effects of the four satellite rainfall products on the probability density of daily precipitation were evaluated based on the two statistics of the probability density function: Brier score (BS) and Skill score (Sscore). BS is the mean square error of the probability prediction; the smaller the BS, the better the simulation effect of the product [58]. BS (103) is the calculation result after BS is multiplied by 1000. Sscore is the degree of overlap between the simulated probability distribution and the measured value; the larger the Sscore value, the better is the model performance [59]. The correlation coefficient (CC) represents the agreement between the satellite rainfall data and site observations. The larger the CC, the higher the correlation [60]. Percent bias (PBIAS) was used to assess the percentage bias between satellite rainfall data and site observations, with positive PBIAS values indicating overestimation of rainfall products and negative values indicating underestimation [61,62]. The Nash–Sutcliffe efficiency (NSE) is a normalized statistic that determines the relative magnitude of the residual variance (“noise”) compared to the measured data variance (“information”) [63]. NSE indicates how well the plot of the observed versus simulated data fits the 1:1 line. Essentially, the closer it is to 1, the more accurate the model is. The ratio of the root mean square error to the standard deviation (RMSE) of measured data (RSR) standardizes RMSE using the standard deviation of observations and combines both error indices [64]. RSR incorporates the benefits of error index statistics and includes a scaling/normalization factor so that the resulting statistic and reported values can be applied to various constituents. The RSR varies from the optimal value of 0, which indicates zero RMSE or residual variation, and therefore a perfect model simulation, to a large positive value. The lower the RSR, the lower the RMSE, and the better the model simulation performance.
The ability of satellite rainfall products to detect extreme rainfall is critical for evaluating their applications in debris flow hazard forecasting. In this study, a series of extreme rainfall indicators were extracted from satellite rainfall products and meteorological station observation data. By fitting and comparing the results, the ability of the four satellite rainfall products to monitor extreme rainfall events in the HMR was evaluated using the RSR. Reference to several indicators of the Climate Change Detection and Monitoring and Index [65] include: the maximum consecutive wet days (CWD), the number of days with a precipitation amount greater than 25 mm (R25mm), annual total precipitation when daily precipitation is greater than the 95 percentile (R95p), the annual maximum 1-day precipitation amount (Rx1day), the annual maximum 5-day precipitation amount (Rx5day), and the simple daily intensity index (SDII). Details of the extreme rainfall indicators have been described in Table S1 of the supplementary material.
Finally, the overall performance of the four satellite rainfall products in simulating the daily sequence and extreme rainfall in the HMR was comprehensively scored using the TOPSIS model. The TOPSIS model obtains the relative proximity between the evaluation object and the optimal scheme by calculating the distance between each evaluation object and the optimal and worst indicator values. The TOPSIS method is detailed by Li et al. [66]. In this study, “high level indicators” include the BS, PBIAS, NSE, and RSR. The “low level indicators” include the CC and Sscore. The comprehensive indicator score (CI) was used to characterize the quality of the results. The higher the CI value, the better the comprehensive evaluation result. The TOPSIS model is described in detail in the “The technique for order preference by similarity to ideal solution (TOPSIS) model” section of the supplemental material.
2.3.2. Extraction of Antecedent Rainfall and Classification of Rainfall Patterns in the HMR
The rainfall conditions of the current day of debris flow (that is, intraday rainfall conditions) and the antecedent effective rainfall conditions were considered as antecedent rainfall. The former includes intraday rainfall, the maximum 3-h rainfall, the maximum 6-h rainfall, and the maximum 12-h rainfall of the current day of debris flow. The latter should be considered along with the possible effects of soil water saturation. The antecedent cumulative effective rainfall (ER) was calculated by applying the decay constant ():
where is the cumulative daily rainfall on the day of the debris flow (i.e., the intraday rainfall). is the cumulative daily rainfall on the ith day before the debris flow occurrence day. Yang et al. [48] found that the corresponding rainfall is representative when N = 7 in Dazhou, Southwest China. Zhuang et al. [67] also found that the effect of rainfall on soil moisture was negligible after 7 days in Xi’an, China. Based on this, the N value was set to seven in this study. According to previous studies on the decay factor in China [65], the k value was set to 0.9. - are all antecedent effective rainfall conditions, and ER_7 is the antecedent cumulative effective rainfall.
To elucidate the relationship between debris flow occurrence and the rainfall process, Ni et al. [49] proposed the concept of a rainfall pattern, which reflects the corresponding rainfall process. The classification of rainfall patterns was calculated according to the proportion of intraday rainfall within the antecedent cumulative effective rainfall (). This study references the concepts of rainfall patterns and classifies them accordingly. When is greater than 60%, the rainfall pattern is considered an intraday rainfall-dominated pattern (IRD pattern). Rainfall processes with between 40% and 60% were considered as intraday-antecedent-rainfall-balanced (IARB), patterns, and rainfall processes with less than 40% were considered as antecedent-rainfall-dominated (IRD) patterns.
2.3.3. Calculation of Critical Rainfall and Empirical Rainfall Threshold Model for Triggering Debris Flow
First, the critical rainfall under different warning levels was defined according to the empirical cumulative distribution function (ECDF) and cumulative probability. The cumulative probability of debris flow at 50%, 75%, and 90% represent the three levels of low, medium, and high warning indications, respectively. The calculation of the ECDF and cumulative probability was performed in the R programming language. The empirical cumulative E-D curve was then fitted according to the critical antecedent cumulative rainfall (the rainfall on the occurrent day of the debris flow and the accumulated effective rainfall from 1 to 7 days before the occurrence) under different early warning levels.
The E-D curve, a common rainfall threshold, reveals a linear increase in cumulative rainfall with rainfall duration under rainfall conditions that lead to debris flows [3,21]. The formula for the E–D rainfall threshold is expressed as follows:
where E is the cumulative effective rainfall (mm), D is the rainfall duration (h), is a scaling constant, and is the shape parameter.
3. Results
3.1. Evaluation of Satellite Rainfall Products
Daily rainfall series from 2000 to 2020 were obtained based on the CMORPH, GPM, MSWEP, and PERSIANN rainfall datasets and compared with rainfall gauge observations, which were used as the benchmark dataset throughout the analysis. The relationship between the daily rainfall recorded by rainfall gauges and data from four satellite rainfall products was explored. Their performance in simulating rainfall events was evaluated.
Figure 2 displays the statistical distribution of station observations in the HMR and the daily mean of the daily series of rainfall outputs from different satellites. The average daily rainfall in the region ranges from 0 mm to 40 mm (Figure 2a). Overall, the GPM and CMORPH data relatively underestimated the daily rainfall at the same probability density, whereas the MSWEP and PERSIANN data exhibited an overestimation of daily rainfall. CMORPH and MSWEP were closer to the observations at the same cumulative probability density. From the probability mean square error of the product rainfall data and the degree of overlap between the probability distribution and the observed value, the mean BS () and Sscore values of CMORPH are both the most consistent among the four products (Table 2), which are 0.92 and 0.06, respectively, with GPM times of 0.92 and 0.05, respectively. However, the GPM value performed better for the concentration of values at 43 stations with BS and Sscore values. MSWEP performed the least consistently on both and had the highest degree of dispersion within the station (Figure 2b,c).
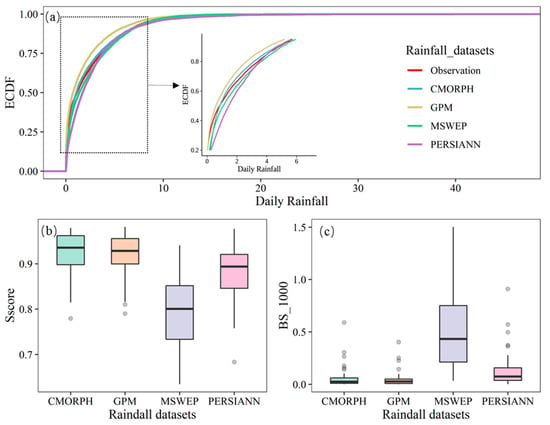
Figure 2.
Comparison of rainfall datasets on probability density. (a) Empirical cumulative distribution function (ECDF) curves for different rainfall datasets, (b,c) boxplots of the Sscore and BS of the four satellite rainfall products, respectively. BS_1000 is BS ().

Table 2.
Mean indicators value and comprehensive indicators score (CI) of the four satellite rainfall products in terms of daily precipitation and extreme precipitation.
A scatter density map of the observations and daily data of the satellite rainfall products is shown in Figure 3. The daily average data of MSWEP had the highest correlation with the observations, with a value of 0.78, followed by CMORPH (0.66). In addition to evaluating the consistency indicators of the mean value of satellite rainfall at the stations, the daily sequence consistency of each station in the satellite rainfall simulation area was evaluated. First, from the point of view of the mean value (Table 2), the PBIAS value of CMORPH was at least 16%, followed by MSWEP, which was 17%. From the point of view of the mean value of stations, the overall daily series is higher than the observation value, which is different from the previous cumulative distribution results. This further shows that the comparison results obtained from the mean point of view are open to question. The NSE value of CMORPH was the highest at 0.72, and the NSE value of PERSIANN was the lowest at −1.27. The RSR value of MSWEP was the smallest, at 0.62, and the RSR values of GPM and CMORPH were equivalent to 0.84. It can be observed that MSWEP exhibits the best performance in CC, RSR, and NSE. PERSIANN underperformed all consistency indicators.
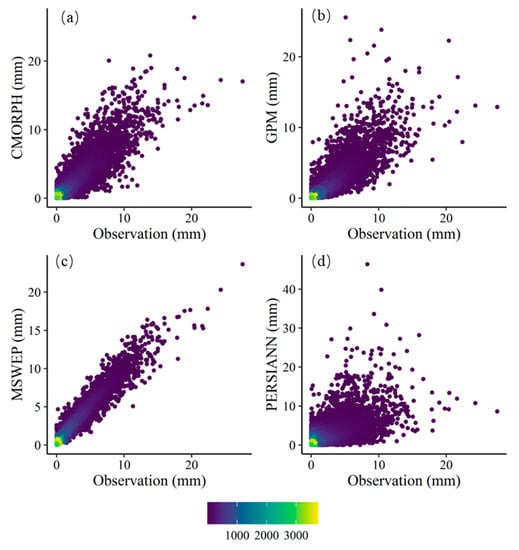
Figure 3.
Scatter density map of the observations and daily data of (a) CMORPH, (b) GPM, (c) MSWEP and (d) PERSIANN datasets.
Figure 4 displays the spatial distributions of CC, PBIAS, NSE, and RSR for the four satellite rainfall products over the HMR. The CC values of the CMORPH were the most dispersed, ranging from 0.29 to 0.75. MSWEP had the highest CC value, which ranged from 0.6 to 0.93, with more than half of the stations having a CC value exceeding 0.82. The PBIAS value of MSWEP was the most concentrated, ranging from −20.3% to 55.1%, followed by GPM, which had values ranging from −53.6% to 23%, and the PBIAS values of PERSIANN were the most scattered, ranging from −70.1% to 26.3%. Among the 43 stations, the PBIAS of GPM was negative at 37 stations, indicating that the GPM data underestimated daily rainfall data. Rainfall data for the remaining three satellite products were positive for the PBIAS at more than half of the stations. The NSE values of MSWEP were also best distributed across stations, ranging from 0.27 to 0.84, with more than half of the stations having an NSE value over 0.67. The NSE distributions for CMORPH and GPM follow closely, ranging from −0.1 to 0.44 and from −0.01 to 0.44, respectively. More than half of the stations estimated by CMORPH had NSE values above 0.32, and more than 21 stations in the GPM simulations had NSE values above 0.29. Most of the sites simulated by PERSIANN had NSE values less than 0. The RSR value of GPM is the most concentrated, in the range of 0.75–1, followed by CMORPH, ranging from 0.75 to 1.05. The RSR distribution of the MSWEP is relatively scattered, but the value of RSR was most consistent, between 0.4 and 0.86.
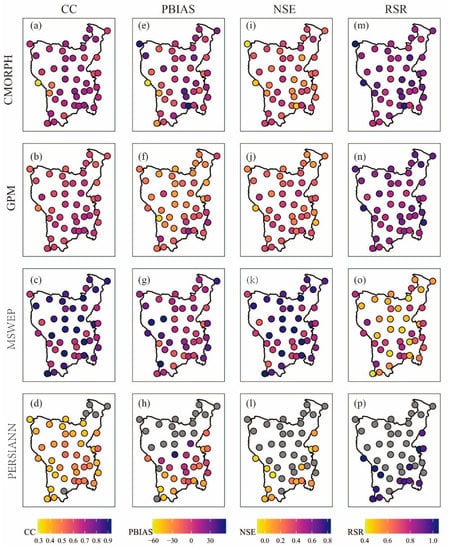
Figure 4.
Spatial distribution of CC (a–d), PBIAS (e–h), NSE (i–l), and RSR (m–p) for four satellite rainfall products over HMR. Gray dots indicate that the value is outside the indicated range.
The performances of the four satellite rainfall products in the simulated extreme rainfall conditions in the HMR are also compared in Figure 5. First, based on the RSR to evaluate the performance of the four satellite rainfall products in the six extreme climate indicator simulations, the RSR values of Rx1day and Rx5day were lower. The RSR values of CMORPH, GPM, MSWEP, and PERSIANN were 0.68, 0.73, 0.47, and 1.45 for Rx1day, respectively, and their RSR values for Rx1day were 0.82, 0.9, 0.62, and 1.71, respectively. This shows that the four satellite rainfall products outperformed the other four indices for Rx1day and Rx1day. CMORPH, MSWEP, and PERSIANN showed the least consistency in the persistence index (CWD), with RSR values of 2.02, 5.73, and 2.85, respectively. The GPM had the worst performance on SDII, with an RSR value of 2.18. The results showed that the performance of the four rainfall products in simulating the persistence of rainfall was relatively poor, and the performance in simulating extreme rainfall events was better. In terms of different extreme rainfall indicators, CMORPH had the lowest RSR distribution in SDII, indicating that it had the strongest ability to simulate SDII. GPM has the lowest degree of discretization in the RSR of CWD and R25mm, and its overall RSR value is also the smallest (Table 2), indicating that GPM performs the best in CWD and R25mm among the four products. MSWEP showed the least consistency than the other three satellite products in terms of SDII and CWD, but performed best on R95P, Rx1day, and Rx5day. PERSIANN had the largest degree of discretization and distribution difference in R25mm, R95P, Rx1day, and Rx1day.
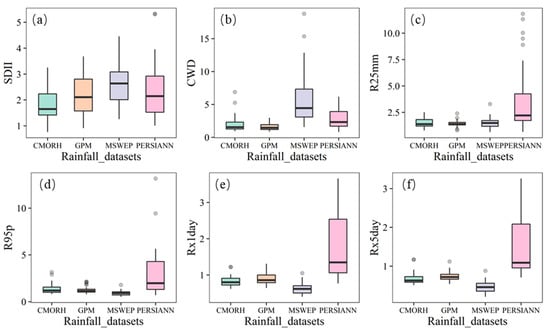
Figure 5.
Boxplots showing the RSR values of the four satellite rainfall products at (a) SDII, (b) CWD, (c) R25mm, (d) R95p, (e) Rx1day, and (f) Rx5day.
The performances of the four satellite rainfall products in simulating the daily rainfall and extreme rainfall conditions in the HMR through the TOPSIS model are presented in Table 2. The CI values for assessing the consistency of daily precipitation for CMORPH are the highest at 0.69, followed closely by GPM with a CI value of 0.68, indicating that CMORPH performed best in the simulated daily data. In terms of the comprehensive assessment results of extreme rainfall, MSWEP performed the best with a CI value of 0.75, followed by CMORPH with a value of 0.65. From the overall performance of daily rainfall and extreme rainfall, CMORPH exhibited the best performance among the four satellite rainfall products, with a CI value of 0.72. GPM was the second highest, and the CI value was 0.7.
3.2. Antecedent Rainfall of Debris Flows
The intraday rainfall conditions and the previous 1- to 7-day effective rainfall conditions for debris flow-inducing rainfall events (DREs) for the four satellite rainfall products were reconstructed, based on the spatio-temporal attribute information of the debris flow points. If ER_7 constructed by the satellite rainfall product is less than 20 mm, it is considered that the product fails to capture the rainfall event of the debris flow. Based on this, the reconstruction rates of correctly captured DREs for the four satellite rainfall products were compared (Table 3). It can be seen that CMORPH captured the most DREs, with a number of 376, which also shows that the reconstruction rate is the highest, reaching 89%. MSWEP was performed by 368 with a reconstruction rate of 87%. The remaining two products have a lower reconstruction rate, both below 75%. Thus, the CMORPH dataset also has the highest ability to reconstruct rainfall events that trigger debris flow. Based on the ratio of the rainfall on the day when the debris flow occurred and the accumulated effective rainfall in the previous seven days, a statistical analysis was carried out on the different rainfall patterns that caused the debris flow in the HMR. It can be seen from Table 3, that among the reconstruction results of the four satellite rainfall products, the ARD pattern had the highest proportion, almost reaching 50% of the total, followed by the IARB pattern, and the IAD pattern had the smallest proportion. Therefore, from the comparison of the number of rainfall patterns, it can be seen that the formation and initiation of debris flows in the HMR are dominated by antecedent cumulative effective rainfall, and debris flows can also be caused when the daily precipitation or rainfall intensity is not high.

Table 3.
Summary of rainfall event reconstruction for DREs and different rainfall patterns.
CMORPH data, which perform well in simulating rainfall and reconstructing rainfall events that trigger debris flows, were selected to analyze the critical rainfall conditions of debris flows in the HMR. First, to clarify the characteristics of different rainfall patterns leading to debris flows in the HMR, the antecedent rainfall in the HMR and three rainfall patterns were calculated. Figure 6a,b shows boxplots of intraday rainfall conditions and antecedent cumulative effective rainfall conditions of the debris flow in the HMR, respectively. The results show that, although the number of ARD patterns is the largest among the three patterns, the daily rainfall conditions in the entire HMR are generally more similar to the IARB pattern. The IRD pattern dominated by intraday rainfall had the highest intraday rainfall conditions, whereas the ARD pattern dominated by antecedent cumulative effective rainfall had the lowest intraday rainfall conditions. It is worth noting that from the distribution of antecedent rainfall conditions, the antecedent rainfall conditions under the ARD pattern are also relatively low among the three models, and the antecedent rainfall conditions under the IRD and IARB patterns are comparable.
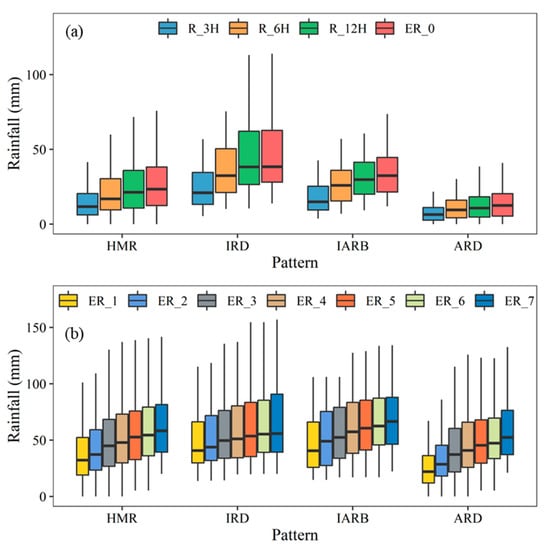
Figure 6.
Boxplots of (a) the intraday rainfall conditions and (b) cumulative 7-day effective rainfall conditions.
Figure 7 shows the empirical cumulative distribution function curves for HMR under different rainfall patterns. Overall, the intraday rainfall, the maximum 3-h rainfall, the maximum 6-h rainfall, and the maximum 12-h rainfall of the intraday of the low warning level (cumulative probability of 50%) are 23.5 mm, 11.7 mm, 16.9 mm, and 21.3 mm, respectively. The cumulative 7-day effective rainfall at the low warning level was 58.4 mm. The critical rainfall conditions increased with the warning level. The critical daily rainfall for medium (cumulative probability of 75%) and high warning levels (cumulative probability of 90%) were 38.2 mm and 56.7 mm, respectively. The critical cumulative 7-day effective rainfall for medium and high warning levels were 81.7 mm and 105.8 mm, respectively. From the perspective of different rainfall patterns, under the same warning level, the IRD pattern had the highest critical intraday rainfall conditions, followed by the IARB pattern, and the ARD pattern was the smallest. The critical daily rainfall values of low, medium, and high warning levels in the IRD pattern are 38.4 mm, 62.6 mm, and 75.8 mm, respectively, and the corresponding values in the IARB pattern are 32.5 mm, 44.6 mm, and 56.7 mm, respectively. The critical daily rainfall values for low, medium, and high warning levels in the ARD pattern were 12.5 mm, 20.4 mm, and 30.5 mm, respectively. However, there are differences in the order of the antecedent cumulative rainfall conditions for different rainfall patterns under different warning levels. Under the low warning condition, the critical cumulative 7-day effective rainfall of the IARB pattern was the highest at 66.7 mm, followed by the IRD pattern (55.9 mm) and the ARD pattern (52.5 mm) with the smallest values. Under the medium warning level, the critical cumulative 7-day rainfall of the IRD pattern was the highest, followed by that of the IARB pattern, and the lowest in the ARD pattern. The critical values are 90.8 mm, 88.1 mm, and 76.5 mm. The critical cumulative 7-day effective rainfall corresponding to the high warning level of the IRD pattern was the highest, followed by the corresponding value of the IARB pattern, and the corresponding value of the ARD pattern was the smallest. The corresponding critical values are 90.8 mm and 88.1 mm. mm, and 76.5 mm.
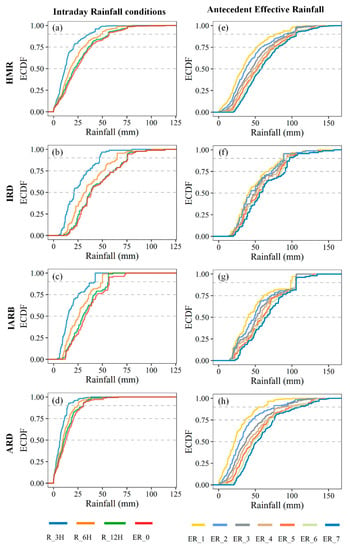
Figure 7.
ECDF curves of intraday rainfall conditions (a–d) and cumulative 7-day effective rainfall conditions (e–h).
3.3. Rainfall Thresholds of Debris Flow
Based on the above results, it can be observed that under different warning levels, there are differences in the antecedent rainfall conditions of different rainfall patterns that trigger debris flows. Therefore, it is necessary to analyze the relationship between the cumulative effective rainfall and rainfall duration for different rainfall patterns. The E-D rainfall thresholds of debris flow in the HMR under different early warning levels were analyzed according to the intraday rainfall and the cumulative effective rainfall on days 1–7 in Figure 7. Figure 8a–c shows the E-D rainfall threshold curves for the HMR and different rainfall patterns under low, medium, and high warning levels, respectively. The results show that the value of the E-D rainfall threshold in the HMR is between 5.84 and 24.36, and the value between 0.44 and 0.29. As the warning level increases, the values of all E-D rainfall threshold curves show an increasing trend, whereas the values show the opposite trend. This shows that, with an increase in the warning level, the effect of short-term rainfall on debris flow is more obvious during the effective rainfall period. Among the different rainfall patterns, the value of the E-D rainfall threshold curve of the IRD pattern was the highest, ranging from 19.54 to 57, followed by the corresponding values of the IARB pattern, ranging from 10.88 to 31.24, and the corresponding value of the IAD pattern was the smallest, ranging from 1.53 to 5.07. The result of the value is the opposite of that of the value. The value of the ARD pattern was the largest with a value from 0.68 to 0.6, the corresponding value of the IARB pattern was the second, between 0.35 and 0.25, and the corresponding value of the IRD pattern was the smallest, ranging from 0.2 to 0.1. The difference in the initial threshold values between the different rainfall patterns was obvious. With an increase in rainfall duration, the difference in the rainfall threshold curves gradually decreased. The initial rainfall threshold was much higher than the difference at the end, which also illustrates the consistency of the antecedent effective accumulated rainfall leading to debris flow.
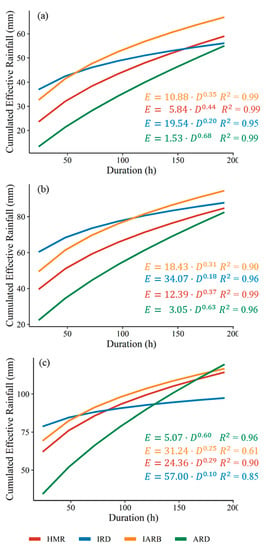
Figure 8.
Rainfall thresholds for debris flow initiation for (a) low warning level, (b) medium warning level, and (c) high warning level of different rainfall patterns.
4. Discussion
The performance of four satellite rainfall product datasets in terms of daily rainfall and extreme rainfall in the HMR was evaluated using multiple evaluation indicators. The results show that CMORPH is optimal in terms of overall performance in several aspects, followed by GPM. The advantages of CMORPH in simulating rainfall in other regions were also reflected. Tang et al. [27] evaluated the performance of rainfall product datasets in mainland China and believed that the CMORPH consistency indicators were also higher than those of other products used for comparison. In terms of systematic errors, it had the lowest value. Other studies have also shown that reprocessed bias-corrected CMORPH consistently performs better than the widely used TMPA in terms of daily rainfall and 3 h of rainfall in the United States and other global neighboring regions [68]. This may be due to the high spatiotemporal resolution of the CMORPH [68,69]. CMORPH was slightly inferior to MSWEP in reproducing extreme rainfall in some regions. The main reason is that the CMORPH has a certain underestimation of the daily precipitation, while MSWEP mainly overestimates daily precipitation. Nonetheless, CMORPH has certain advantages over the other satellite datasets. For example, Chen et al. [70] analyzed satellite rainfall datasets (near real-time Global Satellite Mapping of Precipitation (GSMaP_NRT), PERSIANN, and CMORPH) for heavy rainfall events in northern China and indicated that CMORPH was superior to storm-scale accumulated precipitation and relatively overestimated heavy rainfall. Tian et al. [71] also found that CMORPH has lower uncertainty on shorter timescales. In the compared results, the overall performance of PERSIANN is the poorest, which may be related not only to its lower resolution but also to factors such as the inversion algorithm. Wei et al. [72] believed that regarding the algorithm, the CMORPH (in the service of IMERG) and Kalman filter (same as GSMaP) techniques are more effective algorithms for precipitation retrieval based on remote sensing information compared with other methods. However, the PERSIANN algorithm is not optimal for estimating raw precipitation using IR data, such as PERSIANN outcomes, which have also been reported by Ashouri et al. [73] and Li et al. [74]. Correspondingly, CMORPH also shows an advantage over the other three satellite rainfall product datasets in terms of rainfall reconstructions that trigger debris flows. This result was also confirmed in other regions. Brunetti et al. [69] found that CMORPH and SM2RASC performed best when comparing TMPA, SM2RAIN, CMORPH, and PERSIANN data in the detection of Italian landslides and attributed the main results to the high spatiotemporal resolution of CMORPH. Jia et al. [37] also pointed out that CMORPH has a high Hanssen–Kuiper skill score when evaluating the performance of satellite product data for global landslide prediction.
In terms of the rainfall threshold calculation of debris flows, the critical intraday rainfall and critical antecedent effective rainfall under different warning levels were defined according to the cumulative probability. Based on CMORPH, the calculated results of the critical intraday rainfall and the critical antecedent cumulative effective rainfall at the low warning level of debris flow in the HMR are 38.4 mm and 55.9 mm, respectively. The results of this study (average of approximately 48.2 mm) are lower than the critical cumulative 7-day rainfall of the Hengduan Mountains calculated in previous studies [39] based on TRMM. One reason for this result is the discrepancy in critical rainfall due to differences in the satellite rainfall product data used. In addition, it is also more important that when selecting antecedent rainfall conditions, invalid data with cumulative rainfall of less than 20 mm were excluded. In addition to the overall analysis of the antecedent rainfall of the HMR, this study also compared different rainfall patterns and analyzed the critical rainfall under different rainfall patterns. It can be seen that nearly half of the rainfall patterns of debris flow are dominated by cumulative 7-day effective rainfall. It was found that although the difference between different rainfall patterns was small when the rainfall duration reached seven days, the difference was more obvious when the rainfall duration was shorter, which further illustrates the important role of antecedent cumulative effective precipitation on the impact of debris flow. By classifying and characterizing the different rainfall patterns that trigger debris flows, the response of debris flows to rainfall processes can be better understood, and a reference can be provided for predicting an early warning of critical daily rainfall conditions for debris flows [49].
The empirical E-D rainfall threshold curves for the HMR and the different rainfall patterns were defined based on the antecedent cumulative effective rainfall. The overall threshold of debris flows in the HMR obtained in this study was compared to the results of previous studies in this area. It was found that the rainfall threshold under the low warning level in this study was similar to the results of Guo et al. [75] in the Wenchuan earthquake area and Zhuang et al. [44] in the Jiangjia Gully, Yunnan. The rainfall data used in both studies were from ground gauges. These rain-gauges provided high-resolution rainfall data (with a resolution of 0.1 mm in precipitation and 1 min in observation intervals). The availability of satellite rainfall data for detecting debris flow events in the Hengduan Mountain region is also demonstrated. However, different rainfall patterns have different rainfall thresholds, which further illustrates the necessity of analyzing different rainfall pattern thresholds.
In addition, the results of this study also have some uncertainties and limitations due to spatial differences in a large-scale region, incomplete records of debris flows, and inevitable uncertainties about satellite rainfall products. Firstly, debris flow formation conditions mainly include geomorphological conditions, material conditions, and triggering conditions. In addition to rainfall conditions, the debris flow itself is closely related to regional spatial characteristics. Due to the spatial heterogeneity of debris flows caused by the special geological environment and regional climate, the results of this study cannot respond to local debris flow conditions, which is one of the limitations of this study. Therefore, it is necessary to combine small-scale regional characteristics in future studies. Secondly, another uncertainty of the study results was increased by the incomplete inventory of debris flows collected in this study. Although the number of debris flow events has increased compared to previous studies, it is still incomplete. The time distribution of debris flow data is uneven, and there are phenomena such as under-reporting of data; therefore, it is possible to underestimate the incidence of debris flow in some areas. Owing to the accuracy of information collection, for example, the occurrence time of some debris flows cannot be specified to a certain time point, and only the information that occurred in the morning or afternoon is given; therefore, there are certain limitations in the calculation. Finally, as with other satellite-based rainfall products, large-scale rainfall data introduce inevitable uncertainty. The comparison of rainfall sequences used in this study for ease of comparison is based on daily data, mainly because of the limitations of the time scale of large-scale ground station observations. However, it can be seen from the results of the study that the comparison results of the daily rainfall data and the comparison of the rainfall threshold results do not conflict, thereby confirming the feasibility of this operation. To facilitate the comparison of satellite rainfall products, the rainfall time step of the rainfall threshold calculation in this study was 3 h, which may have a high temporal resolution in other studies. Studies [19] have shown that the temporal resolution of rainfall does not seem to affect the validation process or threshold performance metrics. Therefore, the results of this study can provide a reference for early warning of debris flow in HMR.
5. Conclusions
Based on rainfall gauge observations from 2000 to 2020, this study evaluated the applicability of four satellite rainfall products (CMORPH, GPM, MSWEP, and PER-SIANN) in the HMR in terms of daily and extreme precipitation. The critical antecedent rainfall conditions and the relationship between antecedent rainfall and rainfall duration of large-scale debris flows were explored by considering different rainfall patterns.
The study found that CMORPH showed good performance both in terms of the consistency of the daily rainfall series and extreme precipitation, although it tended to underestimate the rainfall in the study area. CMORPH also showed great advantages in the extraction and analysis of antecedent rainfall, with a reconstruction rate of 89%. The overall performance of GPM is slightly inferior to that of CMORPH. The reason is due to its poor ability to simulate extreme precipitation persistence indicators, which also results in a lower reconstruction rate of antecedent rainfall.
It is found that the ARD pattern accounts for about half of all rainfall patterns triggering debris flows, indicating that the debris flows in the study area were mainly triggered by antecedent effective rainfall. Therefore, in addition to intraday rainfall conditions, long-duration rainfall conditions are an important factor that cannot be ignored. In addition, there are also differences in the antecedent rainfall conditions of different rainfall patterns, which also shows that considering the rainfall patterns can help to describe the rainfall threshold curve of debris flows more precisely. It is found that the α values of all E-D rainfall threshold curves show an increasing trend as the warning level increases, whereas the β values show the opposite trend. It shows that more attention should be paid to the short-duration rainfall conditions under higher debris flow warning conditions.
Combined with the comparison results of the rainfall threshold fitted in this study and previous studies, it is believed that CMORPH can be used to predict the occurrence of debris flow in the HMR. Satellite rainfall products can be used to compensate for the uneven distribution of ground-based observations. Further efforts are required to combine the results of this study with debris flow susceptibility mapping techniques that take into account the geomorphological and material conditions for the purpose of a more refined regional debris flow warning.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/rs14122731/s1, Table S1: Definitions of the extreme rainfall indicators used in this study. Refs. [66,76] are cited in the supplementary materials.
Author Contributions
Conceptualization, J.L., Z.Y. and Z.L.; methodology, J.L., Z.Y. and Z.L.; software, J.L. and X.L.; validation, J.L., Z.Y. and Z.L.; formal analysis, J.L.; investigation, R.W.; resources, Z.Y.; data curation, X.Z.; writing—original draft preparation, J.L.; writing—review and editing, J.L., Z.Y. and Z.L.; visualization, J.L.; supervision, Z.Y., Z.L. and R.W.; project administration, Z.Y.; funding acquisition, Z.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported and funded by the Strategic Priority Research Program of the Chinese Academy of Sciences (XDA23090302; XDA20060202).
Data Availability Statement
The data, materials, and codes of this article can be obtained by contacting the authors at lij.16s@igsnrr.ac.cn and zfliu@igsnrr.ac.cn.
Acknowledgments
We are grateful to the public data portal for providing the satellite rainfall products datasets.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Prenner, D.; Kaitna, R.; Mostbauer, K.; Hrachowitz, M. The Value of Using Multiple Hydrometeorological Variables to Predict Temporal Debris Flow Susceptibility in an Alpine Environment. Water Resour. Res. 2018, 54, 6822–6843. [Google Scholar] [CrossRef]
- Destro, E.; Marra, F.; Nikolopoulos, E.I.; Zoccatelli, D.; Creutin, J.D.; Borga, M. Spatial estimation of debris flows-triggering rainfall and its dependence on rainfall return period. Geomorphology 2017, 278, 269–279. [Google Scholar] [CrossRef]
- Innes, J.L. Debris Flows. Prog. Phys. Geogr. 1983, 7, 469–501. [Google Scholar] [CrossRef]
- Thouret, J.C.; Antoine, S.; Magill, C.; Ollier, C. Lahars and debris flows: Characteristics and impacts. Earth-Sci. Rev. 2020, 201, 103003. [Google Scholar] [CrossRef]
- Banihabib, M.E.; Tanhapour, M. An empirical equation to determine the threshold for rainfall-induced landslides developing to debris flows. Landslides 2020, 17, 2055–2065. [Google Scholar] [CrossRef]
- Valenzuela, P.; Dominguez-Cuesta, M.J.; Garcia, M.A.M.; Jimenez-Sanchez, M. Rainfall thresholds for the triggering of landslides considering previous soil moisture conditions (Asturias, NW Spain). Landslides 2018, 15, 273–282. [Google Scholar] [CrossRef]
- Segoni, S.; Piciullo, L.; Gariano, S.L. A review of the recent literature on rainfall thresholds for landslide occurrence. Landslides 2018, 15, 1483–1501. [Google Scholar] [CrossRef]
- Marin, R.J.; Garcia, E.F.; Aristizabal, E. Effect of basin morphometric parameters on physically-based rainfall thresholds for shallow landslides. Eng. Geol. 2020, 278, 105855. [Google Scholar] [CrossRef]
- Cannon, S.H.; Gartner, J.E.; Wilson, R.C.; Bowers, J.C.; Laber, J.L. Storm rainfall conditions for floods and debris flows from recently burned areas in southwestern Colorado and southern California. Geomorphology 2008, 96, 250–269. [Google Scholar] [CrossRef]
- Marra, F.; Nikolopoulos, E.I.; Creutin, J.D.; Borga, M. Space-time organization of debris flows-triggering rainfall and its effect on the identification of the rainfall threshold relationship. J. Hydrol. 2016, 541, 246–255. [Google Scholar] [CrossRef]
- Peres, D.J.; Cancelliere, A. Derivation and evaluation of landslide-triggering thresholds by a Monte Carlo approach. Hydrol. Earth Syst. Sci. 2014, 18, 4913–4931. [Google Scholar] [CrossRef] [Green Version]
- Kean, J.W.; Staley, D.M.; Cannon, S.H. In situ measurements of post-fire debris flows in southern California: Comparisons of the timing and magnitude of 24 debris-flow events with rainfall and soil moisture conditions. J. Geophys. Res.-Earth Surf. 2011, 116, F04019. [Google Scholar] [CrossRef]
- Monsieurs, E.; Dewitte, O.; Depicker, A.; Demoulin, A. Towards a Transferable Antecedent Rainfall-Susceptibility Threshold Approach for Landsliding. Water 2019, 11, 2202. [Google Scholar] [CrossRef] [Green Version]
- Smolikova, J.; Blahut, J.; Vilimek, V. Analysis of rainfall preceding debris flows on the Smedavska hora Mt. Jizerske hory Mts. Czech Republic. Landslides 2016, 13, 683–696. [Google Scholar] [CrossRef]
- Guzzetti, F.; Peruccacci, S.; Rossi, M.; Stark, C.P. Rainfall thresholds for the initiation of landslides in central and southern Europe. Meteorol. Atmos. Phys. 2007, 98, 239–267. [Google Scholar] [CrossRef]
- Bout, B.; Lombardo, L.; van Westen, C.J.; Jetten, V.G. Integration of two-phase solid fluid equations in a catchment model for flashfloods, debris flows and shallow slope failures. Environ. Model. Softw. 2018, 105, 1–16. [Google Scholar] [CrossRef]
- Bogaard, T.; Greco, R. Invited perspectives: Hydrological perspectives on precipitation intensity-duration thresholds for landslide initiation: Proposing hydro-meteorological thresholds. Nat. Hazards Earth Syst. Sci. 2018, 18, 31–39. [Google Scholar] [CrossRef] [Green Version]
- Chikalamo, E.E.; Mavrouli, O.C.; Ettema, J.; van Westen, C.J.; Muntohar, A.S.; Mustofa, A. Satellite-derived rainfall thresholds for landslide early warning in Bogowonto Catchment, Central Java, Indonesia. Int. J. Appl. Earth Obs. Geoinf. 2020, 89, 102093. [Google Scholar] [CrossRef]
- Gariano, S.L.; Melillo, M.; Peruccacci, S.; Brunetti, M.T. How much does the rainfall temporal resolution affect rainfall thresholds for landslide triggering? Nat. Hazards 2020, 100, 655–670. [Google Scholar] [CrossRef] [Green Version]
- Nikolopoulos, E.I.; Destro, E.; Maggioni, V.; Marra, F.; Borga, M. Satellite Rainfall Estimates for Debris Flow Prediction: An Evaluation Based on Rainfall Accumulation-Duration Thresholds. J. Hydrometeorol. 2017, 18, 2207–2214. [Google Scholar] [CrossRef]
- Peruccacci, S.; Brunetti, M.T.; Luciani, S.; Vennari, C.; Guzzetti, F. Lithological and seasonal control on rainfall thresholds for the possible initiation of landslides in central Italy. Geomorphology 2012, 139, 79–90. [Google Scholar] [CrossRef]
- Jordanova, G.; Gariano, S.L.; Melillo, M.; Peruccacci, S.; Brunetti, M.T.; Auflic, M.J. Determination of Empirical Rainfall Thresholds for Shallow Landslides in Slovenia Using an Automatic Tool. Water 2020, 12, 1449. [Google Scholar] [CrossRef]
- Bezak, N.; Mikos, M. Changes in the rainfall event characteristics above the empirical global rainfall thresholds for landslide initiation at the pan-European level. Landslides 2021, 18, 1859–1873. [Google Scholar] [CrossRef]
- Rossi, M.; Luciani, S.; Valigi, D.; Kirschbaum, D.; Brunetti, M.T.; Peruccacci, S.; Guzzetti, F. Statistical approaches for the definition of landslide rainfall thresholds and their uncertainty using rain gauge and satellite data. Geomorphology 2017, 285, 16–27. [Google Scholar] [CrossRef]
- Nikolopoulos, E.I.; Crema, S.; Marchi, L.; Marra, F.; Guzzetti, F.; Borga, M. Impact of uncertainty in rainfall estimation on the identification of rainfall thresholds for debris flow occurrence. Geomorphology 2014, 221, 286–297. [Google Scholar] [CrossRef]
- Posner, A.J.; Georgakakos, K.P. Soil moisture and precipitation thresholds for real-time landslide prediction in El Salvador. Landslides 2015, 12, 1179–1196. [Google Scholar] [CrossRef]
- Tang, G.; Clark, M.P.; Papalexiou, S.M.; Ma, Z.; Hong, Y. Have satellite precipitation products improved over last two decades? A comprehensive comparison of GPM IMERG with nine satellite and reanalysis datasets. Remote Sens. Environ. 2020, 240, 111697. [Google Scholar] [CrossRef]
- Camici, S.; Ciabatta, L.; Massari, C.; Brocca, L. How reliable are satellite precipitation estimates for driving hydrological models: A verification study over the Mediterranean area. J. Hydrol. 2018, 563, 950–961. [Google Scholar] [CrossRef]
- Lei, H.J.; Li, H.Y.; Zhao, H.Y.; Ao, T.Q.; Li, X.D. Comprehensive evaluation of satellite and reanalysis precipitation products over the eastern Tibetan plateau characterized by a high diversity of topographies. Atmos. Res. 2021, 259, 105661. [Google Scholar] [CrossRef]
- Xavier, A.C.F.; Rudke, A.P.; Serrao, E.A.D.; Terassi, P.M.D.; Pontes, P.R.M. Evaluation of Satellite-Derived Products for the Daily Average and Extreme Rainfall in the Mearim River Drainage Basin (Maranhao, Brazil). Remote Sens. 2021, 13, 4393. [Google Scholar] [CrossRef]
- de Siqueira, R.A.; Vila, D.A.; Afonso, J.M.D. The Performance of the Diurnal Cycle of Precipitation from Blended Satellite Techniques over Brazil. Remote Sens. 2021, 13, 734. [Google Scholar] [CrossRef]
- Getirana, A.; Kirschbaum, D.; Mandarino, F.; Ottoni, M.; Khan, S.; Arsenault, K. Potential of GPM IMERG Precipitation Estimates to Monitor Natural Disaster Triggers in Urban Areas: The Case of Rio de Janeiro, Brazil. Remote Sens. 2020, 12, 4095. [Google Scholar] [CrossRef]
- Ramadhan, R.; Marzuki, M.; Yusnaini, H.; Muharsyah, R.; Suryanto, W.; Sholihun, S.; Vonnisa, M.; Battaglia, A.; Hashiguchi, H. Capability of GPM IMERG Products for Extreme Precipitation Analysis over the Indonesian Maritime Continent. Remote Sens. 2022, 14, 412. [Google Scholar] [CrossRef]
- Hong, Y.; Adler, R.; Huffman, G. Evaluation of the potential of NASA multi-satellite precipitation analysis in global landslide hazard assessment. Geophys. Res. Lett. 2006, 33, L22402. [Google Scholar] [CrossRef]
- Kirschbaum, D.; Stanley, T. Satellite-Based Assessment of Rainfall-Triggered Landslide Hazard for Situational Awareness. Earths Future 2018, 6, 505–523. [Google Scholar] [CrossRef]
- He, S.S.; Wang, J.; Liu, S.N. Rainfall Event-Duration Thresholds for Landslide Occurrences in China. Water 2020, 12, 494. [Google Scholar] [CrossRef] [Green Version]
- Jia, G.Q.; Tang, Q.H.; Xu, X.M. Evaluating the performances of satellite-based rainfall data for global rainfall-induced landslide warnings. Landslides 2020, 17, 283–299. [Google Scholar] [CrossRef]
- Wang, N.; Lombardo, L.; Gariano, S.L.; Cheng, W.M.; Liu, C.J.; Xiong, J.N.; Wang, R.B. Using satellite rainfall products to assess the triggering conditions for hydro-morphological processes in different geomorphological settings in China. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102350. [Google Scholar] [CrossRef]
- Liu, S.; Wei, L.; Hu, K.H. Topographical and geological variation of effective rainfall for debris-flow occurrence from a large-scale perspective. Geomorphology 2020, 358, 107134. [Google Scholar] [CrossRef]
- Guo, X.J.; Cui, P.; Li, Y. Debris flow warning threshold based on antecedent rainfall: A case study in Jiangjia Ravine, Yunnan, China. J. Mt. Sci. 2013, 10, 305–314. [Google Scholar] [CrossRef]
- Long, K.; Zhang, S.J.; Wei, F.Q.; Hu, K.H.; Zhang, Q.; Luo, Y. A hydrology-process based method for correlating debris flow density to rainfall parameters and its application on debris flow prediction. J. Hydrol. 2020, 589, 125124. [Google Scholar] [CrossRef]
- Wei, F.; Hu, K.; Zhang, J.; Jiang, Y.; Chen, J. Determination of effective antecedent rainfall for debris flow forecast based on soil moisture content observation in Jiangjia Gully, China. Monit. Simul. Prev. Remediat. Dense Debris Flows II 2008, 60, 13–22. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.J.; Xu, C.X.; Wei, F.Q.; Hu, K.H.; Xu, H.; Zhao, L.Q.; Zhang, G.P. A physics-based model to derive rainfall intensity-duration threshold for debris flow. Geomorphology 2020, 351, 106930. [Google Scholar] [CrossRef]
- Zhuang, J.Q.; Cui, P.; Wang, G.H.; Chen, X.Q.; Iqbal, J.; Guo, X.J. Rainfall thresholds for the occurrence of debris flows in the Jiangjia Gully, Yunnan Province, China. Eng. Geol. 2015, 195, 335–346. [Google Scholar] [CrossRef]
- Zhou, W.; Tang, C. Rainfall thresholds for debris flow initiation in the Wenchuan earthquake-stricken area, southwestern China. Landslides 2014, 11, 877–887. [Google Scholar] [CrossRef]
- Chang, M.; Dou, X.Y.; Hales, T.C.; Yu, B. Patterns of rainfall-threshold for debris-flow occurrence in the Wenchuan seismic region, Southwest China. Bull. Eng. Geol. Environ. 2021, 80, 2117–2130. [Google Scholar] [CrossRef]
- Guo, X.J.; Cui, P.; Li, Y.; Ma, L.; Ge, Y.G.; Mahoney, W.B. Intensity-duration threshold of rainfall-triggered debris flows in the Wenchuan Earthquake affected area, China. Geomorphology 2016, 253, 208–216. [Google Scholar] [CrossRef]
- Yang, H.J.; Wei, F.Q.; Ma, Z.F.; Guo, H.Y.; Su, P.C.; Zhang, S.J. Rainfall threshold for landslide activity in Dazhou, southwest China. Landslides 2020, 17, 61–77. [Google Scholar] [CrossRef]
- Ni, H.Y.; Song, Z. Response of debris flow occurrence to daily rainfall pattern and critical rainfall condition in the Anning River-Zemu River Fault Zone, SW China. Bull. Eng. Geol. Environ. 2020, 79, 1735–1747. [Google Scholar] [CrossRef]
- Gupta, V.; Jain, M.K.; Singh, P.K.; Singh, V. An assessment of global satellite-based precipitation datasets in capturing precipitation extremes: A comparison with observed precipitation dataset in India. Int. J. Climatol. 2020, 40, 3667–3688. [Google Scholar] [CrossRef]
- Hartke, S.H.; Wright, D.B.; Kirschbaum, D.B.; Stanley, T.A.; Li, Z. Incorporation of Satellite Precipitation Uncertainty in a Landslide Hazard Nowcasting System. J. Hydrometeorol. 2020, 21, 1741–1759. [Google Scholar] [CrossRef] [PubMed]
- Joyce, R.J.; Xie, P. Kalman Filter–Based CMORPH. J. Hydrometeorol. 2011, 12, 1547–1563. [Google Scholar] [CrossRef]
- Skofronick-Jackson, G.; Petersen, W.A.; Berg, W.; Kidd, C.; Stocker, E.F.; Kirschbaum, D.B.; Kakar, R.; Braun, S.A.; Huffman, G.J.; Iguchi, T.; et al. The Global Precipitation Measurement (Gpm) Mission for Science and Society. Bull. Am. Meteorol. Soc. 2017, 98, 1679–1695. [Google Scholar] [CrossRef] [PubMed]
- Jin, D.; Oreopoulos, L.; Lee, D.; Tan, J.; Cho, N. Cloud–Precipitation Hybrid Regimes and Their Projection onto IMERG Precipitation Data. J. Appl. Meteorol. Climatol. 2021, 60, 733–748. [Google Scholar] [CrossRef]
- Beck, H.E.; Wood, E.F.; Pan, M.; Fisher, C.K.; Miralles, D.G.; van Dijk, A.I.J.M.; McVicar, T.R.; Adler, R.F. MSWEP V2 Global 3-Hourly 0.1° Precipitation: Methodology and Quantitative Assessment. Bull. Am. Meteorol. Soc. 2019, 100, 473–500. [Google Scholar] [CrossRef] [Green Version]
- Hong, Y.; Hsu, K.L.; Sorooshian, S.; Gao, X.G. Precipitation Estimation from Remotely Sensed Imagery using an Artificial Neural Network Cloud Classification System. J. Appl. Meteorol. 2004, 43, 1834–1852. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, P.; Shearer, E.J.; Tran, H.; Ombadi, M.; Hayatbini, N.; Palacios, T.; Huynh, P.; Braithwaite, D.; Updegraff, G.; Hsu, K.; et al. The CHRS Data Portal, an easily accessible public repository for PERSIANN global satellite precipitation data. Sci. Data 2019, 6, 180296. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brier, G.W. Verification of forecasts expressed in terms of probability. Mon. Weather Rev. 1950, 78, 1–3. [Google Scholar] [CrossRef]
- Perkins, S.E.; Pitman, A.J.; Holbrook, N.J.; Mcaneney, J. Evaluation of the AR4 Climate Models’ Simulated Daily Maximum Temperature, Minimum Temperature, and Precipitation over Australia Using Probability Density Functions. J. Clim. 2007, 20, 4356. [Google Scholar] [CrossRef]
- Yilmaz, K.K.; Gupta, H.V.; Wagener, T. A process-based diagnostic approach to model evaluation: Application to the NWS distributed hydrologic model. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef] [Green Version]
- Sorooshian, S.; Duan, Q.Y.; Gupta, V.K. Calibration of Rainfall-Runoff Models—Application of Global Optimization to the Sacramento Soil-Moisture Accounting Model. Water Resour. Res. 1993, 29, 1185–1194. [Google Scholar] [CrossRef]
- Yapo, P.O.; Gupta, H.V.; Sorooshian, S. Automatic calibration of conceptual rainfall-runoff models: Sensitivity to calibration data. J. Hydrol. 1996, 181, 23–48. [Google Scholar] [CrossRef]
- Pushpalatha, R.; Perrin, C.; Le Moine, N.; Andreassian, V. A review of efficiency criteria suitable for evaluating low-flow simulations. J. Hydrol. 2012, 420, 171–182. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. Asabe 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Zhang, X.B.; Alexander, L.; Hegerl, G.C.; Jones, P.; Tank, A.K.; Peterson, T.C.; Trewin, B.; Zwiers, F.W. Indices for monitoring changes in extremes based on daily temperature and precipitation data. Wiley Interdiscip. Rev.-Clim. Chang. 2011, 2, 851–870. [Google Scholar] [CrossRef]
- Li, J.; Liu, Z.; Yao, Z.; Wang, R. Comprehensive assessment of Coupled Model Intercomparison Project Phase 5 global climate models using observed temperature and precipitation over mainland Southeast Asia. Int. J. Climatol. 2019, 39, 4139–4153. [Google Scholar] [CrossRef]
- Zhuang, J.-Q.; Iqbal, J.; Peng, J.-B.; Liu, T.-M. Probability prediction model for landslide occurrences in Xi’an, Shaanxi Province, China. J. Mt. Sci. 2014, 11, 345–359. [Google Scholar] [CrossRef]
- Xie, P.; Joyce, R.; Wu, S.; Yoo, S.-H.; Yarosh, Y.; Sun, F.; Lin, R. Reprocessed, Bias-Corrected CMORPH Global High-Resolution Precipitation Estimates from 1998. J. Hydrometeorol. 2017, 18, 1617–1641. [Google Scholar] [CrossRef]
- Brunetti, M.T.; Melillo, M.; Peruccacci, S.; Ciabatta, L.; Brocca, L. How far are we from the use of satellite rainfall products in landslide forecasting? Remote Sens. Environ. 2018, 210, 65–75. [Google Scholar] [CrossRef]
- Chen, S.; Hu, J.; Zhang, A.; Min, C.; Huang, C.; Liang, Z. Performance of near real-time Global Satellite Mapping of Precipitation estimates during heavy precipitation events over northern China. Theor. Appl. Climatol. 2019, 135, 877–891. [Google Scholar] [CrossRef]
- Tian, Y.; Peters-Lidard, C.D.; Choudhury, B.J.; Garcia, M. Multitemporal analysis of TRMM-based satellite precipitation products for land data assimilation applications. J. Hydrometeorol. 2007, 8, 1165–1183. [Google Scholar] [CrossRef]
- Wei, L.Y.; Jiang, S.H.; Ren, L.L.; Wang, M.H.; Zhang, L.Q.; Liu, Y.; Yuan, F.; Yang, X.L. Evaluation of seventeen satellite-, reanalysis-, and gauge-based precipitation products for drought monitoring across mainland China. Atmos. Res. 2021, 263, 105813. [Google Scholar] [CrossRef]
- Ashouri, H.; Hsu, K.-L.; Sorooshian, S.; Braithwaite, D.K.; Knapp, K.R.; Cecil, L.D.; Nelson, B.R.; Prat, O.P. PERSIANN-CDR: Daily Precipitation Climate Data Record from Multisatellite Observations for Hydrological and Climate Studies. Bull. Am. Meteorol. Soc. 2015, 96, 69–83. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Tang, G.; Hong, Y. Cross-evaluation of ground-based, multi-satellite and reanalysis precipitation products: Applicability of the Triple Collocation method across Mainland China. J. Hydrol. 2018, 562, 71–83. [Google Scholar] [CrossRef]
- Guo, X.J.; Cui, P.; Li, Y.; Zhang, J.Q.; Ma, L.; Mahoney, W.B. Spatial features of debris flows and their rainfall thresholds in the Wenchuan earthquake-affected area. Landslides 2016, 13, 1215–1229. [Google Scholar] [CrossRef]
- Hwang, C.L.; Yoon, K. Multiple Attribute Decision Making: Methods and Applications: A State-of-the-Art Survey; Springer: Berlin, Germany; New York, NY, USA, 1981; 259p. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).