Abstract
Since anomaly targets in hyperspectral images (HSIs) with high spatial resolution appear as connected areas instead of single pixels or subpixels, both spatial and spectral information of HSIs can be exploited for a hyperspectal anomaly detection (AD) task. This article proposes a hyperspectral AD method based on Wasserstein distance (WD) and spatial filtering (called AD-WDSF). Based on the assumption that both background and anomaly targets obey the multivariate Gaussian distribution, background and anomaly target distributions are estimated in the local regions of HSIs. Subsequently, the anomaly intensity of test pixels centered in the local regions are determined via measuring the WD between background and anomaly target distributions. Lastly, spatial filters, i.e., guided filter (GF), total variation curvature filter (TVCF), and Maxtree filter, are exploited to further refine detection results. Experimental results conducted on two real hyperspectral data sets demonstrate that the proposed method achieves competitive detection performance compared with the state-of-the-art AD methods.
1. Introduction
Hyperspectral anomaly detection (AD) has been an active research area for several decades. since it is significant in broad domains, such as marine monitoring [1] and environment monitoring [2]. In practice, hyperspectral AD is a challenging task because there is no prior knowledge about background and anomaly targets. As material composition is unique, anomalies in hyperspectral images (HSIs) possess distinctive spectral characteristics from their surrounding background. Moreover, due to the spatial resolution of HSIs increasing, anomaly objects appear as small connected areas compared to background. Thus, it is likely to distinguish anomaly targets of interest from the background based on the spectral and spatial information of HSIs.
Among the open literature, numerous algorithms have been developed to resolve the hyperspectral AD problem. The Reed Xiaoli (RX) detector proposed by Reed and Yu [3] is a milestone work for AD, which depends on the assumption that background obeys the multivariate Gaussian distribution. Then, anomalies are detected by calculating the Mahalanobis distances between test pixels and the estimated statistical model. Since the RX detector characterizes background information from an entire HSI, an unsatisfactory model may be estimated when anomalies contaminate background statistics. To mitigate the influence of anomalies on background statistics, AD methods that estimate the background information in the local regions of HSIs have been exploited. For instance, the local RX (LRX) detector [4] characterizes the background by local statistics in the fixed dual windows of HSIs. The superpixel based dual window RX (SPDWRX) AD detector [5] uses superpixel segmentation to adaptively determine the dual window for LRX detection, where the background in each superpixel is estimated by the local Gaussian model. Besides, Gaussian mixture model (GMM) is another strategy for modeling background statistics from multicomponent scenes [6]. Cluster based anomaly detection (CBAD) [7] is a classical AD method based on GMM, which segments a HSI into different homogeneous clusters and estimates background statistics over clusters. Then, anomalies in each cluster are detected by the Mahalanobis distances between test pixels and the background clutter statistics. According to these works, the core idea of statistical based AD algorithms is to estimate the background distribution, then detect anomalies by calculating the Mahalanobis distances between test pixels and the estimated model.
To avoid estimating statistical models for HSIs, representation-based methods have been developed for hyperspectral AD. Representation-based methods can be divided into two categories: sparse representation-based and low-rank representation-based. Sparse representation-based methods assume that the background pixel can be linearly represented by its neighborhood pixels, while the anomalous pixel cannot. For example, with this assumption, a collaborative representation-based detector (CRD) is proposed in [8], where background is estimated by surrounding spatial neighborhoods via a dual-window strategy and anomalies are identified by subtracting the predicted background from the original image. Low-rank representation-based algorithms transform the hyperspectral AD problem into a low-rank matrix decomposition problem [9,10,11]. For instance, an AD method based on low-rank and sparse representation (LRASR) is proposed in [12], which decomposes a HSI into background and residual parts. Then, anomalies are determined by the response of the residual parts.
Apart from the statistical-based and representation-based AD algorithms, spatial-based and spatial–spectral-based methods have been recently proposed for AD due to an increase in the spatial resolution of HSIs [13,14,15,16]. For spatial-based AD methods, anomalies are detected by exploiting the texture and structure information of images. For instance, based on the hypothesis that anomaly objects in HSIs appear as small areas compared to background, a structure tensor and guided filter (STGF) based AD method is proposed in [17]. In this method, morphological attribute operators are applied in the selected band images to remove background and preserve anomalies. Then, guided filter (GF) is conducted to further refine detection results. For spatial–spectral-based AD methods, both spatial and spectral features are used for hyperspectral AD. Lei et al. [18] proposed a spatial–spectral feature extraction-based hyperspectral AD method. In spectral domain, discriminative spectral features are extracted through a deep belief network (DBN), and anomalies are detected by the Mahalanobis distance method. In spatial domain, morphological attribute operators and GF are used to detect anomalies that appear as small areas. Then, the two detection results are fused by a linear function. Wang et al. [19] proposed a multiple features and isolation forest-based detector (MFIFD) for hyperspectral AD. The spectral feature, Gabor feature, extended morphological profile (EMP) feature, and extend multiattribute profile (EMAP) feature are extracted from HSI. Then, the complementary properties of spectral and spatial features are used to build isolation forests, and the anomaly score for each test pixel is calculated based on the path lengths in isolation forests. Most importantly, the spatial–spectral-based works prove that the detection performance will be unsatisfactory if only one aspect (spatial or spectral) is exploited.
Along with the development of hyperspectral imaging technology, HSIs with high spatial and spectral resolution can be captured. Anomalies in HSIs generally appear as area targets instead of single pixels or subpixels, which motivate us to extract knowledge from both background and anomaly target for the AD task. Moreover, the above works prove that using both spatial and spectral information is superior to using one aspect. Therefore, we propose a hyperspectral AD algorithm based on Wasserstein distance (WD) and spatial filtering (called AD-WDSF) in this article. Based on the assumption that both background and anomaly targets obey the multivariate Gaussian distribution, background and anomaly target models are estimated from the dual windows of HSI. Then, a modified WD is exploited to measure the dissimilarity between background and anomaly target distributions, and the anomaly response of test pixels centered in the dual windows can be determined based on the evaluated distances. Finally, spatial filters, i.e., GF, total variation curvature filter (TVCF), and Maxtree filter, are utilized to further refine detection results.
The main contributions of our work can be mainly summarized as follows.
- To our knowledge, no studies have been reported on how to estimate the anomaly target distribution and detect anomalies via the dissimilarity between background and anomaly target distributions. With the assumption that both background and anomaly target obey the multivariate Gaussian distribution, the background and anomaly target distributions are estimated in the local regions of HSI and the anomaly intensity of test pixels centered in the local regions are evaluated by the dissimilarity between two distributions, which opens up an innovative way for anomalous area target detection.
- To determine anomalies based on the background and anomaly target distributions, a modified WD is developed to measure the dissimilarity between two distributions, which can effectively improve the discrimination capacity between anomalies and background compared with the original one.
- GF, TVCF, and Maxtree filter are exploited to refine detection results. It is demonstrated that the combination of multiple filters can significantly improve AD performance.
2. Methodology
As illustrated in Figure 1, the proposed AD method mainly consist of three parts: anomaly detection withWD, rectification with guided filtering, and background suppression with spatial features. For the first stage, the background and anomaly target distributions are estimated by local Gaussian models in the dual windows of HSI, where the anomaly target model characterizes from the information in inner window region and the background model evaluates from the information in outer window region. Then, a modified WD is exploited to measure the dissimilarity between distributions, and the initial detection map is achieved based on the evaluated values. For the middle stage, GF is utilized to smooth the initial detection map based on a given guidance image, which is conductive to improve the anomaly responses of pixels. For the last stage, based on the connectivity, gradient, and area size attributes of anomaly targets, TVCF and Maxtree filter are conducted on the rectified detection map to suppress background information.

Figure 1.
Schematic of the hyperspectral AD algorithm based on Wassertein distance and spatial filtering.
2.1. Anomaly Detection with Wasserstein Distance
Similar to the LRX detector, the AD with WD conducts detection in a local window centered around each pixel. As shown in Figure 1, the local window is separated into two regions, i.e., inner window region and outer window region. In this method, the inner window region is considered as anomalous area target, and the outer window region is taken as background. Based on the assumption that both background and anomaly target can be characterized by the multivariate Gaussian distribution, the mean vectors and variance matrices of inner and outer window regions are computed, which are denoted as and for inner window region, and and for outer window region. Then, the anomaly target and background distributions are denoted as t∼N (, ) and b∼N (, ), respectively.
WD [20,21] has its root in optimal transport theory. What is more, the optimal transport problem has been extended to the case of Gaussian Stationary stochastic processes as well as Gaussian random field [22,23,24]. Thus, WD can be used to form a metric between two Gaussian random vectors, which has provided a successful framework for the comparison of objects on many domains such as computer vision and image retrieval [25]. In this part, WD is taken as the distance metric between the anomaly target and background distributions, which is measured by
From the above expression, the mean vector and variance matrix play the equally important role in evaluating the dissimilarity between anomaly target and background distributions. Since the intensity of pixels varies in different categories, the mean vector and variance matrix show different significance in measuring the dissimilarity between two distributions. Thus, we modify the WD by attaching two weight parameters (i.e., > 0 and > 0) to the two terms, which is denoted as
Then, the anomaly degree of each test pixel centered in the dual window can be measured based on the modified WD. The larger value reveals the greater anomaly degree of the test pixel, that is, the test pixel is more likely to be a anomalous pixel. Finally, the initial detection map is achieved based on the measured values, which is denoted as A.
2.2. Rectification with Guided Filtering
Since pixels belonging to the same object generally have high spatial correlation and tend to have similar response values in the detection map, GF is applied to smooth the initial detection map, which is conducive to enhance the response of anomaly pixels. According to the GF model in [26], a guidance image is the key of filtering because the filtering output is a local linear transform of guidance image. In this method, the structure tensor [27] is utilized to construct a guidance image that contains the abundant spatial information (e.g., structure and texture information) of original HSI. For a HSI, the structure tensor of a band image I at pixel i is illustrated as
where and denote the gradients at pixel i along x and y directions, respectively. The structure tensor is a semi-definite matrix and can be decomposed as
where and are the non-negative eigenvalues, and and are the corresponding eigenvectors. The trace is the sum of eigenvalues, i.e., =+, which can be utilized to measure the edge and corner response of a region. Thus, the sum of the trace in a band image reveals the image structure information, which is expressed as
where n is the number of pixels in the band image. The larger value indicates the more structure information contained in the band image. To select band images with abundant spatial information, we sort the corresponding values of all band images in a descending order, and the first p percent band images are chosen, which are denoted as , , …, . The guidance image is the average of the selected band images, which is denoted as
Then, pixel response in the initial detection map is rectified as
where is the filtering output of pixel i. and are the linear coefficients in the local window , which are expressed as
where and are the mean and variance of in , is the number of pixels in , and is the mean of in . Since the pixel i is involved in all the overlapping windows that cover i, the value of in Equation (7) is not identical when it is computed in different windows. Thus, we rewrite it as
where and are the average coefficients of all windows overlapping pixel i.
2.3. Background Suppression with Spatial Features
The rectified detection map may include the anomaly targets as well as background information, e.g., the edges that present unique spectral feature compared to their surrounding pixels. Based on the spatial attributes of anomaly targets, TVCF and Maxtree filter are utilized to suppress the background information and preserve anomaly targets. To enhance the contrast between anomalies and background before spatial filtering, the detection map is adjusted by an exponential nonlinear function, which is expressed as
where is an adjusted parameter.
TVCF [16,28] provides a rapid approximate solution for the variational problems in image processing. Based on the piecewise constant assumption, TVCF adopts a pixel-local analytical solution and conducts a local filter projection operator for the variational model. In general, TVCF is used for image smoothing and denoising with prior knowledge of total-variation (TV) regularization. For this AD task, TVCF is exploited to extract background information with contrast edges. Then, the detection result is refined by subtracting the background information from the rectified detection map. The detailed description is as follows.
For a center pixel (i, j) in the rectified detection map Q, the projection distances in a local pixel neighborhood can be calculated, which are denoted as
Then, the pixel response is updated by the minimal projection distance, which is formulated as
where . From Equations (12) and (13), the center pixel will not be smoothed if it is an edge point. Consequently, the background image with contrast edges can be achieved after a large number of iterations. The detection result is refined by suppressing the background information, which is expressed as
Maxtree [29,30,31] is a data structure that describes an entire image through the hierarchical relationship of connected components (CCs) resulting from different thresholds. Filtering an image using Maxtree contains three steps: build a Maxtree of images using the appropriate connectivity rule, remove some of tree nodes based on attribute criteria, and reconstruct the image. Since anomaly targets appear as small connected areas in spatial domain and the response values of anomaly targets are usually larger than these of background, Maxtree representation of the rectified detection map can be built based on response values and pruned based on area size attribute. Then, anomaly targets are removed and background information is preserved in the reconstructed image, and the detection result is refined by subtracting the reconstructed image from the detection map. The detailed description is as follows.
For the rectified detection map, a set of CCs can be achieved from the threshold decomposition of upper level sets. There is an inclusion relationship between CCs: the CC corresponding to a large threshold is included in the CC corresponding to a small threshold. The resulting CCs are ordered by inclusion and structured in a tree, where the root node represents the entire detection map and the tree leaves represent the areas with maximal response values. In other words, the Maxtree describes the entire detection map through its hierarchical property of threshold decomposition. The AD task is transformed as the search for tree nodes that correspond to anomaly targets, where the area size attribute is applied to perform this search. The Maxtree representation and filtering process are illustrated in Figure 2, where the reconstructed detection map is denoted as . The anomaly targets are extracted by the differential operation between the original detection map and the reconstructed detection map, which is represented as
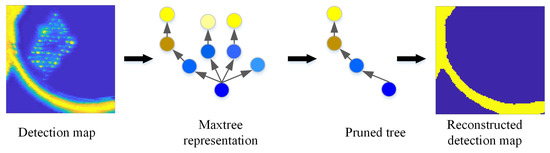
Figure 2.
Schematic of the Maxtree representation and filtering process.
To further improve the AD performance, the detection results achieved by TVCF and Maxtree filter are fused via a linear function, which is denoted as
3. Experimental Results and Analysis
In this section, two real hyperspectral data sets are first introduced. Then, extensive experiments are conducted on the two data sets to evaluate the performance of the proposed AD-WDS method.
3.1. Hyperspectral Data Sets
There are two real hyperspectral data sets, which are consisted of 15 images captured over different scenes. The detailed information is listed as follows.
- Airport-Beach-Urban Data Set [13]: The Airport-Beach-Urban (ABU) data set contains 13 HSIs with pixels and the corresponding references. The ABU data set is captured by the Airborne Visible/Infrared Imaging Spectrometer (AVIRIS) and Reflective Optics System Imaging Spectrometer (ROSIS-03) sensors in the airport, beach, and urban scenes. Since flight heights are different, the spatial resolutions of images and the scales of anomalies are different, which can be observed in Figure 3, Figure 4 and Figure 5.
 Figure 3. Detection maps of the compared AD methods.The sample images from top to bottom are airport-1, airport-2, airport-3, and airport-4, respectively. (a) Color composites of airport scene; (b) Reference map; (c) GRX; (d) LRX; (e) CRD; (f) LRASR; (g) ADLR; (h) KIFD; (i) Proposed.
Figure 3. Detection maps of the compared AD methods.The sample images from top to bottom are airport-1, airport-2, airport-3, and airport-4, respectively. (a) Color composites of airport scene; (b) Reference map; (c) GRX; (d) LRX; (e) CRD; (f) LRASR; (g) ADLR; (h) KIFD; (i) Proposed.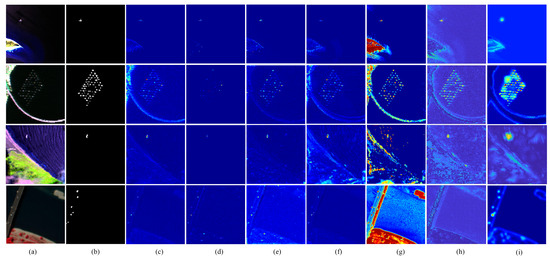 Figure 4. Detection maps of the compared AD methods. The sample images from top to bottom are beach-1, beach-2, beach-3, and beach-4, respectively. (a) Color composites of beach scene; (b) Reference map; (c) GRX; (d) LRX; (e) CRD; (f) LRASR; (g) ADLR; (h) KIFD; (i) Proposed.
Figure 4. Detection maps of the compared AD methods. The sample images from top to bottom are beach-1, beach-2, beach-3, and beach-4, respectively. (a) Color composites of beach scene; (b) Reference map; (c) GRX; (d) LRX; (e) CRD; (f) LRASR; (g) ADLR; (h) KIFD; (i) Proposed.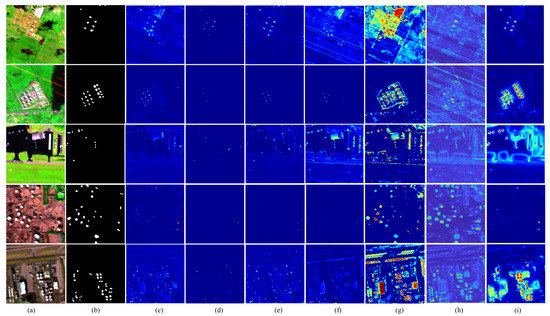 Figure 5. Detection maps of the compared AD methods. The sample mages from top to bottom are urban-1, urban-2, urban-3, urban-4, and urban-5, respectively. (a) Color composites of urban scene; (b) Reference map; (c) GRX; (d) LRX; (e) CRD; (f) LRASR; (g) ADLR; (h) KIFD; (i) Proposed.
Figure 5. Detection maps of the compared AD methods. The sample mages from top to bottom are urban-1, urban-2, urban-3, urban-4, and urban-5, respectively. (a) Color composites of urban scene; (b) Reference map; (c) GRX; (d) LRX; (e) CRD; (f) LRASR; (g) ADLR; (h) KIFD; (i) Proposed. - AVIRIS Data Set [32]: The AVIRIS data set contains two HSIs captured by AVIRIS sensor in San Diego, CA, USA. The AVIRIS-1 is with pixels and 244 spectral bands, where three planes with total number of 58 pixels are taken as anomalies. The AVIRIS-2 is with pixels and 189 spectral bands, where three air crafts with a total number of 143 pixels are considered as anomalies. The sample images and their reference maps are given in Figure 6.
 Figure 6. Detection maps of the compared AD methods. The sample images from top to bottom are AVIRIS-1, and AVIRIS-2, respectively. (a) Color composites of urban scene; (b) Reference map; (c) GRX; (d) LRX; (e) CRD; (f) LRASR; (g) ADLR; (h) KIFD; (i) Proposed.
Figure 6. Detection maps of the compared AD methods. The sample images from top to bottom are AVIRIS-1, and AVIRIS-2, respectively. (a) Color composites of urban scene; (b) Reference map; (c) GRX; (d) LRX; (e) CRD; (f) LRASR; (g) ADLR; (h) KIFD; (i) Proposed.
3.2. Detection Performance
To evaluate the detection performance of the proposed AD-WDSF method, five state-of-the-art AD algorithms are utilized for comparison, including GRX [4], LRX [4], CRD [8], a AD method based on low-rank and SR (LRASR) [12], an abundance-and dictionary-based low-rank decomposition (ADLR) [10], and a Kernel Isolation Forest-based hyperspectral anomaly Detection method (KIFD) [33]. For the LRX and CRD, the inner window size ranges from 3 to 19, the outer window size varies from 5 to 21, and the regularization parameter contained in CRD sets to 0.01. For the LRASR method, the parameters set to , , and . For the ADLR method, the number of endmembers ranges from 5 to 30, the bw ranges from 0.2 to 0.3, and . For the KIFD method, the first principal components set is 300. For the proposed AD-WDSF method, the weight parameter ranges from 1 to 4 and varies from 0.1 to 0.5, the inner and outer window sizes are set to and , the parameter p varies from to , and the adjusted parameter ranges from 0.01 to 5.
The detection performance of AD algorithms are evaluated by the two most widely used metrics, i.e., the receiver operating characteristic (ROC) [34] and the area under the curve (AUC) [35]. The ROC curve can be plotted by the true positive rate (TPR) and the false positive rate (FPR) at various thresholds. The ROC curve indicates a good detection performance when nearing to the upper leftmost corner. The AUC can be calculated as the area of a ROC curve. The larger AUC score reveals the better detection performance.
For the above AD algorithms, the detection maps of 15 HSIs contained in two hyperspectral data sets are presented in Figure 3, Figure 4, Figure 5 and Figure 6, respectively. From the detection maps, it can be observed that the RX, LRASR, ADLR, and KIFD methods tend to highlight targets while preserve numerous background information, which decreases the AD accuracy. Moreover, the four methods are sensitive to strip noise as shown in the urban-1 scene, where the strip noise is detected as anomalies. The LRX method can suppress background information and remove the interference of strip noise, whereas it misses anomaly targets in most of scenes. The CRD method shows stable detection performance, but it also highlights background signals and misses anomalies in some scenes, e.g., beach-2 and urban-4 scenes. Compared with other methods, the proposed AD-WDSF can effectively detect the locations and shapes of anomaly targets while suppress the background information. However, it can be found that the high contrast edges in images are likely to be detected as anomalies.
From the ROC results shown in Figure 7, the proposed AD-WDSF is superior to the most comparison methods, because the corresponding curves are closer to the upper leftmost corner. The ROC results are consistent with the AUC scores reported in Table 1, where the proposed method achieve larger AUC value than other methods in most scenes. It also can be found that the AUC scores achieved by the proposed method are close to 1. Thus, we can conclude that the AD-WDSF shows competitive detection performance compared with the state-of-the-art AD methods.
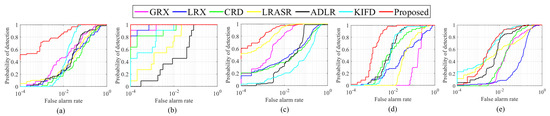
Figure 7.
ROC curves of the compared AD methods on five images. (a) airport-4; (b) beach-3; (c) urban-2; (d) AVIRIS-1; (e) AVIRIS-2.

Table 1.
AUC Scores of the compared AD algorithms on ABU and AVIRIS data sets.
3.3. Ablation Experiments
In this section, ablation experiments are conducted to evaluate the performance of each part contained in the AD-WDSF method. There are four combination algorithms. The first is AD based on WD (called AD-WD). The second is AD based on WD and GF (called AD-WD-GF). The third is AD based on WD, GF, and TVCF (called AD-WD-GF-TVCF). The fourth is AD based on WD, GF, and Maxtree filter (called AD-WD-GF-Maxtree).
The ablation experiments are conducted on the ABU and AVIRIS data sets. The detection maps for four images, i.e., airport-1, beach-2, urban-2, and AVIRIS-1, are presented in Figure 8. The AUC values of all images are presented in Table 2. From the visual and quantitative results, the AD-WD method can effectively detect anomaly targets and achieve high AUC scores for most of images, whereas the detection performance on the images with multiple small targets or numerous contrast edges is unsatisfactory, e.g., beach-2 scene. The AD-WD-GF method can smooth the local areas and enhance the response of anomaly targets, which improves the detection accuracy as reported in Table 2. However, the background signals contained in detection maps are also enhanced, which can be observed from the detection maps of beach-2 and AVIRIS-1 scenes. From the background information achieved by AD-WD-GF-TVCF method, the detection map is smoothed and only pixels with large gradients are preserved. In other words, the contrast edges can be detected, and the background information can be effectively suppressed. However, the detection performance is degraded when anomaly targets on the edges are taken as background signals and removed from the detection map, such as the detection map of airport-1 shown in Figure 8 and the AUC score of beach-4 presented in Table 2. Based on the background information achieved by AD-WD-GF-Maxtree method, the anomaly targets with high response values and small area sizes can be removed from the detection map, as the detection map of beach-2 shown in Figure 8. However, Maxtree filter will not work if the response values between anomaly targets and background are similar, which can be found from the detection map of urban-2 and the AUC score of urban-1.
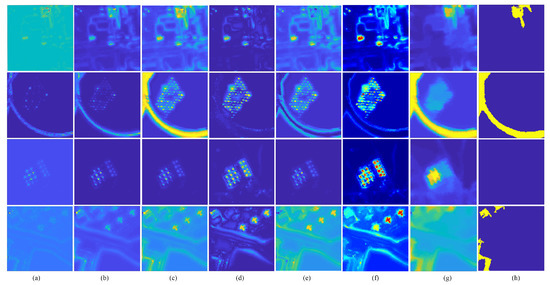
Figure 8.
Detection maps of the four combination methods. The sample images from top to bottom are airport-1, beach-2, urban-2, and AVIRIS-1, respectively. (a) AD-WD; (b) AD-WD-GF; (c) adjusted detection map achieved by the exponential nonlinear function; (d) AD-WD-GF-TVCF; (e) AD-WD-GF-Maxtree; (f) AD-WDSF; (g) background information achieved by AD-WD-GF-TVCF; (h) background information achieved by AD-WD-GF-Maxtree.

Table 2.
AUC Values of the combination methods on ABU and AVIRIS data sets.
From the overall detection result shown in Table 2, it can be observed that the strategy combining the multiple spatial filter outperforms the strategy adopting only one filter. In other words, the combination of multiple filters can significantly improve the AD performance.
3.4. Parameter Analysis
This section analyzes the effects of parameter settings on detection performance. The parameters include the inner and outer window sizes (, ) in the AD based on WD, the weight parameters and in the updated WD, the first p percent bands selected for constructing guidance image, and the adjusted parameter contained in the exponential nonlinear function. The influences of inner and outer window sizes (, ) on detection performance are reported in Table 3. From the AUC scores shown in Table 3, it can be observed that the small inner and outer window sizes are conducive to improve detection performance, especially for scenes with small area targets, e.g., airport-3 and urban-5 scenes. Figure 9 illustrates the effects of the weight parameters and over AUC values on five images. As the results shown in Figure 9, the AUC score is higher when is larger than 1, and the AUC value slightly or sharply decreases when is close to 1. In other words, the large and small are beneficial to obtain perfect detection performance, which demonstrates that the updated WD is superior to the original one. The impacts of the parameters p and over AUC values on five images are presented in Figure 10. As the results shown in the left of Figure 10, the AUC score tends to be stable or fluctuates within a small range when the parameter p varies from to . From the the results shown in the right of Figure 10, the AUC scores for five images are quite large when the parameters ranges from 0.01 to 1, and the AUC scores for some images sharply decrease when the the parameters sets to a larger value, e.g., 1 and 10. Consequently, the high AUC score is associated with the small for most of scenes.

Table 3.
Effects of dual window size (, ) on detection performance.

Figure 9.
Effects of the weight parameters and over AUC values on five images. (a) airport-4; (b) beach-3; (c) urban-2; (d) AVIRIS-1; (e) AVIRIS-2.
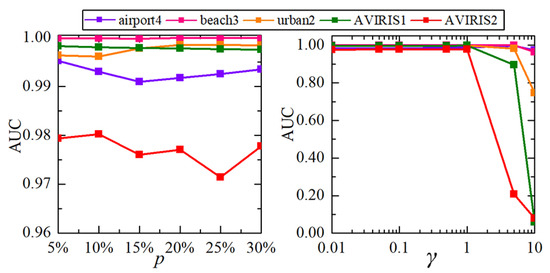
Figure 10.
Effect of the parameters p and over AUC values on five images.
3.5. Comparison of Metrics between Gaussian Random Vectors
With the assumption that both the background and anomaly area target obey the multivariate Gaussian distribution in the local regions of HSIs, the metrics between Gaussian random vectors are used to estimate the dissimilarity between two distributions, and the anomaly response of each pixel centered in the dual window can be achieved based on the evaluated value. To evaluate the detection performance of WD used in the proposed algorithm, two state-of-the-art metrics are exploited for comparison, i.e., Kullback–Leibler (KL) divergence [36] and Bhattacharyya distance (BD) [37].The comparison experiments are conducted on the ABU and AVIRIS data sets.For the three metrics, the AUC scores are represented in Table 4.

Table 4.
Comparison of AUC scores achieved by different metrics.
From the AUC values, it can be observed that the WD can achieve higher scores for all sample images contained in two hyperspectral data sets. In other words, the WD can achieve better detection performance compared with other two metrics. For the KL divergence and BD, the AUC scores of some sample images are high (e.g., beach-1 and beach-3), whereas the AUC values of most sample images are less than 0.6. That is, the detection performance of KL divergence and BD are unsatisfactory, which may be caused by the large inner and outer window sizes of local regions. For KL divergence and BD, the covariance matrix of background and target must be full-rank so that the inner and outer window sizes need to be large to get enough observation samples. In our experiments, the inner window size ranges from 29 to 35, and the outer window size varies from 41 to 49. However, the sizes of anomaly targets are usually smaller than the inner window sizes due to the limited spatial resolution of HSIs. Hence, the inner window regions may contain the background characteristics, which decreases the detection performance. To sum up, WD is more effective in hyperspectral AD task compared with other two metrics.
4. Conclusions
In this paper, we propose a novel method called AD-WDSF for hyperspectral AD task. The proposed AD-WDSF algorithm makes full use of the spectral and spatial information of HSIs in the AD processes. Considering that anomaly targets in HSIs appear as connected areas, the AD-WDSF estimates the background and anomaly target distributions in the local regions of HSIs, then the anomalous pixels centered in the local regions are detected via measuring the dissimilarity between two distributions. Based on the connectivity, gradient, and area size attributes of anomaly targets, multiple spatial filters are exploited to refine the detection result. Experiments conducted on two real hyperspectral data sets demonstrate that the AD-WDSF outperforms the compared state-of-the-art methods. However, there are still some unresolved issues. Specifically, the parameter setting in this method is empirical and laborious, and some detection results still contain background information. These aspects deserve improvements in future work.
Author Contributions
Conceptualization, X.C. and Y.W.; methodology, X.C.; software, X.C.; validation, X.C., M.W. and C.G.; formal analysis, C.G.; investigation, X.C.; resources, X.C.; data curation, X.C. and C.G.; writing—original draft preparation, X.C. and C.G.; writing—review and editing, X.C.; visualization, X.C.; supervision, Y.W.; project administration, Y.W.; funding acquisition, Y.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Key Research Project of Zhejiang Lab (No.2021MH0AC01).
Data Availability Statement
Hyperspectral data is available at http://xudongkang.weebly.com/, accessed on 19 May 2022.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Freitas, S.; Silva, H.; Silva, E. Remote Hyperspectral Imaging Acquisition and Characterization for Marine Litter Detection. Remote Sens. 2021, 13, 2536. [Google Scholar] [CrossRef]
- Han, X.; Zhang, H.; Sun, W. Spectral Anomaly Detection Based on Dictionary Learning for Sea Surfaces. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1502505. [Google Scholar] [CrossRef]
- Reed, I.; Yu, X. Adaptive multiple-band CFAR detection of an optical pattern with unknown spectral distribution. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 1760–1770. [Google Scholar] [CrossRef]
- Molero, J.M.; Garzón, E.M.; García, I.; Plaza, A. Analysis and Optimizations of Global and Local Versions of the RX Algorithm for Anomaly Detection in Hyperspectral Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 801–814. [Google Scholar] [CrossRef]
- Ren, L.; Zhao, L.; Wang, Y. A Superpixel-Based Dual Window RX for Hyperspectral Anomaly Detection. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1233–1237. [Google Scholar] [CrossRef]
- Qu, J.; Du, Q.; Li, Y.; Tian, L.; Xia, H. Anomaly Detection in Hyperspectral Imagery Based on Gaussian Mixture Model. IEEE Trans. Geosci. Remote Sens. 2021, 59, 9504–9517. [Google Scholar] [CrossRef]
- Carlotto, M. A cluster-based approach for detecting man-made objects and changes in imagery. IEEE Trans. Geosci. Remote Sens. 2005, 43, 374–387. [Google Scholar] [CrossRef]
- Li, W.; Du, Q. Collaborative Representation for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1463–1474. [Google Scholar] [CrossRef]
- Zhang, Y.; Du, B.; Zhang, L.; Wang, S. A Low-Rank and Sparse Matrix Decomposition-Based Mahalanobis Distance Method for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1376–1389. [Google Scholar] [CrossRef]
- Qu, Y.; Wang, W.; Guo, R.; Ayhan, B.; Kwan, C.; Vance, S.; Qi, H. Hyperspectral Anomaly Detection Through Spectral Unmixing and Dictionary-Based Low-Rank Decomposition. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4391–4405. [Google Scholar] [CrossRef]
- Cheng, X.; Xu, Y.; Zhang, J.; Zeng, D. Hyperspectral Anomaly Detection via Low-Rank Decomposition and Morphological Filtering. IEEE Geosci. Remote Sens. Lett. 2022, 19, 5511905. [Google Scholar] [CrossRef]
- Xu, Y.; Wu, Z.; Li, J.; Plaza, A.; Wei, Z. Anomaly Detection in Hyperspectral Images Based on Low-Rank and Sparse Representation. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1990–2000. [Google Scholar] [CrossRef]
- Li, S.; Zhang, K.; Hao, Q.; Duan, P.; Kang, X. Hyperspectral Anomaly Detection With Multiscale Attribute and Edge-Preserving Filters. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1605–1609. [Google Scholar] [CrossRef]
- Jiang, K.; Xie, W.; Li, Y.; Lei, J.; He, G.; Du, Q. Semisupervised spectral learning with generative adversarial network for hyperspectral anomaly detection. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5224–5236. [Google Scholar] [CrossRef]
- Song, X.; Aryal, S.; Ting, K.M.; Liu, Z.; He, B. Spectral-Spatial Anomaly Detection of Hyperspectral Data Based on Improved Isolation Forest. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5516016. [Google Scholar] [CrossRef]
- Xiang, P.; Song, J.; Qin, H.; Tan, W.; Li, H.; Zhou, H. Visual Attention and Background Subtraction with Adaptive Weight for Hyperspectral Anomaly Detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 2270–2283. [Google Scholar] [CrossRef]
- Xie, W.; Jiang, T.; Li, Y.; Jia, X.; Lei, J. Structure Tensor and Guided Filtering-Based Algorithm for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4218–4230. [Google Scholar] [CrossRef]
- Lei, J.; Xie, W.; Yang, J.; Li, Y.; Chang, C.I. Spectral–Spatial Feature Extraction for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8131–8143. [Google Scholar] [CrossRef]
- Wang, R.; Nie, F.; Wang, Z.; He, F.; Li, X. Multiple Features and Isolation Forest-Based Fast Anomaly Detector for Hyperspectral Imagery. IEEE Trans. Geosci. Remote Sens. 2020, 58, 6664–6676. [Google Scholar] [CrossRef]
- Kolouri, S.; Nadjahi, K.; Simsekli, U.; Badeau, R.; Rohde, G.K. Generalized Sliced Wasserstein Distances. In Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 6–12 December 2019. [Google Scholar]
- Panaretos, V.M.; Zemel, Y. Statistical Aspects of Wasserstein Distances. Annu. Rev. Stat. Its Appl. 2019, 6, 405–431. [Google Scholar] [CrossRef] [Green Version]
- Zorzi, M. Optimal Transport Between Gaussian Stationary Processes. IEEE Trans. Autom. Control 2021, 66, 4939–4944. [Google Scholar] [CrossRef]
- Ramponi, F.; Ferrante, A.; Pavon, M. A Globally Convergent Matricial Algorithm for Multivariate Spectral Estimation. IEEE Trans. Autom. Control 2009, 54, 2376–2388. [Google Scholar] [CrossRef] [Green Version]
- Ferrante, A.; Pavon, M.; Ramponi, F. Hellinger Versus Kullback–Leibler Multivariable Spectrum Approximation. IEEE Trans. Autom. Control 2008, 53, 954–967. [Google Scholar] [CrossRef]
- Kolouri, S.; Park, S.R.; Thorpe, M.; Slepcev, D.; Rohde, G.K. Optimal Mass Transport: Signal processing and machine-learning applications. IEEE Signal Process. Mag. 2017, 34, 43–59. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Sun, J.; Tang, X. Guided Image Filtering. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1397–1409. [Google Scholar] [CrossRef]
- Qu, J.; Lei, J.; Li, Y.; Dong, W.; Zeng, Z.; Chen, D. Structure Tensor-Based Algorithm for Hyperspectral and Panchromatic Images Fusion. Remote Sens. 2018, 10, 373. [Google Scholar] [CrossRef] [Green Version]
- Gong, Y.; Sbalzarini, I.F. Curvature Filters Efficiently Reduce Certain Variational Energies. IEEE Trans. Image Process. 2017, 26, 1786–1798. [Google Scholar] [CrossRef] [Green Version]
- Salembier, P.; Liesegang, S.; López-Martínez, C. Ship Detection in SAR Images Based on Maxtree Representation and Graph Signal Processing. IEEE Trans. Geosci. Remote Sens. 2019, 57, 2709–2724. [Google Scholar] [CrossRef] [Green Version]
- Carlinet, E.; Géraud, T. A comparative review of component tree computation algorithms. IEEE Trans. Image Process. 2014, 23, 3885–3895. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, Y.; Carlinet, E.; Géraud, T.; Najman, L. Hierarchical segmentation using tree-based shape spaces. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 457–469. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Wang, X.; Zhong, Y.; Zhang, L. Hyperspectral anomaly detection via locally enhanced low-rank prior. IEEE Trans. Geosci. Remote Sens. 2020, 58, 6995–7009. [Google Scholar] [CrossRef]
- Li, S.; Zhang, K.; Duan, P.; Kang, X. Hyperspectral Anomaly Detection With Kernel Isolation Forest. IEEE Trans. Geosci. Remote Sens. 2020, 58, 319–329. [Google Scholar] [CrossRef]
- Kerekes, J. Receiver Operating Characteristic Curve Confidence Intervals and Regions. IEEE Geosci. Remote Sens. Lett. 2008, 5, 251–255. [Google Scholar] [CrossRef] [Green Version]
- Flach, P.A.; Hernández-Orallo, J.; Ramirez, C.F. A coherent interpretation of AUC as a measure of aggregated classification performance. In Proceedings of the ICML, Bellevue, WA, USA, 28 June–2 July 2011. [Google Scholar]
- Zorzi, M. On the robustness of the Bayes and Wiener estimators under model uncertainty. Automatica 2017, 83, 133–140. [Google Scholar] [CrossRef] [Green Version]
- Kailath, T. The Divergence and Bhattacharyya Distance Measures in Signal Selection. IEEE Trans. Commun. Technol. 1967, 15, 52–60. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).