Quantitative Evaluation of Grassland SOS Estimation Accuracy Based on Different MODIS-Landsat Spatio-Temporal Fusion Datasets
Abstract
:1. Introduction
2. Materials
2.1. Study Area
2.2. Data Resources
2.2.1. Remote Sensing Data
2.2.2. Ground Sampling Points Data
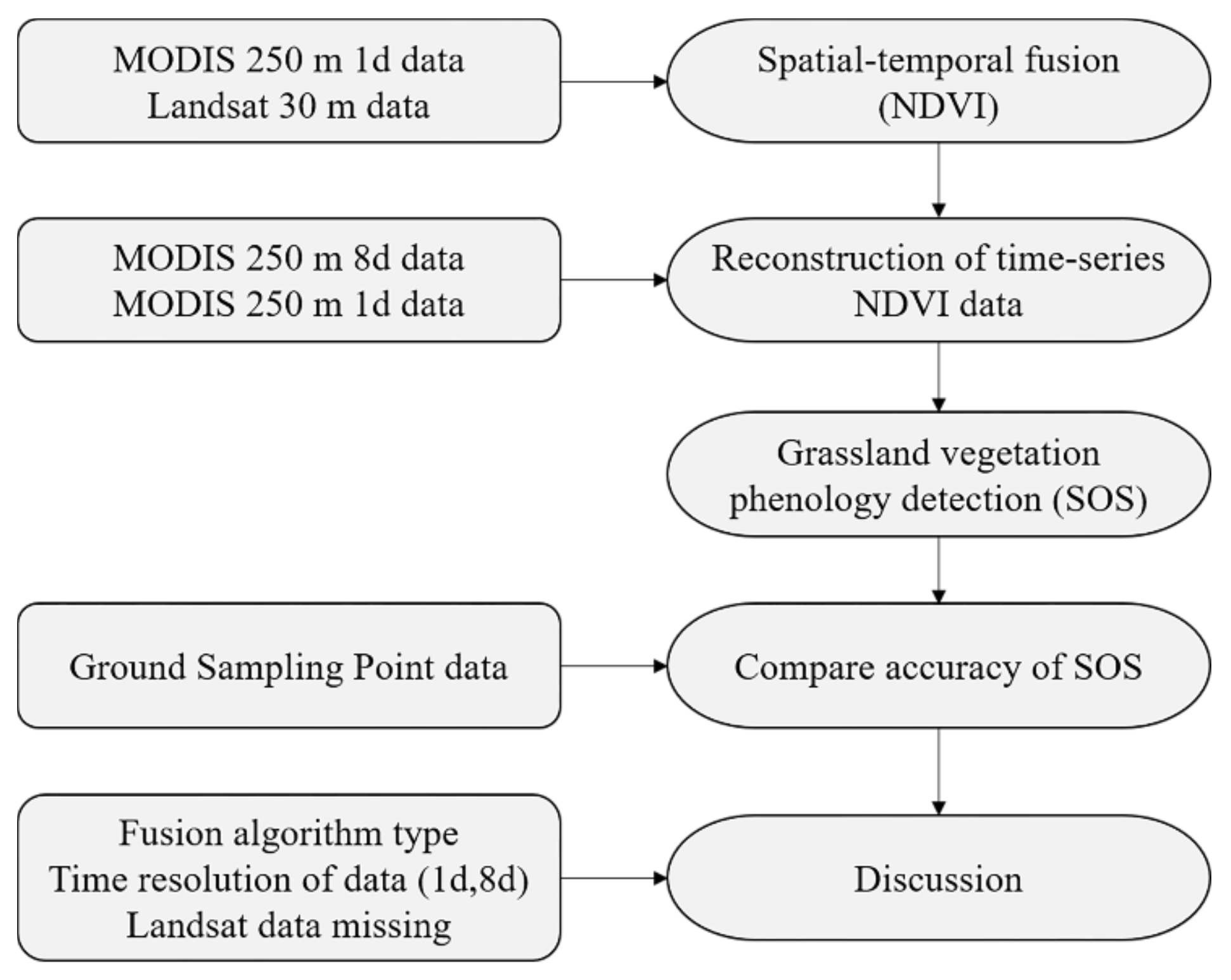
3. Methods
3.1. MODIS NDVI-Landsat NDVI Spatio-Temporal Fusion
3.2. Times-Series NDVI Vegetation Index Reconstruction
3.3. Inversion of Grassland Vegetation Phenology
3.4. Accuracy Assessment
4. Results
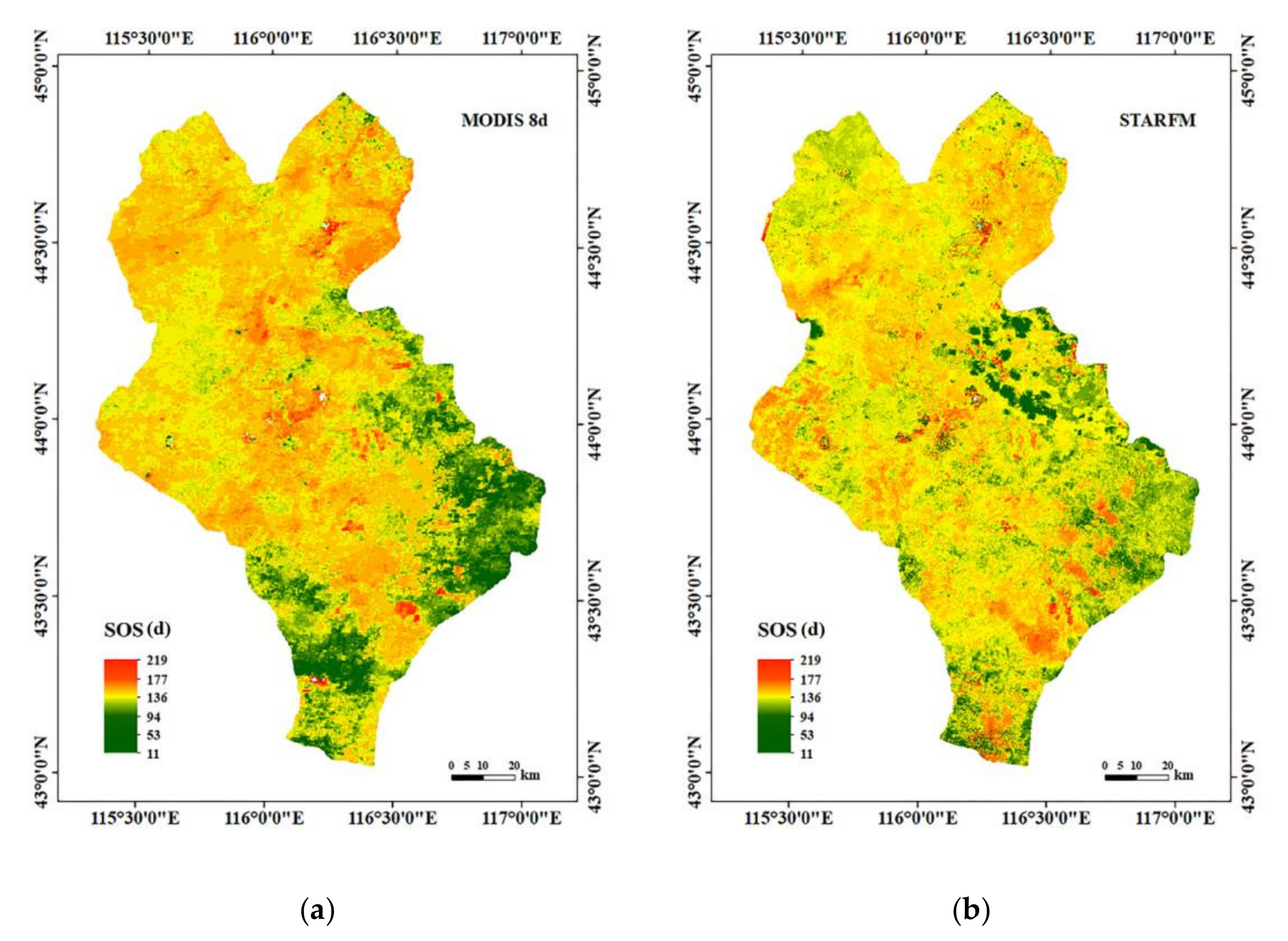
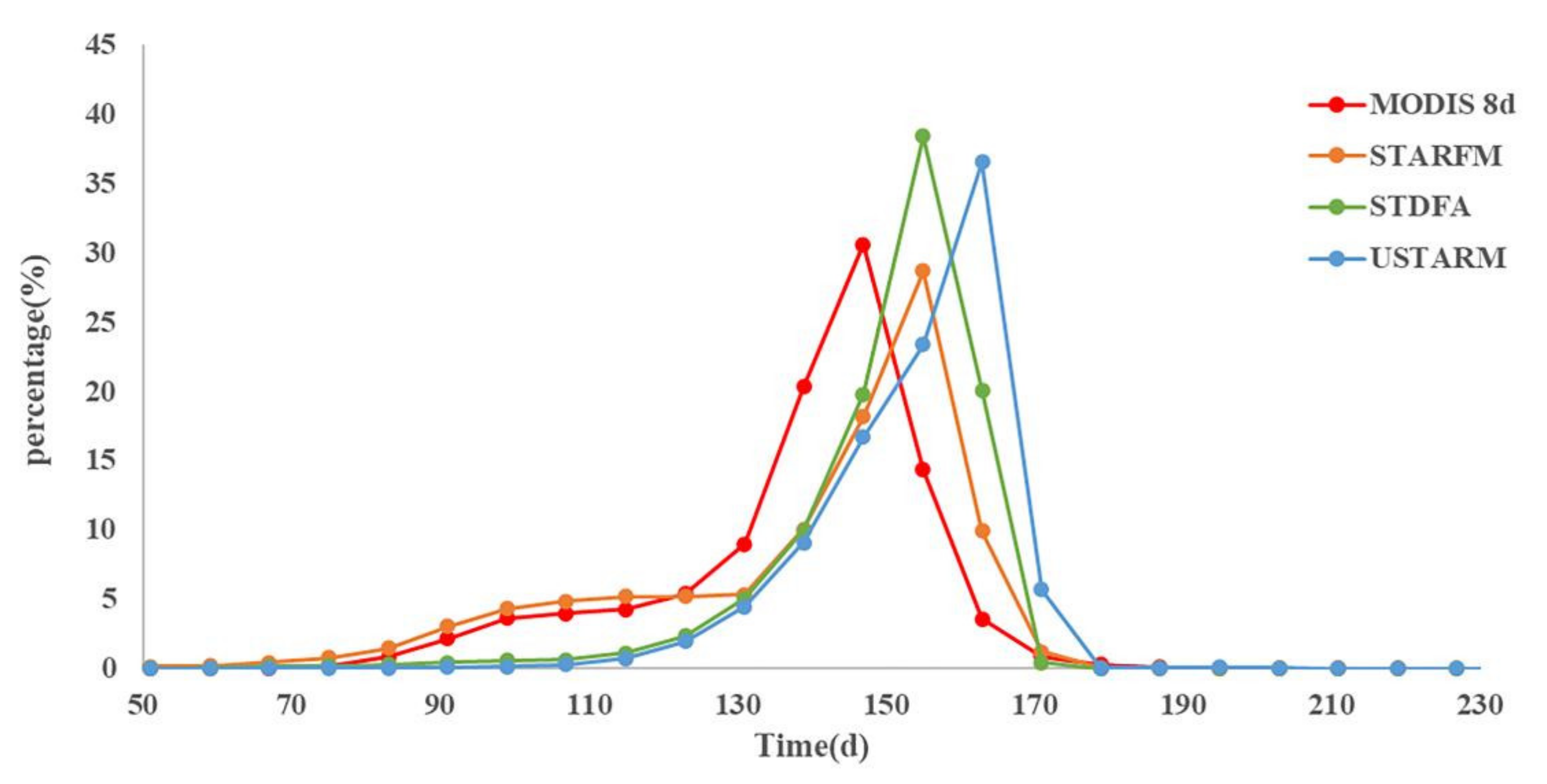
4.1. Grassland SOS from Remote Sensing Approaches
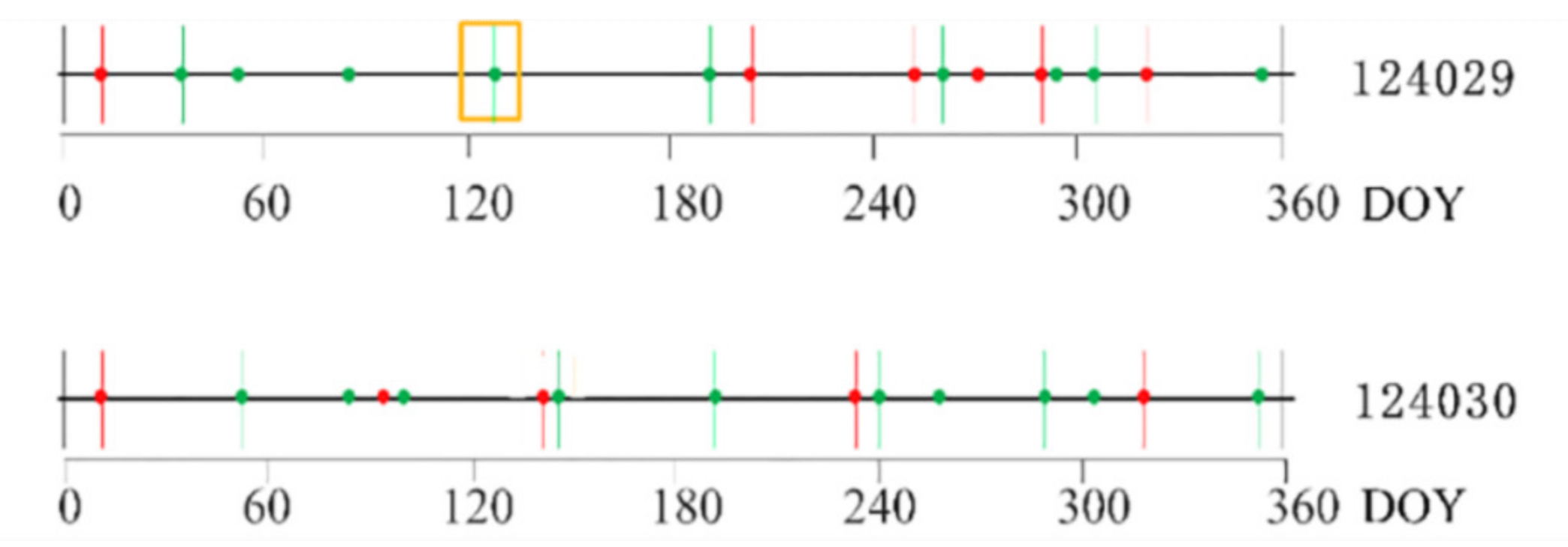
4.2. SOS Inversion Accuracy Analysis with Ground Sampling Data
5. Discussion
5.1. Analysis of SOS Inversion Results for Different Algorithms
5.2. Correlation Analysis of Different NDVI Time Series
5.3. The Impact of Missing Landsat Data during SOS
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Altesor, A.; Oesterheld, M.; Leoni, E.; Lezama, F.; Rodriguez, C. Effect of grazing on community structure and productivity of a Uruguayan grassland. Plant Ecol. 2005, 179, 83–91. [Google Scholar] [CrossRef]
- Lu, P.L.; Yu, Q.; He, Q.T. Responses of plant phenology to climatic change. Acta Ecol. Sin. 2006, 26, 929. [Google Scholar] [CrossRef]
- Cleland, E.E.; Chiariello, N.R.; Loarie, S.R.; Mooney, H.A.; Field, C.B. Diverse responses of phenology to global changes in a grassland ecosystem. Proc. Natl. Acad. Sci. USA 2006, 103, 13740–13744. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yoshie, F. Effects of growth temperature and winter duration on leaf phenology of a spring ephemeral (Gagea lutea) and a summergreen forb (Maianthemum dilatatum). J. Plant Res. 2008, 121, 483–492. [Google Scholar] [CrossRef] [PubMed]
- Hou, J.; Du, L.T.; Liu, K.; Hu, Y.; Zhu, Y.G. Characteristics of vegetation activity and its responses to climate change in desert/grassland biome transition zones in the last 30years based on GIMMS3g. Theor. Appl. Climatol. 2019, 136, 915–928. [Google Scholar] [CrossRef]
- Wang, G.C.; Huang, Y.; Wei, Y.R.; Zhang, W.; Li, T.T.; Zhang, Q. Inner Mongolian grassland plant phenological changes and their climatic drivers. Sci. Total Environ. 2019, 683, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Lee, R.; Yu, F.; Price, K.P.; Ellis, J.; Shi, P. Evaluating vegetation phenological patterns in Inner Mongolia using NDVI time-series analysis. Int. J. Remote Sens. 2002, 23, 2505–2512. [Google Scholar] [CrossRef]
- Myneni, R.B.; Keeling, C.D.; Tucker, C.J.; Asrar, G.; Nemani, R.R. Increased plant growth in the northern high latitudes from 1981 to 1991. Nature 1997, 386, 698–702. [Google Scholar] [CrossRef]
- Garonna, I.; de Jong, R.; Schaepman, M.E. Variability and evolution of global land surface phenology over the past three decades (1982–2012). Glob. Change Biol. 2016, 22, 1456–1468. [Google Scholar] [CrossRef]
- Gu, S.; Tang, Y.H.; Cui, X.Y.; Kato, T.; Du, M.Y.; Li, Y.N.; Zhao, X.Q. Energy exchange between the atmosphere and a meadow ecosystem on the Qinghai-Tibetan Plateau. Agric. For. Meteorol. 2005, 129, 175–185. [Google Scholar] [CrossRef]
- Schwartz, M.D.; Ahas, R.; Aasa, A. Onset of spring starting earlier across the Northern Hemisphere. Glob. Change Biol. 2006, 12, 343–351. [Google Scholar] [CrossRef]
- Menzel, A.; Sparks, T.H.; Estrella, N.; Roy, D.B. Altered geographic and temporal variability in phenology in response to climate change. Glob. Ecol. Biogeogr. 2006, 15, 498–504. [Google Scholar] [CrossRef]
- Reed, B.C.; Brown, J.F. Trend analysis of time-series phenology derived from satellite data. In Proceedings of the 3rd International Workshop on the Analysis of Multi-Temporal Remote Sensing Images, Biloxi, MS, USA, 16–18 May 2005; pp. 166–168. [Google Scholar]
- White, M.A.; Thornton, P.E.; Running, S.W. A continental phenology model for monitoring vegetation responses to interannual climatic variability. Glob. Biogeochem. Cycle 1997, 11, 217–234. [Google Scholar] [CrossRef]
- Stockli, R.; Vidale, P.L. European plant phenology and climate as seen in a 20-year AVHRR land-surface parameter dataset. Int. J. Remote Sens. 2004, 25, 3303–3330. [Google Scholar] [CrossRef]
- Zhou, J.H.; Cai, W.T.; Qin, Y.; Lai, L.M.; Guan, T.Y.; Zhang, X.L.; Jiang, L.H.; Du, H.; Yang, D.W.; Cong, Z.T.; et al. Alpine vegetation phenology dynamic over 16years and its covariation with climate in a semi-arid region of China. Sci. Total Environ. 2016, 572, 119–128. [Google Scholar] [CrossRef]
- Zhang, Q.; Kong, D.D.; Shi, P.J.; Singh, V.P.; Sun, P. Vegetation phenology on the Qinghai-Tibetan Plateau and its response to climate change (1982–2013). Agric. For. Meteorol. 2018, 248, 408–417. [Google Scholar] [CrossRef]
- Shen, X.J.; Liu, B.H.; Xue, Z.S.; Jiang, M.; Lu, X.G.; Zhang, Q. Spatiotemporal variation in vegetation spring phenology and its response to climate change in freshwater marshes of Northeast China. Sci. Total Environ. 2019, 666, 1169–1177. [Google Scholar] [CrossRef]
- Reed, B.C.; Brown, J.F.; Vanderzee, D.; Loveland, T.R.; Merchant, J.W.; Ohlen, D.O. Measuring phenological variability from satellite imagery. J. Veg. Sci. 1994, 5, 703–714. [Google Scholar] [CrossRef]
- Jeong, S.J.; Ho, C.H.; Gim, H.J.; Brown, M.E. Phenology shifts at start vs. end of growing season in temperate vegetation over the Northern Hemisphere for the period 1982–2008. Glob. Change Biol. 2011, 17, 2385–2399. [Google Scholar] [CrossRef]
- Hmimina, G.; Dufrene, E.; Pontailler, J.Y.; Delpierre, N.; Aubinet, M.; Caquet, B.; de Grandcourt, A.; Burban, B.; Flechard, C.; Granier, A.; et al. Evaluation of the potential of MODIS satellite data to predict vegetation phenology in different biomes: An investigation using ground-based NDVI measurements. Remote Sens. Environ. 2013, 132, 145–158. [Google Scholar] [CrossRef]
- Zhou, Q.; Rover, J.; Brown, J.; Worstell, B.; Howard, D.; Wu, Z.T.; Gallant, A.L.; Rundquist, B.; Burke, M. Monitoring Landscape Dynamics in Central US Grasslands with Harmonized Landsat-8 and Sentinel-2 Time Series Data. Remote Sens. 2019, 11, 328. [Google Scholar] [CrossRef] [Green Version]
- Brown, J.F.; Howard, D.; Wylie, B.; Frieze, A.; Ji, L.; Gacke, C. Application-Ready Expedited MODIS Data for Operational Land Surface Monitoring of Vegetation Condition. Remote Sens. 2015, 7, 16226–16240. [Google Scholar] [CrossRef] [Green Version]
- Kovalskyy, V.; Roy, D.P.; Zhang, X.; Ju, J.C. The suitability of multi-temporal web-enabled Landsat data NDVI for phenological monitoring—A comparison with flux tower and MODIS NDVI. Remote Sens. Lett. 2012, 3, 325–334. [Google Scholar] [CrossRef]
- Snyder, K.A.; Huntington, J.L.; Wehan, B.L.; Morton, C.G.; Stringham, T.K. Comparison of Landsat and Land-Based Phenology Camera Normalized Difference Vegetation Index (NDVI) for Dominant Plant Communities in the Great Basin. Sensors 2019, 19, 1139. [Google Scholar] [CrossRef] [Green Version]
- Yan, L.; Roy, D.P. Large-Area Gap Filling of Landsat Reflectance Time Series by Spectral-Angle-Mapper Based Spatio-Temporal Similarity (SAMSTS). Remote Sens. 2018, 10, 609. [Google Scholar] [CrossRef] [Green Version]
- Gao, F.; Masek, J.; Schwaller, M.; Hall, F. On the blending of the Landsat and MODIS surface reflectance: Predicting daily Landsat surface reflectance. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2207–2218. [Google Scholar] [CrossRef]
- Zhu, X.L.; Cai, F.Y.; Tian, J.Q.; Williams, T.K.A. Spatiotemporal Fusion of Multisource Remote Sensing Data: Literature Survey, Taxonomy, Principles, Applications, and Future Directions. Remote Sens. 2018, 10, 527. [Google Scholar] [CrossRef] [Green Version]
- Zhukov, B.; Oertel, D.; Lanzl, F.; Reinhackel, G. Unmixing-based multisensor multiresolution image fusion. IEEE Trans. Geosci. Remote Sens. 1999, 37, 1212–1226. [Google Scholar] [CrossRef]
- Hilker, T.; Wulder, M.A.; Coops, N.C.; Linke, J.; McDermid, G.; Masek, J.G.; Gao, F.; White, J.C. A new data fusion model for high spatial- and temporal-resolution mapping of forest disturbance based on Landsat and MODIS. Remote Sens. Environ. 2009, 113, 1613–1627. [Google Scholar] [CrossRef]
- Zhu, X.L.; Chen, J.; Gao, F.; Chen, X.H.; Masek, J.G. An enhanced spatial and temporal adaptive reflectance fusion model for complex heterogeneous regions. Remote Sens. Environ. 2010, 114, 2610–2623. [Google Scholar] [CrossRef]
- Huang, B.; Song, H.H. Spatiotemporal Reflectance Fusion via Sparse Representation. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3707–3716. [Google Scholar] [CrossRef]
- Wu, M.Q.; Niu, Z.; Wang, C.Y.; Wu, C.Y.; Wang, L. Use of MODIS and Landsat time series data to generate high-resolution temporal synthetic Landsat data using a spatial and temporal reflectance fusion model. J. Appl. Remote Sens. 2012, 6, 063507. [Google Scholar] [CrossRef]
- Song, H.H.; Huang, B. Spatiotemporal Satellite Image Fusion Through One-Pair Image Learning. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1883–1896. [Google Scholar] [CrossRef]
- Xie, D.F.; Zhang, J.S.; Zhu, X.F.; Pan, Y.Z.; Liu, H.L.; Yuan, Z.M.Q.; Yun, Y. An Improved STARFM with Help of an Unmixing-Based Method to Generate High Spatial and Temporal Resolution Remote Sensing Data in Complex Heterogeneous Regions. Sensors 2016, 16, 207. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Song, H.H.; Liu, Q.S.; Wang, G.J.; Hang, R.L.; Huang, B. Spatiotemporal Satellite Image Fusion Using Deep Convolutional Neural Networks. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2018, 11, 821–829. [Google Scholar] [CrossRef]
- Liu, W.J.; Zeng, Y.N.; Li, S.N.; Pi, X.Y.; Huang, W. An Improved Spatiotemporal Fusion Approach Based on Multiple Endmember Spectral Mixture Analysis. Sensors 2019, 19, 2443. [Google Scholar] [CrossRef] [Green Version]
- Walker, J.J.; de Beurs, K.M.; Wynne, R.H. Dryland vegetation phenology across an elevation gradient in Arizona, USA, investigated with fused MODIS and Landsat data. Remote Sens. Environ. 2014, 144, 85–97. [Google Scholar] [CrossRef]
- Gao, F.; Anderson, M.C.; Zhang, X.Y.; Yang, Z.W.; Alfieri, J.G.; Kustas, W.P.; Mueller, R.; Johnson, D.M.; Prueger, J.H. Toward mapping crop progress at field scales through fusion of Landsat and MODIS imagery. Remote Sens. Environ. 2017, 188, 9–25. [Google Scholar] [CrossRef] [Green Version]
- Onojeghuo, A.O.; Blackburn, G.A.; Wang, Q.M.; Atkinson, P.M.; Kindred, D.; Miao, Y.X. Rice crop phenology mapping at high spatial and temporal resolution using downscaled MODIS time-series. GISci. Remote Sens. 2018, 55, 659–677. [Google Scholar] [CrossRef] [Green Version]
- Lyu, X.; Li, X.B.; Dang, D.L.; Dou, H.S.; Xuan, X.J.; Liu, S.Y.; Li, M.Y.; Gong, J.R. A new method for grassland degradation monitoring by vegetation species composition using hyperspectral remote sensing. Ecol. Indic. 2020, 114, 106310. [Google Scholar] [CrossRef]
- Jarihani, A.A.; McVicar, T.R.; Van Niel, T.G.; Emelyanova, I.V.; Callow, J.N.; Johansen, K. Blending Landsat and MODIS Data to Generate Multispectral Indices: A Comparison of “Index-then-Blend” and “Blend-then-Index” Approaches. Remote Sens. 2014, 6, 9213–9238. [Google Scholar] [CrossRef] [Green Version]
- Di Bella, C.; Faivre, R.; Ruget, F.; Seguin, B.; Guerif, M.; Combal, B.; Weiss, A.; Rebella, C. Remote sensing capabilities to estimate pasture production in France. Int. J. Remote Sens. 2004, 25, 5359–5372. [Google Scholar] [CrossRef]
- Holben, B.N. Characteristics of maximum-value composite images from temporal AVHRR data. Int. J. Remote Sens. 1986, 7, 1417–1434. [Google Scholar] [CrossRef]
- Guo, J.; Yang, X.C.; Niu, J.M.; Jin, Y.X.; Xu, B.; Shen, G.; Zhang, W.B.; Zhao, F.; Zhang, Y.J. Remote sensing monitoring of green-up dates in the Xilingol grasslands of northern China and their correlations with meteorological factors. Int. J. Remote Sens. 2019, 40, 2190–2211. [Google Scholar] [CrossRef]
- Jonsson, P.; Eklundh, L. Seasonality extraction by function fitting to time-series of satellite sensor data. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1824–1832. [Google Scholar] [CrossRef]
- Jonsson, P.; Eklundh, L. TIMESAT—A program for analyzing time-series of satellite sensor data. Comput. Geosci. 2004, 30, 833–845. [Google Scholar] [CrossRef] [Green Version]
- Xin, Q.C.; Broich, M.; Zhu, P.; Gong, P. Modeling grassland spring onset across the Western United States using climate variables and MODIS-derived phenology metrics. Remote Sens. Environ. 2015, 161, 63–77. [Google Scholar] [CrossRef]




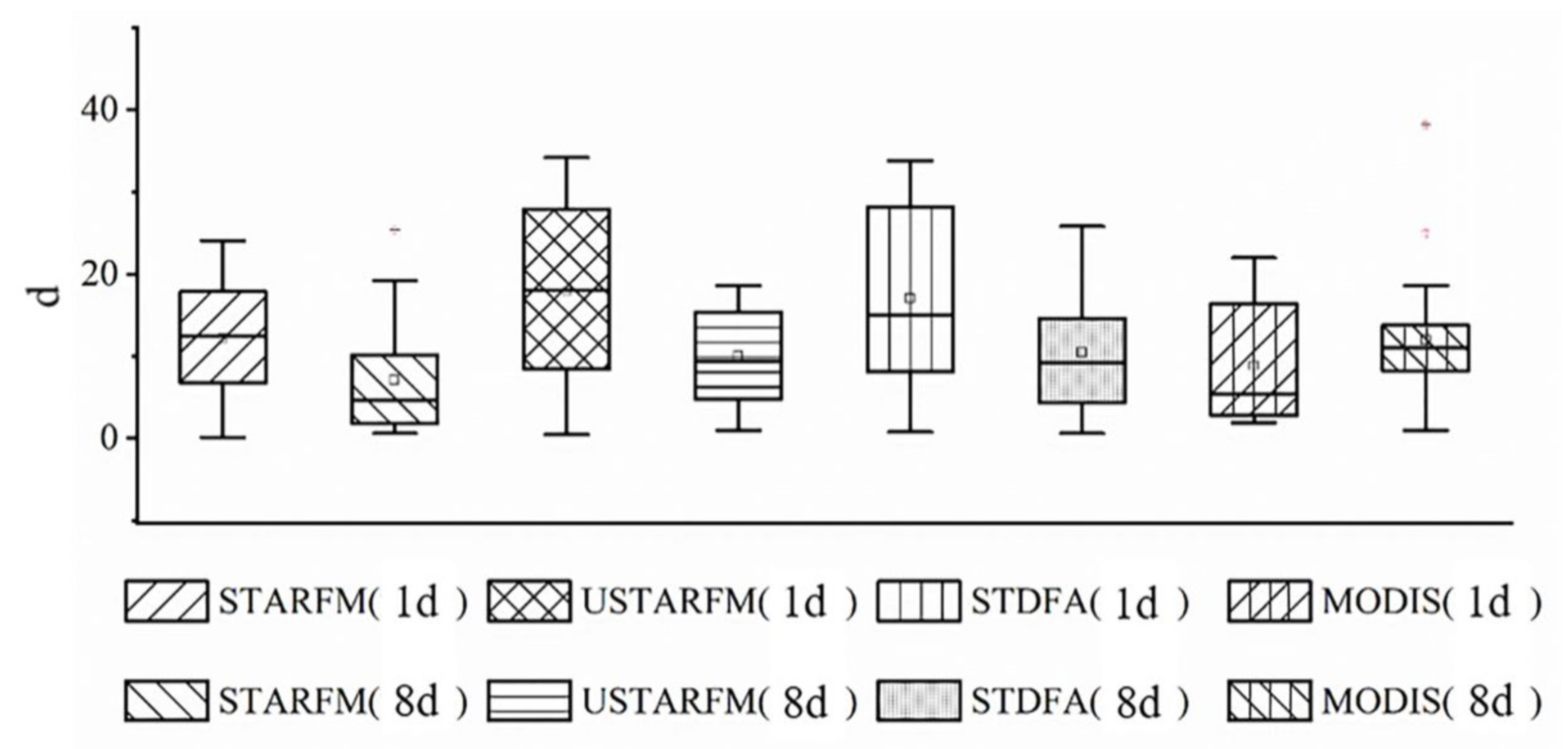
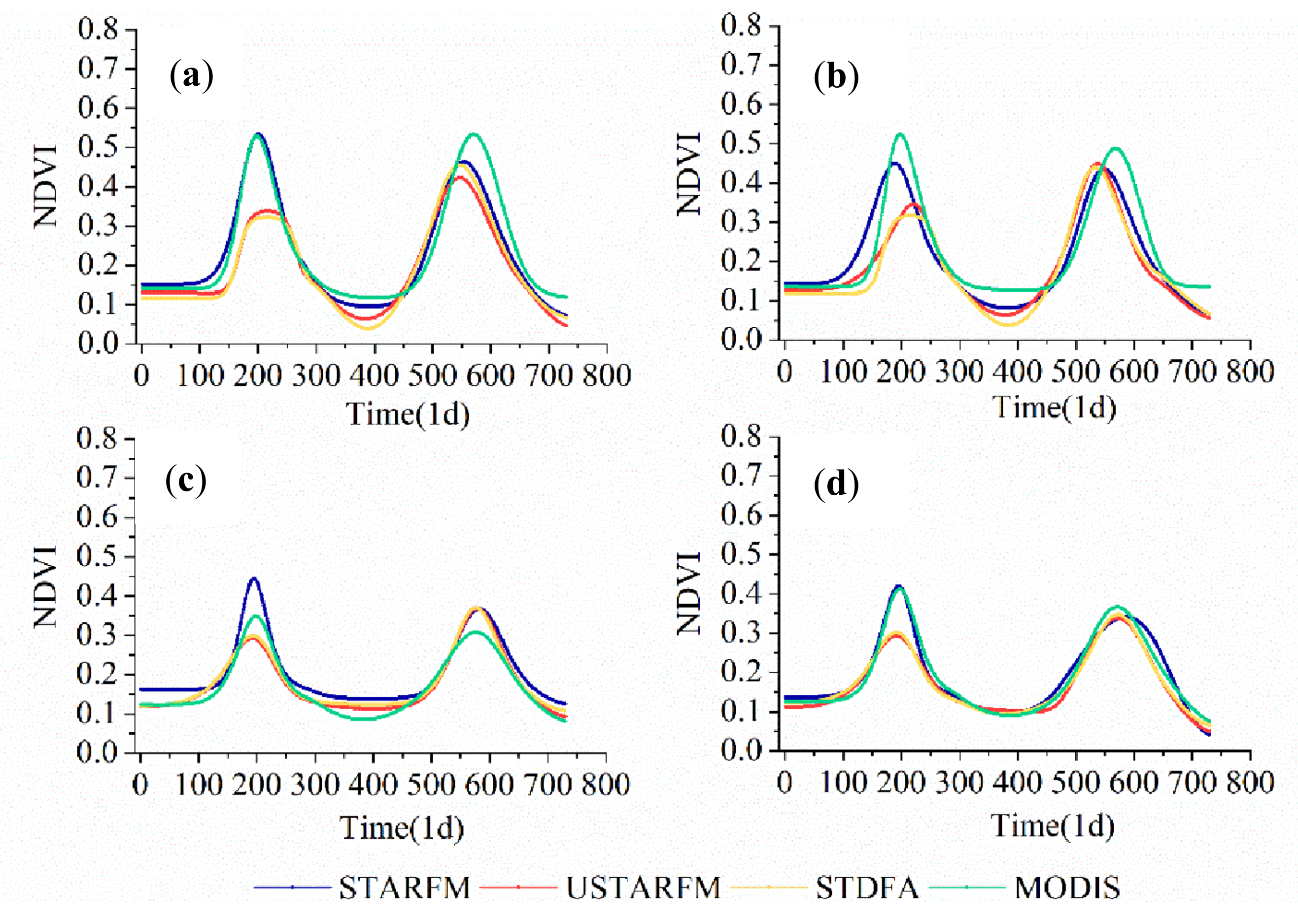
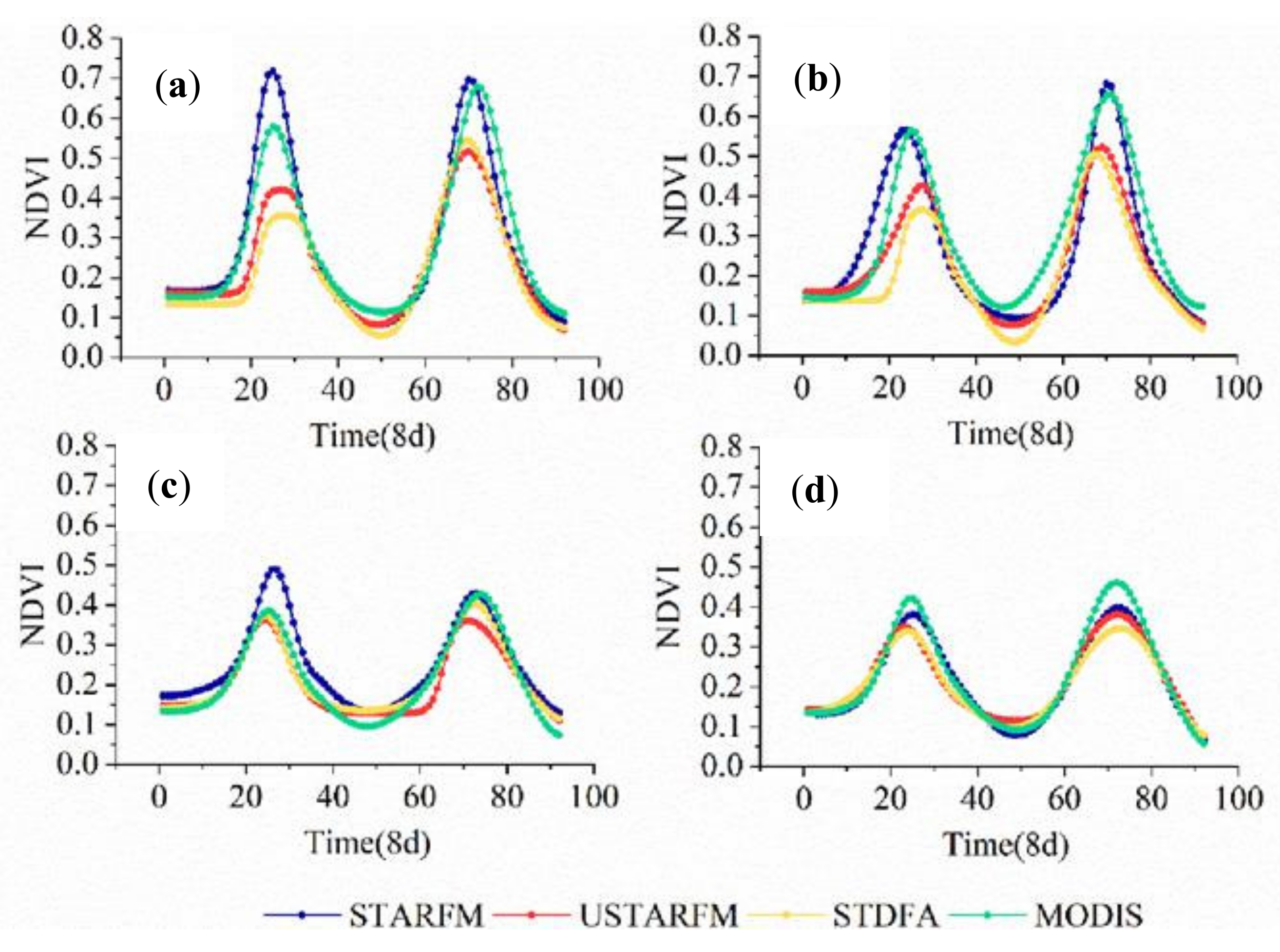

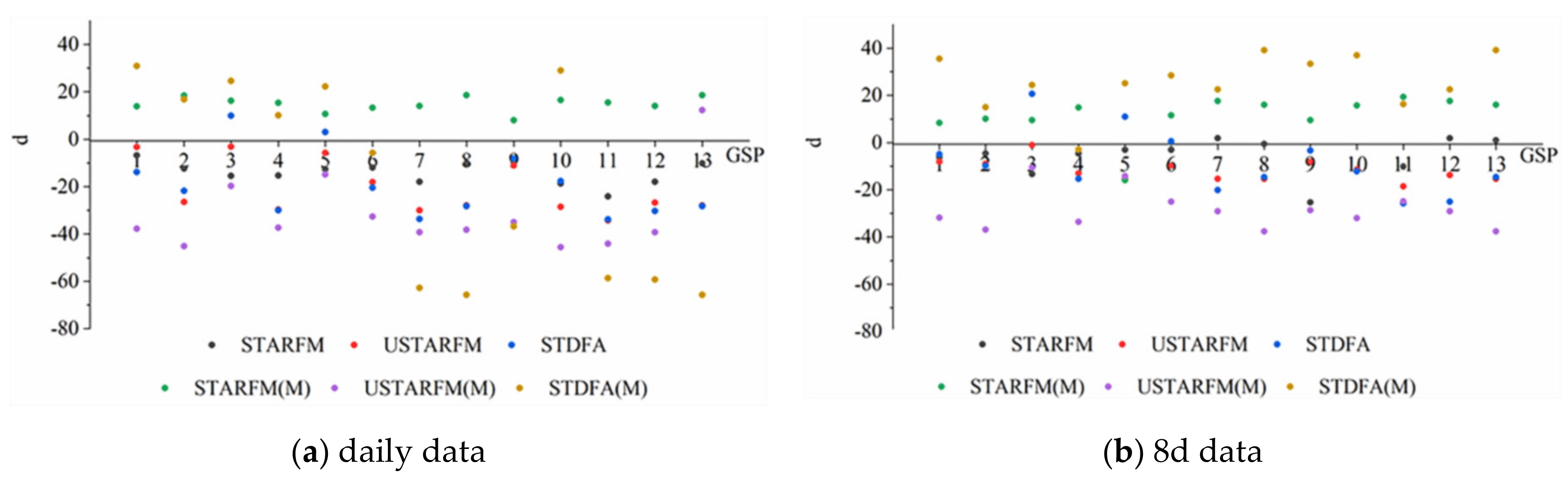
| Datasets | ||||||||
|---|---|---|---|---|---|---|---|---|
| RMSE | 13.7d | 9.7d | 20.6d | 11.0d | 20.2d | 12.6d | 11.3d | 14.3d |
| GSP | ||||||
|---|---|---|---|---|---|---|
| a * | 0.963 | 0.964 | 0.902 | 0.950 | 0.901 | 0.916 |
| b * | 0.915 | 0.917 | 0.846 | 0.941 | 0.846 | 0.931 |
| c * | 0.971 | 0.977 | 0.952 | 0.969 | 0.954 | 0.961 |
| d * | 0.981 | 0.993 | 0.995 | 0.983 | 0.968 | 0.982 |
| Data Source | STARFM | USTARFM | STDFA | |||
|---|---|---|---|---|---|---|
| Processing Method | Full * | Missing | Full | Missing | Full | Missing |
| Daily | 14.8d | 15.2d | 23.6d | 35.5d | 23.6d | 43.1d |
| 8d data | 9.5d | 14.5d | 12.7d | 29.7d | 15.6d | 28.2d |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Y.; Du, P.; Zhang, M.; Bai, X.; Lei, R.; Yang, X. Quantitative Evaluation of Grassland SOS Estimation Accuracy Based on Different MODIS-Landsat Spatio-Temporal Fusion Datasets. Remote Sens. 2022, 14, 2542. https://doi.org/10.3390/rs14112542
Cao Y, Du P, Zhang M, Bai X, Lei R, Yang X. Quantitative Evaluation of Grassland SOS Estimation Accuracy Based on Different MODIS-Landsat Spatio-Temporal Fusion Datasets. Remote Sensing. 2022; 14(11):2542. https://doi.org/10.3390/rs14112542
Chicago/Turabian StyleCao, Yungang, Puying Du, Min Zhang, Xueqin Bai, Ruodan Lei, and Xiuchun Yang. 2022. "Quantitative Evaluation of Grassland SOS Estimation Accuracy Based on Different MODIS-Landsat Spatio-Temporal Fusion Datasets" Remote Sensing 14, no. 11: 2542. https://doi.org/10.3390/rs14112542
APA StyleCao, Y., Du, P., Zhang, M., Bai, X., Lei, R., & Yang, X. (2022). Quantitative Evaluation of Grassland SOS Estimation Accuracy Based on Different MODIS-Landsat Spatio-Temporal Fusion Datasets. Remote Sensing, 14(11), 2542. https://doi.org/10.3390/rs14112542





