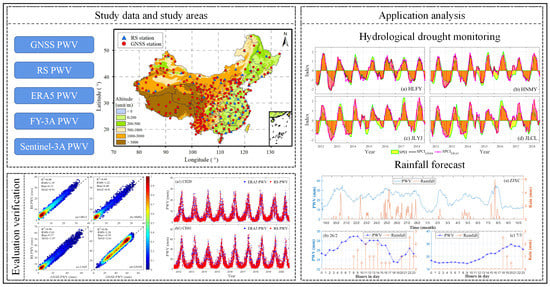
Comprehensive Precipitable Water Vapor Retrieval and Application Platform Based on Various Water Vapor Detection Techniques
Abstract
:1. Introduction
2. Data and Theory Description
2.1. The CPRAP Usage Data Description
2.1.1. GNSS and RS PWV Data
2.1.2. ERA5 PWV Data
2.1.3. FY-3A/MERSI and Sentinel-3A/OLCI PWV Data
2.2. Theory and Method of Retrieving PWV
2.2.1. PWV Derived from GNSS
2.2.2. PWV Derived from Radiosonde
2.2.3. PWV Derived from ERA5
2.2.4. PWV Derived from Remote Sensing Satellite
- (1)
- The weighted mean value of the three water vapor absorption channels is combined based on the sensitivity and the PWV is obtained according to the equation [47]:where is the PWV values derived from each water vapor absorption channel; is the normalized weighting parameters correspond to each band and subscription i refers to the channel.
- (2)
- The weighting parameter of each band is calculated based on the sensitivity of the transmission in each of the channels to the PWV.where is the transmittance variation in one unit length; is the PWV variation in one unit length. It is computed numerically from simulated curves of transmittance versus precipitable water vapor; is sensitivity.
3. Evaluation and Application of PWV Derived from CPRAP
3.1. Performance of CPRAP-Derived PWV
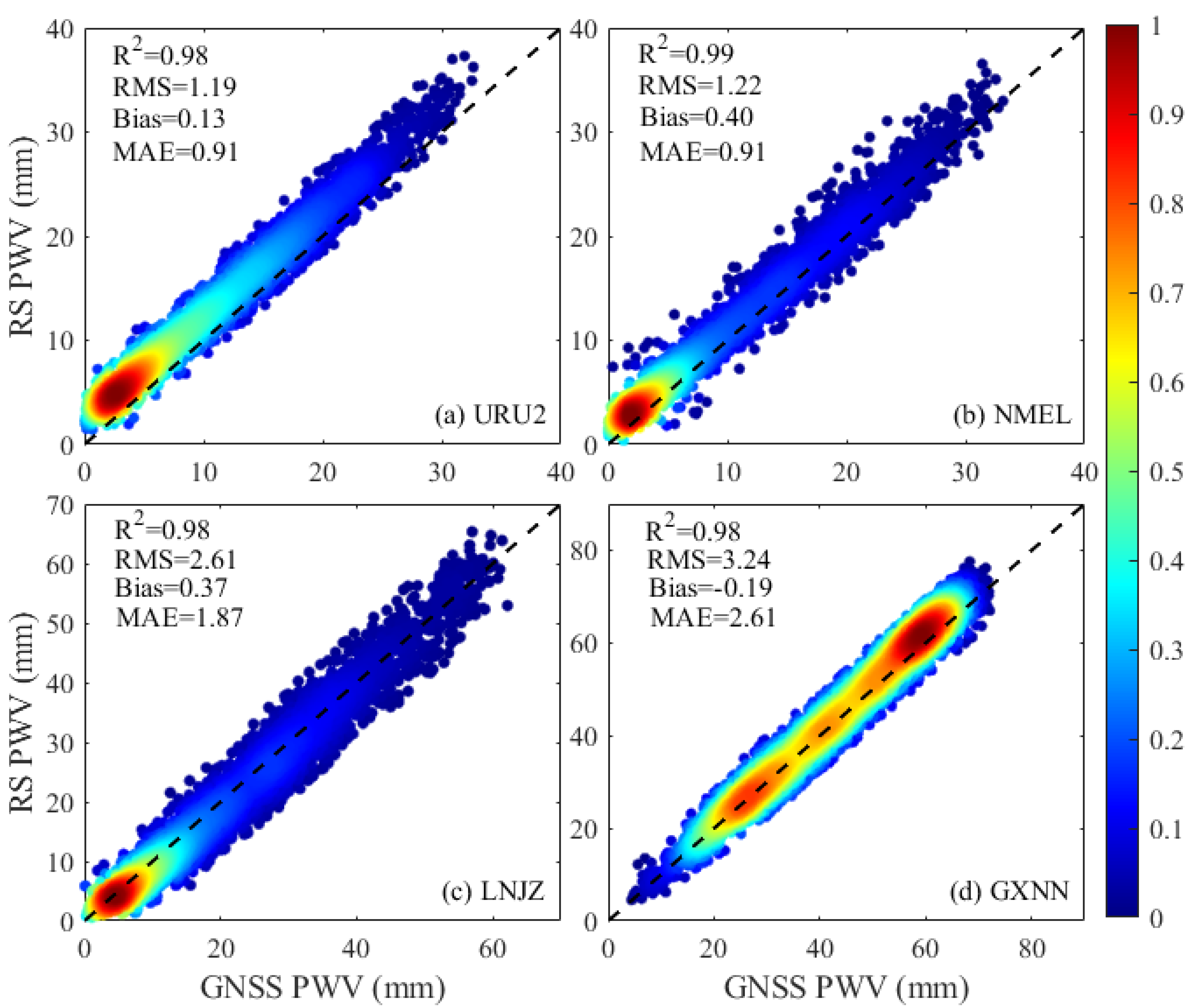
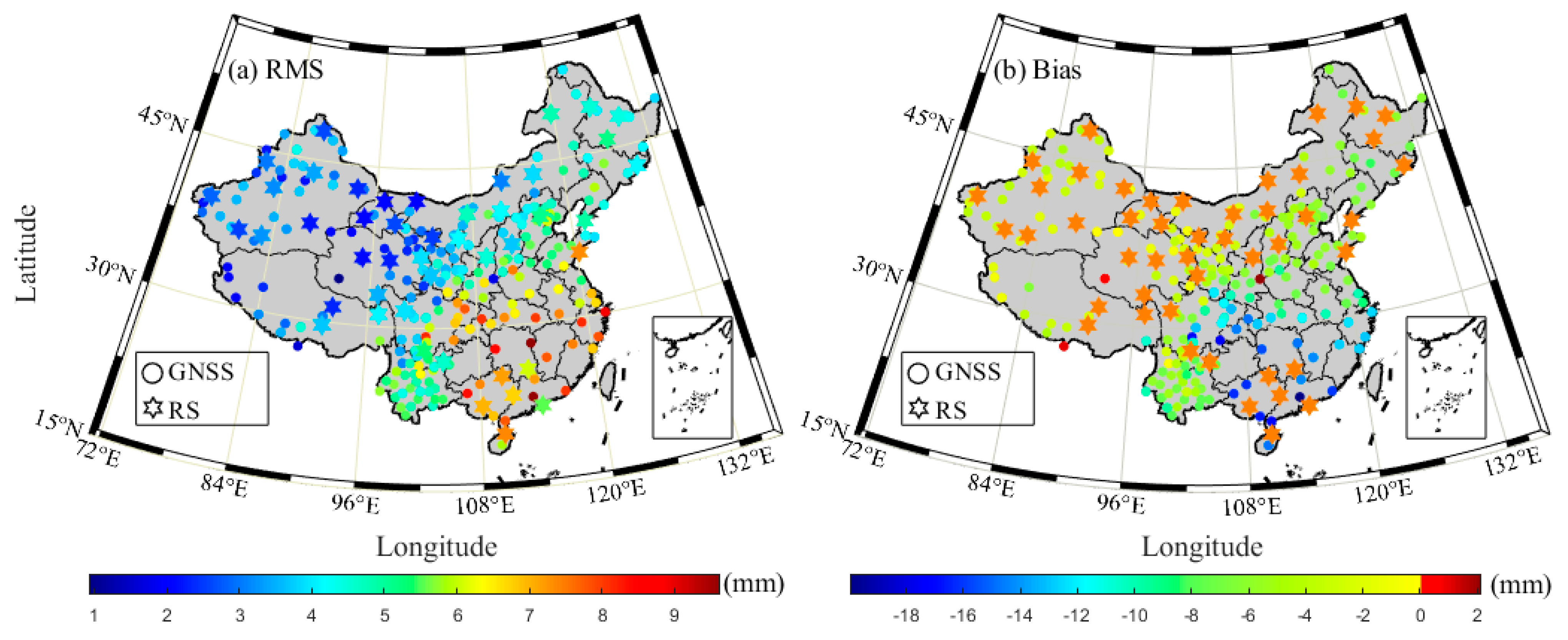
3.1.1. Accuracy Analysis of GNSS-Derived PWV
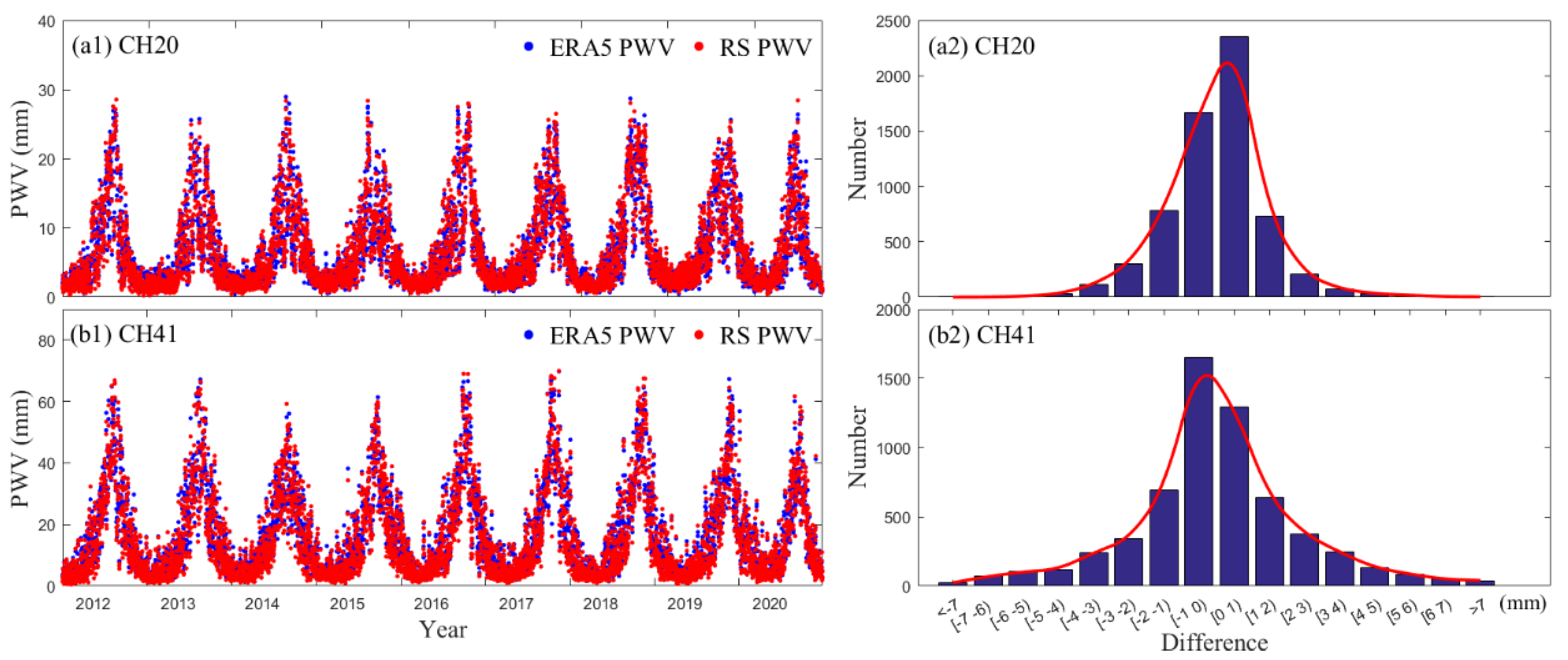
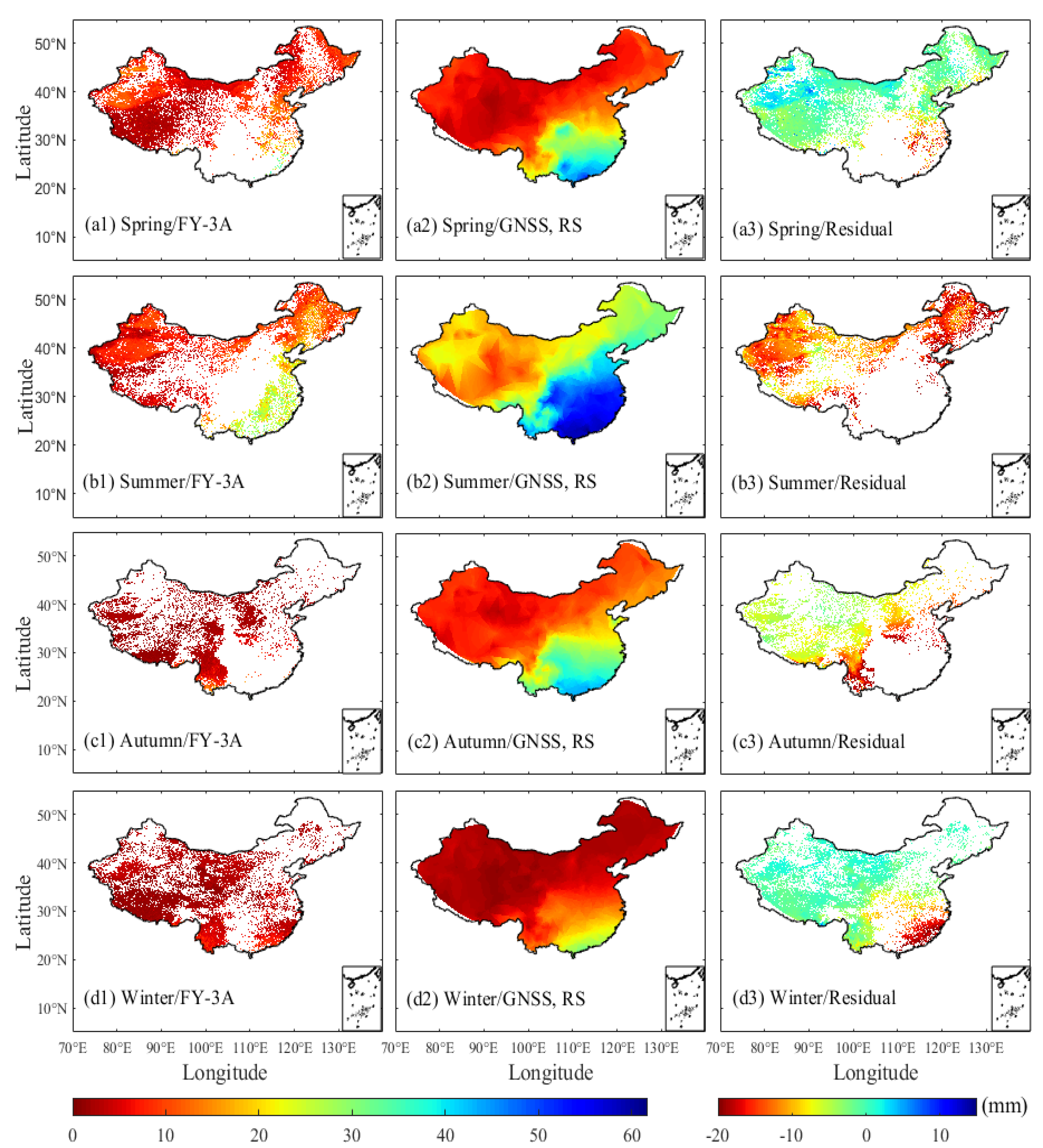
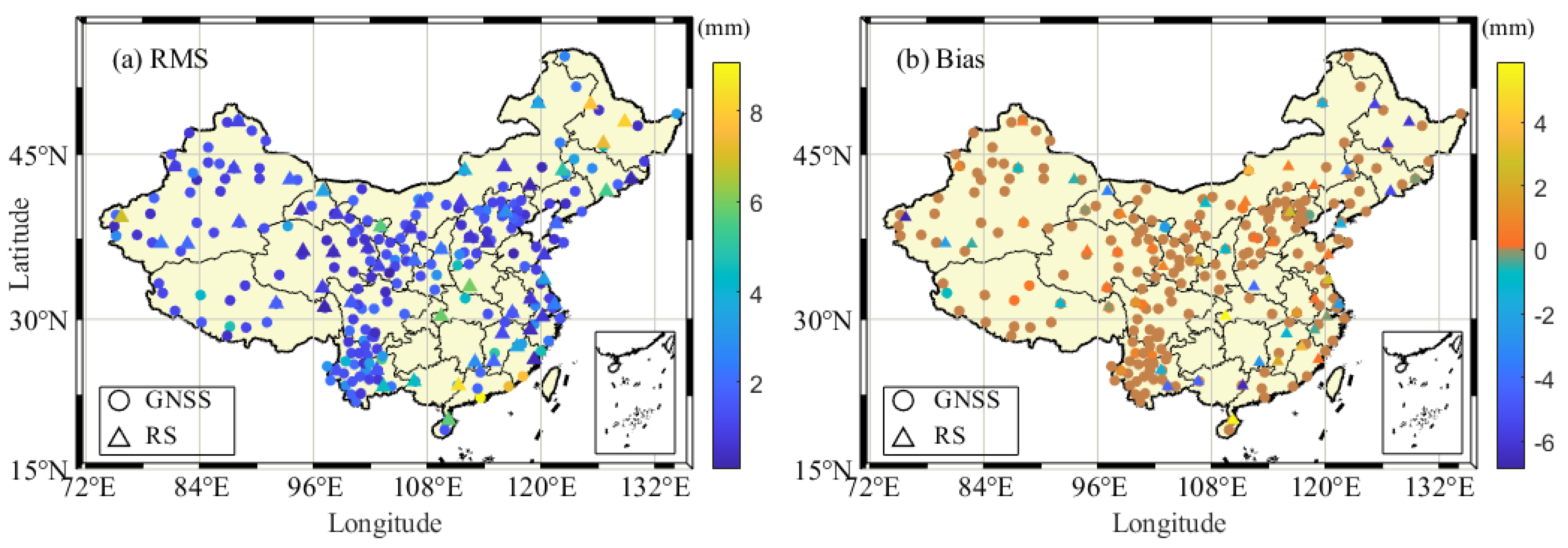
3.1.2. Accuracy Analysis of ERA5-Derived PWV Product
3.1.3. Accuracy Analysis of Satellite-Derived PWV Product
3.2. Application of CPRAP-Derived PWV
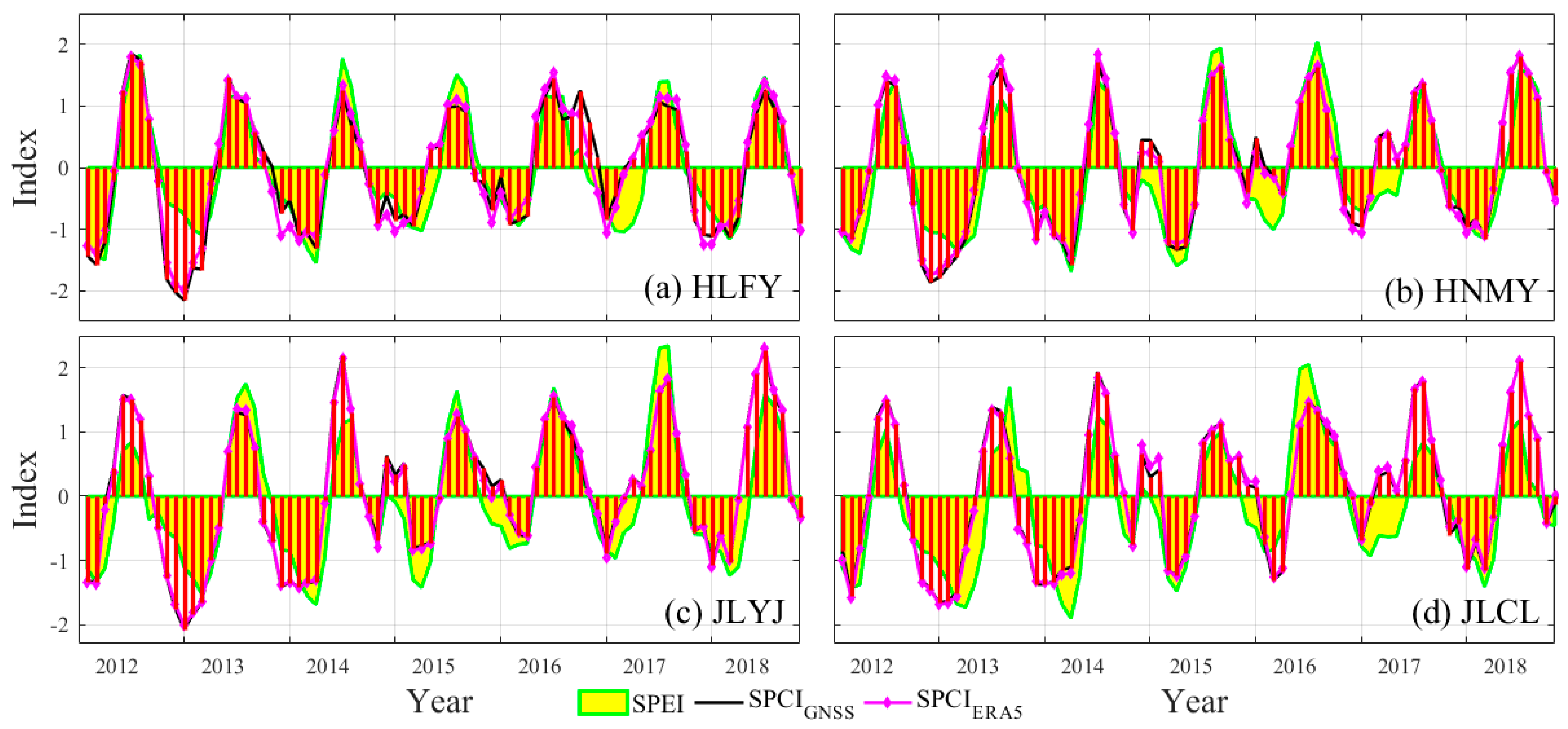
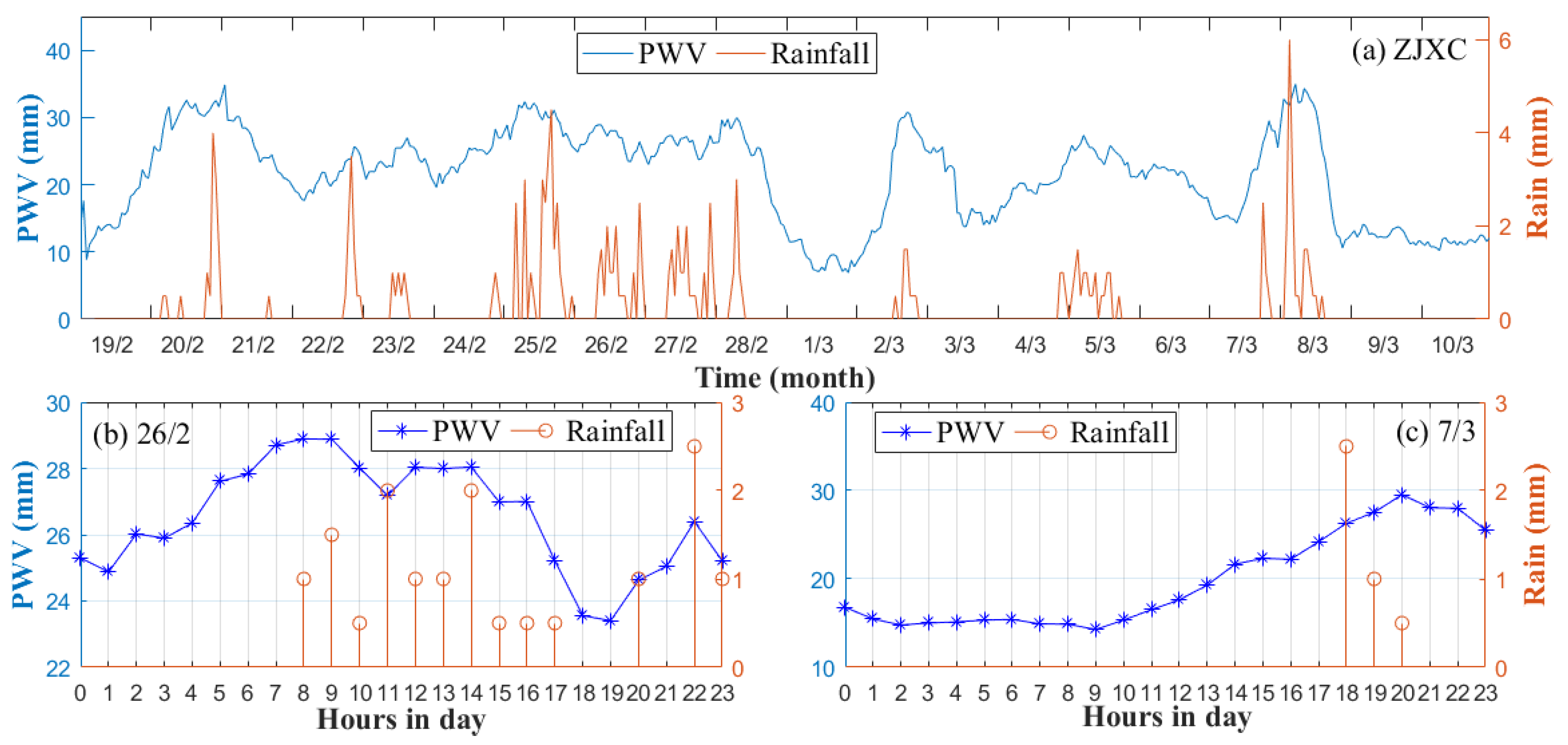
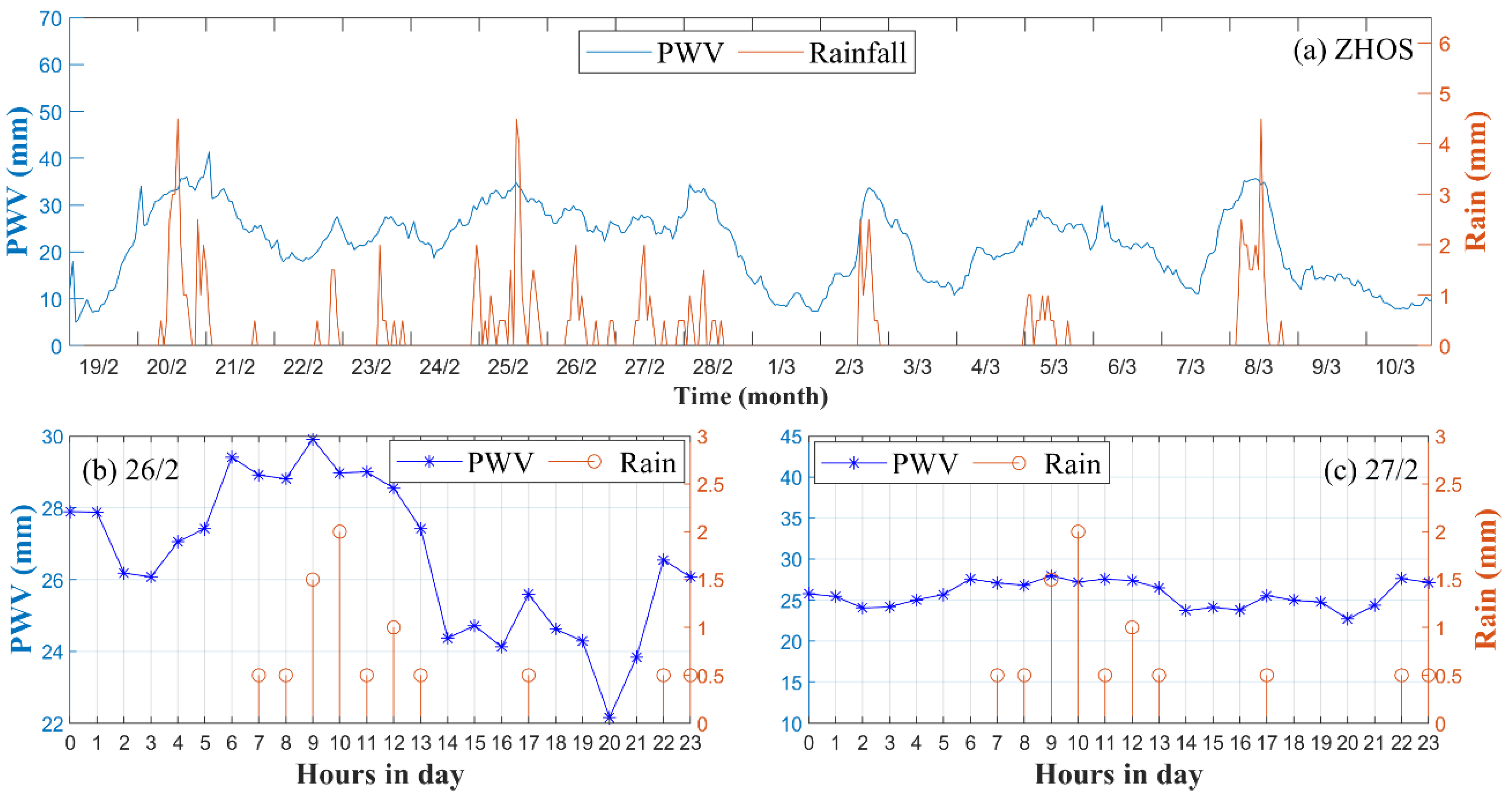
3.2.1. Application of CPRAP for Drought Monitoring
3.2.2. Application of CPRAP for Rainfall Monitoring
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jin, S.; Li, Z.; Cho, J. Integrated water vapor fifield and multiscale variations over China from GPS measurements. J. Appl. Meteorol. Climatol. 2008, 47, 3008–3015. [Google Scholar] [CrossRef]
- Huang, L.; Mo, Z.; Xie, S.; Liu, L.; Chen, J.; Kang, C.; Wang, S. Spatiotemporal characteristics of GNSS-derived precipitable water vapor during heavy rainfall events in Guilin, China. Satell. Navig. 2021, 2, 1–17. [Google Scholar] [CrossRef]
- Wong, M.S.; Jin, X.; Liu, Z.; Nichol, J.; Chan, P.W. Multi-sensors study of precipitable water vapour over mainland China. Int. J. Climatol. 2015, 35, 3146–3159. [Google Scholar] [CrossRef]
- Li, Z.; Sun, Y.; Li, T.; Ding, Y.; Hu, T. Future changes in East Asian summer monsoon circulation and precipitation under 1.5 to 5 °C of warming. Earth’s Future 2019, 7, 1391–1406. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Q.; Yao, W.; Yao, Y.; Li, X. An improved GNSS tropospheric tomography method with the GPT2w model. GPS Solut. 2020, 24, 1–13. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, Q.; Yao, W.; Ma, X.; Yao, Y.; Liu, L. Short-term rainfall forecast model based on the improved BP–NN algorithm. Sci. Rep. 2019, 9, 19751. [Google Scholar] [CrossRef]
- Zhang, B.; Yao, Y. Precipitable water vapor fusion based on a generalized regression neural network. J. Geod. 2021, 95, 1–14. [Google Scholar] [CrossRef]
- Pérez-Ramírez, D.; Whiteman, D.N.; Smirnov, A.; Lyamani, H.; Holben, B.N.; Pinker, R.; Andrade, M.; Alados-Arboledas, L. Evaluation of AERONET precipitable water vapor versus microwave radiometry, GPS and radiosondes at ARM sites. J. Geophys. Res. Atmos. 2014, 119, 9596–9613. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Long, D. An improvement in accuracy and spatiotemporal continuity of the MODIS precipitable water vapor product based on a data fusion approach. Remote Sens. Environ. 2020, 248, 111966. [Google Scholar] [CrossRef]
- Li, H.; Wang, X.; Choy, S.; Wu, S.; Jiang, C.; Zhang, J.; Qiu, C.; Li, L.; Zhang, K. A New Cumulative Anomaly-based Model for the Detection of Heavy Precipitation Using GNSS-derived Tropospheric Products. IEEE Trans. Geosci. Remote Sens. 2021, 60, 4105718. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, H.; Liang, H.; Lou, Y.; Cai, Y.; Cao, Y.; Zhou, Y.; Liu, W. On the suitability of ERA5 in hourly GPS precipitable water vapor retrieval over China. J. Geod. 2019, 93, 1897–1909. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Herring, T.A.; Rocken, C.; Anthes, R.A.; Ware, R.H. GPS meteorology: Remote sensing of atmospheric water vapor using the Global Positioning System. J. Geophys. Res. Atmos. 1992, 97, 15787–15801. [Google Scholar] [CrossRef]
- Zhang, W.; Lou, Y.; Huang, J.; Zheng, F.; Cao, Y.; Liang, H.; Shi, C.; Liu, J. Multiscale Variations of Precipitable Water Over China Based on 1999–2015 Ground-Based GPS Observations and Evaluations of Reanalysis Products. J. Clim. 2018, 31, 945–962. [Google Scholar] [CrossRef]
- Zhao, Q.; Yang, P.; Yao, W.; Yao, Y. Hourly PWV dataset derived from GNSS observations in China. Sensors 2020, 20, 231. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, L.; Jiang, W.; Liu, L.; Chen, H.; Ye, S. A new global grid model for the determination of atmospheric weighted mean temperature in GPS precipitable water vapor. J. Geod. 2019, 93, 159–176. [Google Scholar] [CrossRef]
- Gao, W.; Gao, J.; Yang, L.; Wang, M.; Yao, W. A novel modeling strategy of weighted mean temperature in China using RNN and LSTM. Remote Sens. 2021, 13, 3004. [Google Scholar] [CrossRef]
- Wang, S.; Xu, T.; Nie, W.; Jiang, C.; Yang, Y.; Fang, Z.; Li, M.; Zhang, Z. Evaluation of precipitable water vapor from five reanalysis products with Ground-Based GNSS observations. Remote Sens. 2020, 12, 1817. [Google Scholar] [CrossRef]
- Lu, Q.; Hu, J.; Wu, C.; Qi, C.; Wu, S.; Xu, N.; Sun, L.; Li, X.; Liu, H.; Guo, Y.; et al. Monitoring the performance of the Fengyun satellite instruments using radiative transfer models and NWP fields. J. Quant. Spectrosc. Radiat. Transf. 2020, 107239. [Google Scholar] [CrossRef]
- He, J.; Liu, Z. Comparison of satellite-derived precipitable water vapor through near-infrared remote sensing channels. IEEE Trans. Geosci. Remote Sens. 2019, 57, 10252–10262. [Google Scholar] [CrossRef]
- Gong, S.; Hagan, D.F.; Wu, X.; Wang, G. Spatio-temporal analysis of precipitable water vapour over northwest china utilizing MERSI/FY-3A products. Int. J. Remote Sens. 2018, 39, 3094–3110. [Google Scholar] [CrossRef]
- Xu, J.; Liu, Z. The First Validation of Sentinel-3 OLCI Integrated Water Vapor Products Using Reference GPS Data in Mainland China. IEEE Trans. Geosci. Remote Sens. 2021, 60, 4102817. [Google Scholar] [CrossRef]
- Altamimi, Z.; Collilieux, X.; Métivier, L. ITRF2008, an improved solution of the international terrestrial reference frame. J. Geod. 2011, 85, 457–473. [Google Scholar] [CrossRef] [Green Version]
- Yuan, Y.; Zhang, K.; Rohm, W.; Choy, S.; Norman, R.; Wang, C.S. Real-time retrieval of precipitable water vapor from GPS precise point positioning. J. Geophys. Res. Atmos. 2014, 119, 10044–10057. [Google Scholar] [CrossRef]
- Ssenyunzi, R.C.; Oruru, B.; D’ujanga, F.M.; Realini, E.; Barindelli, S.; Tagliaferro, G.; von Engeln, A.; van de Giesen, N. Performance of ERA5 data in retrieving Precipitable Water Vapour over East African tropical region. Adv. Space Res. 2020, 65, 1877–1893. [Google Scholar] [CrossRef]
- Jiang, P.; Ye, S.R.; Liu, Y.Y.; Zhang, J.J.; Xia, P.F. Near real-time water vapor tomography using ground-based GPS and meteorological data: Long-term experiment in Hong Kong. Annales Geophysicae. Copernic. GmbH 2014, 32, 911–923. [Google Scholar] [CrossRef] [Green Version]
- Durre, I.; Vose, R.S.; Wuertz, D.B. Overview of the integrated global radiosonde archive. J. Clim. 2006, 19, 53–68. [Google Scholar] [CrossRef] [Green Version]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Yang, J.; Dong, C. Products and Application of New Generation Chinese Polar-orbit Meteorological Satellite; Science Press: Beijing, China, 2011; pp. 240–244. [Google Scholar]
- Sun, L.; Hu, X.; Guo, M.; Xu, N. Multisite calibration tracking for FY-3A MERSI solar bands. IEEE Transact. Geosci. Remote Sens. 2012, 50, 4929–4942. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, S.; Ding, N.; Holden, L.; Wang, X.; Zheng, N. GNSS-RS tomography: Retrieval of tropospheric water vapor fields using GNSS and RS observations. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–13. [Google Scholar] [CrossRef]
- Segarra, J.; Buchaillot, M.L.; Araus, J.L.; Kefauver, S.C. Remote sensing for precision agriculture: Sentinel-2 improved features and applications. Agronomy 2020, 10, 641. [Google Scholar] [CrossRef]
- Donlon, C.; Berruti, B.; Buongiorno, A.; Ferreira, M.H.; Féménias, P.; Frerick, J.; Goryl, P.; Klein, U.; Laur, H.; Mavrocordatos, C.; et al. The global monitoring for environment and security (GMES) sentinel-3 mission. Remote Sens. Environ. 2012, 120, 37–57. [Google Scholar] [CrossRef]
- Solheim, F.S.; Vivekanandan, J.; Ware, R.H.; Rocken, C. Propagation delays induced in GPS signals by dry air, water vapor, hydrometeors and other particulates. J. Geophys. Res. Atmos. 1999, 104, 9663–9670. [Google Scholar] [CrossRef]
- Li, X.; Dick, G.; Ge, M.; Heise, S.; Wickert, J.; Bender, M. Real-time GPS sensing of atmospheric water vapor: Precise point positioning with orbit, clock, and phase delay corrections. Geophys. Res. Lett. 2014, 41, 3615–3621. [Google Scholar] [CrossRef] [Green Version]
- Saastamoinen, J. Contributions to the theory of atmospheric refraction. Bull. Géodésique 1973, 107, 13–34. [Google Scholar] [CrossRef]
- Böhm, J.; Möller, G.; Schindelegger, M.; Pain, G.; Weber, R. Development of an improved empirical model for slant delays in the troposphere (GPT2w). GPS Solut. 2015, 19, 433–441. [Google Scholar] [CrossRef] [Green Version]
- Huang, L.; Liu, L.; Chen, H.; Jiang, W. An improved atmospheric weighted mean temperature model and its impact on GNSS precipitable water vapor estimates for China. GPS Solut. 2019, 23, 1–16. [Google Scholar] [CrossRef]
- Kirkland, E.J. Bilinear interpolation. In Advanced Computing in Electron Microscopy; Springer: Boston, MA, USA, 2010; pp. 261–263. [Google Scholar]
- Huang, L.; Peng, H.; Liu, L.; Xiong, S.; Xie, S.; Chen, J.; Li, J.; He, H. GNSS precipitable water vapor retrieval with the aid of NWM data for China. Earth Space Sci. 2021, 8, e2020EA001550. [Google Scholar] [CrossRef]
- Suparta, W.; Iskandar, A.; Singh, M.S.J.; Ali, M.A.M.; Yatim, B.; Yatim, A.N.M. Analysis of GPS water vapor variability during the 2011 La Niña event over the western Pacific Ocean. Ann. Geophys. 2013, 56, R0330. [Google Scholar] [CrossRef]
- Ferreira, A.P.; Nieto, R.; Gimeno, L. Completeness of radiosonde humidity observations based on the Integrated Global Radiosonde Archive. Earth Syst. Sci. Data 2019, 11, 603–627. [Google Scholar] [CrossRef] [Green Version]
- Von Storch, H.; Zwiers, F.W. Statistical Analysis in Climate Research; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Huang, L.; Zhu, G.; Liu, L.; Chen, H.; Jiang, W. A global grid model for the correction of the vertical zenith total delay based on a sliding window algorithm. GPS Solut. 2021, 25, 1–14. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, K.; Wu, S.; Fan, S.; Cheng, Y. Water vapor-weighted mean temperature and its impact on the determination of precipitable water vapor and its linear trend. J. Geophys. Res. Atmos. 2016, 121, 2849–2857. [Google Scholar] [CrossRef]
- Liangke, H.U.A.N.G.; Zhixiang, M.O.; Lilong, L.I.U.; Shaofeng, X.I.E. An empirical model for the vertical correction of precipitable water vapor considering the time-varying lapse rate for Mainland China. Acta Geod. Et Cartogr. Sin. 2021, 50, 1320. [Google Scholar]
- Yang, P.; Zhao, Q.; Li, Z.; Yao, W.; Yao, Y. High temporal resolution global PWV dataset of 2005–2016 by using a neural network approach to determine the mean temperature of the atmosphere. Adv. Space Res. 2021, 67, 3087–3097. [Google Scholar] [CrossRef]
- Gao, B.C.; Kaufman, Y.J. Water vapor retrievals using Moderate Resolution Imaging Spectroradiometer (MODIS) near-infrared channels. J. Geophys. Res. 2003, 108, 4389. [Google Scholar] [CrossRef]
- Preusker, R.; Carbajal Henken, C.; Fischer, J. Retrieval of Daytime Total Column Water Vapour from OLCI Measurements over Land Surfaces. Remote Sens. 2021, 13, 932. [Google Scholar] [CrossRef]
- Fischer, J.; Bennartz, R. Retrieval of Total Water Vapour Content From MERIS Measurements. Available online: https://earth.esa.int/eogateway/documents/20142/37627/MERIS%20ATBD%202-04 (accessed on 21 April 2022).
- Xu, J.; Liu, Z. Radiance-based retrieval of total water vapor content from sentinel-3A OLCI NIR channels using ground-based GPS measurements. Int. J. Appl. Earth Obs. Geoinf. 2021, 104, 102586. [Google Scholar] [CrossRef]
- Li, X.; Dick, G.; Lu, C.; Ge, M.; Nilsson, T.; Ning, T.; Wickert, J.; Schuh, H. Multi-GNSS meteorology: Real-time retrieving of atmospheric water vapor from BeiDou, Galileo, GLONASS and GPS observations. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6385–6393. [Google Scholar] [CrossRef] [Green Version]
- Bai, J.; Lou, Y.; Zhang, W.; Zhou, Y.; Zhang, Z.; Shi, C. Assessment and calibration of MODIS precipitable water vapor products based on GPS network over China. Atmos. Res. 2021, 254, 105504. [Google Scholar] [CrossRef]
- Zhao, Q.; Ma, X.; Yao, W.; Liu, Y.; Yao, Y. A drought monitoring method based on precipitable water vapor and precipitation. J. Clim. 2020, 33, 10727–10741. [Google Scholar] [CrossRef]
- Jiang, W.; Yuan, P.; Chen, H.; Cai, J.; Li, Z.; Chao, N.; Sneeuw, N. Annual variations of monsoon and drought detected by GPS: A case study in Yunnan, China. Sci. Rep. 2017, 7, 1–10. [Google Scholar]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration Bernard 10740 JOURNAL OF CLIMATE VOLUME 33 index. J. Climate 2010, 23, 1696–1718. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Wang, X.; Wu, S.; Zhang, K.; Chen, X.; Qiu, C.; Zhang, S.; Zhang, J.; Xie, M.; Li, L. Development of an improved model for prediction of short-term heavy precipitation based on GNSS-derived PWV. Remote Sens. 2020, 12, 4101. [Google Scholar] [CrossRef]
- Li, H.; Wang, X.; Wu, S.; Zhang, K.; Chen, X.; Zhang, J.; Qiu, C.; Zhang, S.; Li, L. An improved model for detecting heavy precipitation using GNSS-derived zenith total delay measurements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 5392–5405. [Google Scholar] [CrossRef]

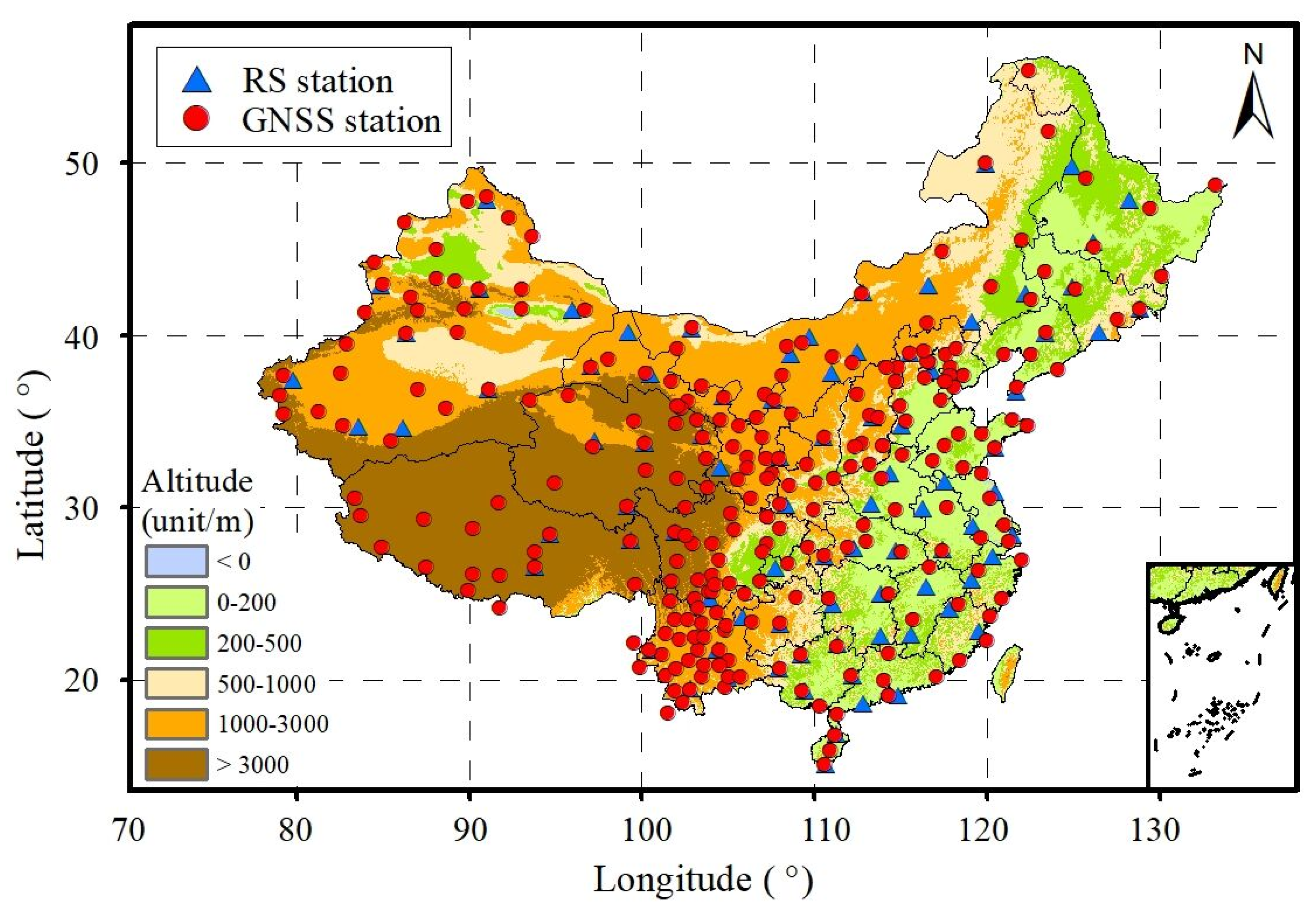


| Category | Resource | Period | Spatial-Temporal Resolution | Source | |
|---|---|---|---|---|---|
| Ground-Based | GNSS | 1 January 2012–31 December 2020 | 1 h | Station (260) | ftp://ftp.cgps.ac.cn/products/ (accessed on 24 April 2022) |
| RS | 1 January 2012–31 December 2020 | 12 h | Station (87) | ftp://ftp.ncdc.noaa.gov/ (accessed on 24 April 2022) | |
| Reanalysis-Based | ERA5 | 1 January 2012–31 December 2020 | 1 h | 0.25° × 0.25° | https://www.ecmwf.int/ (accessed on 24 April 2022) |
| Space-Based | FY-3A/MERSI | 1 January 2012–31 December 2013 | 5 min | 1 km × 1 km | http://satellite.nsmc.org.cn/ (accessed on 24 April 2022) |
| Sentinel-3A/OLCI | 1 March 2019–4 March 2020 | 5 min | 0.3 km × 0.3 km | https://scihub.copernicus.eu/ (accessed on 24 April 2022) | |
| Index | RMS | Bias | MAE | |
|---|---|---|---|---|
| Value | ||||
| Mean | 2.15 | 0.05 | 1.65 | |
| Max | 3.24 | 0.61 | 3.54 | |
| Min | 0.86 | −0.69 | 0.66 | |
| Type | Comparison with RS | Comparison with GNSS | |||||
|---|---|---|---|---|---|---|---|
| Index | RMS | Bias | MAE | RMS | Bias | MAE | |
| Mean | 1.90 | −0.05 | 1.51 | 1.86 | 0.11 | 1.48 | |
| Max | 3.61 | 0.24 | 2.85 | 4.72 | 0.27 | 4.01 | |
| Min | 0.79 | −0.26 | 0.62 | 0.9 | −0.54 | 0.71 | |
| Type | Comparison with RS | Comparison with GNSS | |||||
|---|---|---|---|---|---|---|---|
| Index | RMS | Bias | MAE | RMS | Bias | MAE | |
| Mean | 4.46 | 0.56 | 3.61 | 4.61 | −0.33 | 3.79 | |
| Max | 9.26 | 1.56 | 8.03 | 11.38 | 5.91 | 8.71 | |
| Min | 0.98 | −0.42 | 0.78 | 2.00 | −8.71 | 1.57 | |
| Type | Comparison with RS | Comparison with GNSS | |||||
|---|---|---|---|---|---|---|---|
| Index | RMS | Bias | MAE | RMS | Bias | MAE | |
| Mean | 2.47 | −0.63 | 1.58 | 2.95 | 0.01 | 1.37 | |
| Max | 8.40 | −6.88 | 6.88 | 10.82 | 0.84 | 7.51 | |
| Min | 0.09 | −0.42 | 0.01 | 0.24 | −0.89 | 0.07 | |
| Stations | ||
|---|---|---|
| Mean. | 0.875 | 0.865 |
| HLFY | 0.88 | 0.86 |
| HNMY | 0.90 | 0.90 |
| JLYJ | 0.88 | 0.87 |
| JLCL | 0.84 | 0.83 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Q.; Zhang, X.; Wu, K.; Liu, Y.; Li, Z.; Shi, Y. Comprehensive Precipitable Water Vapor Retrieval and Application Platform Based on Various Water Vapor Detection Techniques. Remote Sens. 2022, 14, 2507. https://doi.org/10.3390/rs14102507
Zhao Q, Zhang X, Wu K, Liu Y, Li Z, Shi Y. Comprehensive Precipitable Water Vapor Retrieval and Application Platform Based on Various Water Vapor Detection Techniques. Remote Sensing. 2022; 14(10):2507. https://doi.org/10.3390/rs14102507
Chicago/Turabian StyleZhao, Qingzhi, Xiaoya Zhang, Kan Wu, Yang Liu, Zufeng Li, and Yun Shi. 2022. "Comprehensive Precipitable Water Vapor Retrieval and Application Platform Based on Various Water Vapor Detection Techniques" Remote Sensing 14, no. 10: 2507. https://doi.org/10.3390/rs14102507
APA StyleZhao, Q., Zhang, X., Wu, K., Liu, Y., Li, Z., & Shi, Y. (2022). Comprehensive Precipitable Water Vapor Retrieval and Application Platform Based on Various Water Vapor Detection Techniques. Remote Sensing, 14(10), 2507. https://doi.org/10.3390/rs14102507