Digital Mapping of Soil Organic Carbon with Machine Learning in Dryland of Northeast and North Plain China
Abstract
:1. Introduction
2. Materials and Methods
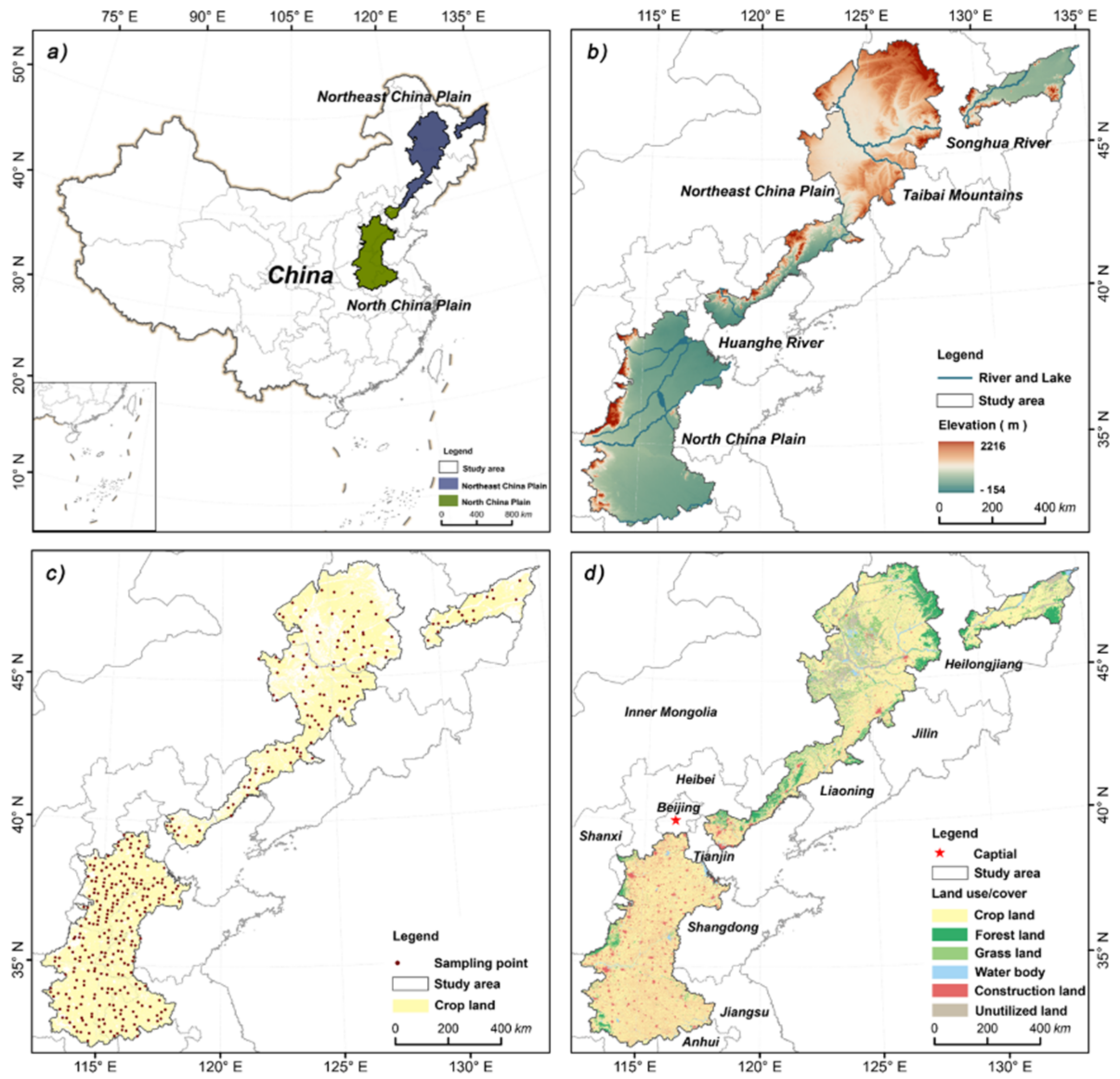
2.1. Study Area
2.2. Soil Data
2.3. Environmental Covariates
2.4. Modeling Methodology
2.4.1. Feature Selection
2.4.2. Model Development
2.4.3. Model Validation
2.4.4. Uncertainty Assessment
3. Results
3.1. Descriptive Statistics for SOC
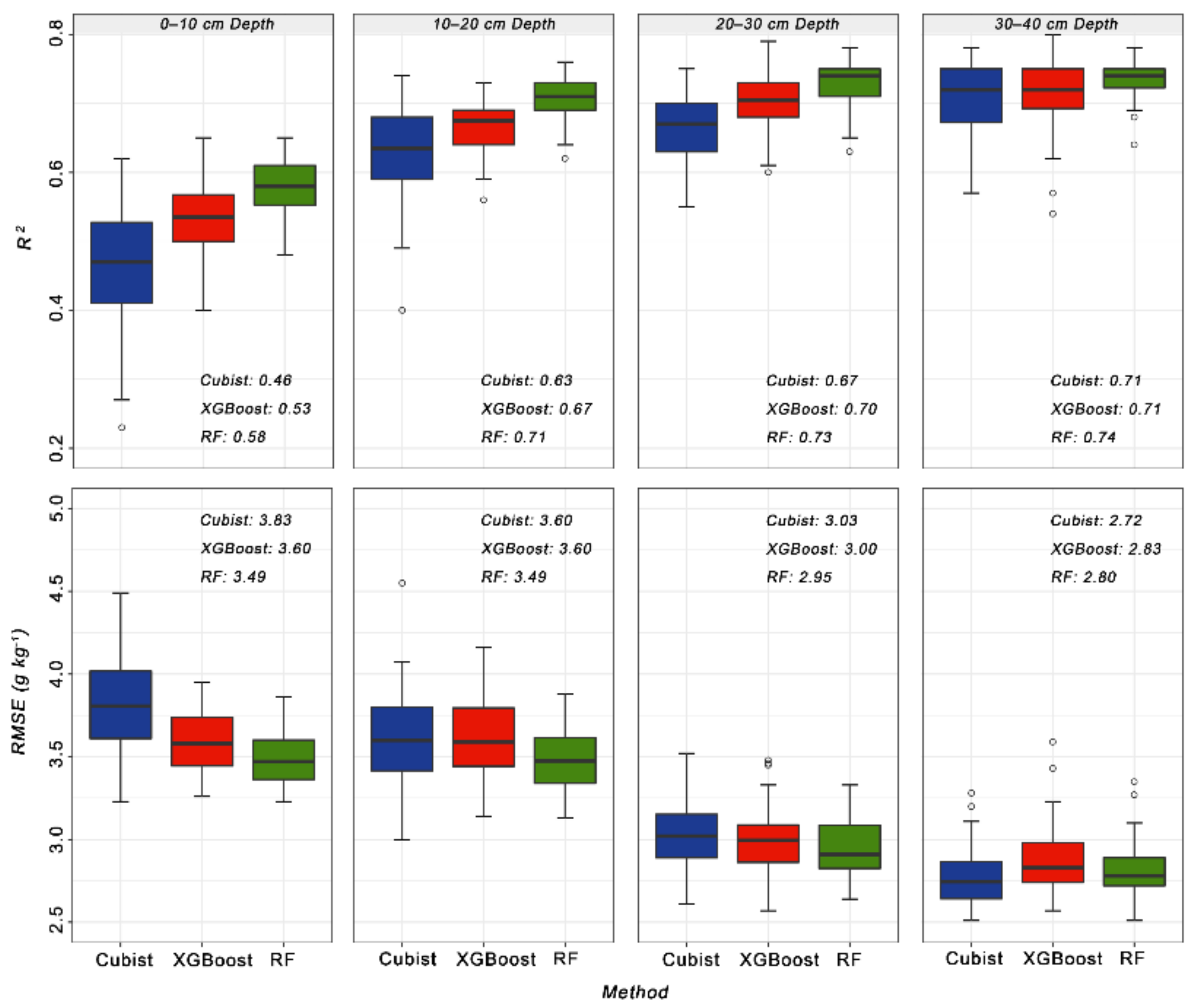
3.2. Model Evaluation and Comparison
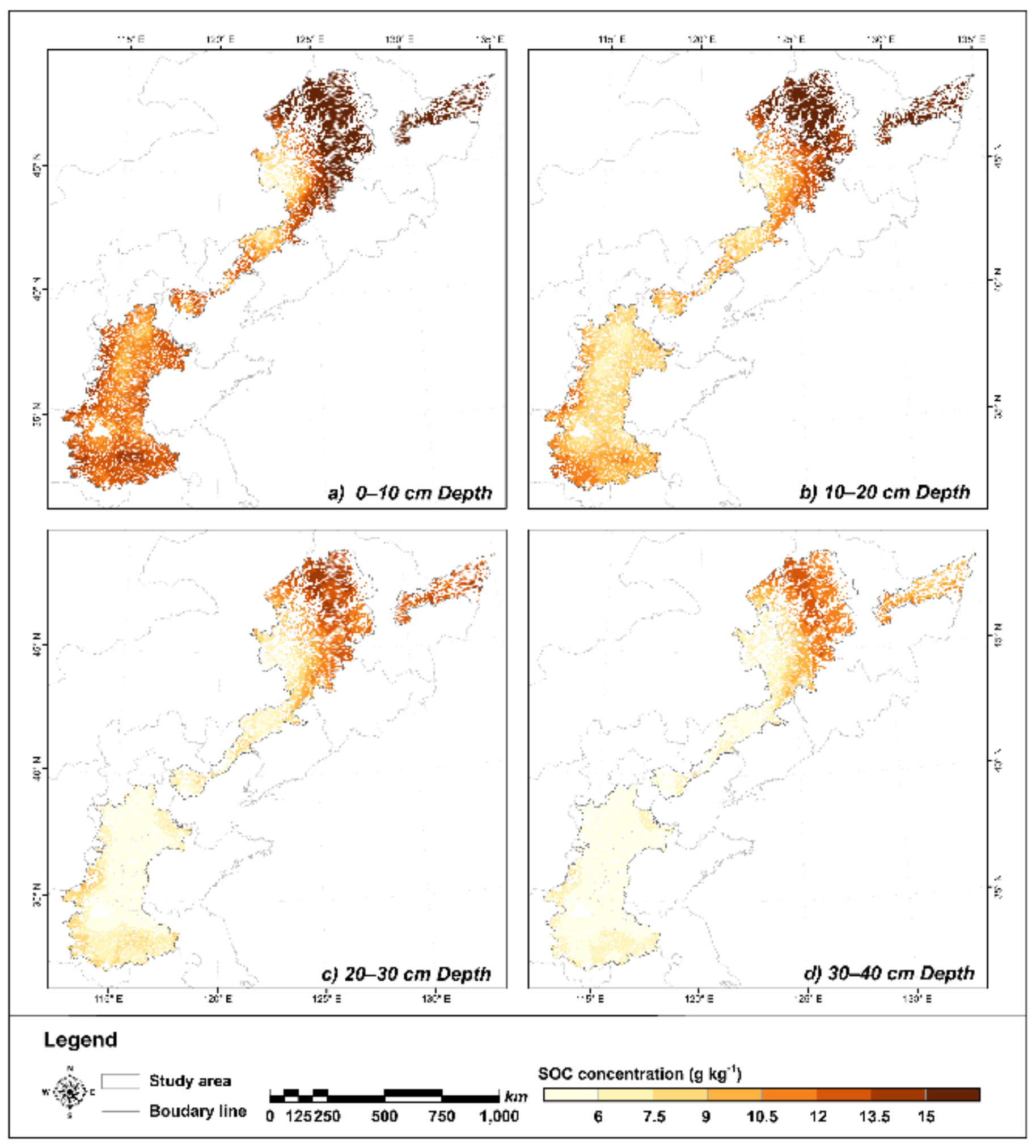
3.3. Spatial Distribution Pattern of SOC
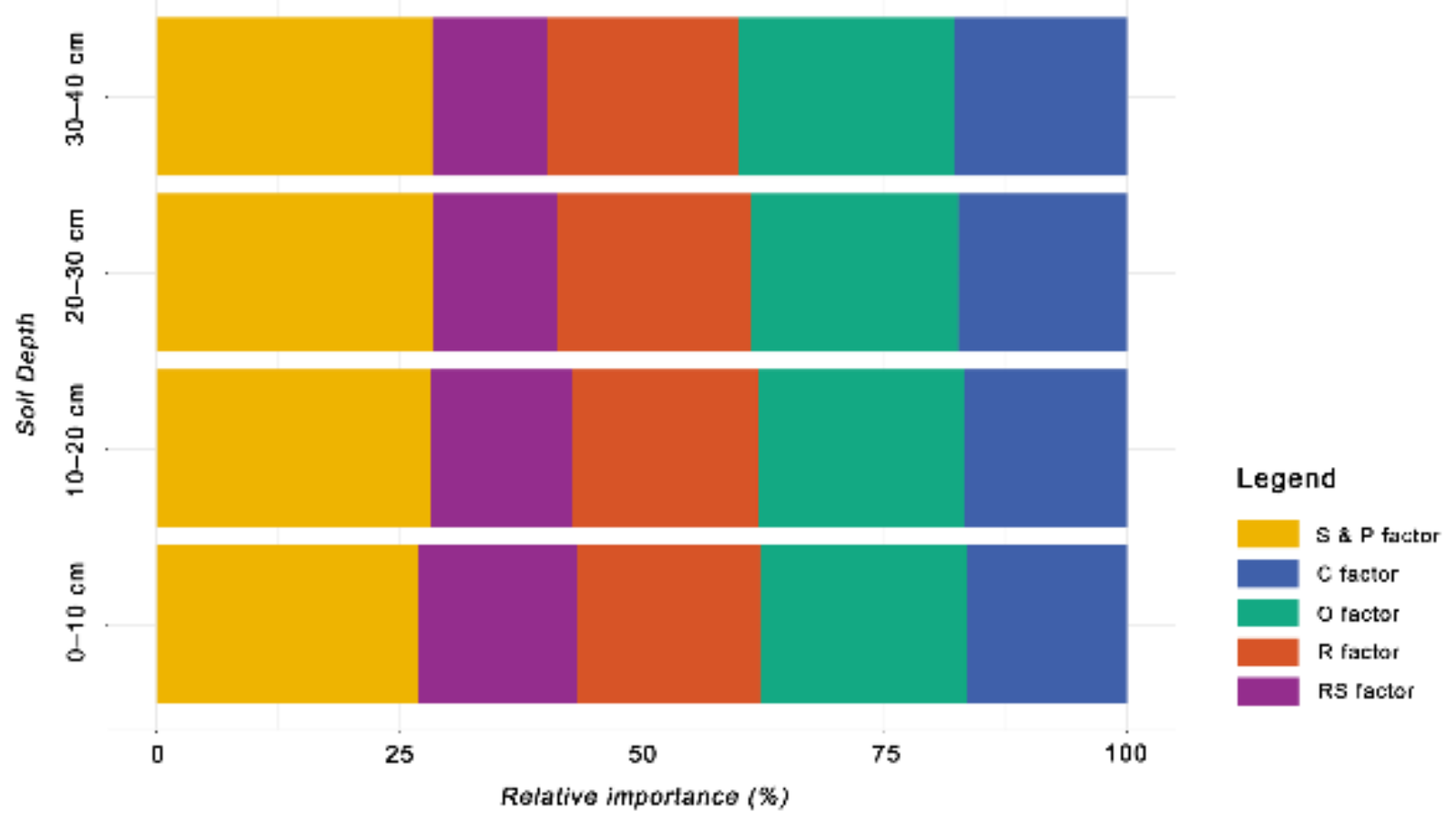
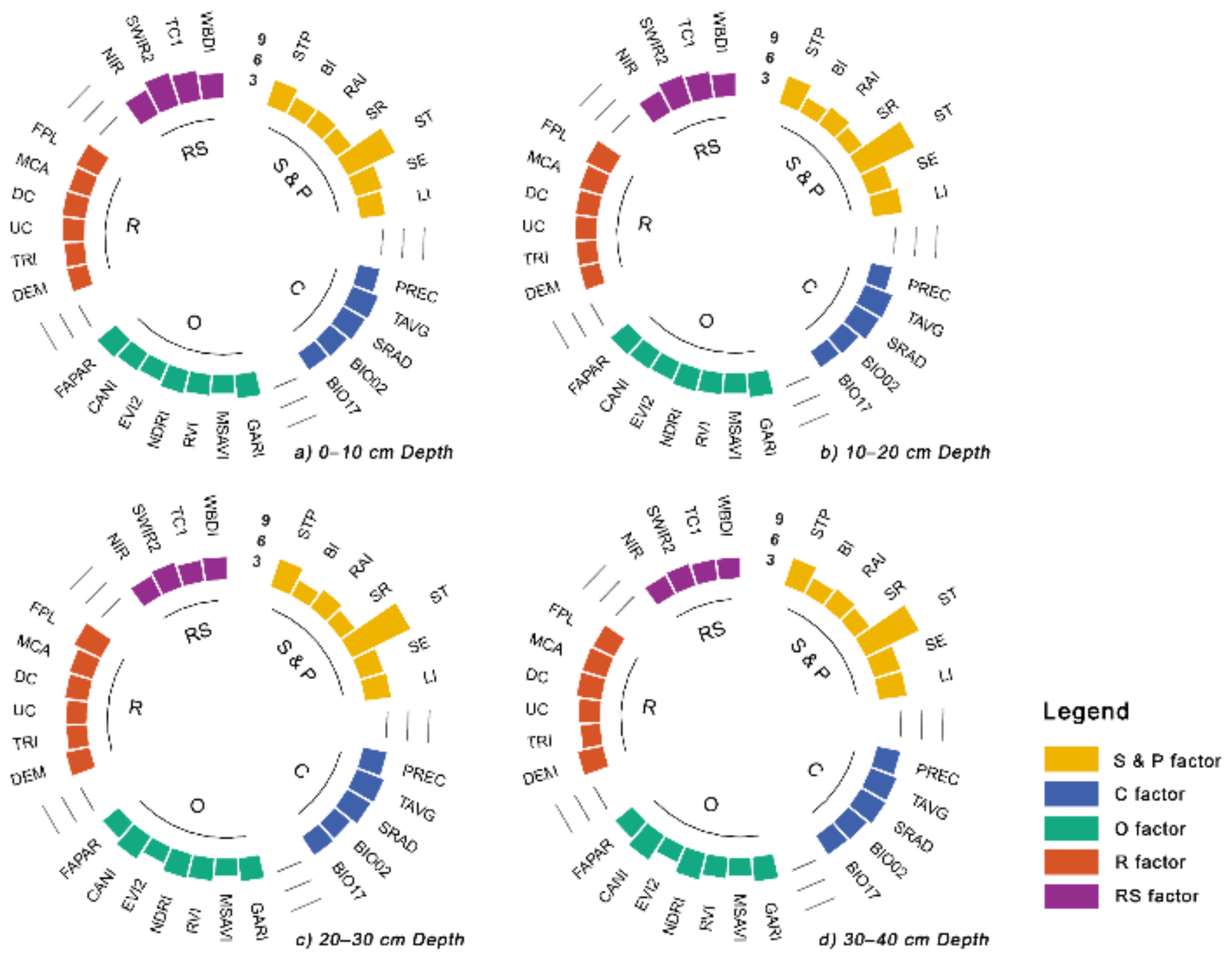
3.4. Relative Importance of Environmental Covariates
4. Discussion
4.1. Model Performance
4.2. Spatial Distribution Pattern of SOC and Controlling Factors
4.3. Digital SOC Mapping and Its Uncertainty
4.4. Limitations and Perspectives
5. Conclusions
- Compared with XGBoost and Cubist, RF was the optimal model for predicting regional SOC, with the highest accuracy and the lowest uncertainty.
- The SOC overall increased from south to north and decreased with increasing depth. In the North Plain, the SOC was higher in the margin, while it increased with latitude in the Northeast Plain, with high values in the typical black soil region.
- The spatial variation was mainly influenced by the soil and parent material, organism, relief and climate.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Owusu, S.; Yigini, Y.; Olmedo, G.F.; Omuto, C.T. Spatial prediction of soil organic carbon stocks in Ghana using legacy data. Geoderma 2020, 360, 114008. [Google Scholar] [CrossRef]
- Houghton, J.T.; Ding, Y.; Griggs, D.J.; Noguer, M.; van der Linden, P.J.; Dai, X.; Maskell, K.; Johnson, C. Climate Change 2001: The Scientific Basis; Cambridge University Press: New York, NY, USA, 2001. [Google Scholar]
- Lal, R. Soil carbon sequestration impacts on global climate change and food security. Science 2004, 304, 1623–1627. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, S.; Arrouays, D.; Leatitia Mulder, V.; Poggio, L.; Minasny, B.; Roudier, P.; Libohova, Z.; Lagacherie, P.; Shi, Z.; Hannam, J.; et al. Digital mapping of GlobalSoilMap soil properties at a broad scale: A review. Geoderma 2022, 409, 115567. [Google Scholar] [CrossRef]
- Goldstein, A.; Turner, W.R.; Spawn, S.A.; Anderson-Teixeira, K.J.; Cook-Patton, S.; Fargione, J.; Gibbs, H.K.; Griscom, B.; Hewson, J.H.; Howard, J.F.; et al. Protecting irrecoverable carbon in Earth’s ecosystems. Nat. Clim. Change 2020, 10, 287–295. [Google Scholar] [CrossRef]
- Paustian, K.; Lehmann, J.; Ogle, S.; Reay, D.; Robertson, G.P.; Smith, P. Climate-smart soils. Nature 2016, 532, 49–57. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zeraatpisheh, M.; Ayoubi, S.; Mirbagheri, Z.; Mosaddeghi, M.R.; Xu, M. Spatial prediction of soil aggregate stability and soil organic carbon in aggregate fractions using machine learning algorithms and environmental variables. Geoderma Reg. 2021, 27, e00440. [Google Scholar] [CrossRef]
- Tubiello, F.N.; Salvatore, M.; Ferrara, A.F.; House, J.; Federici, S.; Rossi, S.; Biancalani, R.; Condor Golec, R.D.; Jacobs, H.; Flammini, A.; et al. The Contribution of Agriculture, Forestry and other Land Use activities to Global Warming, 1990–2012. Glob. Chang Biol. 2015, 21, 2655–2660. [Google Scholar] [CrossRef] [Green Version]
- Lagacherie, P.; McBratney, A. Spatial soil information systems and spatial soil inference systems: Perspectives for digital soil mapping. Dev. Soil Sci. 2006, 31, 3–22. [Google Scholar] [CrossRef]
- Chen, S.; Martin, M.P.; Saby, N.P.A.; Walter, C.; Angers, D.A.; Arrouays, D. Fine resolution map of top-and subsoil carbon sequestration potential in France. Sci. Total Environ. 2018, 630, 389–400. [Google Scholar] [CrossRef]
- Zeraatpisheh, M.; Bakhshandeh, E.; Hosseini, M.; Alavi, S.M. Assessing the effects of deforestation and intensive agriculture on the soil quality through digital soil mapping. Geoderma 2020, 363, 114139. [Google Scholar] [CrossRef]
- Zhang, G.; Liu, F.; Song, X. Recent progress and future prospect of digital soil mapping: A review. J. Integr. Agric. 2017, 16, 2871–2885. [Google Scholar] [CrossRef]
- Hong, Y.; Chen, S.; Chen, Y.; Linderman, M.; Mouazen, A.M.; Liu, Y.; Guo, L.; Yu, L.; Liu, Y.; Cheng, H.; et al. Comparing laboratory and airborne hyperspectral data for the estimation and mapping of topsoil organic carbon: Feature selection coupled with random forest. Soil Tillage Res. 2020, 199, 104589. [Google Scholar] [CrossRef]
- Taghizadeh-Mehrjardi, R.; Khademi, H.; Khayamim, F.; Zeraatpisheh, M.; Heung, B.; Scholten, T. A Comparison of Model Averaging Techniques to Predict the Spatial Distribution of Soil Properties. Remote Sens. 2022, 14, 472. [Google Scholar] [CrossRef]
- Lamichhane, S.; Kumar, L.; Wilson, B. Digital soil mapping algorithms and covariates for soil organic carbon mapping and their implications: A review. Geoderma 2019, 352, 395–413. [Google Scholar] [CrossRef]
- Zhou, Y.; Xue, J.; Chen, S.; Zhou, Y.; Liang, Z.; Wang, N.; Shi, Z. Fine-resolution mapping of soil total nitrogen across China based on weighted model averaging. Remote Sens. 2020, 12, 85. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.X.; Minasny, B.; Malone, B.P.; Mcbratney, A.B. Pedology and digital soil mapping (DSM). Eur. J. Soil Sci. 2019, 70, 216–235. [Google Scholar] [CrossRef]
- Chen, S.; Arrouays, D.; Angers, D.A.; Chenu, C.; Barre, P.; Martin, M.P.; Saby, N.P.A.; Walter, C. National estimation of soil organic carbon storage potential for arable soils: A data-driven approach coupled with carbon-landscape zones. Sci. Total Environ. 2019, 666, 355–367. [Google Scholar] [CrossRef]
- Zhuo, Z.; Chen, Q.; Zhang, X.; Chen, S.; Gou, Y.; Sun, Z.; Huang, Y.; Shi, Z. Soil organic carbon storage, distribution, and influencing factors at different depths in the dryland farming regions of Northeast and North China. Catena 2022, 210, 105934. [Google Scholar] [CrossRef]
- Chen, Q.; Shi, Z.; Chen, S.; Gou, Y.; Zhuo, Z. Role of Environment Variables in Spatial Distribution of Soil C, N, P Ecological Stoichiometry in the Typical Black Soil Region of Northeast China. Sustainability 2022, 14, 2636. [Google Scholar] [CrossRef]
- Zhou, Y.; Hartemink, A.E.; Shi, Z.; Liang, Z.; Lu, Y. Land use and climate change effects on soil organic carbon in North and Northeast China. Sci. Total Environ. 2019, 647, 1230–1238. [Google Scholar] [CrossRef]
- Tang, H.; Liu, Y.; Li, X.; Muhammad, A.; Huang, G. Carbon sequestration of cropland and paddy soils in China: Potential, driving factors, and mechanisms. Greenh. Gases Sci. Technol. 2019, 9, 872–885. [Google Scholar] [CrossRef]
- Yao, Y.; Tang, H.; Tang, P.; Yu, S.; Wang, D.; Si, H.; Chen, Y.; He, Y. Soil organic matter spatial distribution change over the past 20 years and its causes in Northeast. In Proceedings of the 2013 Second International Conference on Agro-Geoinformatics (Agro-Geoinformatics), Fairfax, VA, USA, 12–16 August 2013; pp. 433–438. [Google Scholar]
- Zhuo, Z.; Xing, A.; Cao, M.; Li, Y.; Zhao, Y.; Guo, X.; Huang, Y. Identifying the position of the compacted layer by measuring soil penetration resistance in a dryland farming region in Northeast China. Soil Use Manag. 2020, 36, 494–506. [Google Scholar] [CrossRef]
- Lessmann, M.; Ros, G.H.; Young, M.D.; de Vries, W. Global variation in soil carbon sequestration potential through improved cropland management. Glob. Change Biol. 2022, 28, 1162–1177. [Google Scholar] [CrossRef] [PubMed]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- IUSS Working Group WRB. World Reference Base for Soil Resources 2014, Update 2015 International Soil Classification System for Naming Soils and Creating Legends for Soil Maps; Food and Agriculture Organization of the United Nations: Rome, Italy, 2015. [Google Scholar]
- Jarvis, A.; Reuter, H.I.; Nelson, A.; Guevara, E. Hole-Filled SRTM for the Globe Version 4. CGIAR-CSI SRTM 90m Database. Available online: http://srtm.csi.cgiar.org (accessed on 9 November 2018).
- Bao, S. Soil Agro-Chemistrical Analysis; China Agriculture Press: Beijing, China, 2000; Volume 2030, pp. 30–107. [Google Scholar]
- McBratney, A.B.; Santos, M.L.M.; Minasny, B. On digital soil mapping. Geoderma 2003, 117, 3–52. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, G.L.; Song, X.D.; Li, D.C.; Zhao, Y.G.; Yang, J.L.; Wu, H.Y.; Yang, F. High-resolution and three-dimensional mapping of soil texture of China. Geoderma 2020, 361, 114061. [Google Scholar] [CrossRef]
- Wold, S.; Esbensen, K.; Geladi, P. Principal component analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar] [CrossRef]
- Crist, E.P.; Cicone, R.C. A Physically-Based Transformation of Thematic Mapper Data—The Tm Tasseled Cap. IEEE Trans. Geosci. Remote Sens. 1984, 22, 256–263. [Google Scholar] [CrossRef]
- Fick, S.E.; Hijmans, R.J. WorldClim 2: New 1-km spatial resolution climate surfaces for global land areas. Int. J. Climatol. 2017, 37, 4302–4315. [Google Scholar] [CrossRef]
- Hijmans, R.J.; Cameron, S.E.; Parra, J.L.; Jones, P.G.; Jarvis, A. Very high resolution interpolated climate surfaces for global land areas. Int. J. Climatol. 2005, 25, 1965–1978. [Google Scholar] [CrossRef]
- Fischer, G.; Nachtergaele, F.; Prieler, S.; van Velthuizen, H.; Verelst, L.; Wiberg, D. Global Agro-Ecological Zones Assessment for Agriculture (GAEZ 2008); IIASA: Laxenburg, Austria; FAO: Rome, Italy, 2008; Volume 10. [Google Scholar]
- Hartmann, J.; Moosdorf, N. The new global lithological map database GLiM: A representation of rock properties at the Earth surface. Geochem. Geophy. Geosystems 2012, 13, 1–37. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021. [Google Scholar]
- Taghizadeh-Mehrjardi, R.; Nabiollahi, K.; Kerry, R. Digital mapping of soil organic carbon at multiple depths using different data mining techniques in Baneh region, Iran. Geoderma 2016, 266, 98–110. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Welikala, R.A.; Fraz, M.M.; Dehmeshki, J.; Hoppe, A.; Tah, V.; Mann, S.; Williamson, T.H.; Barman, S.A. Genetic algorithm based feature selection combined with dual classification for the automated detection of proliferative diabetic retinopathy. Comput. Med. Imaging Graph. 2015, 43, 64–77. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wadoux, A.M.J.C.; Minasny, B.; McBratney, A.B. Machine learning for digital soil mapping: Applications, challenges and suggested solutions. Earth-Sci. Rev. 2020, 210, 103359. [Google Scholar] [CrossRef]
- Quinlan, J.R. Combining instance-based and model-based learning. In Proceedings of the Tenth International Conference on Machine Learning, San Francisco, CA, USA, 27–29 July 1993; pp. 236–243. [Google Scholar]
- Minasny, B.; McBratney, A.B. Regression rules as a tool for predicting soil properties from infrared reflectance spectroscopy. Chemom. Intell. Lab. Syst. 2008, 94, 72–79. [Google Scholar] [CrossRef]
- Ma, Z.; Shi, Z.; Zhou, Y.; Xu, J.; Yu, W.; Yang, Y. A spatial data mining algorithm for downscaling TMPA 3B43 V7 data over the Qinghai–Tibet Plateau with the effects of systematic anomalies removed. Remote Sens. Environ. 2017, 200, 378–395. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Wang, N.; Xue, J.; Peng, J.; Biswas, A.; He, Y.; Shi, Z. Integrating Remote Sensing and Landscape Characteristics to Estimate Soil Salinity Using Machine Learning Methods: A Case Study from Southern Xinjiang, China. Remote Sens. 2020, 12, 4118. [Google Scholar] [CrossRef]
- Wilding, L. Spatial variability: Its documentation, accomodation and implication to soil surveys. In Proceedings of the Soil Spatial Variability, Las Vegas, NV, USA, 30 November–1 December 1984; pp. 166–194. [Google Scholar]
- Jansen, S. Hands-On Machine Learning for Algorithmic Trading: Design and Implement Investment Strategies Based on Smart Algorithms that Learn from Data Using Python; Packt Publishing Ltd.: Birmingham, UK, 2018. [Google Scholar]
- Gomes, L.C.; Faria, R.M.; de Souza, E.; Veloso, G.V.; Schaefer, C.E.G.R.; Fernandes, E.I. Modelling and mapping soil organic carbon stocks in Brazil. Geoderma 2019, 340, 337–350. [Google Scholar] [CrossRef]
- Liu, F.; Wu, H.; Zhao, Y.; Li, D.; Yang, J.; Song, X.; Shi, Z.; Zhu, A.; Zhang, G. Mapping high resolution National Soil Information Grids of China. Sci. Bull. 2021, 63, 328–340. [Google Scholar] [CrossRef]
- Viscarra Rossel, R.A.; Lee, J.; Behrens, T.; Luo, Z.; Baldock, J.; Richards, A. Continental-scale soil carbon composition and vulnerability modulated by regional environmental controls. Nat. Geosci. 2019, 12, 547–552. [Google Scholar] [CrossRef]
- Wiesmeier, M.; Urbanski, L.; Hobley, E.; Lang, B.; von Lutzow, M.; Marin-Spiotta, E.; van Wesemael, B.; Rabot, E.; Liess, M.; Garcia-Franco, N.; et al. Soil organic carbon storage as a key function of soils—A review of drivers and indicators at various scales. Geoderma 2019, 333, 149–162. [Google Scholar] [CrossRef]
- Hobley, E.; Wilson, B.; Wilkie, A.; Gray, J.; Koen, T. Drivers of soil organic carbon storage and vertical distribution in Eastern Australia. Plant Soil 2015, 390, 111–127. [Google Scholar] [CrossRef]
- Gray, J.M.; Bishop, T.F.A.; Wilson, B.R. Factors controlling soil organic carbon stocks with depth in eastern Australia. Soil Sci. Soc. Am. J. 2015, 79, 1741–1751. [Google Scholar] [CrossRef] [Green Version]
- Xue, J.; Wang, Y.; Teng, H.; Wang, N.; Li, D.; Peng, J.; Biswas, A.; Shi, Z. Dynamics of Vegetation Greenness and Its Response to Climate Change in Xinjiang over the Past Two Decades. Remote Sens. 2021, 13, 4063. [Google Scholar] [CrossRef]
- Brady, N.C.; Weil, R.R.; Weil, R.R. The Nature and Properties of Soils; Prentice Hall: Upper Saddle River, NJ, USA, 2008; Volume 13. [Google Scholar]
- Rial, M.; Martinez Cortizas, A.; Rodriguez-Lado, L. Understanding the spatial distribution of factors controlling topsoil organic carbon content in European soils. Sci. Total Environ. 2017, 609, 1411–1422. [Google Scholar] [CrossRef]
- Adhikari, K.; Hartemink, A.E.; Minasny, B.; Bou Kheir, R.; Greve, M.B.; Greve, M.H. Digital mapping of soil organic carbon contents and stocks in Denmark. PLoS ONE 2014, 9, e105519. [Google Scholar] [CrossRef]
- Ramifehiarivo, N.; Brossard, M.; Grinand, C.; Andriamananjara, A.; Razafimbelo, T.; Rasolohery, A.; Razafimahatratra, H.; Seyler, F.; Ranaivoson, N.; Rabenarivo, M.; et al. Mapping soil organic carbon on a national scale: Towards an improved and updated map of Madagascar. Geoderma Reg. 2017, 9, 29–38. [Google Scholar] [CrossRef]
- Kumar, L.; Skidmore, A.K.; Knowles, E. Modelling topographic variation in solar radiation in a GIS environment. Int. J. Geogr. Inf. Sci. 1997, 11, 475–497. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Liang, Z.; Chen, S.; Yang, Y.; Zhao, R.; Shi, Z.; Rossel, R.A.V. National digital soil map of organic matter in topsoil and its associated uncertainty in 1980′s China. Geoderma 2019, 335, 47–56. [Google Scholar] [CrossRef]
- Chen, S.C.; Richer-de-Forges, A.C.; Mulder, V.L.; Martelet, G.; Loiseau, T.; Lehmann, S.; Arrouays, D. Digital mapping of the soil thickness of loess deposits over a calcareous bedrock in central France. Catena 2021, 198, 105062. [Google Scholar] [CrossRef]
- Ma, Y.; Minasny, B.; Welivitiya, W.D.P.; Malone, B.P.; Willgoose, G.R.; McBratney, A.B. The feasibility of predicting the spatial pattern of soil particle-size distribution using a pedogenesis model. Geoderma 2019, 341, 195–205. [Google Scholar] [CrossRef]
- Arrouays, D.; Lagacherie, P.; Hartemink, A.E. Digital soil mapping across the globe. Geoderma Reg. 2017, 9, 1–4. [Google Scholar] [CrossRef]
- Chen, S.C.; Mulder, V.L.; Heuvelink, G.B.M.; Poggio, L.; Caubet, M.; Dobarco, M.R.; Walter, C.; Arrouays, D. Model averaging for mapping topsoil organic carbon in France. Geoderma 2020, 366, 114237. [Google Scholar] [CrossRef]
- Don, A.; Schumacher, J.; Freibauer, A. Impact of tropical land-use change on soil organic carbon stocks—A meta-analysis. Glob. Change Biol. 2011, 17, 1658–1670. [Google Scholar] [CrossRef] [Green Version]
- Viscarra Rossel, R.A.; Webster, R.; Bui, E.N.; Baldock, J.A. Baseline map of organic carbon in Australian soil to support national carbon accounting and monitoring under climate change. Glob. Change Biol. 2014, 20, 2953–2970. [Google Scholar] [CrossRef]



| Name | Cod | Scale | Factor | Type |
|---|---|---|---|---|
| Soil Temperature | STP | 10,000 m | S&P 1 | N 6 |
| Reflectance Absorption Index | BI | 30 m | S&P 1 | N 6 |
| Stress Related | RAI | 30 m | S&P 1 | N 6 |
| Brightness Index | SR | 30 m | S&P 1 | N 6 |
| Soil Type | ST | 1000 m | S&P 1 | C 7 |
| Soil Erosion | SE | 1000 m | S&P 1 | C 7 |
| Lithology | LI | 2000 m | S&P 1 | C 7 |
| Mean Precipitation | PREC | 1000 m | C 2 | N 6 |
| Mean Temperature | TAVG | 1000 m | C 2 | N 6 |
| Solar Radiation | SRAD | 1000 m | C 2 | N 6 |
| Mean Diurnal Range | BIO02 | 1000 m | C 2 | N 6 |
| Precipitation of Driest Quarter | BIO17 | 1000 m | C 2 | N 6 |
| Green Atmospherically Resistant Vegetation Index | GARI | 30 m | O 3 | N 6 |
| Modified Soil Adjusted Vegetation Index | MSAVI | 30 m | O 3 | N 6 |
| Ratio Vegetation Index | RVI | 30 m | O 3 | N 6 |
| Normalized Difference Red/Green Redness Index | NDRI | 30 m | O 3 | N 6 |
| Two-Band Enhanced Vegetation Index | EVI2 | 30 m | O 3 | N 6 |
| Canopy Index | CANI | 30 m | O 3 | N 6 |
| Fraction of Absorbed Photosynthetic Active Radiation | FAPAR | 500 m | O 3 | N 6 |
| Elevation | DEM | 90 m | R 4 | N 6 |
| Terrain Ruggedness Index | TRI | 90 m | R 4 | N 6 |
| Upslope Curvature | UC | 90 m | R 4 | N 6 |
| Downslope Curvature | DC | 90 m | R 4 | N 6 |
| Modified Catchment Area | MCA | 90 m | R 4 | N 6 |
| Flow Path Length | FPL | 90 m | R 4 | N 6 |
| Near-Infrared Band | NIR | 30 m | RS 5 | N 6 |
| Shortwave Infrared 2 Band | SWIR2 | 30 m | RS 5 | N 6 |
| Tasseled Cap 1 | TC1 | 30 m | RS 5 | N 6 |
| Wetness Brightness Difference Index | WBDI | 30 m | RS 5 | N 6 |
| Depth | Min 5 | 1st Qu 7 | Median | Mean | 3rd Qu 8 | Max 6 | SD | CV (%) 9 | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|---|---|---|
| SOC 0–10 1 | 2.88 | 9.15 | 12.04 | 12.56 | 15.36 | 31.15 | 4.86 | 38.66 | 0.71 | 3.80 |
| SOC 10–20 2 | 2.02 | 6.81 | 8.87 | 10.11 | 11.78 | 30.60 | 4.98 | 49.22 | 1.37 | 5.01 |
| SOC 20–30 3 | 0.96 | 4.56 | 6.26 | 7.58 | 9.14 | 25.26 | 4.53 | 59.79 | 1.42 | 4.83 |
| SOC 30–40 4 | 0.60 | 3.57 | 4.91 | 6.37 | 7.66 | 20.95 | 4.17 | 65.46 | 1.52 | 4.88 |
| Depth | Cubist | XGBoost | RF | ||||||
|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | RRMSE | R2 | RMSE | RRMSE | R2 | RMSE | RRMSE | |
| SOC 0–10 1 | 0.46 | 3.83 | 0.32 | 0.53 | 3.60 | 0.30 | 0.58 | 3.49 | 0.29 |
| SOC 10–20 2 | 0.63 | 3.60 | 0.35 | 0.67 | 3.60 | 0.35 | 0.71 | 3.49 | 0.34 |
| SOC 20–30 3 | 0.67 | 3.03 | 0.39 | 0.70 | 3.00 | 0.38 | 0.73 | 2.95 | 0.38 |
| SOC 30–40 4 | 0.71 | 2.72 | 0.41 | 0.71 | 2.83 | 0.43 | 0.74 | 2.80 | 0.43 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Xue, J.; Chen, S.; Wang, N.; Shi, Z.; Huang, Y.; Zhuo, Z. Digital Mapping of Soil Organic Carbon with Machine Learning in Dryland of Northeast and North Plain China. Remote Sens. 2022, 14, 2504. https://doi.org/10.3390/rs14102504
Zhang X, Xue J, Chen S, Wang N, Shi Z, Huang Y, Zhuo Z. Digital Mapping of Soil Organic Carbon with Machine Learning in Dryland of Northeast and North Plain China. Remote Sensing. 2022; 14(10):2504. https://doi.org/10.3390/rs14102504
Chicago/Turabian StyleZhang, Xianglin, Jie Xue, Songchao Chen, Nan Wang, Zhou Shi, Yuanfang Huang, and Zhiqing Zhuo. 2022. "Digital Mapping of Soil Organic Carbon with Machine Learning in Dryland of Northeast and North Plain China" Remote Sensing 14, no. 10: 2504. https://doi.org/10.3390/rs14102504
APA StyleZhang, X., Xue, J., Chen, S., Wang, N., Shi, Z., Huang, Y., & Zhuo, Z. (2022). Digital Mapping of Soil Organic Carbon with Machine Learning in Dryland of Northeast and North Plain China. Remote Sensing, 14(10), 2504. https://doi.org/10.3390/rs14102504









