Abstract
Soil texture and particle size fractions (PSFs) are a critical characteristic of soil that influences most physical, chemical, and biological properties of soil; furthermore, reliable spatial predictions of PSFs are crucial for agro-ecological modeling. Here, series of hybridized artificial neural network (ANN) models with bio-inspired metaheuristic optimization algorithms such as a genetic algorithm (GA-ANN), particle swarm optimization (PSO-ANN), bat (BAT-ANN), and monarch butterfly optimization (MBO-ANN) algorithms, were built for predicting PSFs for the Mazandaran Province of northern Iran. In total, 1595 composite surficial soil samples were collected, and 64 environmental covariates derived from terrain, climatic, remotely sensed, and categorical datasets were used as predictors. Models were tested using a repeated 10-fold nested cross-validation approach. The results indicate that the hybridized ANN methods were far superior to the reference approach using ANN with a backpropagation training algorithm (BP-ANN). Furthermore, the MBO-ANN approach was consistently determined to be the best approach and yielded the lowest error and uncertainty. The MBO-ANN model improved the predictions in terms of RMSE by 20% for clay, 10% for silt, and 24% for sand when compared to BP-ANN. The physiographical units, soil types, geology maps, rainfall, and temperature were the most important predictors of PSFs, followed by the terrain and remotely sensed data. This study demonstrates the effectiveness of bio-inspired algorithms for improving ANN models. The outputs of this study will support and inform sustainable soil management practices, agro-ecological modeling, and hydrological modeling for the Mazandaran Province of Iran.
1. Introduction
Soil texture is one of the most critical physical properties of soil and is classified based on the relative proportions of sand, silt, and clay. These individual particle-size fractions (PSFs) are a type of compositional soil data and have important impacts on the behavior of other physical, chemical, and biological properties of soil; furthermore, it is a major control of soil fertility [1,2,3,4]. For example, the buffering capacity of soils [5], fertilizer application rates [6,7], soil carbon maintenances [8,9], and taxonomic-based diagnostic horizon definitions [10] are greatly dependent on soil PSFs and textural classes. Moreover, soil PSFs are the most widely used input for developing pedotransfer functions, which are used to predict soil characteristics that are difficult to measure, which are in turn used for hydrogeological, erosion, and environmental modeling purposes [11,12,13,14]. Hence, providing high-resolution spatial data related to soil PSFs is of great interest to researchers.
Globally, soil surveying practices have largely transitioned towards the use of digital soil mapping (DSM) approaches as a means to reduce the cost and time required to develop soil maps and leverage the advances in modern technologies related to computing, remote sensing (RS), machine learning (ML), and geographical information systems. Within a DSM framework, different statistical methods are used to infer the relationships between soil response variables (e.g., soil texture and PSFs) and a suite of environmental covariates to predict soil variability in unsampled locations. Typically, these environmental covariates may be derived from digital elevation models (DEM), geomorphological data, climatic data, and RS data for predicting PSFs [11,15,16].
The use of ML models has become increasingly prevalent for predicting the spatial distribution of soil properties. When predicting soil PSFs, various ML-based DSM studies have included the use of artificial neural networks (ANNs) [17,18,19,20,21], boosted regression tree (BRT) [19,22,23], Random Forest (RF) [18,24], and artificial neuro-fuzzy inference system (ANFIS) [16,25]. Despite the variety of ML models that a DSM practitioner may apply, existing literature does not seem to suggest that one model is universally better than others; furthermore, model comparison studies have shown that different models have the potential to generate drastically different outputs when given the same input data [26].
When predicting PSFs, however, ANNs have been shown to be particularly effective, and they are the most widespread approach due to their accuracy and flexibility [17,18,19,20,21]. However, this model has several considerable shortcomings, such as inconsistent architectures for different applications, coupled with the process required to tune and fit a neural network, which is a time-consuming procedure that is largely based on trial and error [27,28]. Conventionally, ANNs have been fitted using a backpropagation (BP) algorithm; however, state-of-the-art approaches using bio-inspired, metaheuristic, optimization algorithms have become increasingly prevalent, including the genetic algorithm (GA) [29], particle swarm optimization (PSO) [30], ant lion optimization (ALO) [31], spotted hyena optimizer (SHO) [32], binary spring search algorithm (BSSA) [33], grey wolf algorithm (GWO) [34], genetic optimization resampling based particle filtering (GORPF) algorithm [35], and ant colony optimization (ACO) [16]—all of which may be hybridized with ANNs to address the aforementioned disadvantages.
The separate estimation of each particle size class does not guarantee that the sand, silt, and clay percentages will sum to 100% for all predicted locations. To reduce the uncertainty and unreliability in spatially predicting PSFs, soil PSFs must be treated as compositional data (i.e., sum to a constant value) [3,12,14]. To address this, different types of transformations include the additive, centered, and isometric log-ratio transformations [12,14]. A unique feature of the ANN model is its ability to use a softmax transform function in the output layer. The softmax function, also known as a softargmax or a normalized exponential function, is very similar to the additive log-ratio transform, which ensures that the sand, silt, and clay fractions sum to unity [12].
Within the DSM literature, the use of these optimization techniques is limited, and a comprehensive comparison has yet to be carried out on individual soil properties—in particular, compositional soil data, such as PSFs. Hence, the main objectives of this study were: (1) to develop and test the performance of metaheuristic, optimization algorithms that were hybridized with ANNs for predicting soil PSFs using existing soil survey; (2) to rank the explanatory power of individual environmental covariates for predicting the distribution of soil PSFs for a case study in northern Iran; and (3) to map the spatial distribution of soil PSFs and soil textural classes at a provincial scale. This study was carried out in the Mazandaran Province of northern Iran, which is an agriculturally significant region with intensive crop production and diverse soil types. Due to the nonuniform impacts of the soil forming factors, coupled with the unique eco-hydrological characteristics of the area, the surficial soil texture is highly diverse across the province.
2. Materials and Methods
2.1. Study Area
The Mazandaran Province located in the northern region of Iran, within 50°31′21″ E to 53°56′52″ E longitudes and 36°38′06″ N to 36°54′59″ N latitudes, has an areal extent of 23,833 km² (Figure 1). Forestlands, rangelands, croplands, and orchards are the dominant landcover types, occupying 46%, 24%, 10% and 4% of the total area, respectively. The soils of the province are mostly fertile and, due to the suitable climatic conditions, play a significant role in producing various crops (e.g., rice, wheat, and corn) and fruit trees (e.g., citrus and kiwi) in Iran. The elevation ranges from <5 m above mean sea level in the northern region, along the shoreline of the Caspian Sea, to >3000 m above mean sea level in the southern region, along the Alborz Mountain chains. According to the De Martonne methodology for climate classification [36], the Mazandaran Province is described as having a mixture of very humid, humid, Mediterranean, and semi-humid climatic conditions. Within the province, the rainfall in the eastern part is about 400 mm and increases along a westward gradient to 1400 mm; hence, the soil moisture regime is classified as xeric, ustic, and udic along that same gradient. The predominant soil temperature regime class is classified as being thermic and followed by mesic and cryic [37]. The most important soil environmental factor, which influences the soil development and variability at the provincial scale, is climate, followed by the relief, parent material, and vegetation, which control local-scale soil variation [38,39]. The dominant physiographic unit in this landscape are mountains (76%), followed by piedmont plains (6%), flood plains (6%), flood basins (5%), hills (2%), alluvial plains (2%), plateaus (0.2%), and alluvial fans (0.2%); in addition, miscellaneous land types occupy 3% of the total area. The main soil orders include Mollisols (39%), Entisols (17%), Inceptisols (7%), Alfisols (5%), and Ultisols (0.002%) and the remaining parts of the landscape consist of rocky outcrops, badlands, and waterbodies (32%).
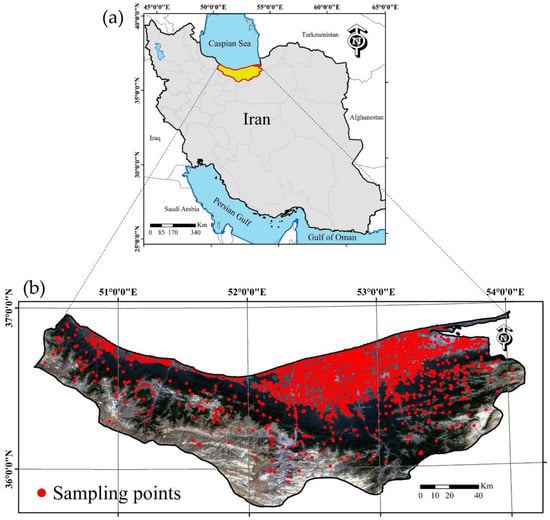
Figure 1.
Localization of the Mazandaran province in Iran (a); and spatial distribution of soil sampling locations within the Mazandaran Province (b).
2.2. Soil Data
The soil texture data for this study were acquired by the Mazandaran Agricultural Research, Education and Extension Organization (AREEO) in Sari, Iran and consists of 1595 surficial soil samples collected between 2014 and 2018. All samples were collected from the 0–20 cm depth increment and their corresponding geographical coordinates were recorded using a global positioning system (GPS) device. Apart from those samples that were randomly sampled in uncultivated areas, more than half of the samples were acquired from croplands and orchards using a gridded sample design with a 2 km × 2 km grid spacing (Figure 1). All samples were air-dried and passed through a 2 mm sieve for measuring the PSFs using the Bouyoucos hydrometer method [40]. A computer program was used for converting the PSFs to soil textural classes based on the classification system of the United States Department of Agriculture (USDA) [41].
2.3. Environmental Covariates
To represent the possible pedogenetic and hydro-ecological process involved in controlling the spatial distribution of PSFs, a large set of environmental covariates was generated for Mazandaran Province. The four main data sources included terrain-derived attributes, RS reflectance data, climatic characteristics, and digitized polygon maps. As tabulated in Table A1, 64 environmental covariates that represented the SCORPAN factors [42] were used to predict soil PSFs.
Geologic, soil taxonomic, and physiographic maps in the polygon format were included as categorical covariates and the remaining 61 variables were based on continuous data. Using the SAGA GIS software, 18 topographic covariates were derived from a digital elevation model (DEM) at a 30 m spatial resolution. The terrain attributes included slope, aspect, catchment area, catchment slope, channel networks base level, elevation, flow accumulation, multi-resolution valley bottom flatness index (MrVBF) [43], topographic openness (NegOpen and PoOpen), plane curvature, relative slope position, slope-length (LS) factor, topographic wetness index (TWI), total insolation, upslope curvature, valley depth, vertical distance to channel networks, and wind effect.
The 41 satellite-derived covariates were acquired based on the median values of optical satellite data from Landsat 8 (Operational Land Imager) and Sentinel-2 imagery taken during 2014–2018. The individual spectral bands were used as covariates; furthermore, additional band ratios were calculated: normalized difference vegetation index (NDVI), enhanced vegetation index (EVI) [44], transformed vegetation index (TVI) [45], soil adjusted vegetation index (SAVI) [16], brightness index (BI) [46], normalized difference water index (NDWI) [47], land surface water index (LSWI) [48], clay index [49], salinity index [50], carbonate index [51], and gypsum index [52]. Furthermore, five datasets were acquired from MODIS images at a 1 km spatial resolution: near-infrared (858 nm) reflectance band, daytime land surface temperature, NDVI, SAVI, and soil brightness index. Lastly, data representing the mean annual rainfall (mm) and mean annual temperature (°C) data for the 1970–2000 period were acquired at a 1000 m spatial resolution from the WorldClim data repository to represent the climatic factors that control the soil forming process for the region [53].
All environmental covariates were aggregated (average resampling) or disaggregated (bilinear resampling) to a common grid of a 30 m × 30 m spatial resolution and rescaled using Z-score standardization. With respect to the categorical covariates, they were all transformed into dummy variables.
Selection of Environmental Covariates
A feature selection technique was applied to identify the most suitable covariates for implementation in the model [54]. Here, a correlation-based feature selection method, which was fully automated. Here, an optimal covariate should be highly correlated with the soil response variables and not be correlated to any other relevant covariates [55]. The correlation-based feature selection method consists of two steps: (1) the selection of relevant covariates; and (2) the identification and removal of irrelevant covariates from the original database [55]. The correlation-based feature selection method removed more than half of the environmental covariates and selected only 23 covariates. It should be noted that the calibration and testing of the ML models was carried out based on the 23 selected environmental covariates.
2.4. Predictive Models
The proposed ANN-based algorithms, which are among the most efficient neural computing methods, include genetic algorithm (GA-ANN), particle swarm optimization (PSO-ANN), bat (Bat-ANN), and monarch butterfly optimization (MBO-ANN). The training for ANN was performed with various evolutionary algorithms to unveil the most efficient method. A multi-layered feed-forward perceptron neural network with three main layers (one input, one hidden, and one output) was used to identify the non-linear relationships between PSFs and environmental covariates. The neurons between the three layers are interconnected weighted connection (i.e., synapses) [56]. By running the ANN model, the weighted predictors from an input layer are added to a bias coefficient, and the results pass through the transfer function in the hidden and output layers to produce an output (i.e., PSFs). Figure 2 depicts a flowchart of the training process via the proposed hybridization methods. In this study, 2–20 neurons in the hidden layers were tested and the best architecture was selected considering the lowest mean squared error (MSE). In brief, the proposed ANNs consist of 23 neurons (i.e., covariates) in the input layer and three neurons (i.e., clay, silt, and sand contents) in the output layer. Sigmoid functions were used as the transfer functions in the hidden layers and softmax transfer functions were used in the output layers.
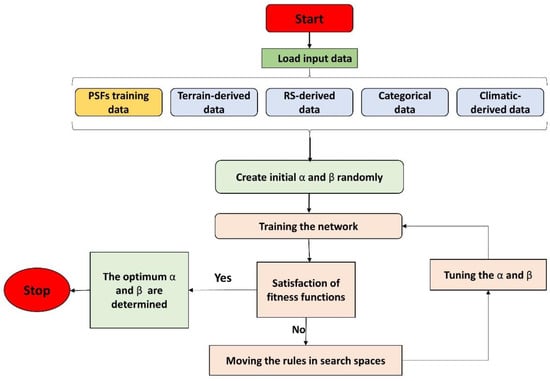
Figure 2.
Flowchart diagram of the ANN training using metaheuristic optimization algorithms. α and β represent the weights and biases, respectively.
The soil texture data are multivariate data with clay, silt, and sand fractions that must sum up to 100%. The strict requirement of summing to 100% is not met in most unsampled locations without pre-treatment of the PSFs data. Therefore, in this study, the predicted sand, silt, and clay fractions in the output layer of ANNs are passed through a softmax transfer function to address the compositional constrains [12]. The softmax transfer function takes, as input, a vector (i.e., the predicted clay, silt, and sand fractions), and normalizes it into values ranging from 0 to 1. whereby the vector adds up to 1. Finally, the returned values from the softmax transfer function are multiplied by 100.
The local optima, convergence rate, and training time of the neural networks are greatly affected by their weights and biases, thus resulting in the need for optimizing the ANN parameters during the iteration process [57]. The hybridization of ANN with bio-inspired, optimization algorithms has the potential to be a powerful tool, which may overcome these challenges [28,57]. Hence, four bio-inspired, metaheuristic algorithms, namely, GA, BAT, PSO, and MBO, were trained to predict the PSFs as the target variables. Table 1 shows the hyper-parameter settings of the four metaheuristic algorithms, which were hybridized with ANN. The performances of these bio-inspired training algorithms were compared with the commonly used backpropagation algorithm (BP-ANN) for predicting PSFs. A brief description of each training algorithms is provided in the following subsections.

Table 1.
The hyper-parameters settings of algorithms used in this study.
2.4.1. Backpropagation (BP) Algorithm
The BP neural network, which uses the Levenberg–Marquardt algorithm, is the simplest in terms of implementation and is also the most popular approach used for training neural networks [58]. BP is a type of supervised learning algorithm, which adjusts the weights and biases according to the target value(s). BP starts by randomly selecting initial weights and then comparing the outputs with the given target value(s) to calculate the difference in MSE [59]. The errors are then backpropagated through the earlier layers via a negative gradient descent direction for adjusting the weights and bias until at least one stopping criteria is reached. The maximum number of epochs and the MSE of the network output for each target PSFs were the two stopping criteria and were set as 500 and 0 in this study, respectively. It should be noted that the BP algorithm is a type of hill-climbing algorithm, whereby the algorithm may get “trapped” in local minima; furthermore, BP algorithms also tend to overfit the data [56].
2.4.2. Genetic Algorithm (GA)
A GA is frequently used for hybridization with an ANN. This algorithm mimics the process of natural selection and the survival-of-the-fittest for optimizing the weights and bias of neural network connections [60]. GA commences with a random population with individual chromosomes as solutions, whereby the genes of the chromosomes are the random values. Each solution/generation’s conditions are calculated with fitness values to select the parents to produce the children in the next solution/generation. Upon sequential generations, the chromosomes of the population tend to achieve the best solutions. The crossover and mutation are two operators mostly used by the GA algorithm to generate new offspring. In this study, the hyperparameter settings are described in Table 1.
2.4.3. Particle Swarm Optimization (PSO)
PSO is a metaheuristic algorithm, which was first proposed in 1995 [61]. It is modeled based on the swarming nature of insects and birds. By tuning the model parameters, PSO algorithms are used for hybridization with different machine learning techniques—particularly with ANN models. To optimize an ANN with PSO, a recently outlined procedure was used [62]. PSO starts with random populations for a given fitness function. The individual solutions are “particles” in a population with random velocities and positions. The fitness value of particles is then calculated to get the required value for the best fitness function. Particles adjust their movement to the best local position with the best fitness, accompanied by other particles’ best position in global optimization. Here, the local velocity adjustment of particles on their best fitness and the other particles’ experience is considered in the PSO algorithm. The first step of the algorithm terminates following the mass movement. This process is repeated until the stopping criteria are met. By changing the particle’s position and velocity from their solution space, PSO optimizes the weights and biases of ANN [57]. The cost function (fitness function) of the ith particle can be defined in the terms of RMSE in Equation (1):
where, wi is the weights; bi is the biases; E is the cost value; Tpls is the target value; Ppls is the predicted output; O is the neuron numbers; and S is the number of training samples.
2.4.4. Bat Algorithms (BAT)
The BAT algorithm is inspired by the echolocation ability of bats in finding their prey with global optimization [63]. The BAT algorithm begins the local position’s optimization with random fly followed by the sequential iterations to achieve the best local solution along with the optimum global location. Bats use echolocation for sensing the distances in search space for a global optimum. In this algorithm, bats at a position, Xi, fly randomly with velocity, Vi, to emit pulses at a frequency, fi, loudness, Ai, and emission rate, ri. In this study, the minimum (fmin) and maximum (fmax) frequencies were set as 0 and 1, respectively. Bats automatically adjust fi, and ri is changed based on the adjacency of their prey. Ai changes between 1, as a large positive value (A0), and 0 as a minimum value (Amin). The rules apply an initial population of bats to update Xi and Vi with initial random values of fi for n virtual bats to select the best solution in local search with following equations:
where Ɵ is a vector with randomly generated values (0 to 1) and Xbest is the optimal local position of current bats. Subsequently, the new solution is generated using a random walk algorithm that selects the best local solution for a globally-optimal position of the bat in each iteration and balancing the Ai (loudness) and ri (pulse emission rate) [63,64]. The algorithm initiates by randomly selecting an initial population of bats, and the weights and biases in an ANN. Afterward, the BAT algorithms assign the best solution for the output of the trained ANN. Subsequently, by searching in local space, a new solution is generated. Each local space with a satisfactory new solution will be substituted with an optimal global solution. These procedures are repeated until the maximum number of iterations (e.g., 100) is met and whereby the optimal values of weights and biases are found.
2.4.5. Monarch Butterfly Optimization (MBO) Algorithm
The MBO algorithm is a global-solving, metaheuristic algorithm with a high convergence rate for high-dimensional data [65] and was initially proposed in 2019 [66]. This algorithm mimics the migratory behavior of individual monarch butterflies between northern USA (Land1) to southern Mexico (Land2). MBO initiates with random generation of the population to form a local solution. Afterward, all populations are ranked by fitness functions. The ranked populations are separated into subpopulations, identified as Land1 and Land2, to consider the pre-defined fixed ratio of population p. The original population is kept unchanged by these two operators independently and where the objective is to simultaneously minimize the fitness functions. The migration operator generates the new candidate solutions/individuals and is adjusted by the migration ratio using the following equation:
where xi is the position of a butterfly i; t is the generation number; k is the element of xi at a generation of t + 1; r1 is the randomly generated position in Land1; r2 is the randomly generated position in Land2; p is the ratio of butterfly in Lands; and ri is equal to the product of the period (peri) parameter, which was set to 1.2, and a random number (rand) between 0 and 1.
The butterfly adjusting operator tunes the positioning behavior of other butterflies, j, in global best positions using the following equation:
where xbest is the best monarch butterfly position in Land1 and Land2; t is the current generation number; r3 is the randomly generated from Land2; BAR is the butterfly adjusting ratio; dxk is kth element of the walk step; and α= (Smax/t2) is the weighing factor with maximum walk step (Smax). The models’ weights and biases are encoded as the k elements of a D-dimensional vectors. In the process of optimization using MBO, the initial random weights and biases are updated at each generation with the best position of the monarch butterflies that achieve the optimal fitness functions. Here, MBO calculates the best weights and biases by allocating the best monarch butterflies’ positions in a forward path and obtains the mean square error of fitness functions for ANN training. This process periodically continues until the lowest RMSE of fitness is achieved or the maximum generation (e.g., 100) is met.
2.5. Accuracy Assessment and Uncertainty Analysis
For evaluating the performances of the hybridized ANN models in predicting the PSFs for Mazandaran Province, the soil data were randomly partitioned into two sets. Here, 70% of the data were randomly selected to calibrate the ANN models, and the remaining 30% of the data were used to test the models and determine the accuracy metrics. When training the ANN models, the calibration dataset was further subdivided into training and validating datasets, whereby 80% of the data were used to train the ANN models, and the remaining 20% were used to validate the model. The nested cross-validation process was repeated 10 times to account for the effects of the internal (bootstrapping) and external randomness within the modeling procedure, thereby ensuring stability in the accuracy metrics [67].
The metrics used to evaluate model accuracy included mean absolute error (MAE), RMSE, coefficient of determination (R2), and Lin’s concordance correlation coefficient (CCC), which are formulated as follows:
where n is the number of samples in the cross-validation dataset; Mi and Pi are the measured and predicted PSFs for each sampling points, respectively; M′ and P′ are the means for the measured and predicted PSFs values, respectively; and σM and σp are the variances of measured and predicted PSFs values. The model with the highest R2 and CCC and the lowest MAE and RMSE values was determined to be the best hybridization of ANN for predicting PSFs and soil textural classes.
For analyzing the uncertainty of hybridized ANN, the PSF maps generated by each iteration of the models were used to calculate the mean and standard deviation (SD) of the PSF for each pixel. Then, the confidence interval (CI) was calculated as the prediction mean ± 1.64SD (standard deviation) for the given 90% CI. It should be noted that only the mean of the PSF contents for each pixel is presented.
3. Results
3.1. Summary Statistics
Table 2 shows the descriptive statistics of the measured topsoil sand, silt, and clay contents for the study area. The silt contents were the highest in this area, with an average of 45.2%, whereas the clay and sand contents were 31.4% and 23.4%, respectively. Considering the high silt contents, the soils were typically classified as clay loam, according to the USDA system of soil texture classification. The coefficient of variation (CV) was the highest for sand values (63%), which indicates high heterogeneity with a wide range of sand spread across Mazandaran Province; in contrast, clay and silt had a CV of 39% and 25%, respectively. The sand and clay values had high variability over the study area with CV > 35% [68], while the silt values had moderate variability (15% < CV < 35%). Regardless of the PSFs, the mean and medium values were similar, which suggests that the PSFs closely resembled a normal distribution and was further confirmed by the low skewness and kurtosis.

Table 2.
Summary statistics of PSFs data for the Mazandaran Province (n = 1595).
The distribution of the soil textural classes for all sample points, according to the USDA soil texture triangle, is plotted in Figure 3. Here, the plot indicates that there was a wide range of soil texture classes over the study area (Figure 3), which included eight out of the 12 possible texture classes: sand, loamy sand, sandy loam, loam, silt loam, silt, sandy clay loam, clay loam, silty clay loam, sandy clay, silty clay, and clay.
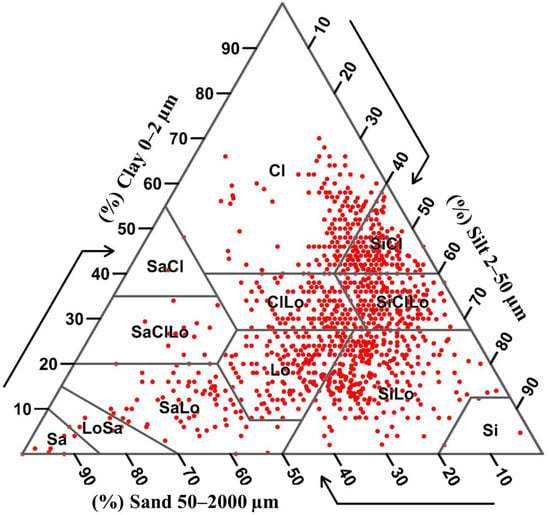
Figure 3.
Distribution of soil texture classes for all samples based on the USDA soil texture triangle. (Cl: clay; SiCl: silty clay; SiClLo: silty clay loam; SaCl: sandy clay; SaClLo: sandy clay loam; ClLo: clay loam; Si: silt; SiLo: silt loam; Lo: loam; Sa: sand; LoSa: loamy sand; SaLo: sandy loam).
The high variability in PSFs could be attributed to the variability in parent materials, topography, elevations, soil weathering rates, land uses and management practices, and other environmental elements [11]. The selective removal of particles that were <63 μm in diameter on steep slopes in the study area via soil erosion processes may have been a controlling factor on the accumulation of finer soil particles in the low-lying areas [69].
3.2. Accuracy Assessment and Uncertainty Analysis
The performances of the five ANN models (i.e., BP-ANN, GA-ANN, PSO-ANN, Bat-ANN, and MBO-ANN) for predicting three components of PSFs were compared in terms of MAE, RMSE, R2, and CCC. Once the ANN models were trained using the aforementioned algorithms, the optimal weights and biases of each input covariates were assigned to predict the PSFs [57,70]. Table 3 indicates the mean values of the accuracy metrics, calculated using the testing data from the repeated, nested 10-fold cross-validation procedure. As shown in Table 3, the accuracy of the ANN models varied amongst the different optimization learning algorithms. In terms of R2 and CCC statistics, MBO-ANN was the most effective in predicting clay contents with mean accuracy values of MAE = 5.6%, RMSE = 6.4%, R2 = 0.68 and CCC = 0.69. In comparison, BP-ANN, the reference approach, had substantially lower R2 (0.50) and CCC (0.51) and slightly higher MAE (6.5%) and RMSE (8%). Furthermore, BP-ANN was also considerably outperformed by the GA-ANN, PSO-ANN, and Bat-ANN models for clay predictions with CCC values of 0.68, 0.62, and 0.66, respectively. Across all ANN hybridizations, there were considerable gains in CCC values for clay predictions, whereby an increase of 35%, 33%, 29%, and 22% was observed for MBO-ANN, GA-ANN, Bat-ANN, and PSO-ANN, respectively, when compared to the reference BP-ANN model. These results indicate that the bio-spired algorithms hybridized with neural network greatly enhanced the accuracy of clay prediction.

Table 3.
Accuracy metrics of the five ANN models for predicting PSFs based on repeated 10-fold cross-validation.
Similar trends of R2, CCC, MAE, and RMSE values were observed for the silt and sand predictions. With these PSFs, the results also showed that the BP-ANN model had the lowest R2 and CCC and highest errors (MAE and RMSE). Again, the MBO-ANN model resulted in silt and sand predictions that had the highest accuracy across all five hybridized models. Furthermore, the improvement of prediction using the hybridization of ANN with bio-inspired algorithms was most pronounced for the silt prediction in comparison to the clay and sand predictions. With respect to the silt predictions, the MBO-ANN algorithm was an improvement on the BP-ANN algorithm by increasing R2 from 0.32 to 0.62 (93.8% increase) and CCC from 0.25 to 0.65 (160% increase) and decreasing MAE from 5.76% to 4.81% (16.5% decrease) and RMSE from 7.34% to 6.60% (10.1% decrease). Again, similar to the clay predictions, MBO-ANN was the most effective bio-inspired hybridization of ANN followed by GA-ANN, PSO-ANN, and Bat-ANN, respectively.
With respect to the sand predictions, the MBO-ANN model was, again, the most effective approach amongst the hybridized models, yielding the highest R2 (0.70) and CCC (0.71) values and lowest RMSE (6.59%) and MAE (5.74%) values. In comparison with the traditional BP-ANN model, the bio-inspired hybridized algorithms improved the sand predictions across all accuracy metrics when compared to BP-ANN. Specifically, with respect to CCC, the improvements for the MBO-ANN, GA-ANN, Bat-ANN, and PSO-ANN were 45%, 43%, 29%, and 29%, respectively.
When evaluating the uncertainty estimates, ideally, 90% of test data with corresponding observed values should fall within the confidence interval (CI) range for each of the PSFs (Table 4). Here, the evaluation of the uncertainty estimates showed a similar trend with respect to how the various ANN models performed, whereby the MBO-ANN results were the most optimal in generating uncertainty estimates because 85%, 83%, and 88% of the clay, silt, and sand observations, respectively, fell within the defined CI. Conversely, the bootstrapping of the BP-ANN model was the least effective in generating uncertainty estimates because only 78%, 72%, and 81% of the observed values fell within the 90% confidence interval range.

Table 4.
The percentages (%) of three PSFs that fall within the 90% prediction intervals predicted by hybridized-ANN models.
3.3. Covariate Importance
The weight values assigned to each input parameter by the ANN model were used to identify the most important covariates for predicting the PSFs. In this study, the relative importance (RI) of the covariates, were categorized as follows: weakly relevant (RI < 2%), slightly relevant (2% < RI < 4%), moderately relevant (4% < RI < 6%), and strongly relevant (RI > 6%). The RI values of all covariates are shown in Figure 4, where it shows that there was a wide range of RI amongst the covariates when predicting PSFs.
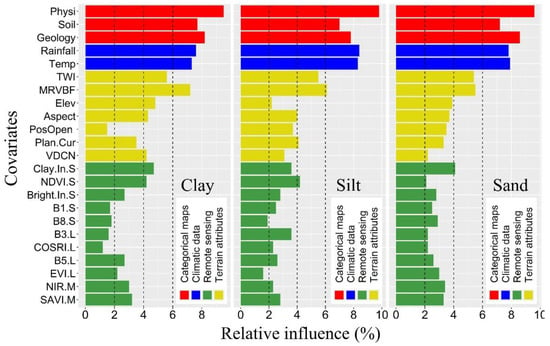
Figure 4.
The relative influence of environmental covariates for predicting clay, silt, and sand contents using the MBO-ANN algorithm. (Refer to Table A1 for covariate codes).
The number of covariates with weakly, slightly, moderately, and strongly relevant contribution for PSFs prediction are shown in Table 5. The most critical factor controlling the PSFs was represented by the categorical data, which represented the study area’s soil, geologic, and physiographic variability. These covariates were then followed by climatic, terrain-derived, and RS-derived data, respectively. The categorical maps, along with the two climatic datasets (rainfall and temperature), were the most strongly relevant covariates across all PSFs predictions for the study area.

Table 5.
The number of covariates with relevance contribution in predicting PSFs.
By calculating the mean RI based on the covariate source, it was observed that data derived from the categorical maps were consistently ranked the highest for the clay predictions with a mean RI = 8.5%. The importance of the categorical data was then followed by climatic data (7.5%), terrain-derived data (4.4%), MODIS-derived data (3.1%), Sentinel-2-derived data (3.0%), and Landsat-derived data (1.9%), respectively. When the covariates were evaluated on an induvial basis, the physiography map had the highest RI value (9.5%), indicating the most important driving factor for clay spatial distribution, followed by the geology map (8.2%), soil map (7.7%), rainfall (7.6%), temperature (7.3%), MRVBF (7.2%), topographic wetness index (TWI) (5.6%), and the Sentinel-2-derived clay index (4.7%), respectively (Figure 4).
The importance of the covariates for predicting silt content were also similar, whereby the climatic data and categorical maps were ranked the highest and yielded a mean RI of 8.4% and 8.2%, respectively. The importance of these data sources was then followed by terrain-derived data, which had a mean RI of 4.1% and the remote sensing data, which had a mean RI of 3.0%, 2.6%, and 2.5% for the Sentinel-2-, MODIS, and Landsat-derived data, respectively. Similar to the clay predictions, the physiographic map was determined to be the most important covariate for silt predictions with RI = 9.8%, and followed by rainfall (8.4%), temperature (8.3%), geologic map (7.8%), soil map (7.0%), and MRVBF (6.1%), respectively (Figure 4).
The ranking of the mean RI values by data source for the sand predictions were the same as for the clay predictions where the categorical maps had the highest mean RI of 8.5% and was subsequently followed by the climatic data (7.9%), terrain-derived data (3.9%), and remote sensing data, where the MODIS-, Sentinel-2-, and Landsat-derived data had a mean RI of 3.4%, 2.9%, and 2.5%, respectively. Again, the physiographic map, geologic map, temperature, rainfall, soil type map, MRVBF, and TWI were the most important covariates for sand predictions with the RI values of 9.6%, 8.6%, 7.9%, 7.8%, 7.2%, 5.5%, and 5.4%, respectively (Figure 4).
3.4. Spatial Prediction of Soil PSFs
The continuous map of clay, silt, and sand fractions and USDA soil texture classes for the whole region was produced using the MBO-ANN model due to its superior performance in comparison to the other approaches (Figure 5). Furthermore, the MBO-ANN model, when coupled with the softmax transfer function in its output layer guarantees the summation of PSFs to 100%, which is necessary for precise predictions of PSFs (see the Supplementary Materials). Based on a visual assessment of the predictions, the silt contents were relatively higher compared with the clay and sand contents along the central strip of the study area. The predicted PSF maps, produced using the MBO-ANN model, were also reclassified in accordance to the USDA soil texture classification system (Figure 5).
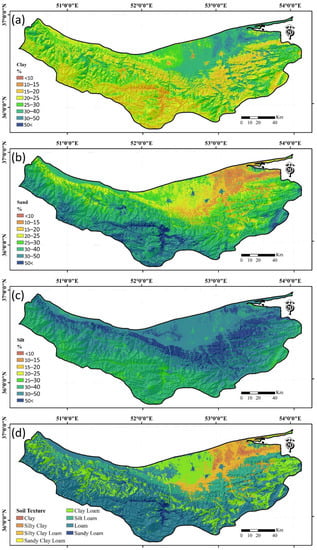
Figure 5.
Continues maps produced using the MBO-ANN model for the Mazandaran Province of: surficial clay content (a); surficial sand content (b); and surficial silt content (c); and textual classes (d).
Eight main USDA textural classes were identified: clay, silty clay, and silty clay loam classes were mapped in the northeastern region; the silty clay loam class dominated the central region; the silt loam, loam, and sandy loam texture classes dominated the southern regions of the province; and sandy clay loam soil texture class had a limited distribution in the study areas (Figure 5).
With respect to the predicted clay contents, there was a relatively higher abundance of clay in the northeastern region of the province, which corresponds with a flood basin on the low-lying area and where the fine-textured materials are dominant. Here, the clay contents were >40% and were mainly distributed at low elevations (<10 m) and where fine-textured parent materials are present (Figure 5).
In comparison, the sand content was low in the northeastern; however, was it substantially higher in the southern and southeastern regions, where the soils are mostly degraded and the coarse-textured parent materials are exposed. In addition, the thin coastline (about 10–20 m from shorelines), adjacent to the Mazandaran Province, includes a sand dune that was omitted from this study given that these areas were not mapped as soils by surveyors. With respect to the silt predictions, the map showed highest amounts of silt along the central region of the study area along an east to west direction. This area of high silt contents corresponds with the presence of a loess deposit and loess-derived soils, which are highest in the eastern region of the province [71].
4. Discussion
4.1. Environmental Covariates
The categorical maps, along with the two climatic datasets (rainfall and temperature), were the most strongly relevant covariates across all PSFs predictions for the study area. Soil taxonomic type, represented as great soil groups, was strongly relevant in explaining the total variation of PSFs soil in Mazandaran Province. The soil survey data were traditionally derived from the physiographic units in Iran and provide information directly related to the spatial patterns of PSFs; furthermore, the geological map also provided information on the soil parent material and its associated mineralogy—a key determinant of soil texture. By using these datasets as covariates, there is the potential to renew and improve upon existing soil textural and PSF maps for the Mazandaran Province using DSM approaches. The relationship between these datasets and PSFs was apparent in this study; for example, the spatial distribution of alluvial plains and flood basins were two physiographic units of the northeastern region of the study areas, which also coincided with the high clay contents that were observed. The information such as soil type and land cover could explain the considerable variation of PSFs [22,24,72,73]. Therefore, these results would seem to indicate that, for study areas where detailed and accurate soil maps exist, it would be beneficial to include them as a covariate in predicting PSFs [18]. Of the terrain-derived data, MRVBF was the most important—especially for the prediction of clay and silt. Here, MRVBF was effective in characterizing the low-lying terrains and the depositional features of the landscape, where fine particles tend to accumulate [43]. In cultivated alluvial/flood plains of low-lying areas, the use of land surface temperature data from MODIS was a promising covariate, particularly where the soils were clearly bare over a year [74].
RS-derived covariates were not strongly relevant for predicting PSFs in this study. The main reason was attributed to the effect of surficial soil moisture and roughness, the presence of vegetation canopy, and, in some cases, due to the low spatial resolution of the RS data [75,76]. All covariates derived from Landsat and MODIS imagery were classified as being weakly to slightly relevant covariates, whereas two covariates derived from the Sentinel-2 were moderately important. Specifically, the clay index was moderately relevant for predicting all PSFs, while NDVI was moderately relevant for predicting the clay and silt fractions (Table 4). With respect to the clay index of Sentinel-2, there was a negative relationship with soil clay content [77]. The soil texture mapping using Sentinel-2 data performance had a good discrimination for extremely different soil texture classes (e.g., sandy loam versus clay), whereas neighboring soil texture classes (e.g., sandy clay loam and clay class) had high uncertainty [75].
The weak relationship between the Landsat data and PSFs was most likely associated with lower spatial resolution of the images (i.e., 90 m) and the time of imagery acquisition [78]. A poor relationship between Landsat data and the sand and silt fractions was also reported for PSFs prediction in large-scale studies [79,80]. However, high correlations between clay contents and Landsat 7 images, particularly with Band 7, have been reported in other studies [81]. In comparison, the higher spectral and spatial resolution (10 m) of the Sentinel-2 data may have been the main reason the covariates derived from this data source had higher RI. Similar to this study, the covariates derived from Sentinel-2 data resulted in satisfactory/good predictors of clay contents for soils in the Czech Republic [82].
Although several variables were determined to not be important, accounting for them in the prediction process still has the potential to enhance the spatial predictions of PSFs [11,83,84]. PSFs have a complex, nonlinear hierarchal relationship between many covariates that were determined to be effective, and machine learning models are designed to discover these relationships. It could be concluded that the coarse-resolution categorical maps could potentially capture the average soil PSFs at large spatial extents and scales other covariates related to local terrain and vegetation would be more effective in capturing soil erosional and depositional processes.
4.2. Performance of Hybridized Models and Output Maps
The poorest model performance for the PSF predictions resulted from the BP-ANN (i.e., traditional implementation of ANN) and was substantially improved upon by using bio-inspired optimization algorithms. The MBO algorithm was the most effective approach within the studied bio-inspired algorithms while PSO was the lowest-performing hybridization for clay predictions. The prediction accuracy of clay in this large-scale study for the proposed model was better than that of other studies [20,85,86] ranging 9.2–12.2% for RMSE and 0.33–0.54 for R2. By considering the multispectral (VNIR–SWIR) ASTER data as covariates for mapping the surface clay content at large scales, the results yielded the R2 of 0.61% [87] that is close but still lower than our findings. The prediction accuracy was close to another finding [20] with R2 of 0.71 and RMSE of 7.3% but much better than many other studies [85,86,88,89]. The slightly lower model performance for predicting silt contents in the MBO-ANN model with lower R2 and CCC compared with clay and sand contents may be due to the poorer relationship between the auxiliary covariates and silt content that is in agreement with other findings [24,85,86], which declared the low performance was due to high variability.
Regarding to the accuracy and uncertainty analysis, it was concluded that the hybridized ANN using bio-inspired algorithms resulted in a vast improvement in comparison to the standard reference approach using BP-ANN by potentially overcoming challenges such as the local minima and low convergence issues [90,91]. Consistently, the MBO-ANN model outperformed all other hybridizations when mapping PSFs, which was likely attributed to its ability to optimize the initial input parameters (e.g., thresholds and weights) for ANN by the MBO algorithm, thereby resulting in the suitable convergence of the neural network towards a global optimum solution and effectively capturing the nonlinear relationships between variables [92]. Although the MBO-ANN approach was able to handle the large set of input variables in predicting the spatial distribution of PSFs, its processing time was longer than that of BP-ANN; furthermore, the use of the other bio-inspired hybridizations with ANN were also longer, but acceptable. From this study, the increased computational demand and processing time was warranted given the level of improvement when compared to the BP-ANN approach, as evidenced by all accuracy metrics.
Theses soil textural class maps reflected the contribution of environmental covariates that were used to generate the PSFs prediction maps. These maps can also potentially improve land surface modeling for future studies. From a soil management perspective, information on the spatial distribution of clay in the northern region is important for decision makers in order to improve agricultural practices and the management of paddy fields and orchards. In particular, the application of potassium fertilizer is greatly dependent on the clay contents of the study area due to the ability of clay minerals to bind/fix the potassium in interlayers spaces and cause its unavailability for plant uptake.
5. Conclusions
Provincial-scale information on soil texture is crucial for the management of soil resources and agricultural production planning by decision makers. By using a large set of environmental covariates derived from terrain, remotely sensed, climatic, and categorical data as the main sources of data, series of hybridized ANN models were built for predicting PSFs and tested using a 10-fold cross-validation. The softmax transfer function was used in the output layer of the ANN models to normalize the predicted clay, silt, and sand contents, leading to the summation of PSFs to 100% in unsampled locations. Of the 64 environmental covariates used, categorical data, which consist of physiographic maps, maps of soil types, and geologic maps, were the most effective variables for predicting the spatial distribution of PSFs. The importance of these categorical inputs was subsequently followed by the climatic data, terrain data, and RS-derived covariates, respectively. Where available, existing map products generated using conventional approaches (i.e., existing categorical maps) could have the potential of being refined using DSM approaches for future mapping of PSFs at the provincial scale.
When compared to the reference ANN approach, BP-ANN, the bio-inspired optimization algorithms substantially improved the predictions of PSFs, whereby the results indicate that MBO-ANN resulted in the best performance across all accuracy metrics and PSFs. Furthermore, the MBO-ANN approach also resulted in the lowest uncertainty in comparison to BP-ANN. It could be concluded that the application of bio-inspired computational algorithms is a promising alternative to the conventional BP-ANN—especially given that the computational demands were not substantially greater. The high-resolution PSFs maps generated in this study can be used for integrated management of soils along with sustainable development strategies at the provincial scale. Furthermore. The maps can be used as inputs to support future environmental and hydrological modeling activities.
Supplementary Materials
The following are available online at https://www.mdpi.com/2072-4292/13/5/1025/s1.
Author Contributions
Conceptualization, M.E. and R.T.-M.; methodology, R.T.-M. and T.S.; software, R.T.-M.; validation, M.E., A.M., and T.S.; formal analysis, R.T.-M. and T.S.; investigation, M.E. and R.T.-M.; resources, A.C.; data curation, A.C.; writing—original draft preparation, M.E. and R.T.-M.; writing—review and editing, A.M., B.H., and T.S.; visualization, R.T.-M.; and supervision, M.E. and R.T.-M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy restrictions.
Acknowledgments
This study was financially supported by the Sari Agricultural Sciences and Natural Resources University (SANRU) (under grant No. T161-1369). The work of Ruhollah Taghizadeh-Mehrjardi was supported by the Alexander von Humboldt Foundation under the grant number: Ref 3.4-1164573-IRN-GFHERMES-P. Amir Mosavi would like to acknowledge his support from Alexander von Humboldt Foundation. Ruhollah Taghizadeh-Mehrjardi and Thomas Scholten thank the German Research Foundation (DFG) for supporting this research through the Collaborative Research Center (SFB 1070) “Resource Cultures” (subprojects Z, S and B02) and the DFG Cluster of Excellence “Machine Learning—New Perspectives for Science”, EXC 2064/1, project number 390727645. We acknowledge support by Open Access Publishing Fund of University of Tübingen.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Covariates initially considered for predicting the distribution of PSFs.
Table A1.
Covariates initially considered for predicting the distribution of PSFs.
| No. | Covariates | Code | Definition |
|---|---|---|---|
| 1 | Geology map | Geology | Polygon map prepared by SWRI |
| 2 | Soil map | Soil | Polygon map prepared by SWRI |
| 3 | Physiography map | Physi | Polygon map prepared by SWRI |
| 4 | Annual rainfall (mm) | Rainfall | It is derived from the monthly rainfall values |
| 5 | Mean annual temperature (°C) | Temp | It is derived from the monthly temperature values |
| 6 | Aspect (°C) | Aspect | The compass direction of the maximum rate of change |
| 7 | Catchment area | Cat.Area | Area from which rainfall flows into a river |
| 8 | Catchment slope (degrees) | Cat.Slo. | Average gradient above flow path |
| 9 | Channel networks base level | CNBL | The interpolated channel network base level elevations |
| 10 | Elevation (m) | Elev | Height above sea level |
| 11 | Flow accumulation (number of cells) | Fl.Ac | Calculates accumulated flow |
| 12 | Multi-resolution Valley Bottom Flatness Index | MRVBF | Measure of flatness and lowness |
| 13 | Openness | NegOpen | How wide a landscape can be viewed from any position |
| 14 | Openness | PosOpen | How wide a landscape can be viewed from any position |
| 15 | Plan curvature (radians / m) | Plan.Cur | The curvature of a contour line |
| 16 | Relative Slope Position | Re.Slope.Posi | The position of one point relative to the ridge and valley of a slope |
| 17 | Slope Length factor | LS factor | Slope Length and Steepness factor |
| 18 | Topographic Wetness index | TWI | ln (specific catchment area/slope angle) |
| 19 | Total Insolation (kWh / m2) | To.In | Calculate the total incoming solar radiation |
| 20 | Upslope Curvature | Ups.Cur | The distance weighted average local curvature |
| 21 | Valley Depth (m) | Va.Dep | The vertical distance to a channel network base level |
| 22 | Vertical distance to channel networks (m) | VDCN | The altitude above the channel network |
| 23 | Wind Effect | WE | The Wind Effect is a dimensionless index |
| 24 | Coastal aerosol of Sentinel-2 | B1.S | Wavelength of 0.442 μm |
| 25 | Blue band of Sentinel-2 | B2.S | Wavelength of 0.492 μm |
| 26 | Green band of Sentinel-2 | B3.S | Wavelength of 0.559 μm |
| 27 | Red band of Sentinel-2 | B4.S | Wavelength of 0.664 μm |
| 28 | Vegetation Red Edge of Sentinel-2 | B5.S | Wavelength of 0.704 μm |
| 29 | Vegetation Red Edge of Sentinel-2 | B6.S | Wavelength of 0.740 μm |
| 30 | Vegetation Red Edge of Sentinel-2 | B7.S | Wavelength of 0.782 μm |
| 31 | Near-infra red of Sentinel-2 | B8.S | Wavelength of 0.832 μm |
| 32 | Shortwave IR-1 band of Sentinel-2 | B9.S | Wavelength of 0.945 μm |
| 33 | Shortwave IR-2 band of Sentinel-2 | B10.S | Wavelength of 1.373 μm |
| 34 | Normalized Difference Vegetation Index | NDVI.S | (NIR−GREEN / NIR + GREEN) |
| 35 | Enhanced Vegetation Index of Sentinel-2 | EVI.S | (2.5 × (Band4 − Band3)/(Band4 + 6× Band 3–7.7 × Band1 + 1) |
| 36 | Transformed vegetation index of Sentinel-2 | TVI.S | (Band5 − Band3/ Band5 + Band3) |
| 37 | Soil Adjusted Vegetation Index of Sentinel-2 | SAVI.S | (Band4 − Band3/ Band4 + Band3 + 0.5) × (1 + 0.5)) |
| 38 | Land Surface Water Index of Sentinel-2 | LSWI.S | (NIR − shortwave infrared)/ (NIR+shortwave infrared) |
| 39 | Brightness Index of Sentinel-2 | Bright.In.S | ((RED)2 + (NIR)2)0.5 |
| 40 | Clay Index of Sentinel-2 | Clay.In.S | (SWIR-1 / SWIR-2) |
| 41 | Normalized Difference Salinity Index of Sentinel-2 | Salin.In.S | (Red-NIR)/(Red + NIR) |
| 42 | Carbonate Index of Sentinel-2 | Carbonat.In.S | (RED / GREEN) |
| 43 | Gypsum index of Sentinel-2 | Gypsum.In.S | (SWIR-1 − NIR) / (SWIR-1 + NIR) |
| 44 | Blue band of Landsat-8 | B1.L | Wavelength of 0.450–0.515 μm of Landsat 8 spectral band |
| 45 | Green band of Landsat-8 | B2.L | Wavelength of 0.525–0.600 μm of Landsat 8 spectral band |
| 46 | Red band of Landsat-8 | B3.L | Wavelength of 0.630–0.680 μm of Landsat 8 spectral band |
| 47 | Near infrared band of Landsat-8 | B4.L | Wavelength of 0.845–0.885 μm of Landsat 8 spectral band |
| 48 | Shortwave Infrared-1 band of Landsat-8 | B5.L | Wavelength of 1.560–1.660 μm of Landsat 8 spectral band |
| 49 | Shortwave Infrared-2 band of Landsat-8 | B6.L | Wavelength of 2.100–2.300 μm of Landsat 8 spectral band |
| 50 | Normalized Difference Vegetation Index of Landsat-8 | NDVI.L | (NIR − RED) / (NIR + RED) |
| 51 | Enhanced Vegetation Index of Landsat-8 | EVI.L | (NIR − RED) / (NIR + C1 × RED−C2 × BLUE + L) |
| 52 | Soil Adjusted Vegetation Index of Landsat-8 | SAVI.L | (1 + L) × (NIR − RED) / (NIR + RED + L) |
| 53 | Normalized difference moisture index of Landsat-8 | NDMI.L | (Band4 − Band5/ Band4 + Band5) |
| 54 | Combined spectral response index of Landsat-8 | COSRI.L | [Blue + Green)/(Red + NIR)] × NDVI.L |
| 55 | Brightness Index of Landsat-8 | Bright.In.L | ((RED)2 + (NIR)2)0.5 |
| 56 | Clay Index of Landsat-8 | Clay.In.L | (SWIR-1/SWIR-2) |
| 57 | Salinity Index of Landsat-8 | Salinity.In.L | Band 3/Band 4 |
| 58 | Carbonate Index of Landsat-8 | Carbon.In.L | (RED / GREEN) |
| 59 | Gypsum index of Landsat-8 | Gypsum.In.L | (SWIR-1 − NIR) / (SWIR-1 + NIR) |
| 60 | MODIS Night Temperature | Temp.M | Land Surface Temperature/Emissivity Daily L3 Global 1km |
| 61 | MODIS Near Infrared | NIR.M | Wavelength of 0.841–0.876 μm of MODIS spectral band |
| 62 | Normalized Difference Vegetation Index of MODIS | NDVI.M | (NIR – GREEN / NIR+ GREEN) |
| 63 | Soil Adjusted Vegetation Index of MODIS | SAVI.M | (1 + L) × ( NIR − RED) / (NIR + RED + L) |
| 64 | Brightness Index of MODIS | Brigh.Index.M | ((MODIS RED)2 + (MODIS NIR)2)0.5 |
Note: Red: Categorical maps; Blue: Climatic data; Yellow: Terrain attributes; Green: Remote sensing.
References
- Kome, G.K.; Enang, R.K.; Tabi, F.O.; Yerima, B.P.K. Influence of Clay Minerals on Some Soil Fertility Attributes: A Review. Open J. Soil Sci. 2019, 9, 155–188. [Google Scholar] [CrossRef]
- Morgan, R.; Quinton, J.; Smith, R.; Govers, G.; Poesen, J.; Auerswald, K.; Chisci, G.; Torri, D.; Styczen, M. The European Soil Erosion Model (EUROSEM): A dynamic approach for predicting sediment transport from fields and small catchments. Earth Surf. Process. Landf. J. Br. Geomorphol. Group 1998, 23, 527–544. [Google Scholar] [CrossRef]
- Poggio, L.; Gimona, A. 3D mapping of soil texture in Scotland. Geoderma Reg. 2017, 9, 5–16. [Google Scholar] [CrossRef]
- Wang, W.J.; Dalal, R.C.; Moody, P.W.; Smith, C.J. Relationships of soil respiration to microbial biomass, substrate availability and clay content. Soil Biol. Biochem. 2003, 35, 273–284. [Google Scholar] [CrossRef]
- Koseva, I.S.; Watmough, S.A.; Aherne, J. Estimating base cation weathering rates in Canadian forest soils using a simple texture-based model. Biogeochemistry 2010, 101, 183–196. [Google Scholar] [CrossRef]
- Ghiri, M.N.; Abtahi, A. Factors affecting potassium fixation in calcareous soils of southern Iran. Arch. Agron. Soil Sci. 2012, 58, 335–352. [Google Scholar] [CrossRef]
- Goli-Kalanpa, E.; Roozitalab, M.; Malakouti, M. Potassium availability as related to clay mineralogy and rates of potassium application. Commun. Soil Sci. Plant Anal. 2008, 39, 2721–2733. [Google Scholar] [CrossRef]
- Vaughan, E.; Matos, M.; Ríos, S.; Santiago, C.; Marín-Spiotta, E. Clay and climate are poor predictors of regional-scale soil carbon storage in the US Caribbean. Geoderma 2019, 354, 113841. [Google Scholar] [CrossRef]
- Xu, H.; Liu, K.; Zhang, W.; Rui, Y.; Zhang, J.; Wu, L.; Colinet, G.; Huang, Q.; Chen, X.; Xu, M. Long-term fertilization and intensive cropping enhance carbon and nitrogen accumulated in soil clay-sized particles of red soil in South China. J. Soils Sediments 2020, 20, 1824–1833. [Google Scholar] [CrossRef]
- Bockheim, J.; Hartemink, A. Distribution and classification of soils with clay-enriched horizons in the USA. Geoderma 2013, 209, 153–160. [Google Scholar] [CrossRef]
- Amirian-Chakan, A.; Minasny, B.; Taghizadeh-Mehrjardi, R.; Akbarifazli, R.; Darvishpasand, Z.; Khordehbin, S. Some practical aspects of predicting texture data in digital soil mapping. Soil Tillage Res. 2019, 194, 104289. [Google Scholar] [CrossRef]
- Wadoux, A.M.C. Using deep learning for multivariate mapping of soil with quantified un-certainty. Geoderma 2019, 351, 59–70. [Google Scholar] [CrossRef]
- Wang, Z.; Shi, W. Mapping soil particle-size fractions: A comparison of compositional kriging and log-ratio kriging. J. Hydrol. 2017, 546, 526–541. [Google Scholar] [CrossRef]
- Walvoort, D.J.; de Gruijter, J.J. Compositional kriging: A spatial interpolation method for compositional data. Math. Geol. 2001, 33, 951–966. [Google Scholar] [CrossRef]
- Pahlavan-Rad, M.R.; Akbarimoghaddam, A. Spatial variability of soil texture fractions and pH in a flood plain (case study from eastern Iran). Catena 2018, 160, 275–281. [Google Scholar] [CrossRef]
- Taghizadeh-Mehrjardi, R.; Toomanian, N.; Khavaninzadeh, A.; Jafari, A.; Triantafilis, J. Predicting and mapping of soil particle-size fractions with adaptive neuro-fuzzy inference and ant colony optimization in central I ran. Eur. J. Soil Sci. 2016, 67, 707–725. [Google Scholar] [CrossRef]
- Zhao, Z.; Chow, T.L.; Rees, H.W.; Yang, Q.; Xing, Z.; Meng, F.-R. Predict soil texture distributions using an artificial neural network model. Comput. Electron. Agric. 2009, 65, 36–48. [Google Scholar] [CrossRef]
- Song, X.-D.; Liu, F.; Zhang, G.-L.; Li, D.-C.; Zhao, Y.-G. Estimation of Soil Texture at a Regional Scale Using Local Soil-Landscape Models. Soil Sci. 2016, 181, 435–445. [Google Scholar] [CrossRef]
- Wu, W.; Li, A.-D.; He, X.-H.; Ma, R.; Liu, H.-B.; Lv, J.-K. A comparison of support vector machines, artificial neural network and classification tree for identifying soil texture classes in southwest China. Comput. Electron. Agric. 2018, 144, 86–93. [Google Scholar] [CrossRef]
- Ding, X.; Zhao, Z.; Yang, Q.; Chen, L.; Tian, Q.; Li, X.; Meng, F.-R. Model prediction of depth-specific soil texture distributions with artificial neural network: A case study in Yunfu, a typical area of Udults Zone, South China. Comput. Electron. Agric. 2020, 169, 105217. [Google Scholar] [CrossRef]
- Khanbabakhani, E.; Torkashvand, A.M.; Mahmoodi, M.A. The possibility of preparing soil texture class map by artificial neural networks, inverse distance weighting, and geostatistical methods in Gavoshan dam basin, Kurdistan Province, Iran. Arab. J. Geosci. 2020, 13, 1–14. [Google Scholar] [CrossRef]
- Wang, Z.; Shi, W.; Zhou, W.; Li, X.; Yue, T. Comparison of additive and isometric log-ratio transformations combined with machine learning and regression kriging models for mapping soil particle size fractions. Geoderma 2020, 365, 114214. [Google Scholar] [CrossRef]
- Greve, M.H.; Kheir, R.B.; Greve, M.B.; Bøcher, P.K. Quantifying the ability of environmental parameters to predict soil texture fractions using regression-tree model with GIS and LIDAR data: The case study of Denmark. Ecol. Indic. 2012, 18, 1–10. [Google Scholar] [CrossRef]
- Akpa, S.I.; Odeh, I.O.; Bishop, T.F.; Hartemink, A.E. Digital mapping of soil particle-size fractions for Nigeria. Soil Sci. Soc. Am. J. 2014, 78, 1953–1966. [Google Scholar] [CrossRef]
- Mehrabi-Gohari, E.; Matinfar, H.R.; Jafari, A.; Taghizadeh-Mehrjardi, R.; Triantafilis, J. The Spatial Prediction of Soil Texture Fractions in Arid Regions of Iran. Soil Syst. 2019, 3, 65. [Google Scholar] [CrossRef]
- Heung, B.; Ho, H.C.; Zhang, J.; Knudby, A.; Bulmer, C.E.; Schmidt, M.G. An overview and comparison of machine-learning techniques for classification purposes in digital soil mapping. Geoderma 2016, 265, 62–77. [Google Scholar] [CrossRef]
- Vaheddoost, B.; Guan, Y.; Mohammadi, B. Application of hybrid ANN-whale optimization model in evaluation of the field capacity and the permanent wilting point of the soils. Environ. Sci. Pollut. Res. 2020, 27, 13131–13141. [Google Scholar] [CrossRef] [PubMed]
- Nabipour, N.; Dehghani, M.; Mosavi, A.; Shamshirband, S. Short-Term Hydrological Drought Forecasting Based on Different Nature-Inspired Optimization Algorithms Hybridized With Artificial Neural Networks. IEEE Access 2020, 8, 15210–15222. [Google Scholar] [CrossRef]
- Taghavifar, H.; Khalilarya, S.; Jafarmadar, S. Diesel engine spray characteristics prediction with hybridized artificial neural network optimized by genetic algorithm. Energy 2014, 71, 656–664. [Google Scholar] [CrossRef]
- Termeh, S.V.R.; Kornejady, A.; Pourghasemi, H.R.; Keesstra, S. Flood susceptibility mapping using novel ensembles of adaptive neuro fuzzy inference system and metaheuristic algorithms. Sci. Total Environ. 2018, 615, 438–451. [Google Scholar] [CrossRef]
- Liu, Y.; Xie, S.; Zheng, L.; Li, T.; Sun, Y.; Ma, L.; Lin, Z.; Grathwohl, P.; Lohmann, R. Air-soil diffusive exchange of PAHs in an urban park of Shanghai based on polyethylene passive sampling: Vertical distribution, vegetation influence and diffusive flux. Sci. Total Environ. 2019, 689, 734–742. [Google Scholar] [CrossRef]
- Moayedi, H.; Gör, M.; Khari, M.; Foong, L.K.; Bahiraei, M.; Bui, D.T. Hybridizing four wise neural-metaheuristic paradigms in predicting soil shear strength. Measurement 2020, 156, 107576. [Google Scholar] [CrossRef]
- Dehghani, M.; Montazeri, Z.; Dehghani, A.; Malik, O.P.; Morales-Menendez, R.; Dhiman, G.; Nouri, N.; Ehsanifar, A.; Guerrero, J.M.; Ramirez-Mendoza, R.A. Binary Spring Search Algorithm for Solving Various Optimization Problems. Appl. Sci. 2021, 11, 1286. [Google Scholar] [CrossRef]
- Mohammadi, B.; Guan, Y.; Aghelpour, P.; Emamgholizadeh, S.; Pillco Zolá, R.; Zhang, D. Simulation of Titicaca Lake Water Level Fluctuations Using Hybrid Machine Learning Technique Integrated with Grey Wolf Optimizer Algorithm. Water 2020, 12, 3015. [Google Scholar] [CrossRef]
- Zhou, N.; Lau, L.; Bai, R.; Moore, T. A Genetic Optimization Resampling Based Particle Filtering Algorithm for Indoor Target Tracking. Remote Sens. 2021, 13, 132. [Google Scholar] [CrossRef]
- De Martonne, E. Une nouvelle function climatologique: L’indice d’aridité. Meteorologie 1926, 2, 449–459. [Google Scholar]
- Emadi, M.; Shahriari, A.R.; Sadegh-Zadeh, F.; Jalili Seh-Bardan, B.; Dindarlou, A. Geostatistics-based spatial distribution of soil moisture and temperature regime classes in Mazandaran province, northern Iran. Arch. Agron. Soil Sci. 2016, 62, 502–522. [Google Scholar] [CrossRef]
- Emadi, M.; Baghernejad, M.; Bahmanyar, M.A.; Morovvat, A. Changes in soil inorganic phosphorous pools along a precipitation gradient in northern Iran. Int. J. For. Soil Eros. (IJFSE) 2012, 2, 143–147. [Google Scholar]
- Khormali, F.; Ghergherechi, S.; Kehl, M.; Ayoubi, S. Soil formation in loess-derived soils along a subhumid to humid climate gradient, Northeastern Iran. Geoderma 2012, 179, 113–122. [Google Scholar] [CrossRef]
- Gee, G.W.; Bauder, J.W. Particle-size analysis. Methods Soil Anal. 1986, 5, 383–411. [Google Scholar]
- Gerakis, A.; Baer, B. A computer program for soil textural classification. Soil Sci. Soc. Am. J. 1999, 63, 807–808. [Google Scholar] [CrossRef]
- McBratney, A.B.; Mendonça Santos, M.L.; Minasny, B. On digital soil mapping. Geoderma 2003, 117, 3–52. [Google Scholar] [CrossRef]
- Gallant, J.C.; Dowling, T.I. A multiresolution index of valley bottom flatness for mapping depositional areas. Water Resour. Res. 2003, 39, 1347. [Google Scholar] [CrossRef]
- Wang, Z.; Shi, W. Robust variogram estimation combined with isometric log-ratio transformation for improved accuracy of soil particle-size fraction mapping. Geoderma 2018, 324, 56–66. [Google Scholar] [CrossRef]
- Mutanga, O.; Skidmore, A.K. Narrow band vegetation indices overcome the saturation problem in biomass estimation. Int. J. Remote Sens. 2004, 25, 3999–4014. [Google Scholar] [CrossRef]
- Escadafal, R. Soil spectral properties and their relationships with environmental parameters-examples from arid regions. In Imaging Spectrometry—A Tool for Environmental Observations; Springer: Dordrecht, The Netherlands, 1994; pp. 71–87. [Google Scholar]
- Serrano, J.; Shahidian, S.; Marques da Silva, J. Evaluation of normalized difference water index as a tool for monitoring pasture seasonal and inter-annual variability in a Mediterranean agro-silvo-pastoral system. Water 2019, 11, 62. [Google Scholar] [CrossRef]
- Xiao, X.; Hollinger, D.; Aber, J.; Goltz, M.; Davidson, E.A.; Zhang, Q.; Moore III, B. Satellite-based modeling of gross primary production in an evergreen needleleaf forest. Remote Sens. Environ. 2004, 89, 519–534. [Google Scholar] [CrossRef]
- Dogan, O.K.; Akyurek, Z.; Beklioglu, M. Identification and mapping of submerged plants in a shallow lake using quickbird satellite data. J. Environ. Manag. 2009, 90, 2138–2143. [Google Scholar] [CrossRef]
- Khan, N.M.; Rastoskuev, V.V.; Sato, Y.; Shiozawa, S. Assessment of hydrosaline land degradation by using a simple approach of remote sensing indicators. Agric. Water Manag. 2005, 77, 96–109. [Google Scholar] [CrossRef]
- Nield, S.; Boettinger, J.; Ramsey, R. Digitally mapping gypsic and natric soil areas using Landsat ETM data. Soil Sci. Soc. Am. J. 2007, 71, 245–252. [Google Scholar] [CrossRef]
- Boettinger, J.; Ramsey, R.; Bodily, J.; Cole, N.; Kienast-Brown, S.; Nield, S.; Saunders, A.; Stum, A. Landsat spectral data for digital soil mapping. In Digital Soil Mapping with Limited Data; Springer: Dordrecht, The Netherlands, 2008; pp. 193–202. [Google Scholar]
- Fick, S.E.; Hijmans, R.J. WorldClim 2: New 1-km spatial resolution climate surfaces for global land areas. Int. J. Climatol. 2017, 37, 4302–4315. [Google Scholar] [CrossRef]
- Karegowda, A.G.; Manjunath, A.; Jayaram, M. Comparative study of attribute selection using gain ratio and correlation based feature selection. Int. J. Inf. Technol. Knowl. Manag. 2010, 2, 271–277. [Google Scholar]
- Hall, D.B. Zero-inflated Poisson and binomial regression with random effects: A case study. Biometrics 2000, 56, 1030–1039. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1998. [Google Scholar]
- Lazzús, J.; Vega-Jorquera, P.; Palma-Chilla, L.; Stepanova, M.; Romanova, N. D st Index Forecast Based on Ground-Level Data Aided by Bio-Inspired Algorithms. Space Weather 2019, 17, 1487–1506. [Google Scholar] [CrossRef]
- Zhang, W.; Goh, A.T. Multivariate adaptive regression splines and neural network models for prediction of pile drivability. Geosci. Front. 2016, 7, 45–52. [Google Scholar] [CrossRef]
- Abeyrathna, K.D.; Jeenanunta, C. Training Artificial Neural Networks With Improved Particle Swarm Optimization: Case of Electricity Demand Forecasting in Thailand. In Handbook of Research on Advancements of Swarm Intelligence Algorithms for Solving Real-World Problems; IGI Global: Hershey, PA, USA, 2020; pp. 63–77. [Google Scholar]
- Sarangi, P.K.; Singh, N.; Swain, D.; Chauhan, R.; Singh, R. Short term load forecasting using neuro genetic hybrid approach: Results analysis with different network architectures. J. Theor. Appl. Inf. Technol. 2009, 5, 109–116. [Google Scholar]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the MHS’95, Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Shariati, M.; Mafipour, M.S.; Mehrabi, P.; Bahadori, A.; Zandi, Y.; Salih, M.N.; Nguyen, H.; Dou, J.; Song, X.; Poi-Ngian, S. Application of a hybrid artificial neural network-particle swarm optimization (ANN-PSO) model in behavior prediction of channel shear connectors embedded in normal and high-strength concrete. Appl. Sci. 2019, 9, 5534. [Google Scholar] [CrossRef]
- Yang, X.-S. A new metaheuristic bat-inspired algorithm. In Nature Inspired Cooperative Strategies for Optimization (NICSO 2010); Springer: Berlin/Heidelberg, Germany, 2010; pp. 65–74. [Google Scholar]
- Dong, J.; Wu, L.; Liu, X.; Li, Z.; Gao, Y.; Zhang, Y.; Yang, Q. Estimation of daily dew point temperature by using bat algorithm optimization based extreme learning machine. Appl. Therm. Eng. 2020, 165, 114569. [Google Scholar] [CrossRef]
- Devikanniga, D.; Raj, R.J.S. Classification of osteoporosis by artificial neural network based on monarch butterfly optimisation algorithm. Healthc. Technol. Lett. 2018, 5, 70–75. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.-G.; Deb, S.; Cui, Z. Monarch butterfly optimization. Neural Comput. Appl. 2019, 31, 1995–2014. [Google Scholar] [CrossRef]
- Hitziger, M.; Ließ, M. Comparison of three supervised learning methods for digital soil mapping: Application to a complex terrain in the Ecuadorian Andes. Appl. Environ. Soil Sci. 2014, 2014, 809495. [Google Scholar] [CrossRef]
- Wilding, L. Spatial variability: Its documentation, accomodation and implication to soil surveys. In Proceedings of the Soil Spatial Variability, Las Vegas NV, USA, 30 November–1 December 1984; pp. 166–194. [Google Scholar]
- Kiani-Harchegani, M.; Sadeghi, S.H.; Asadi, H. Comparing grain size distribution of sediment and original soil under raindrop detachment and raindrop-induced and flow transport mechanism. Hydrol. Sci. J. 2018, 63, 312–323. [Google Scholar] [CrossRef]
- Lazzús, J.; Vega, P.; Rojas, P.; Salfate, I. Forecasting the Dst index using a swarm-optimized neural network. Space Weather 2017, 15, 1068–1089. [Google Scholar] [CrossRef]
- Khormali, F.; Kehl, M. Micromorphology and development of loess-derived surface and buried soils along a precipitation gradient in Northern Iran. Quat. Int. 2011, 234, 109–123. [Google Scholar] [CrossRef]
- Akpa, S.I.; Odeh, I.O.; Bishop, T.F.; Hartemink, A.E.; Amapu, I.Y. Total soil organic carbon and carbon sequestration potential in Nigeria. Geoderma 2016, 271, 202–215. [Google Scholar] [CrossRef]
- Law-Ogbomo, K.; Nwachokor, M. Variability in selected soil physic-chemical properties of five soils formed on different parent materials in southeastern Nigeria. Res. J. Agric. Biol. Sci 2010, 6, 14–19. [Google Scholar]
- Wang, D.-C.; Zhang, G.-L.; Zhao, M.-S.; Pan, X.-Z.; Zhao, Y.-G.; Li, D.-C.; Macmillan, B. Retrieval and mapping of soil texture based on land surface diurnal temperature range data from MODIS. PLoS ONE 2015, 10, e0125814. [Google Scholar] [CrossRef] [PubMed]
- Gomez, C.; Dharumarajan, S.; Féret, J.-B.; Lagacherie, P.; Ruiz, L.; Sekhar, M. Use of sentinel-2 time-series images for classification and uncertainty analysis of inherent biophysical property: Case of soil texture mapping. Remote Sens. 2019, 11, 565. [Google Scholar] [CrossRef]
- Luo, H.; Zheng, Y. The camparison of citrus canopy spectral characteristics obtained by the HJ-1A/HSI and ASD field spectrometer. In Proceedings of the 2012 9th International Conference on Fuzzy Systems and Knowledge Discovery, Chongqing, China, 29–31 May 2012; pp. 1977–1980. [Google Scholar]
- Bousbih, S.; Zribi, M.; Pelletier, C.; Gorrab, A.; Lili-Chabaane, Z.; Baghdadi, N.; Ben Aissa, N.; Mougenot, B. Soil texture estimation using radar and optical data from Sentinel-1 and Sentinel-2. Remote Sens. 2019, 11, 1520. [Google Scholar] [CrossRef]
- Lagacherie, P. Digital soil mapping: A state of the art. In Digital Soil Mapping with Limited Data; Springer: Dordrecht, The Netherlands, 2008; pp. 3–14. [Google Scholar]
- Shahriari, M.; Delbari, M.; Afrasiab, P.; Pahlavan-Rad, M.R. Predicting regional spatial distribution of soil texture in floodplains using remote sensing data: A case of southeastern Iran. Catena 2019, 182, 104149. [Google Scholar] [CrossRef]
- De Carvalho Junior, W.; Lagacherie, P.; da Silva Chagas, C.; Calderano Filho, B.; Bhering, S.B. A regional-scale assessment of digital mapping of soil attributes in a tropical hillslope environment. Geoderma 2014, 232, 479–486. [Google Scholar] [CrossRef]
- Liao, K.; Xu, S.; Wu, J.; Zhu, Q. Spatial estimation of surface soil texture using remote sensing data. Soil Sci. Plant Nutr. 2013, 59, 488–500. [Google Scholar] [CrossRef]
- Gholizadeh, A.; Žižala, D.; Saberioon, M.; Borůvka, L. Soil organic carbon and texture retrieving and mapping using proximal, airborne and Sentinel-2 spectral imaging. Remote Sens. Environ. 2018, 218, 89–103. [Google Scholar] [CrossRef]
- Da Silva Chagas, C.; de Carvalho Junior, W.; Bhering, S.B.; Calderano Filho, B. Spatial prediction of soil surface texture in a semiarid region using random forest and multiple linear regressions. Catena 2016, 139, 232–240. [Google Scholar] [CrossRef]
- Bishop, T.; McBratney, A. A comparison of prediction methods for the creation of field-extent soil property maps. Geoderma 2001, 103, 149–160. [Google Scholar] [CrossRef]
- Adhikari, K.; Kheir, R.B.; Greve, M.B.; Bøcher, P.K.; Malone, B.P.; Minasny, B.; McBratney, A.B.; Greve, M.H. High-resolution 3-D mapping of soil texture in Denmark. Soil Sci. Soc. Am. J. 2013, 77, 860–876. [Google Scholar] [CrossRef]
- Muzzamal, M.; Huang, J.; Nielson, R.; Sefton, M.; Triantafilis, J. Mapping soil particle-size fractions using additive log-ratio (ALR) and isometric log-ratio (ILR) transformations and proximally sensed ancillary data. Clays Clay Miner. 2018, 66, 9–27. [Google Scholar] [CrossRef]
- Gasmi, A.; Gomez, C.; Lagacherie, P.; Zouari, H. Surface soil clay content mapping at large scales using multispectral (VNIR–SWIR) ASTER data. Int. J. Remote Sens. 2019, 40, 1506–1533. [Google Scholar] [CrossRef]
- Mulder, V.L.; Lacoste, M.; Richer-de-Forges, A.; Arrouays, D. GlobalSoilMap France: High-resolution spatial modelling the soils of France up to two meter depth. Sci. Total Environ. 2016, 573, 1352–1369. [Google Scholar] [CrossRef] [PubMed]
- Hengl, T.; Heuvelink, G.B.; Kempen, B.; Leenaars, J.G.; Walsh, M.G.; Shepherd, K.D.; Sila, A.; MacMillan, R.A.; de Jesus, J.M.; Tamene, L. Mapping soil properties of Africa at 250 m resolution: Random forests significantly improve current predictions. PLoS ONE 2015, 10, e0125814. [Google Scholar] [CrossRef]
- Kouchami-Sardoo, I.; Shirani, H.; Esfandiarpour-Boroujeni, I.; Besalatpour, A.; Hajabbasi, M. Prediction of soil wind erodibility using a hybrid Genetic algorithm–Artificial neural network method. Catena 2020, 187, 104315. [Google Scholar] [CrossRef]
- Mohamad, E.T.; Faradonbeh, R.S.; Armaghani, D.J.; Monjezi, M.; Majid, M.Z.A. An optimized ANN model based on genetic algorithm for predicting ripping production. Neural Comput. Appl. 2017, 28, 393–406. [Google Scholar] [CrossRef]
- Abeyrathna, K.D.; Jeenanunta, C. Hybrid particle swarm optimization with genetic algorithm to train artificial neural networks for short-term load forecasting. Int. J. Swarm Intell. Res. (IJSIR) 2019, 10, 1–14. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).