Hyperspectral Data Compression Using Fully Convolutional Autoencoder
Abstract
:1. Introduction
- Development of a spectral signals compressor based on deep convolutional autoencoder (SSCNet), analysing its learning process and evaluating it in terms of compression and spectral signal reconstruction over spectral datasets and Imagenet-ILSVRC2012 benchmark.
- Definition of two datasets come from the ESA repository (Lombardia Sentinel-2 satellite imagery and VIRTIS-Rosetta hyperspectral data) and development of a python parser useful to read and handle the calibrated data images.
- Release the PyTorch code for SSCNet, the pretrained models and the parser software available in [28].
2. Spectral Signals Compressor Network
3. Experimental Results
3.1. Datasets
3.1.1. Lombardia Sentinel-2 Dataset
3.1.2. VIRTIS-Rosetta dataset
3.1.3. Normalization
| Algorithm 1 Pseudo code of the training step. We apply a min/max normalization per channel taking all min/max from a preprocessing dataset step; then, we feed into SSCNet , which returns the compressed data. Finally, we use the compressed data and feed it into the SSCNet decoder module for the image reconstruction. The total error will be given from the binary cross-entropy error between the decoded image reconstructed and the original source, and the error backpropagation is applied for the learning process. |
|
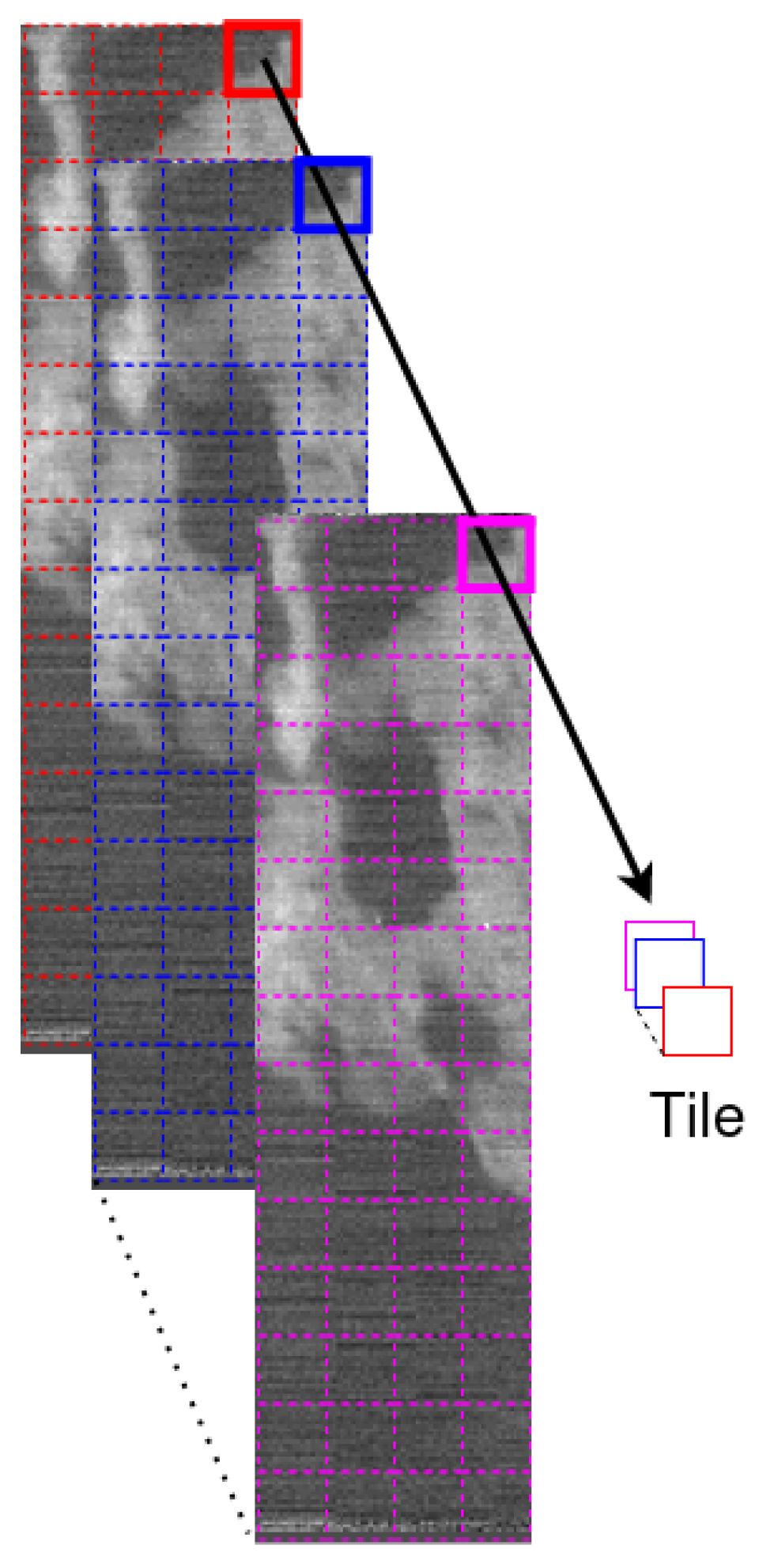
3.2. Training Batch Strategy in High-Spatial Resolution Input
3.3. Generalization Capability
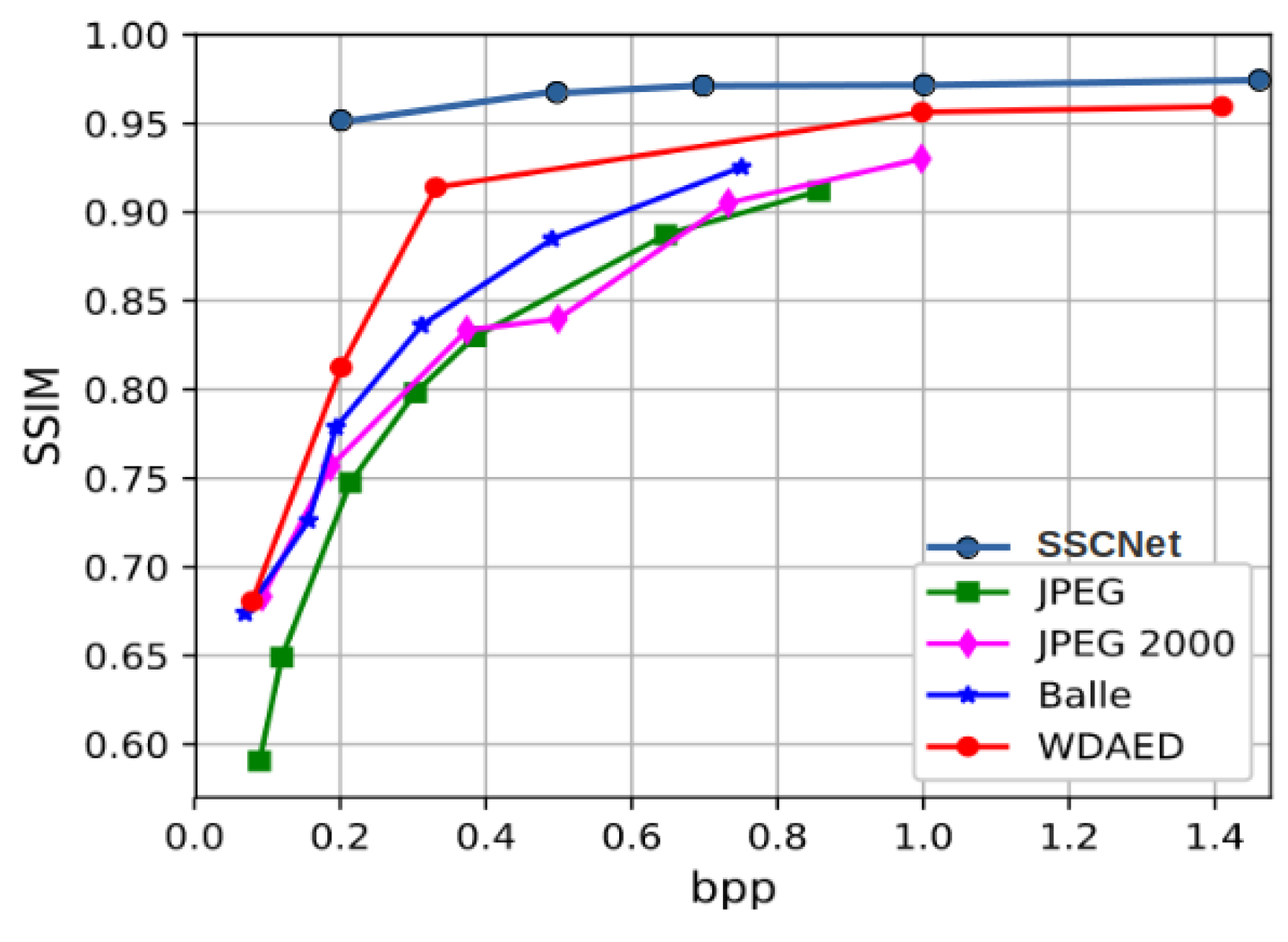
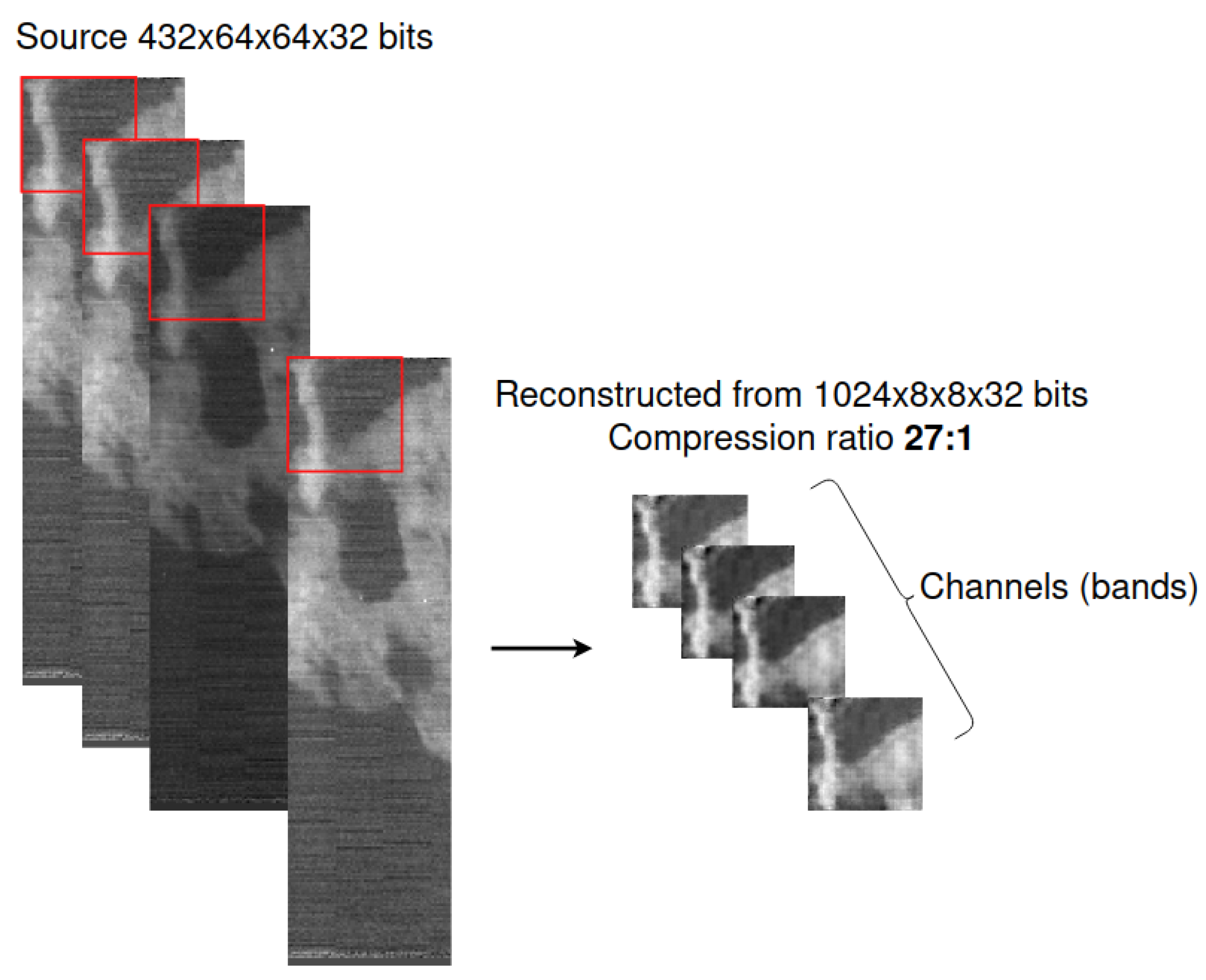
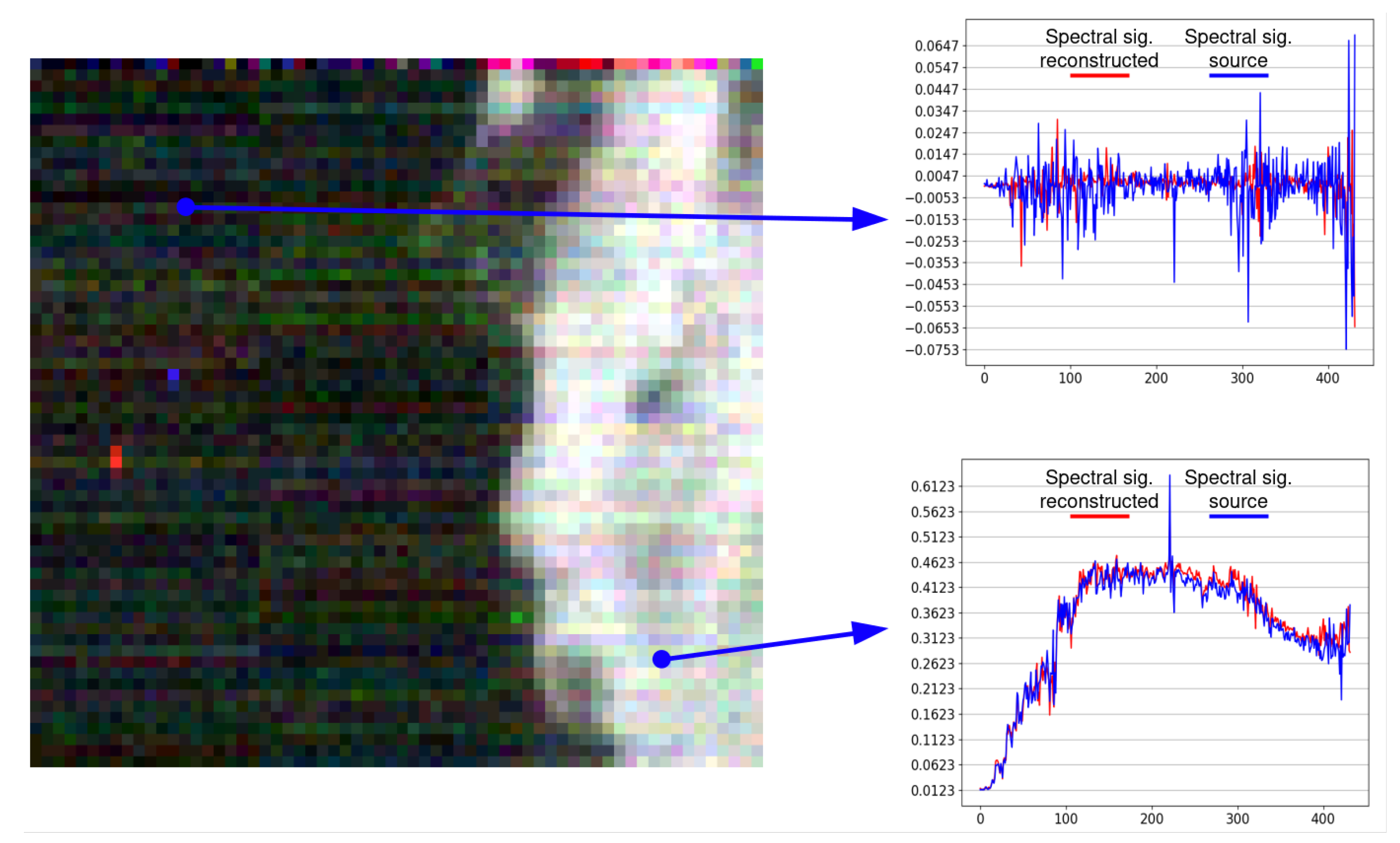
3.4. Coding and Spectral Signal Reconstruction Efficiency
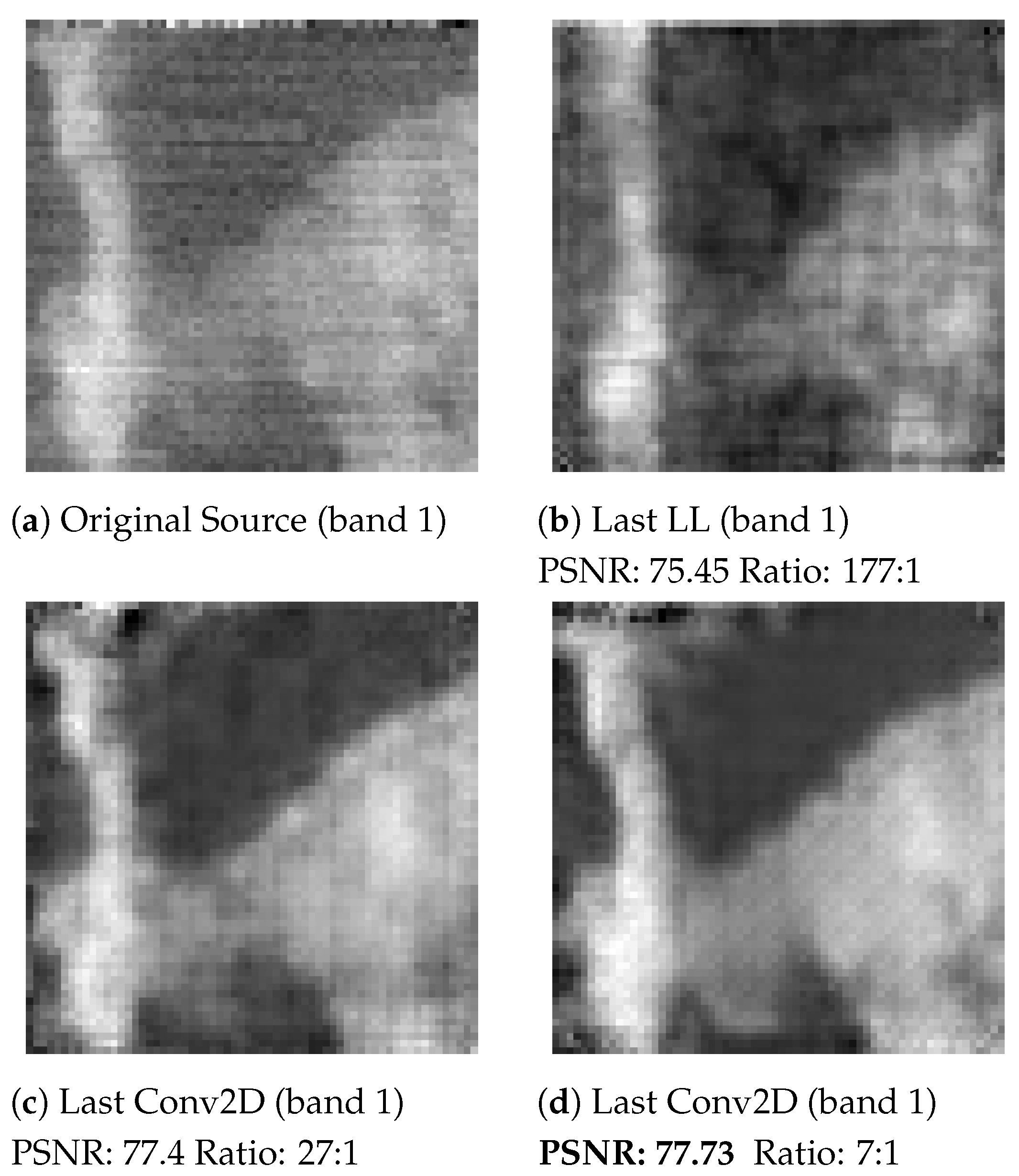
SSCNet with Last Convolutional Layer
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- La Grassa, R.; Gallo, I.; Landro, N. σ2R loss: A weighted loss by multiplicative factors using sigmoidal functions. Neurocomputing 2022, 470, 217–225. [Google Scholar] [CrossRef]
- Yuan, Y.; Chen, X.; Wang, J. Object-contextual representations for semantic segmentation. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 173–190. [Google Scholar]
- Wang, X.; Xie, L.; Dong, C.; Shan, Y. Real-esrgan: Training real-world blind super-resolution with pure synthetic data. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, Canada, 11–18 October 2021; pp. 1905–1914. [Google Scholar]
- Sun, W.; Chen, Z. Learned image downscaling for upscaling using content adaptive resampler. IEEE Trans. Image Process. 2020, 29, 4027–4040. [Google Scholar] [CrossRef] [Green Version]
- Webb, S. Deep learning for biology. Nature 2018, 554, 555–558. [Google Scholar] [CrossRef] [Green Version]
- Shen, D.; Wu, G.; Suk, H.I. Deep learning in medical image analysis. Annu. Rev. Biomed. Eng. 2017, 19, 221–248. [Google Scholar] [CrossRef] [Green Version]
- Xiong, Y.; Zuo, R.; Carranza, E.J.M. Mapping mineral prospectivity through big data analytics and a deep learning algorithm. Ore Geol. Rev. 2018, 102, 811–817. [Google Scholar] [CrossRef]
- Gallo, I.; La Grassa, R.; Landro, N.; Boschetti, M. Sentinel 2 Time Series Analysis with 3D Feature Pyramid Network and Time Domain Class Activation Intervals for Crop Mapping. ISPRS Int. J. Geo-Inf. 2021, 10, 483. [Google Scholar] [CrossRef]
- Rothrock, B.; Kennedy, R.; Cunningham, C.; Papon, J.; Heverly, M.; Ono, M. Spoc: Deep learning-based terrain classification for mars rover missions. In Proceedings of the AIAA SPACE 2016, Long Beach, CA, USA, 13–16 September 2016; p. 5539. [Google Scholar]
- Rao, Q.; Frtunikj, J. Deep learning for self-driving cars: Chances and challenges. In Proceedings of the 1st International Workshop on Software Engineering for AI in Autonomous Systems, Gothenburg, Sweden, 28 May 2018; pp. 35–38. [Google Scholar]
- Zhang, S.; Yao, L.; Sun, A.; Tay, Y. Deep learning based recommender system: A survey and new perspectives. ACM Comput. Surv. 2019, 52, 1–38. [Google Scholar] [CrossRef] [Green Version]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. Adv. Neural Inf. Process. Syst. 2014, 27. [Google Scholar]
- Cheng, Z.; Sun, H.; Takeuchi, M.; Katto, J. Deep convolutional autoencoder-based lossy image compression. In Proceedings of the 2018 Picture Coding Symposium (PCS), San Francisco, CA, USA, 24–27 June 2018; pp. 253–257. [Google Scholar]
- Makhzani, A.; Shlens, J.; Jaitly, N.; Goodfellow, I.; Frey, B. Adversarial autoencoders. arXiv 2015, arXiv:1511.05644. [Google Scholar]
- Chen, Z.; Wu, B.; Liu, W.C. Mars3DNet: CNN-based high-resolution 3D reconstruction of the Martian surface from single images. Remote Sens. 2021, 13, 839. [Google Scholar] [CrossRef]
- Marmanis, D.; Datcu, M.; Esch, T.; Stilla, U. Deep learning earth observation classification using ImageNet pretrained networks. IEEE Geosci. Remote Sens. Lett. 2015, 13, 105–109. [Google Scholar] [CrossRef] [Green Version]
- Wallace, G.K. The JPEG still picture compression standard. IEEE Trans. Consum. Electron. 1992, 38, xviii–xxxiv. [Google Scholar] [CrossRef]
- Christopoulos, C.; Skodras, A.; Ebrahimi, T. The JPEG2000 still image coding system: An overview. IEEE Trans. Consum. Electron. 2000, 46, 1103–1127. [Google Scholar] [CrossRef] [Green Version]
- CCSDS. Image Data Compression Report. Available online: https://public.ccsds.org/Pubs/120x1g3.pdf (accessed on 5 April 2022).
- Nvidia. Nvidia embedded-systems. Available online: https://www.nvidia.com/it-it/autonomous-machines/embedded-systems/ (accessed on 2 April 2022).
- Mishra, D.; Singh, S.K.; Singh, R.K. Wavelet-based deep auto encoder-decoder (wdaed)-based image compression. IEEE Trans. Circuits Syst. Video Technol. 2020, 31, 1452–1462. [Google Scholar] [CrossRef]
- Akyazi, P.; Ebrahimi, T. Learning-based image compression using convolutional autoencoder and wavelet decomposition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Long Beach, CA, USA, 16–17 June 2019. [Google Scholar]
- Palsson, B.; Sigurdsson, J.; Sveinsson, J.R.; Ulfarsson, M.O. Hyperspectral unmixing using a neural network autoencoder. IEEE Access 2018, 6, 25646–25656. [Google Scholar] [CrossRef]
- Deng, C.; Cen, Y.; Zhang, L. Learning-based hyperspectral imagery compression through generative neural networks. Remote Sens. 2020, 12, 3657. [Google Scholar] [CrossRef]
- Toderici, G.; Vincent, D.; Johnston, N.; Jin Hwang, S.; Minnen, D.; Shor, J.; Covell, M. Full resolution image compression with recurrent neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 5306–5314. [Google Scholar]
- Ballé, J.; Laparra, V.; Simoncelli, E.P. End-to-end optimized image compression. arXiv 2016, arXiv:1611.01704. [Google Scholar]
- Vahdat, A.; Kautz, J. Nvae: A deep hierarchical variational autoencoder. Adv. Neural Inf. Process. Syst. 2020, 33, 19667–19679. [Google Scholar]
- La Grassa, R.; Cristina, R.; Gabriele, C.; Ignazio, G. SSCNet. 2022. Available online: https://gitlab.com/riccardo2468/spectral-signals-compressor-network (accessed on 15 April 2022).
- Community, P. BCE Loss Documentation. Available online: https://pytorch.org/docs/stable/generated/torch.nn.BCELoss.html (accessed on 5 April 2022).
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Coradini, A.; Capaccioni, F.; Drossart, P.; Arnold, G.; Ammannito, E.; Angrilli, F.; Barucci, A.; Bellucci, G.; Benkhoff, J.; Bianchini, G.; et al. VIRTIS: An imaging spectrometer for the Rosetta mission. Space Sci. Rev. 2007, 128, 529–559. [Google Scholar] [CrossRef]
- Politi, R.; Piccioni, G.; Henry, F.; Erard, S.; Jacquinod, S.; Drossart, P. VIRTIS-VEX Data Manual. Available online: https://www.cosmos.esa.int/documents/772136/977578/VIRTIS-VEX_Data_Manual_DRAFT.pdf/66410ef7-e8b9-4312-b492-ce7f0a5e84ad (accessed on 3 April 2022).
- NASA. Planetary Data System, Rosetta Data Repository Nasa. Available online: https://pds-smallbodies.astro.umd.edu/data_sb/missions/rosetta/ (accessed on 26 April 2022).
- Huang, L.; Qin, J.; Zhou, Y.; Zhu, F.; Liu, L.; Shao, L. Normalization techniques in training dnns: Methodology, analysis and application. arXiv 2020, arXiv:2009.12836. [Google Scholar]
- LeCun, Y.A.; Bottou, L.; Orr, G.B.; Müller, K.R. Efficient backprop. In Neural Networks: Tricks of the Trade; Springer: Berlin/Heidelberg, Germany, 2012; pp. 9–48. [Google Scholar]
- Ghassemi, S.; Magli, E. Convolutional neural networks for on-board cloud screening. Remote Sens. 2019, 11, 1417. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Simoncelli, E.P.; Bovik, A.C. Multiscale structural similarity for image quality assessment. In Proceedings of the 37th Asilomar Conference on Signals, Systems & Computers, Pacific Grove, CA, USA, 9–12 November 2003; Volume 2, pp. 1398–1402. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed] [Green Version]



| Bands | PSNR | SSIM | FSIM |
|---|---|---|---|
| 1 | 48.106 | 0.984 | 0.984 |
| 2 | 49.427 | 0.988 | 0.984 |
| 3 | 49.553 | 0.987 | 0.983 |
| 4 | 50.914 | 0.993 | 0.991 |
| 5 | 49.205 | 0.990 | 0.990 |
| 6 | 48.085 | 0.987 | 0.989 |
| 7 | 44.259 | 0.967 | 0.975 |
| 8 | 50.581 | 0.993 | 0.991 |
| 9 | 50.458 | 0.992 | 0.991 |
| Bands | PSNR | SSIM | FSIM |
|---|---|---|---|
| 1 | 48.440 | 0.985 | 0.985 |
| 2 | 49.709 | 0.988 | 0.985 |
| 3 | 49.783 | 0.988 | 0.984 |
| 4 | 51.318 | 0.993 | 0.991 |
| 5 | 49.569 | 0.991 | 0.991 |
| 6 | 48.542 | 0.988 | 0.990 |
| 7 | 44.527 | 0.969 | 0.977 |
| 8 | 51.043 | 0.993 | 0.992 |
| 9 | 50.876 | 0.992 | 0.991 |
| Bands | PSNR | SSIM |
|---|---|---|
| 1 | 0.6895 | 0.10152 |
| 2 | 0.5673 | 0.0000 |
| 3 | 0.4620 | 0.10121 |
| 4 | 0.7872 | 0.0000 |
| 5 | 0.7343 | 0.1009 |
| 6 | 0.9414 | 0.1012 |
| 7 | 0.6018 | 0.2063 |
| 8 | 0.9051 | 0.0000 |
| 9 | 0.8216 | 0.0000 |
| JPEG Ratio (2.5):1 | JPEG2000 Ratio (9.7):1 | SSCNet Ratio 20:1 | ||||
|---|---|---|---|---|---|---|
| Bands | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM |
| 1 | 19.171 | 0.908 | 35.317 | 0.925 | 48.440 | 0.985 |
| 2 | 19.302 | 0.906 | 36.249 | 0.923 | 49.709 | 0.988 |
| 3 | 19.404 | 0.899 | 35.710 | 0.912 | 49.783 | 0.988 |
| 4 | 21.722 | 0.945 | 36.219 | 0.929 | 51.318 | 0.993 |
| 5 | 21.561 | 0.948 | 36.570 | 0.932 | 49.569 | 0.991 |
| 6 | 21.523 | 0.949 | 36.354 | 0.931 | 48.542 | 0.988 |
| 7 | 18.798 | 0.916 | 35.767 | 0.929 | 44.527 | 0.969 |
| 8 | 21.866 | 0.943 | 37.444 | 0.946 | 51.043 | 0.993 |
| 9 | 21.904 | 0.942 | 35.847 | 0.938 | 50.876 | 0.992 |
| Compression Ratio SSCNet | avg PSNR |
|---|---|
| 7:1 () last conv | 67.677 |
| 27:1 () last conv | 66.79 |
| 177:1 () | 64.845 |
| 353:1 () | 64.841 |
| 1769:1 () | 64.729 |
| Ref. [24] GNN model (VGG16 + CNN Decoder) | |
| 177:1 () | 60.87 |
| 353:1 () | 60.87 |
| 1769:1 () | 60.71 |
| 36k:1 () | 59.44 |
| Model | P (M) | Train T(s) | Test T Enc(s) | Test T Dec(s) | Test G Time |
|---|---|---|---|---|---|
| SSCNet conv | 8 (enc) 6.7 (dec) | 35,020 | 0.219 | 0.125 | ∼0.34 |
| SSCNet linear | 171 (enc) 168 (dec) | 39,578 | 0.220 | 0.120 | ∼0.34 |
| [24] GNN model | 175 (enc) 0.683 (dec) | 30,074 | 0.116 | 0.090 | ∼0.20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
La Grassa, R.; Re, C.; Cremonese, G.; Gallo, I. Hyperspectral Data Compression Using Fully Convolutional Autoencoder. Remote Sens. 2022, 14, 2472. https://doi.org/10.3390/rs14102472
La Grassa R, Re C, Cremonese G, Gallo I. Hyperspectral Data Compression Using Fully Convolutional Autoencoder. Remote Sensing. 2022; 14(10):2472. https://doi.org/10.3390/rs14102472
Chicago/Turabian StyleLa Grassa, Riccardo, Cristina Re, Gabriele Cremonese, and Ignazio Gallo. 2022. "Hyperspectral Data Compression Using Fully Convolutional Autoencoder" Remote Sensing 14, no. 10: 2472. https://doi.org/10.3390/rs14102472
APA StyleLa Grassa, R., Re, C., Cremonese, G., & Gallo, I. (2022). Hyperspectral Data Compression Using Fully Convolutional Autoencoder. Remote Sensing, 14(10), 2472. https://doi.org/10.3390/rs14102472








