Observation on the Droplet Ranging from 2 to 16 μm in Cloud Droplet Size Distribution Based on Digital Holography
Abstract
:1. Introduction
2. Theory
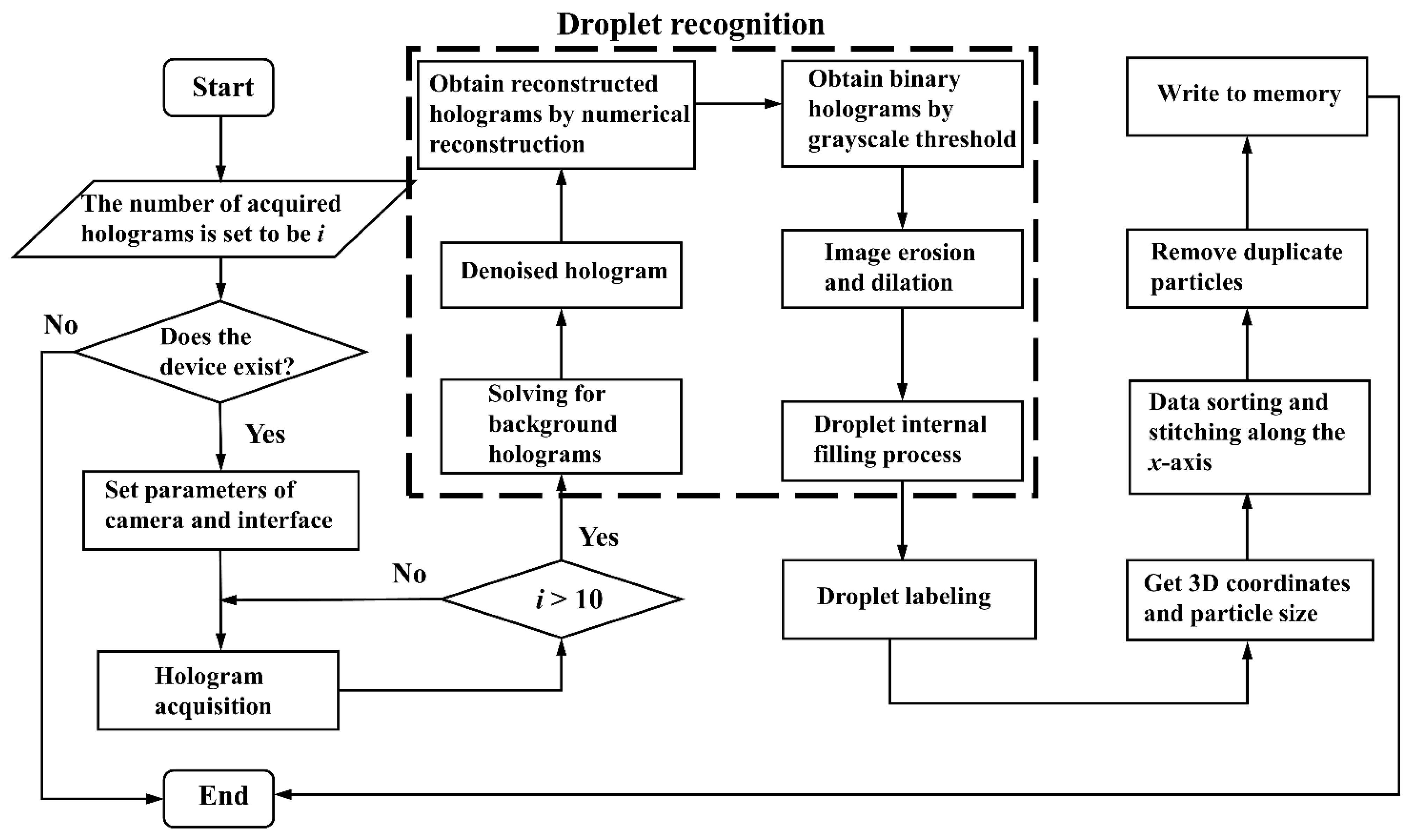
3. Experimental Setup
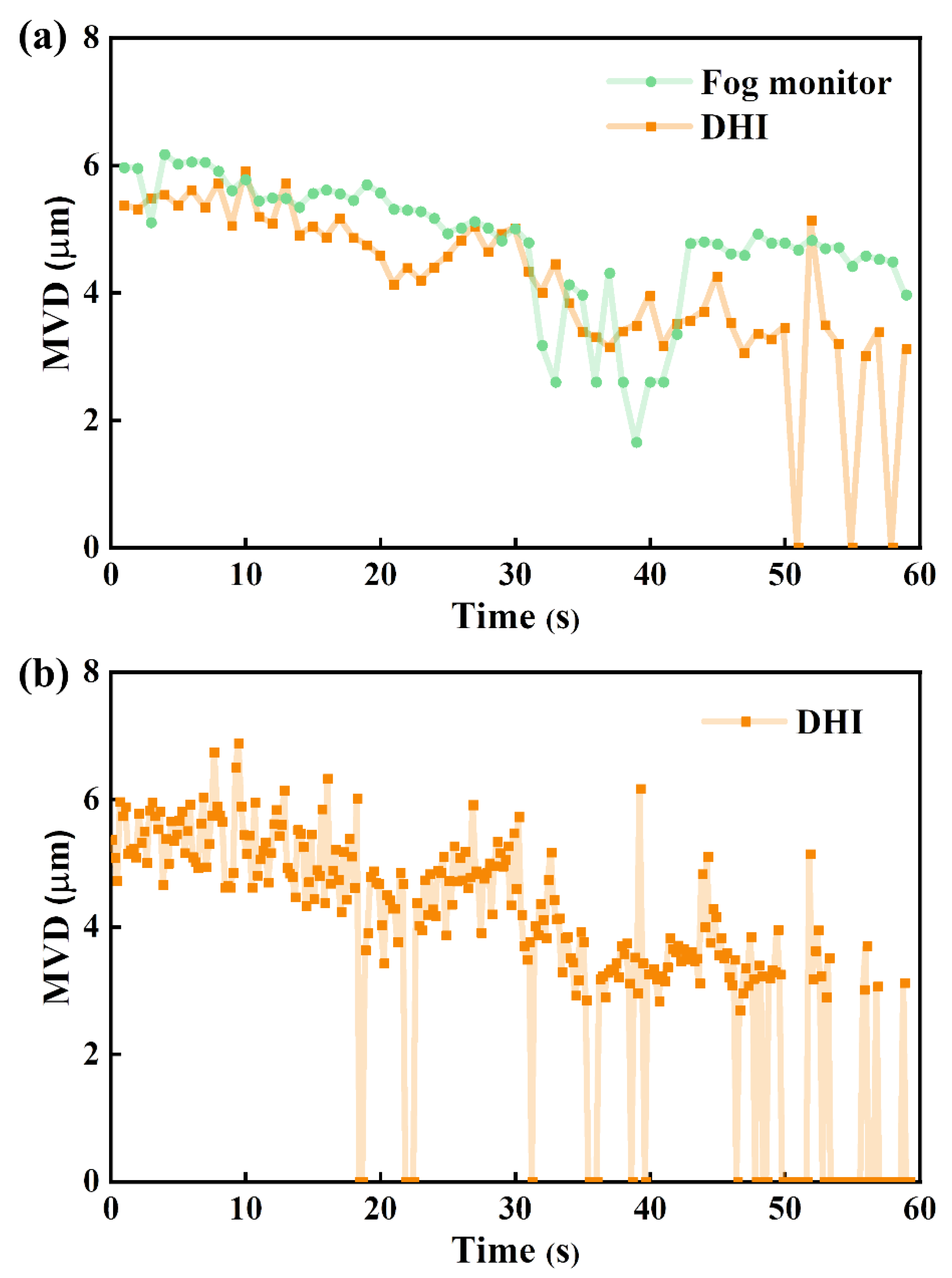
4. Results Analysis and Discussion
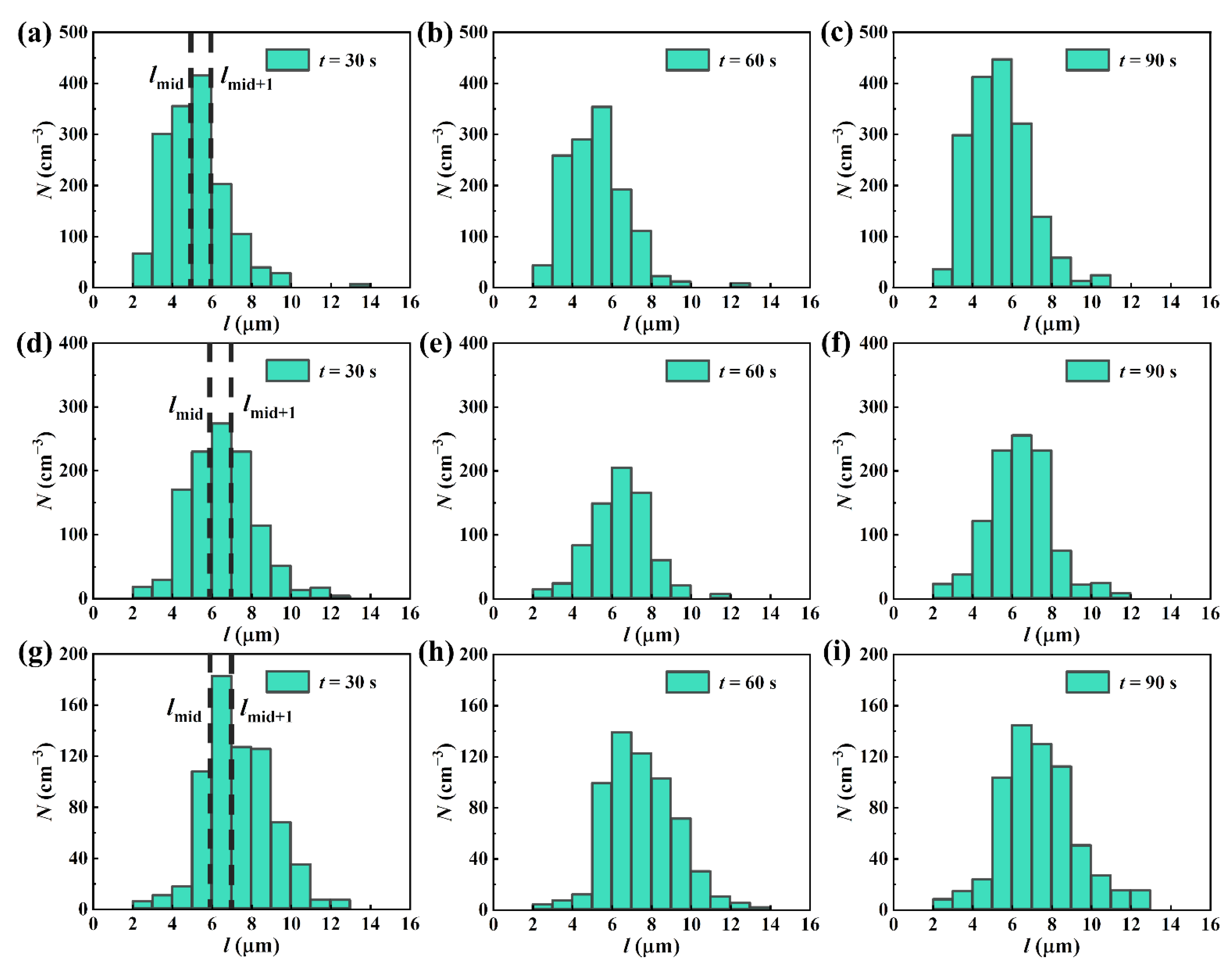
4.1. Size Distribution
4.2. Microphysical Parameters
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bhatia, K.; Vecchi, G.; Murakami, H.; Underwood, S.; Kossin, J. Projected response of tropical cyclone intensity and intensification in a global climate model. J. Clim. 2018, 31, 8281–8303. [Google Scholar] [CrossRef]
- Gettelman, A.; Morrison, H.; Santos, S.; Bogenschutz, P. Advanced two-moment bulk microphysics for global models. Part II: Global model solutions and aerosol–cloud interactions. J. Clim. 2015, 28, 1288–1307. [Google Scholar] [CrossRef]
- Lohmann, U.; Stier, P.; Hoose, C.; Ferrachat, S.; Kloster, S.; Roeckner, E.; Zhang, J. Cloud microphysics and aerosol indirect effects in the global climate model ECHAM5-HAM. Atmos. Chem. Phys. 2007, 7, 3425–3446. [Google Scholar] [CrossRef] [Green Version]
- Revell, L.E.; Kremser, S.; Hartery, S.; Harvey, M.; Mulcahy, J.P.; Williams, J.; Morgenstern, O.; McDonald, A.J.; Varma, V.; Bird, L.; et al. The sensitivity of Southern Ocean aerosols and cloud microphysics to sea spray and sulfate aerosol production in the HadGEM3-GA7.1 chemistry-climate model. Atmos. Chem. Phys. 2019, 19, 15447–15466. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Fan, J.; Li, Z.; Rosenfeld, D. Impacts of cloud microphysics parameterizations on simulated aerosol-cloud interactions for deep convective clouds over Houston. Atmos. Chem. Phys. 2021, 21, 2363–2381. [Google Scholar] [CrossRef]
- Shaw, R.A.; Cantrell, W.; Chen, S.; Chuang, P.; Donahue, N.; Feingold, G.; Kollias, P.; Korolev, A.; Kreidenweis, S.; Krueger, S.; et al. Cloud–aerosol–turbulence interactions: Science priorities and concepts for a large-scale laboratory facility. Bull. Amer. Meteorol. Soc. 2020, 101, E1026–E1035. [Google Scholar] [CrossRef]
- Dias, A.; Ehrhart, S.; Vogel, A.; Williamsonet, C.; Almeida, J.; Kirkby, J.; Mathot, S.; Mumford, S.; Onnela, A. Temperature uniformity in the CERN CLOUD chamber. Atmos. Meas. Tech. 2017, 10, 5075–5088. [Google Scholar] [CrossRef] [Green Version]
- Zhao, X.; Heidinger, A.K.; Walther, A. Climatology analysis of aerosol effect on marine water cloud from long-term satellite climate data records. Remote Sens. 2016, 8, 300. [Google Scholar] [CrossRef] [Green Version]
- Desai, N.; Chandrakar, K.K.; Chang, K.; Cantrell, W.; Shaw, R.A. Influence of Microphysical Variability on Stochastic Condensation in a Turbulent Laboratory Cloud. J. Atmos. Sci. 2018, 75, 189–201. [Google Scholar] [CrossRef]
- Chandrakar, K.K.; Saito, I.; Yang, F.; Cantrell, W.; Gotoh, T.; Shaw, R.A. Droplet size distributions in turbulent clouds: Experimental evaluation of theoretical distributions. Q. J. R. Meteorol. Soc. 2020, 146, 483–504. [Google Scholar] [CrossRef]
- Beals, M.J.; Fugal, J.P.; Shaw, R.A.; Lu, J.; Spuler, S.M.; Stith, J.L. Holographic measurements of inhomogeneous cloud mixing at the centimeter scale. Science 2015, 350, 87–90. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pinsky, M.B.; Khain, A.P.; Shapiro, M. Collisions of cloud droplets in a turbulent flow. Part IV: Droplet hydrodynamic interaction. J. Atmos. Sci. 2007, 64, 2462–2482. [Google Scholar] [CrossRef]
- Chen, R.; Chang, F.L.; Li, Z.; Ferraro, R.; Weng, F. Impact of the vertical variation of cloud droplet size on the estimation of cloud liquid water path and rain detection. J. Atmos. Sci. 2007, 64, 3843–3853. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Wang, X.; Chen, J.; Zhu, C.; Li, W.; Li, C.; Liu, L.; Xu, C.; Wen, L.; Xue, L.; et al. Chemical composition and droplet size distribution of cloud at the summit of Mount Tai, China. Atmos. Chem. Phys. 2017, 17, 9885–9896. [Google Scholar] [CrossRef] [Green Version]
- Lu, C.; Liu, Y.; Yum, S.S.; Chen, J.; Zhu, L.; Gao, S.; Yin, Y.; Jia, X.; Wang, Y. Reconciling contrasting relationships between relative dispersion and volume-mean radius of cloud droplet size distributions. J. Geophys. Res. Atmos. 2020, 125, e2019JD031868. [Google Scholar] [CrossRef]
- Broekhuizen, K.; Chang, R.Y.W.; Leaitch, W.R.; Li, S.M.; Abbatt, J.P.D. Closure between measured and modeled cloud condensation nuclei (CCN) using size-resolved aerosol compositions in downtown Toronto. Atmos. Chem. Phys. 2006, 6, 2513–2524. [Google Scholar] [CrossRef] [Green Version]
- Petters, M.D.; Kreidenweis, S.M. A single parameter representation of hygroscopic growth and cloud condensation nuclus activity. Atmos. Chem. Phys. 2007, 7, 1961–1971. [Google Scholar] [CrossRef] [Green Version]
- Huang, Z.; Nee, J.B.; Chiang, C.W.; Zhang, S.; Jin, H.; Wang, W.; Zhou, T. Real-Time Observations of Dust-Cloud Interactions Based on Polarization and Raman Lidar Measurements. Remote Sens. 2018, 10, 1017. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Lee, Y.N.; Daum, P.H.; Jayne, J.; Alexander, M.L. Effects of aerosol organics on cloud condensation nucleus (CCN) concentration and first indirect aerosol effect. Atmos. Chem. Phys. 2008, 8, 6325–6339. [Google Scholar] [CrossRef] [Green Version]
- Riipinen, I.; Pierce, J.R.; Yli-Juuti, T.; Nieminen, T.; Hakkinen, S.; Ehn, M.; Junninen, H.; Lehtipalo, K.; Petaja, T.; Slowik, J.; et al. Organic condensation: A vital link connecting aerosol formation to cloud condensation nuclei (CCN) concentrations. Atmos. Chem. Phys. 2011, 11, 3865–3878. [Google Scholar] [CrossRef] [Green Version]
- Lambe, A.T.; Onasch, T.B.; Massoli, P.; Croasdale, D.R.; Wright, J.P.; Ahern, A.T.; Williams, L.R.; Worsnop, D.R.; Brune, W.H.; Davidovits, P. Laboratory studies of the chemical composition and cloud condensation nuclei (CCN) activity of secondary organic aerosol (SOA) and oxidized primary organic aerosol (OPOA). Atmos. Chem. Phys. 2011, 11, 8913–8928. [Google Scholar] [CrossRef] [Green Version]
- Gunthe, S.S.; Rose, D.; Su, H.; Garland, R.M.; Achtert, P.; Nowak, A.; Wiedensohler, A.; Kuwata, M.; Takegawa, N.; Kondo, Y.; et al. Cloud condensation nuclei (CCN) from fresh and aged air pollution in the megacity region of Beijing. Atmos. Chem. Phys. 2011, 11, 11023–11039. [Google Scholar] [CrossRef] [Green Version]
- Zheng, G.; Kuang, C.; Uin, J.; Watson, T.; Wang, J. Large contribution of organics to condensational growth and formation of cloud condensation nuclei (CCN) in the remote marine boundary layer. Atmos. Chem. Phys. 2020, 20, 12515–12525. [Google Scholar] [CrossRef]
- Bauer, H.; Ciebl, H.; Hitzenberger, R.; Kasper-Giebl, A.; Reischl, G.; Zibuschka, F.; Puxbaum, H. Airborne bacteria as cloud condensation nuclei. J. Geophys. Res.-Atmos. 2003, 108, 4658. [Google Scholar] [CrossRef]
- Gustafson, W.I., Jr.; Chapman, E.G.; Ghan, S.J.; Easter, R.C.; Fast, J.D. Impact on modeled cloud characteristics due to simplified treatment of uniform cloud condensation nuclei during NEAQS 2004. Geophys. Res. Lett. 2007, 34, L19809. [Google Scholar] [CrossRef]
- Kumar, M.; Birhman, A.S.; Kannan, S.; Shakher, C. Measurement of initial displacement of canine and molar in human maxilla under different canine retraction methods using digital holographic interferometry. Opt. Eng. 2018, 57, 094106. [Google Scholar] [CrossRef]
- Das, B.; Yelleswarapu, C.S. Dual plane in-line digital holographic microscopy. Opt. Lett. 2010, 35, 3426–3428. [Google Scholar] [CrossRef]
- Sang, X.; Yu, C.; Yu, M.; Hsu, D. Applications of digital holography to measurements and optical characterization. Opt. Eng. 2011, 50, 091311. [Google Scholar] [CrossRef]
- Pan, G.; Jun, W.; Cheng-Cheng, Z.; Jia-Bin, T.; Jing-Jing, L.; Qing, Y.; Deng-Xin, H. Simultaneous measurement of cloud microphysical parameters based on digital holographic interferometry. Acta Phys. Sin. 2021, 70, 099201. [Google Scholar] [CrossRef]
- Bellanger, C.; Brignon, A.; Colineau, J.; Huignard, J.P. Coherent fiber combining by digital holography. Opt. Lett. 2008, 33, 2937–2939. [Google Scholar] [CrossRef]
- Alvarez, A.S.; Manuel, H.; Santoyo, F.M.; Anaya, T.S. Strain determination in bone sections with simultaneous 3D digital holographic interferometry. Opt. Lasers Eng. 2014, 57, 101–108. [Google Scholar] [CrossRef]
- Kumar, M.; Shakher, C. Experimental characterization of the hygroscopic properties of wood during convective drying using digital holographic interferometry. Appl. Opt. 2016, 55, 960–968. [Google Scholar] [CrossRef] [PubMed]
- Sánchez, A.; Manuel, H.; Santoyo, F.M.; Saucedo-A, T.; Reyes, R. Simultaneous 3D digital holographic interferometry for strain measurements validated with FEM. Opt. Lasers Eng. 2014, 52, 178–183. [Google Scholar] [CrossRef]
- Kumar, V.; Kumar, M.; Shakher, C. Measurement of natural convective heat transfer coefficient along the surface of a heated wire using digital holographic interferometry. Appl. Opt. 2014, 53, G74–G83. [Google Scholar] [CrossRef] [PubMed]
- Gorthi, S.S.; Rajshekhar, G.; Rastogi, P. Strain estimation in digital holographic interferometry using piecewise polynomial phase approximation based method. Opt. Express 2010, 18, 560–565. [Google Scholar] [CrossRef] [Green Version]
- Vincitorio, F.; Bahuer, L.; Fiorucci, M.P.; López, A.J.; Ramil, A. Improvement of crack detection on rough materials by digital holographic interferometry in combination with non-uniform thermal loads. Optik 2018, 163, 43–48. [Google Scholar] [CrossRef]
- Sheng, J.; Malkiel, E.; Katz, J. Digital holographic microscope for measuring three-dimensional particle distributions and motions. Appl. Optics. 2006, 45, 3893–3901. [Google Scholar] [CrossRef]
- Yu, X.; Hong, J.; Liu, C.; Kim, M.K. Review of digital holographic microscopy for three-dimensional profiling and tracking. Opt. Eng. 2014, 53, 112306. [Google Scholar] [CrossRef] [Green Version]
- Dubois, F.; Callens, N.; Yourassowsky, C.; Hoyos, M.; Kurowski, P.; Monnom, O. Digital holographic microscopy with reduces spatial coherence for three-dimensional particle flow analysis. Appl. Opt. 2006, 45, 864–871. [Google Scholar] [CrossRef]
- Latychevskaia, T.; Fink, H.W. Holographic time-resolved particle tracking by means of three-dimensional volumetric deconvolution. Opt. Express 2014, 22, 20994–21003. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.J.; Seo, K.W.; Choi, Y.S.; Sohn, M.H. Three-dimensional motion measurements of free-swimming microorganisms using digital holographic microscopy. Meas. Sci. Technol. 2011, 22, 064004. [Google Scholar] [CrossRef]
- Dimiduk, T.G.; Perry, R.W.; Fung, J.; Manoharan, V.N. Random-subset fitting of digital holograms for fast three-dimensional particle tracking. Appl. Opt. 2014, 53, G177–G183. [Google Scholar] [CrossRef] [PubMed]
- Marquet, P.; Depeursinge, C.; Magistretti, P.J. Exploring Neural Cell Dynamics with Digital Holographic Microscopy. Annu. Rev. Biomed. Eng. 2013, 15, 407–431. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Krenkel, M.; Toepperwien, M.; Alves, F.; Salditt, T. Three-dimensional single-cell imaging with X-ray waveguides in the holographic regime. Acta Crystallogr. Sect. A 2017, 73, 282–292. [Google Scholar] [CrossRef] [Green Version]
- Langehanenberg, P.; Kemper, B.; Dirksen, D.; Bally, G. Autofocusing in digital holographic phase contrast microscopy on pure phase objects for live cell imaging. Appl. Opt. 2008, 47, D176–D182. [Google Scholar] [CrossRef]
- Bartels, M.; Krenkel, M.; Haber, J.; Wilke, R.N.; Salditt, T. X-Ray Holographic Imaging of Hydrated Biological Cells in Solution. Phys. Rev. Lett. 2015, 114, 048103. [Google Scholar] [CrossRef] [Green Version]
- Singh, A.S.G.; Anand, A.; Leitgeb, R.A.; Javidi, B. Lateral shearing digital holographic imaging of small biological specimens. Opt. Express 2012, 20, 23617–23622. [Google Scholar] [CrossRef]
- Chen, C.; Liu, T.; Liu, Y.; Yang, B.; Su, Y. Learning-Based Clutter Mitigation with Subspace Projection and Sparse Representation in Holographic Subsurface Radar Imaging. Remote Sens. 2022, 14, 682. [Google Scholar] [CrossRef]
- Ivashov, S.I.; Capineri, L.; Bechtel, T.D.; Razevig, V.V.; Inagaki, M.; Gueorguiev, N.L.; Kizilay, A. Design and Applications of Multi-Frequency Holographic Subsurface Radar: Review and Case Histories. Remote Sens. 2021, 13, 3487. [Google Scholar] [CrossRef]
- Kreis, T.M. Frequency analysis of digital holography with reconstruction by convolution. Opt. Eng. 2002, 41, 1829–1839. [Google Scholar] [CrossRef]
- Picart, P.; Tankam, P. Analysis and adaptation of convolution algorithms to reconstruct extended objects in digital holography. Appl. Opt. 2013, 52, A240–A253. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, S.; Tan, W.; Chen, S.; Chen, H.; Guo, P.; Sun, Z.; Hu, R.; Xu, Q.; Zhang, M.; et al. Retrieval of Water Cloud Optical and Microphysical Properties from Combined Multiwavelength Lidar and Radar Data. Remote Sens. 2021, 13, 4396. [Google Scholar] [CrossRef]
- Tav, J.; Masson, O.; Burnet, F.; Paulat, P.; Bourrianne, T.; Conil, S.; Pourcelot, L. Determination of fog-droplt deposition velocity fron a simple weighing method. Aerosol Air Qual. Res. 2018, 18, 103–113. [Google Scholar] [CrossRef]
- Wei, M.; Xu, C.; Chen, J.; Zhu, C.; Li, J.; Lv, G. Characteristics of bacterial community in cloud water at Mt Tai: Similarity and disparity under polluted and non-polluted cloud episodes. Atmos. Chem. Phys. 2017, 17, 5253–5270. [Google Scholar] [CrossRef] [Green Version]
- Alfonso, L.; Raga, G.B.; Baumgardner, D. The impact of fluctuations and correlations in droplet growth by collision–coalescence revisited–Part 2: Observational evidence of gel formation in warm clouds. Atmos. Chem. Phys. 2019, 19, 14917–14932. [Google Scholar] [CrossRef] [Green Version]
- La, I.; Yum, S.S.; Gultepe, I.; Yeom, J.M.; Song, J.I.; Cha, J.W. Influence of Quasi-Periodic Oscillation of Atmospheric Variables on Radiation Fog over A Mountainous Region of Korea. Atmosphere 2020, 11, 230. [Google Scholar] [CrossRef] [Green Version]
- Liu, Q.; Wu, B.; Wang, Z.; Hao, T. Fog droplet size distribution and the interaction between fog droplets and fine particles during dense fog in Tianjin, China. Atmosphere 2020, 11, 258. [Google Scholar] [CrossRef] [Green Version]
- Weston, M.; Francis, D.; Nelli, N.; Fonseca, R.; Temimi, M.; Addad, Y. The first characterization of fog microphysics in the United Arab Emirates, an arid region on the Arabian Peninsula. Earth Space Sci. 2022, 9, e2021EA002032. [Google Scholar] [CrossRef]
- Koike, M.; Ukita, J.; Ström, J.; Tunved, P.; Shiobara, M.; Vitale, V.; Lupi, A.; Baumgardner, D.; Ritter, C.; Hermansen, O.; et al. Year-round in situ measurements of Arctic low-level clouds: Microphysical properties and their relationships with aerosols. J. Geophys. Res.-Atmos. 2019, 124, 1798–1822. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.; Zhang, M.; Perrie, W.; Chang, R.; Chen, X.; Duplessis, P.; Wheeler, M. Boundary layer parameterizations to simulate fog over Atlantic Canada waters. Earth Space Sci. 2020, 7, e2019EA000703. [Google Scholar] [CrossRef] [Green Version]











Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, P.; Wang, J.; Gao, Y.; Liu, J.; Hua, D. Observation on the Droplet Ranging from 2 to 16 μm in Cloud Droplet Size Distribution Based on Digital Holography. Remote Sens. 2022, 14, 2414. https://doi.org/10.3390/rs14102414
Gao P, Wang J, Gao Y, Liu J, Hua D. Observation on the Droplet Ranging from 2 to 16 μm in Cloud Droplet Size Distribution Based on Digital Holography. Remote Sensing. 2022; 14(10):2414. https://doi.org/10.3390/rs14102414
Chicago/Turabian StyleGao, Pan, Jun Wang, Yangzi Gao, Jingjing Liu, and Dengxin Hua. 2022. "Observation on the Droplet Ranging from 2 to 16 μm in Cloud Droplet Size Distribution Based on Digital Holography" Remote Sensing 14, no. 10: 2414. https://doi.org/10.3390/rs14102414
APA StyleGao, P., Wang, J., Gao, Y., Liu, J., & Hua, D. (2022). Observation on the Droplet Ranging from 2 to 16 μm in Cloud Droplet Size Distribution Based on Digital Holography. Remote Sensing, 14(10), 2414. https://doi.org/10.3390/rs14102414




