Efficient Shallow Network for River Ice Segmentation
Abstract
:1. Introduction
2. Background
2.1. River Ice Segmentation
2.2. Depthwise Separable Convolution
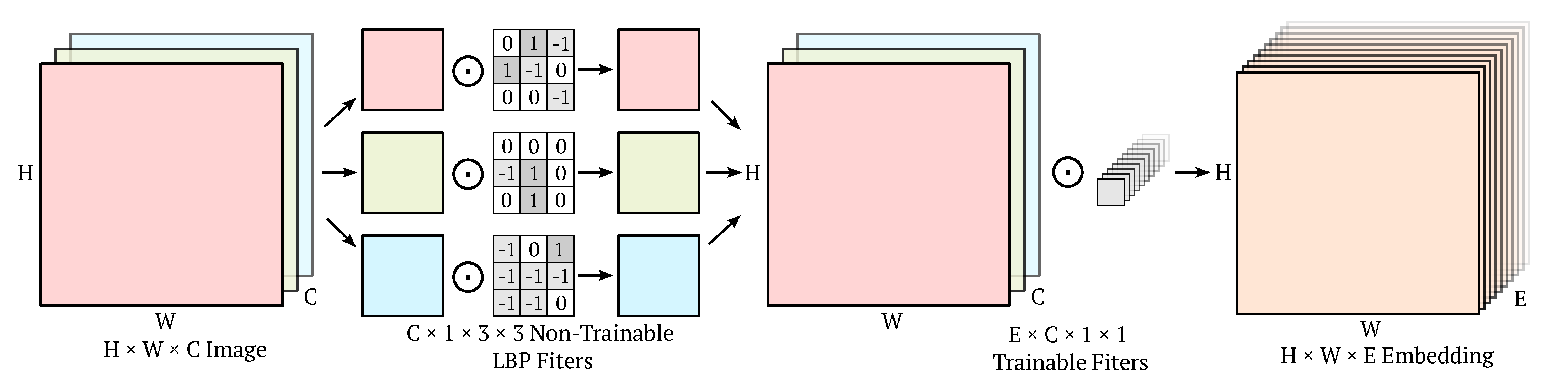
2.3. Local Binary Convolution
2.4. Efficient Networks
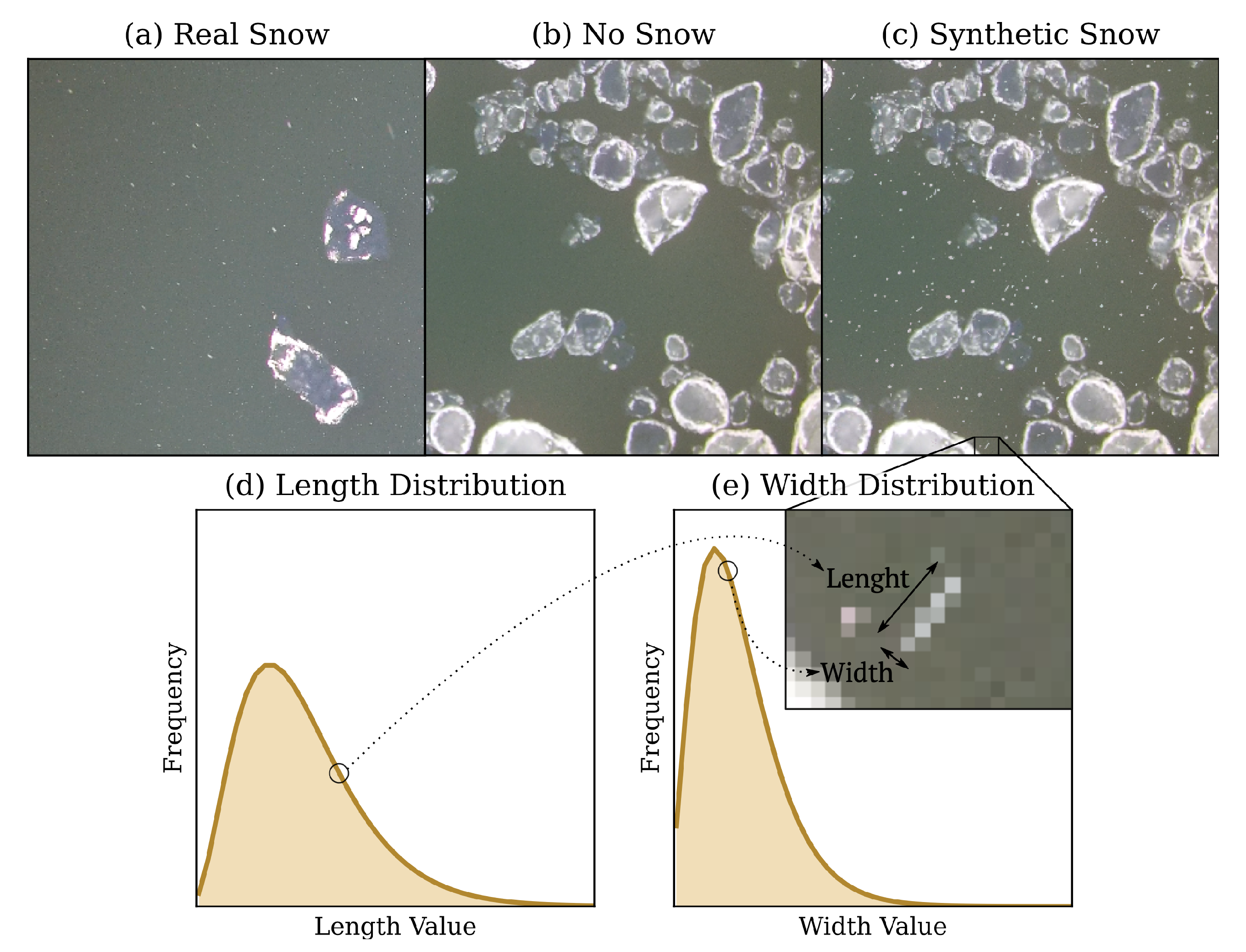
2.5. Dataset
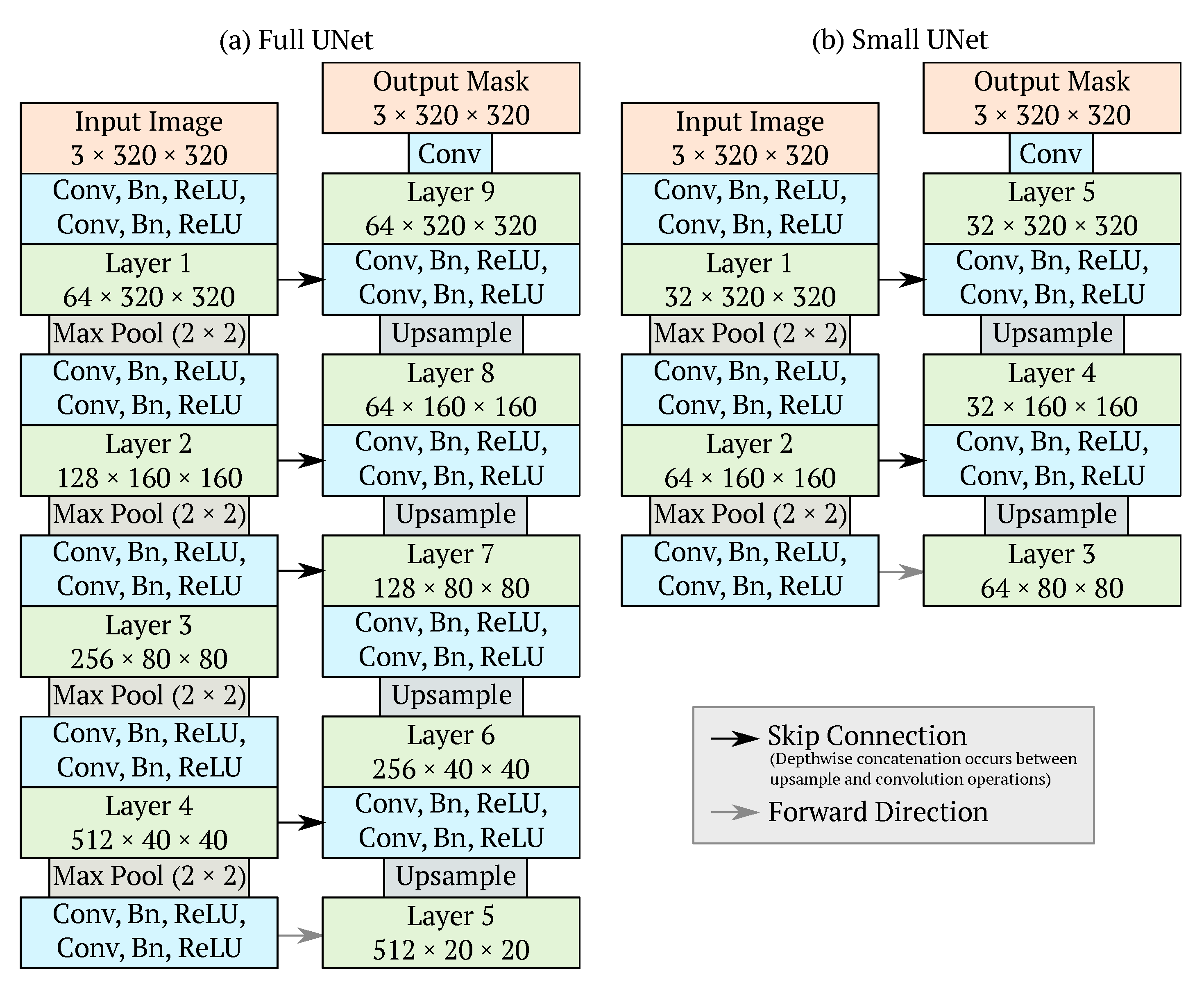
3. Methodology
3.1. Architecture
3.2. Experiments
4. Results and Discussion
4.1. Metrics
- Mean Pixel Accuracy is simply the ratio of correctly classified pixels to total labelled pixels per class, averaged over the total number of classes. For k classes, Mean Pixel Accuracy can be calculated bywhere is the total number of pixels both classified and labelled as class j, and is the total number of pixels labelled as class j.
- Mean Intersect over Union is the ratio of the intersection of the predicted segmentation with the ground truth to the union of the predicted segmentation with the ground truth.where k is the number of classes, is the total number of pixels both classified and labelled as class j, is the number of pixels labelled as class i but classified as class j, and is the total number of pixels labelled as class j but classified as class i.
4.2. Model Comparison
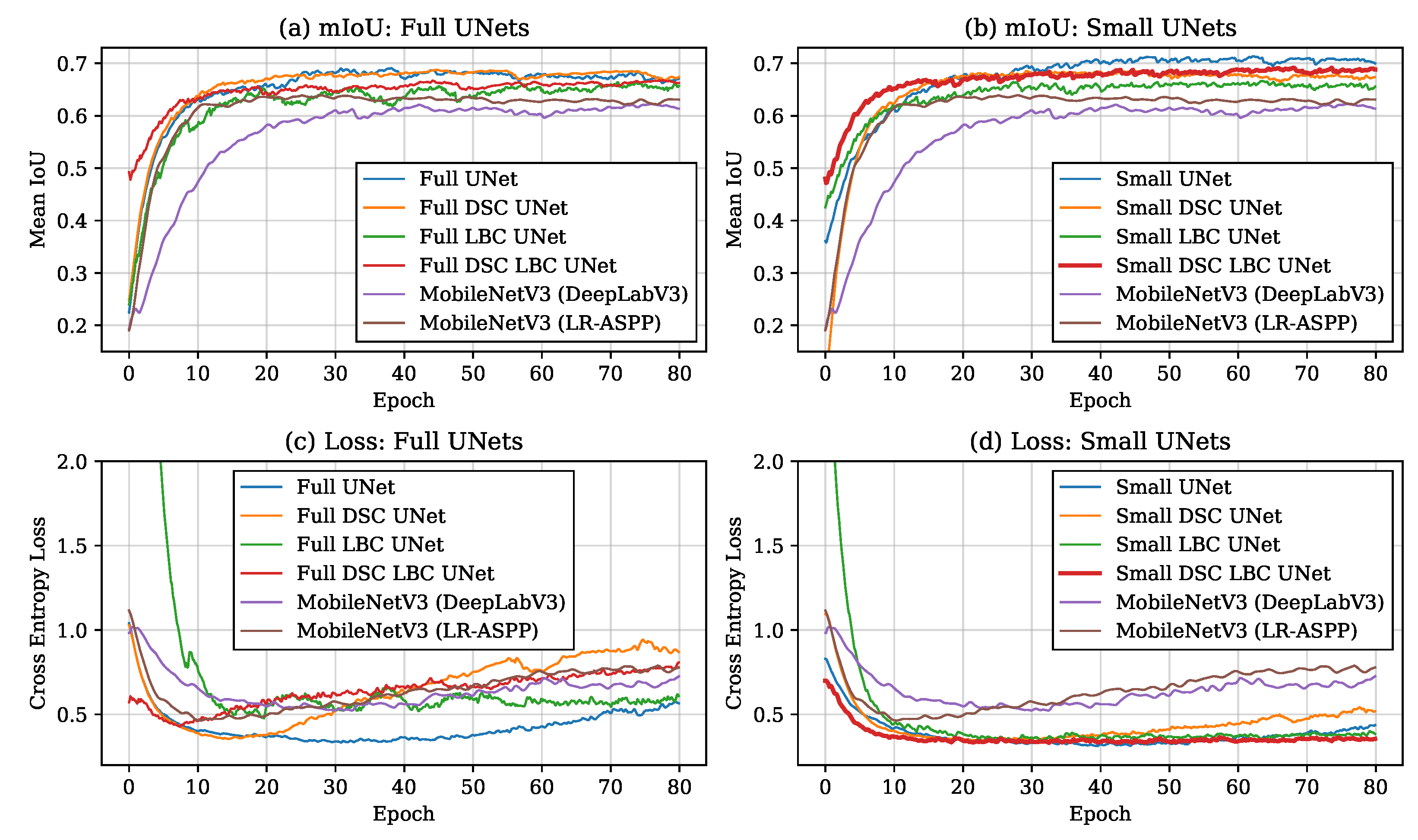
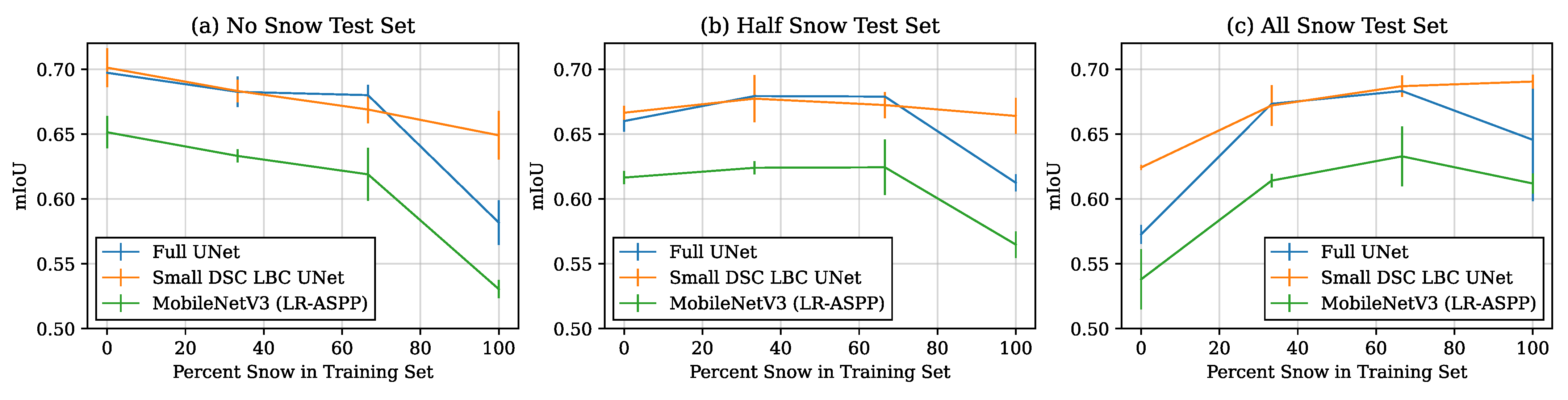
4.3. Training Curves and Generalization Ability
4.4. Performance-Latency Trade-Off
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
Appendix A. Direct Comparison to Previous Work
| Model | Anchor Ice Recall | Frazil Ice Recall | Ice + Water Recall | Ice + Water Recall (fw) |
|---|---|---|---|---|
| Previous UNet [1] | 73.75 | 84.27 | 85.13 | 88.69 |
| Small DSC LBC UNet | 74.18 | 87.28 | 86.84 | 90.57 |
| MobileNetV3 (LR-ASPP) | 77.35 | 80.22 | 84.32 | 86.99 |
| Model | Anchor Ice Precision | Frazil Ice Precision | Ice + Water Precision | Ice + Water Precision (fw) |
| Previous UNet [1] | 54.89 | 71.17 | 73.19 | 81.73 |
| Small DSC LBC UNet | 56.59 | 73.17 | 74.78 | 84.70 |
| MobileNetV3 (LR-ASPP) | 48.50 | 65.82 | 68.29 | 79.54 |
References
- Singh, A.; Kalke, H.; Loewen, M.; Ray, N. River ice segmentation with deep learning. IEEE Trans. Geosci. Remote Sens. 2020, 58, 7570–7579. [Google Scholar] [CrossRef] [Green Version]
- Hicks, F. An Overview of River Ice Problems: CRIPE07 Guest Editorial. Cold Regions Sci. Technol. 2009, 55, 175–185. [Google Scholar] [CrossRef]
- Beltaos, S. Progress in the study and management of river ice jams. Cold Reg. Sci. Technol. 2008, 51, 2–19. [Google Scholar] [CrossRef]
- Kalke, H.; Loewen, M. Support vector machine learning applied to digital images of river ice conditions. Cold Reg. Sci. Technol. 2018, 155, 225–236. [Google Scholar] [CrossRef]
- Peters, D.L.; Prowse, T.D. Regulation effects on the lower Peace River, Canada. Hydrol. Process. 2001, 15, 3181–3194. [Google Scholar] [CrossRef]
- Piesold, K. Fluvial Geomorphology and Sediment Transport Technical Data Report; BC Hydro: Vancouver, BC, Canada, 2011. [Google Scholar]
- Kalke, H.; Loewen, M.; McFarlane, V.; Jasek, M. Observations of anchor ice formation and rafting of sediments. In Proceedings of the 18th Workshop on the Hydraulics of Ice Covered Rivers, Quebec City, QC, Canada, 18–20 August 2015. [Google Scholar]
- Kalke, H.; McFarlane, V.; Schneck, C.; Loewen, M. The transport of sediments by released anchor ice. Cold Reg. Sci. Technol. 2017, 143, 70–80. [Google Scholar] [CrossRef]
- Ansari, S.; Rennie, C.D.; Clark, S.P.; Seidou, O. Application of a Fast Superpixel Segmentation Algorithm in River Ice Classification. In Proceedings of the 20th Workshop on the Hydraulics of Ice Covered Rivers, Ottawa, ON, Canada, 14–16 May 2019. [Google Scholar]
- Zhang, X.; Jin, J.; Lan, Z.; Li, C.; Fan, M.; Wang, Y.; Yu, X.; Zhang, Y. ICENET: A semantic segmentation deep network for river ice by fusing positional and channel-wise attentive features. Remote Sens. 2020, 12, 221. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Zhou, Y.; Jin, J.; Wang, Y.; Fan, M.; Wang, N.; Zhang, Y. ICENETv2: A Fine-Grained River Ice Semantic Segmentation Network Based on UAV Images. Remote Sens. 2021, 13, 633. [Google Scholar] [CrossRef]
- Van Beeck, K.; Tuytelaars, T.; Scarramuza, D.; Goedemé, T. Real-time embedded computer vision on UAVs. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 3–10. [Google Scholar]
- Yang, X.; Chen, J.; Dang, Y.; Luo, H.; Tang, Y.; Liao, C.; Chen, P.; Cheng, K.T. Fast depth prediction and obstacle avoidance on a monocular drone using probabilistic convolutional neural network. IEEE Trans. Intell. Transp. Syst. 2019, 32, 156–167. [Google Scholar] [CrossRef]
- Jiao, Z.; Zhang, Y.; Xin, J.; Mu, L.; Yi, Y.; Liu, H.; Liu, D. A deep learning based forest fire detection approach using UAV and YOLOv3. In Proceedings of the 2019 1st International Conference on Industrial Artificial Intelligence (IAI), Shenyang, China, 22–26 July 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–5. [Google Scholar]
- Yang, Q.; Shi, L.; Han, J.; Yu, J.; Huang, K. A near real-time deep learning approach for detecting rice phenology based on UAV images. Agric. For. Meteorol. 2020, 287, 107938. [Google Scholar] [CrossRef]
- Nagi, A.S.; Kumar, D.; Sola, D.; Scott, K.A. RUF: Effective Sea Ice Floe Segmentation Using End-to-End RES-UNET-CRF with Dual Loss. Remote Sens. 2021, 13, 2460. [Google Scholar] [CrossRef]
- Wagner, P.M.; Hughes, N.; Bourbonnais, P.; Stroeve, J.; Rabenstein, L.; Bhatt, U.; Little, J.; Wiggins, H.; Fleming, A. Sea-ice information and forecast needs for industry maritime stakeholders. Polar Geogr. 2020, 43, 160–187. [Google Scholar] [CrossRef]
- Ansari, S.; Rennie, C.; Seidou, O.; Malenchak, J.; Zare, S. Automated monitoring of river ice processes using shore-based imagery. Cold Reg. Sci. Technol. 2017, 142, 1–16. [Google Scholar] [CrossRef]
- Bharathi, P.; Subashini, P. Texture based color segmentation for infrared river ice images using K-means clustering. In Proceedings of the 2013 International Conference on Signal Processing, Image Processing & Pattern Recognition, Coimbatore, India, 7–8 February 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 298–302. [Google Scholar]
- Kalke, H.; Loewen, M. Predicting surface ice concentration using machine learning. In Proceedings of the 19th Workshop on the Hydraulics of Ice Covered Rivers, Whitehorse, YT, Canada, 9–12 July 2017. [Google Scholar]
- Chen, L.C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-decoder with atrous separable convolution for semantic image segmentation. In Proceedings of the European conference on computer vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 801–818. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Chollet, F. Xception: Deep Learning With Depthwise Separable Convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Zhang, X.; Zhou, X.; Lin, M.; Sun, J. Shufflenet: An extremely efficient convolutional neural network for mobile devices. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 6848–6856. [Google Scholar]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. Mobilenetv2: Inverted residuals and linear bottlenecks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4510–4520. [Google Scholar]
- Howard, A.; Sandler, M.; Chu, G.; Chen, L.C.; Chen, B.; Tan, M.; Wang, W.; Zhu, Y.; Pang, R.; Vasudevan, V.; et al. Searching for mobilenetv3. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27–28 October 2019; pp. 1314–1324. [Google Scholar]
- Juefei-Xu, F.; Naresh Boddeti, V.; Savvides, M. Local binary convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 19–28. [Google Scholar]
- Ojala, T.; Pietikainen, M.; Maenpaa, T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 971–987. [Google Scholar] [CrossRef]
- Ahonen, T.; Hadid, A.; Pietikainen, M. Face description with local binary patterns: Application to face recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 2037–2041. [Google Scholar] [CrossRef] [PubMed]
- Tan, M.; Chen, B.; Pang, R.; Vasudevan, V.; Sandler, M.; Howard, A.; Le, Q.V. Mnasnet: Platform-aware neural architecture search for mobile. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 2820–2828. [Google Scholar]
- Chen, L.C.; Papandreou, G.; Schroff, F.; Adam, H. Rethinking atrous convolution for semantic image segmentation. arXiv 2017, arXiv:1706.05587. [Google Scholar]
- Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 834–848. [Google Scholar] [CrossRef] [Green Version]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar]
- Paszke, A.; Chaurasia, A.; Kim, S.; Culurciello, E. Enet: A deep neural network architecture for real-time semantic segmentation. arXiv 2016, arXiv:1606.02147. [Google Scholar]
- Yu, C.; Wang, J.; Peng, C.; Gao, C.; Yu, G.; Sang, N. Bisenet: Bilateral segmentation network for real-time semantic segmentation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 325–341. [Google Scholar]
- Li, H.; Xiong, P.; Fan, H.; Sun, J. Dfanet: Deep feature aggregation for real-time semantic segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–17 June 2019; pp. 9522–9531. [Google Scholar]
- Chen, W.; Gong, X.; Liu, X.; Zhang, Q.; Li, Y.; Wang, Z. Fasterseg: Searching for faster real-time semantic segmentation. arXiv 2019, arXiv:1912.10917. [Google Scholar]
- Jacob, B.; Kligys, S.; Chen, B.; Zhu, M.; Tang, M.; Howard, A.; Adam, H.; Kalenichenko, D. Quantization and training of neural networks for efficient integer-arithmetic-only inference. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2704–2713. [Google Scholar]
- Krishnamoorthi, R. Quantizing deep convolutional networks for efficient inference: A whitepaper. arXiv 2018, arXiv:1806.08342. [Google Scholar]
- Frankle, J.; Carbin, M. The lottery ticket hypothesis: Finding sparse, trainable neural networks. arXiv 2018, arXiv:1803.03635. [Google Scholar]
- Hinton, G.; Vinyals, O.; Dean, J. Distilling the knowledge in a neural network. arXiv 2015, arXiv:1503.02531. [Google Scholar]
- Singh, A.; Kalke, H.; Loewen, M.; Ray, N. Alberta River Ice Segmentation Dataset; IEEE Dataport: New York, NY, USA, 2019. [Google Scholar] [CrossRef]
- Schindler, A.; Lidy, T.; Rauber, A. Comparing Shallow versus Deep Neural Network Architectures for Automatic Music Genre Classification. In Proceedings of the FMT, St. Polten, Austria, 23–24 November 2016; pp. 17–21. [Google Scholar]
- Pasupa, K.; Sunhem, W. A comparison between shallow and deep architecture classifiers on small dataset. In Proceedings of the 2016 8th International Conference on Information Technology and Electrical Engineering (ICITEE), Yogyakarta, Indonesia, 5–6 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–6. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. Pytorch: An imperative style, high-performance deep learning library. Adv. Neural Inf. Process. Syst. 2019, 32, 8026–8037. [Google Scholar]
- Tieleman, T.; Hinton, G. Divide the gradient by a running average of its recent magnitude. COURSERA Neural Netw. Mach. Learn. 2012, 42, 26–31. [Google Scholar]
- Bradski, G. Dr. Dobb’s Journal of Software Tools; The OpenCV Library’: Hilton Head, SC, USA, 2000. [Google Scholar]
- Krähenbühl, P.; Koltun, V. Efficient inference in fully connected crfs with gaussian edge potentials. In Advances in Neural Information Processing Systems 24 (NIPS 2011), Proceedings of the 24th International Conference on Neural Information Processing Systems, Red Hook, NY, USA, 12–15 December 2011; Curran Associates Inc.: Red Hook, NY, USA, 2011; pp. 109–117. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Singh, A. River_ice_segmentation. In GitHub Repository; GitHub: San Francisco, CA, USA, 2021. [Google Scholar]

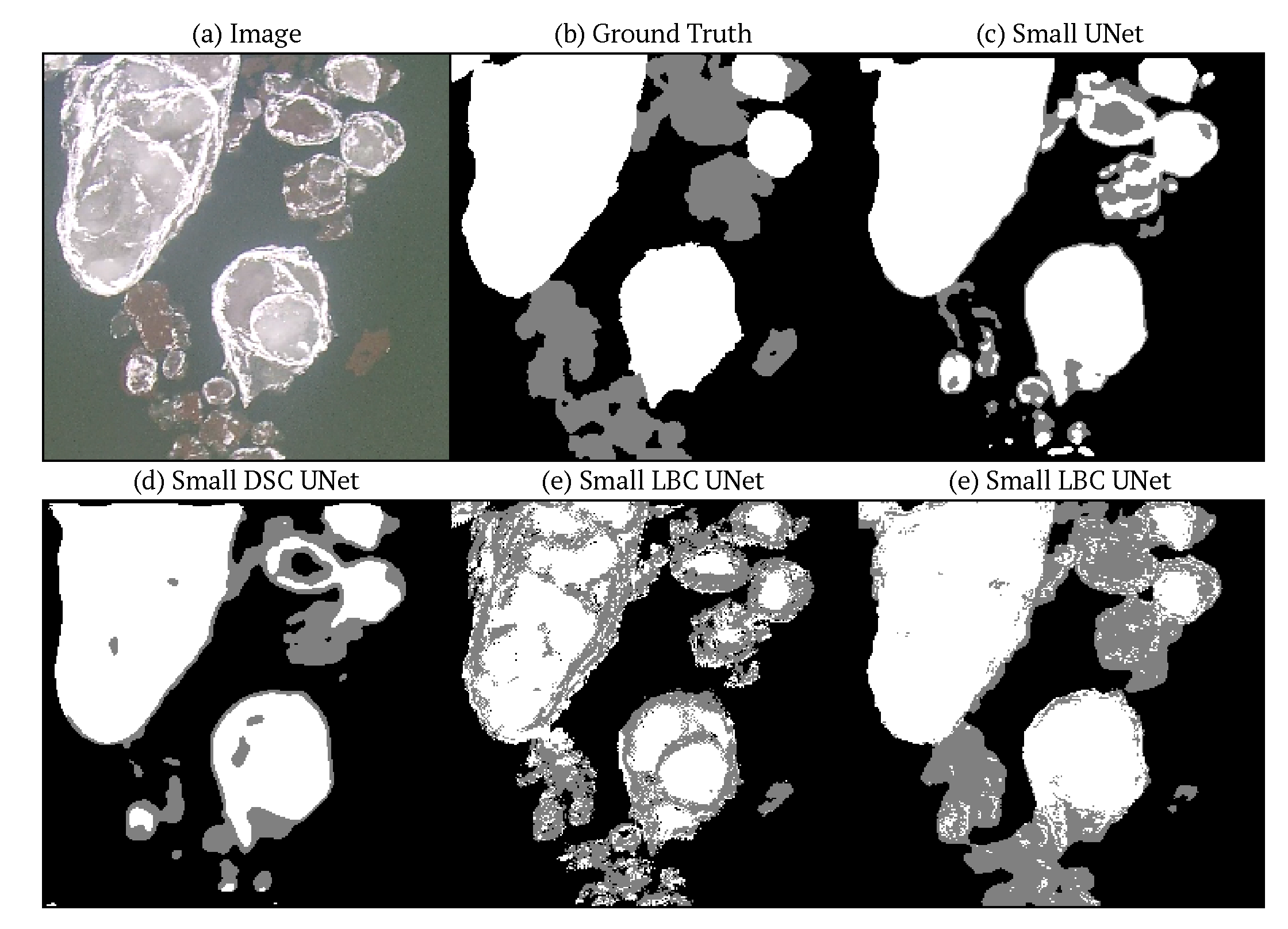
| Model | mIoU | mPA | Total Params | Trainable Params | Mult-Adds | Memory |
|---|---|---|---|---|---|---|
| Full UNet | 69.7 | 82.7 | 17,267,523 | 17,267,523 | 62,764 M | 1542 MB |
| Full DSC UNet | 69.7 | 82.9 | 1,983,713 | 1,983,713 | 7717 M | 2242 MB |
| Full LBC UNet | 67.7 | 82.2 | 16,498,842 | 794,697 | 71,048 M | 1164 MB |
| Full DSC LBC UNet | 69.1 | 82.7 | 821,220 | 794,697 | 3402 M | 1104 MB |
| Small UNet | 71.2 | 85.0 | 260,451 | 260,451 | 8237 M | 622 MB |
| Small DSC UNet | 70.4 | 84.3 | 35,777 | 35,777 | 1123 M | 936 MB |
| Small LBC UNet | 69.7 | 83.8 | 253,050 | 13,353 | 9479 M | 468 MB |
| Small DSC LBC UNet | 70.1 | 83.5 | 16,260 | 13,353 | 637 M | 466 MB |
| MobileNetV3 (DeepLabV3) | 63.7 | 78.5 | 11,020,851 | 11,020,851 | 3898 M | 589 MB |
| MobileNetV3 (LR-ASPP) | 65.1 | 80.0 | 3,218,478 | 3,218,478 | 826 M | 307 MB |
| Model | mIoU | mPA |
|---|---|---|
| Full UNet | 58.1 | 71.0 |
| Full DSC UNet | 57.6 | 72.0 |
| Full LBC UNet | 56.5 | 70.5 |
| Full DSC LBC UNet | 62.9 | 76.8 |
| Small UNet | 58.9 | 71.0 |
| Small DSC UNet | 59.1 | 71.1 |
| Small LBC UNet | 57.0 | 71.7 |
| Small DSC LBC UNet | 62.4 | 76.1 |
| MobileNetV3 (DeepLabV3) | 49.7 | 62.3 |
| MobileNetV3 (LR-ASPP) | 53.0 | 62.8 |
| Model | GPU Train (FPS) | GPU Inference (FPS) | CPU Train (FPS) | CPU Inference (FPS) |
|---|---|---|---|---|
| Full UNet | 10.59 | 21.69 | 0.72 | 1.29 |
| Full DSC UNet | 10.25 | 21.79 | 1.36 | 2.30 |
| Full LBC UNet | 11.17 | 21.83 | 0.92 | 1.18 |
| Full DSC LBC UNet | 16.07 | 21.98 | 2.23 | 2.99 |
| Small UNet | 18.82 | 21.88 | 3.21 | 4.83 |
| Small DSC UNet | 18.00 | 21.93 | 3.71 | 5.62 |
| Small LBC UNet | 19.35 | 22.07 | 3.94 | 4.69 |
| Small DSC LBC UNet | 19.57 | 22.47 | 5.78 | 6.54 |
| MobileNetV3 (DeepLabV3) | 13.27 | 20.88 | 3.27 | 8.00 |
| MobileNetV3 (LR-ASPP) | 15.54 | 21.19 | 6.32 | 12.35 |
| mIoU Threshold | Small DSC LBC UNet Time | MobileNetV3 (LR-ASPP) Time |
|---|---|---|
| 48 | 2.16 s | 18.05 s |
| 52 | 15.57 s | 24.70 s |
| 56 | 20.24 s | 31.83 s |
| 60 | 27.51 s | 43.70 s |
| 64 | 43.08 s | 481.17 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sola, D.; Scott, K.A. Efficient Shallow Network for River Ice Segmentation. Remote Sens. 2022, 14, 2378. https://doi.org/10.3390/rs14102378
Sola D, Scott KA. Efficient Shallow Network for River Ice Segmentation. Remote Sensing. 2022; 14(10):2378. https://doi.org/10.3390/rs14102378
Chicago/Turabian StyleSola, Daniel, and K. Andrea Scott. 2022. "Efficient Shallow Network for River Ice Segmentation" Remote Sensing 14, no. 10: 2378. https://doi.org/10.3390/rs14102378
APA StyleSola, D., & Scott, K. A. (2022). Efficient Shallow Network for River Ice Segmentation. Remote Sensing, 14(10), 2378. https://doi.org/10.3390/rs14102378






