Non-Uniform Synthetic Aperture Radiometer Image Reconstruction Based on Deep Convolutional Neural Network
Abstract
:1. Introduction
- The G-matrix method measures the G-matrix of the system response, and then uses the measured G-matrix to reconstruct the brightness temperature image of the measured data by using the regularization algorithm. There are many very small singular values in the G-matrix of the impulse response of a non-uniform sampling synthetic aperture radiometer system. These small singular values are caused by the non-uniform arrangement of element antennas. When the G-matrix reconstruction method is used for image reconstruction, a stable solution cannot be obtained.
- Based on the ideal situation, the FFT method can meet the Fourier transformation relationship between the visibility function and the brightness temperature image. Through the measured visibility function, the anti-Fourier transform is transformed and rebuilds the brightness temperature image. Although a stable solution can be obtained by using the FFT method, the FFT method requires that the sampling points in the frequency domain are evenly distributed, while the sampling points of the non-uniform sampling synthetic aperture radiometer on the UV plane are non-uniform, which will introduce large errors into the inversion image.
2. Related Works
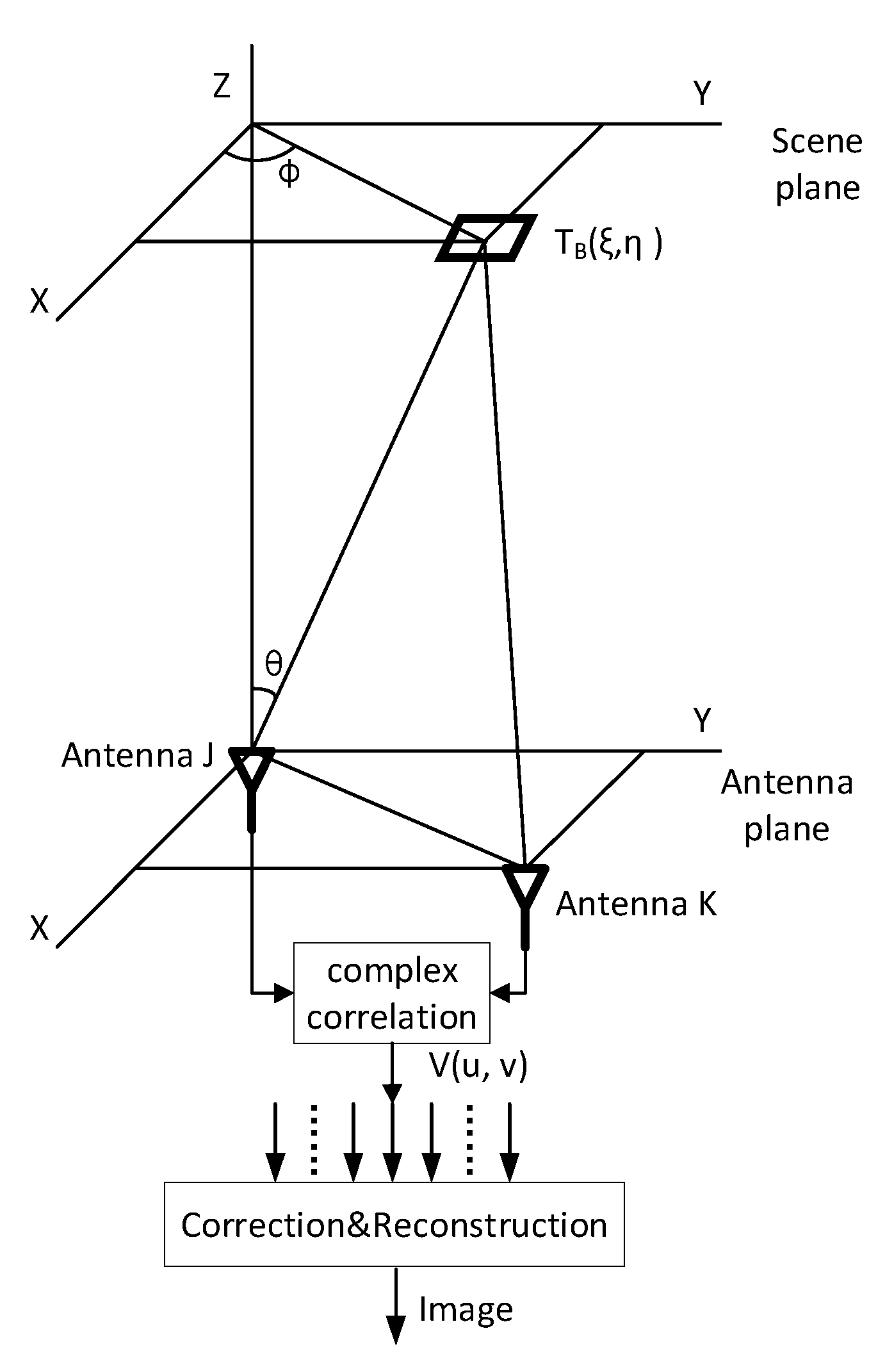
2.1. Non-Uniform Synthetic Aperture Radiometer Model
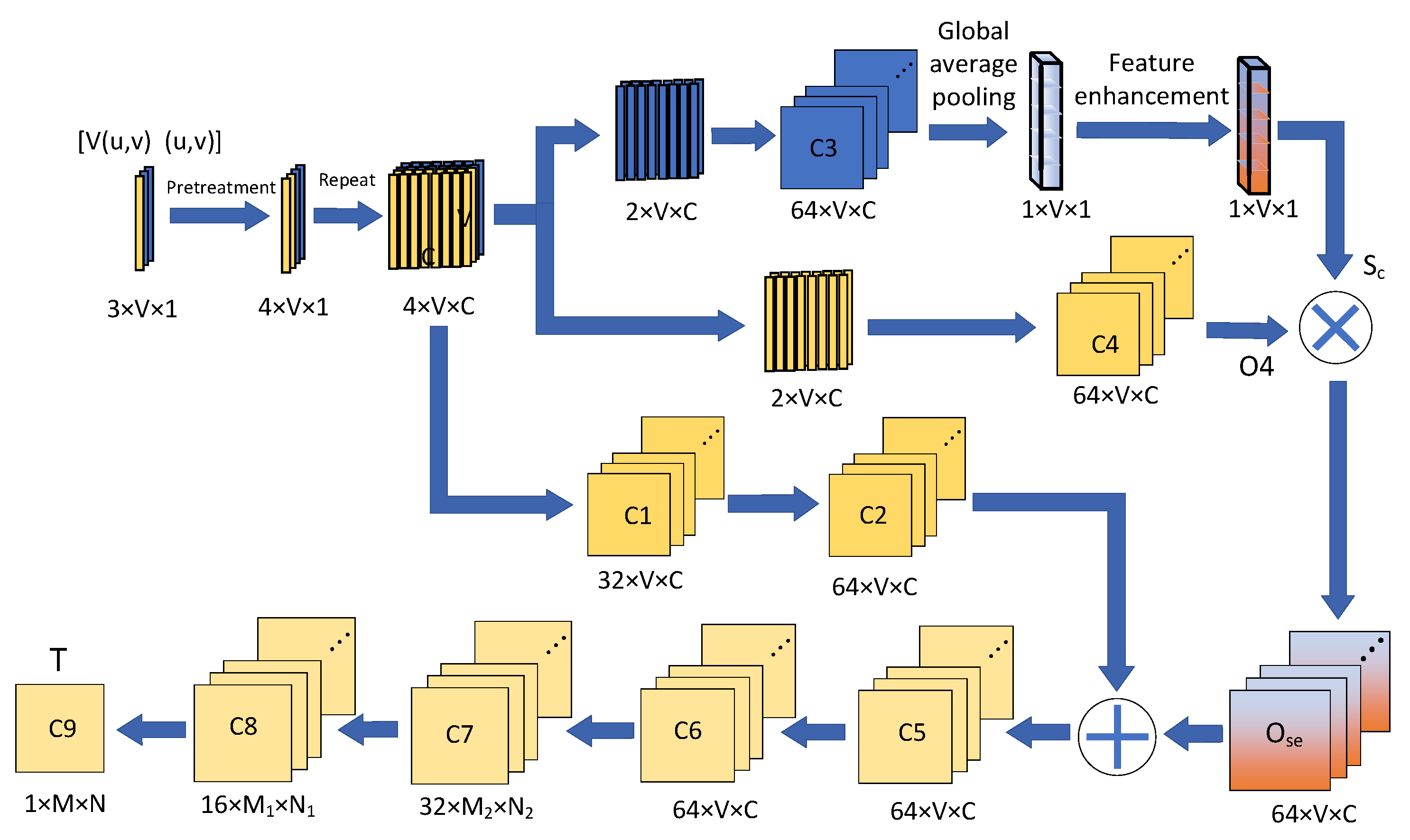
2.2. Definition of the Related Neural Network
3. Dataset and Learning for ISAR-CNN
3.1. Dataset Generation
- From the UC Merced (UCM) dataset (created by researchers at the University of California, Merced, CA, USA) of 21 different categories of remote sensing images, an image was selected and converted to grayscale. In order to correspond to the scale of the conventional microwave brightness temperature image, we mapped the scale of the image from 0–255 to 2.7–300 (in the practical application of Earth remote sensing, the scene brightness temperature is mostly distributed between 2.7 K and 300 K, and the simulated scene covers the dynamic range of the whole scene brightness temperature distribution). Then, we used this image as the original scene brightness temperature image ().
- is then input into the ideal non-uniform synthetic aperture radiometer simulation program to generate the simulated non-uniform synthetic aperture radiometer visibilities function and its corresponding UV plane coordinates . In the non-uniform synthetic aperture radiometer simulation program, the antenna array is set to a randomly distributed 51-element antenna array, and the antenna array is shown in Figure 2 (the X-axes and Y-axes represent the relative position of the antenna distribution, and the unit is the multiple of the wavelength). The receiving frequency was set to 33.5 GHz.
- (size of 1 269) and (size of 1 269) were combined as one input data , with a size of 3 269.
- and (size of 79 79) were combined as one sample.
- After each image in the UCM dataset undergoes steps 1–4, we can obtain multiple samples to form dataset ().
- Randomly select 90% of the data from dataset () as the training dataset (), and the remaining 10% of the data from dataset () is then used for network testing as the testing dataset ()
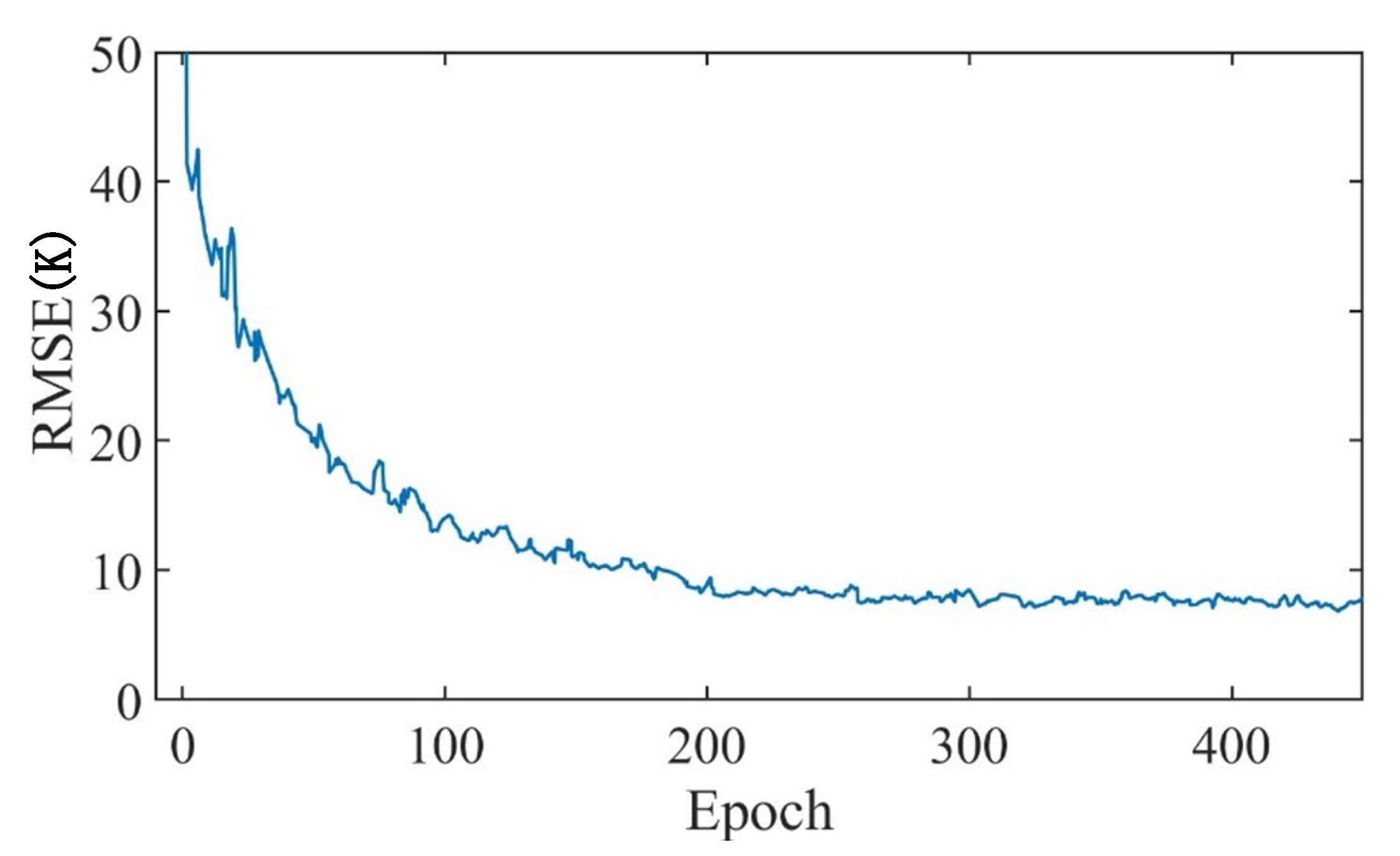
3.2. Learning for IASR-CNN
4. Experiments and Result Analysis
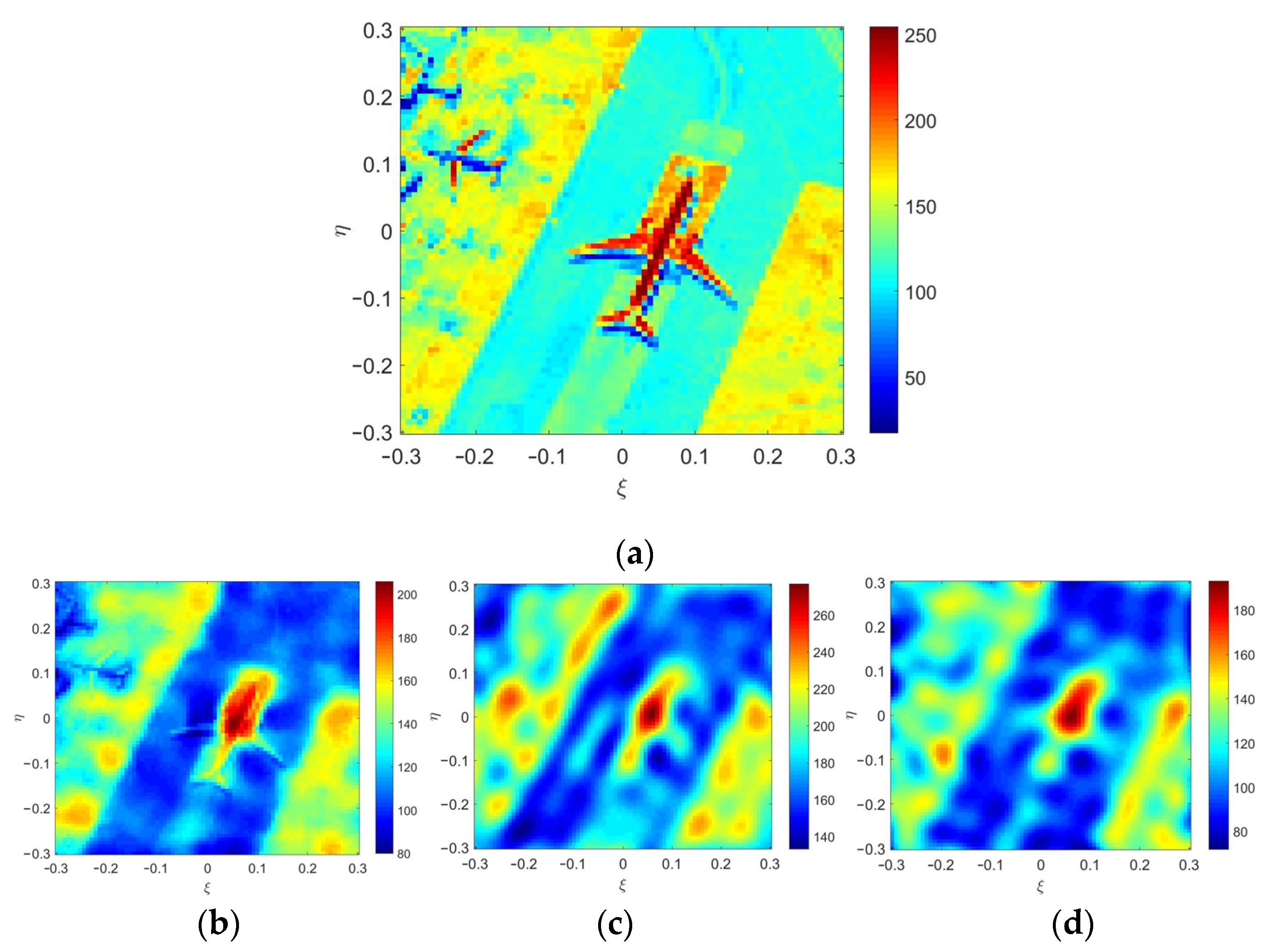
4.1. Ideal Simulation Results
4.2. Simulation Results with Errors
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.; Delwart, S.; Cabot, F.; Boutin, J.; Escorihuela, M.; Font, J.; Reul, N.; Gruhier, C.; et al. The SMOS mission: New tool for monitoring key elements of the global water cycle. Proc. IEEE 2010, 98, 666–687. [Google Scholar] [CrossRef] [Green Version]
- Shao, X.; Junor, W.; Zenick, R.; Rogers, A.; Dighe, K. Passive interferometric millimeter-wave imaging: Achieving big results with a constellation of small satellites. Proc. SPIE 2004, 5410, 270–277. [Google Scholar]
- Corbella, I.; Torres, F.; Camps, A.; Duffo, N.; all-Llossera, M.V. Brightness-temperature retrieval methods in synthetic aperture radiometers. IEEE Trans. Geosci. Remote Sens. 2009, 47, 285–294. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, H.; Wu, J.; He, J.; Zhang, C. Statistical analysis for performance of detection and imaging of dynamic targets using the geostationary interferometric microwave sounder. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2018, 11, 3–11. [Google Scholar] [CrossRef]
- Feng, L.; Li, Q.; Chen, K.; Li, Y.; Tong, X.; Wang, X.; Lu, H.; Li, Y. The gridding method for image reconstruction of nonuniform aperture synthesis radiometers. IEEE Geosci. Remote Sens. Lett. 2015, 12, 274–278. [Google Scholar] [CrossRef]
- Feng, L.; Wu, M.; Li, Q.; Chen, K.; Li, Y.; He, Z.; Tong, J.; Tu, L.; Xie, H.; Lu, H. Array factor forming for image reconstruction of one-dimensional nonuniform aperture synthesis radiometers. IEEE Geosci. Remote Sens. Lett. 2016, 13, 237–241. [Google Scholar] [CrossRef]
- Chen, L.; Ma, W.; Wang, Y.; Zhou, H. Array Factor Forming with Regularization for Aperture Synthesis Radiometric Imaging with an Irregularly Distributed Array. IEEE Geosci. Remote Sens. Lett. 2020, 17, 97–101. [Google Scholar] [CrossRef]
- Fessler, J.A.; Sutton, B.P. Nonuniform fast Fourier transforms using min–max interpolation. IEEE Trans. Signal Process. 2003, 51, 560–574. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Qi, X.; Jiang, Y.; Liao, W.; Du, Y. Reconstruction algorithm for staggered synthetic aperture radar with modified second-order keystone transform. J. Appl. Remote Sens. 2021, 15, 026511. [Google Scholar] [CrossRef]
- Mukherjee, S.; Zimmer, A.; Kottayil, N.K.; Sun, X.; Ghuman, P.; Cheng, I. CNN-based InSAR Denoising and Coherence Metric. In Proceedings of the 2018 IEEE SENSORS, New Delhi, India, 28–31 October 2018. [Google Scholar]
- Xiao, C.; Li, Q.; Lei, Z.; Zhao, G.; Chen, Z.; Huang, Y. Image Reconstruction with Deep CNN for Mirrored Aperture Synthesis. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5303411. [Google Scholar] [CrossRef]
- Dou, H.; Gui, L.; Li, Q.; Chen, L.; Bi, X.; Wu, Y.; Lei, Z.; Li, Y.; Chen, K.; Lang, L.; et al. Initial Results of Microwave Radiometric Imaging with Mirrored Aperture Synthesis. IEEE Trans. Geosci. Remote Sens. 2019, 55, 8105–8117. [Google Scholar] [CrossRef]
- Oveis, A.H.; Guisti, E.; Ghio, S.; Martorella, M. A Survey on the Applications of Convolutional Neural Networks for Synthetic Aperture Radar: Recent Advances. IEEE Aerosp. Electron. Syst. Mag. 2022, 37, 18–42. [Google Scholar] [CrossRef]
- Thompson, A.R.; Moran, J.M.; Swenson, G.W. Interferometry and Synthesis in Radio Astronomy, 2nd ed.; Wiley: Weinheim, Germany, 2001. [Google Scholar]
- Lin, T.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal loss for dense object detection. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 99, 2999–3007. [Google Scholar]
- Butora, R.; Camps, A. Noise maps in aperture synthesis radiometric images due to cross-correlation of visibility noise. Radio Sci. 2003, 38, 1067–1074. [Google Scholar] [CrossRef]
- Xu, X.; Li, W.; Ran, Q.; Du, Q.; Gao, L.; Zhang, B. Multisource Remote Sensing Data Classification Based on Convolutional Neural Network. IEEE Trans. Geosci. Remote Sens. 2018, 56, 937–949. [Google Scholar] [CrossRef]
- Zhu, B.; Liu, J.Z.; Cauley, S.F.; Rosen, B.R.; Rosen, M.S. Image reconstruction by domain-transform manifold learning. Nature 2018, 555, 487–492. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Y.; Ren, Y.; Miao, W.; Lin, Z.; Gao, H.; Shi, S. Microwave SAIR Imaging Approach Based on Deep Convolutional Neural Network. IEEE Trans. Geosci. Remote Sens. 2019, 57, 10376–10389. [Google Scholar] [CrossRef]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L. MobileNetV2: Inverted Residuals and Linear Bottlenecks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 4510–4520. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G.; Albanie, S. Squeeze-and-Excitation Networks. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Hyun, C.M.; Kim, H.P.; Lee, S.M.; Lee, S.; Seo, J.K. Deep learning for undersampled MRI reconstruction. Phys. Med. Biol. 2018, 63, 135007. [Google Scholar] [CrossRef]





| Method | RMSE (K) | PSNR (dB) |
|---|---|---|
| IASR–CNN method | 9.4718 | 24.6375 |
| Grid method | 15.3268 | 20.6268 |
| AFF method | 14.8785 | 21.8099 |
| Method | RMSE |
|---|---|
| IASR–CNN method | 1.35 × 10−4 |
| Grid method | 2.21 × 10−4 |
| AFF method | 1.76 × 10−4 |
| Method | Time (s) |
|---|---|
| IASR–CNN method | 0.016 |
| Grid method | 0.19 |
| AFF method | 0.85 |
| Variable Noise Intensities | 50% | 60% | 70% | 80% | 90% |
|---|---|---|---|---|---|
| 0 | 9.8924 | 9.7922 | 9.7757 | 9.6031 | 9.5327 |
| 0.1 | 10.7056 | 10.6691 | 10.5176 | 10.3349 | 10.2615 |
| 0.2 | 12.8341 | 12.7241 | 12.2785 | 12.0975 | 11.9740 |
| 0.3 | 15.3358 | 15.1270 | 14.9058 | 14.5469 | 14.1078 |
| Variable Noise Intensities | 50% | 60% | 70% | 80% | 90% |
|---|---|---|---|---|---|
| 0 | 23.9786 | 24.0357 | 24.2759 | 24.3040 | 24.3436 |
| 0.1 | 23.1031 | 23.2295 | 23.3485 | 23.4191 | 23.5625 |
| 0.2 | 22.0849 | 22.5657 | 22.6787 | 22.8003 | 22.9299 |
| 0.3 | 20.3953 | 20.8124 | 21.1419 | 21.3134 | 22.0037 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, C.; Wang, X.; Dou, H.; Li, H.; Lv, R.; Wu, Y.; Song, G.; Wang, W.; Zhai, R. Non-Uniform Synthetic Aperture Radiometer Image Reconstruction Based on Deep Convolutional Neural Network. Remote Sens. 2022, 14, 2359. https://doi.org/10.3390/rs14102359
Xiao C, Wang X, Dou H, Li H, Lv R, Wu Y, Song G, Wang W, Zhai R. Non-Uniform Synthetic Aperture Radiometer Image Reconstruction Based on Deep Convolutional Neural Network. Remote Sensing. 2022; 14(10):2359. https://doi.org/10.3390/rs14102359
Chicago/Turabian StyleXiao, Chengwang, Xi Wang, Haofeng Dou, Hao Li, Rongchuan Lv, Yuanchao Wu, Guangnan Song, Wenjin Wang, and Ren Zhai. 2022. "Non-Uniform Synthetic Aperture Radiometer Image Reconstruction Based on Deep Convolutional Neural Network" Remote Sensing 14, no. 10: 2359. https://doi.org/10.3390/rs14102359
APA StyleXiao, C., Wang, X., Dou, H., Li, H., Lv, R., Wu, Y., Song, G., Wang, W., & Zhai, R. (2022). Non-Uniform Synthetic Aperture Radiometer Image Reconstruction Based on Deep Convolutional Neural Network. Remote Sensing, 14(10), 2359. https://doi.org/10.3390/rs14102359






