Parameter Estimation for Sea Clutter Pareto Distribution Model Based on Variable Interval
Abstract
:1. Introduction
2. Method
2.1. The PDF of the GP Distribution
2.2. The MoM of GP Distribution
2.3. BiP Parameter Estimation
2.4. Truncated Moment Estimation
2.5. The VIE Method
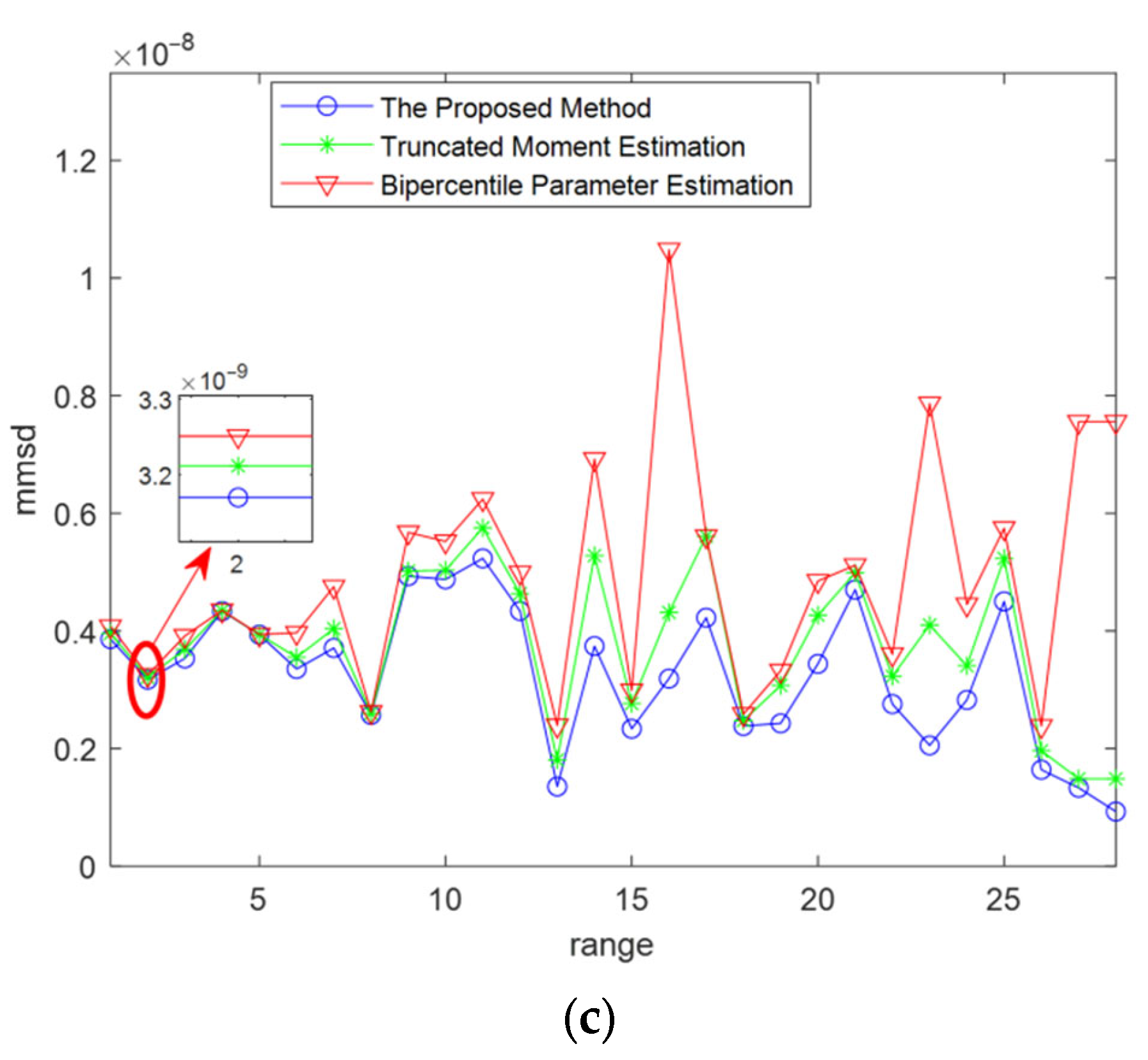
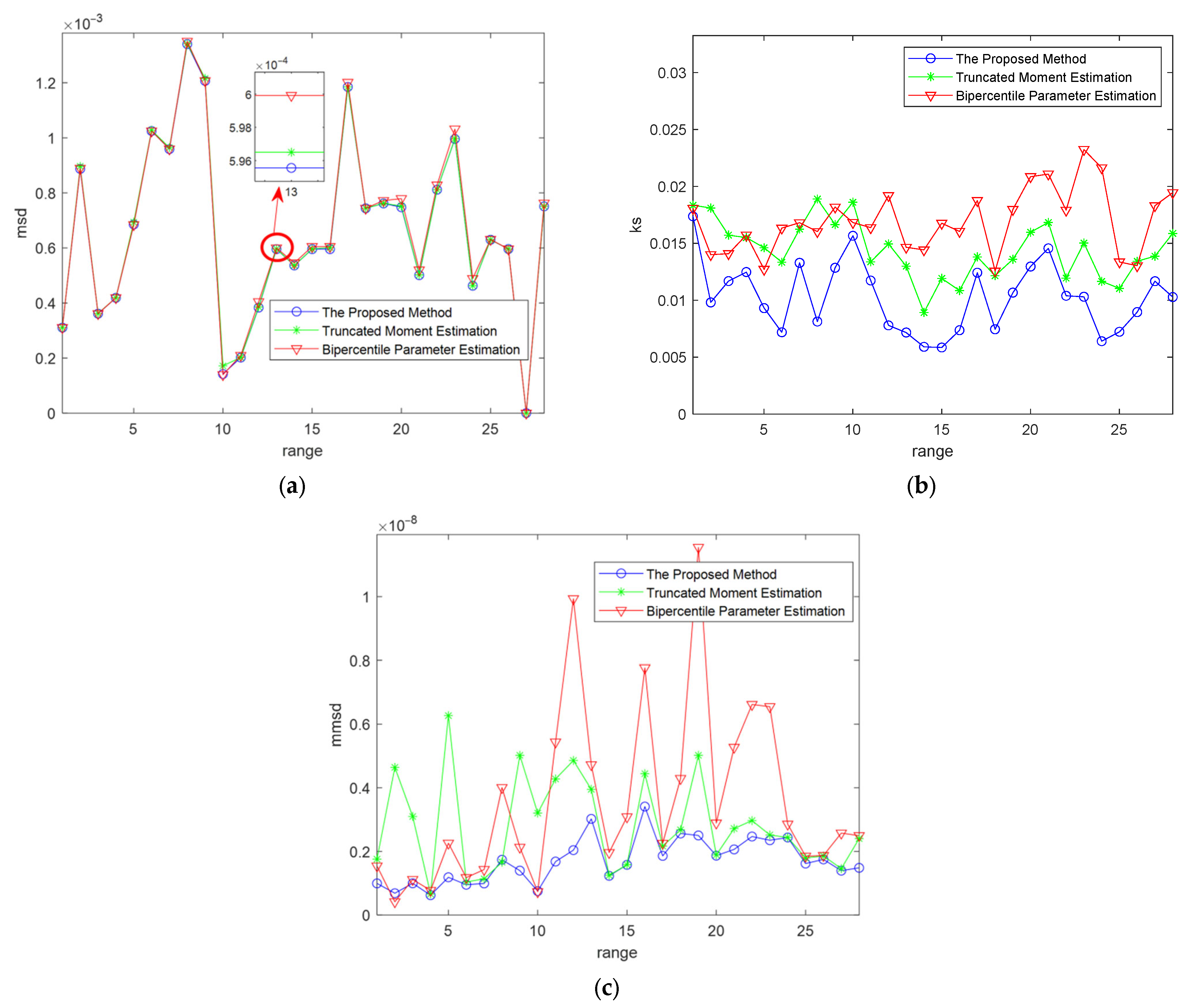
2.6. Histogram Statistics and GOF Test
- (1)
- The calculation of MSD is defined as:where represents the frequency of sea clutter sequence in histogram, represents the PDF of fit model, k represents the sequence number of the sea clutter sequence, N represents the length of sea clutter sequence.
- (2)
- The calculation of K-S distance is defined as:where KSD represents the K-S distance, represents the CDF of the fit model, and represents the empirical CDF of the sample sequence.
- (3)
- The calculation of MMSD is defined as:where the definition of and are same as MSD, represents the sample aggregation of tail. If the smallest is the detection threshold, the function is CFAR detection, is the false alarm probability.
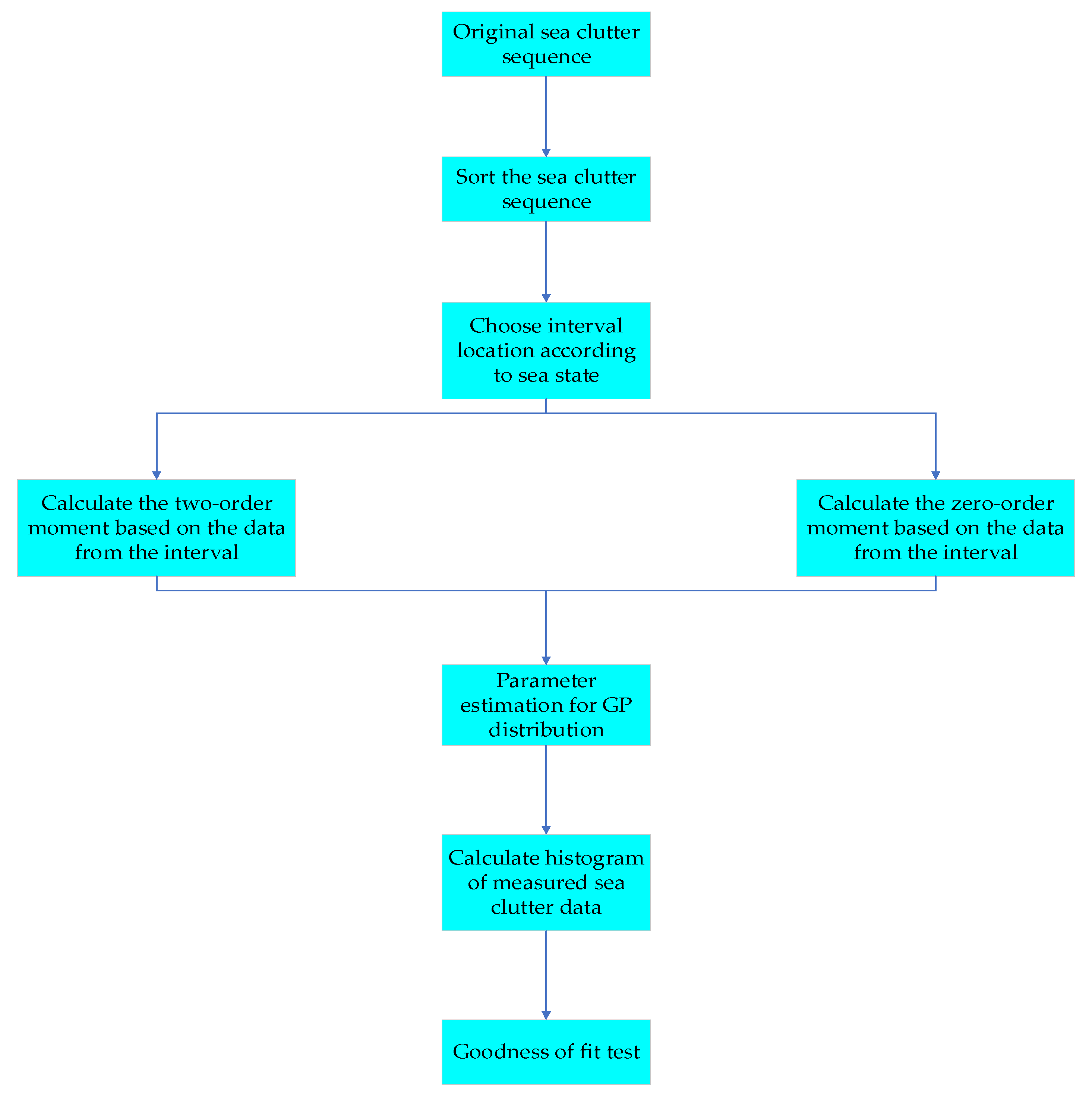
- Step 1: Radar echo acquisition and preprocessing. Sort the original sea clutter time sequence according to the criterion from smallest to largest and obtain the sorted sea clutter sequence .
- Step 2: Variable interval location selection. Select the sea clutter data form the sorted sea clutter sequence based on the sea state.
- Step 3: Parameter estimation for GP distribution. Calculate the one-order and two-order moments based on the data from interval and estimate the parameters of GP distribution through simultaneous equations.
- Step 4: Goodness of fit test. Calculate the fit errors between the histogram of measured sea clutter data and the fit model based on the MSD, K-S distance and MMSD algorithm.
3. Results and Discussion
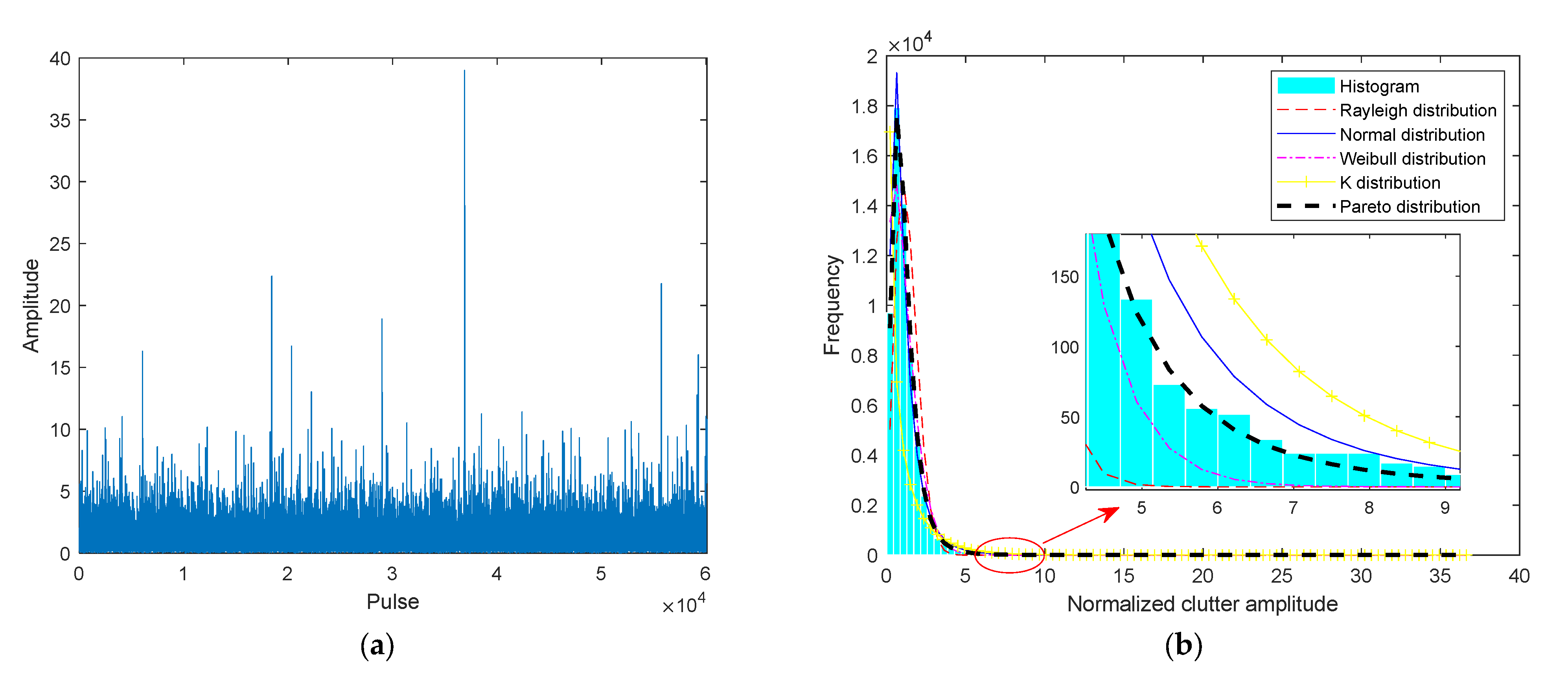
3.1. Real Sea Clutter Datasets Introduction
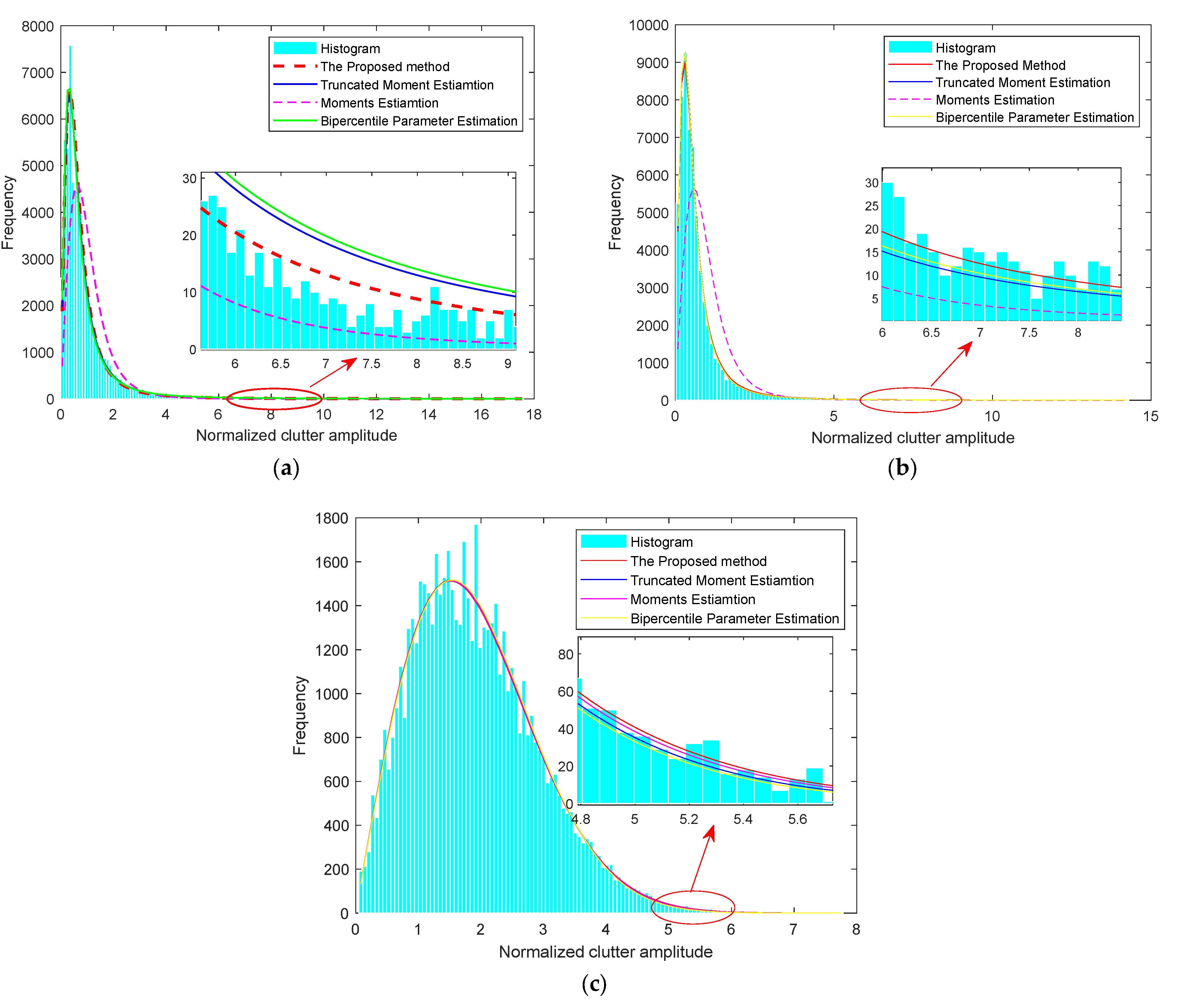
3.2. Parameter Estimation Analysis of Statistical Model
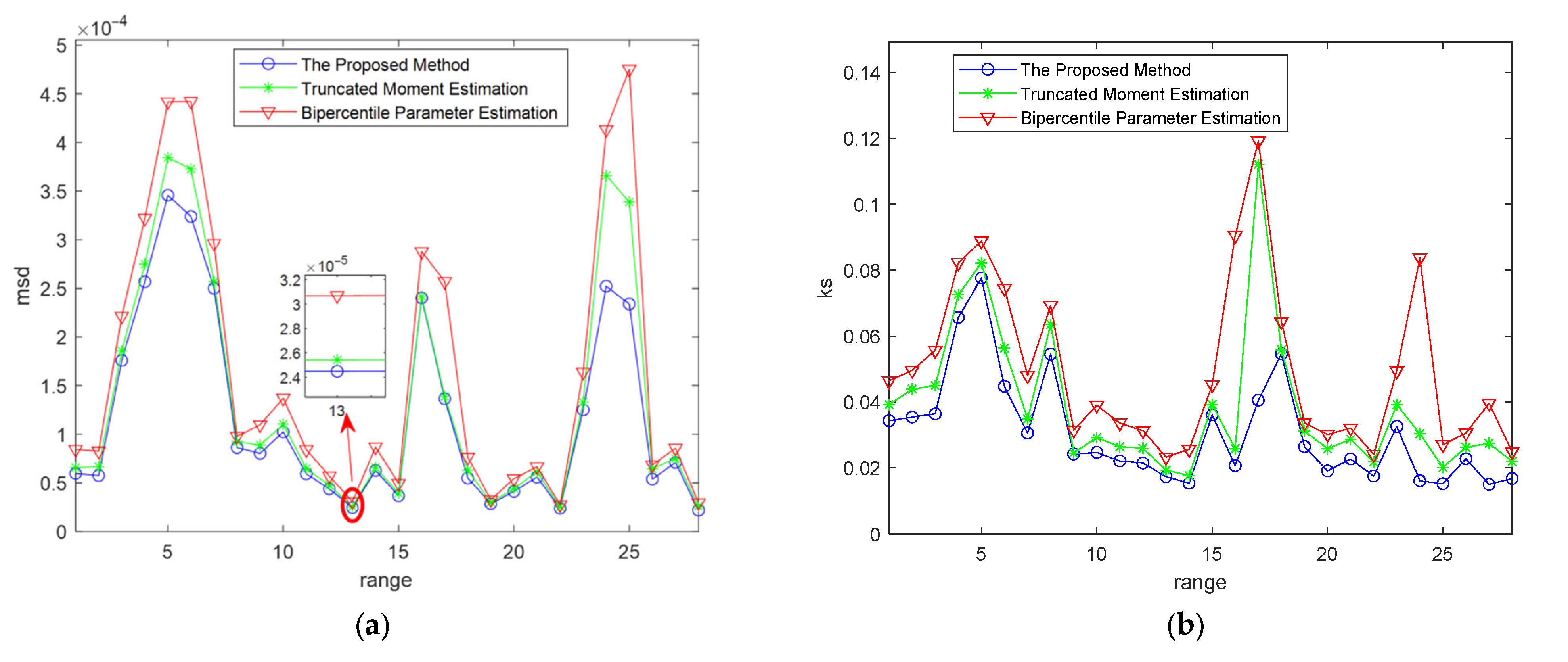
3.3. Analysis of the GOF Results
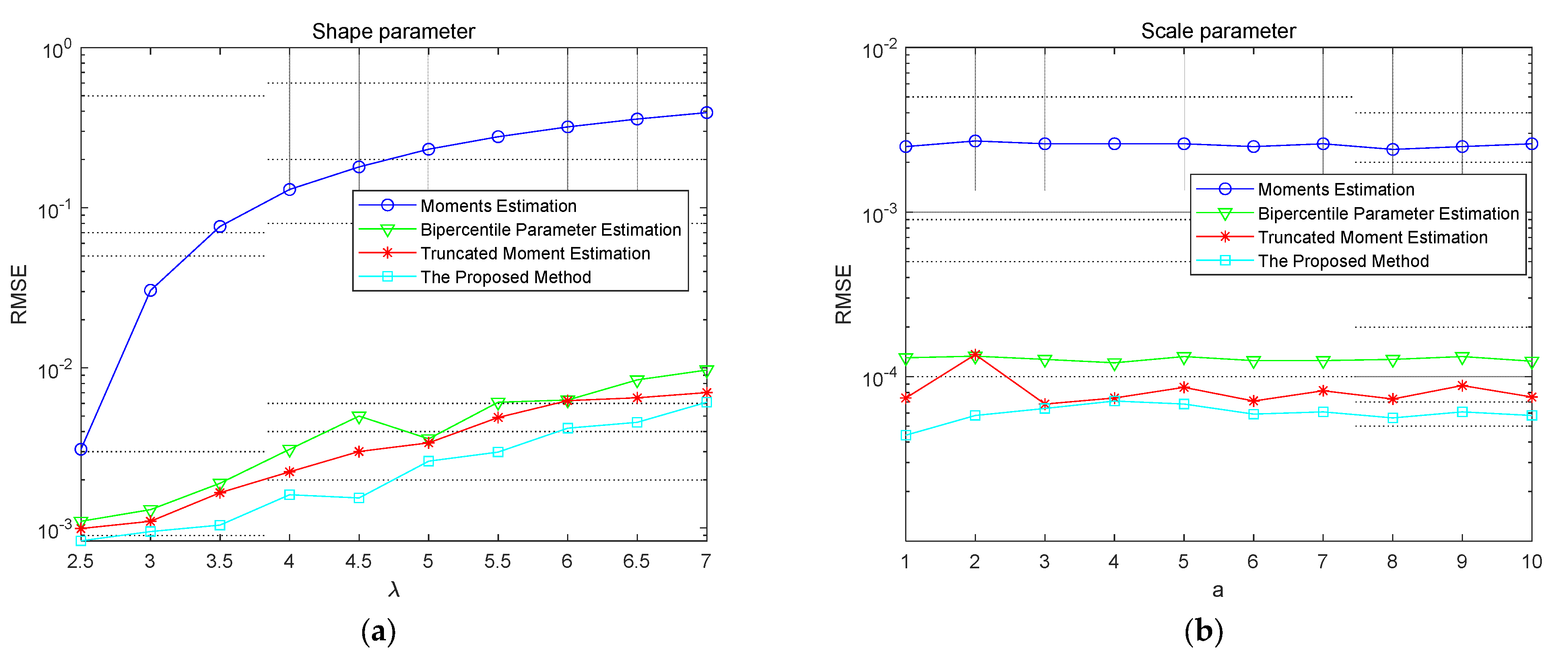
3.4. Parameter Performance Analysis through Monte Carlo Experiments
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ward, K.; Tough, R.; Watts, S. Sea Clutter: Scattering, the K Distribution and Radar Performance, 2nd ed.; The Institution of Engineering and Technology: London, UK, 2013. [Google Scholar]
- Ward, K.D.; Tough, R.J.A.; Watts, S. Sea clutter: Scattering, the K distribution and radar performance. Waves Random Complex Media 2013, 17, 233–234. [Google Scholar] [CrossRef]
- Ravid, R.; Levanon, N. Maximum-likelihood CFAR for Weibull background. Radar Signal Processing Iee Proc. F 1992, 139, 256–264. [Google Scholar] [CrossRef]
- Weik, M.H. Rayleigh distribution. In Encyclopedia of Statistical Sciences; Elsevier Ltd.: Amsterdam, The Netherlands, 2000; p. 1416. [Google Scholar]
- Xin, Z.; Liao, G.; Yang, Z.; Zhang, Y.; Dang, H. Analysis of Distribution Using Graphical Goodness of Fit for Airborne SAR Sea-Clutter Data. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5719–5728. [Google Scholar] [CrossRef]
- Fan, Y.; Tao, M.; Su, J.; Wang, L. Analysis of goodness-of-fit method based on local property of statistical model for airborne sea clutter data. Digit. Signal Process. 2020, 99, 102653. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, F.; Liu, Y.; Wu, H.; Wu, W.; Zhou, A. A Study of Accelerated Life Test of White OLED Based on Maximum Likelihood Estimation Using Lognormal Distribution. IEEE Trans. Electron Devices 2012, 59, 3401–3404. [Google Scholar] [CrossRef]
- Levanon, N. Order statistic CFAR for Weibull background. IEE Proc. Part F 1990, 137, 157–162. [Google Scholar]
- Sarhan, A.M.; Zaindin, M. Modified Weibull distribution. Appl. Sci. 2009, 55, 189–200. [Google Scholar]
- Carretero-Moya, J.; Gismero-Menoyo, J.; Blanco-del-Campo, Á.; Asensio-Lopez, A. Statistical Analysis of a High-Resolution Sea-Clutter Database. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2024–2037. [Google Scholar] [CrossRef]
- Johnsen, T. Characterization of X-band radar sea-clutter in a limited fetch condition from low to high grazing angles. In Proceedings of the 2015 IEEE Radar Conference, Arlington, VA, USA, 10–15 May 2015; pp. 109–114. [Google Scholar]
- Huang, P.; Zou, Z.; Xia, X.-G.; Liu, X.; Liao, G. A Statistical Model Based on Modified Generalized-K Distribution for Sea Clutter. IEEE Geosci. Remote Sens. Lett. 2021, 19, 8015805. [Google Scholar] [CrossRef]
- Arnold, B. Pareto Distributions, 2nd ed.; Taylor & Francis: Abingdon, UK, 2015; pp. 41–47. [Google Scholar]
- Farshchian, M.; Posner, F.L. The Pareto distribution for low grazing angle and high resolution X-band sea clutter. In Proceedings of the 2010 IEEE Radar Conference, Arlington, VA, USA, 10–14 May 2010. [Google Scholar]
- Weinberg, G.V. An Investigation of the Pareto Distribution as a Model for High Grazing Angle Clutter; Defence Science and Technology Organisation: Canberra, Australia, 2011. [Google Scholar]
- Rosenberg, L.; Bocquet, S. The Pareto distribution for high grazing angle sea-clutter. In Proceedings of the IEEE Geoscience & Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 4209–4212. [Google Scholar]
- Weinberg, G.V. Constant false alarm rate detectors for pareto clutter models. IET Radar Sonar Navig. 2013, 7, 153–163. [Google Scholar] [CrossRef]
- Shang, X.; Song, H. Radar detection based on compound-Gaussian model with inverse gamma texture. IET Radar Sonar Navig. 2011, 5, 315–321. [Google Scholar] [CrossRef]
- Stinco, P.; Greco, M.; Gini, F. Adaptive detection in compound-Gaussian clutter with inverse-gamma texture. In Proceedings of the 2011 IEEE CIE International Conference on Radar, Chengdu, China, 24–27 October 2011. [Google Scholar]
- Chen, S.; Kong, L.; Yang, J. Adaptive Detection in Compound-Gaussian Clutter with Inverse Gaussian Texture. Cancer Res. 2013, 54, 2462–2467. [Google Scholar] [CrossRef] [Green Version]
- Sangston, K.J.; Gini, F.; Greco, M.S. Coherent Radar Target Detection in Heavy-Tailed Compound-Gaussian Clutter. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 64–77. [Google Scholar] [CrossRef]
- Weinberg, G.V. Coherent multilook detection for targets in Pareto distributed clutter. Electron. Lett. 2012, 47, 822–824. [Google Scholar] [CrossRef]
- Banks, H.T.; Kunisch, K. Parameter Estimation: Basic Concepts and Examples; Birkhäuser Boston: Cambridge, MA, USA, 1989; pp. 53–91. [Google Scholar]
- Balleri, A.; Nehorai, A.; Wang, J. Maximum likelihood estimation for compound-gaussian clutter with inverse gamma texture. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 775–779. [Google Scholar] [CrossRef]
- Xu, S.; Wang, L.; Shui, P.; Li, X.; Zhang, J. Iterative maximum likelihood and zFlogz estimation of parameters of compound-Gaussian clutter with inverse gamma texture. In Proceedings of the 2018 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Qingdao, China, 14–16 September 2018; pp. 1–6. [Google Scholar]
- Weinberg, G.V. Estimation of Pareto clutter parameters using order statistics and linear regression. Electron. Lett. 2013, 49, 845. [Google Scholar] [CrossRef]
- Alexopoulos, A.; Weinberg, G.V. Fractional order Pareto distributions with application to X-band maritime radar clutter. Radar Sonar Navig. IET 2015, 9, 817–826. [Google Scholar] [CrossRef]
- Mezache, A.; Chalabi, I.; Soltani, F.; Sahed, M. Estimating the Pareto plus noise distribution parameters using non-integer order moments and [zlog(z)] approaches. Radar Sonar Navig. IET 2016, 10, 192–204. [Google Scholar] [CrossRef] [Green Version]
- Chan, D.; Rey, A.; Gambini, J.; Frery, A.C. Low-Cost Robust Estimation for the Single-Look Model Using the Pareto Distribution. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1879-188. [Google Scholar] [CrossRef]
- Mehanaoui, A.; Laroussi, T.; Mezache, A. New Pareto clutter parameters estimators based on log-moments and fractional negative-moments. In Proceedings of the 2017 Seminar on Detection Systems Architectures and Technologies (DAT), Algiers, Algeria, 20–22 February 2017; pp. 1–5. [Google Scholar]
- Shui, P.; Yu, H.; Shi, L.; Yang, C. Explicit Bipercentile Parameter Estimation of Compound-Gaussian Clutter with Inverse Gamma Distributed Texture. IET Radar Sonar Navig. 2018, 12, 202–208. [Google Scholar] [CrossRef]
- Hao, J.C. Research on the Parameter Moment Estimation Method of Sea Clutter Amplitude Distribution Based on Compound Gaussian Model. Master’s Thesis, Xidian University, Xian, China, 2017. [Google Scholar]
- Yang, C.; Wei, Y.; Yang, W. Simulation of compound k-distribution sea clutter. In Proceedings of the IEEE Radar, Cie International Conference, Beijing, China, 8–10 October 1996. [Google Scholar]
- Yang, J.L.; Wan, J.W. New Method for the Simulation of Coherent K-distributed Clutter. In Proceedings of the CIE International Conference on Radar, Shanghai, China, 16–19 October 2006; pp. 1–4. [Google Scholar]
- Jie, Z.; Dong, C.; Sun, D.K. Distribution Sea Clutter Modeling and Simulation Based on ZMNL. In Proceedings of the IEEE International Conference on Intelligent Computation Technology & Automation, Nanchang, China, 14–15 June 2015. [Google Scholar]
- Angelliaume, S.; Rosenberg, L.; Ritchie, M. Modeling the Amplitude Distribution of Radar Sea Clutter. Remote Sens. 2019, 11, 319. [Google Scholar] [CrossRef] [Green Version]
- Huang, D.; Zeng, D.Z.; Long, T. A new method for modeling and simulation of coherent correlated K-distributed clutter. In Proceedings of the IET International Radar Conference, Guilin, China, 20–22 April 2009. [Google Scholar]
- Yanhui, H.; Feng, L.; Baobao, Z.; Shunjun, W. Simulation of Coherent Correlation K-distribution Sea Clutter Based on SIRP. In Proceedings of the 2006 CIE International Conference on Radar, Shanghai, China, 16–19 October 2006; pp. 1–4. [Google Scholar]
- Bocquet, S. Simulation of correlated Pareto distributed sea clutter. In Proceedings of the 2013 International Conference on Radar, Adelaide, Australia, 9–12 September 2013; pp. 258–261. [Google Scholar]
- Bocquet, S.; Rosenberg, L.; Watts, S. Simulation of coherent sea clutter with inverse gamma texture. In Proceedings of the 2014 International Radar Conference, Lille, France, 3–17 October 2014; pp. 1–6. [Google Scholar]

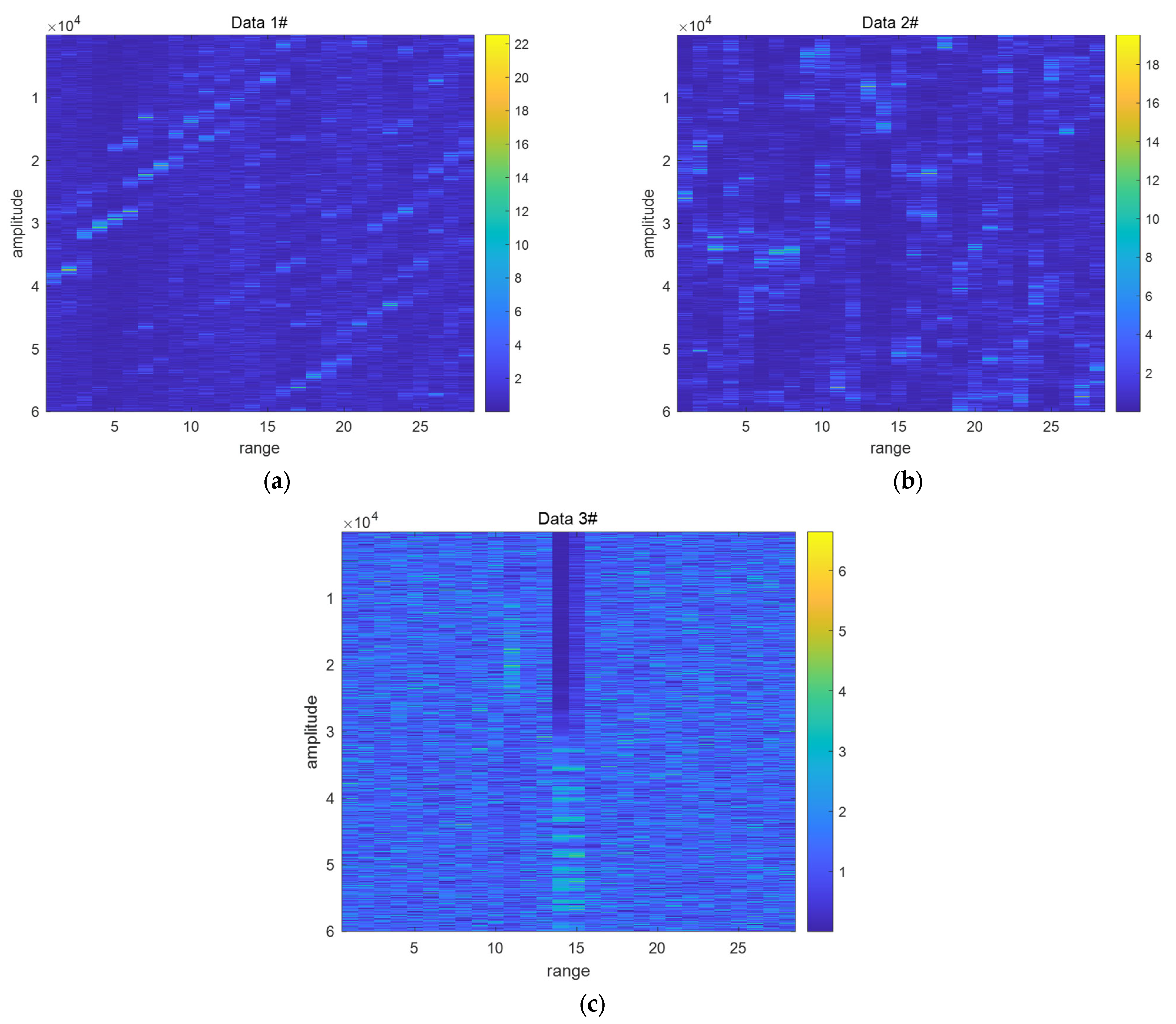

| Parameter Type | Data 1# | Data 2# | Data 3# |
|---|---|---|---|
| Radar height | 30 m | 30 m | 30 m |
| Band width | 5 MHz | 5 MHz | 5 MHz |
| Range resolution | 30 m | 30 m | 30 m |
| Beam width | 0.9° | 0.9° | 0.9° |
| PRF | 1000 Hz | 1000 Hz | 1000 Hz |
| Frequency | 9.3 GHz | 9.3 GHz | 9.3 GHz |
| Operation mode | Grazing | Grazing | Grazing |
| Sea state | 4 | 3 | 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, Y.; Chen, D.; Tao, M.; Su, J.; Wang, L. Parameter Estimation for Sea Clutter Pareto Distribution Model Based on Variable Interval. Remote Sens. 2022, 14, 2326. https://doi.org/10.3390/rs14102326
Fan Y, Chen D, Tao M, Su J, Wang L. Parameter Estimation for Sea Clutter Pareto Distribution Model Based on Variable Interval. Remote Sensing. 2022; 14(10):2326. https://doi.org/10.3390/rs14102326
Chicago/Turabian StyleFan, Yifei, Duo Chen, Mingliang Tao, Jia Su, and Ling Wang. 2022. "Parameter Estimation for Sea Clutter Pareto Distribution Model Based on Variable Interval" Remote Sensing 14, no. 10: 2326. https://doi.org/10.3390/rs14102326
APA StyleFan, Y., Chen, D., Tao, M., Su, J., & Wang, L. (2022). Parameter Estimation for Sea Clutter Pareto Distribution Model Based on Variable Interval. Remote Sensing, 14(10), 2326. https://doi.org/10.3390/rs14102326







