Next Article in Journal
Harmonizing Definitions and Methods to Estimate Deforestation at the Lacandona Tropical Region in Southern Mexico
Next Article in Special Issue
Assessing Surface Urban Heat Island Related to Land Use/Land Cover Composition and Pattern in the Temperate Mountain Valley City of Kathmandu, Nepal
Previous Article in Journal
Climatological Aspects of Active Fires in Northeastern China and Their Relationship to Land Cover
Previous Article in Special Issue
Heterogeneous Urban Thermal Contribution of Functional Construction Land Zones: A Case Study in Shenzhen, China
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 14
Issue 10
10.3390/rs14102318
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

The Seasonality of Surface Urban Heat Islands across Climates

by
Panagiotis Sismanidis
1,*,
Benjamin Bechtel
1,
Mike Perry
2 and
Darren Ghent
2
1
Institute of Geography, Ruhr-University Bochum, 44801 Bochum, Germany
2
National Centre for Earth Observation, Department of Physics and Astronomy, University of Leicester, Leicester LE1 7RH, UK
*
Author to whom correspondence should be addressed.
Remote Sens. 2022, 14(10), 2318; https://doi.org/10.3390/rs14102318
Submission received: 3 April 2022 / Revised: 5 May 2022 / Accepted: 6 May 2022 / Published: 11 May 2022
(This article belongs to the Special Issue Geographical Analysis and Modeling of Urban Heat Island Formation)
Browse Figures
Versions Notes

Abstract

:
In this work, we investigate how the seasonal hysteresis of the Surface Urban Heat Island Intensity (SUHII) differs across climates and provide a detailed typology of the daytime and nighttime SUHII hysteresis loops. Instead of the typical tropical/dry/temperate/continental grouping, we describe Earth’s climate using the Köppen–Geiger system that empirically maps Earth’s biome distribution into 30 climate classes. Our thesis is that aggregating multi-city data without considering the biome of each city results in temporal means that fail to reflect the actual SUHII characteristics. This is because the SUHII is a function of both urban and rural features and the phenology of the rural surroundings can differ considerably between cities, even in the same climate zone. Our investigation covers all the densely populated areas of Earth and uses 18 years (2000–2018) of land surface temperature and land cover data from the European Space Agency’s Climate Change Initiative. Our findings show that, in addition to concave-up and -down shapes, the seasonal hysteresis of the SUHII also exhibits twisted, flat, and triangle-like patterns. They also suggest that, in wet climates, the daytime SUHII hysteresis is almost universally concave-up, but they paint a more complex picture for cities in dry climates.

1. Introduction

Cities are generally warmer than their surroundings. This phenomenon is known as the Urban Heat Island (UHI) and is one of the clearest examples of human-induced climate modification [1]. UHIs increase the cooling energy demand, aggravate the feeling of thermal discomfort, and influence air quality [2,3,4,5,6]. As such, they impact the health and welfare of the urban population and increase the carbon footprint of cities [7,8,9]. The root cause of an UHI is the transformation of the natural landscape to a corrugated, mostly manufactured, and less vegetated surface [10]. The radiative, aerodynamic, thermal, and moisture properties of man-made surfaces are fundamentally different to natural ones, leading to reduced evapotranspiration and the uptake, storage, and release of more heat [1,11]. The relative warmth of the urban atmosphere, surface, and substrate leads to four distinct UHI types that are governed by a different mix of physical processes. These four types are the canopy layer, boundary layer, surface, and subsurface UHI.
Surface UHIs (SUHI) result from modifications of the surface energy balance at urban facets, canyons, and neighborhoods [1,12,13,14]. They exhibit complex spatial and temporal patterns that are strongly related to land cover and are usually estimated from remotely-sensed Land Surface Temperature (LST) data with a kilometer or sub-kilometer spatial resolution [10,15,16,17]. These data are retrieved from satellite observations of the surface-emitted thermal infrared radiation and provide a spatially continuous representation of the urban surface at the satellite overpass time. The difference between the urban and rural LST is known as the SUHI Intensity (SUHII) and is controlled primarily by differences in the evapotranspiration and aerodynamic roughness [11,18,19]. The SUHII varies rapidly in space and time as the surface conditions, the weather, and the incoming radiation change, and it is generally strongest during the daytime and summertime [13,20,21,22,23]. These variations are driven by changes in both the urban and the rural LST [24,25] and not only by the urban as it is usually assumed. The dependency of the SUHII on the characteristics of the rural reference area makes it inappropriate for urban heat mitigation [24] and complicates the analysis of multi-city SUHII data [25].
The seasonal variation of the SUHII has been extensively studied on local [15,26,27,28,29,30,31,32], regional [33,34,35,36,37,38,39,40], and global [13,22,37,41] levels, primarily by analyzing monthly and seasonal means. A global study of 419 cities with more than one million inhabitants estimated that the 2003–2008 mean daytime SUHII is 1.9 K for the summertime and 1.1 K for the wintertime (the corresponding nighttime means are 1.0 K) [22]. A more recent work that examines 9500 cities and a longer time period (2000–2017) reports lower daytime means—1.3 K for the summertime and 0.4 K for the wintertime—and that the majority (87%) of urban areas exhibit positive daytime SUHIIs [23]. It also reports that in warm temperate and snow cities, the SUHII peaks in June–July and is least in November–December, while in arid and equatorial cities, it hardly shows any seasonality. Independent works investigating the seasonal variation of the SUHII in India [35], Europe [33], China [36], and North America [37,38] corroborate most of these findings and show that the SUHII is stronger in temperate and continental cities than in arid and semi-arid. They also show that negative SUHIIs occur primarily in dry areas in summer [23,38].
One of the most interesting findings, however, is that the SUHII, when plotted against the rural LST, exhibits a rate-dependent seasonal hysteresis that strongly depends on local climate conditions [26,29,33,34,42]. This means that the seasonal variation of the SUHII exhibits a looping pattern whose shape is controlled primarily by the local climate and that its magnitude (at any point in time) depends on both present (relative to that timepoint) and recent past effects. This hysteresis is first reported in Zhou et al. [33], where seven distinct and geographically separated types of SUHII hysteresis are identified in Europe. A plausible explanation for the seasonal hysteresis of the SUHII is given in Manoli et al. [42], where it is hypothesized that this behavior is the result of time lags between the surface energy budget of urban and rural areas. Testing this hypothesis using a coarse-grained SUHI model [43], the SUHII hysteresis of wet (London, Milan, and Paris) and dry (Madrid and Nicosia) cities in Europe was replicated and led the authors to conclude that in wet climates, the shape of the daytime hysteresis is controlled by the time lag between solar radiation and the air temperature, whereas in seasonally dry climates, it is controlled by the time lag between solar radiation and the rainfall. The former generates a concave-up loop that is positive throughout the year and peaks in summer, while the latter is a concave-down loop that peaks in spring and is negative during summer and autumn [42].
These findings improve our understanding about the influence of the local climate conditions on the SUHII and it is worth further investigation and testing. The first step toward this direction is to extend the work of Zhou et al. [33] in cities outside of Europe and consistently describe the SUHII seasonal hysteresis in every climate inhabited by humans. This paper aims to address this gap and derive a complete typology of the SUHII hysteresis loops for both the daytime and nighttime. In this regard, we ask: (i) what is the shape of the SUHII hysteresis loops in every densely populated climate; (ii) when is the SUHII strongest and weakest within the year; (iii) what these values are; and (iv) how they relate to the seasonal variation of the precipitation and solar radiation? To answer these questions, we use 18 years (2000–2018) of global LST and land cover data from the European Space Agency’s Climate Change Initiative (ESA-CCI). To characterize the climate of each city, we use the Köppen–Geiger classification system [44] that empirically maps Earth’s biome distribution (i.e., vegetation zones) in 30 climate classes. The SUHII is a function of both urban and rural features [24,25], and the phenology of the rural surroundings can differ considerably between cities, even within the same climate zone (i.e., tropical, dry, temperate, continental, and polar). Controlling the city biomes is especially important over dry and tropical regions where cities exhibiting positive and negative SUHIIs may coexist (e.g., in India [35]). In such cases, aggregating multi-city SUHII data can result in temporal means that fail to reflect the actual SUHII characteristics and lead to erroneous conclusions.
Following this introduction, in Section 2, we describe our method for calculating the SUHII and deriving the hysteresis loops. In Section 3 and Section 4, we present our results and discuss how they differ between climates, and in Section 5, we provide our conclusions.

2. Materials and Methods

2.1. ESA-CCI MODIS LST

The ESA-CCI project on Land Surface Temperature (LST_cci) provides validated LST products across all land surfaces of the Earth over the past 20 to 25 years. In this work, we use the 0.01° daily 2000–2018 LST_cci Terra MODIS (Moderate Resolution Imaging Spectroradiometer) product (v.1.0) for the focus areas presented in Figure 1. Terra MODIS is a multispectral sun-synchronous satellite instrument that crosses the equator at 10:30 (local solar time) in the descending orbit and 22:30 in the ascending orbit and views almost the entire surface of the Earth every day. The LST_cci MODIS LST are retrieved as a linear combination of the 11.0 µm and 12.0 µm clear-sky brightness temperatures (BT) using a Generalized Split-Window (GSW) algorithm [45]. The GSW coefficients depend on the satellite view angle and the water vapor and are derived by linearly regressing simulated BT and LST for various conditions. The land surface emissivity is used explicitly in the GSW formulation and is obtained from the Baseline Fit Emissivity Database of the Cooperative Institute for Meteorological Satellite Studies (CIMSS) [46], while the cloud masks are from the MOD35_L2 operational product. A strong point of the LST_cci MODIS data is that they provide a detailed quantification of the uncertainty of each pixel using three uncertainty components: the random (uran), the locally correlated (uloc), and the systematic (usys). The employed uncertainty model is described in detail in Ghent et al. [47] and is equally applicable across different surface temperature domains. In this work, we use the total LST uncertainty (utotal) of each pixel, by combining uran, uloc, and usys using Equation (1).
u total = u ran 2 + u loc 2 + u sys 2

2.2. Present Köppen–Geiger Climate Classification Map

The present (1980–2016) Köppen–Geiger climate map from Beck et al. [44] classifies Earth’s climate into five main classes and 30 sub-classes (Figure 1). The five main classes are the tropical, dry, temperate, continental, and polar, while the sub-classes reflect differences in seasonal precipitation and level of heat. It is derived from an ensemble of four independent high-resolution (~1 km) climatic maps of air temperature and precipitation that have been topographically corrected and adjusted to reflect the period 1980–2016. The classification is based on threshold values and the seasonality of monthly air temperature and precipitation, and it is applied to each climatic dataset combination separately (12 in total; for full details, see [44]). The final climate map is derived from the 12 individual maps by selecting, for each grid-cell, the most common Köppen–Geiger climate class. A corresponding confidence map is also derived by dividing the frequency of occurrence of the most common class by the ensemble size and converting these fractions to percentages [44]. In general, class confidence levels are generally lower in the vicinity of borders between climate zones, especially in high-latitude regions where the climatic data have higher uncertainty.

2.3. City Delineation and SUHII Calculation

To delineate the cities in the focus areas of Figure 1, we use land cover (LC) data from the ESA-CCI Land Cover project [48]. This data product provides annual high-resolution (300 m) LC maps that classify the global surface in 37 classes according to the United Nations Land Cover Classification System (UNLCCS) with an overall accuracy of 75.4% [48]. To process the LC data, we first resample them to the 0.01° × 0.01° LST grid by calculating the LC fractions of each grid cell. Then, for each year from 2000 to 2018, we create a binary urban mask of all the pixels that have an urban fraction of at least 95%, a water fraction equal to 0%, and are more than ~2 km away from the coastline. To eliminate single pixels and small objects from the resulting masks, we apply a morphological operator that removes any objects with eight or fewer connected pixels using scikit-image v.0.18.1 [49]. Finally, we segment the filtered masks into clusters that correspond to cities and label all the instances of each city with the same unique ID. Our method follows the principle of the City Clustering Algorithm [50], which has been used in several SUHII studies due to its ability to describe the extent of a city more accurately than administrative or population data [18,22,33].
To select appropriate rural pixels for each city, we use the Boundary Generation Algorithm (BGA) [33] that iteratively expands a rural buffer around each city until its size is approximately that of the urban area. To ensure consistency in the SUHII estimates over time, we create a single rural buffer per city that is representative for all the years between 2000 and 2018. In our implementation of BGA, we do not use all the pixels in each new ring but filter them according to the following rules: the rural LC fraction of each candidate pixel is at least 95% for every year between 2000 and 2018; the corresponding urban and water LC fractions are equal to 0%; and the elevation of each candidate pixel does not differ by more than ±200 m from the median elevation of the corresponding city. Here, we define as rural LC the aggregate class that is derived by summing the LC fractions presented in Table 1 (the resulting class closely resembles LCZ B, C, D, and F [51]). To ensure that only rural pixels adjacent to each city are selected, the search zone of BGA is limited to within 30 pixels from the city boundary.
Following standard practice [1,13,22,33], we calculate SUHII as the difference between the mean urban (LSTurban) and rural LST (LSTrural) for each date d (Equation (2)).
SUHII ( d ) =   LST urban ( d ) − LST rural ( d ) ,
We apply Equation (2) to each city (separately for daytime and nighttime), using the corresponding urban and rural masks to select the respective MODIS pixels. Before we calculate the urban and rural means, we quality-filter the LST data of each group, keeping only the values that range from 240 K to 360 K and have a total uncertainty equal or better than 2 K. In addition to these two checks, we also apply a median absolute deviation test to remove any remaining outliers (the test statistics are calculated separately for the urban and rural pixels of each city, using the corresponding LST for each year). To evaluate our SUHII estimates, we compare them with reference SUHIIs derived from MOD11A1 v.6.0 LST using the method described above (the results are presented in Appendix A).

2.4. Data Analysis

Our goal is to analyze the seasonal hysteresis of SUHII vs. LSTrural as a function of climate. To do this, we use the ~1 km Köppen–Geiger present climate map from Beck et al. [44] and assign each city to a climate class. To reduce misclassifications, we keep only the cities where the climate confidence flag is at least 90%. We also discard any climate classes with insufficient SUHII data (<10% of clear-sky days) and/or fewer than 10 cities. To derive each class’s hysteresis loop, we first calculate the 2000–2018 SUHII and LSTrural monthly means for each city. We do this using only the dates where at least 70% of the urban and rural pixels are available. Before we calculate the monthly means, we subtract from each date 80 days (i.e., the approximate day-of-year of spring equinox) if it is a north hemisphere city and 265 days if it is south. This, in essence, results in a custom calendar where the corresponding south and north hemisphere equinoxes and solstices are in sync. To derive the SUHII hysteresis loop for each climate class, we average the hysteresis loops from the individual cities located in that class. For this calculation, we use only the cities with complete loops, i.e., loops without missing months. To describe and compare the resulting hysteresis patterns, we use the loop direction, the minimum and maximum SUHII (calculated using the absolute values), and the month when these values occur. In contrast to Zhou et al. [33], we do not approximate the LSTrural and SUHII time series of each city with a Fourier series but follow a data-driven approach that relies on the good quality and the large volume of the collected data.
To investigate the influence of precipitation and solar radiation on the shape of the resulting loops, we use precipitation data (v2020) from the Global Precipitation Climatology Centre (GPCC) [52] and at-surface clear-sky downwelling shortwave fluxes (SW) [53] from the CERES Level-3b Energy Balanced and Filled Climate Data Record (v4.1). Both datasets provide global coverage, are available at monthly resolution, and cover the study period (2000–2018). To extract the corresponding precipitation and SW time series for each city, we use the coordinates of the urban polygon centroid. This is because the grid-cell size of the precipitation and SW data (0.5° × 0.5° for the former and 1° × 1° for the latter) is much coarser than that of the LST data. To derive the climate-class monthly means, we first calculate the 2000–2018 mean precipitation and SW value per month and city and then aggregate the data from the relevant cities, as performed for SUHII and LSTrural. To analyze the seasonality of SUHII and LSTrural versus that of precipitation, and SW per climate class, we study their co-seasonality and determine the months of minimum and maximum.

3. Results

3.1. Delineated Cities and SUHII Climatology

Using the City Clustering Algorithm [50], we delineate 1511 global cities in one tropical, two dry, five temperate, and three continental Köppen–Geiger classes (Table 2). The location and the number of cities per class is presented in Figure 2, while their characteristics (area, elevation, and percentage of coastal/inland cities) are discussed in Appendix B. From these 11 classes, 10 include more than 50 cities, 6 more than 100 cities, and 1 more than 300 cities. The majority (90.5%) of them are located in Asia (40.0%), Europe (27.5%), and North America (23.0%), and only 9.5% are in Africa (5.9%), South America (2.7%), and Oceania (0.9%). In Figure 2, we also present the daytime (~10:30 local time) and nighttime (~22:30 local time) SUHII climatology of each class as the bivariate distribution of the daily SUHII and LSTrural that we have randomly sampled using the months as strata.
The tropical class is the Aw (tropical savanna), which comprises African, Asian, and South American cities (Figure 2A). The Aw climate has two distinct seasons—a wet and a dry—and is warm throughout the year. This weak seasonality is evident in the SUHII climatologies in Figure 2A, which are shaped like convex blobs. The interquartile range (shown as [Q25, Q75], where Q25 and Q75 are the first and third quartiles) of the Aw SUHII is [−0.4 K, 3.1 K] for the daytime and [0.5 K, 2.2 K] for the nighttime. The corresponding LSTrural values are [306 K, 315 K] and [293.7 K, 298.9 K], respectively, which make the Aw the climate with the least intra-annual variation in our analysis (the corresponding means are shown in Table 3). The dry classes are the BSh (hot semi-arid) and the BSk (cold semi-arid). They are intermediate climates between desert and humid climates and are usually dominated by grasslands and shrubs. In our analysis, the BSh is represented mainly by cities in India, Africa, Mexico, and the Middle East, while the BSk is represented by cities in Europe and Asia. The shape of the BSh and BSk SUHII climatologies is more complex than that of the Aw and clearly influenced by seasons (Figure 2B,C). The interquartile range of the daytime SUHII (and LSTrural) is [−2.0 K, 0.8 K] ([305.7 K, 319.8 K]) for the BSh and [−1.4 K, 1.2 K] ([283.7 K, 310.3 K]) for the BSk. The corresponding nighttime values are [1.1 K, 2.8 K] ([288.0, K 298.9 K]) and [1.0 K, 2.8 K] ([270.1 K, 290.6 K]), respectively. The key characteristic of these two dry climates is that daytime SUHIIs are mostly negative, especially when the LSTrural is maximum.
The five temperate classes are the Csa (hot-summer Mediterranean), Cfa (humid subtropical), Cfb (oceanic), Cwa (dry-winter humid subtropical), and Cwb (dry-winter humid highland). Temperate climates are generally defined as environments with moderate rainfall, sporadic droughts, mild-to-warm summers, and cool-to-cold winter. They occur in mid-latitude regions and have four seasons (winter, spring, summer, and autumn). The Csa exhibits wet winters and hot, dry summers and is water deficient during part of the growing season. This makes the daytime climatology of the Csa (Figure 2D) to be considerably different than that of the other temperate climates. It has a concave-down shape with negative summertime SUHIIs and an interquartile range of [−1.1 K, 1.3 K] for the SUHII and [294.2 K, 313.1 K] for the LSTrural. In contrast, the shape of the Csa nighttime climatology is convex and always positive with an interquartile range of [0.9 K, 2.5 K] and [282.4 K, 293.8 K], respectively. The Cfa is represented by cities in North and South America, Europe, Australia, and Asia (Figure 2E), while the Cfb is represented by cities in western Europe (Figure 2F). Their daytime (and nighttime) climatologies exhibit almost identical concave-up shapes, with the SUHII and LSTrural peaking almost simultaneously. The daytime interquartile range of the SUHII (and LSTrural) is [0.3 K, 3.2 K] ([292.9 K, 309.1 K]) for the Cfa and [0.4 K, 3.0 K] ([282.0 K, 301.5 K]) for the Cfb. The corresponding nighttime values are [0.7 K, 2.2 K] ([279.6 K, 294.8 K]) and [0.4 K, 1.9 K] ([275.1 K, 285.9 K]). The last two temperate classes, namely the Cwa and Cwb, are represented mainly by cities in Asia and Central America, respectively. The Cwa is a monsoon-influenced climate with dry winters and hot summers, while the Cwb is a climate mainly found in tropical and subtropical highlands with cold, dry winters and rainy summers. They both exhibit a completely different daytime SUHII climatology than the other temperate climates. The shape of the Cwa climatology is presented in Figure 2G, while that of the Cwb is in Figure 2H. The interquartile range of the daytime SUHII (and LSTrural) is [−0.1 K, 2.5 K] ([298.0, 311.0]) for the Cwa and [−1.0 K, 3.4 K] ([301.1 K, 310.0 K]) for the Cwb. The corresponding nighttime values are [1.0 K, 2.5 K] ([286.2 K, 298.1 K]) and [1.1 K, 3.4 K] ([282.5 K, 290.1 K]), respectively.
The three continental Köppen–Geiger classes are the Dfa (hot-summer humid continental), Dfb (warm-summer humid continental), and Dwa (monsoon-influenced hot-summer humid continental). The Dfa is represented mainly by cities in North America (Figure 2I), while the Dfb (Figure 2J) and the Dwa (Figure 2K) are represented by cities in Europe and Asia, respectively. Continental climates occur within large landmasses away from the moderating effect of oceans and are characterized by an extreme range of annual near-surface air temperatures. They exhibit four distinct seasons (winter, spring, summer, and autumn) with warm-to-hot summers and cold, snowy winters. The shapes of the Dfa, Dfb, and Dwa climatologies (Figure 2I–K) are almost identical and quite similar to that of the Cfa and Cfb (Figure 2E,F). When the LSTrural is below 300 K, the daytime SUHII of continental climates is rather constant and close to 1 K. Above 300 K, the SUHII increases considerably and peaks when the LSTrural is maximum. The shape of the corresponding nighttime climatologies are rather flat and featureless like all the other climates presented in Figure 2. The interquartile range of the daytime SUHII is [0.3 K, 3.3 K] for the Dfa, [0.2 K, 2.7 K] for the Dfb, and [−0.5 K, 2.5 K] for the Dwa. The corresponding nighttime values are [0.5 K, 2.1 K], [0.4 K, 2.4 K], and [1.1 K, 2.8 K]. The extreme range of continental annual temperatures is evident in the interquartile range of the daytime LSTrural, which is [282.9 K, 304.8 K] for the Dfa, [275.2 K, 302.4 K] for the Dfb, and [282.5 K, 306.7 K] for the Dwa. The corresponding nighttime values are [271.5 K, 290.2 K], [268.9 K, 285.7 K], and [270.1 K, 292.3 K].

3.2. SUHII Seasonal Hysteresis

The daytime SUHII hysteresis loops of the examined climate classes are presented in Figure 3. Overall, their shape matches well that of the SUHII climatologies and provides a clearer view of how the SUHII and LSTrural vary within the year. They are the most different for temperate climates (Table 2), where each sub-class exhibits a distinct looping pattern. The daytime Cfa and Cfb hysteresis loops exhibit a concave-up pattern, as the model of Manoli et al. [42] suggests, with the SUHII and LSTrural peaking almost simultaneously. The shape of the Csa loop exhibits a weak concave-down pattern, while that of the Cwa exhibits a twisted concave-up pattern. The shape of the Cwb daytime loop is convex (triangle-like), as is the case for the Aw. For cities in the Dfa, Dfb, and Dwa continental climates, the daytime SUHII hysteresis shows a concave-up pattern that is flat when the LSTrural is below ~300 K and peaks rapidly as the LSTrural increases. Similarly, to the Cfa and Cfb climates, the SUHII and LSTrural of the Dfa, Dfb, and Dwa become maximum almost simultaneously. For the BSh and BSk semi-arid climates, the daytime SUHII loops are rather flat. This result does not agree well with the shapes of the individual city loops shown in Figure 3 (grey lines). Further investigations focusing on the BSh cities show that the shape of the individual hysteresis loops differs with geographic location and can take the form of concave-down, flat, twisted, and triangle-like loops (Figure 4). These differences are attributed primarily to differences in the characteristics of the surrounding rural areas, which exert a strong influence on the SUHII [24,25], and suggest that semi-arid cities should be classified into even finer groups. Our analysis also shows that the shape of the humid temperate and continental loops is more stable than that of the dry-climate loops. This observation corroborates the remark of Manoli et al. [42] that the shape of dry-climate loops is more susceptible to perturbations in the seasonality and the magnitude of rainfall. The direction of the daytime loops is clockwise in all cases, except for the Aw, BSh, Cwa, Cwb, and Dwa (Figure 3).
In Figure 5, we present the seasonal variation of the daytime SUHII, SW, and precipitation for each Köppen–Geiger class examined in this work. We focus on these two variables because they have been shown to play a key role in the seasonality of the SUHII [42]. For the Aw cities we observe that the SUHII peaks when the SW and precipitation are almost maximum. This is also the case for the Cwb cities in our analysis, which are located mainly in elevated regions within the tropics and the subtropics (Figure 2H). In temperate and continental climates (Cfa, Cfb, Dfa, and Dfb), where the precipitation is rather constant throughout the year, the SUHII appears to vary mainly with the SW. This, however, is not the case for the Cwa and Dwa variates that exhibit a monsoonal tendency with a much higher precipitation in summer than in winter. In these climates, the SUHII intensifies as the summertime precipitation peaks, which suggests that monsoons influence the concave-up hysteresis of the SUHII in the Cwa and Dwa. The climate class with the most distinct behavior is the hot-summer Mediterranean (Csa), where the precipitation decreases as the SW increases. The anti-correlation between the SW and precipitation during spring and summer makes the Csa SUHII-SW-precipitation loop the only one with a clockwise direction (Figure 5). The daytime SUHII of the Csa cities peaks in late spring/early summer and then starts to drop as the precipitation approaches its minimum and SW its maximum. During this phase, a significant portion of the natural vegetation begins to dry due to water stress [54]. Under such water-limited conditions, the evapotranspiration of rural areas decreases, which impacts their ability to cool [11,42]. In dry-climate cities, the precipitation is low throughout the year and does not vary much with the SW (monsoon-influenced cities in India make the bulk of the examined BSh cities and are responsible for the precipitation peak in Figure 5). The SUHII of the BSh and BSk cities does not vary with the SW either; however, as discussed above, this result is a fluke caused by averaging dissimilar SUHII loops (see Figure 3 and Figure 4). Overall, Figure 5 shows that the SUHII of tropical, temperature, and continental cities is generally strongest when the SW and precipitation peak. Under these conditions, the vegetation surrounding each city reaches peak greenness, which in turn suggests that the observed SUHII increase should not be attributed solely to an increase in the urban LST.
The corresponding nighttime hysteresis loops are rather similar and exhibit mostly flat and concave-up patterns (Figure 6). In humid temperate and continental climates, the SUHII increases and decreases almost in sync with the LSTrural, while in dry climates, the shape of the nighttime hysteresis loops is mainly flat. The looping direction is always clockwise and the classes with the most distinct nighttime loops are the BSh for the dry climates, the Cfb for the temperate, and the Dwa for the continental. Contrary to the daytime, the shape of the individual BSh and BSk nighttime hysteresis loops are more alike and better represented by the mean loop (Figure 6). In respect to the seasonal variation of the precipitation and SW, the nighttime SUHII of the Csa, Cfa, Cfb, Dfa, and Dfb cities is strongest when the SW peaks (Figure 7). In contrast, the nighttime SUHII of the Aw cities is weakest when the precipitation and SW peak.
In Figure 3 and Figure 6, we also include the SUHII hysteresis of the dry, temperate, and continental parent classes (dashed lines) that we derive using the individual loops from all the relevant cities. The results support our thesis that aggregating multi-city data without considering the biome of each city can result in temporal means that fail to reflect the actual SUHII characteristics and show that the shape of each parent-class loop is determined by the climate sub-class with the most cities. This is particularly the case for the Cfa and Cfb, where the daytime temperate parent-class loop reflects their shape and is not representative of the other temperate sub-classes (e.g., Csa or Cwb, as seen in Figure 3).

3.3. Month of Minimum and Maximum SUHII

The month when the SUHII of each hysteresis loop is maximum and minimum in absolute values is shown with black dots in Figure 8 and Figure 9 (the corresponding magnitudes are provided in Table 4). The colored dots refer to the individual city loops and indicate the variability in the examined cities. For the Aw cities, the daytime SUHII is strongest in September (4.3 ± 0.8 K) and weakest in February (−0.1 ± 0.7 K). The peak occurs four months later than that of the daytime LSTrural and one month later than that of the precipitation (Figure 8). The nighttime SUHII peaks in January (1.4 ± 0.2 K) and is least in September (0.8 ± 0.2 K), whereas the Aw LSTrural is maximum in May and minimum in December/January.
The daytime SUHII and LSTrural of semi-arid cities is generally strongest in summer. The nighttime SUHII peaks in November (1.9 ± 0.2 K) for the BSh and in June (2.0 ± 0.2 K) for the BSk, while the LSTrural peaks in August. In hot-Mediterranean (Csa) cities, the daytime SUHII is warmest in May (1.5 ± 0.4 K) and the LSTrural in August. In contrast, the nighttime SUHII peaks in July (1.8 ± 0.2 K) when the precipitation is minimum and the LSTrural is almost maximum. The month when the Csa SUHII and LSTrural are weakest is January (Figure 9). The Csa is the only temperate climate where the daytime SUHII peak occurs in spring and not in summer.
In wet temperate climates, the SUHII is strongest in summer. It peaks in August for the Cfa and in June/July for the Cfb. The corresponding SUHII magnitudes are 3.6 ± 0.3 K and 4.0 ± 0.2 K for the daytime and 1.7 ± 0.1 K and 1.9 ± 0.1 K for the nighttime (Table 4). The LSTrural and SW also peak in summer, while the precipitation is relative constant throughout the year (this explains the pronounced dispersion of the Cfa and Cfb colored dots in Figure 8 and Figure 9). The SUHII is weakest in December/January for both climate classes, with the Cfa exhibiting a slightly greater magnitude (~0.9 K vs. 0.4 K). The daytime SUHII of the Cwa and Cwb cities is maximum in August/September and minimum in December. This is also the case for the precipitation, SW, and LSTrural. The maximum daytime SUHII is equal to 4.1 ± 0.5 K for the Cwa and 3.8 ± 1.3 K for the Cwb, while the corresponding minimums are 0.0 ± 0.2 K and 0.2 ± 0.6 K, respectively (Table 4). The nighttime SUHII peaks earlier than the LSTrural (in April/May vs. July/August) and is equal to 1.9 ± 0.2 K for the Cwa and 2.2 ± 1.1 K for the Cwb.
In continental climates (Dfa, Dfb, and Dwa), the SUHII and LSTrural are warmest in July/August. The only exception is the Dwa where the nighttime SUHII peaks in February (Figure 8). The precipitation also peaks in July, while the SW peaks in June. The maximum daytime SUHII is 3.9 ± 0.4 K for the Dfa, 3.3 ± 0.2 K for the Dfb, and 5.2 ± 0.3 K for the Dwa. The corresponding nighttime values are 1.9 ± 0.1 K, 2.2 ± 0.1 K, and 2.4 ± 0.2 K. The daytime SUHII minimums occur in November/December and the nighttime in January/December, except for the Dwa which occurs in August (Figure 9). The corresponding values are ~0 K for the daytime and 0.7 ± 0.1 K (Dfa, Dfb) and 1.5 ± 0.1 K (Dwa) for the nighttime. Figure 8 and Figure 9 also show that the daytime and nighttime, minimum and maximum SUHII do not always occur in the same month. We attribute this to the different mechanisms that drive the SUHII during the day and night.

4. Discussion

In this work, we revisit the topic of SUHII seasonality and how it differs across climates. Instead of the typical tropical/dry/temperate/continental grouping, we describe Earth’s climate using the Köppen–Geiger system that empirically maps Earth’s biome distribution into 30 climate classes [44]. This climate classification system has proven to be a highly suitable means for aggregating complex climate gradients into simple but ecologically meaningful classes [44]. As such, it is regularly used across a range of disciplines for regionalizing variables [55]. We find this property particularly suitable for our work because it allows an indirect control of the biome of each city. Even though a global vegetation map would provide more accurate labels about the city biomes, this approach also leads to a sufficient discrimination between the examined tropical, temperate, and continental cities. This is because climate is the basis for most plant vegetation systems, and the regional extend of each biome is primarily determined by it.
Previous studies investigating the characteristics of the SUHII on a global level have largely neglected to control the biome of each city, despite the fact that it exerts a strong influence on the SUHII. The SUHII is a function of both urban and rural features [24,25], and the phenology of the rural surroundings can differ considerably between urban areas even within the same climate zone. This implies that failing to control this parameter when aggregating multi-city data can result in temporal means that do not reflect the actual SUHII dynamics of each group. Our findings support this thesis and show that the seasonality of tropical, dry, temperate, and continental SUHIIs differs considerably during the daytime. They also reveal that in dry and temperate climates, the SUHII seasonal dynamics exhibit considerable intra-class variations that cannot be represented by the parent class. The comparison between the SUHII characteristics (i.e., hysteresis, range, and month of minimum/maximum) of the temperate parent class and the corresponding sub-classes provides clear evidence of this and suggests that the parent-class characteristics reflect those of the dominant sub-class. This suggests that using parent-class summaries to make inferences about the SUHII characteristics of cities in non-dominant climate sub-classes should be avoided or exercised with caution. In contrast to daytime data, this issue does not appear to affect the analysis and aggregation of nighttime SUHIIs as much, particularly because they exhibit less inter- and intra-class annual variation.
The derived SUHII hysteresis loops reveal the strong influence that local climate conditions exert on daytime SUHIIs and suggest that almost every climate class exhibits a unique daytime looping pattern. For temperate climates, our results replicate the daytime concave-up and -down patterns observed in Europe [33,42] and present the convex and twisted hysteresis of temperate dry-winter cities in America and Asia. They also show that the daytime hysteresis of continental cities in Asia, Europe, and North America is always concave-up, with a rather constant SUHII when the LSTrural is below 300 K. For cities in dry semi-arid climates, we found a rather flat SUHII seasonality, like Chakraborty and Lee [23]. However, examining the individual daytime loops of semi-arid cities, we observed a variety of flat, twisted, triangle-like, and concave-up patterns that depend strongly on geographic location. This finding suggests that dry-climate SUHIIs should be grouped into even finer classes that describe the rural features in more detail (e.g., using the land cover fractions).
Overall, our results provide the most complete typology of daytime and nighttime hysteresis loops to date. This information improves our understanding about the global SUHII dynamics and can guide the analysis of multi-city SUHII data from different climates. The development of a consistent framework for analyzing global SUHI data has been the focus of many papers over the years [10,13,23,39]. Our work contributes to this goal by proposing a consistent method for delineating cities and demonstrating the impact of improper data aggregation. Future efforts should introduce further controls and investigate how the seasonal hysteresis of the SUHII varies as a function of urban form and function. These two attributes exhibit considerable heterogeneity [56,57] on a global level and have been shown to influence the SUHII [10,58]. Here, we overlook this issue primarily because we use coarse resolution data (~1 km) and a custom definition of urban areas that selects only pixels that form densely built-up clusters with almost no vegetation. The employed definition improves the consistency of the derived multi-city SUHII data by mitigating the influence of urban green. However, it also results in city polygons that are smaller, more fragmented, and with more gaps in comparison to city polygons retrieved from administrative or land cover data. This work is also one of the first to use data from the new ESA-CCI LST product that has been designed to meet the requirements of the Global Climate Observing System (GCOS) for climate applications.
In respect to other global SUHII studies [13,23], our study includes fewer cities. This is mainly due to the minimum city size threshold that we use to ensure that the employed cities are adequately resolved in the ~1 km LST data. A consequence of this decision is that our SUHII estimates are warmer than that from other studies (this is because the SUHII and city size are positive correlated [58,59]). We are also skeptical about the direct use of the findings presented here and in similar works for informing heat mitigation actions. This is due to the dependency of the SUHII on the characteristics of the reference rural areas [24,25] and also because the canopy-layer UHIs—which are the ones that should be mitigated—differ significantly from the SUHIs [12,17] and do not exhibit any pronounced seasonal hysteresis [26]. Nevertheless, this information can help us better understand how rural and urban land covers react to time-lags between radiation forcing and precipitation, which might provide further insights about urban heat.

5. Conclusions

The seasonal variation of the SUHII exhibits distinct hysteretic patterns that depend on the local climate conditions and in particular on the seasonal availability of energy and water. In this work, we use the new ESA-CCI LST data product for the Terra MODIS and characterize the seasonal hysteresis of the SUHII in almost every Köppen–Geiger climate class inhabited by humans. Our results advance the state-of-the-art and provide the most complete typology of daytime and nighttime SUHII hysteresis loops to date. They reveal that in addition to concave-up and -down shapes, the seasonal hysteresis of the daytime SUHII can also exhibit twisted, flat, and triangle-like patterns, and that nighttime loops are mostly flat and concave-up. They suggest that, in wet climates, the daytime SUHII hysteresis is almost universally concave-up but paint a more complex picture for dry climate cities, where the reference rural areas are more heterogenous and actual evapotranspiration is less than potential evapotranspiration. They also show that aggregating SUHII data from cities in different biomes results in temporal means that do not reflect the actual SUHII characteristics. Even though our results cannot and should not be used for urban heat mitigation, they improve our understanding about the global SUHI variability and the influence that rural surroundings exert on SUHII.

Author Contributions

Conceptualization, P.S. and B.B.; methodology, P.S. and B.B.; software, P.S.; validation, P.S.; formal analysis, P.S.; investigation, P.S. and B.B.; resources, M.P. and D.G.; data curation, P.S.; writing—original draft preparation, P.S.; writing—review and editing, P.S., B.B. and D.G.; visualization, P.S.; supervision, B.B.; project administration, P.S. and B.B.; funding acquisition, B.B. and D.G. All authors have read and agreed to the published version of the manuscript.

Funding

This work has received funding from the European Space Agency within the framework of the Land Surface Temperature project under the Climate Change Initiative, contract number 4000123553/18/I-NB, and the ENLIGHT project, funded by the German Research Foundation (DFG) under grant No. 437467569.

Data Availability Statement

The LST, LC, and climate data that support the findings of this study are openly available at http://gws-access.ceda.ac.uk/public/esacci_lst, https://cds.climate.copernicus.eu/portfolio/dataset/satellite-land-cover, and https://doi.org/10.6084/m9.figshare.6396959, respectively (all accessed on 5 May 2022). The SUHII and rural LST means that support the findings of this work are openly available in Zenodo at https://zenodo.org/record/6535187, reference number 6535187.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
BGABoundary Generation Algorithm
BTBrightness Temperatures
CIMSSCooperative Institute for Meteorological Satellite Studies
ESA-CCIEuropean Space Agency’s Climate Change Initiative
GCOSGlobal Climate Observing System
GPCCGlobal Precipitation Climatology Centre
GSWGeneralized Split-Window
LCLand Cover
LCZLocal Climate Zones
LSTLand Surface Temperature
LST_cciESA-CCI project on Land Surface Temperature
MODISModerate Resolution Imaging Spectroradiometer
RMSDRoot-Mean-Square-Deviation
SDStandard Deviation
SUHISurface Urban Heat Island
SUHIISurface Urban Heat Island Intensity
SWAt-surface clear-sky downwelling shortwave fluxes
UHIUrban Heat Island
UNLCCSUnited Nations Land Cover Classification System

Appendix A

Table A1 presents the agreement between the 2000–2018 SUHII data estimated from the LST_cci MODIS product (v.1.0) and the well-established MOD11A1 LST v.6.0 product. We retrieve the MOD11A1 SUHII data for all the focus areas of Figure 1 using the method described in Section 2.3. To quantify the agreement between the two SUHII datasets, we use the Root-Mean-Square-Deviation (RMSD) and Pearson’s correlation coefficient. Our results show that the daytime and nighttime LST_cci and MOD11A1 SUHII data agree well, with the RMSD ranging from 0.5 to 1.1 K at daytime and 0.1 K to 0.7 K at nighttime. The correlation coefficient ranges from 0.90 to 0.97 and is generally higher during the daytime.
Table
Table A1. The Root-Mean-Square-Deviation (RMSD) and the correlation coefficient between the 2000–2018 LST_cci and MOD11A1 (v.6.0) SUHII for each Köppen–Geiger climate class.
Table A1. The Root-Mean-Square-Deviation (RMSD) and the correlation coefficient between the 2000–2018 LST_cci and MOD11A1 (v.6.0) SUHII for each Köppen–Geiger climate class.
ClimateRMSD (K)CorrelationObservations
DaytimeNighttimeDaytimeNighttimeDaytimeNighttime
Aw0.60.10.970.92929731,831
BSh0.80.50.960.91339313,180
BSk0.60.50.970.94939225,613
Csa0.70.50.940.91282811,988
Cfa0.80.50.940.9019,40164,639
Cfb0.60.60.920.9010,15026,337
Cwa0.60.40.970.92551926,964
Cwb0.60.40.950.95469974
Dfa1.10.40.940.9113,95129,807
Dfb0.60.60.920.9420,87344,667
Dwa0.50.40.970.9514,77541,282

Appendix B

Figure A1 presents the characteristics (area, elevation, and percentage of inland/coastal cities) of the examined cities per Köppen–Geiger climate class. The mean city elevation ranges from 98 m in the Dwa to 1928 m in the Cwb. The pooled mean and the standard deviation (SD) of the elevation means is 400 ± 503 m, while the median of the means is 220 m. The climate classes with the most pronounced elevation differences are the BSk and Cwb, where the interquartile range (ΔQ) is 966 m and 611 m, respectively. The classes where the urban elevations differ the least are the Cfa (ΔQ = 132 m), Cfb (101 m), and Dwa (117 m). The mean city size (Figure A1B) ranges from 32 km2 in the Cfb and BSk to 159 km2 in the Cwb. The pooled mean (±SD) is 57 ± 36 km2 and the median of the means is 48 km2. The size distributions are heavily skewed to the right and appear to follow Zipf’s Law. The class with the largest cities (≥500 km2) is the Cfa (11), followed by the Cfb (3) and Dfa (3). The classes with the greatest variation in city size are the Csa (the SD is 396 km2) and the Cwb (258 km2), while the ones with the least variation are the BSk (43 km2), Cwa (46 km2), and Dfb (53 km2). The percentage of inland and coastal cities for each climate is presented in Figure A1C (we assign a city as coastal if at least one point of its boundary is 10 km or less from the coast). Inland cities make up most of the urban areas in each class. The median and the mean (±SD) percentage for these classes is 84% and 82% (±12%), respectively. The only class with no coastal cities is the Cwb, which corresponds to subtropical highlands.
Remotesensing 14 02318 g0a1 550
Figure A1. The distribution of city elevations (A) and sizes (B) and the percentage of inland and coastal cities (C) per Köppen–Geiger climate class.
Figure A1. The distribution of city elevations (A) and sizes (B) and the percentage of inland and coastal cities (C) per Köppen–Geiger climate class.
Remotesensing 14 02318 g0a1

References

  1. Oke, T.R.; Mills, G.; Christen, A.; Voogt, J.A. Urban Climates, 1st ed.; Cambridge University Press: Cambridge, UK, 2017; ISBN 978-1-139-01647-6. [Google Scholar]
  2. Santamouris, M. On the Energy Impact of Urban Heat Island and Global Warming on Buildings. Energy Build. 2014, 82, 100–113. [Google Scholar] [CrossRef]
  3. Sismanidis, P.; Keramitsoglou, I.; Barberis, S.; Dorotić, H.; Bechtel, B.; Kiranoudis, C.T. PLANHEAT’s Satellite-Derived Heating and Cooling Degrees Dataset for Energy Demand Mapping and Planning. Remote Sens. 2019, 11, 2048. [Google Scholar] [CrossRef] [Green Version]
  4. Keramitsoglou, I.; Sismanidis, P.; Analitis, A.; Butler, T.; Founda, D.; Giannakopoulos, C.; Giannatou, E.; Karali, A.; Katsouyanni, K.; Kendrovski, V.; et al. Urban Thermal Risk Reduction: Developing and Implementing Spatially Explicit Services for Resilient Cities. Sustain. Cities Soc. 2017, 34, 56–68. [Google Scholar] [CrossRef]
  5. Sailor, D.J.; Baniassadi, A.; O’Lenick, C.R.; Wilhelmi, O.V. The Growing Threat of Heat Disasters. Environ. Res. Lett. 2019, 14, 054006. [Google Scholar] [CrossRef]
  6. Sarrat, C.; Lemonsu, A.; Masson, V.; Guedalia, D. Impact of Urban Heat Island on Regional Atmospheric Pollution. Atmos. Environ. 2006, 40, 1743–1758. [Google Scholar] [CrossRef]
  7. Baccini, M.; Biggeri, A.; Accetta, G.; Kosatsky, T.; Katsouyanni, K.; Analitis, A.; Anderson, H.R.; Bisanti, L.; DʼIppoliti, D.; Danova, J.; et al. Heat Effects on Mortality in 15 European Cities. Epidemiology 2008, 19, 711–719. [Google Scholar] [CrossRef]
  8. Zafeiratou, S.; Analitis, A.; Founda, D.; Giannakopoulos, C.; Varotsos, K.V.; Sismanidis, P.; Keramitsoglou, I.; Katsouyanni, K. Spatial Variability in the Effect of High Ambient Temperature on Mortality: An Analysis at Municipality Level within the Greater Athens Area. Int. J. Environ. Res. Public Health 2019, 16, 3689. [Google Scholar] [CrossRef] [Green Version]
  9. Santamouris, M.; Paraponiaris, K.; Mihalakakou, G. Estimating the Ecological Footprint of the Heat Island Effect over Athens, Greece. Clim. Chang. 2007, 80, 265–276. [Google Scholar] [CrossRef]
  10. Bechtel, B.; Demuzere, M.; Mills, G.; Zhan, W.; Sismanidis, P.; Small, C.; Voogt, J. SUHI Analysis Using Local Climate Zones—A Comparison of 50 Cities. Urban Clim. 2019, 28, 100451. [Google Scholar] [CrossRef]
  11. Zhao, L.; Lee, X.; Smith, R.B.; Oleson, K. Strong Contributions of Local Background Climate to Urban Heat Islands. Nature 2014, 511, 216–219. [Google Scholar] [CrossRef]
  12. Parlow, E. Regarding Some Pitfalls in Urban Heat Island Studies Using Remote Sensing Technology. Remote Sens. 2021, 13, 3598. [Google Scholar] [CrossRef]
  13. Clinton, N.; Gong, P. MODIS Detected Surface Urban Heat Islands and Sinks: Global Locations and Controls. Remote Sens. Environ. 2013, 134, 294–304. [Google Scholar] [CrossRef]
  14. Chrysoulakis, N.; Grimmond, S.; Feigenwinter, C.; Lindberg, F.; Gastellu-Etchegorry, J.-P.; Marconcini, M.; Mitraka, Z.; Stagakis, S.; Crawford, B.; Olofson, F.; et al. Urban Energy Exchanges Monitoring from Space. Sci. Rep. 2018, 8, 11498. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  15. Keramitsoglou, I.; Kiranoudis, C.T.; Ceriola, G.; Weng, Q.; Rajasekar, U. Identification and Analysis of Urban Surface Temperature Patterns in Greater Athens, Greece, Using MODIS Imagery. Remote Sens. Environ. 2011, 115, 3080–3090. [Google Scholar] [CrossRef]
  16. Sismanidis, P.; Keramitsoglou, I.; Kiranoudis, C.T. A Satellite-Based System for Continuous Monitoring of Surface Urban Heat Islands. Urban Clim. 2015, 14, 141–153. [Google Scholar] [CrossRef]
  17. Voogt, J.A.; Oke, T.R. Thermal Remote Sensing of Urban Climates. Remote Sens. Environ. 2003, 86, 370–384. [Google Scholar] [CrossRef]
  18. Venter, Z.S.; Chakraborty, T.; Lee, X. Crowdsourced Air Temperatures Contrast Satellite Measures of the Urban Heat Island and Its Mechanisms. Sci. Adv. 2021, 7, eabb9569. [Google Scholar] [CrossRef]
  19. Li, D.; Liao, W.; Rigden, A.J.; Liu, X.; Wang, D.; Malyshev, S.; Shevliakova, E. Urban Heat Island: Aerodynamics or Imperviousness? Sci. Adv. 2019, 5, eaau4299. [Google Scholar] [CrossRef] [Green Version]
  20. Stewart, I.D.; Krayenhoff, E.S.; Voogt, J.A.; Lachapelle, J.A.; Allen, M.A.; Broadbent, A.M. Time Evolution of the Surface Urban Heat Island. Earth’s Future 2021, 9, e2021EF002178. [Google Scholar] [CrossRef]
  21. Sismanidis, P.; Keramitsoglou, I.; Kiranoudis, C.T. Diurnal Analysis of Surface Urban Heat Island Using Spatially Enhanced Satellite Derived LST Data. In Proceedings of the 2015 Joint Urban Remote Sensing Event (JURSE), Lausanne, Switzerland, 30 March–1 April 2015; pp. 1–4. [Google Scholar]
  22. Peng, S.; Piao, S.; Ciais, P.; Friedlingstein, P.; Ottle, C.; Bréon, F.-M.; Nan, H.; Zhou, L.; Myneni, R.B. Surface Urban Heat Island Across 419 Global Big Cities. Environ. Sci. Technol. 2012, 46, 696–703. [Google Scholar] [CrossRef]
  23. Chakraborty, T.; Lee, X. A Simplified Urban-Extent Algorithm to Characterize Surface Urban Heat Islands on a Global Scale and Examine Vegetation Control on Their Spatiotemporal Variability. Int. J. Appl. Earth Obs. Geoinf. 2019, 74, 269–280. [Google Scholar] [CrossRef]
  24. Martilli, A.; Krayenhoff, E.S.; Nazarian, N. Is the Urban Heat Island Intensity Relevant for Heat Mitigation Studies? Urban Clim. 2020, 31, 100541. [Google Scholar] [CrossRef]
  25. Yang, X.; Yao, L. Reexamining the Relationship between Surface Urban Heat Island Intensity and Annual Precipitation: Effects of Reference Rural Land Cover. Urban Clim. 2022, 41, 101074. [Google Scholar] [CrossRef]
  26. Zhou, B.; Lauwaet, D.; Hooyberghs, H.; De Ridder, K.; Kropp, J.P.; Rybski, D. Assessing Seasonality in the Surface Urban Heat Island of London. J. Appl. Meteorol. Climatol. 2016, 55, 493–505. [Google Scholar] [CrossRef] [Green Version]
  27. Haashemi, S.; Weng, Q.; Darvishi, A.; Alavipanah, S.K. Seasonal Variations of the Surface Urban Heat Island in a Semi-Arid City. Remote Sens. 2016, 8, 352. [Google Scholar] [CrossRef] [Green Version]
  28. Bechtel, B. Robustness of Annual Cycle Parameters to Characterize the Urban Thermal Landscapes. IEEE Geosci. Remote Sens. Lett. 2012, 9, 876–880. [Google Scholar] [CrossRef]
  29. Bechtel, B. Multitemporal Landsat Data for Urban Heat Island Assessment and Classification of Local Climate Zones. In Proceedings of the 2011 Joint Urban Remote Sensing Event, Munich, Germany, 11–13 April 2011; pp. 129–132. [Google Scholar]
  30. Mathew, A.; Khandelwal, S.; Kaul, N. Investigating Spatial and Seasonal Variations of Urban Heat Island Effect over Jaipur City and Its Relationship with Vegetation, Urbanization and Elevation Parameters. Sustain. Cities Soc. 2017, 35, 157–177. [Google Scholar] [CrossRef]
  31. Aslam, B.; Maqsoom, A.; Khalid, N.; Ullah, F.; Sepasgozar, S. Urban Overheating Assessment through Prediction of Surface Temperatures: A Case Study of Karachi, Pakistan. IJGI 2021, 10, 539. [Google Scholar] [CrossRef]
  32. Zhao, Z.; Sharifi, A.; Dong, X.; Shen, L.; He, B.-J. Spatial Variability and Temporal Heterogeneity of Surface Urban Heat Island Patterns and the Suitability of Local Climate Zones for Land Surface Temperature Characterization. Remote Sens. 2021, 13, 4338. [Google Scholar] [CrossRef]
  33. Zhou, B.; Rybski, D.; Kropp, J.P. On the Statistics of Urban Heat Island Intensity. Geophys. Res. Lett. 2013, 40, 5486–5491. [Google Scholar] [CrossRef]
  34. Bechtel, B.; Sismanidis, P.; Voogt, J.; Zhan, W. Seasonal Surface Urban Heat Island Analysis. In Proceedings of the 2019 Joint Urban Remote Sensing Event (JURSE), Vannes, France, 21–24 May 2019; pp. 1–4. [Google Scholar]
  35. Shastri, H.; Barik, B.; Ghosh, S.; Venkataraman, C.; Sadavarte, P. Flip Flop of Day-Night and Summer-Winter Surface Urban Heat Island Intensity in India. Sci. Rep. 2017, 7, 40178. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  36. Zhou, D.; Zhao, S.; Zhang, L.; Sun, G.; Liu, Y. The Footprint of Urban Heat Island Effect in China. Sci. Rep. 2015, 5, 11160. [Google Scholar] [CrossRef] [PubMed]
  37. Chakraborty, T.; Hsu, A.; Manya, D.; Sheriff, G. A Spatially Explicit Surface Urban Heat Island Database for the United States: Characterization, Uncertainties, and Possible Applications. ISPRS J. Photogramm. Remote Sens. 2020, 168, 74–88. [Google Scholar] [CrossRef]
  38. Imhoff, M.L.; Zhang, P.; Wolfe, R.E.; Bounoua, L. Remote Sensing of the Urban Heat Island Effect across Biomes in the Continental USA. Remote Sens. Environ. 2010, 114, 504–513. [Google Scholar] [CrossRef] [Green Version]
  39. Schwarz, N.; Lautenbach, S.; Seppelt, R. Exploring Indicators for Quantifying Surface Urban Heat Islands of European Cities with MODIS Land Surface Temperatures. Remote Sens. Environ. 2011, 115, 3175–3186. [Google Scholar] [CrossRef]
  40. Li, X.; Stringer, L.C.; Dallimer, M. The Role of Blue Green Infrastructure in the Urban Thermal Environment across Seasons and Local Climate Zones in East Africa. Sustain. Cities Soc. 2022, 80, 103798. [Google Scholar] [CrossRef]
  41. Liu, Z.; Zhan, W.; Lai, J.; Bechtel, B.; Lee, X.; Hong, F.; Li, L.; Huang, F.; Li, J. Taxonomy of Seasonal and Diurnal Clear-Sky Climatology of Surface Urban Heat Island Dynamics across Global Cities. ISPRS J. Photogramm. Remote Sens. 2022, 187, 14–33. [Google Scholar] [CrossRef]
  42. Manoli, G.; Fatichi, S.; Bou-Zeid, E.; Katul, G.G. Seasonal Hysteresis of Surface Urban Heat Islands. Proc. Natl. Acad. Sci. USA 2020, 117, 7082–7089. [Google Scholar] [CrossRef]
  43. Manoli, G.; Fatichi, S.; Schläpfer, M.; Yu, K.; Crowther, T.W.; Meili, N.; Burlando, P.; Katul, G.G.; Bou-Zeid, E. Magnitude of Urban Heat Islands Largely Explained by Climate and Population. Nature 2019, 573, 55–60. [Google Scholar] [CrossRef]
  44. Beck, H.E.; Zimmermann, N.E.; McVicar, T.R.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and Future Köppen-Geiger Climate Classification Maps at 1-Km Resolution. Sci. Data 2018, 5, 180214. [Google Scholar] [CrossRef] [Green Version]
  45. Wan, Z.; Dozier, J. A Generalized Split-Window Algorithm for Retrieving Land-Surface Temperature from Space. IEEE Trans. Geosci. Remote Sens. 1996, 34, 892–905. [Google Scholar] [CrossRef] [Green Version]
  46. Seemann, S.W.; Borbas, E.E.; Knuteson, R.O.; Stephenson, G.R.; Huang, H.-L. Development of a Global Infrared Land Surface Emissivity Database for Application to Clear Sky Sounding Retrievals from Multispectral Satellite Radiance Measurements. J. Appl. Meteorol. Climatol. 2008, 47, 108–123. [Google Scholar] [CrossRef]
  47. Ghent, D.; Veal, K.; Trent, T.; Dodd, E.; Sembhi, H.; Remedios, J. A New Approach to Defining Uncertainties for MODIS Land Surface Temperature. Remote Sens. 2019, 11, 1021. [Google Scholar] [CrossRef] [Green Version]
  48. ESA. ESA CCI Land Cover Product User Guide. 2017; p. 105. Available online: http://maps.elie.ucl.ac.be/CCI/viewer/download/ESACCI-LC-Ph2-PUGv2_2.0.pdf (accessed on 5 May 2022).
  49. van der Walt, S.; Schönberger, J.L.; Nunez-Iglesias, J.; Boulogne, F.; Warner, J.D.; Yager, N.; Gouillart, E.; Yu, T. Scikit-Image: Image Processing in Python. PeerJ 2014, 2, e453. [Google Scholar] [CrossRef]
  50. Rozenfeld, H.D.; Rybski, D.; Gabaix, X.; Makse, H.A. The Area and Population of Cities: New Insights from a Different Perspective on Cities. Am. Econ. Rev. 2011, 101, 2205–2225. [Google Scholar] [CrossRef] [Green Version]
  51. Stewart, I.D.; Oke, T.R. Local Climate Zones for Urban Temperature Studies. Bull. Am. Meteorol. Soc. 2012, 93, 1879–1900. [Google Scholar] [CrossRef]
  52. Schneider, U.; Becker, A.; Finger, P.; Meyer-Christoffer, A.; Ziese, M.; Rudolf, B. GPCC’s New Land Surface Precipitation Climatology Based on Quality-Controlled in Situ Data and Its Role in Quantifying the Global Water Cycle. Theor. Appl. Climatol. 2014, 115, 15–40. [Google Scholar] [CrossRef] [Green Version]
  53. Doelling, D.R.; Sun, M.; Nguyen, L.T.; Nordeen, M.L.; Haney, C.O.; Keyes, D.F.; Mlynczak, P.E. Advances in Geostationary-Derived Longwave Fluxes for the CERES Synoptic (SYN1deg) Product. J. Atmos. Ocean. Technol. 2016, 33, 503–521. [Google Scholar] [CrossRef]
  54. Gouveia, C.M.; Trigo, R.M.; Beguería, S.; Vicente-Serrano, S.M. Drought Impacts on Vegetation Activity in the Mediterranean Region: An Assessment Using Remote Sensing Data and Multi-Scale Drought Indicators. Glob. Planet. Chang. 2017, 151, 15–27. [Google Scholar] [CrossRef] [Green Version]
  55. Peel, M.C.; Finlayson, B.L.; Mcmahon, T.A. Updated World Map of the Köppen-Geiger Climate Classification. Hydrol. Earth Syst. Sci. Discuss. 2007, 11, 1633–1644. [Google Scholar] [CrossRef] [Green Version]
  56. Taubenböck, H.; Debray, H.; Qiu, C.; Schmitt, M.; Wang, Y.; Zhu, X.X. Seven City Types Representing Morphologic Configurations of Cities across the Globe. Cities 2020, 105, 102814. [Google Scholar] [CrossRef]
  57. Demuzere, M.; Bechtel, B.; Middel, A.; Mills, G. Mapping Europe into Local Climate Zones. PLoS ONE 2019, 14, e0214474. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  58. Liu, H.; Huang, B.; Zhan, Q.; Gao, S.; Li, R.; Fan, Z. The Influence of Urban Form on Surface Urban Heat Island and Its Planning Implications: Evidence from 1288 Urban Clusters in China. Sustain. Cities Soc. 2021, 71, 102987. [Google Scholar] [CrossRef]
  59. Zhou, B.; Rybski, D.; Kropp, J.P. The Role of City Size and Urban Form in the Surface Urban Heat Island. Sci. Rep. 2017, 7, 4791. [Google Scholar] [CrossRef] [PubMed]
Remotesensing 14 02318 g001 550
Figure 1. Areas of dense human habitation and the focus areas of this work. The present Köppen–Geiger climate zones are also shown.
Figure 1. Areas of dense human habitation and the focus areas of this work. The present Köppen–Geiger climate zones are also shown.
Remotesensing 14 02318 g001
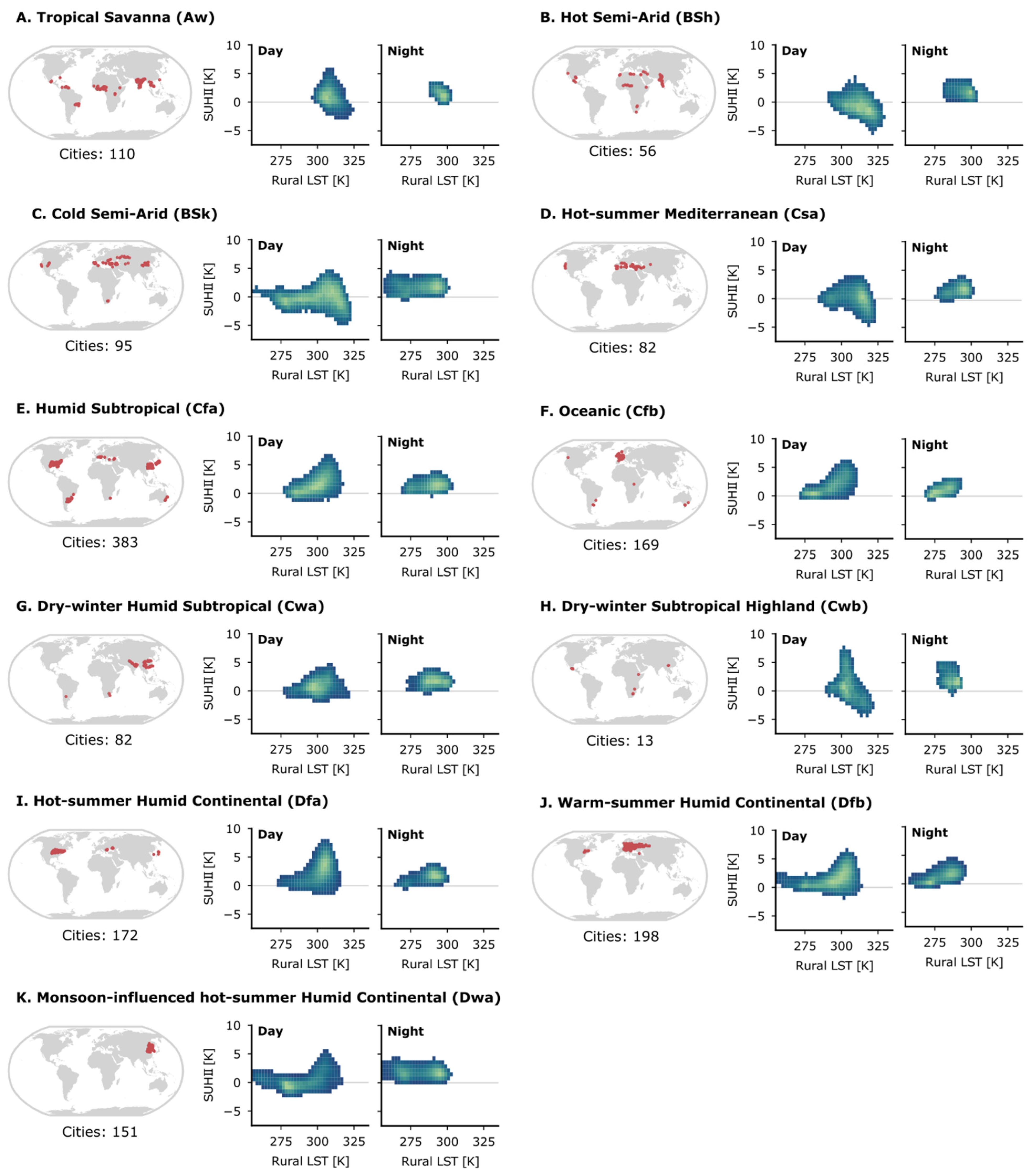
Remotesensing 14 02318 g002 550
Figure 2. The location and number of delineated cities per Köppen–Geiger climate class and the corresponding daytime and nighttime SUHII climatologies visualized as the bivariate distribution of daily SUHII and rural LST. Each distribution presents all the possible combinations of SUHII and rural LST and is unique and characteristic of the respective climate class. The colors indicate how likely each combination is: yellow indicates the most likely and blue the least.
Figure 2. The location and number of delineated cities per Köppen–Geiger climate class and the corresponding daytime and nighttime SUHII climatologies visualized as the bivariate distribution of daily SUHII and rural LST. Each distribution presents all the possible combinations of SUHII and rural LST and is unique and characteristic of the respective climate class. The colors indicate how likely each combination is: yellow indicates the most likely and blue the least.
Remotesensing 14 02318 g002
Remotesensing 14 02318 g003 550
Figure 3. The daytime SUHII hysteresis loops for each Köppen–Geiger climate class (colored lines). Each black dot represents a month (the start and end points correspond to spring equinox), and the change in color indicates the direction of each loop. The solid grey loops represent the individual city loops per climate class, and the dashed one represents the corresponding parent-class loops.
Figure 3. The daytime SUHII hysteresis loops for each Köppen–Geiger climate class (colored lines). Each black dot represents a month (the start and end points correspond to spring equinox), and the change in color indicates the direction of each loop. The solid grey loops represent the individual city loops per climate class, and the dashed one represents the corresponding parent-class loops.
Remotesensing 14 02318 g003
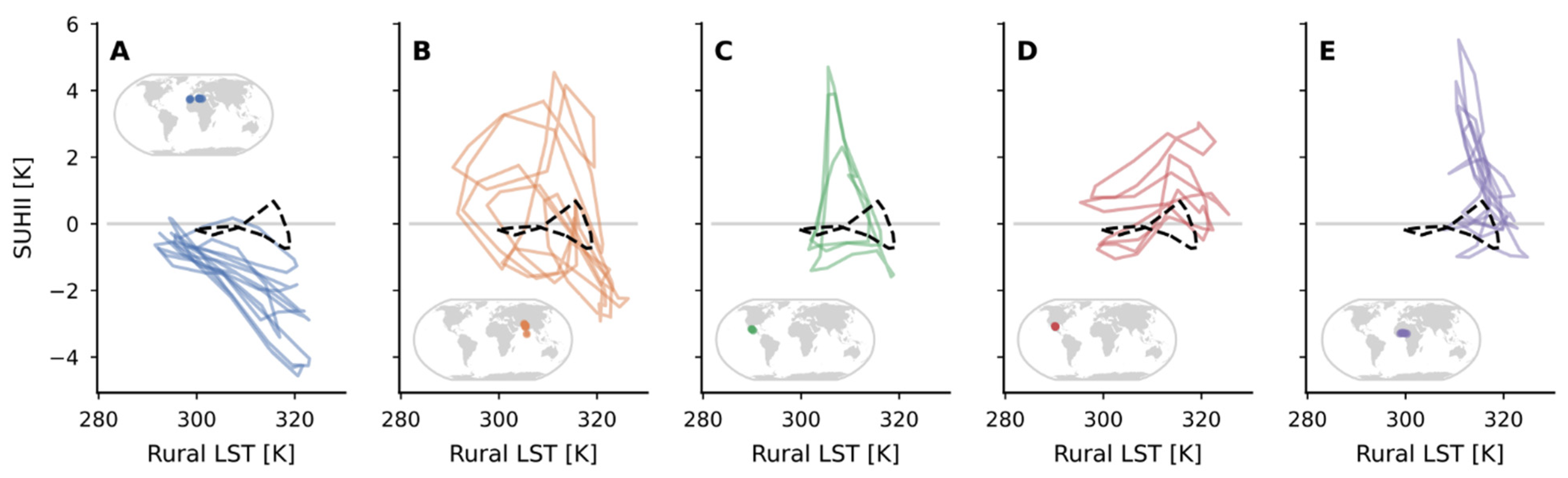
Remotesensing 14 02318 g004 550
Figure 4. The individual daytime SUHII hysteresis loops for hot semi-arid (BSh) cities in North Africa (A), South Asia (B), Central America—Mexico (C), Central America—USA (D), and West Africa (E). The dashed line is the mean BSh loop from Figure 3.
Figure 4. The individual daytime SUHII hysteresis loops for hot semi-arid (BSh) cities in North Africa (A), South Asia (B), Central America—Mexico (C), Central America—USA (D), and West Africa (E). The dashed line is the mean BSh loop from Figure 3.
Remotesensing 14 02318 g004
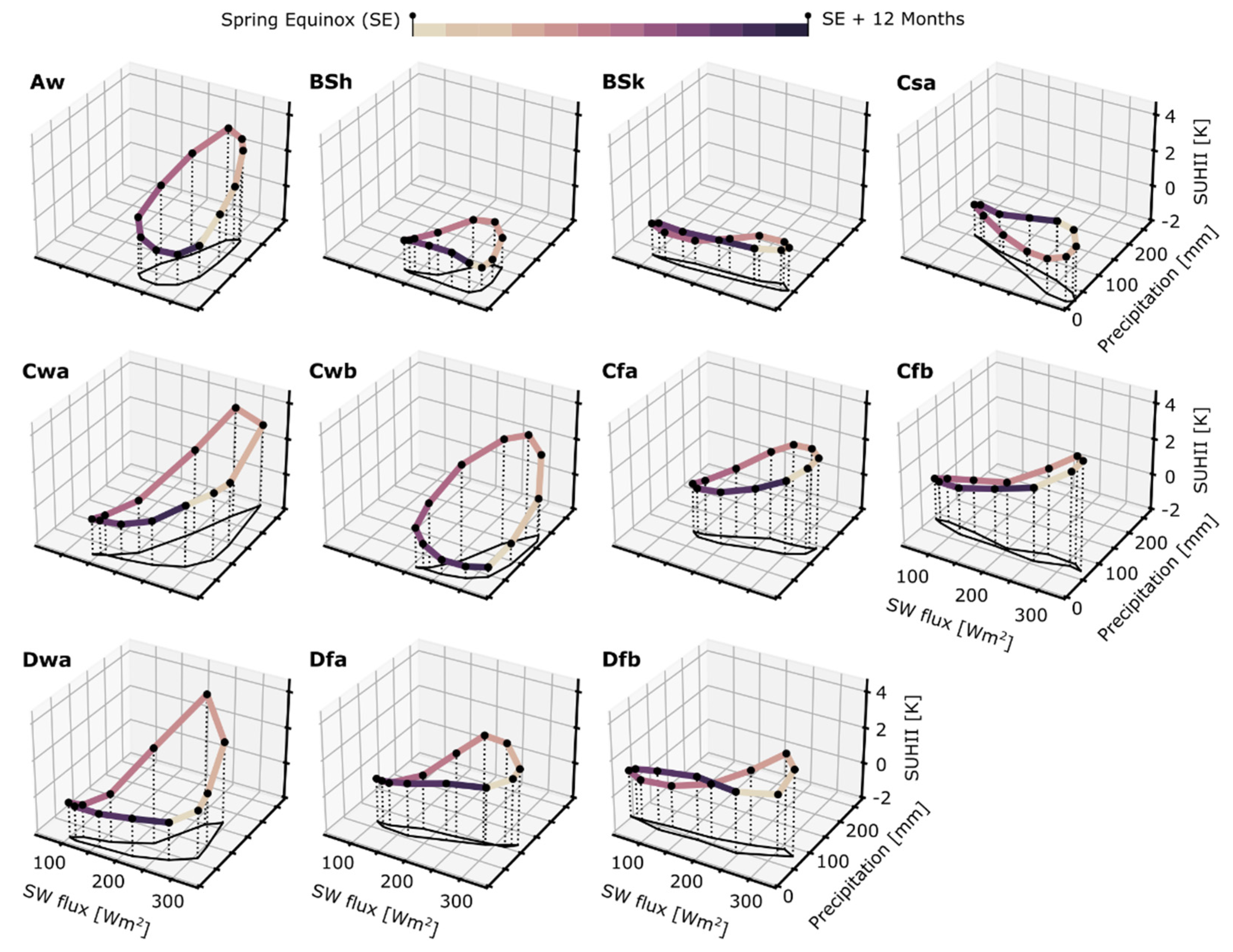
Remotesensing 14 02318 g005 550
Figure 5. The seasonal variation of precipitation, clear-sky at-surface downwelling shortwave radiation flux (SW), and daytime SUHII for each Köppen–Geiger climate class examined in this work. Each dot represents a month (the start and end points correspond to spring equinox). The monthly means refer to the years 2000-2018 and the color of the line indicates the direction of each loop.
Figure 5. The seasonal variation of precipitation, clear-sky at-surface downwelling shortwave radiation flux (SW), and daytime SUHII for each Köppen–Geiger climate class examined in this work. Each dot represents a month (the start and end points correspond to spring equinox). The monthly means refer to the years 2000-2018 and the color of the line indicates the direction of each loop.
Remotesensing 14 02318 g005
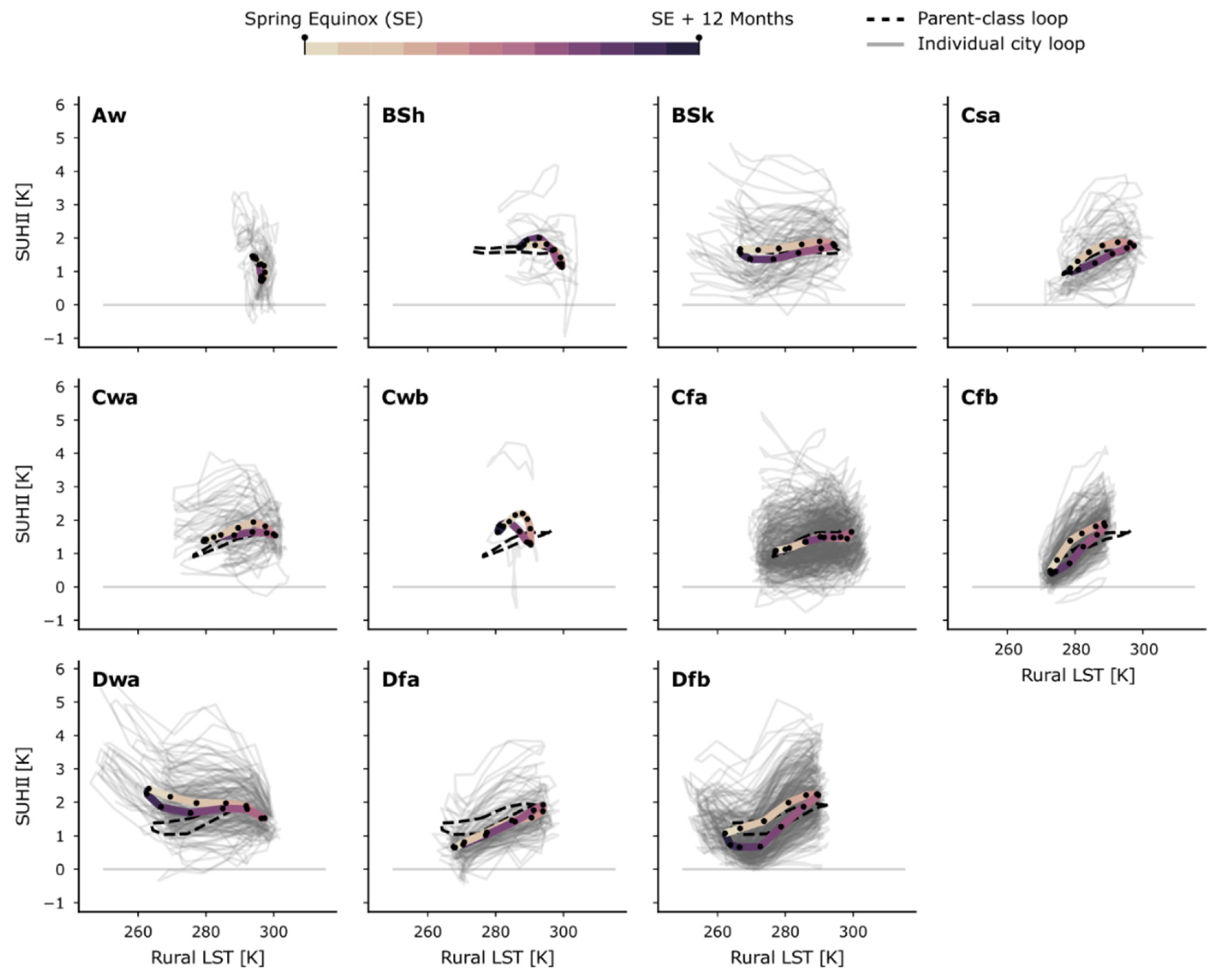
Remotesensing 14 02318 g006 550
Figure 6. The nighttime SUHII hysteresis loops for each Köppen–Geiger climate class (colored lines). Each black dot represents a month (the start and end points correspond to spring equinox), and the change in color indicates the direction of each loop. The solid grey loops represent the individual city loops of each climate class, and the dashed one represents the corresponding parent-class loops.
Figure 6. The nighttime SUHII hysteresis loops for each Köppen–Geiger climate class (colored lines). Each black dot represents a month (the start and end points correspond to spring equinox), and the change in color indicates the direction of each loop. The solid grey loops represent the individual city loops of each climate class, and the dashed one represents the corresponding parent-class loops.
Remotesensing 14 02318 g006
Remotesensing 14 02318 g007 550
Figure 7. The seasonal variation of precipitation, clear-sky at-surface downwelling shortwave radiation flux (SW) and nighttime SUHII for each Köppen–Geiger climate class examined in this work. Each dot represents a month (the start and end points correspond to spring equinox). The monthly means refer to the years 2000–2018, and the color of the line indicates the direction of each loop.
Figure 7. The seasonal variation of precipitation, clear-sky at-surface downwelling shortwave radiation flux (SW) and nighttime SUHII for each Köppen–Geiger climate class examined in this work. Each dot represents a month (the start and end points correspond to spring equinox). The monthly means refer to the years 2000–2018, and the color of the line indicates the direction of each loop.
Remotesensing 14 02318 g007
Remotesensing 14 02318 g008 550
Figure 8. The month when SUHII, rural LST, SW, and precipitation are strongest per climate class. The colored dots represent the individual SUHII loops and the black dots the Köppen–Geiger climate-class mean loop (BSh and BSk are not included).
Figure 8. The month when SUHII, rural LST, SW, and precipitation are strongest per climate class. The colored dots represent the individual SUHII loops and the black dots the Köppen–Geiger climate-class mean loop (BSh and BSk are not included).
Remotesensing 14 02318 g008
Remotesensing 14 02318 g009 550
Figure 9. The month when SUHII, rural LST, SW flux, and precipitation are minimum. The colored dots represent the individual SUHII loops, and the black dots the Köppen–Geiger climate-class mean loop (BSh and BSk are not included).
Figure 9. The month when SUHII, rural LST, SW flux, and precipitation are minimum. The colored dots represent the individual SUHII loops, and the black dots the Köppen–Geiger climate-class mean loop (BSh and BSk are not included).
Remotesensing 14 02318 g009
Table
Table 1. The rural LC component classes.
Table 1. The rural LC component classes.
IDESA-CCI Land Cover Class
10Rainfed croplands
11Rainfed croplands with herbaceous cover
12Rainfed croplands with tree or shrub cover
20Irrigated croplands
30Mosaic croplands (>50%) with natural vegetation
40Mosaic natural vegetation (>50%) with croplands
110Mosaic herbaceous cover (>50%) with trees and shrubs
120Shrublands
121Evergreen shrublands
122Deciduous shrublands
130Grasslands
140Lichens and mosses
150Sparse vegetation
151Sparse trees
152Sparse shrubs
153Sparse herbaceous cover
200Bare areas
201Consolidated bare areas
Table
Table 2. The Köppen–Geiger climate classes analyzed in this work.
Table 2. The Köppen–Geiger climate classes analyzed in this work.
IDParent ClassDescription
AwTropicalTropical savanna with dry-winter characteristics
BShDryHot semi-arid
BSkCold semi-arid
CsaTemperateHot-summer mediterranean
CfaHumid subtropical
CfbOceanic
CwaDry-winter humid subtropical
CwbDry-winter subtropical highland
DfaContinentalHot-summer humid continental
DfbWarm-summer humid continental
DwaMonsoon-influenced hot-summer humid continental
Table
Table 3. The mean and the standard deviation (SD) of the 2000–2018 daily SUHII and rural LST shown in Figure 2.
Table 3. The mean and the standard deviation (SD) of the 2000–2018 daily SUHII and rural LST shown in Figure 2.
ClimateSUHII (K)Rural LST (K)
DaytimeNighttimeDaytimeNighttime
MeanSDMeanSDMeanSDMeanSD
Aw1.32.71.41.2311.07.0296.24.0
BSh−0.62.32.01.3312.39.6293.46.7
BSk−0.12.11.91.3296.517.0279.713.0
Csa0.02.01.71.2303.611.0287.87.3
Cfa1.82.21.51.2301.011.0287.39.3
Cfb1.71.91.21.1292.111.4280.56.9
Cwa1.22.01.81.2304.510.2291.58.3
Cwb1.23.12.21.6305.57.2286.05.1
Dfa1.92.31.41.2293.813.6280.611.1
Dfb1.51.91.51.4288.217.0276.311.5
Dwa1.12.32.11.4294.416.2280.214.3
Table
Table 4. The minimum and maximum SUHII (and the 95% confidence intervals) for the Köppen–Geiger climate-class means shown in Figure 8 and Figure 9 (black dots).
Table 4. The minimum and maximum SUHII (and the 95% confidence intervals) for the Köppen–Geiger climate-class means shown in Figure 8 and Figure 9 (black dots).
ClimateMaximum SUHII (K)Minimum SUHII (K)
DaytimeNighttimeDaytimeNighttime
Aw4.3 ± 0.81.4 ± 0.2−0.1 ± 0.70.8 ± 0.2
BSh-1.9 ± 0.2-1.1 ± 0.3
BSk-2.0 ± 0.2-1.4 ± 0.2
Csa1.5 ± 0.41.8 ± 0.20.0 ± 0.20.9 ± 0.2
Cfa3.6 ± 0.31.7 ± 0.10.7 ± 0.11.1 ± 0.1
Cfb4.0 ± 0.21.9 ± 0.10.4 ± 0.10.4 ± 0.1
Cwa4.1 ± 0.51.9 ± 0.20.0 ± 0.21.4 ± 0.1
Cwb3.8 ± 1.32.2 ± 1.10.2 ± 0.61.3 ± 1.1
Dfa3.9 ± 0.41.9 ± 0.10.4 ± 0.10.7 ± 0.1
Dfb3.3 ± 0.22.2 ± 0.10.3 ± 0.10.7 ± 0.1
Dwa5.2 ± 0.32.4 ± 0.20.0 ± 0.11.5 ± 0.1
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Sismanidis, P.; Bechtel, B.; Perry, M.; Ghent, D. The Seasonality of Surface Urban Heat Islands across Climates. Remote Sens. 2022, 14, 2318. https://doi.org/10.3390/rs14102318

AMA Style

Sismanidis P, Bechtel B, Perry M, Ghent D. The Seasonality of Surface Urban Heat Islands across Climates. Remote Sensing. 2022; 14(10):2318. https://doi.org/10.3390/rs14102318

Chicago/Turabian Style

Sismanidis, Panagiotis, Benjamin Bechtel, Mike Perry, and Darren Ghent. 2022. "The Seasonality of Surface Urban Heat Islands across Climates" Remote Sensing 14, no. 10: 2318. https://doi.org/10.3390/rs14102318

APA Style

Sismanidis, P., Bechtel, B., Perry, M., & Ghent, D. (2022). The Seasonality of Surface Urban Heat Islands across Climates. Remote Sensing, 14(10), 2318. https://doi.org/10.3390/rs14102318

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop