Multi-Temporal Landsat-8 Images for Retrieval and Broad Scale Mapping of Soil Copper Concentration Using Empirical Models
Abstract
:1. Introduction
- Instead of just using a single remote sensing image (SI), multi-temporal images (MTIs) of the same area are considered;
- Instead of just using the original Landsat data, various feature extraction scenarios are evaluated;
- A number of regression models are compared and contrasted to improve overall accuracy;
- The complete data processing pipeline (multi-temporal data, feature extraction and model selection) can produce maps consistent with ancillary ground-truth information.
2. Theoretical Background
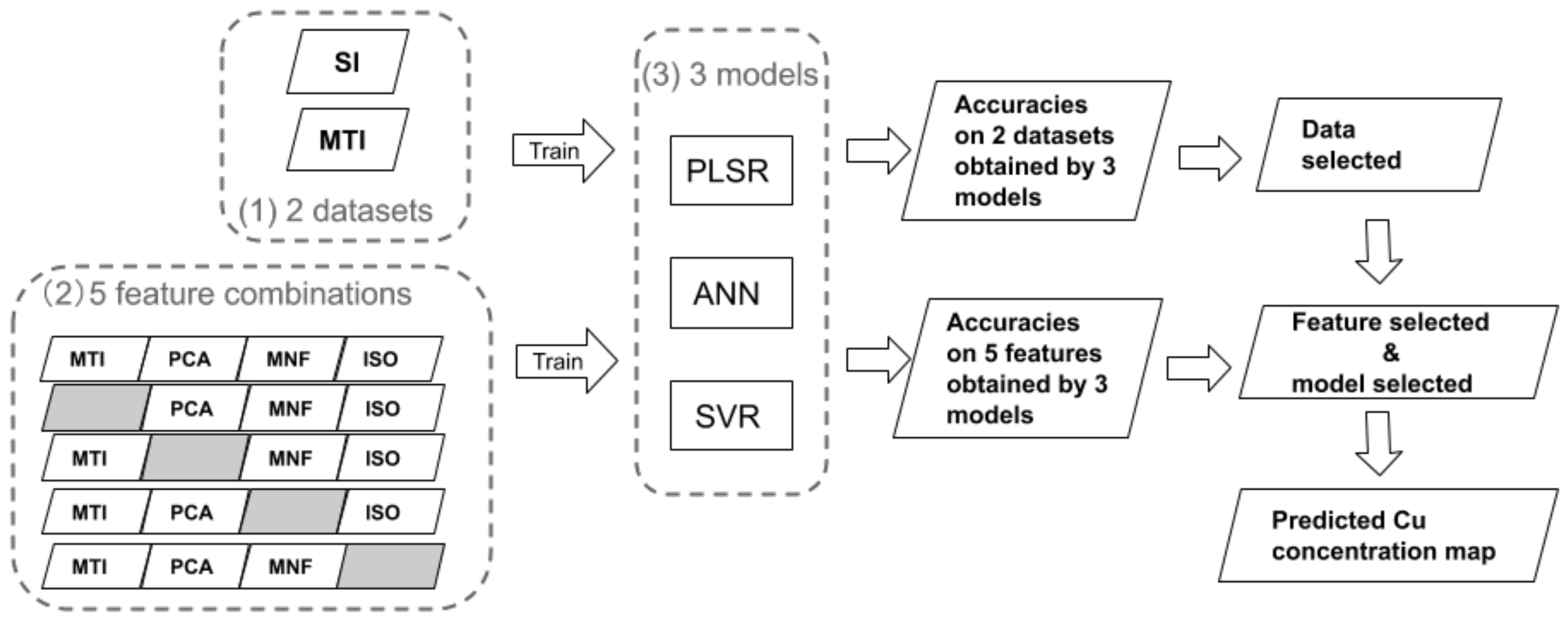
3. Materials and Methods
3.1. Study Area and Soil Samples
3.2. Multi-Temporal Images of Landsat-8
3.3. Feature Selection
3.3.1. Feature Extraction
3.3.2. Feature Importance Measure
3.4. Regression Methods
3.4.1. Partial Least Square Regression, PLSR
3.4.2. Artificial Neural Network, ANN
3.4.3. Support Vector Regression, SVR
3.5. Accuracy Measure
3.6. Cross-Validation Estimation
4. Results
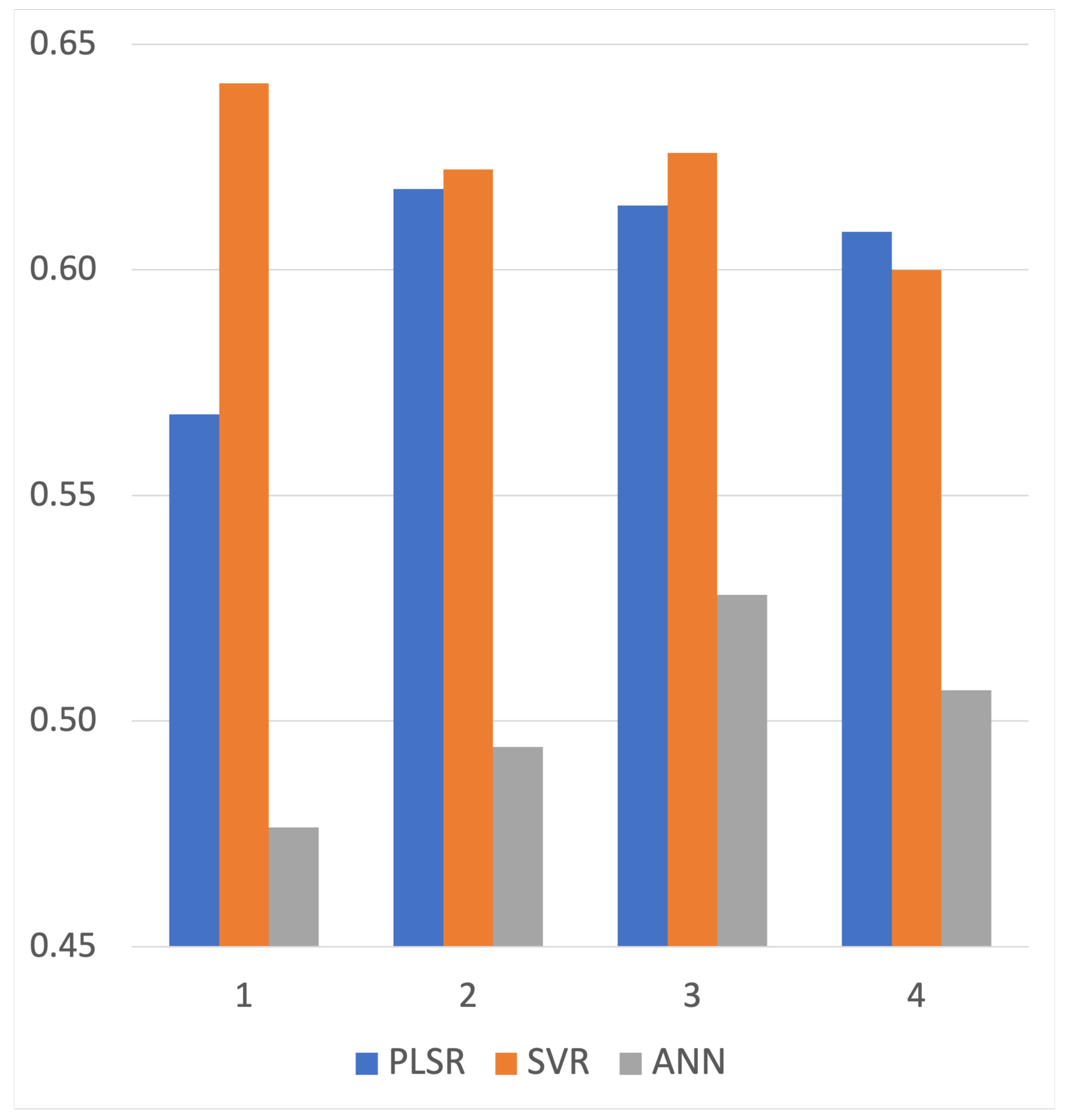
4.1. Comparison between Single and Multi-Temporal Images of Landsat-8
4.2. Feature Evaluation and Selection
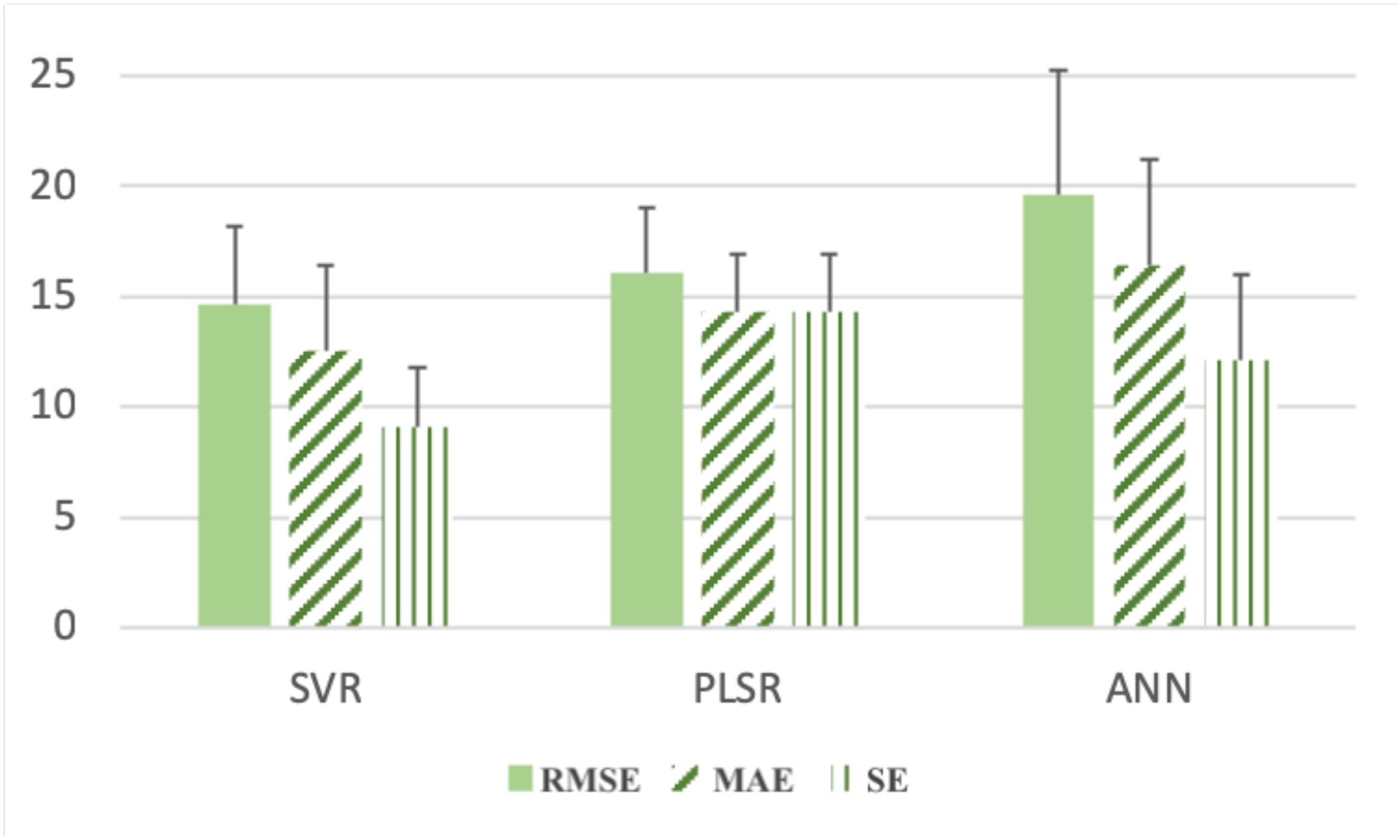
4.3. Model Selection
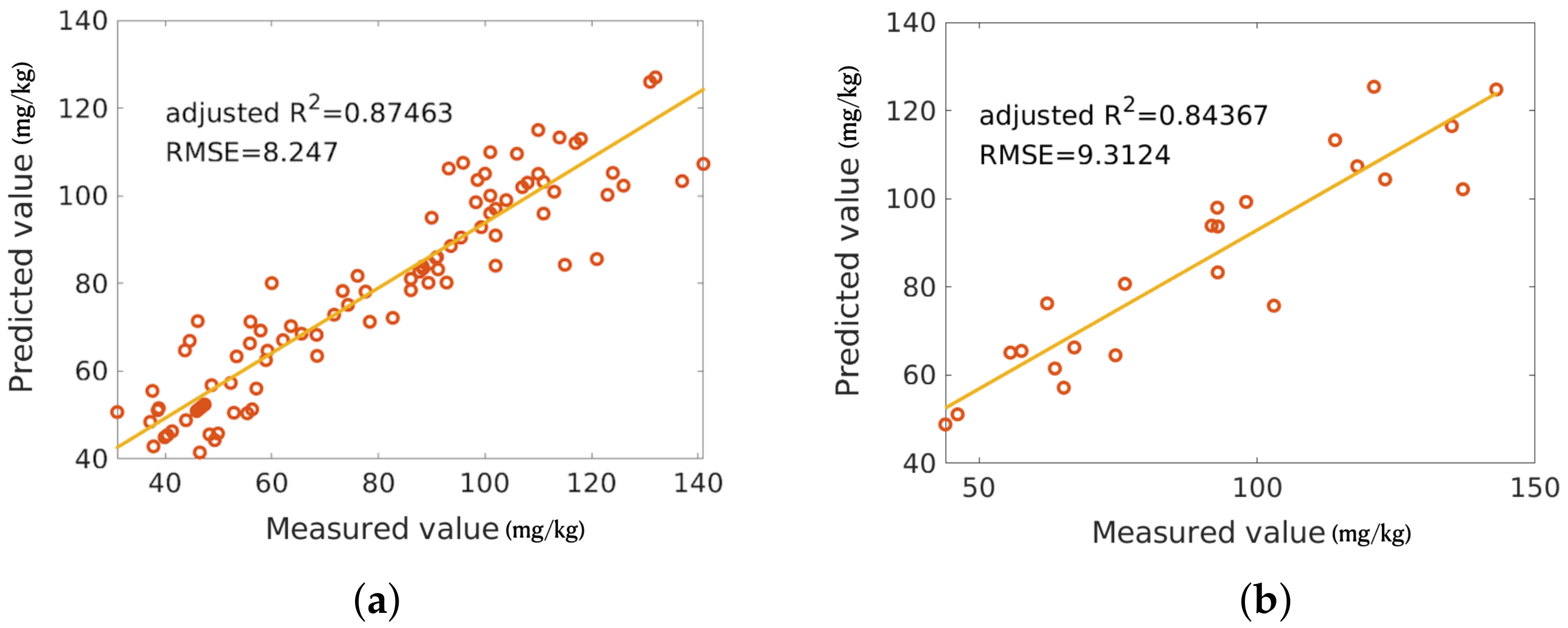
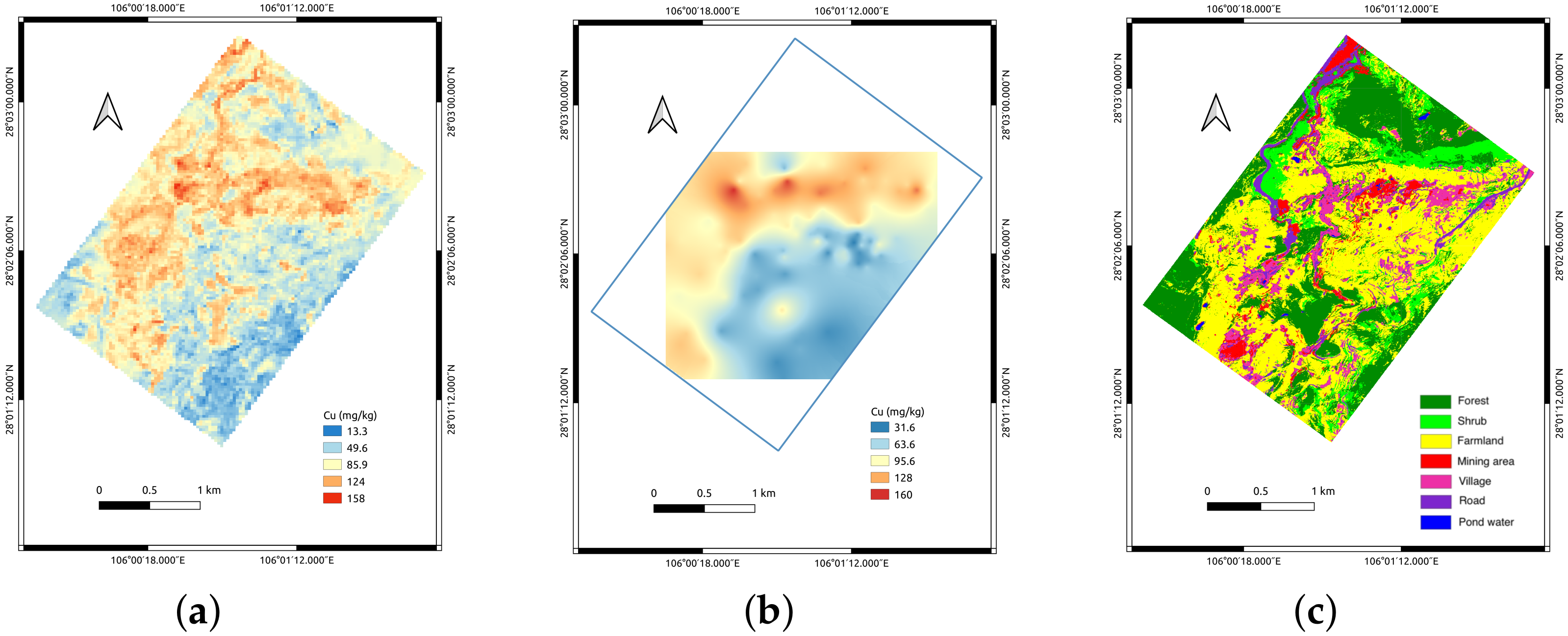
4.4. Soil Cu Concentration Mapping
5. Discussion
5.1. Benefits of Using Multi-Temporal Landsat-8 Images
5.2. Feature Selection
5.3. Regressor Comparison
5.4. Cu Concentration Mapping
5.5. Uncertainty Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Wild, A. Soils and the Environment; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Alloway, B.J. Heavy Metals in Soils: Trace Metals and Metalloids in Soils and Their Bioavailability; Springer Science & Business Media: New York, NY, USA, 2012; Volume 22. [Google Scholar]
- McBratney, A.B.; Odeh, I.O.; Bishop, T.F.; Dunbar, M.S.; Shatar, T.M. An overview of pedometric techniques for use in soil survey. Geoderma 2000, 97, 293–327. [Google Scholar] [CrossRef]
- Slonecker, T.; Fisher, G.B.; Aiello, D.P.; Haack, B. Visible and infrared remote imaging of hazardous waste: A review. Remote Sens. 2010, 2, 2474–2508. [Google Scholar] [CrossRef] [Green Version]
- Choe, E.; Kim, K.W.; Bang, S.; Yoon, I.H.; Lee, K.Y. Qualitative analysis and mapping of heavy metals in an abandoned Au-Ag mine area using NIR spectroscopy. Environ. Geol. 2009, 58, 477–482. [Google Scholar] [CrossRef]
- JiA, J.; Song, Y.; Yuan, X.; Yang, Z. Diffuse reflectance spectroscopy study of heavy metals in agricultural soils of the Changjiang River Delta, China. In Proceedings of the 19th World Congress of Soil Science, Brisbane, Australia, 1–6 August 2010. [Google Scholar]
- Choe, E.; van der Meer, F.; van Ruitenbeek, F.; van der Werff, H.; de Smeth, B.; Kim, K.W. Mapping of heavy metal pollution in stream sediments using combined geochemistry, field spectroscopy, and hyperspectral remote sensing: A case study of the Rodalquilar mining area, SE Spain. Remote Sens. Environ. 2008, 112, 3222–3233. [Google Scholar] [CrossRef]
- Maliki, A.A.; Bruce, D.; Owens, G. Capabilities of remote sensing hyperspectral images for the detection of lead contamination: A review. In Proceedings of the ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Melbourne, Australia, 25 August–1 September 2012; Volume 55. [Google Scholar]
- Liu, Y.; Li, W.; Wu, G.; Xu, X. Feasibility of estimating heavy metal contaminations in floodplain soils using laboratory-based hyperspectral data—A case study along Le’an River, China. Geo-Spat. Inf. Sci. 2011, 14, 10–16. [Google Scholar] [CrossRef] [Green Version]
- Wang, F.; Gao, J.; Zha, Y. Hyperspectral sensing of heavy metals in soil and vegetation: Feasibility and challenges. ISPRS J. Photogramm. Remote Sens. 2018, 136, 73–84. [Google Scholar] [CrossRef]
- Hong-Yan, R.; Zhuang, D.F.; Singh, A.; Jian-Jun, P.; Dong-Sheng, Q.; Run-He, S. Estimation of As and Cu contamination in agricultural soils around a mining area by reflectance spectroscopy: A case study. Pedosphere 2009, 19, 719–726. [Google Scholar]
- Zhang, X.; Huang, C.; Liu, B.; Tong, Q. Inversion of soil Cu concentration based on band selection of hyperspetral data. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 3680–3683. [Google Scholar]
- Phiri, D.; Morgenroth, J. Developments in Landsat land cover classification methods: A review. Remote Sens. 2017, 9, 967. [Google Scholar] [CrossRef] [Green Version]
- Kalma, J.D.; McVicar, T.R.; McCabe, M.F. Estimating land surface evaporation: A review of methods using remotely sensed surface temperature data. Surv. Geophys. 2008, 29, 421–469. [Google Scholar] [CrossRef]
- Quattrochi, D.A.; Luvall, J.C. Thermal Remote Sensing in Land Surface Processing; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Skakun, S.; Vermote, E.; Roger, J.C.; Franch, B. Combined use of Landsat-8 and Sentinel-2A images for winter crop mapping and winter wheat yield assessment at regional scale. AIMS Geosci. 2017, 3, 163. [Google Scholar] [CrossRef]
- Wallis, C.I.; Homeier, J.; Peña, J.; Brandl, R.; Farwig, N.; Bendix, J. Modeling tropical montane forest biomass, productivity and canopy traits with multispectral remote sensing data. Remote Sens. Environ. 2019, 225, 77–92. [Google Scholar] [CrossRef]
- Ali, A.M.; Darvishzadeh, R.; Skidmore, A.K. Retrieval of specific leaf area from Landsat-8 surface reflectance data using statistical and physical models. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3529–3536. [Google Scholar] [CrossRef]
- Middinti, S.; Thumaty, K.C.; Gopalakrishnan, R.; Jha, C.S.; Thatiparthi, B.R. Estimating the leaf area index in Indian tropical forests using Landsat-8 OLI data. Int. J. Remote Sens. 2017, 38, 6769–6789. [Google Scholar] [CrossRef]
- Sadeghi, M.; Babaeian, E.; Tuller, M.; Jones, S.B. The optical trapezoid model: A novel approach to remote sensing of soil moisture applied to Sentinel-2 and Landsat-8 observations. Remote Sens. Environ. 2017, 198, 52–68. [Google Scholar] [CrossRef] [Green Version]
- Amani, M.; Parsian, S.; MirMazloumi, S.M.; Aieneh, O. Two new soil moisture indices based on the NIR-red triangle space of Landsat-8 data. Int. J. Appl. Earth Obs. Geoinf. 2016, 50, 176–186. [Google Scholar] [CrossRef]
- Aldabaa, A.A.A.; Weindorf, D.C.; Chakraborty, S.; Sharma, A.; Li, B. Combination of proximal and remote sensing methods for rapid soil salinity quantification. Geoderma 2015, 239, 34–46. [Google Scholar] [CrossRef] [Green Version]
- Guerschman, J.P.; Paruelo, J.; Bella, C.D.; Giallorenzi, M.; Pacin, F. Land cover classification in the Argentine Pampas using multi-temporal Landsat TM data. Int. J. Remote Sens. 2003, 24, 3381–3402. [Google Scholar] [CrossRef]
- Zurita-Milla, R.; Gómez-Chova, L.; Guanter, L.; Clevers, J.G.; Camps-Valls, G. Multitemporal unmixing of medium-spatial-resolution satellite images: A case study using MERIS images for land-cover mapping. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4308–4317. [Google Scholar] [CrossRef]
- Mattia, F.; Satalino, G.; Pauwels, V.; Alexander, L. Soil moisture retrieval through a merging of multi-temporal L-band SAR data and hydrologic modelling. Hydrol. Earth Syst. Sci. 2009, 13, 343–356. [Google Scholar] [CrossRef] [Green Version]
- Kurvonen, L.; Pulliainen, J.; Hallikainen, M. Retrieval of biomass in boreal forests from multitemporal ERS-1 and JERS-1 SAR images. IEEE Trans. Geosci. Remote Sens. 1999, 37, 198–205. [Google Scholar] [CrossRef] [Green Version]
- Tang, J.; Alelyani, S.; Liu, H. Feature selection for classification: A review. In Data Classification: Algorithms and Applications; CRC Press: Boca Raton, FL, USA, 2014; p. 37. [Google Scholar]
- Xiaobo, Z.; Jiewen, Z.; Povey, M.J.; Holmes, M.; Hanpin, M. Variables selection methods in near-infrared spectroscopy. Anal. Chim. Acta 2010, 667, 14–32. [Google Scholar] [CrossRef]
- Balabin, R.M.; Smirnov, S.V. Variable selection in near-infrared spectroscopy: Benchmarking of feature selection methods on biodiesel data. Anal. Chim. Acta 2011, 692, 63–72. [Google Scholar] [CrossRef]
- Wang, J.; Shi, T.; Yu, D.; Teng, D.; Ge, X.; Zhang, Z.; Yang, X.; Wang, H.; Wu, G. Ensemble machine-learning-based framework for estimating total nitrogen concentration in water using drone-borne hyperspectral imagery of emergent plants: A case study in an arid oasis, NW China. Environ. Pollut. 2020, 266, 115412. [Google Scholar] [CrossRef]
- Wang, J.; Hu, X.; Shi, T.; He, L.; Hu, W.; Wu, G. Assessing toxic metal chromium in the soil in coal mining areas via proximal sensing: Prerequisites for land rehabilitation and sustainable development. Geoderma 2022, 405, 115399. [Google Scholar] [CrossRef]
- Wu, Y.; Chen, J.; Wu, X.; Tian, Q.; Ji, J.; Qin, Z. Possibilities of reflectance spectroscopy for the assessment of contaminant elements in suburban soils. Appl. Geochem. 2005, 20, 1051–1059. [Google Scholar] [CrossRef]
- Pinheiro, É.; Ceddia, M.; Clingensmith, C.; Grunwald, S.; Vasques, G. Prediction of soil physical and chemical properties by visible and near-infrared diffuse reflectance spectroscopy in the central Amazon. Remote Sens. 2017, 9, 293. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Li, X.; Yu, K.; Cheng, F.; He, Y. Hyperspectral Imaging for Determining Pigment Contents in Cucumber Leaves in Response to Angular Leaf Spot Disease. Sci. Rep. 2016, 6, 27790. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Mistele, B.; Hu, Y.; Chen, X.; Schmidhalter, U. Reflectance estimation of canopy nitrogen content in winter wheat using optimised hyperspectral spectral indices and partial least squares regression. Eur. J. Agron. 2014, 52, 198–209. [Google Scholar] [CrossRef]
- Di, W.U.; Nie, P.; Joel, C.; Yong, H.E.; Wang, Z.; Hongxi, W.U. Application of visible and near infrared spectroscopy for rapid and non-invasive quantification of common adulterants in Spirulina powder. J. Food Eng. 2011, 102, 278–286. [Google Scholar]
- Wei, C.; Huang, J.; Wang, X.; Blackburn, G.A.; Zhang, Y.; Wang, S.; Mansaray, L.R. Hyperspectral characterization of freezing injury and its biochemical impacts in oilseed rape leaves. Remote Sens. Environ. 2017, 195, 56–66. [Google Scholar] [CrossRef] [Green Version]
- Fang, Y.; Xu, L.; Peng, J.; Wang, H.; Wong, A.; Clausi, D.A. Retrieval and mapping of heavy metal concentration in soil using time seies Landsat 8 imagery. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing & Spatial Information Sciences, Beijing, China, 7–10 May 2018; Volume 42. [Google Scholar]
- Geospatial Data Cloud. Available online: http://www.gscloud.cn/ (accessed on 8 April 2018).
- Strobl, C.; Boulesteix, A.L.; Zeileis, A.; Hothorn, T. Bias in random forest variable importance measures: Illustrations, sources and a solution. BMC Bioinform. 2007, 8, 25. [Google Scholar] [CrossRef] [Green Version]
- Xu, L.; Li, J.; Brenning, A. A comparative study of different classification techniques for marine oil spill identification using RADARSAT-1 imagery. Remote Sens. Environ. 2014, 141, 14–23. [Google Scholar] [CrossRef]
- Guyon, I.; Elisseeff, A. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Minu, S.; Shetty, A.; Gopal, B. Review of preprocessing techniques used in soil property prediction from hyperspectral data. Cogent Geosci. 2016, 2, 1145878. [Google Scholar] [CrossRef]
- Farifteh, J.; Van der Meer, F.; Atzberger, C.; Carranza, E. Quantitative analysis of salt-affected soil reflectance spectra: A comparison of two adaptive methods (PLSR and ANN). Remote Sens. Environ. 2007, 110, 59–78. [Google Scholar] [CrossRef]
- Yu, H.; Liu, M.; Du, B.; Wang, Z.; Hu, L.; Zhang, B. Mapping Soil Salinity/Sodicity by using Landsat OLI Imagery and PLSR Algorithm over Semiarid West Jilin Province, China. Sensors 2018, 18, 1048. [Google Scholar] [CrossRef] [Green Version]
- Verrelst, J.; Camps-Valls, G.; Muñoz-Marí, J.; Rivera, J.P.; Veroustraete, F.; Clevers, J.G.; Moreno, J. Optical remote sensing and the retrieval of terrestrial vegetation bio-geophysical properties—A review. ISPRS J. Photogramm. Remote Sens. 2015, 108, 273–290. [Google Scholar] [CrossRef]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Zhang, G.P. Neural networks for classification: A survey. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 2000, 30, 451–462. [Google Scholar] [CrossRef] [Green Version]
- Jaroenpoj, S.; Yu, J.; Ness, J. Development of artificial neural network models for biogas production from co-digestion of leachate and pineapple peel. Glob. Environ. Eng. 2015, 1, 42–47. [Google Scholar] [CrossRef] [Green Version]
- Fard, R.S.; Matinfar, H.R. Capability of vis-NIR spectroscopy and Landsat-8 spectral data to predict soil heavy metals in polluted agricultural land (Iran). Arab. J. Geosci. 2016, 9, 745. [Google Scholar] [CrossRef]
- Kemper, T.; Sommer, S. Estimate of heavy metal contamination in soils after a mining accident using reflectance spectroscopy. Environ. Sci. Technol. 2002, 36, 2742–2747. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
- Verrelst, J.; Malenovskỳ, Z.; Van der Tol, C.; Camps-Valls, G.; Gastellu-Etchegorry, J.P.; Lewis, P.; North, P.; Moreno, J. Quantifying vegetation biophysical variables from imaging spectroscopy data: A review on retrieval methods. Surv. Geophys. 2018, 40, 589–629. [Google Scholar] [CrossRef] [Green Version]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef] [Green Version]
- Karasuyama, M.; Nakano, R. Optimizing SVR hyperparameters via fast cross-validation using AOSVR. In Proceedings of the 2007 International Joint Conference on Neural Networks, Orlando, FL, USA, 12–17 August 2007; pp. 1186–1191. [Google Scholar]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Hand, D.J. Construction and Assessment of Classification Rules; Wiley: Chichester, UK, 1997; Volume 15. [Google Scholar]
- Childs, C. Interpolating surfaces in ArcGIS spatial analyst. Arcuser 2004, 3235, 569. [Google Scholar]
- Ozdogan, M. The spatial distribution of crop types from MODIS data: Temporal unmixing using Independent Component Analysis. Remote Sens. Environ. 2010, 114, 1190–1204. [Google Scholar] [CrossRef]
- Vuolo, F.; Neuwirth, M.; Immitzer, M.; Atzberger, C.; Ng, W.T. How much does multi-temporal Sentinel-2 data improve crop type classification? Int. J. Appl. Earth Obs. Geoinf. 2018, 72, 122–130. [Google Scholar] [CrossRef]
- Çimen, M.; Kisi, O. Comparison of two different data-driven techniques in modeling lake level fluctuations in Turkey. J. Hydrol. 2009, 378, 253–262. [Google Scholar] [CrossRef]
- Balabin, R.M.; Lomakina, E.I. Support vector machine regression (SVR/LS-SVM)—An alternative to neural networks (ANN) for analytical chemistry? Comparison of nonlinear methods on near infrared (NIR) spectroscopy data. Analyst 2011, 136, 1703–1712. [Google Scholar] [CrossRef]
- Inoue, Y.; Sakaiya, E.; Zhu, Y.; Takahashi, W. Diagnostic mapping of canopy nitrogen content in rice based on hyperspectral measurements. Remote Sens. Environ. 2012, 126, 210–221. [Google Scholar] [CrossRef]
- Shi, T.; Hu, X.; Guo, L.; Su, F.; Tu, W.; Hu, Z.; Liu, H.; Yang, C.; Wang, J.; Zhang, J.; et al. Digital mapping of zinc in urban topsoil using multisource geospatial data and random forest. Sci. Total Environ. 2021, 792, 148455. [Google Scholar] [CrossRef]


| 2013 | 2014 | 2015 | 2016 | 2017 |
|---|---|---|---|---|
| 16 June 2013 | 6 August 2014 a | 3 April 2015 a | 8 June 2016 | 19 February 2017 |
| 6 August 2014 b | 3 April 2015 b | 26 July 2015 | ||
| 9 October 2014 | 8 July 2015 | |||
| 28 December 2014 |
| PLSR | SVR | ANN | |||||
|---|---|---|---|---|---|---|---|
| Mean | Std.dev | Mean | Std.dev | Mean | Std.dev | ||
| Adjusted R | MTI | 0.568 | 0.131 | 0.641 | 0.160 | 0.476 | 0.197 |
| SI | 0.368 | 0.148 | 0.433 | 0.237 | 0.249 | 0.185 | |
| RMSE | MTI | 16.997 | 3.178 | 15.515 | 3.426 | 20.651 | 5.664 |
| SI | 16.257 | 3.014 | 14.636 | 3.508 | 23.305 | 6.213 | |
| MAE | MTI | 15.215 | 3.021 | 12.498 | 3.914 | 17.673 | 5.444 |
| SI | 19.493 | 2.752 | 16.711 | 4.857 | 22.994 | 5.310 | |
| SE | MTI | 15.215 | 3.021 | 9.099 | 2.691 | 12.910 | 4.270 |
| SI | 19.493 | 2.752 | 11.874 | 3.915 | 14.504 | 4.461 | |
| PLSR | SVR | ANN | PLSR | SVR | ANN | ||
|---|---|---|---|---|---|---|---|
| Mean | Std.dev. | ||||||
| Adjusted R | C1 | 0.608 | 0.600 | 0.507 | 0.134 | 0.169 | 0.183 |
| C2 | 0.103 | 0.254 | 0.144 | 0.119 | 0.233 | 0.154 | |
| C3 | 0.556 | 0.626 | 0.498 | 0.117 | 0.143 | 0.206 | |
| C4 | 0.614 | 0.593 | 0.528 | 0.109 | 0.164 | 0.186 | |
| C5 | 0.601 | 0.577 | 0.498 | 0.132 | 0.158 | 0.186 | |
| RMSE | C1 | 16.384 | 14.741 | 20.338 | 3.543 | 3.806 | 5.407 |
| C2 | 14.809 | 20.707 | 27.151 | 4.858 | 4.910 | 8.275 | |
| C3 | 17.920 | 15.314 | 20.522 | 4.569 | 3.519 | 6.533 | |
| C4 | 16.365 | 15.335 | 19.598 | 3.571 | 3.385 | 5.628 | |
| C5 | 16.532 | 15.515 | 21.511 | 2.952 | 3.426 | 5.741 | |
| MAE | C1 | 14.475 | 13.698 | 16.717 | 2.955 | 4.140 | 4.722 |
| C2 | 24.426 | 20.835 | 26.282 | 3.854 | 5.491 | 5.900 | |
| C3 | 15.872 | 13.193 | 17.028 | 2.961 | 3.675 | 5.576 | |
| C4 | 14.246 | 13.702 | 16.423 | 2.786 | 3.865 | 4.732 | |
| C5 | 14.691 | 14.340 | 17.378 | 2.738 | 3.636 | 4.957 | |
| SE | C1 | 14.475 | 9.189 | 12.595 | 2.955 | 2.831 | 3.931 |
| C2 | 24.426 | 12.995 | 16.786 | 3.854 | 3.920 | 5.942 | |
| C3 | 15.872 | 9.552 | 12.931 | 2.961 | 2.884 | 5.040 | |
| C4 | 14.246 | 9.481 | 12.125 | 2.786 | 2.624 | 3.852 | |
| C5 | 14.691 | 9.579 | 13.118 | 2.738 | 2.594 | 3.826 | |
| Importance Order | PLSR | SVR | ANN |
|---|---|---|---|
| 1 | OB | OB | OB |
| 2 | PCA | ISOMAP | PCA |
| 3 | ISOMAP | MNF | ISOMAP |
| 4 | MNF | PCA | MNF |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, Y.; Xu, L.; Wong, A.; Clausi, D.A. Multi-Temporal Landsat-8 Images for Retrieval and Broad Scale Mapping of Soil Copper Concentration Using Empirical Models. Remote Sens. 2022, 14, 2311. https://doi.org/10.3390/rs14102311
Fang Y, Xu L, Wong A, Clausi DA. Multi-Temporal Landsat-8 Images for Retrieval and Broad Scale Mapping of Soil Copper Concentration Using Empirical Models. Remote Sensing. 2022; 14(10):2311. https://doi.org/10.3390/rs14102311
Chicago/Turabian StyleFang, Yuan, Linlin Xu, Alexander Wong, and David A. Clausi. 2022. "Multi-Temporal Landsat-8 Images for Retrieval and Broad Scale Mapping of Soil Copper Concentration Using Empirical Models" Remote Sensing 14, no. 10: 2311. https://doi.org/10.3390/rs14102311
APA StyleFang, Y., Xu, L., Wong, A., & Clausi, D. A. (2022). Multi-Temporal Landsat-8 Images for Retrieval and Broad Scale Mapping of Soil Copper Concentration Using Empirical Models. Remote Sensing, 14(10), 2311. https://doi.org/10.3390/rs14102311







