The Feasibility of Leaf Reflectance-Based Taxonomic Inventories and Diversity Assessments of Species-Rich Grasslands: A Cross-Seasonal Evaluation Using Waveband Selection
Abstract
:1. Introduction
- (1)
- Determine whether the species within the community could be separated using classification models and to what extent the classification of these species changed over time;
- (2)
- Explore the temporal stability of band selection during classification and test the transferability of classification models across sampling dates;
- (3)
- Test whether the species that were more easily classified displayed particular leaf traits or were more phylogenetically distant from other species within the community;
- (4)
- Examine the importance of the biochemical traits of a leaf in classification over time.
2. Materials and Methods
2.1. Experimental System
2.2. Leaf Spectra Acquisition and Pre-Processing
2.3. Spectral Dissimilarity within and between Species
2.4. Sparse PLS-DA for the Class Determination of Species
2.5. Assessment of Waveband Selection and Model Stability
2.6. Grounds for the “Ease” of Species Separation
- (1)
- Species that were taxonomically or phylogenetically more distinctive were easier to classify;
- (2)
- Species with smaller, and therefore harder to measure, leaves were harder to classify (due to increased noise within the leaf clip dataset);
- (3)
- The leaf longevity that is typical of this species affected the ease of species classification;
- (4)
- The leaf surface defence mechanisms affected the ease of species classification;
- (5)
- The amount of bi-directional leaf reflectance affected the ease of species classification;
- (6)
- The spectral distance between pairs of species-specific spectra compared to inter-specific spectral distances (as denoted by the Kolmogorov–Smirnov statistic D) was a good predictor of the ease of species classification.
2.7. Use of the PRO-COSINE Radiative Transfer Model to Understand the Biochemical Basis of Shifting Waveband Importance
3. Results
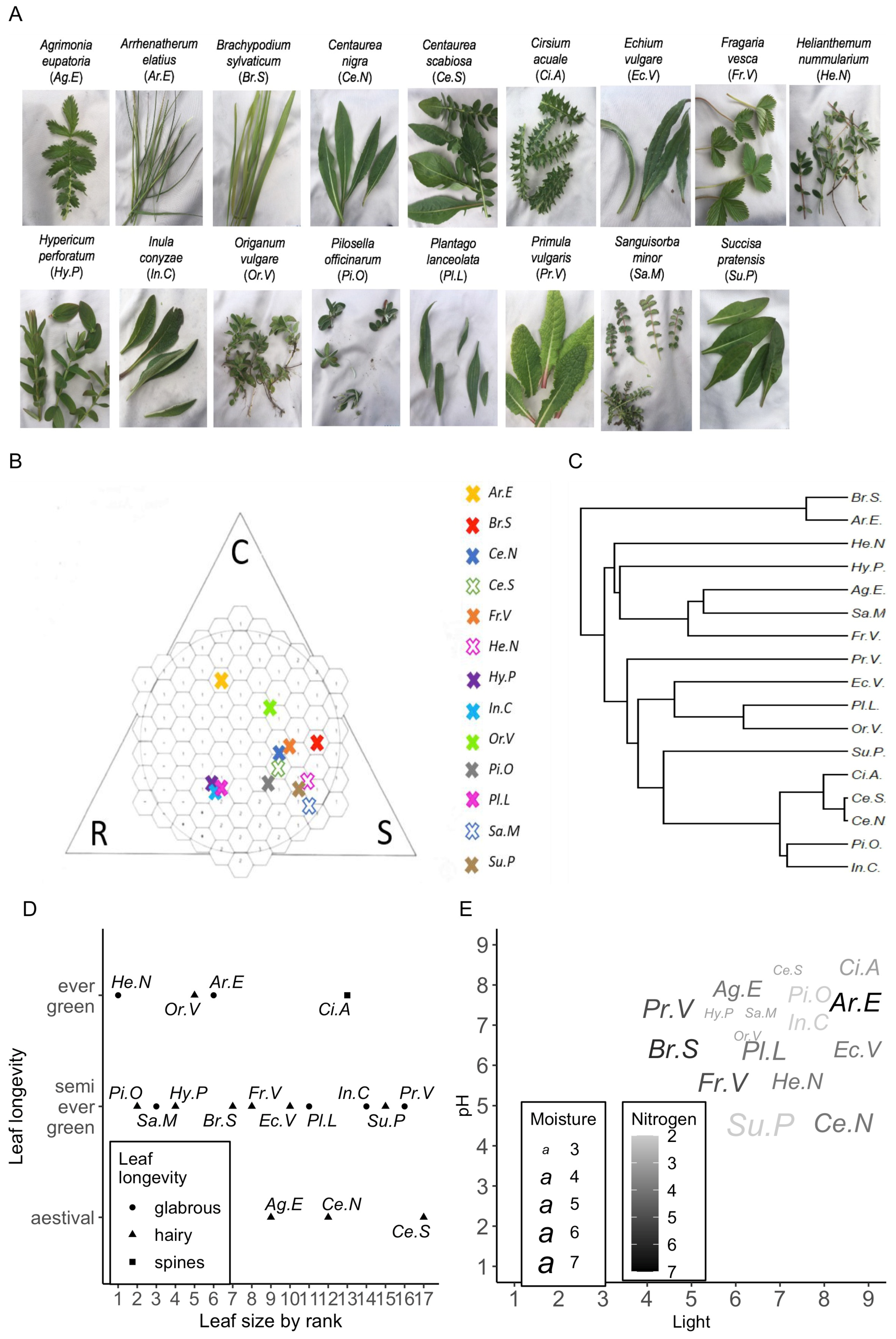
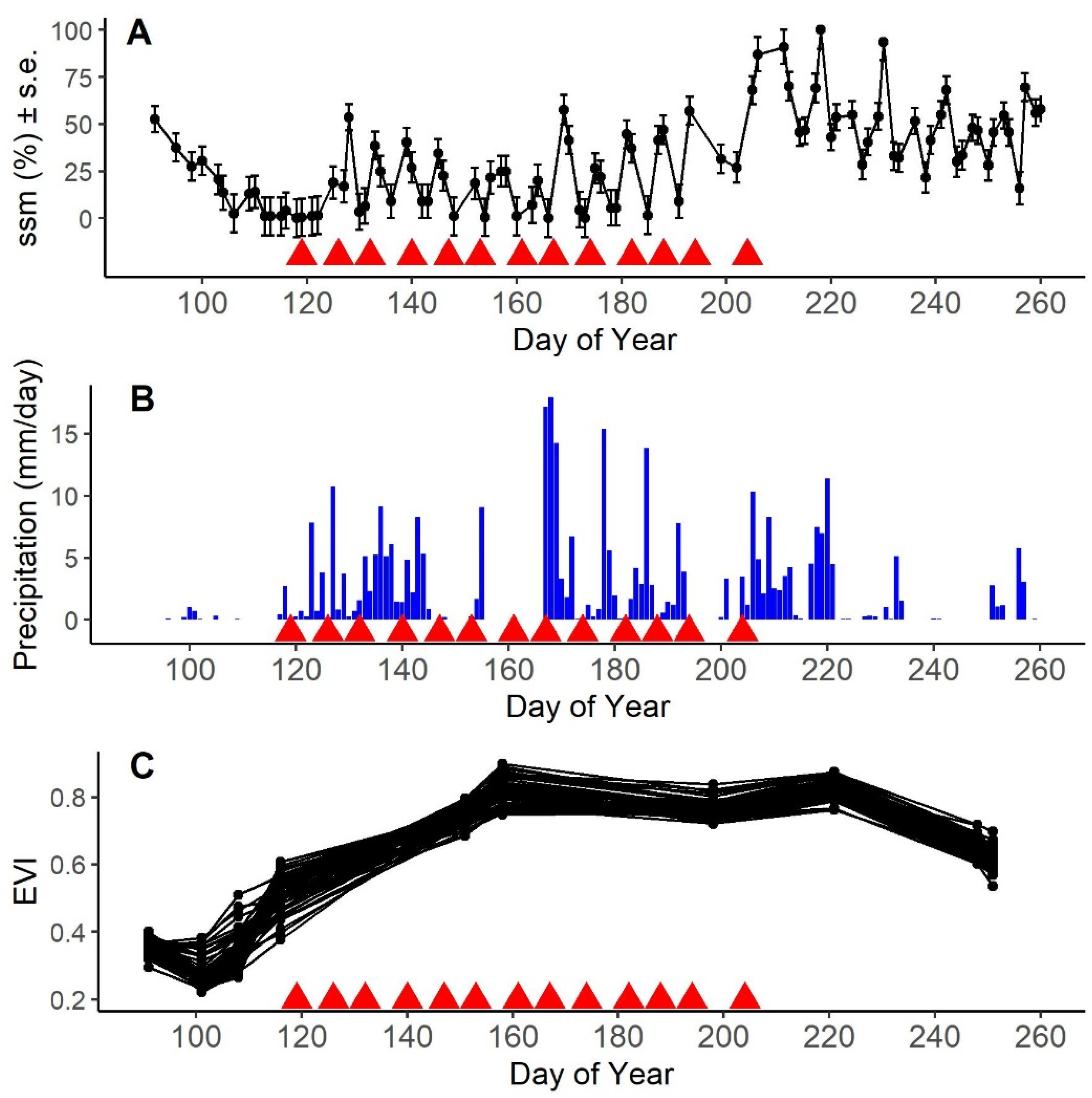
3.1. Ecological Context of the Plant Community and Timing of Sampling Campaign
3.2. Spectral Distance over Time
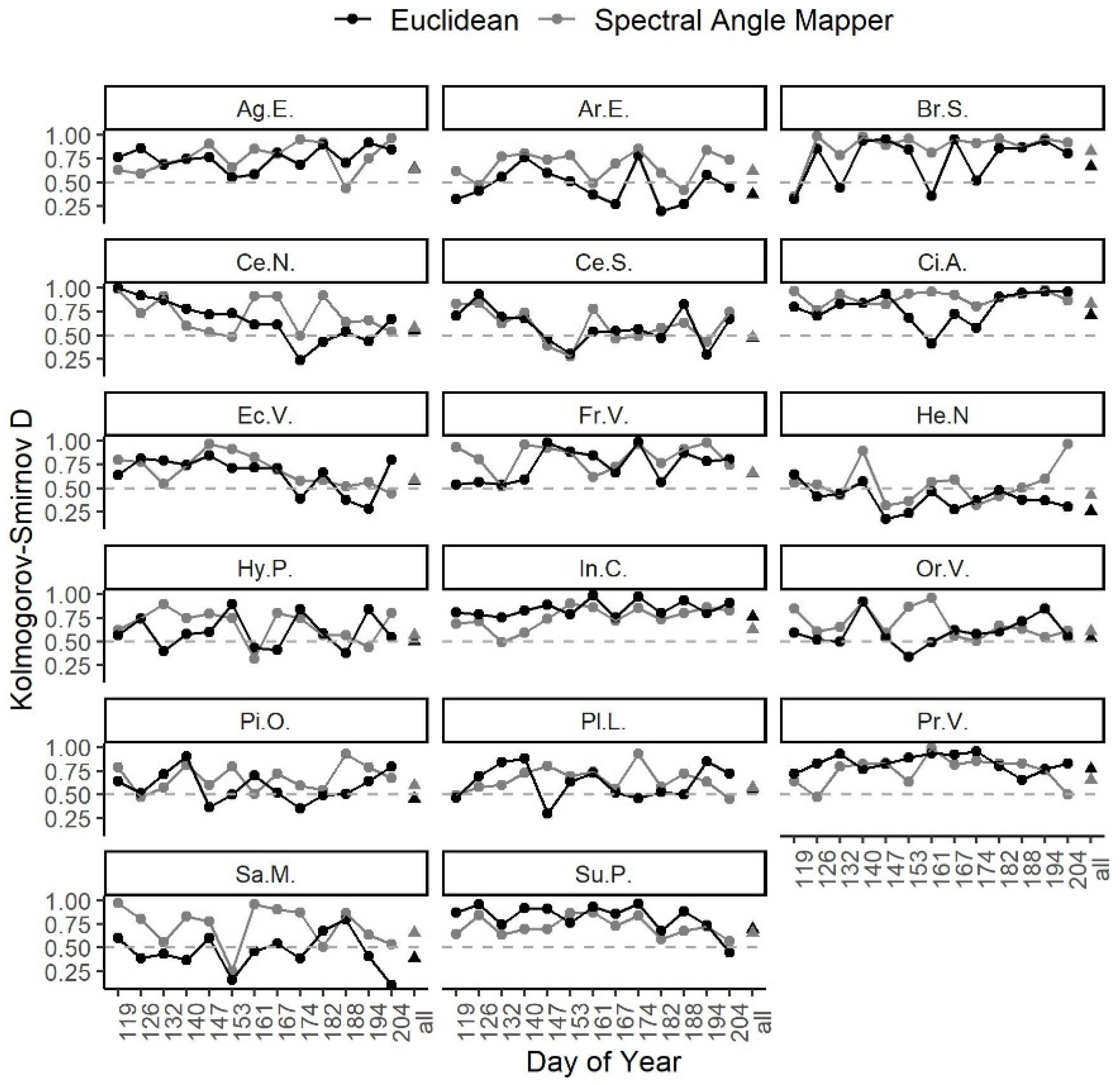
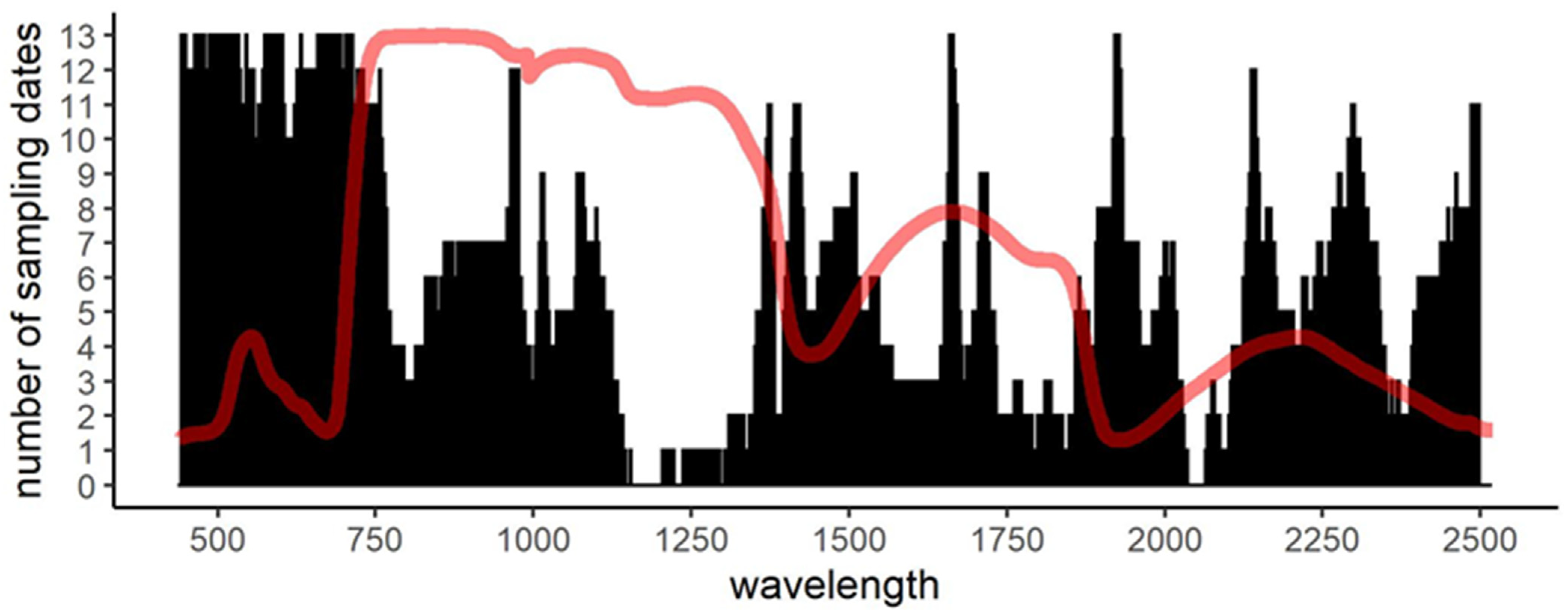
3.3. Performance of PLS-DA over Time: Waveband and Model Stability
3.4. Ease of Species Separability
3.5. Phylogenetic and Morphological Drivers of Species Separability
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Critchley, C.N.R.; Burke, M.J.W.; Stevens, D.P. Conservation of lowland semi-natural grasslands in the UK: A review of botanical monitoring results from agri-environment schemes. Biol. Conserv. 2004, 115, 263–278. [Google Scholar] [CrossRef]
- de Bello, F.; Lavorel, S.; Gerhold, P.; Reier, Ü.; Pärtel, M. A biodiversity monitoring framework for practical conservation of grasslands and shrublands. Biol. Conserv. 2010, 143, 9–17. [Google Scholar] [CrossRef]
- Lark, T.J. Protecting our prairies: Research and policy actions for conserving America’s grasslands. Land Use Policy 2020, 97, 104727. [Google Scholar] [CrossRef]
- Mansour, K.; Mutanga, O.; Everson, T.; Adam, E. Discriminating indicator grass species for rangeland degradation assessment using hyperspectral data resampled to AISA Eagle resolution. ISPRS J. Photogramm. Remote Sens. 2012, 70, 56–65. [Google Scholar] [CrossRef]
- Marcinkowska-Ochtyra, A.; Jarocińska, A.; Bzdȩga, K.; Tokarska-Guzik, B. Classification of expansive grassland species in different growth stages based on hyperspectral and LiDAR data. Remote Sens. 2018, 10, 2019. [Google Scholar] [CrossRef] [Green Version]
- Pfitzner, K.; Bartolo, R.; Whiteside, T.; Loewensteiner, D.; Esparon, A. Hyperspectral monitoring of non-native tropical grasses over phenological seasons. Remote Sens. 2021, 13, 738. [Google Scholar] [CrossRef]
- Meireles, J.E.; Cavender-Bares, J.; Townsend, P.A.; Ustin, S.; Gamon, J.A.; Schweiger, A.K.; Schaepman, M.E.; Asner, G.P.; Martin, R.E.; Singh, A.; et al. Leaf reflectance spectra capture the evolutionary history of seed plants. New Phytol. 2020, 228, 485–493. [Google Scholar] [CrossRef]
- Irisarri, J.G.N.; Oesterheld, M.; Verón, S.R.; Paruelo, J.M. Grass species differentiation through canopy hyperspectral reflectance. Int. J. Remote Sens. 2009, 30, 5959–5975. [Google Scholar] [CrossRef]
- Punalekar, S.; Verhoef, A.; Tatarenko, I.V.; Van Der Tol, C.; Macdonald, D.M.J.; Marchant, B.; Gerard, F.; White, K.; Gowing, D. Characterization of a highly biodiverse floodplain meadow using hyperspectral remote sensing within a plant functional trait framework. Remote Sens. 2016, 8, 112. [Google Scholar] [CrossRef] [Green Version]
- Petibon, F.; Czyż, E.A.; Ghielmetti, G.; Hueni, A.; Kneubühler, M.; Schaepman, M.E.; Schuman, M.C. Uncertainties in measurements of leaf optical properties are small compared to the biological variation within and between individuals of European beech. Remote Sens. Environ. 2021, 264, 112601. [Google Scholar] [CrossRef]
- Wang, R.; Gamon, J.A.; Schweiger, A.K.; Cavender-Bares, J.; Townsend, P.A.; Zygielbaum, A.I.; Kothari, S. Influence of species richness, evenness, and composition on optical diversity: A simulation study. Remote Sens. Environ. 2018, 211, 218–228. [Google Scholar] [CrossRef]
- Price, J.C. How unique are spectral signatures? Remote Sens. Environ. 1994, 49, 181–186. [Google Scholar] [CrossRef]
- Yang, X.; Tang, J.; Mustard, J.F.; Wu, J.; Zhao, K.; Serbin, S.; Lee, J.E.; Noda, H.M.; Muraoka, H.; Nasahara, K.N. Seasonal variability of multiple leaf traits captured by leaf spectroscopy at two temperate deciduous forests. Agric. For. Meteorol. 2016, 179, 108236. [Google Scholar] [CrossRef] [Green Version]
- Chavana-Bryant, C.; Malhi, Y.; Wu, J.; Asner, G.P.; Anastasiou, A.; Enquist, B.J.; Cosio Caravasi, E.G.; Doughty, C.E.; Saleska, S.R.; Martin, R.E.; et al. Leaf aging of Amazonian canopy trees as revealed by spectral and physiochemical measurements. New Phytol. 2017, 214, 1049–1063. [Google Scholar] [CrossRef] [Green Version]
- Guo, C.; Ma, L.; Yuan, S.; Wang, R. Morphological, physiological and anatomical traits of plant functional types in temperate grasslands along a large-scale aridity gradient in northeastern China. Sci. Rep. 2017, 7, 40900. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Serbin, S.P.; Singh, A.; McNeil, B.E.; Kingdon, C.C.; Townsend, P.A. Spectroscopic determination of leaf morphological and biochemical traits for northern temperate and boreal tree species. Ecol. Appl. 2014, 24, 1651–1669. [Google Scholar] [CrossRef] [Green Version]
- Asner, G.P.; Martin, R.E. Canopy phylogenetic, chemical and spectral assembly in a lowland Amazonian forest. New Phytol. 2011, 189, 999–1012. [Google Scholar] [CrossRef]
- Hesketh, M.; Sánchez-Azofeifa, G.A. The effect of seasonal spectral variation on species classification in the Panamanian tropical forest. Remote Sens. Environ. 2012, 118, 73–82. [Google Scholar] [CrossRef]
- Dudley, K.L.; Dennison, P.E.; Roth, K.L.; Roberts, D.A.; Coates, A.R. A multi-temporal spectral library approach for mapping vegetation species across spatial and temporal phenological gradients. Remote Sens. Environ. 2015, 167, 121–134. [Google Scholar] [CrossRef]
- Wang, R.; Gamon, J.A.; Cavender-Bares, J.; Townsend, P.A.; Zygielbaum, A.I. The spatial sensitivity of the spectral diversity-biodiversity relationship: An experimental test in a prairie grassland. Ecol. Appl. 2018, 28, 541–556. [Google Scholar] [CrossRef] [Green Version]
- Schweiger, A.K.; Cavender-Bares, J.; Townsend, P.A.; Hobbie, S.E.; Madritch, M.D.; Wang, R.; Tilman, D.; Gamon, J.A. Plant spectral diversity integrates functional and phylogenetic components of biodiversity and predicts ecosystem function. Nat. Ecol. Evol. 2018, 2, 976–982. [Google Scholar] [CrossRef] [PubMed]
- Carlson, K.M.; Asner, G.P.; Hughes, R.F.; Ostertag, R.; Martin, R.E. Hyperspectral remote sensing of canopy biodiversity in Hawaiian lowland rainforests. Ecosystems 2007, 10, 536–549. [Google Scholar] [CrossRef]
- Féret, J.B.; Asner, G.P. Spectroscopic classification of tropical forest species using radiative transfer modeling. Remote Sens. Environ. 2011, 115, 2415–2422. [Google Scholar] [CrossRef]
- Gholizadeh, H.; Gamon, J.A.; Helzer, C.J.; Cavender-Bares, J. Multi-temporal assessment of grassland α- and β-diversity using hyperspectral imaging. Ecol. Appl. 2020, 30, e02145. [Google Scholar] [CrossRef] [PubMed]
- Thornley, R.; Gerard, F.F.; White, K.; Verhoef, A. Intra-annual taxonomic and phenological drivers of spectral variance in grasslands. Remote Sens. Environ. 2022, 271, 112908. [Google Scholar] [CrossRef]
- Imran, H.A.; Gianelle, D.; Scotton, M.; Rocchini, D.; Dalponte, M.; Macolino, S.; Sakowska, K.; Pornaro, C.; Vescovo, L. Potential and limitations of grasslands α-diversity prediction using fine-scale hyperspectral imagery. Remote Sens. 2021, 13, 2649. [Google Scholar] [CrossRef]
- Maschler, J.; Atzberger, C.; Immitzer, M. Individual tree crown segmentation and classification of 13 tree species using Airborne hyperspectral data. Remote Sens. 2018, 10, 1218. [Google Scholar] [CrossRef] [Green Version]
- Dalponte, M.; Ørka, H.O.; Ene, L.T.; Gobakken, T.; Næsset, E. Tree crown delineation and tree species classification in boreal forests using hyperspectral and ALS data. Remote Sens. Environ. 2014, 140, 306–317. [Google Scholar] [CrossRef]
- Lopatin, J.; Fassnacht, F.E.; Kattenborn, T.; Schmidtlein, S. Mapping plant species in mixed grassland communities using close range imaging spectroscopy. Remote Sens. Environ. 2017, 201, 12–23. [Google Scholar] [CrossRef]
- Peerbhay, K.Y.; Mutanga, O.; Ismail, R. Commercial tree species discrimination using airborne AISA Eagle hyperspectral imagery and partial least squares discriminant analysis (PLS-DA) in KwaZulu-Natal, South Africa. ISPRS J. Photogramm. Remote Sens. 2013, 79, 19–28. [Google Scholar] [CrossRef]
- Zhong, Y.; Hu, X.; Luo, C.; Wang, X.; Zhao, J.; Zhang, L. WHU-Hi: UAV-borne hyperspectral with high spatial resolution (H2) benchmark datasets and classifier for precise crop identification based on deep convolutional neural network with CRF. Remote Sens. Environ. 2020, 250, 112012. [Google Scholar] [CrossRef]
- Vaiphasa, C.; Skidmore, A.K.; de Boer, W.F.; Vaiphasa, T. A hyperspectral band selector for plant species discrimination. ISPRS J. Photogramm. Remote Sens. 2007, 62, 225–235. [Google Scholar] [CrossRef]
- Fassnacht, F.E.; Latifi, H.; Stereńczak, K.; Modzelewska, A.; Lefsky, M.; Waser, L.T.; Straub, C.; Ghosh, A. Review of studies on tree species classification from remotely sensed data. Remote Sens. Environ. 2016, 186, 64–87. [Google Scholar] [CrossRef]
- Hennessy, A.; Clarke, K.; Lewis, M. Hyperspectral Classification of Plants: A Review of Waveband Selection Generalisability. Remote Sens. 2020, 12, 113. [Google Scholar] [CrossRef] [Green Version]
- Fitter, A.H.; Peat, H.J. The Ecological Flora Database. J. Ecol. 1994, 82, 415–425. Available online: http://www.ecoflora.co.uk (accessed on 2 February 2022). [CrossRef]
- Grime, J.P. Trait convergence and trait divergence in herbaceous plant communities: Mechanisms and consequences. J. Veg. Sci. 2006, 17, 255. [Google Scholar] [CrossRef]
- Grime, J.P.; Hodgeson, J.G.; Hunt, R. The Autecological Accounts. In Comparative Plant Ecology; Oxford University Press: Oxford, UK, 1998; pp. 53–646. [Google Scholar]
- Alexander, L.V.; Jones, P.D. Updated precipitation series for the U.K. and discussion of recent extremes. Atmos. Sci. Lett. 2001, 1, 142–150. [Google Scholar] [CrossRef]
- Schweiger, A.K. Spectral field campaigns: Planning and data collection. In Remote Sensing of Plant Biodiversity; Cavender-Bares, J., Gamon, J.A., Townsend, P.A., Eds.; Springer Nature: Cham, Switzerland, 2020; pp. 385–423. [Google Scholar]
- Lehnert, L.W.; Meyer, H.; Obermeier, W.A.; Silva, B.; Regeling, B.; Thies, B.; Bendix, J. Hyperspectral data analysis in R: The hsdar package. J. Stat. Softw. 2019, 89, 1–23. [Google Scholar] [CrossRef] [Green Version]
- Kruse, F.A.; Lefkoff, A.B.; Boardman, J.W.; Heidebrecht, K.B.; Shapiro, A.T.; Barloo, P.J.; Goetz, A.F.H. The Spectral Image Processing System (SIPS)- Interactive Visualization and Analysis of Imaging Spectrometer Data. Remote Sens. Environ. 1993, 44, 145–163. [Google Scholar] [CrossRef]
- Marsaglia, G.; Tsang, W.W.; Wang, J. Evaluating Kolmogorov’s distribution. J. Stat. Softw. 2003, 8, 1–4. [Google Scholar] [CrossRef]
- Ruiz-Perez, D.; Guan, H.; Madhivanan, P.; Mathee, K.; Narasimhan, G. So you think you can PLS-DA? BMC Bioinform. 2020, 21 (Suppl. 1), 1–10. [Google Scholar] [CrossRef] [PubMed]
- Mehmood, T.; Sæbø, S.; Liland, K.H. Comparison of variable selection methods in partial least squares regression. J. Chemom. 2020, 34, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Feret, J.B.; François, C.; Asner, G.P.; Gitelson, A.A.; Martin, R.E.; Bidel, L.P.R.; Ustin, S.L.; le Maire, G.; Jacquemoud, S. PROSPECT-4 and 5: Advances in the leaf optical properties model separating photosynthetic pigments. Remote Sens. Environ. 2008, 112, 3030–3043. [Google Scholar] [CrossRef]
- Saccenti, E.; Timmerman, M.E. Approaches to sample size determination for multivariate data: Applications to PCA and PLS-DA of omics data. J. Proteome Res. 2016, 15, 2379–2393. [Google Scholar] [CrossRef]
- Lee, L.C.; Liong, C.Y.; Jemain, A.A. Partial least squares-discriminant analysis (PLS-DA) for classification of high-dimensional (HD) data: A review of contemporary practice strategies and knowledge gaps. Analyst 2018, 143, 3526–3539. [Google Scholar] [CrossRef]
- Rohart, F.; Gautier, B.; Singh, A.; Lê Cao, K.A. mixOmics: An R package for ‘omics feature selection and multiple data integration. BioRxiv 2017, 13, 1–19. [Google Scholar] [CrossRef] [Green Version]
- R Core Team, R. A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021; Available online: https://www.R-project.org/ (accessed on 18 March 2022).
- Lê Cao, K.A.; Boitard, S.; Besse, P. Sparse PLS discriminant analysis: Biologically relevant feature selection and graphical displays for multiclass problems. BMC Bioinform. 2011, 12, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Jin, Y.; Qian, H.V. PhyloMaker: An R package that can generate very large phylogenies for vascular plants. Ecography 2019, 42, 1353–1359. [Google Scholar] [CrossRef] [Green Version]
- Sims, D.A.; Gamon, J.A. Relationships between leaf pigment content and spectral reflectance across a wide range of species, leaf structures and developmental stages. Remote Sens. Environ. 2002, 81, 337–354. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Baret, F. PROSPECT: A model of leaf optical properties spectra. Remote Sens. Environ. 1990, 34, 75–91. [Google Scholar] [CrossRef]
- Jay, S.; Bendoula, R.; Hadoux, X.; Féret, J.B.; Gorretta, N. A physically-based model for retrieving foliar biochemistry and leaf orientation using close-range imaging spectroscopy. Remote Sens. Environ. 2016, 177, 220–236. [Google Scholar] [CrossRef] [Green Version]
- Li, D.; Cheng, T.; Jia, M.; Zhou, K.; Lu, N.; Yao, X.; Tian, Y.; Zhu, Y.; Cao, W. PROCWT: Coupling PROSPECT with continuous wavelet transform to improve the retrieval of foliar chemistry from leaf bidirectional reflectance spectra. Remote Sens. Environ. 2018, 206, 1–14. [Google Scholar] [CrossRef]
- Wan, L.; Zhang, J.; Xu, Y.; Huang, Y.; Zhou, W.; Jiang, L.; He, Y.; Cen, H. PROSDM: Applicability of PROSPECT model coupled with spectral derivatives and similarity metrics to retrieve leaf biochemical traits from bidirectional reflectance. Remote Sens. Environ. 2021, 267, 112761. [Google Scholar] [CrossRef]
- Verrelst, J.; Rivera, J.P.; Moreno, J. ARTMO’s global sensitivity analysis (GSA) toolbox to quantify driving variables of leaf and canopy radiative transfer models. EARSeL eProceedings 2015, 2, 1–11. [Google Scholar]
- Hovi, A.; Forsström, P.; Mõttus, M.; Rautiainen, M. Evaluation of accuracy and practical applicability of methods for measuring leaf reflectance and transmittance spectra. Remote Sens. 2018, 10, 25. [Google Scholar] [CrossRef] [Green Version]
- Conti, L.; Malavasi, M.; Galland, T.; Komárek, J.; Lagner, O.; Carmona, C.P.; de Bello, F.; Rocchini, D.; Šímová, P. The relationship between species and spectral diversity in grassland communities is mediated by their vertical complexity. Appl. Veg. Sci. 2021, 24, 1–8. [Google Scholar] [CrossRef]
- Gholizadeh, H.; Gamon, J.A.; Zygielbaum, A.I.; Wang, R.; Schweiger, A.K.; Cavender-Bares, J. Remote sensing of biodiversity: Soil correction and data dimension reduction methods improve assessment of α-diversity (species richness) in prairie ecosystems. Remote Sens. Environ. 2018, 206, 240–253. [Google Scholar] [CrossRef]
- Murchie, E.H.; Horton, P. Acclimation of photosynthesis to irradiance and spectral quality in British plant species: Chlorophyll content, photosynthetic capacity and habitat preference. Plant Cell Environ. 1997, 20, 438–448. [Google Scholar] [CrossRef]
- Douzas, G.; Bacao, F.; Fonseca, J.; Khudinyan, M. Imbalanced learning in land cover classification: Improving minority classes’ prediction accuracy using the geometric SMOTE algorithm. Remote Sens. 2019, 11, 3040. [Google Scholar] [CrossRef] [Green Version]
- Banerjee, B.P.; Raval, S. A particle swarm optimization based approach to pre-tune programmable hyperspectral sensors. Remote Sens. 2021, 13, 3295. [Google Scholar] [CrossRef]
- Roelofsen, H.D.; van Bodegom, P.M.; Kooistra, L.; Witte, J.P.M. Predicting leaf traits of herbaceous species from their spectral characteristics. Ecol. Evol. 2014, 4, 706–719. [Google Scholar] [CrossRef] [PubMed]
- Falcioni, R.; Moriwaki, T.; Pattaro, M.; Herrig Furlanetto, R.; Nanni, M.R.; Camargos Antunes, W. High resolution leaf spectral signature as a tool for foliar pigment estimation displaying potential for species differentiation. J. Plant Physiol. 2020, 249, 153161. [Google Scholar] [CrossRef] [PubMed]

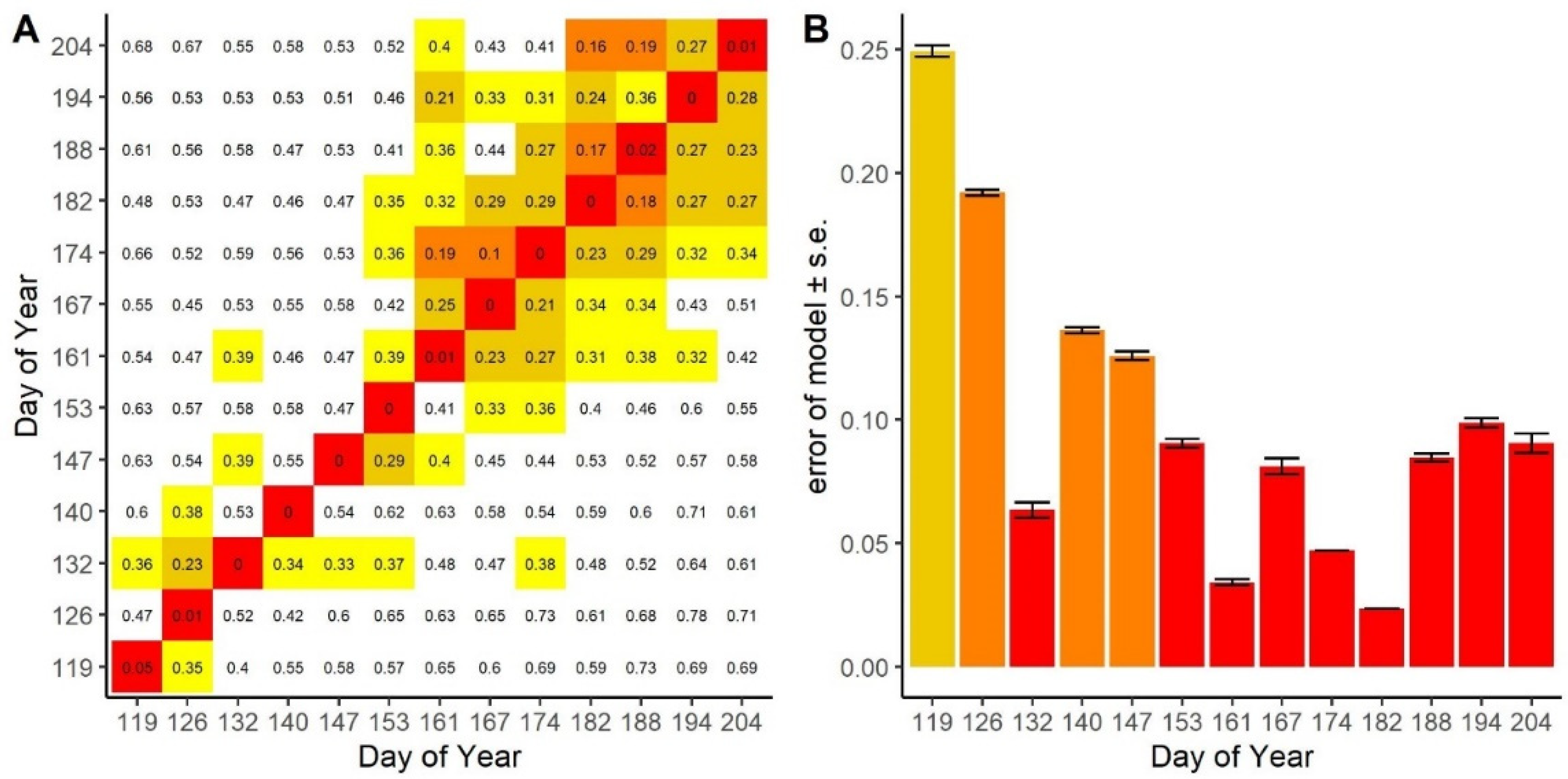
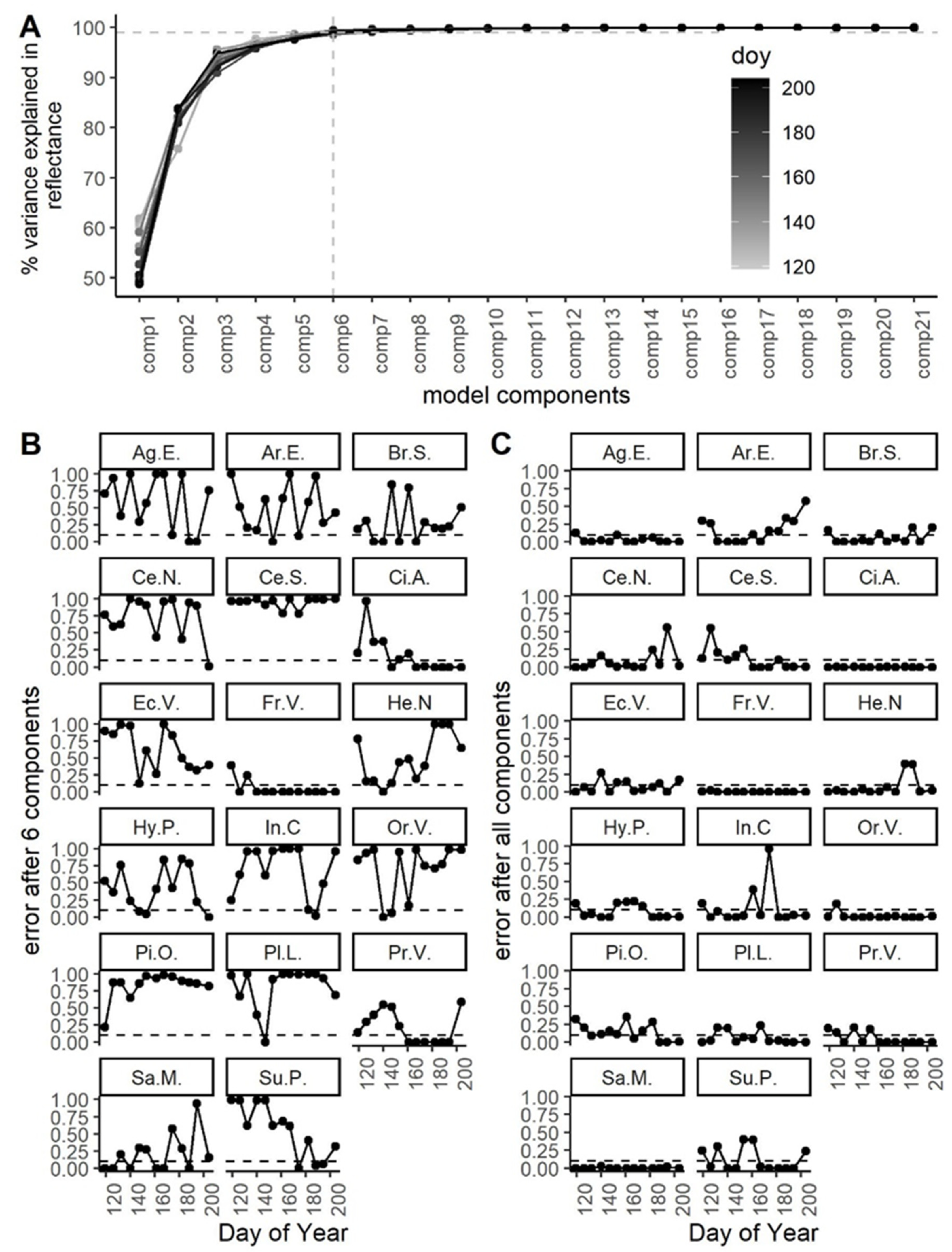


| Sampling Date | Date | Day of Year (DoY) | Cumulative Distance (Euclidean) | Cumulative Distance (Spectral Angle Mapper) | Model Error (Range of 10 Runs; 2 d.p.) | Number of Components (Range of 10 Runs) | Number of Unique Wavelengths (Range of 10 Runs) |
|---|---|---|---|---|---|---|---|
| 1 | 29 April | 119 | 12,398,267 | 4970 | 0.1–0.11 | 18–20 | 467–576 |
| 2 | 6 May | 126 | 12,504,256 | 4874 | 0.09–0.1 | 20–21 | 444–541 |
| 3 | 12 May | 132 | 11,961,457 | 4889 | 0.07–0.11 | 18–20 | 518–663 |
| 4 | 20 May | 140 | 13,740,155 | 5087 | 0.07–0.11 | 15–21 | 438–630 |
| 5 | 27 May | 147 | 13,645,126 | 5041 | 0.04–0.04 | 16–17 | 439–554 |
| 6 | 2 June | 153 | 12,610,071 | 4940 | 0.08–0.11 | 20–21 | 436–555 |
| 7 | 10 June | 161 | 11,830,265 | 4778 | 0.08–0.08 | 19–20 | 442–658 |
| 8 | 16 June | 167 | 12,367,520 | 4824 | 0.04–0.08 | 18–20 | 493–621 |
| 9 | 23 June | 174 | 11,581,843 | 4691 | 0.02–0.05 | 20–21 | 582–683 |
| 10 | 1 July | 182 | 12,825,589 | 5014 | 0.08–0.12 | 16–19 | 403–545 |
| 11 | 7 July | 188 | 12,582,159 | 5119 | 0.04–0.08 | 19–20 | 463–574 |
| 12 | 13 July | 194 | 12,329,164 | 5104 | 0.05–0.08 | 19–21 | 583–641 |
| 13 | 23 July | 204 | 13,851,285 | 5146 | 0.05–0.07 | 19–20 | 300–593 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thornley, R.H.; Verhoef, A.; Gerard, F.F.; White, K. The Feasibility of Leaf Reflectance-Based Taxonomic Inventories and Diversity Assessments of Species-Rich Grasslands: A Cross-Seasonal Evaluation Using Waveband Selection. Remote Sens. 2022, 14, 2310. https://doi.org/10.3390/rs14102310
Thornley RH, Verhoef A, Gerard FF, White K. The Feasibility of Leaf Reflectance-Based Taxonomic Inventories and Diversity Assessments of Species-Rich Grasslands: A Cross-Seasonal Evaluation Using Waveband Selection. Remote Sensing. 2022; 14(10):2310. https://doi.org/10.3390/rs14102310
Chicago/Turabian StyleThornley, Rachael Helen, Anne Verhoef, France F. Gerard, and Kevin White. 2022. "The Feasibility of Leaf Reflectance-Based Taxonomic Inventories and Diversity Assessments of Species-Rich Grasslands: A Cross-Seasonal Evaluation Using Waveband Selection" Remote Sensing 14, no. 10: 2310. https://doi.org/10.3390/rs14102310
APA StyleThornley, R. H., Verhoef, A., Gerard, F. F., & White, K. (2022). The Feasibility of Leaf Reflectance-Based Taxonomic Inventories and Diversity Assessments of Species-Rich Grasslands: A Cross-Seasonal Evaluation Using Waveband Selection. Remote Sensing, 14(10), 2310. https://doi.org/10.3390/rs14102310







