1. Introduction
The goal of remote sensing scene image classification is to correctly classify the input remote sensing images. Due to the wide application of remote sensing image classification in natural disaster detection, land cover analysis, urban planning and national defense security [
1,
2,
3,
4], the classification of remote sensing scene images has attracted extensive attention. In order to improve the performance of remote sensing scene classification, many methods have been proposed. Among them, convolutional neural networks have become one of the most successful deep learning methods with their strong feature extraction ability. Convolutional neural networks are widely used in image classification [
5] and target detection [
6]. Many excellent neural networks have been designed for image classification. For example, Li et al. [
7] proposed a deep feature fusion network for remote sensing scene classification. Zhao et al. [
8] proposed a multi-topic framework combining local spectral features, global texture features and local structure features to fuse features. Wang et al. [
9] used an attention mechanism to adaptively select the key parts of each image, and then fused the features to generate more representative features.
In recent years, designing a convolutional neural network to achieve the optimal trade-off between classification accuracy and running speed has become a research hotspot. SqueezeNet [
10] designed a lightweight network by squeezing and extending modules to reduce parameter weight. In the SqueezeNet structure, three strategies are mainly used to reduce the parameters of the model. Firstly, partial 3 × 3 convolution is replaced by 1 × 1 convolution, then the number of input channels of 3 × 3 convolution kernel is reduced, and downsampling is carried out in the later part of the network to provide a larger features map for the convolution layer. The traditional convolution is decomposed in MobileNetV1 [
11] to obtain the depthwise separable convolution. The depthwise separable convolution is divided into two independent processes: a lightweight depthwise convolution for spatial filtering and a 1 × 1 convolution for generating features, which separates spatial filtering from the feature generation mechanism. MobileNetV2 [
12] added a linear bottleneck and inverted residuals structure on the basis of MobileNetV1, which further improves the performance of the network. SENet [
13] proposed the SE module, which consists of extrusion and expansion. Firstly, extrusion is accomplished by global average pooling, which transforms the input two-dimensional feature channel into a real number with a global receptive field. Then, expansion is accomplished through the full connection layer, and a set of weighting parameters is obtained. Finally, channel-by-channel weighting is multiplied to complete the re-calibration of the original feature on the channel dimension. NASNet [
14] used the enhanced learning and model search structure to learn a network unit in a small dataset, then stacked the learned units on a large dataset, which solves the problem that the previous neural network search structure cannot be applied to a large dataset. MobileNetV3 [
15] added a SE module and used a neural structure search to search for network configuration and parameters. ResNet [
16] solved performance degradation due to network depth using residual connectivity, and presents an efficient bottleneck structure with satisfactory results. Xception [
17] replaced the convolution operation in the Inception module with depthwise separable convolution and achieves better performance. GoogleNet [
18] used the Inception module to make the network deeper and wider. The Inception module consists of three convolution branches and one pooled branch, and finally four branches were fused through channels.
Grouped convolution was first used in AlexNet [
19]. Due to the limitations of hardware conditions at that time, it was used in AlexNet to slice the network, which made it run parallel with two GPUs and achieved good performance. The validity of grouping convolution is well demonstrated in ResNeXt [
20]. ResNeXt highly modularizes the network structure, building a network architecture by repeating stacked modules. The module is composed of several bottleneck structures, which improves the accuracy of the model without increasing the number of parameters. Traditional channel grouping uses a single grouping form (for example, the number of channels of input features is
,
is the number of groups, and the number of channels in each group is
). Using a single channel group is not conducive to feature extraction; to solve this problem, we proposed a channel multi-group convolution structure. The structure classifies the input features into two types of grouping, the number of channels for each set of features in the first type is
, and the number of channels for each set of features in the other type is
. The channel multi-group structure increases the diversity of features while decreasing the parameters further. To reduce the loss of feature information during the grouping convolution process, residual connection is added to the channel multi-group structure, which can effectively avoid the disappearance of gradient due to network deepening. In order to solve the problem of network performance degradation caused by lack of information interaction between individual groups during group convolution, channel fusion of adjacent features is carried out to increase information interaction and improve network feature representation ability.
The main contributions of this study are as follows.
- (1)
In the shallow layer of the network, a shallow feature extraction module is constructed. The module is composed of three branches. Branch 1 uses two consecutive 3 × 3 convolution for downsampling and feature extraction, branch 2 utilizes max-pooling and 3 × 3 convolution for downsampling and feature extraction. Branch 3 is a shortcut branch. The fused features of branch 1 and branch 2 are shortcut with branch 3. The module can fully extract the shallow feature information, so as to accurately distinguish the target scene.
- (2)
In the deep layer of the network, a channel multi-group fusion module is constructed for the extraction of deep features, which divided the input features into features with channel number of and channel number of , increasing the diversity of features.
- (3)
To solve the problem of lack of information interaction for features between groups due to group convolution, in the channel multi-group module, the channel fusion of adjacent features is utilized to increase the information exchange, which significantly improves the performance of the network.
- (4)
A lightweight convolutional neural network is constructed based on channel multi-group fusion (LCNN-CMGF) for remote sensing scene image classification, which includes shallow feature extraction module and channel multi-group fusion module. Moreover, a variety of experiments are carried out under the conditions of four datasets of UCM21, RSSCN7, AID and NWPU45, and the experimental results prove the proposed LCNN-CMGF method achieves the trade-off between model classification accuracy and running speed.
The rest of this paper is as follows. In
Section 2, the overall structure, shallow feature extraction module and channel multi-group module of the proposed LCNN-CMGF method are described in detail.
Section 3 provides the experimental results and analysis. In
Section 4, several visualization methods are adopted to evaluate the proposed LCNN-GMGF method. The conclusion of this paper is given in
Section 5.
2. Methods
2.1. The Overall Structure of Proposed LCNN-CMGF Methods
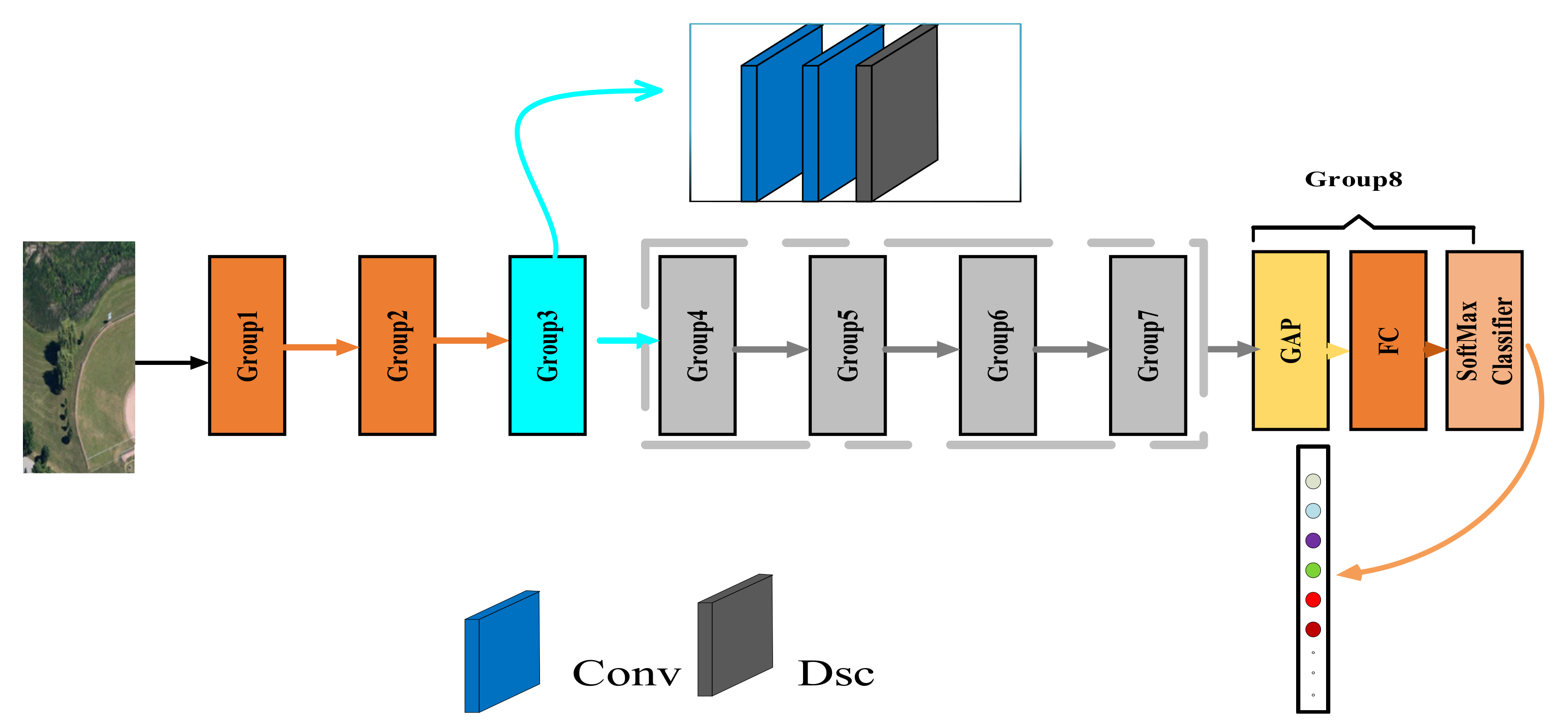
As shown in
Figure 1, the proposed network structure is divided into eight groups, the first three being used to extract shallow information from remote sensing images. Groups 1 and 2 adopt a proposed shallow downsampling structure, which is introduced in
Section 2.2 in detail. Group 3 uses a hybrid convolution method combining standard convolution and depthwise separable convolution for feature extraction. Depthwise separable convolution has a significant reduction in the number of parameters compared with standard convolution. Assuming that the input feature size is
, the convolution kernel size is
and the output feature size is
, the parameter quantity of standard convolution is:
The parameter quantities of depthwise separable convolution is:
The ratio
of depthwise separable convolution to standard convolution is:
According to Equation (3), when the convolution kernel size
is equal to 3 × 3, due to
, the parameter quantity of standard convolution is approximately 9 times that of depthwise separable convolution, and when the convolution kernel size
is equal to 5 × 5, the parameter of standard convolution is approximately 25 times that of depthwise separable convolution. With the increase in convolution kernel size, the parameter will be further reduced. However, depthwise separable convolution can inevitably lead to the loss of some feature information while significantly reducing the amount of parameters, and then make the learning ability of the network decline. Therefore, we propose to use the hybrid convolution of standard convolution and depthwise separable convolution for feature extraction, which not only reduces the weight parameters, but also improves the learning ability of the network. From group 4 to group 7, channel multi-group fusion structure is used to further extract deep feature information. Channel multi-group fusion structure can generate a large number of features with a few parameters to increase the feature diversity. Assuming that the input feature size is
, the convolution kernel size is
and the output feature size is
, the parameter quantity of standard convolution is
Divide the input features into
groups along the channel dimension, then the feature size of each group is
, the corresponding convolution kernel size is
, and the output feature size of each group is
. Connect the obtained t group features along the channel dimension to obtain that the final output feature size is
. The parameter quantity of the whole process is
As shown in Equations (4) and (5), the parameter quantity of group convolution is
of the standard convolution parameter quantity, that is, under the condition of the same parameter quantity, the number of features obtained by group convolution is
times of the standard convolution, which increases the feature diversity and effectively improves the classification accuracy. The details are described in
Section 2.3. Group 8 consists of a global average pooling layer (GAP), a fully connected layer (FC), and a softmax classifier to convert the convolutionally extracted feature information into probabilities for each scenario. Because features extracted by convolution contain spatial information, which is destroyed if features derived by convolution are directly mapped to the feature vector through a fully connected layer, and global average pooling does not. Assuming that the output of the last convolution layer is
,
represents cascading operations along the batch dimension, and
represents the set of real numbers. In addition,
,
,
,
represent the number of samples per training, the height of the feature, the width of the feature, and the number of channels, respectively. Suppose the result of global average pooling is
, then the processing process of any
with the global average pooling layer can be represented as
As shown in Equation (6), global average pooling more intuitively maps the features of the last layer convolution output to each class. Additionally, the global average pooling layer does not require weight parameters, which can avoid overfitting phenomena during training the model. Finally, a softmax classifier is used to output probability values for each scenario.
2.2. The Three-Branch Shallow Downsampling Structure
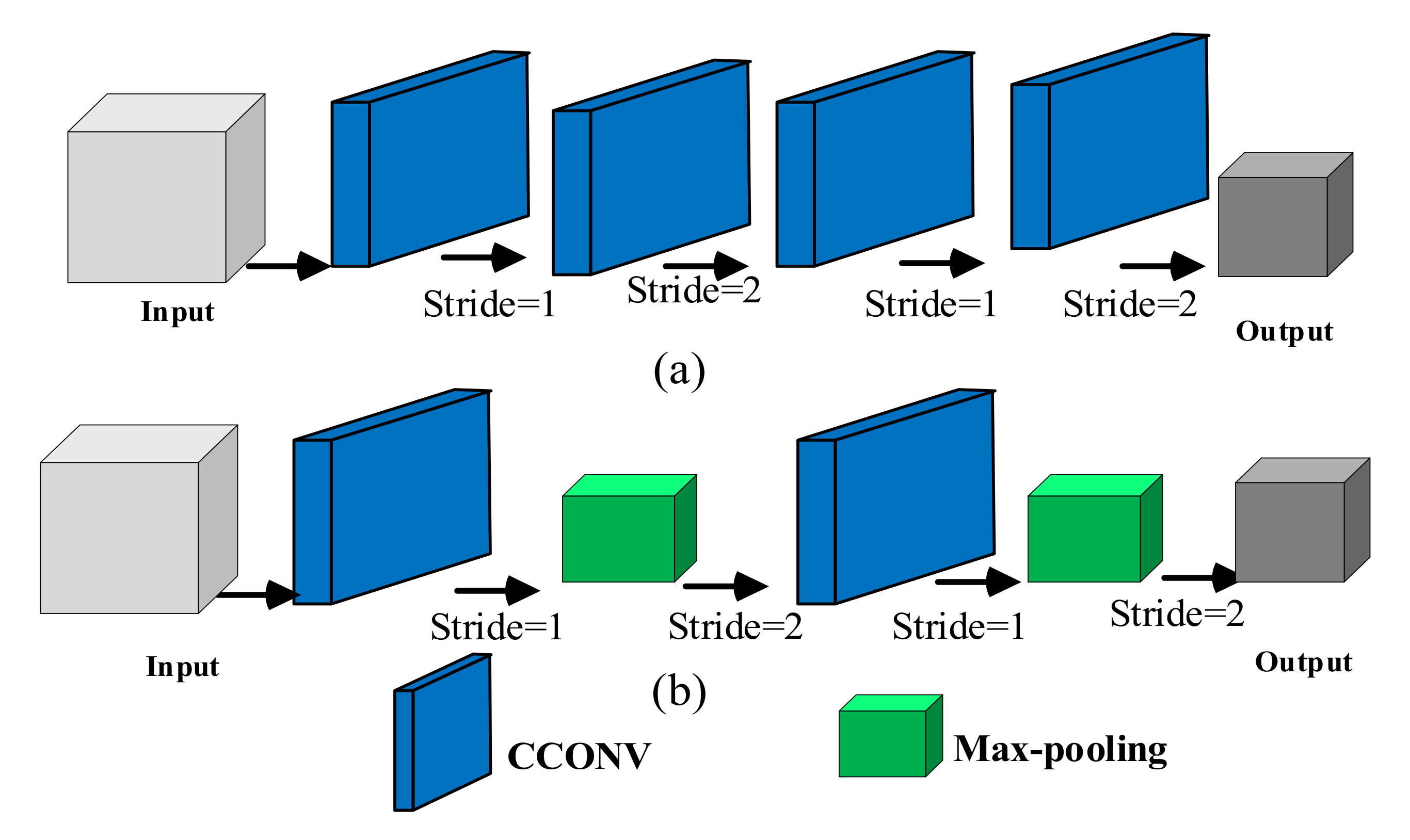
Max-pooling downsampling is a nonlinear downsampling method. For small convolutional neural networks, better nonlinearity can be obtained by using maximum pool downsampling. On the contrary, for deep neural networks, multi-layer superimposed convolutional downsampling can learn better nonlinearity than max-pooling according to the training set, as shown in
Figure 2.
Figure 2a,b represents convolution downsampling and max-pooling downsampling, respectively. The convolution downsampling in
Figure 2a first uses the 3 × 3 convolution with step size of 1 for feature extraction of the input data, and then uses the 3 × 3 convolution with step size of 2 for downsampling. In the max-pooling downsampling in
Figure 2b, the input feature is extracted by 3 × 3 convolution with step size of 1, and then the max-pooling downsampling with step size of 2 is adopted. Combining max-pooling downsampling and convolutional downsampling, we propose a three-branch downsampling structure as shown in
Figure 3 for feature extraction, and use the input features to compensate the downsampling features, which can not only extract strong semantic features, but also retain shallow information.
In groups 1 and 2 of the network, we use the structure shown in
Figure 3 to extract shallow features. The structure is divided into three branches. The first branch uses 3 × 3 convolution with step size of 2 to obtain
, and then uses 3 × 3 convolution with step size of 1 to extract the shallow features of the image to obtain
. That is
In Equations (7) and (8), represents the activation function , represents batch standardization, represents the input characteristics, represents the convolution kernel with step size , and represents the convolution operation.
The second branch uses the max-pooling with step size of 2 to downsample the input features to obtain
. The most responsive part of the max-pooling selection features enters the next layer, which reduces the redundant information in the network and makes the network easier to be optimized. The max-pooling downsampling can also reduce the estimated mean shift caused by the parameter error of the convolution layer, keep more texture information. Then, the shallow features
are extracted by 3 × 3 convolution with step size of 1. That is
In Equation (9), represents the max-pooling output value in rectangular area related to the m-th feature, and represents the element at the position in rectangular area .
The fused feature
is obtained by fusing the features from Branch 1 and Branch 2. To reduce the loss of feature information caused by the first two branches, a residual branch is constructed to compensate for the loss of information. The fused feature
and the third branch are fused to generate the final output feature
. That is
The in Equation (11) is a residual connection implemented by 1 × 1 convolution.
2.3. Channel Multi-Group Fusion Structure
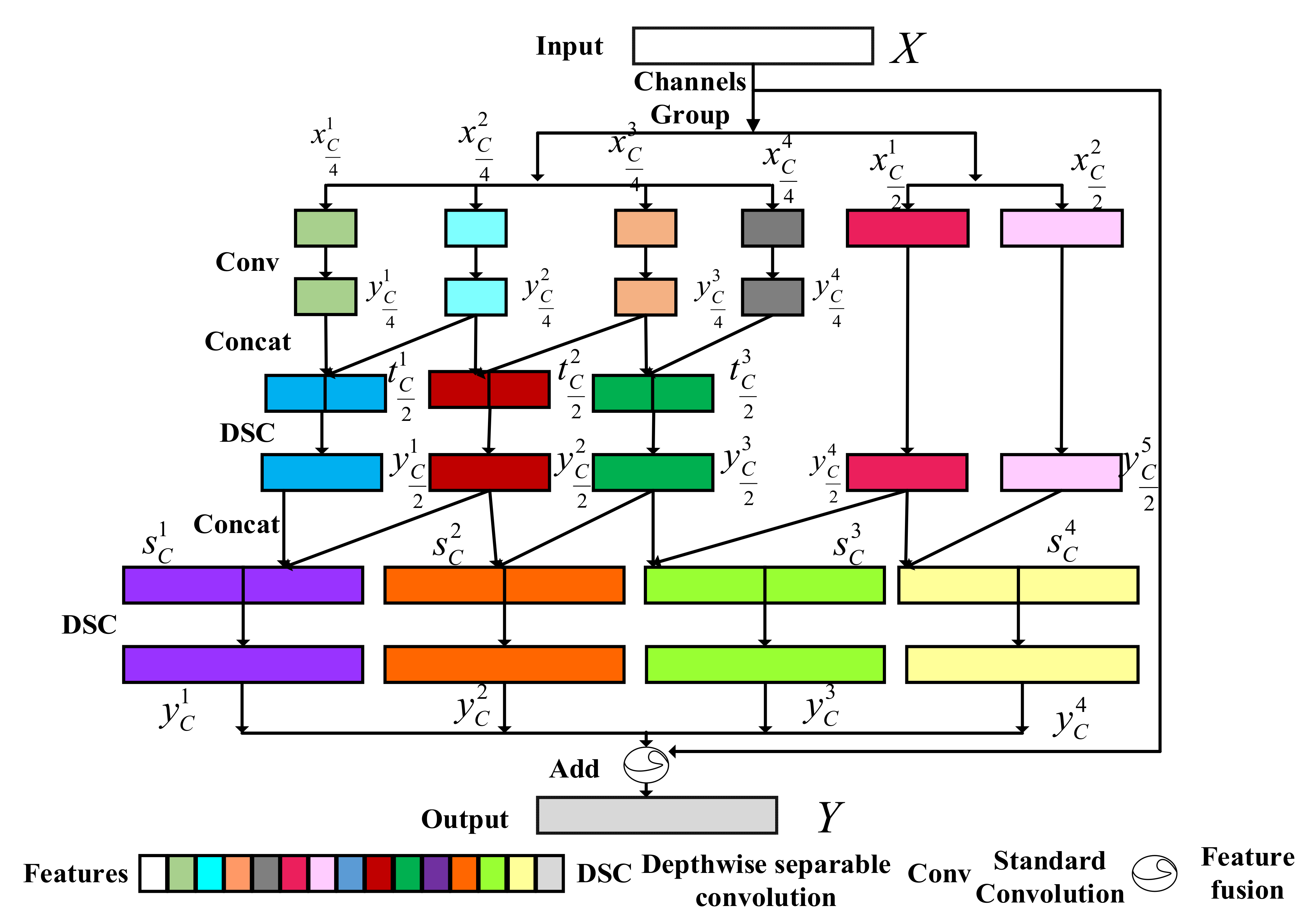
The proposed channel multi-group fusion structure is shown in
Figure 4. It divides the input features with the number of channels
into two parts, one part is composed of 4 features with the number of channels
, and the other part is composed of 2 features with the number of channels
. First, the convolution operations are performed for features with the number of channels
, the adjacent two convolution results are channel concatenated, the number of feature channels after concatenate is
. Then, the convolution operations are performed on features with the number of channels
, the adjacent two features convolution results are channel concatenated, the number of channels of each feature after fusion was
. The convolution operations are performed on features with the number of channels
, and the convolution results are fused to obtain the output features. This process can be described as follows.
Suppose that the input feature is
,
represents the i-th feature with the number of channels
, and
represents the i-th feature with the number of channels
. After channel grouping, the input features can be represented as
,
,
,
,
,
. The convolution operation is performed first for the features
,
,
, and
, where the number of channels is
, and after convolution the results are
,
,
, and
, respectively. Here,
can be represented as
represents the convolution result of the feature , and . represents the m-th channel of the i-th feature with the number of channels , represents the convolution operation, represents the convolution weight, represents the activation function, and represents batch normalization.
The use of grouping convolution can reduce the requirement of computing power, but it will also lead to the lack of information interaction between group features, which makes the extracted features incomplete. The information interaction is enhanced through channel concatenate of two adjacent features
,
and
. The number of feature channels after channel concatenate is
, and
represents the i-th feature after channel concatenate, the channel concatenate operation of feature
and feature
is represented by
, where
is calculated as
The features
,
,
,
,
with the number of channel
are processed by depthwise separable convolution and the results after convolution are
,
,
,
,
respectively.
is calculated as
where
represents the convolution result of the features
and
, and
,
represents the m-th channel of the i-th feature with the number of channels
, and
represents the depthwise separable convolution operation. Then, the adjacent features
,
,
and
are concatenated in the channel dimension. The number of feature channels after concatenate is
, and
represents the i-th feature with the number of channels after concatenate
. The calculation process of
is
The features
,
,
and
with the number of channels
are processed by depthwise separable convolution, respectively. The convolution results are
,
,
and
. The calculation process of
is
Next, the features
,
,
,
are fused and the fusion results and input feature
are shortcut to obtain the final output result
, where
denotes feature fusion.
4. Discussions
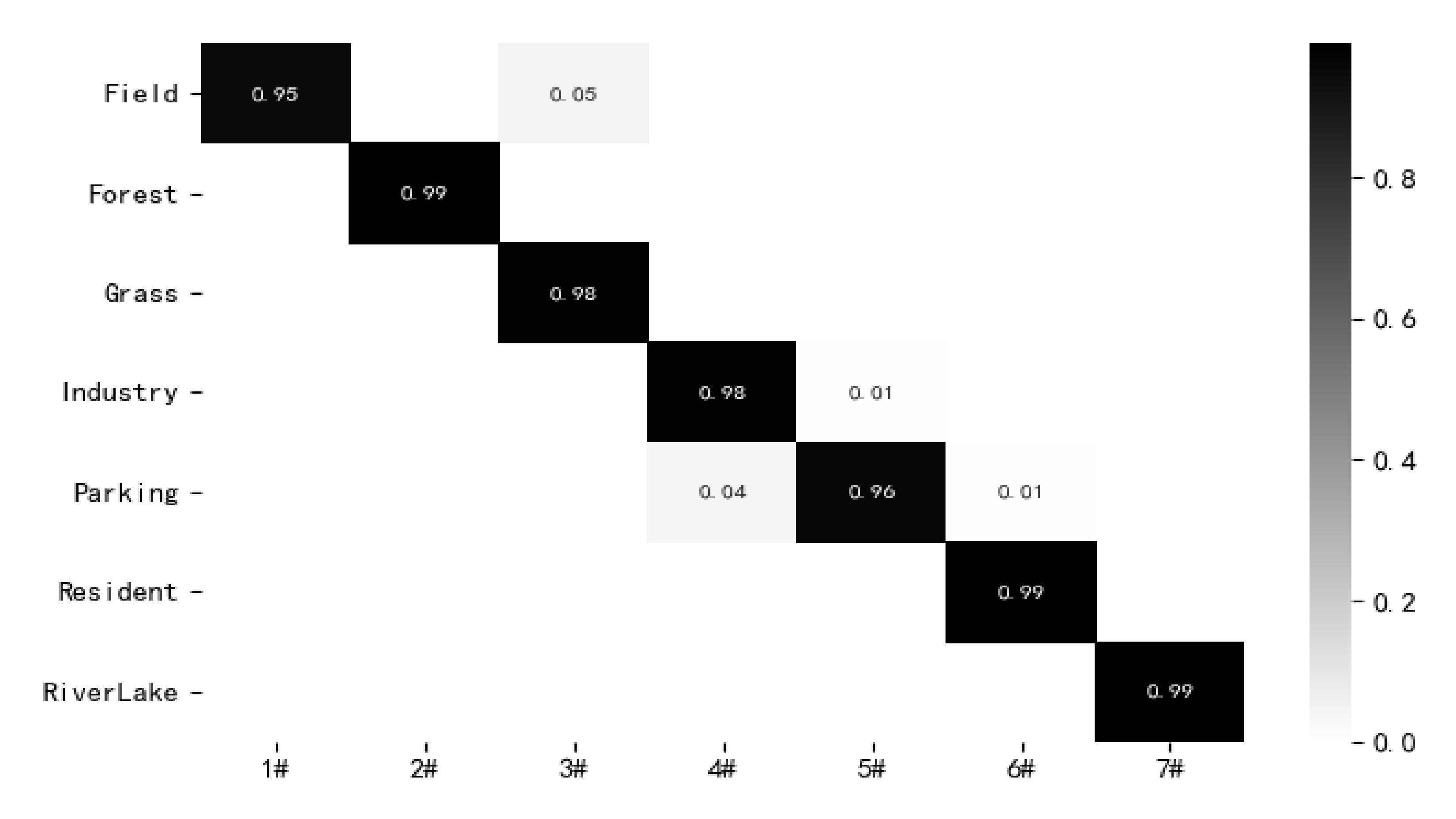
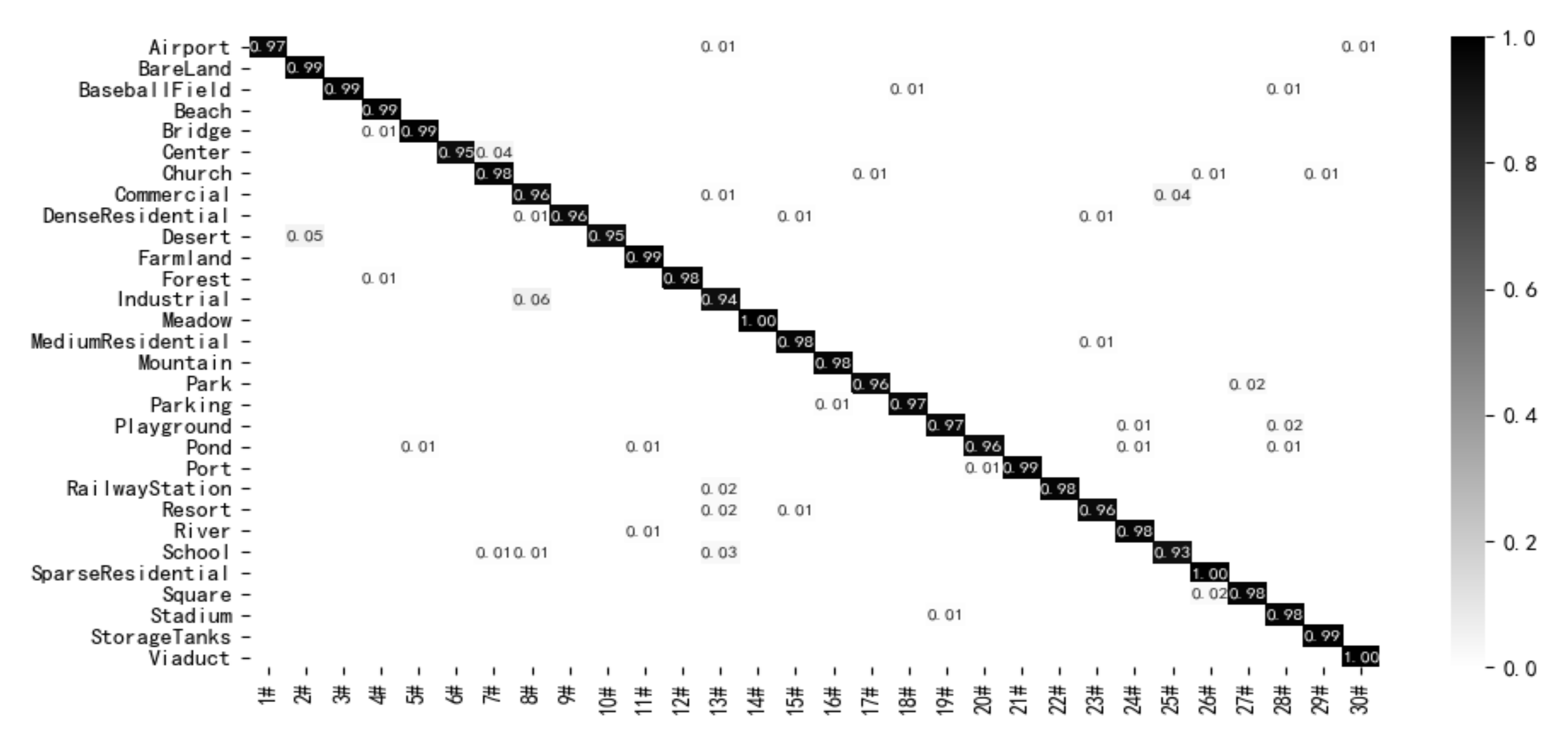
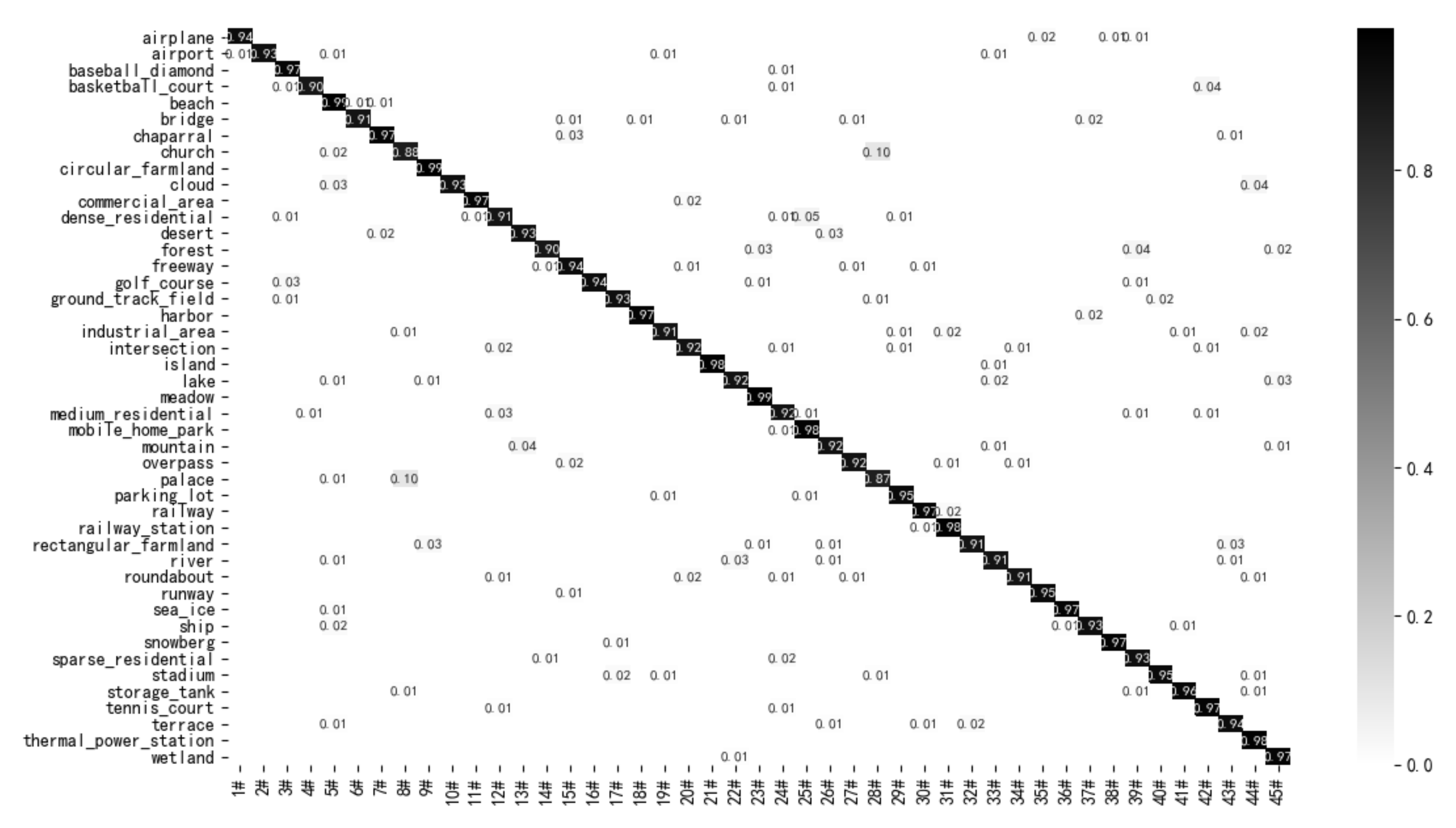
In order to display the feature extraction ability of the proposed method more intuitively, a series of visualization methods are adopted to evaluate the proposed method. Firstly, the feature extraction ability of the proposed method is presented by using the visualization method of Class Activation Map (CAM). The CAM method displays important areas of the image predicted by the model by generating a rough attention map from the last layer of the convolutional neural network. Some images in the UCM21 dataset are chosen for visualization experiments, and the visualization results are shown in
Figure 12. As shown in
Figure 12, the proposed LCNN-CMGF method can highlight semantic objects corresponding to real categories. This shows that the proposed LCNN-CMGF method has a strong ability to locate and recognize objects. In addition, the proposed LCNN-CMGF method can better cover semantic objects and has a wide highlight range.
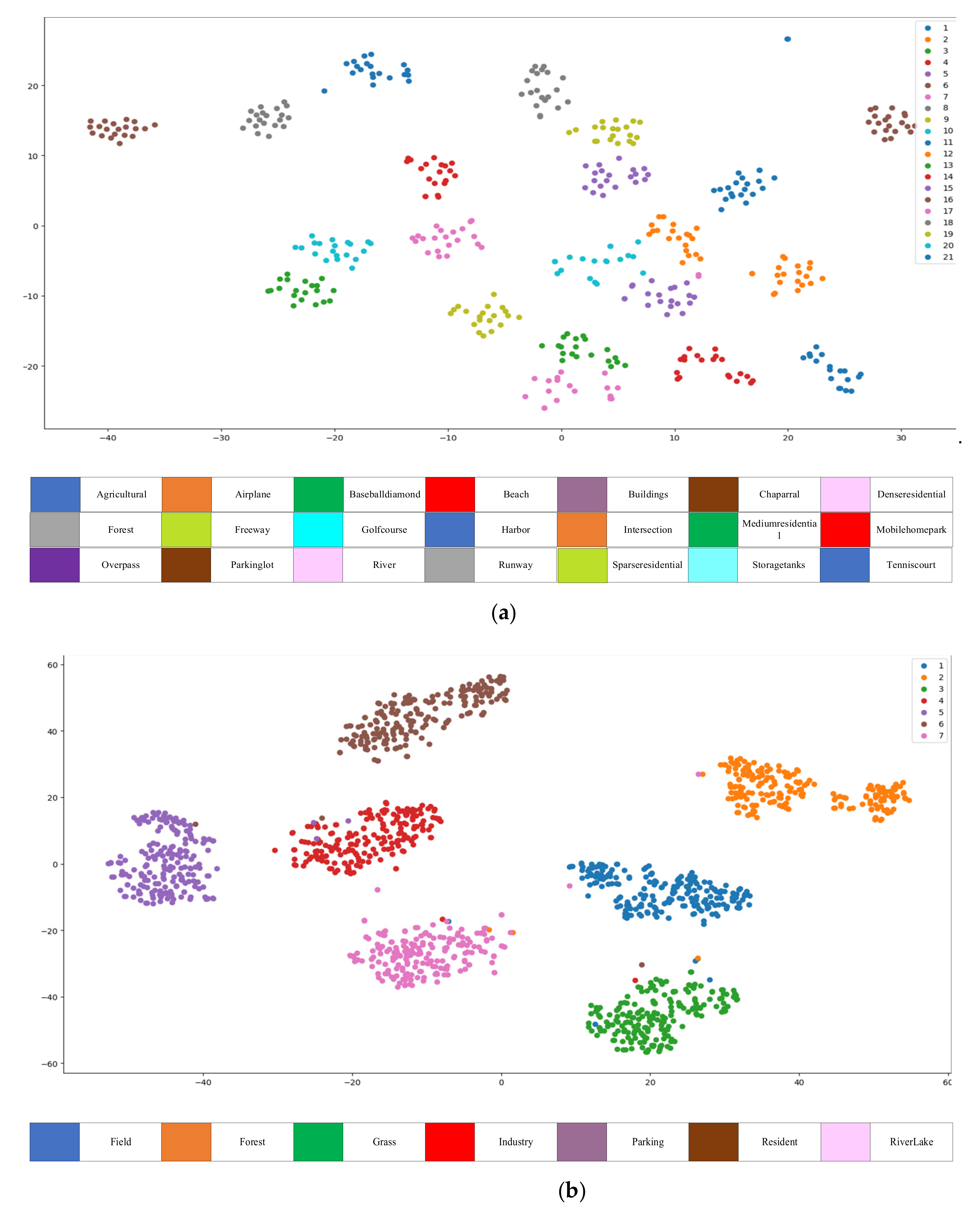
Next, t-distributed stochastic neighbor embedding visualization (T-SNE) method is used to visualize the proposed LCNN-CMGF method and further evaluate the performance of the proposed LCNN-CMGF method. T-SNE is a nonlinear dimensionality reduction algorithm, which usually maps high dimensions to two-dimensional or three-dimensional space for visualization, which can well evaluate the classification effect of the model. The RSSCN7 and UCM21 datasets are used for visualization experiments, and the experimental results are shown in
Figure 13.
As shown in
Figure 13, there is no confusion between single semantic clusters on the UCM21 dataset and the RSSCN7 dataset, which means that the proposed LCNN-CMGF method has better global feature representation, increases the separability and relative distance between single semantic clusters, and can more accurately extract the features of remote sensing scene images and improve the classification accuracy.
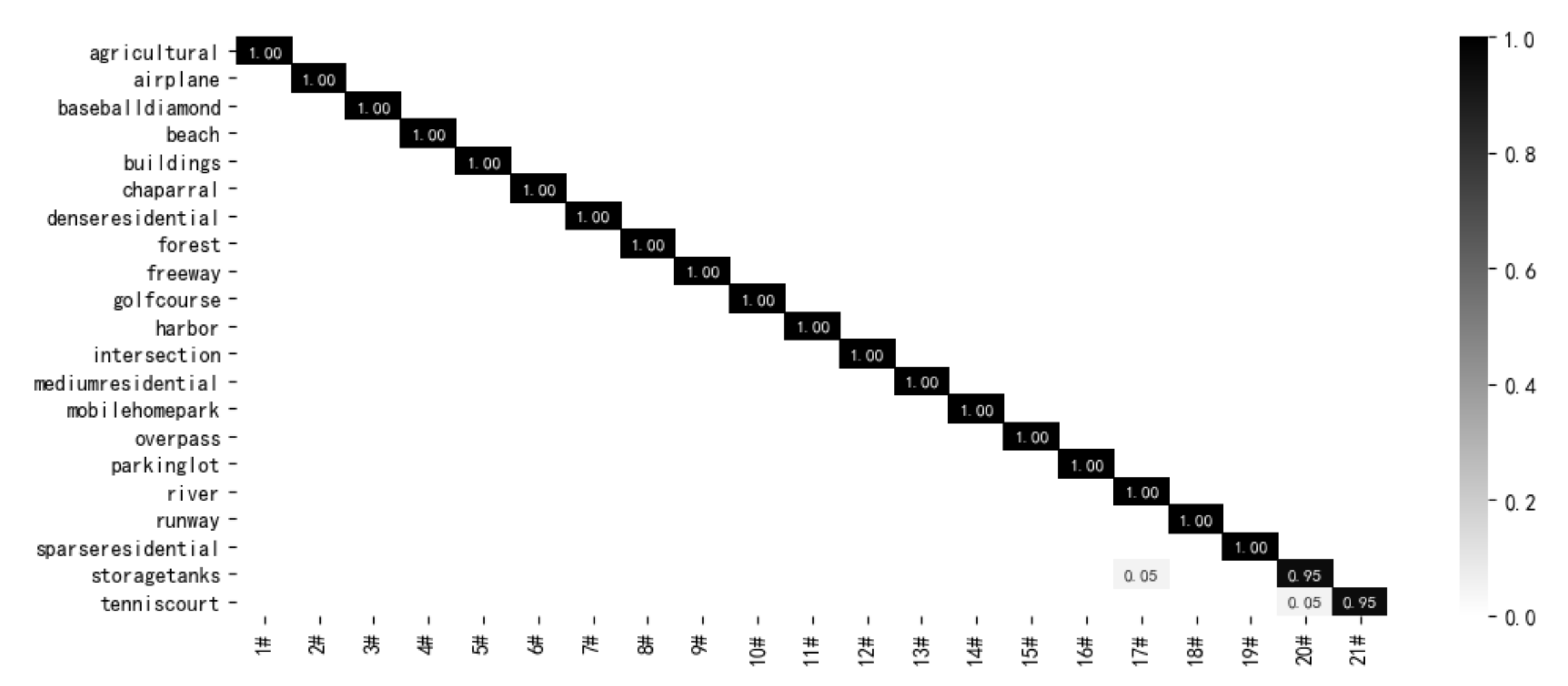
In addition, a randomized prediction experiment is performed on the UCM21 dataset using the LCNN-CMGF method. The results are shown in
Figure 14. From
Figure 14, we can see that the LCNN-CMGF method has more than 99% confidence in remote sensing image prediction, and some of the predictions even reach 100%. This further proves the validity of the proposed method for remote sensing scene image classification.